Open Access Article
Open Access ArticleComplex hydrides as thermal energy storage materials: characterisation and thermal decomposition of Na2Mg2NiH6†
Terry D.
Humphries
 *ab,
Drew A.
Sheppard
a,
Guanqiao
Li
b,
Matthew R.
Rowles
*ab,
Drew A.
Sheppard
a,
Guanqiao
Li
b,
Matthew R.
Rowles
 a,
Mark
Paskevicius
a,
Mark
Paskevicius
 a,
Motoaki
Matsuo
cd,
Kondo-Francois
Aguey-Zinsou
a,
Motoaki
Matsuo
cd,
Kondo-Francois
Aguey-Zinsou
 e,
M. Veronica
Sofianos
e,
M. Veronica
Sofianos
 a,
Shin-ichi
Orimo
bd and
Craig E.
Buckley
a,
Shin-ichi
Orimo
bd and
Craig E.
Buckley
 a
a
aDepartment of Physics and Astronomy, Fuels and Energy Technology Institute, Curtin University, GPO Box U1987, Perth, WA 6845, Australia. E-mail: terry_humphries81@hotmail.com
bWPI-Advanced Institute for Materials Research, Tohoku University, Sendai 980-8577, Japan
cSchool of Science and Technology, Kwansei Gakuin University, Sanda 669-1337, Japan
dInstitute for Materials Research, Tohoku University, Sendai 980-8577, Japan
eMerlin Group, School of Chemical Engineering, The University of New South Wales, Sydney, NSW 2052, Australia
First published on 23rd April 2018
Abstract
Complex transition metal hydrides have been identified as being materials for multi-functional applications holding potential as thermal energy storage materials, hydrogen storage materials and optical sensors. Na2Mg2NiH6 (2Na+·2Mg2+·2H−·[NiH4]4−) is one such material. In this study, the decomposition pathway and thermodynamics have been explored for the first time, revealing that at 225 °C, hydrogen desorption commences with two major decomposition steps, with maximum H2 desorption rates at 278 and 350 °C as measured by differential scanning calorimetry. The first step of decomposition results in the formation of Mg2NiHx (x < 0.3) and NaH, before these compounds decompose into Mg2Ni and Na, respectively. PCI analysis of Na2Mg2NiH6 has determined the thermodynamics of decomposition for the first step to have a ΔHdes and ΔSdes of 83 kJ mol−1 H2 and 140 J K−1 mol−1 H2, respectively. Hydrogen cycling of the first step has been achieved for 10 cycles without any significant reduction in hydrogen capacity, with complete hydrogen desorption within 20 min at 395 °C. Despite the relatively high cost of Ni, the ability to effectively store hydrogen reversibly at operational temperatures of 318–568 °C should allow this material to be considered as a thermal energy storage material.
Introduction
Recent years have seen a resurgence of interest into the synthesis and characterisation of complex metal hydrides1–3 and complex transition metal hydrides (CTMH).4–6 Their thermal stability and hydrogen storage capacity have made this class of materials applicable for implementation as hydrogen storage materials, thermal energy storage (TES) materials7–9 and possibly as neutron moderators or nuclear fuel components in nuclear reactors.10 Furthermore, the rich and diverse chemistry made possible by the variety of cations (i.e. alkali, alkali-earth and rare-earth metals)4,11,12 able to stabilise the transition metal hydride anion may prove useful in the development of multifunctional materials.One of the first CTMHs to be characterised was Mg2NiH4, in 1968.13 This material was reported to reversibly absorb and desorb hydrogen into the alloy of Mg2Ni with an enthalpy and entropy of desorption (ΔHdes) of 64 kJ mol−1 H2 and (ΔSdes) of 122 J K−1 mol−1 H2 (eqn (1)). In fact, upon decomposition, Mg2NiH4 proceeds through a Mg2NiHx (x < 0.3) phase as hydrogen is also dissolved in the Mg2Ni lattice.
| Mg2NiH4 ⇄ Mg2NiH0.3 + 1.85H2 (3.35 wt% H2) | (1) |
The initial study of Mg2NiH4 has fuelled a prolific interest in CTMHs and has led to the substitution of an array of metal centres for Ni in the complex anion (i.e. [NiH4]4−) with many examples found in the literature: [FeH6]4−, [CoH5]4−, [RuH6]4−, [OsH6]4−, [IrH5]4− and [PdH4]4−.4,11,12,14,15 These materials have been extensively characterised, with several crystal structures determined using both neutron and X-ray diffraction (XRD). In addition, their thermodynamics have been determined by pressure-composition-isotherm (PCI) experiments, differential scanning calorimetry (DSC) and thermogravimetric analysis (TGA); while vibrational and nuclear magnetic resonance (NMR) spectroscopies have also been explored.
In the simplest compositions of these systems, all hydrogen atoms are bonded to the transition metal center T resulting in the chemical formula Mmδ+[THn]δ− (T = 3d, 4d, 5d elements; M = alkali, alkali-earth and rare-earth elements; m, n = 1, 2, 3,…).16 The crystal structure of the archetypal compound, Mg2NiH4, consists of a Ni atom, coordinated by a distorted tetrahedron of four hydrogen atoms, forming the [NiH4]4− anion.17 This anion is thus stabilised within a distorted cubic array of Mg2+ cations. The room temperature polymorph of Mg2NiH4 resides in the monoclinic space group C2/c with a = 14.343(5) Å, b = 6.4038(10) Å, c = 6.4830(13), Å and has an average Ni–D bond distance of 1.53(2) Å. A transformation to a high temperature polymorph occurs in the range of 210–245 °C,18 and has been determined to crystallise in a pseudo-CaF2-type structure with a = 6.490 Å. These polymorphs have undergone a plethora of studies to understand their true physical properties, which have recently been detailed in a review article.4
To date there are eight known compounds incorporating the [NiH4]4− complex anion including MMgNiH4 (M = Mg, Sr, Eu, Ca, Yb),4,17,19,20 Na2Mg2NiH6,21,22 LaMg2NiH7 (ref. 23 and 24) and La2MgNi2H8.25 MMgNiH4 (M = Sr, Eu, Ca, Yb) are isostructural, crystalising in the cubic space group P213.12,13 As observed with Mg2NiH4, the [NiH4]4− is coordinated by a distorted cube of two M2+ and two Mg2+ atoms. LaMg2NiH7 and Na2Mg2NiH6 represent a class of materials in which the [NiH4]4− is coordinated by an array of M (M = La, Na, Mg) cations, but are seen as a link between ‘interstitial’ and ‘complex’ metal hydrides due to the inclusion of quasi-isolated H−.21–24
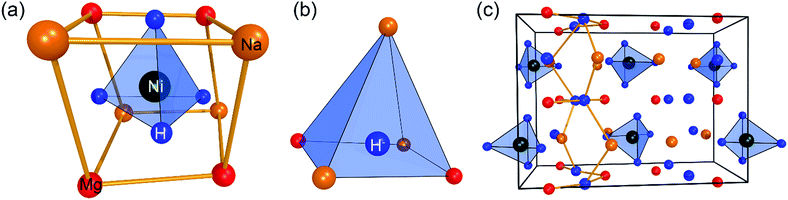
Na2Mg2NiH6 (2Na+·2Mg2+·2H−·[NiH4]4−) was first synthesised in 2007, and the structure, elucidated from neutron-diffraction data, exists in the orthorhombic space group Pnma.21 In 2009, the structure was revised using ab initio structure analysis, along with newly collected diffraction data.22 Although the space group, Pnma, was originally correct, the lattice parameters were revised to be a = 11.433(1) Å, b = 8.4435(8) Å, c = 5.4180(7) Å, along with an alteration in the description of the overall structure. As such, the [NiH4]4− is surrounded by two Na+ and two Mg2+ ions (Fig. 1a), while the quasi-isolated H− ions are coordinated four-fold by 2Mg2+ and 2Na+ ions (Fig. 1b).22 In the deuterated version of this compound, the average Ni–D distance is 1.61(2) Å, which is significantly longer than that of Mg2NiD4, indicating the mutual contribution of both countercations on the [NiD4]4−.26 Overall, the structure of Na2Mg2NiH6 can be described as a stacking of (NaMgH2)+ and (NaMgNiH4)− slabs (Fig. 1c).22
The synthesis of Na2Mg2NiH6 was previously achieved by first synthesising Mg2NiH4 from the hydrogenation of Mg2Ni at 200 °C.22 The product was then mixed in a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 ratio with NaH and ground to a fine powder in an agate mortar, compacted to pellets, put into a steel crucible, and sintered in an autoclave at 300–315 °C under 50 bar H2 for 24 h.
2 ratio with NaH and ground to a fine powder in an agate mortar, compacted to pellets, put into a steel crucible, and sintered in an autoclave at 300–315 °C under 50 bar H2 for 24 h.
The decomposition pathway of Na2Mg2NiH6 has not been elucidated and hence neither have the thermodynamics of decomposition. To date, only four [NiD4]4− complexes have been thermodynamically characterised: Mg2NiH4, LaMg2NiH7, YbMgNiH4 and CaMgNiH4, each with a ΔHdes of 64.4, 94, 111 and 129 kJ mol−1 H2, respectively (Table 1).13,19,20,23 It was originally understood that these values are not directly related to the electronegativity of the M atom, instead that the thermal stability is governed considerably by the ΔHf of the corresponding binary hydride (Table 1).20 Overall, the average electronegativity of the cation, χa, (Allred–Rochow scale) appears to have a stronger influence on the stability of the complex than the stability of the corresponding binary hydride.26 The average χa of Mg2NiH4, LaMg2NiH7, YbMgNiH4 and CaMgNiH4 are 1.23, 1.18, 1.15 and 1.14, which is inversely proportional to the ΔHdes of the complexes (i.e. Mg2NiH4 < LaMg2NiH7 < YbMgNiH4 < CaMgNiH4).
| Space group | Average cation χa | Lattice parameter of deuteride (a, Å) | Average Ni–D bond distance (Å) | ΔHdes (kJ mol−1 H2) | ΔHf MHyc (kJ mol−1 H2) | |
|---|---|---|---|---|---|---|
| a Lattice parameter of hydride. b Errors not provided. c M is La2+, Yb2+, Ca2+, Na+, Sr2+ for the corresponding compound except for Mg2NiH4 where M is Mg; y corresponds to the valence of M. | ||||||
| Mg2NiH4 | C2/c | 1.23 | 14.343![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) (ref. 17) (ref. 17) |
1.53(2)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) (ref. 17) (ref. 17) |
64.4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) (ref. 13) (ref. 13) |
−74.1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) (ref. 27) (ref. 27) |
| LaMg2NiH7 | P21/c | 1.18 | 13.9789(7)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) (ref. 24) (ref. 24) |
1.59(2)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) (ref. 24) (ref. 24) |
94![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) (ref. 23) (ref. 23) |
−209![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) (ref. 28) (ref. 28) |
| YbMgNiH4 | P213 | 1.15 | 6.7114(6)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) (ref. 20) (ref. 20) |
1.608(7)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) (ref. 20) (ref. 20) |
111![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) (ref. 20) (ref. 20) |
−182![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) (ref. 29) (ref. 29) |
| CaMgNiH4 | P213 | 1.14 | 6.7301(4)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) (ref. 19) (ref. 19) |
1.601(8)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) (ref. 19) (ref. 19) |
129![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) (ref. 19) (ref. 19) |
−188![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) (ref. 29) (ref. 29) |
| Na2Mg2NiH6 | Pnma | 1.12 | 11.433(1)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) (ref. 22) (ref. 22) |
1.61(2)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) (ref. 22) (ref. 22) |
— | −117![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) (ref. 30) (ref. 30) |
| EuMgNiH4 | P213 | 1.12 | 6.8486(7)a![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) (ref. 20) (ref. 20) |
— | — | — |
| SrMgNiH4 | P213 | 1.11 | 6.8953(4)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) (ref. 20) (ref. 20) |
1.614(8)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) (ref. 20) (ref. 20) |
— | −188![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) (ref. 29) (ref. 29) |
| La2MgNi2H8 | P 21/c | 1.08 | 11.84482(11)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) (ref. 25) (ref. 25) |
1.58b![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) (ref. 25) (ref. 25) |
— | −209![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) (ref. 28) (ref. 28) |
The decomposition pathway of Na2Mg2NiH6 is studied for the first time in this research. It is anticipated that Na2Mg2NiH6 will decompose in a two-stage process via the formation of a binary hydride (NaH), as observed in other CTMHs (eqn (2) and (3)).4,13,19,20,23 The decomposition pathway has been studied in detail using in situ synchrotron powder X-ray diffraction (SR-XRD) and simultaneous DSC-TGA-MS (DSC-TGA-mass spectrometry) and the thermodynamics of the decomposition process have been determined by PCI measurements. The determination of the decomposition pathway and thermodynamic measurements will ultimately identify the feasibility of this material for technological applications. The synthesis method of Na2Mg2NiH6 has also been optimised allowing for facile manufacturing of this powder for future applications.
| Na2Mg2NiH6 → Mg2NiHx + 2NaH + (2 − x)H2 (x < 0.3, >2.15 wt% H2) | (2) |
| 2NaH → 2Na + H2 (1.27 wt% H2) | (3) |
Experimental
All handling of chemicals and sealable milling canisters was undertaken in an argon-atmosphere Mbraun Unilab glovebox in order to minimise oxygen (O2 < 1 ppm) and water (H2O < 1 ppm) contamination. To synthesise Na2Mg2NiH6, two methods were employed. The majority of the material used in this study employed the two-step synthesis method which entailed the ball-milling of NaH (95%, Sigma-Aldrich), MgH2 (hydrogen storage grade, Sigma-Aldrich) and Ni powder (>99.8%, Sigma-Aldrich) in a stoichiometric ratio of 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2
2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1. Following milling, the samples were generally annealed under a H2 pressure of 50 bar at 315 °C for 20 h. Ball milling was conducted inside an Across International Planetary Ball Mill (PQ-N04) employing tempered steel vials and balls in an Ar atmosphere. A ball-to-powder mass ratio of 40
1. Following milling, the samples were generally annealed under a H2 pressure of 50 bar at 315 °C for 20 h. Ball milling was conducted inside an Across International Planetary Ball Mill (PQ-N04) employing tempered steel vials and balls in an Ar atmosphere. A ball-to-powder mass ratio of 40![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 was employed, with a total milling time of 5 h (15 min milling and 5 min pause) at a speed of 450 rpm.
1 was employed, with a total milling time of 5 h (15 min milling and 5 min pause) at a speed of 450 rpm.
The four-step synthesis method, adapted from previous reports,22 involved the milling of MgH2 (hydrogen storage grade, Sigma Aldrich) and Ni powders at a molar ratio of 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 for 2 h at 400 rpm (ball-to-powder ratio 40
1 for 2 h at 400 rpm (ball-to-powder ratio 40![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1), under argon using a Fritsch Pulverisette 7. The pelletised powder was then annealed at 300 °C for 20 h under 3 bar H2. The resultant brick-red powder was then ball-milled with NaH (95%, Sigma Aldrich) at a molar ratio of 1
1), under argon using a Fritsch Pulverisette 7. The pelletised powder was then annealed at 300 °C for 20 h under 3 bar H2. The resultant brick-red powder was then ball-milled with NaH (95%, Sigma Aldrich) at a molar ratio of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 for 20 h under argon with subsequent heat treatment of the pelletised powder at 300 °C for 20 h under 60 bar H2. The final product was as an olive-green powder.
2 for 20 h under argon with subsequent heat treatment of the pelletised powder at 300 °C for 20 h under 60 bar H2. The final product was as an olive-green powder.
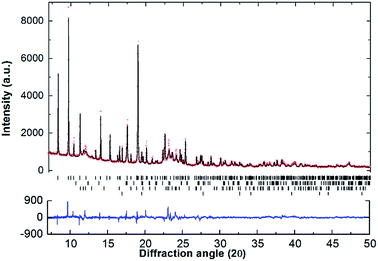
Ex situ powder X-ray diffraction (XRD) was performed using a Bruker D8 Advance diffractometer (λ = CuKα radiation) utilising XRD sample holders covered with a poly(methylmethacrylate) (PMMA) airtight dome to prevent oxygen/moisture contamination during data collection. The PMMA airtight dome results in a broad hump in XRD patterns centred at ∼20° 2θ. Data was acquired over a 2θ range of 20–80°, with step size of 0.02° and count time of 1 s per step. In situ synchrotron powder X-ray diffraction (SR-XRD) was performed at the Australian Synchrotron in Melbourne, Australia.31 The annealed powder was loaded in a borosilicate capillary (outer diameter 0.7 mm, wall thickness 0.01 mm) while inside a glove box, and mounted using a graphite ferrule to a sample holder constructed from Swagelok tube fittings. The sample holder was then connected to a H2 gas filling/vacuum manifold and the capillary heated with a hot air blower with a heating rate of 5 °C min−1 and under a 1 bar H2 atmosphere. One-dimensional SR-XRD patterns (monochromatic X-rays with λ = 0.824890(1) Å) were continuously collected using a Mythen microstrip detector32 with an exposure time of 27 s. The capillary was continuously oscillated through 120° during exposure to improve the powder averaging and ensure even heating. Diffraction patterns were quantitatively analysed with the Rietveld method33 using TOPAS (Bruker-AXS).
The hydrogen sorption properties were examined by measuring PCIs between 370 and 450 °C with a computer controlled Sieverts/volumetric apparatus previously described.27 The digital pressure transducer (Rosemount 3051S) has an accuracy of 0.15%, whilst room temperature measurements were recorded using a 4-wire platinum resistance temperature detector (RTD). The sample temperature was monitored using a K-type thermocouple that was calibrated by the manufacturer to be accurate within 0.1 °C at 419 °C. Above ∼420 °C, the permeation of hydrogen directly through the walls of the stainless-steel sample cell becomes an issue and the measured hydrogen content at each PCI data point has to be corrected for this loss. A full explanation of the correction method has previously been described in detail.34 The cycling experiments were carried out using a High Energy PCTpro E&E. The first decomposition was conducted by heating the sample to 315 °C under 60 bar H2 before reducing the H2 pressure to 0.2 bar. The temperature was then increased to 395 °C at a rate of 10 °C min−1 to promote desorption. Subsequent absorption and desorption cycles were carried out as follows: after the first dehydrogenation, the H2 pressure and temperature were reduced to 0.2 bar and 315 °C, respectively. The hydrogen pressure was then increased to 60 bar to initiate hydrogenation. The temperature was then increased to 395 °C at a rate of 10 °C min−1 before reducing the H2 pressure to 0.2 bar to initiate decomposition. This was repeated to achieve a total of 10 cycles before leaving the sample in the hydrogenated state. Furthermore, 30 cycles where completed with desorption being carried out under an initial back pressure of 0.7 bar H2 for 1 h and absorption being conducted under an initial pressure of 40 bar for 2 h at 395 °C.
DSC-TGA-MS were conducted at 10 °C min−1 under an argon flow of 20 mL min−1 using a Mettler Toledo TGA/DSC 1 coupled with an Omnistar MS. Mass to charge ratios (m/e–m in atomic mass units and e the electronic charge) ranging between 2 and 100 were followed up at a temperature of 400 °C. The instrument was operated within an Ar filled glovebox to avoid contamination during sample handling. The temperature accuracy of this instrument is ±0.2 °C, while the balance has an accuracy of ±20 μg.
Results and discussion
Thermal decomposition experiments
SR-XRD (Fig. 2) of the two-step synthesised olive-green powder was analysed by Rietveld refinement and the lattice parameters were determined to be a = 11.4255(4) Å, b = 8.4413(3) Å, and c = 5.4154(2) Å: in excellent agreement with a = 11.4297(3) Å, b = 8.4430(2) Å and c = 5.4197(1) Å previously determined by neutron diffraction (space group Pnma).22 Further, quantitative analysis determined that the synthesised material consisted of Na2Mg2NiH6 (76.2(3) wt%), MgNi2 (12.1(2) wt%), NaMgH3 (7.3(1) wt%) and NaH (4.4(1) wt%). This is also in close agreement with the four-step synthesis strategy imposed previously for Na2Mg2NiH6 (69 wt%), Mg2NiH4 (4 wt%), NaMgH3 (10 wt%), NaH (3 wt%), and NaOH (14 wt%).22 Overall, the two-step method (eqn (4)) is highly efficient with regards to synthesis time and product purity compared to the previously reported four-step method (eqn (5) and (6)).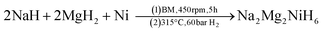 | (4) |
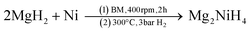 | (5) |
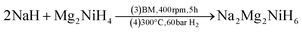 | (6) |
Apart from the report of the original synthesis21 of Na2Mg2NiH6 and the subsequent structure determination by powder neutron diffraction,22 no further experimental studies have been published concerning this material. It is particularly interesting that the decomposition pathway of this compound has not been determined considering the attention its analogue, Mg2NiH4, has received as a hydrogen storage material.4,13,35–43 In this research, initial studies of the decomposition pathway for Na2Mg2NiH6 were carried out by in situ SR-XRD experiments. These experiments allow for the identification of all crystalline species that are present or evolve during decomposition, while simultaneously determining the temperatures at which these processes occur. Fig. 3 illustrates the in situ heating experiment, performed under 1 bar of H2 back pressure, in which the composition of all the crystalline phases were determined as a function of temperature. It is evident that Na2Mg2NiH6 undergoes decomposition in a two- step process which begins at ∼280 °C. As the intensity of the crystalline Na2Mg2NiH6 phase declines, the quantity of the MgNi2, NaH and NaMgH3 phases begin to increase, while Mg2Ni is observed for the first time at ∼320 °C. Above 340 °C, transient NaMgH3 and MgNi2 begin to decrease while Na2Mg2NiH6 can no longer be observed. By 360 °C, NaMgH3 has been totally consumed, whereas the other species, including NaH remain throughout the experiment (Fig. 3 and S1†). Interestingly, PCI analysis does not show an equilibrium plateau for NaMgH3, ex situ XRD diffraction does not exhibit Bragg peaks for NaMgH3, and DSC-TGA-MS only shows a small shoulder (each shown below). Hence, we postulate that NaMgH3 is a transient intermediate in the reaction. The in situ XRD experiment was stopped at ∼410 °C and so the second stage of decomposition was not observed. It is anticipated that the NaH phase would leave Na metal upon decomposition.
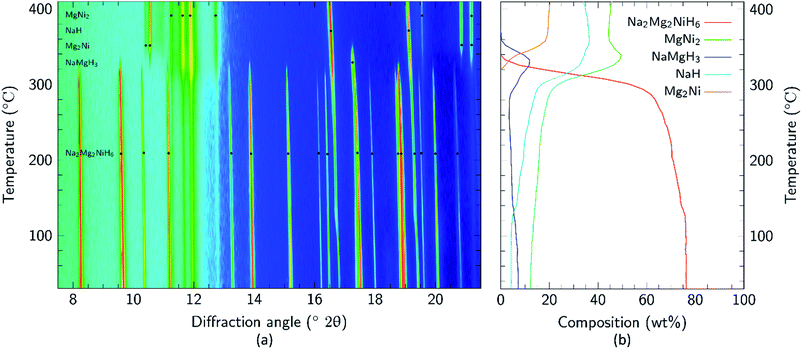 | ||
Fig. 3 (a) Two-dimensional in situ SR-XRD plot for Na2Mg2NiH6 and (b) phase composition of Na2Mg2NiH6 calculated by Rietveld refinement (ΔT/Δt = 5 °C min−1, 1 bar H2, λ = 0.824![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 890(1) Å). 890(1) Å). | ||
Mg poor MgNi2 is formed in a large quantity during the in situ SR-XRD experiment. This is in contrast to ex situ XRD results (see below) and it is therefore concluded that MgNi2 is not normally part of the decomposition process but may merely be a by-product formed due to Mg loss. This may be attributed to the formation of amorphous/nanocrystalline MgO, which would leave Mg2Ni unable to be formed stoichiometrically.
Upon closer inspection, it is apparent that while the decomposition of Na2Mg2NiH6 follows a two-step decomposition pathway, there are also some underlying processes occurring. At ∼100 °C, a distinct expansion of the lattice parameters of NaH are observed from 4.8978 to 4.9094 Å, which is especially apparent for the peak at 2θ = 16.8°. Coincidentally, an exothermic peak at 97 °C is also observed by DSC analysis without a concomitant mass loss detected by TGA (Fig. S2†). This process is associated with the dissolution of NaOH impurities into the NaH lattice. Studies have shown that as little as 10 mol% NaOH (w.r.t. NaH) is capable of causing up to an 11% expansion of the NaH lattice parameters.44 NaOH is not observed in the Na2Mg2NiH6 sample at room temperature (Fig. 2), but was detected in the NaH starting material (3.2 wt% by quantitative XRD analysis). As 30.1 wt% NaH is used as the starting material then at least 0.96 wt% NaOH would be expected in the sample, although this is close to the detection limit of X-ray diffraction, depending on crystallinity. Additional NaOH impurity may also have been introduced during handling of the sample.
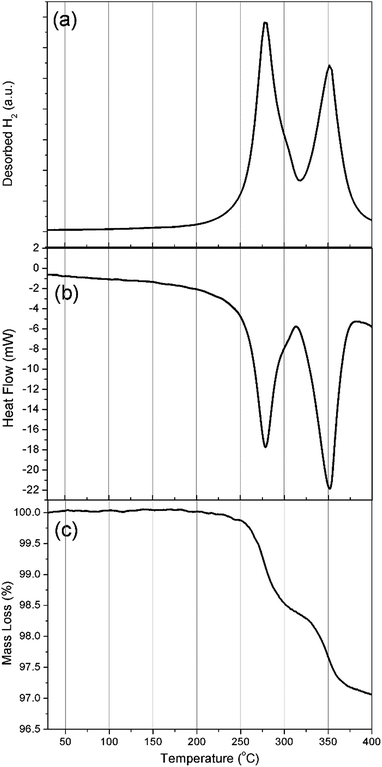
Simultaneous DSC-TGA-MS measurements were carried out to determine the decomposition temperature for Na2Mg2NiH6 and to characterise the associated hydrogen evolution events, (Fig. 4). Each of the DSC, TGA and MS measurements corroborate the in situ SR-XRD data and indicate that hydrogen release occurs in a two-step process (Fig. 4a) with an initial onset temperature of ∼225 °C determined by DSC (Fig. 4b and S3†). DSC measurements indicate that all hydrogen release events are endothermic, with the first exhibiting a maximum hydrogen release rate at 278 °C, with a minor shoulder at 300 °C, followed by a major release at 350 °C. These temperatures are lower than those observed by in situ SR-XRD as DSC-TGA-MS is conducted under a stream of Ar, whereas 1 bar H2 backpressure was placed on the sample during in situ SR-XRD experiments.
TGA measurements (Fig. 4c) determine that, by 400 °C, a total of 3 wt% H2 is released over only two visible mass loss events. This value is 0.8 wt% lower than the theoretical value of 3.8 wt% H2 expected for the total decomposition of Na2Mg2NiH6. As described above, quantitative XRD analysis of the material had determined a 76.2% sample purity and as such only 2.9 wt% H2 is expected to be observed, excluding other hydrogen releasing compounds that may decompose in the same temperature region. The first decomposition step (formation of NaH and 2H2) has an associated mass loss of 1.5 wt% between 250 and 315 °C, which is lower than the 2.5 wt% expected for the decomposition of Na2Mg2NiH6 (1.9 wt% expected accounting for impurities). As seen in Fig. 3b, a small quantity of NaMgH3 is formed during the first stage of decomposition and, as such, would rescind some of the H2 that would be expected to desorb if decomposition were to follow a two-step pathway.
The second mass loss event releases 1.4 wt% hydrogen between 315 and 383 °C. This quantity is close to the theoretical hydrogen capacity for this step corresponding to the decomposition of 2 equivalents of NaH, although when the purity of the material is considered, only 1.1 wt% is expected. The increased capacity corresponds with the decomposition of the NaMgH3 formed and any other hydrogen containing impurity phases. In fact, when the in situ SR-XRD data is considered (Fig. 3b), at 315 °C ∼10 wt% NaMgH3 was determined to be present. Taking the purity of the starting material into consideration, 1.35 wt% H2 is to be expected to be released. This accounts for the 1.4 wt% mass loss observed during the second mass loss event in the TGA measurement. This notion is corroborated by the fact that there is no definite separation between the end of the first decomposition stage and the beginning of the second mass loss event (∼315 °C) by TGA (Fig. 4c), while a small shoulder is also apparent in both the DSC and MS data at 300 °C (Fig. 4 and S3†).
From the experiments carried out so far, it has been determined that the predominant decomposition pathway of Na2Mg2NiH6 is via a two-step process, where Na2Mg2NiH6 forms Na and Mg2Ni with NaMgH3 being formed as an intermediate. Further ex situ XRD data were also collected for Na2Mg2NiH6 material after it was heated to 260 and 330 °C in vacuo. These two temperatures were chosen so as to determine the decomposition products at each of the desorption events observed by TGA. A powder sample heated to 260 °C under vacuum was kept isothermal for 2 h on reaching temperature and, upon analysis by XRD, exhibited peaks for Na2Mg2NiH6, Mg2NiHx (x ≤ 0.3), NaH and a small quantity of MgNi2 (Fig. S4†). No Bragg peaks for NaMgH3 were observed, which may be due to the ex situ XRD experiments being carried out in vacuo, whereas the in situ SR-XRD experiments being carried out under 1 bar H2. This pressure may have allowed for the formation of NaMgH3 which is stable at 1 bar H2 pressure at 382 °C whereas it will decompose under vacuum conditions.45 Further heating of the material to 330 °C, under vacuum, followed by a 12 h isothermal stage yielded predominantly Mg2NiHx, NaH and a small quantity of MgNi2. Mg2NiHx was not modelled during refinement of the in situ SR-XRD data. This is because Mg2NiHx and Mg2Ni exist in the same space group (P6222) and only vary by their lattice parameters.46 Due to the inclusion of H in the lattice, Mg2NiH0.29 has a unit cell volume of 321.4 Å3, whereas Mg2Ni has a unit cell volume of 311.0 Å3. The slight difference in lattice parameters ensures that it is difficult to differentiate between these species, especially when indexing diffraction data measured at high temperatures (due to thermal lattice expansion). Nevertheless, when the materials are cooled to room temperature, these compounds can be distinguished. The detection of Mg2NiHx (x ≤ 0.3) is not unexpected as it is commonly seen during studies of the related Mg2NiH4.46 The Mg2NiHx phases observed in the materials heated to 260 and 330 °C have room temperature unit cell volumes of 318 Å3, indicating that the stoichiometry of H is closer to 0.3 than 0 and that the vestiges of H are difficult to remove from Mg2Ni. The presence of this phase accounts for the reduced hydrogen capacity of the material observed during TGA measurements for the first decomposition step. Therefore, the decomposition of Na2Mg2NiH6 can be explained as
| Na2Mg2NiH6 → Mg2NiHx + 2NaH + (2 − x)H2 (x < 0.3) | (7) |
| 2NaH → 2Na + H2 | (8) |
PCI analysis
Following the determination of the decomposition temperature of Na2Mg2NiH6, PCI measurements were undertaken at five temperatures between 370 and 451 °C to determine the thermodynamics of the H2 desorption process (Fig. 5). Only the first step of this process (eqn (7)) was measured as to inhibit the decomposition of NaH, which inevitably leads to the distillation of Na metal to cooler parts of the instrument.47–49 In regards to technological application, the formation of Na metal is undesirable and the thermodynamics of that process are understood.30 The pressure of the equilibrium plateaux were measured at 0.6 wt%, which allowed for a van't Hoff plot with a corresponding R2 factor of 0.999. As a result, ΔHdes and ΔSdes were determined to be 83 ± 3 kJ mol−1 H2 and 140 ± 4 J K−1 mol−1 H2, respectively. Assuming that Mg2Ni has no thermodynamic or kinetic effect on the decomposition of NaH, then the second stage of decomposition (eqn (8)) will have a ΔHdes and ΔSdes of 117 ± 2 kJ mol−1 H2 and 167 J K−1 mol−1 H2, respectively, based on literature data.30 This gives a total ΔHdes and ΔSdes of 283 ± 6 kJ mol−1 (94.33 ± 3 kJ mol−1 H2) and 447 ± 8 J K−1 mol−1 (149 ± 4 J K−1 mol−1 H2), respectively.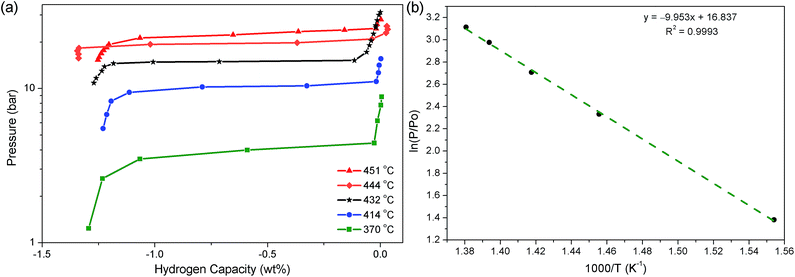 | ||
| Fig. 5 (a) PCI analysis of Na2Mg2NiH6 at selected temperatures and (b) van't Hoff plot of respective H2 desorption equilibrium pressures. | ||
In regards to the analogous compound MgNiH4, Na2Mg2NiH6 is considerably more stable in terms of both enthalpy and entropy. Mg2NiH4 decomposes to Mg2Nix (eqn (1)) with a ΔHdes of 63 kJ mol−1 H2, while ΔS is 120 J K−1 mol−1 H2.13 The ΔHdes of Na2Mg2NiH6 to Mg2Nix and NaH (eqn (7) & (8)) is 31.33 kJ mol−1 larger due to the additional stability achieved by the incorporation of Na+ and H− into the compound.50,51 This effect has been observed previously in analogous compounds of Na2Mg2FeH8 and Mg2FeH6, which have a total ΔHdes of 378 and 261 kJ mol−1, respectively, or 94.5 and 87 kJ mol−1 H2, respectively.50 In Na2Mg2FeH8, the decomposition to 2NaH, 2Mg and Fe has a ΔHdes of 89 kJ mol−1 H2, while ΔHdes of Mg2FeH6 to 2Mg and Fe is 87 J K−1 mol−1 H2. This particular process seems energetically very similar, but the decomposition of Na2Mg2FeH8 to 2NaH, 2Mg and Fe actually proceeds in two steps, via NaMgH3, with the first step having an equilibrium plateau of 100 bar at 380 °C (ΔHdes = 93 kJ mol−1 H2).
Rehydrogenation and cycling experiments
Rehydrogenation experiments were conducted on material that had been decomposed at 415 °C with pressure being kept between 1 and 2 bar H2. This was to ensure total decomposition of all NaMgH3 that may be contained in the sample without decomposing NaH. Samples were then subjected to identical conditions as used for initial synthesis but without formation of pellets (60 bar H2, 315 °C, 20 h). Quantitative Rietveld refinement of the rehydrided products confirmed a composition of 85.3(6) wt% Na2Mg2NiH6, 6.9(4) wt% MgNi2, 2.8(3) wt% NaH, 1.9(2) wt% Ni and only 3.1(3) wt% NaMgH3 showing that rehydrogenation is achievable.Due to early reports,21,22 all hydrogenation experiments up to this point were carried out at H2 pressures exceeding 30 bar. After the determination of the thermodynamics of decomposition of the first step of Na2Mg2NiH6 (eqn (7)), it was deduced that the equilibrium pressure of sorption should be 0.92 bar H2 at 315 °C. An isothermal PCI absorption experiment was conducted at 315 °C (Fig. S5†) resulting in a capacity of 1.2 wt% H2 at an equilibrium pressure of 2.1 bar. XRD analysis of the hydrogenation product indicated that it was predominantly NaMgH3 along with some MgNi2 and NaH (Fig. S6†). Given the desorption pathway and PCI measurements, Na2Mg2NiH6 should have formed under the temperature and pressure applied. Since NaMgH3 is formed instead, which is reported to be less thermodynamically favourable,45 this suggests fast kinetics for the formation of NaMgH3 from the decomposition products and slow kinetics for the formation of Na2Mg2NiH6. Increasing the applied H2 pressure to the decomposition products at 315 °C (in this case to 60 bar) increases the Na2Mg2NiH6 formation kinetics enough to allow it to form.52 However, further investigations would be required to confirm this. In fact, NaMgH3 appears to be a kinetic sink with the necessity for bonding in two moles of NaMgH3 to be broken in order to form 1 mole of Na2Mg2NiH6. Therefore, in order for Na2Mg2NiH6 to be preferentially formed over NaMgH3, a significant hydrogen overpressure of >50 bar is required to be applied during synthesis.
Hydrogen cycling of Na2Mg2NiH6 was conducted 10 times utilising only the first decomposition step (eqn (7), Fig. 6). The first desorption (starting from the pristine state) was carried out by ramping the sample from 315 °C to 395 °C under an initial pressure of 0.2 bar H2. These temperatures and pressures were, used to avoid formation of NaMgH3 during absorption. Within 60 min desorption is almost complete, with 1.36 wt% H2 being desorbed. A further nine cycles were conducted with isothermal hydrogenation at 315 °C and dehydrogenation at 395 °C, respectively. Analysis of the Sieverts data indicates that desorption occurs rapidly and is complete within 30 min with the hydrogen capacity staying consistent within experimental error. Analysis of the material after a final absorption by XRD indicates that the material was cycling through Na2Mg2NiH6, with the final composition being Na2Mg2NiH6 (71.8(5) wt%), NaMgH3 (10.9(2) wt%), NaH (5.3(2) wt%) and MgNi2 (6.6(3)), Mg2NiHx (5.5(5) wt%) (Fig. S7†). Overall, the rate of desorption and the hydrogen capacity is favourable and shows good viability for application.
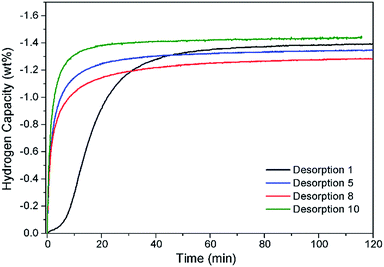 | ||
| Fig. 6 Hydrogen capacity of Na2Mg2NiH6 after ten sorption cycles measured inside a Sieverts apparatus. Tdes = 395 °C and 0.2 bar H2; Tabs = 315 °C and 60 bar H2. | ||
Further hydrogen cycling of Na2Mg2NiH6 was conducted with desorption measured at 400 °C and 0.7 bar H2 initial pressure and absorption at 400 °C and 40 bar H2 pressure (starting from the pristine state). Analysis of the Sieverts data indicates that absorption occurs rapidly and is complete within 3 min for the first 5 cycles (Fig. S8a†). The rate of absorption slowly diminishes over the 30 cycles although hydrogenation is still complete within 6 min after the 30th cycle. The hydrogen capacity of the material also diminishes after the first cycle and over the next nine cycles but appears to stabilise thereafter (Fig. S8b†). The initial capacity is 1.36 wt% H2 on the first absorption but is 1.21 wt% by cycle 30. XRD analysis of the material after the last absorption showed an identical pattern as observed after carrying out the absorption PCT at 315 °C at low pressures (Fig. S5†). This again indicates that NaMgH3 is acting as a kinetic sink and inhibiting formation of Na2Mg2NiH6.
Technological application
If this material were to be technologically viable for high temperature thermal energy storage (TES) applications, a few criteria must be met. Firstly, a relatively high theoretical thermal storage capacity should be upheld. Unfortunately, due to the high molecular weight of 159 amu, Na2Mg2NiH6 – 1st step has a low thermal storage capacity of 1042 kJ kg−1 (Table 2). This is much lower than compounds such as NaBH4 (5709 kJ kg−1) and MgH2 (2811 kJ kg−1) and as such if it were to be implemented, a greater quantity of powder would be required to achieve a similar thermal efficiency. In a similar vein, the theoretical hydrogen capacity of 2.53 wt% is also comparably lower than the wt% H2 of NaBH4 (10.67) and MgH2 (7.66), respectively. This would inhibit its use as a hydrogen storage material. On the other hand, if this material was to be paired with a low temperature metal hydride (LTMH) when implemented as a TES (to store the hydrogen during desorption of H2 during the day), less LTMH would be required as less H2 needs to be stored.8,34| Material | Theoretical H2 capacity (wt%) | ΔHdes (kJ mol−1 H2) | Operating range (°C) | Theoretical thermal storage capacity (kJ kg−1) |
|---|---|---|---|---|
| a Pressures noted correspond to calculated fugacities (pressure = fugacity/compressibility of H2). b Maximum temperature unachievable due to sintering.55 | ||||
| Na2Mg2NiH6 – 1st step | 2.53 | 83 | 318–568 | 1042 |
| NaH0.5F0.5 | 1.53 | 106![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) (ref. 49) (ref. 49) |
470–775 | 803 |
| NaMgH2F | 2.95 | 96.8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) (ref. 34) (ref. 34) |
431–738 | 1416 |
| NaMgH3 – 1st step | 4.01 | 86.6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) (ref. 45) (ref. 45) |
382–683 | 1721 |
| NaH | 4.20 | 116.8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) (ref. 30) (ref. 30) |
426–659 | 2434 |
| NaBH4 | 10.67 | 100.4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) (ref. 53) (ref. 53) |
511–890 | 5709 |
| MgH2 | 7.66 | 74![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) (ref. 54) (ref. 54) |
282–534b | 2811 |
| Mg2FeH6 | 5.47 | 77![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) (ref. 54) (ref. 54) |
304–564 | 2090 |
With a ΔHdes of 83 kJ mol−1, Na2Mg2NiH6 would have an operating temperature of 318–568 °C within a pressure range of 1 and 150 bar. This is in the operating temperature similar to Mg2FeH6, which has already been investigated as a thermal energy storage material on a scale of 211 g and has been shown to cycle at least 23 times.9 The present study has shown that Na2Mg2NiH6 is capable of cycling at least 10 times with full formation of Na2Mg2NiH6 at 315 °C (1.35 wt% H2). Although the pressure and temperature must be controlled during absorption to prevent formation of NaMgH3. The use of a gas booster to store the desorbed hydrogen to maximise volumetric storage will enable full desorption and provide higher gas pressures for absorption. At higher temperatures the material can be cycled at least 30 times through formation of NaMgH3 with a hydrogen capacity of 1.2 wt% H2, although despite the fast kinetics and cyclability this material would contain too much dead weight.
Despite its promise, Na2Mg2NiH6 is unlikely to find technological application due to its material cost. Ni metal is ∼$11 per kg,56 leading to Na2Mg2NiH6 costing ∼$21 per kg, which equates to 72 US$/kWhth. However, there may be alternative applications. For instance, the parent compound, Mg2NiH4, has been shown to form an electrochromic mirror electrode, or switchable mirror, when formed as a thin film.4 This is one aspect of Na2Mg2NiH6 that can be further explored. In addition, Mg2NiH4 has also been shown to be an efficient material to form Ni nanoparticles when hydrolysed.57
Conclusions
The synthesis, thermodynamics and reversible hydrogenation of Na2Mg2NiH6 has been studied in detail to determine its feasibility for technological application as a high temperature hydrogen storage material or as a thermal energy storage material. The incorporation of quasi-isolated H− into this class of complex transition metal hydrides has allowed for increased variety of coordination by cations and increased thermal stability. The original synthesis procedure of Na2Mg2NiH6 involved a four-step method with the requirement of two mixing stages and two annealing stages. This study reports that only one mixing and one annealing stage is required, which results in a reduction of synthesis time by half.The decomposition pathway of Na2Mg2NiH6 has been studied for the first time by in situ SR-XRD and DSC-TGA-MS. Na2Mg2NiH6 is observed to commence hydrogen desorption at 225 °C with two decomposition steps, with maximum H2 desorption rates at 278 °C and 350 °C. The total hydrogen capacity was determined to be 2.9 wt% when heated up to 400 °C if all hydrogen is desorbed (theoretical 3.8 wt% H2). The first step of decomposition is the formation of Mg2NiHx (x < 0.3), and NaH. The second step is the decomposition of NaH. The theoretical hydrogen capacity of 3.8 wt% is not achieved during desorption due to the formation of unreactive MgNi2 during synthesis. PCI analysis of Na2Mg2NiH6 has determined the thermodynamics of decomposition for the first step to have a ΔHdes and ΔSdes of 83 ± 3 kJ mol−1 H2 and 140 ± 4 J K−1 mol−1 H2, respectively. Thermodynamics for the complete decomposition are found to be ΔHdes and ΔSdes of 283 ± 6 kJ mol−1 (94 ± 3 kJ mol−1 H2) and 447 ± 8 J K−1 mol−1 (149 ± 4 J K−1 mol−1 H2), respectively.
Hydrogen cycling of the first step of decomposition has been demonstrated over 10 cycles with no significant reduction in hydrogen capacity. Each cycle desorbed ∼1.35 wt% H2 in under 20 min. It was imperative to apply moderately high pressure to achieve hydrogenation of Na2Mg2NiH6 and to avoid formation of NaMgH3.
Technological implementation of Na2Mg2NiH6 as a high temperature hydride or thermal energy storage material may be hindered by the relatively high cost of the material of $21 per kg, which equates to 72 US$/kWhth. This expense is attributed to the high cost of Ni. Nevertheless, this material would have an operating temperature of 318–568 °C between a pressure range of 1 and 150 bar H2 with impressive cyclability.
With regards to the use of CTMHs as TES materials, it has been shown that the inclusion of sodium, or other metals with high vapour pressures, will inhibit the operating temperatures of the system in order to avoid evaporation and capacity loss. Despite this, a variety of CTMHs have been identified as possible TES materials,4,8,10 although, to date, their thermal properties have not been fully explored.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
CEB, DAS and MP acknowledges the financial support of the Australian Research Council (ARC) for ARC Linkage grant LP120101848, LP150100730 and ARC LIEF grants LE0989180 and LE0775551, which enabled the XRD and gas sorption studies to be done. DAS acknowledges the financial support of a Curtin University Postdoctoral Research Fellowship. MP acknowledges the financial support of the ARC Future Fellowship grant FT160100303. The authors also acknowledge funding from the Australian Synchrotron (ANSTO), which enabled the research at the powder diffraction beamline to be undertaken.Notes and references
- K. Møller, D. Sheppard, D. Ravnsbæk, C. E. Buckley, E. Akiba, H.-W. Li and T. Jensen, Energies, 2017, 10, 1645 CrossRef.
- C. Frommen, M. H. Sørby, M. Heere, T. D. Humphries, J. E. Olsen and B. C. Hauback, Energies, 2017, 10, 2115 CrossRef.
- M. B. Ley, L. H. Jepsen, Y.-S. Lee, Y. W. Cho, J. M. Bellosta von Colbe, M. Dornheim, M. Rokni, J. O. Jensen, M. Sloth, Y. Filinchuk, J. E. Jørgensen, F. Besenbacher and T. R. Jensen, Mater. Today, 2014, 17, 122–128 CrossRef CAS.
- T. D. Humphries, D. A. Sheppard and C. E. Buckley, Coord. Chem. Rev., 2017, 342, 19–33 CrossRef CAS.
- S. Takagi, Y. Iijima, T. Sato, H. Saitoh, K. Ikeda, T. Otomo, K. Miwa, T. Ikeshoji, K. Aoki and S. Orimo, Angew. Chem., Int. Ed., 2015, 54, 5650–5653 CrossRef CAS PubMed.
- S. Takagi and S. Orimo, Scr. Mater., 2015, 109, 1–5 CrossRef CAS.
- D. A. Sheppard, T. D. Humphries and C. E. Buckley, Appl. Phys. A, 2016, 122, 406 CrossRef.
- D. A. Sheppard, M. Paskevicius, T. D. Humphries, M. Felderhoff, G. Capurso, J. Bellosta von Colbe, M. Dornheim, T. Klassen, P. A. Ward, J. A. Teprovich, C. Corgnale, R. Zidan, D. M. Grant and C. E. Buckley, Appl. Phys. A, 2016, 122, 395 CrossRef.
- R. Urbanczyk, M. Meggouh, R. Moury, K. Peinecke, S. Peil and M. Felderhoff, Appl. Phys. A, 2016, 122, 315 CrossRef.
- K. M. Nicholson and D. S. Sholl, Inorg. Chem., 2014, 53, 11833–11848 CrossRef CAS PubMed.
- K. Yvon, Chimia, 1998, 52, 613–619 CAS.
- K. Yvon and G. Renaudin, Hydrides: Solid State Transition Metal Complexes, John Wiley & Sons, Ltd, 2006 Search PubMed.
- J. J. Reilly and R. H. Wiswall, Inorg. Chem., 1968, 7, 2254–2256 CrossRef CAS.
- T. D. Humphries, S. Takagi, G. Li, M. Matsuo, T. Sato, M. H. Sørby, S. Deledda, B. C. Hauback and S. Orimo, J. Alloys Compd., 2015, 645, S347–S352 CrossRef CAS.
- S. F. Parker, Coord. Chem. Rev., 2010, 254, 215–234 CrossRef CAS.
- A. Züttel, M. Hirscher, B. Panella, K. Yvon, S.-i. Orimo, B. Bogdanović, M. Felderhoff, F. Schüth, A. Borgschulte, S. Goetze, S. Suda and M. T. Kelly, Hydrogen as a Future Energy Carrier, Wiley-VCH Verlag GmbH & Co. KGaA, 2008 Search PubMed.
- P. Zolliker, K. Yvon, J. D. Jorgensen and F. J. Rotella, Inorg. Chem., 1986, 25, 3590–3593 CrossRef CAS.
- Z. Gavra, M. H. Mintz, G. Kimmel and Z. Hadari, Inorg. Chem., 1979, 18, 3595–3597 CrossRef CAS.
- B. Huang and K. Yvon, J. Alloys Compd., 1992, 178, 173–179 CrossRef CAS.
- B. Huang, K. Yvon and P. Fischer, J. Alloys Compd., 1994, 204, 5–8 CrossRef.
- K. Kadir and D. Noréus, Inorg. Chem., 2007, 46, 2220–2223 CrossRef CAS PubMed.
- M. Orlova, J.-P. Rapin and K. Yvon, Inorg. Chem., 2009, 48, 5052–5054 CrossRef CAS PubMed.
- M. Di Chio, A. Ziggiotti and M. Baricco, Intermetallics, 2008, 16, 102–106 CrossRef CAS.
- G. Renaudin, L. Guenee and K. Yvon, J. Alloys Compd., 2003, 350, 145–150 CrossRef CAS.
- J.-N. Chotard, Y. Filinchuk, B. Revaz and K. Yvon, Angew. Chem., 2006, 118, 7934–7937 CrossRef.
- T. D. Humphries, D. A. Sheppard and C. E. Buckley, Chem. Commun., 2015, 51, 11248–11251 RSC.
- M. Paskevicius, D. A. Sheppard and C. E. Buckley, J. Am. Chem. Soc., 2010, 132, 5077–5083 CrossRef CAS PubMed.
- H. Yukawa, M. Takagi and M. Morinaga, Bull. Mater. Sci., 1999, 22, 885–890 CrossRef CAS.
- J. F. Herbst, J. Alloys Compd., 2002, 337, 99–107 CrossRef CAS.
- F. D. Manchester and A. San-Martin, Phase Diagrams of Binary Hydrogen Alloys, ASM International, Ohio, 2000 Search PubMed.
- K. S. Wallwork, B. J. Kennedy and D. Wang, Synchrotron Radiation Instrumentation: Ninth International Conference on Synchrotron Radiation Instrumentation, 2007, vol. 879, pp. 879–882 Search PubMed.
- B. Schmitt, C. Brönnimann, E. Eikenberry, F. Gozzo, C. Hörmann, R. Horisberger and B. Patterson, Nucl. Instrum. Methods Phys. Res., Sect. A, 2003, 501, 267–272 CrossRef CAS.
- R. A. Young and R. A. Young, The Rietveld Method, Oxford University Press, 1995 Search PubMed.
- D. A. Sheppard, C. Corgnale, B. Hardy, T. Motyka, R. Zidan, M. Paskevicius and C. E. Buckley, RSC Adv., 2014, 4, 26552–26562 RSC.
- H. Blomqvist and D. Noréus, J. Appl. Phys., 2002, 91, 5141–5148 CrossRef CAS.
- J. P. Darnaudery, M. Pezat, B. Darriet and P. Hagenmuller, Mater. Res. Bull., 1981, 16, 1237–1244 CrossRef CAS.
- G. N. Garcia, J. P. Abriata, J. O. Sofo and G. García, Phys. Rev. B, 1999, 59, 11746–11754 CrossRef CAS.
- R. Martinez-Coronado, M. Retuerto and J. A. Alonso, Int. J. Hydrogen Energy, 2012, 37, 4188–4193 CrossRef CAS.
- W. R. Myers, L. W. W. Wang, T. J. Richardson and M. D. Rubin, J. Appl. Phys., 2002, 91, 4879–4885 CrossRef CAS.
- S. F. Parker, K. P. J. Williams, T. Smith, M. Bortz, B. Bertheville and K. Yvon, Phys. Chem. Chem. Phys., 2002, 4, 1732–1737 RSC.
- Y. Pivak, V. Palmisano, H. Schreuders and B. Dam, J. Mater. Chem. A, 2013, 1, 10972–10978 CAS.
- M. Polanski, T. K. Nielsen, I. Kunce, M. Norek, T. Płociński, L. R. Jaroszewicz, C. Gundlach, T. R. Jensen and J. Bystrzycki, Int. J. Hydrogen Energy, 2013, 38, 4003–4010 CrossRef CAS.
- P. Zolliker, K. Yvon and C. Baerlocher, J. Less-Common Met., 1986, 115, 65–78 CrossRef CAS.
- E. G. Sorte, E. H. Majzoub, T. Ellis-Caleo, B. A. Hammann, G. Wang, D. Zhao, R. C. Bowman and M. S. Conradi, J. Phys. Chem. C, 2013, 117, 23575–23581 CAS.
- D. A. Sheppard, M. Paskevicius and C. E. Buckley, Chem. Mater., 2011, 23, 4298–4300 CrossRef CAS.
- D. Noreus and P. E. Werner, Acta Chem. Scand., Ser. A, 1982, 36, 847–851 CrossRef CAS.
- D. M. Banus, J. J. McSharry and E. A. Sullivan, J. Am. Chem. Soc., 1955, 77, 2007–2010 CrossRef CAS.
- W. Klostermeier and E. U. Franck, Ber. Bunsen-Ges. Phys. Chem., 1982, 86, 606–612 CrossRef CAS.
- T. D. Humphries, D. A. Sheppard, M. R. Rowles, M. V. Sofianos and C. E. Buckley, J. Mater. Chem. A, 2016, 4, 12170–12178 CAS.
- T. D. Humphries, M. Matsuo, G. Li and S.-i. Orimo, Phys. Chem. Chem. Phys., 2015, 17, 8276–8282 RSC.
- S. Takagi, T. D. Humphries, K. Miwa and S. Orimo, Appl. Phys. Lett., 2014, 104, 203901 CrossRef.
- T. Ichikawa, K. Tokoyoda, H. Leng and H. Fujii, J. Alloys Compd., 2005, 400, 245–248 CrossRef CAS.
- Outokumpu, HSC Chemistry, 6.1, 2006 Search PubMed.
- A. Reiser, B. Bogdanovic and K. Schlichte, Int. J. Hydrogen Energy, 2000, 25, 425–430 CrossRef CAS.
- B. Bogdanović, H. Hofmann, A. Neuy, A. Reiser, K. Schlichte, B. Spliethoff and S. Wessel, J. Alloys Compd., 1999, 292, 57–71 CrossRef.
- Metal Prices.com, http://www.metalprices.com/metal/magnesium/magnesium-99-9-usa, accessed 04 December 2016.
- H. Wang, L. Han, H. Hu and D. O. Northwood, J. Alloys Compd., 2009, 470, 539–543 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Quantitative analysis of in situ SR-XRD data; DSC-TPD-MS data; ex situ XRD data; absorption PCI data. See DOI: 10.1039/c8ta00822a |
| This journal is © The Royal Society of Chemistry 2018 |