Open Access Article
Open Access ArticleA multiscale-pore ion exchange membrane for better energy efficiency†
Hyukjin J.
Kwon
 ab,
Bumjoo
Kim
ac,
Geunbae
Lim‡
ab,
Bumjoo
Kim
ac,
Geunbae
Lim‡
 *b and
Jongyoon
Han‡
*b and
Jongyoon
Han‡
 *a
*a
aDepartment of Electrical Engineering and Computer Science, Department of Biological Engineering, Massachusetts Institute of Technology, 77 Massachusetts Avenue, Cambridge, Massachusetts 02139, USA. E-mail: jyhan@mit.edu
bDepartment of Mechanical Engineering, Pohang University of Science and Technology, 77 Cheongam-Ro, Nam-Gu, Pohang, Gyeongbuk, Korea 37673
cKongju National University, Korea
First published on 22nd March 2018
Abstract
Ion exchange membranes (IEMs) have been adopted in various environmental, chemical, and energy applications. However, the formation of ion-depletion regions, caused by concentration polarization near IEMs, often leads to significant energy and efficiency loss. While much research has been devoted to solving this challenge, complete removal of ion-depletion regions is still difficult, especially when the membrane systems are operating under near- or over-limiting conditions. This paper proposes a novel multiscale-pore (MP) IEM to reduce the effect of the ion-depletion region, by allowing a fluid flow through the MP-IEM, thereby limiting the size (and the resulting resistance) of the ion-depletion region. The electrical resistance and energy consumption in MP and conventional IEM-embedded electrochemical systems were investigated, and their performance during water desalination processes were compared. The current–voltage response suggests a secondary ohmic regime attributed to an internal flow rate through the MP-IEM. Moreover, the electrochemical desalination of seawater with MP-IEMs demonstrated up to 75% reduction of energy consumption, compared with conventional IEMs under comparable operating conditions.
Introduction
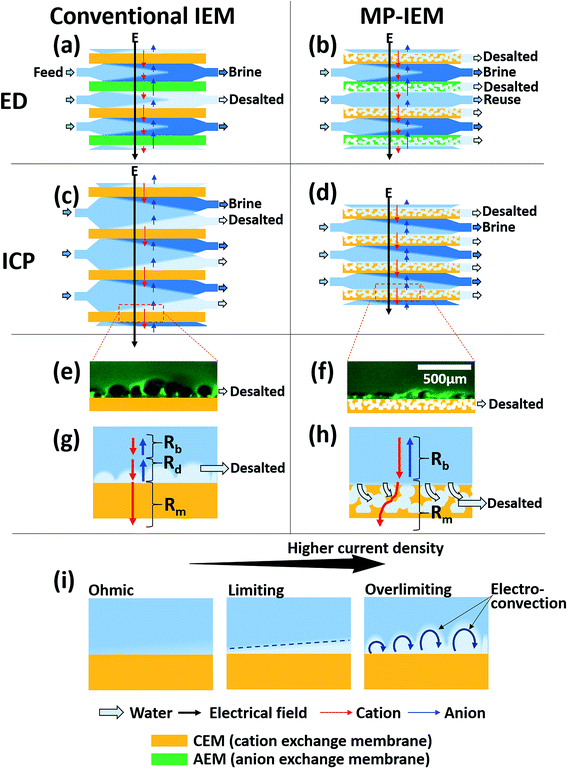
Ion exchange membranes (IEMs) are selective ion conductors due to their ionic permselectivity by nanoscale pores based on the Donnan equilibrium potential. Over the last 50 years, ion-exchange membranes have been utilized in many industrial applications and processes. (1) Environment: electrodialysis (ED) and its related processes for the desalination of seawater and for processing brackish water and seawater or for extracting valuable metals from industrial effluents.1,2 (2) Chemical synthesis and refining: for the chlor-alkali process or for acid refining in the food and pharmaceutical industry. More recently, this application has been extended to the environmentally friendly production of various chemicals.3,4 (3) Energy: ion-exchange membranes have been used as separator membranes in hydrogen–oxygen fuel cell batteries.5 Recently, reverse electrodialysis (RED) has also been suggested for renewable energy generation.6 More recently, ion concentration polarization (ICP) has attracted special attention and shows great potential in processes for the desalination of highly contaminated water, such as flowback water from shale gas mining,7 and biological sample concentration and separation.8When IEMs are used in various applications, the polarization of ion concentration at each side of the membrane (concentration polarization) cannot be avoided. This phenomenon occurs at the membrane–solution interface due to a difference in ion mobility between membrane and solution phases; for example, the ED in Fig. 1(a) comprises alternate cation and anion conductive membranes. In the channel, the anions and cations migrate toward the anode and cathode, respectively, crossing the respective anion-exchange membranes (AEMs) and cation-exchange membranes (CEMs) when an electric potential is applied. For CEMs, the ion concentration is depleted at the cathode side (ion-depletion region) and enhanced at the anode side (ion-enrichment region). The ion-depletion region suppresses ion transfer, resulting in the saturation of the current density (limiting current or diffusion-limited current) as schematically shown in Fig. 1(i). However, excess electric potential can transfer ions through the ion-depletion region and results in overlimiting current. Over the past few decades, intensive research has focused on the discovery of the source and formation of the overlimiting current. Currently, it is widely believed that electro-convection in the ion-depletion region, induced by electro-osmotic instability, could be the main mechanism for ion transfer between the bulk and membrane with overlimiting current [Fig. 1(i)].9–12 Recently, electro-convection and polarization near IEMs have been visualized in three-dimensions, providing significant insight into polarization in the system.13
Concentration polarization is essential in a few applications.7,8 In ICP desalination, the bulky ion-depletion region is physically isolated as desalted product water [Fig. 1(c)]. Biological sample concentration or separation is driven by the intensive gradient of the electric potential in the ion-depletion region. However, in most applications, polarization is an unwanted phenomenon due to the additional electrical resistance caused by the ion-depletion region. For example, it is the main cause that prevents ED efficiency from reaching the theoretical efficiency mainly due to the ion-depletion region near the membrane. Thus, the actual power consumption is several times larger than the power consumption in the absence of polarization.1,14–17 In RED and fuel cells, this polarization effect lowers the power density by interrupting the mass transfer.18 In most of these systems, inefficiencies are related to the difficulty in controlling concentration polarization.
Several attempts have been made to reduce the energy consumption and to increase the limiting current density by mixing the ion-depletion region with the bulk solution. In commercial electrodialysis plants, concentration polarization is controlled by using various feed spacer designs, in order to maximize fluid mixing in the cells.1,2 However, spacers cover part of the membrane and reduces the membrane area available for ion conduction (known as the spacer shadow effect). Therefore, a spacer made of ion-conductive material, an ion conducting spacer, has been suggested to promote turbulence.15–18 More recently, membranes with a specific surface geometry (profiled membranes) have been developed, which promote mixing of the solutions (therefore reducing polarization) without the use of spacers.15,19–21 Although these strategies (flow-driven mixing) can significantly mitigate the effects of ion-depletion regions, they cannot eliminate them altogether, especially at the downstream of the process where reduced ion concentration tends to generate even stronger polarization and depletion.
Another effective strategy to deal with concentration polarization and depletion is to create an ionic conduction path by filling the ED channel with ion exchange (IX) resin beads. The IX beads enhance ion transport, minimizing inherent resistance, and exchange salt ions to aid desalination. This hybrid process consisting of ED and IX, namely electrodeionization (EDI) or continuous deionization (CDI), has been widely used for ultra-pure water production. However, IX resins can cause other problems such as reverse junction formation and water splitting as well as difficulty in system assembly. Unsorted anion and cation exchange resin beads create forward and reverse junctions randomly. Reverse junctions, formed between IX beads of different polarities, interrupt ion migration through the resin;22 water splitting occurs at the forward junction. Although water splitting plays an important role in the electroregeneration of IX resin beads, it also decreases the desalination efficiency for three reasons, namely, it decreases (1) the current efficiency due to the current (from H+ and OH− ions) passing through the membrane,20 (2) electroconvection due to the low Stokes radius of the H+ and OH− ions,23 and (3) the permselectivity of the membrane due to the presence of the water dissociation product near the membrane.24
Recently, notable advances were made in electrical desalination processes, specifically designed to alleviate the energy consumption. Santiago and his group introduced a ‘flow-through electrode capacitance deionization (FTE CD)’ process,25 where a flow driven into microporous (pore size ∼ 1 μm) electrodes in a CDI system enhances ion transport by reducing the thickness of the ion depletion region at electrodes.26 With enhanced ion transport at electrodes, they can reduce the desalination time and enhance the salt removal rate per charge compared to conventional CDI.27 In another example, Bazant and his group introduced a ‘shock electrodialysis’ process to enhance ion transport and thus lower the resistance in the overlimiting regime by using fine glass frit.28,29 Because the material of glass frit itself does not conduct ions at all, glass frit can enhance the current through two possible overlimiting mechanisms which are surface conduction (SC) or electro-osmotic flow (EOF). The dominant mechanism is decided by the pore size of glass frit.12 In order to make SC (ions moving predominantly within the Debye layer) dominant, the pore size should be in the order of a micron or less which might lead to a significant pressure drop. Therefore, EOF is the most likely mechanism applied to shock electrodialysis, as was said in their paper.28,30 EOF is induced by the charged surface of glass frit with relatively larger pores (less than a few hundred micrometers),12,31 and similar to the conventional feed spacer mentioned above, fluid convection by EOF enhances the ion transport in the depletion region. However, EOF-driven mixing is confined within pore space and therefore cannot eliminate the ion-depletion region expanding outside of glass frit or micropores.
In this paper, we suggest a multiscale-pore ion exchange membrane (MP-IEM) to reduce the overall cell resistance (and energy consumption) by using an externally applied pressure-driven flow going into the ion exchange membrane. A conventional IEM with nano-pores was employed to create ion selective permeability with higher mobility than that of the bulk. Moreover, we have added micro-pores (50–300 μm) by a simple salt leaching method in order to allow water flow normal to the membrane, which will confine the ion-depletion region via fluid shearing.32 Through this membrane, the path of water and ions can be controlled by hydraulic pressure and electrical potential, respectively. We previously demonstrated the use of such a large-pore membrane, using a Nafion-coated mesh33 or salt-leached Nafion film,34 but those systems were challenging to scale up and build high-throughput systems. In this work, we are introducing a new membrane structure that can be stacked similarly to standard ED stacks, while maintaining the benefits of an externally driven flow into the ion selective membrane, eliminating the bulk ion depletion region entirely for relatively high current and salt-removal ratio operations. With this novel membrane architecture, the ion-depletion region (desalted region) is extracted through the micro-pores, and thus ionic current can flow from the bulk to the ion exchange membrane directly without passing through the depletion region (severe resistance) suppressing the limiting current phenomenon. This method can be applied to the desalination process to produce fresh water [Fig. 1(b and d)].
This study provides new insight into the polarization phenomenon based on the novel concept of IEMs having an internal flow. In practical terms, this study produces new opportunities to improve the energy efficiency of various ion exchange membrane applications. Herein, we successfully demonstrated an ∼75% reduction in energy consumption in seawater desalination applications.
Results and discussion
Design and preparation of the MP-IEM and its application for desalination
For both means of transport of the ion-depletion region and separation of the channel, the MP-IEM is designed to contain MP (micro-pores + nano-pores) and conventional (only nano-pores) IEM layers. As schematically illustrated in Fig. 2(a), a perfluorinated resin solution was cast with salt crystals to form the MP layer. Subsequently, the conventional IEM layer was coated onto the surface of the MP-IEM layers. To verify the actual performance, we adopted this MP-IEM into an actual platform. Similar to a commercialized ED consisting of a few hundreds of IEM stacks, MP-IEMs can also be stacked to scale up [Fig. 2(b)]. Since the ion pathway is the same as that observed in conventional IEMs, the same polarization is induced, arising from the ion-depletion region at the surface of the MP-IEM. However, under an applied suction flow through the MP-IEM, the ion-depletion region is extracted from the main channel, confined within the micro-pores. | ||
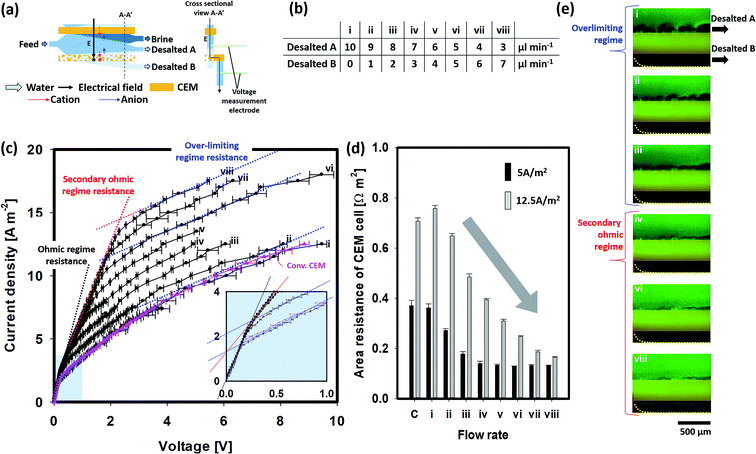
| Fig. 2 (a) Schematics of the fabrication of the MP-IEM comprising MP and conventional IEM layers. (b) Image of the MP-IEM and (c) its SEM image comprising nano-pores for ion transportation and micro-pores for water transportation. Cross-sectional SEM image is shown in the ESI (see S06†). (d) Assembly of a scalable platform with (e) MP-CEM assembly as a key part of this device. (f) Layer by layer fabrication of the device: every plastic component is cut by using a laser cutter and stacked. Membrane assembly can be stacked repeatedly or the area of the membrane can be enlarged to afford a higher flow rate capacity. ED and ICP platforms are produced according to the arrangement of the layers. | ||
The concrete explanation for the working mechanism of the MP-IEM compared to an IEM is shown in Fig. 1(e–h). In the case of the conventional IEM, the microscopy image [Fig. 1(e)] and its schematics [Fig. 1(g)] indicate that the ionic current flow from the bulk concentration solution to the top surface of the conventional IEM must pass through the ion-depletion region, experiencing severe resistance (Rd). In contrast to the conventional IEM, Fig. 1(f and h) demonstrate that most of ions go into the MP-IEM at the top surface of the MP-IEM without passing through the ion-depletion region and there is less ion transport occurring between ion-depleted water within micro-pores and the ion exchange material. To be more specific, the moment the stream meets the micro-porous structure of the MP-IEM surface and then driven into it by the suction flow, hydro-convections are generated. These convections enhance the ion transport considerably between the bulk solution and the MP-IEM generating ion-depleted water. Subsequently, the generated ion-depleted water is isolated within the micro-pores and extracted as fresh water. Although the micro-pores are filled with ion-depleted water which can lead to huge resistance for ionic current, it doesn't count for resistance because it is outside of the main ionic current path (through the microporous part of the membrane, not through the depleted water).
Electrical properties of the MP-IEM
Fig. 3 presents the experimental results of the voltage drop profile by a current swap together with its fluorescence image. To capture images of the extraction of the ion-depletion region, only the first layer (MP) was located to extract the ion-depletion region to the bottom channel (indicated as desalted B) and transfer cations to the upper channel [Fig. 3(a)]. The current–voltage curve usually reflects the electrical properties of the membrane and provides information about the ion transport mechanism, including the polarization phenomenon. Considering the classical theory, the current–voltage curve exhibits three distinguished regimes for the conventional IEM. In the first regime, a linear relationship is observed between the current and voltage drop governed by Ohm's law, the ohmic regime. In the second regime, as the ion-depletion region arises from polarization, a negligible change in current is observed with a change in voltage; this is observed as a plateau (limiting regime) and increases again during the third regime (overlimiting regime).9,11 In this experiment, the second limiting step is not distinguished clearly; this inflection curve was the most commonly encountered in the practical ED process.35The influence of the suction flow (desalted B) on the current–voltage curve was also studied [Fig. 3(c)]. A comparison with the conventional CEM displayed no significant difference between the MP-CEM having an ohmic and an overlimiting regime in the absence of the “desalted B” flow. This indicates that the absence of an internal flow in the MP-CEM does not affect its electrical characteristics. In contrast, when a suction flow was employed, another regime was notably observed between the ohmic and overlimiting regimes. Thus, a slope (effective resistance) higher than that of the overlimiting regime but similar to that of the ohmic regime was observed, indicating that resistance caused by the ion-depletion region was suppressed. We named this regime as the “secondary ohmic regime.” To the best of our knowledge, this unique phenomenon, caused by the suction flow inside the membrane, is reported herein for the first time.
As current density increased, the depletion region is getting bigger and thus the suction flow rate starts to become insufficient to extract the entire depletion region into the MP-IEM. Subsequently, the rest of the depletion region will be formed at the top of the MP-IEM causing resistance like a conventional MP-IEM, resulting in the transition to the overlimiting regime from the secondary ohmic regime. Consequently, the range of the secondary ohmic regime increased with an increase in the suction flow rate. Furthermore, the resistance values in the overlimiting regime (expected to be determined by vortex flows in the main channel) were similar in all of the cases, regardless of the suction flow rate. This indicated that the area resistance of the CEM cell is mainly determined by the ion-depletion region at the surface of the MP-CEM. Note that we use the “area resistance of CEM cell” which includes the resistance of the bulk solution and ion-depletion region as well as the CEM itself while the electrical resistance of the commercial CEM generally means a resistance solely for the membrane materials.
Fig. 3(d and e) illustrate the overall resistance and fluorescence image of the depletion region at a current density of 5 A m−2 at different suction flow rates. They indicate that the area resistance of the CEM cell decreases with an increase in the suction flow, reflecting the transition from the overlimiting regime to the secondary ohmic regime. Moreover, the size of the ion-depletion region observed at the top of the MP-IEM surface shows a clear transition from the vortex-driven overlimiting regime to the near-complete suppression of vortices in the secondary ohmic regime. In the secondary ohmic regime (e.g. as in (iv)), the area resistance of the CEM cell is largely determined by the conductivity of macroporous membranes (much higher than that of the depleted region within the macroporous membrane), resulting in a much lower voltage drop. Fig. 3(e, vi–viii) display the leakage of the bulk solution to the “desalted B” stream due to a higher suction flow when compared to the ion-depletion region. This leakage eventually lowers the current efficiency of desalination. Therefore, for each current density, optimal operating suction flow rates should be determined. This optimal operating point can be found around the inflection point between the suppressed overlimiting and overlimiting regimes in the current–voltage curve. For a current density of 12.5 A m−2 as shown in Fig. 3(d), a higher suction flow was needed to extract the ion-depletion region due to the generally larger ion-depletion region. At this point, roughly the same amount of salt can be removed (determined by the current density and current efficiency) but with the overall area resistance of the CEM cell being approximately quarter of the original resistance. Power consumption is usually calculated as electrical power consumption divided by the flow rate of desalted water, as shown in S01 in the ESI.† Consequently, with the same current density and salt removal, reduction in the overall area resistance of the CEM cell results in a reduction in power consumption. Therefore, from the graph in Fig. 3(d), it is highly expected that there is ∼75% reduction in power consumption at 12.5 A m−2 current density (∼50% for 5 A m−2). Note that the reduction in voltage drop/power consumption is more prominent for higher current density operation, where overall efficiency is critically impaired by the expansion of the ion depleted region. In order to investigate the reduction in power consumption by the MP-IEM considering salt removal, several demonstrations of the actual desalination process are conducted as follows.
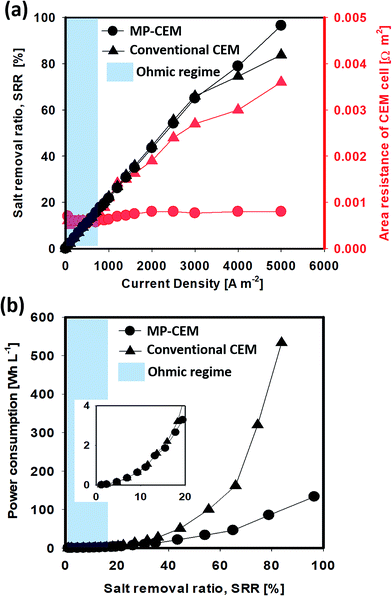
Overview of the area resistance of the MP-IEM cell
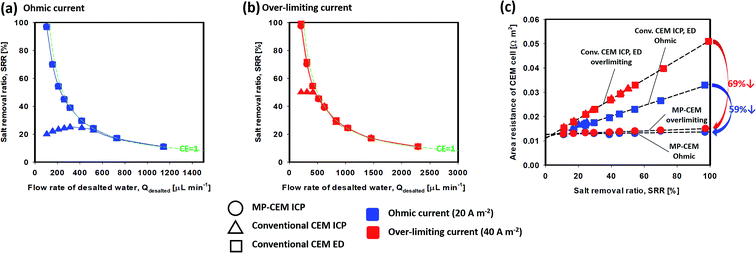
Although the current–voltage response clearly indicates that the area resistance of the cell exhibits a beneficial “secondary ohmic regime”, the salt removal ratio (SRR) must also be taken into consideration for practical application. The various measurements for desalination performance including the SRR are described in the ESI.† From eqn (S5) and (S7),† the salt removal ratio can be described as the product of the theoretical salt removal ratio and current efficiency (CE):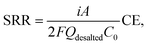 | (1) |
Fig. 4(c) reveals a linear relationship between the area resistance of the CEM cell and the salt removal ratio. It indicates an important fact that the area resistance of the CEM cell is mainly decided by the salt removal ratio (size of the ion-depletion region); therefore, current density and the flow rate of desalted water are the main variables deciding the salt removal ratio. For a better understanding, the resistivity of salt removal (RS, slope of the line) indicating the relationship between salt removal and resistance caused by the ion-depletion region is suggested as follows:
| Rd [Ω m2] = RS·C0·SRR. | (2) |
As previously mentioned in Fig. 1(g and h), the area resistance of the cell consists of the area resistance of the ion-depletion region (Rd), the area resistance of the bulk solution (Rb) and the area resistance of the membrane (Rm) as follows:
| Rcell [Ω m2] = Rd + Rb + Rm. | (3) |
Consequently, the area resistance of the CEM cell can be simply described as follows:
| Rcell [Ω m2] = RS·C0·SRR + (Rb + Rm). | (4) |
From the lines of Fig. 4(c), the value of RS and Rb + Rm can be found as shown in Table 1. From Table 1, one can see that the Rb + Rm values for all three cases are rather similar, but the RS value for the MP-CEM is significantly lower than those for conventional CEMs both in ICP and ED configurations. In addition, it is noteworthy that the RS value is lowered in both ohmic and overlimiting regimes. As the salt removal ratio increases, the Rb + Rm value becomes relatively insignificant while the Rd value becomes the dominant area resistance of the cell, thereby dominating the power consumption. Therefore, a reduction in power consumption is more significant at a higher salt removal ratio (simply because Rd dominates at a higher salt removal ratio).
| Type | Regime | RS [Ω m2 M−1] | R b + Rm [Ω m2] |
|---|---|---|---|
| MP-CEM | Ohmic | 1.04 × 10−3 | 12.66 × 10−3 |
| Overlimiting | 2.49 × 10−3 | 12.59 × 10−3 | |
| Conv. CEM ICP | Ohmic | 26.26 × 10−3 | 10.77 × 10−3 |
| Overlimiting | 40.59 × 10−3 | 11.03 × 10−3 | |
| Conv. CEM ED | Ohmic | 22.98 × 10−3 | 10.63 × 10−3 |
| Overlimiting | 40.48 × 10−3 | 10.86 × 10−3 |
The conventional CEM has a higher RS value, which means that a higher salt removal ratio in the conventional IEM inevitably leads to a thicker ion-depletion region and additional voltage drop (area resistance of the CEM cell). The RS value of the conventional CEM with overlimiting currents is even higher than that of the ohmic regime. In contrast, the MP-CEM exhibits a lower RS value because the flow into the MP-CEM membrane ensures that the thickness of the depletion region is minimized. This clearly indicates that the MP-CEM can lower the electrical resistance in practical desalination processes, enabling high salt removal and high recovery electrical desalination at better energy efficiency. With 100% salt removal, a significant 69% power consumption reduction is expected in the over-limiting regime and a 59% reduction is expected even in the ohmic regime.
Performance comparison with conventional ED operated under optimized conditions
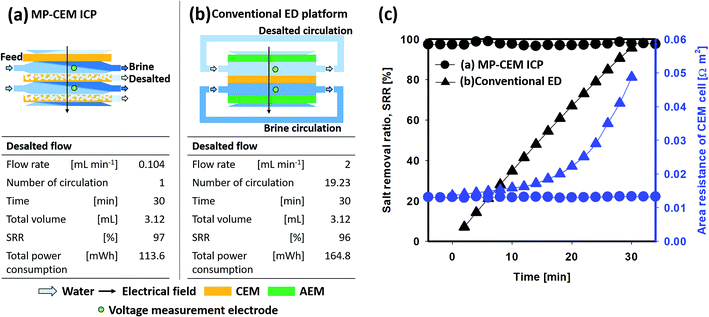
Unfortunately, as mentioned previously, a large energy loss caused by concentration polarization arises under higher current density operation, especially in the overlimiting current regime. Hence, it is often assumed that a current slightly below the limiting current is considered as the ‘optimal’ point. To verify the improvement of the energy efficiency for an actual system under the optimal operating current, the MP-CEM and conventional ED were compared under the same current, membrane size, and volume of produced water but different desalted streams [Fig. 5(a and b)]. The desalted stream from the MP-CEM was collected continuously and exhibited the stable area resistance of the CEM cell and salt concentration [Fig. 5(c)]. However, as previously mentioned in the Introduction, commercialized ED is usually optimized with additional convection induced by spacers to remove the bulky ion-depletion region. To create this additional convection during the operation of ED, a desalted stream was circulated at a high flow velocity (thereby suppressing the ion-depletion region) when the concentration and area resistance of the CEM cell were measured in real time. Initially, the area resistance of the conventional CEM cell was similar to the that of the MP-CEM cell. However, it exponentially increased with time [Fig. 5(c)]. The origin of this effect is due to two reasons: (1) in the ED process, even with the starting current density at sub-limiting values, the process eventually enters the overlimiting regime, resulting in significant polarization and an additional voltage drop, due to precipitous desalting in the dilute channel. (2) The dilute channel eventually reaches near-zero salt concentration, resulting in severe area resistance of the cell. Even in a more typical non-recirculating ED process, the same phenomena would be observed toward the end of the ED channel, which are unavoidable for the production of desalted fresh water (desalted) regardless of the choice of ‘optimal’ ED operating current.Demonstration of energy efficiency improvement in seawater desalination
The current–voltage curves (Fig. 3) and resistance overview (Fig. 4) reveal that the MP-CEM plays a significant role in the reduction of the overall area resistance of the cell, especially in the overlimiting regime, thereby allowing the desalination with higher current density. Yet, desalination demonstrations of Fig. 4 and 5 were conducted at relatively low concentration which is not practical. To verify the decrease in resistance at high concentration, the performances of ICP desalination by conventional and MP-CEMs were compared in seawater desalination. Note that for visualization, this experiment was conducted on a microchip platform. In Fig. 6(a), the ohmic current density does not induce any significant increase in the area resistance of the cell, as observed in Fig. 5, yet at those current values the rate of salt removal is low (less than 20% salt removal at the end of the stage, shaded area). However, the overlimiting regime current is enough to induce a strong polarization, meaning a significantly desalted output stream with an acceptable salt removal ratio. The area resistance of the conventional CEM cell increases gradually with current density falling into the overlimiting regime, while that of the MP-CEM increases only slightly, entering the secondary ohmic regime instead of the overlimiting regime (current–voltage curve in Fig. 3). In the visualization shown in Fig. 1(e and f), it is remarkably observed that the ion-depletion region is extracted inside the MP-IEM with 4000 A m−2. The comparison of the experimental power consumption in Fig. 6(b) clearly demonstrates an improvement of 75% in energy efficiency in desalination with high salt removal. Although, it is clearly verified in this experiment that the MP-IEM can reduce power consumption, the thermodynamic efficiency was low. It was measured as 4.7 for 10 mM solution and 0.68 for seawater, respectively. This low energy efficiency is mainly caused by the extremely high current density compared to the typical current density adopted for commercialized seawater ED which is about 300–500 A m−2. It is reported that as the applied current density increases, the required energy per certain amount of salt also increases.36Methods
Fabrication of IEMs
A Nafion membrane does not comprise micro-pores but only nano-pores. To add micro-pores to this membrane, ground NaCl crystals (Sigma Aldrich, USA) were added to the Nafion solution (Sigma Aldrich, USA) and subsequently leached away. As previously mentioned and shown in Fig. 2(a), the MP-IEM consists of MP and conventional IEM layers. First, to fabricate the MP layer, a few hundred micrometer-sized salt crystals were added to 20 wt% Nafion solution. The resultant mixture was fully solidified in an oven for 3 h at 60 °C. Second, in order to form a conventional IEM layer on top of the MP layer, a diluted 5 wt% Nafion solution was applied by using a brush on the top surface of the dried Nafion-salt crystal mixture in the oven for 60 °C. The solvent from the applied Nafion solution momentarily dissolved the dried Nafion at the top surface of the MP layer and solidified forming a solid bond between the MP and conventional layers. This latter step was repeated five times to create a solid conventional IEM layer without micro-pores. Finally, water was added to dissolve the salt and then the fabricated membrane consists of an ∼800 μm thick MP-IEM layer and ∼200 μm thick conventional IEM layer. Although the thickness of this membrane can be controlled by the amount of the solution, an ∼1000 μm thick MP-IEM was used for convenient handling and experiment for visualization. The membrane was kept wet to maintain its structure. It was cut to an appropriate size for application. The pore size and porosity depend on the size and number of salt crystals.As shown in Fig. 3, to compare the current voltage curve of the MP-IEM to that of conventional IEMs, a conventional IEM was fabricated with identical material and solidification conditions. The conventional IEM was cast in an oven for 60 °C with 20% Nafion solution to form a 300–400 μm thick membrane.
Microfluidic device fabrication for visualization
A microchip was used to determine the electrical characteristics and visualize the ion-depletion region induced by polarization. Polydimethylsiloxane (PDMS) material was used for the top, middle, and bottom frames of the microfluidic device. PDMS with a curing agent (15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ratio, Sylgard 184 Silicone elastomer kit, Dow Corning, USA) was poured into a 3D printed mould (printed by Object3500 with Vero clear material, Stratasys, USA) and cured in an oven at 80 °C to create the frames; these frames included a slot for the membrane and a micro-channel pattern. The membranes and electrodes were inserted between the slots in the frames and assembled by using an oxygen plasma bonder according to a previously reported method. Detailed schematics and fabrication of the microchip platform are shown in S07 in the ESI.† 1 mg mL−1 monosodium negatively charged dye (Alexa 488, Invitrogen, USA) (200 μM) was added to the feed solution to visualize the migration of the ion-depletion region into the MP-IEM by fluorescence microscopy. During the device operation, the flow rates of each channel were controlled by using syringe pumps with a fixed recovery ratio of 0.5. The electrode channels were supplied with an electrolyte solution of the same concentration and composition as the feed.
1 ratio, Sylgard 184 Silicone elastomer kit, Dow Corning, USA) was poured into a 3D printed mould (printed by Object3500 with Vero clear material, Stratasys, USA) and cured in an oven at 80 °C to create the frames; these frames included a slot for the membrane and a micro-channel pattern. The membranes and electrodes were inserted between the slots in the frames and assembled by using an oxygen plasma bonder according to a previously reported method. Detailed schematics and fabrication of the microchip platform are shown in S07 in the ESI.† 1 mg mL−1 monosodium negatively charged dye (Alexa 488, Invitrogen, USA) (200 μM) was added to the feed solution to visualize the migration of the ion-depletion region into the MP-IEM by fluorescence microscopy. During the device operation, the flow rates of each channel were controlled by using syringe pumps with a fixed recovery ratio of 0.5. The electrode channels were supplied with an electrolyte solution of the same concentration and composition as the feed.
Plastic layer-by-layer scalable device fabrication
The membrane area of the microfluidic system was too small to produce fresh water from feed water in the ohmic regime. Thus, to compare the fabricated MP-IEM to a conventional IEM with an ED or ICP platform in the ohmic regime, a relatively high-throughput device, compared to that of a microchip, is necessary. For this reason, experiments for Fig. 4 and 5 were conducted by using a layer-by-layer scalable device which is presented in Fig. 2(f). The mainframe and electrode rinsing channels were made of 3 mm thick acrylic (Plazen, Korea) to form a 3 mm thick rinsing channel for bubble removal at the electrode. An iridium-coated titanium electrode (Titech, Korea) was fixed at the side of the mainframe inside the electrode rinsing channel. 1 mm thick silicon sheets (HSW, Korea) were located at each side of the membrane for the formation of a 1 mm thick concentrated channel and gaskets to prevent any leakage while under compression by bolts. The MP-IEM and 0.5 mm silicon desalted channels were located between two windows (0.5 mm polycarbonate sheet, DSpolychem, Korea and 0.1 mm polyethylene terephthalate sheet, 3M, US) and fixed into the window with tape (3M 371, USA) to separate the desalted channel from the concentrated channel. The MP layer of the MP-IEM is connected to the 0.5 mm thick desalted channel for applying a suction flow and there were 1 mm gaps between MP-IEMs. For comparison with conventional ED, a commercial cation exchange membrane (Nafion N1110, Ion power, USA) and anion exchange membrane (Fumasep, FTAM-E, Germany) were used and the thickness of the membranes were 225 μm and 400 μm, respectively. Both concentrated and desalted channels were 1 mm thick and thus the gap between the IEMs was 1 mm. In every experiment using the layer-by-layer device, the recovery ratio was fixed at 0.5.Electrical characteristic measurement
The ionic resistance of the membrane cell needs to be precisely measured and all the other resistances such as that induced by bubbles trapped in the electrode rinsing channel or overpotential at the electrodes must be ruled out. For this purpose, additional voltage measurement electrodes (Ag/AgCl 0.15, A-M SYSTEMS, USA) were located between the target membranes, measuring the voltage drop using a multimeter (Keysight 34401a, USA); a constant current was applied to the working electrodes at each end of the membrane stack using a source measure unit (Keysight 2902b, USA). Current–voltage curves were afforded by a step-wise increase of the current density through the cell. Subsequently, the system was allowed to reach a steady state for 30 s to measure the voltage. Consequently, the area resistance of the target membrane cell was derived from the slopes of the straight portion by using simple Ohm's law. During the device operation, flow rates through syringes were controlled by using syringe pumps (Harvard apparatus PHD 2000, USA).Conclusion
In commercialized water production, the cost of electrically driven desalination comprises operating and capital costs. In effective operations, the operating cost is mainly due to the electrical energy consumed by salt removal, while the capital cost is mainly the cost of the membrane.15 As the experimental results indicated, this novel MP-IEM can significantly reduce the operating costs over the entire current regime (ohmic to overlimiting, Fig. 4(c)). Efficiency improvement by the MP-IEM was more prominent for limiting and overlimiting regimes, essentially migrating their regimes into a ‘secondary ohmic regime’ with no additional voltage drop associated with higher current/salt removal operation. As a result, the operating current range for electrical desalination that is economically viable was dramatically expanded well into the overlimiting current regime. Regarding the membrane cost, the required membrane area is inversely proportional to the applied current.15 Therefore, applying the overlimiting regime with our MP-IEM can decrease the capital cost of commercial scale electrical desalination. Moreover, since the system size depends on the size of the membrane, it is possible to size the system down to a portable scale for small volume applications such as individual household or emergency uses.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by an Advanced Research Projects Agency-Energy (ARPA-E) grant (DE-AR0000294), as well as a Kuwait-MIT signature project grant (P31475EC01) supported by the Kuwait Foundation for the Advancement of Sciences (KFAS). H. J. Kwon was supported by the Mid-career Researcher Program through the National Research Foundation of Korea (NRF) grant funded by the Korea government (MSIP) (No. 2015R1A2A1A14027903).Notes and references
- R. W. Baker, Membrane Technology and Applications, 2005 Search PubMed.
- H. Strathmann, Ion-Exchange Membrane Separation Processes, Elsevier Science, Amsterdam, 1st edn, 2004 Search PubMed.
- H. Strathmann, A. Grabowski and G. Eigenberger, Ind. Eng. Chem. Res., 2013, 52, 10364–10379 CrossRef CAS.
- H. Jaroszek and P. Dydo, Open Chem., 2016, 14, 1–19 CrossRef CAS.
- S. J. Peighambardoust, S. Rowshanzamir and M. Amjadi, Int. J. Hydrogen Energy, 2010, 35, 9349–9384 CrossRef CAS.
- B. E. Logan and M. Elimelech, Nature, 2012, 488, 313–319 CrossRef CAS PubMed.
- B. Kim, R. Kwak, H. J. Kwon, V. S. Pham, M. Kim, B. Al-Anzi, G. Lim and J. Han, Sci. Rep., 2016, 6, 31850 CrossRef CAS PubMed.
- R. Kwak, S. J. Kim and J. Han, Anal. Chem., 2011, 83, 7348–7355 CrossRef CAS PubMed.
- V. V. Nikonenko, A. V. Kovalenko, M. K. Urtenov, N. D. Pismenskaya, J. Han, P. Sistat and G. Pourcelly, Desalination, 2014, 342, 85–106 CrossRef CAS.
- I. Rubinstein and B. Zaltzman, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 2000, 62, 2238–2251 CrossRef CAS.
- V. Barragán and C. Ruíz-Bauzá, J. Colloid Interface Sci., 1998, 205, 365–373 CrossRef.
- E. V. Dydek, B. Zaltzman, I. Rubinstein, D. S. Deng, A. Mani and M. Z. Bazant, Phys. Rev. Lett., 2011, 107, 118301 CrossRef PubMed.
- S. V. Pham, H. Kwon, B. Kim, J. K. White, G. Lim and J. Han, Phys. Rev. E, 2016, 93, 33114 CrossRef PubMed.
- L. Shaffer and M. Mintz, Electrodialysis, in Principles of Desalination, Academic Press, New York, 2nd edn, 1980 Search PubMed.
- H. Strathmann, Desalination, 2010, 264, 268–288 CrossRef CAS.
- O. Kedem, Desalination, 1975, 16, 105–118 CrossRef CAS.
- J. Weida and L. Dong, Desalination, 1985, 54, 197–206 CrossRef.
- P. Długołecki, J. Dabrowska, K. Nijmeijer and M. Wessling, J. Membr. Sci., 2010, 347, 101–107 CrossRef.
- V. V. Nikonenko, N. D. Pismenskaya, A. G. Istoshin, V. I. Zabolotsky and A. A. Shudrenko, Chem. Eng. Process., 2008, 47, 1118–1127 CrossRef CAS.
- C. Larchet, V. I. Zabolotsky, N. Pismenskaya, V. V. Nikonenko, A. Tskhay, K. Tastanov and G. Pourcelly, Desalination, 2008, 222, 489–496 CrossRef CAS.
- D. A. Vermaas, M. Saakes and K. Nijmeijer, J. Membr. Sci., 2011, 385–386, 234–242 CrossRef.
- A. Grabowski, G. Zhang, H. Strathmann and G. Eigenberger, Sep. Purif. Technol., 2008, 60, 86–95 CrossRef CAS.
- J.-H. Choi, H.-J. Lee and S.-H. Moon, J. Colloid Interface Sci., 2001, 238, 188–195 CrossRef CAS PubMed.
- E. I. Belova, G. Y. Lopatkova, N. D. Pismenskaya, V. V. Nikonenko, C. Larchet and G. Pourcelly, J. Phys. Chem. B, 2006, 110, 13458–13469 CrossRef CAS PubMed.
- M. E. Suss, T. F. Baumann, W. L. Bourcier, C. M. Spadaccini, K. A. Rose, J. G. Santiago and M. Stadermann, Energy Environ. Sci., 2012, 5, 9511 CAS.
- Y. Qu, T. F. Baumann, J. G. Santiago and M. Stadermann, Environ. Sci. Technol., 2015, 49, 9699–9706 CrossRef CAS PubMed.
- Y. Qu, P. G. Campbell, L. Gu, J. M. Knipe, E. Dzenitis, J. G. Santiago and M. Stadermann, Desalination, 2016, 400, 18–24 CrossRef CAS.
- D. Deng, E. V. Dydek, J.-H. Han, S. Schlumpberger, A. Mani, B. Zaltzman and M. Z. Bazant, Langmuir, 2013, 29, 16167–16177 CrossRef CAS PubMed.
- S. Schlumpberger, N. B. Lu, M. E. Suss and M. Z. Bazant, Environ. Sci. Technol. Lett., 2015, 2, 367–372 CrossRef CAS.
- E. V. Dydek and M. Z. Bazant, AIChE J., 2013, 59, 3539–3555 CrossRef CAS.
- S. Nam, I. Cho, J. Heo, G. Lim, M. Z. Bazant, D. J. Moon, G. Y. Sung and S. J. Kim, Phys. Rev. Lett., 2015, 114, 1–5 CrossRef PubMed.
- R. Kwak, V. S. Pham, K. M. Lim and J. Han, Phys. Rev. Lett., 2013, 110, 114501 CrossRef PubMed.
- S. J. Kim, B. Kim, R. Kwak, G. Kim and J. Han, SPIE Nanosyst. Eng. + Med., 2012, p. 85483R Search PubMed.
- H. J. Kwon, B. Kim, G. Lim and J. Han, in μTAS, 2015, pp. 1202–1204 Search PubMed.
- H. Meng, D. Deng, S. Chen and G. Zhang, Desalination, 2005, 181, 101–108 CrossRef CAS.
- Y. Tanaka, J. Membr. Sci., 2003, 215, 265–279 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c7ta10570c |
| ‡ These authors contributed equally to this work. |
| This journal is © The Royal Society of Chemistry 2018 |