Drop mobility on superhydrophobic microstructured surfaces with wettability contrasts

Abstract

Manipulation of drop motion has attracted considerable attention recently as it is pertinent to industrial/biological applications such as microfluidics. Wettability gradients/contrasts applied to microtextured, superhydrophobic surfaces are probable candidates for engineering drop motion by virtue of their wettability controllability and low contact angle hysteresis. In the present work, we present a systematic study of drop mobility induced via wettability contrasts. A millimetre-sized water drop, placed on the boundary between two surfaces with distinct, uniform arrays of pillars, immediately moved toward the surface more densely populated with asperities, which was relatively more hydrophilic. The velocity of the motion was found to increase proportionally with the difference in pillar densities on each surface, in circumstances where the rear side surface had sufficiently small contact angle hysteresis. To elucidate the underlying mechanism of drop motion, we implemented a surface energy analysis for each motion event. Motion was initiated by the excess surface free energy due to drop deformation and directed in favour of energy minimisation. Lastly, we propose a theory to predict the direction of the drop which at the same time acts as the criterion for the motion to ensue.

---

Introduction

Drop manipulation/transport on solid surfaces has attracted significant interest over the past decade due to its importance in the development of bio-medical microfluidics,^1–4 self-cleaning surfaces,^5–9 anti-icing^10–13 and better heat transfer surfaces e.g. dropwise condensation enhancement.^14–17

Capillarity is one of the tactics to drive drop motion due to the fact that surface tension is mainly responsible for the dynamics of micro- or millimetre-sized drops.^18–20 A drop experiencing an imbalance of capillary force will rearrange in order to attain the equilibrium state. In their seminal work, Chaudhury and Whitesides²¹ imposed a spatial wettability gradient combined with low contact angle hysteresis (6–8°) on a silicon wafer using the silanization process. On their surface, water, glycerol and chloroform drops were capable of climbing up to a 15° incline. Following their work, various drop manipulation techniques have been proposed based on introducing heterogeneous surface tension using chemical,^21–25 thermal,^25–28 and electrical^29–32 principles. However, these mechanisms might lead to undesirable side effects in practice, such as chemical compatibility, temperature change, phase change and electrical interference.

The fabrication of micropillars on surfaces is another promising technique to engineer surface wettability. When the liquid completely penetrates the asperities, also known as the Wenzel state,³³ the apparent contact angle in the equilibrium state, denoted as θ_app, is expressed as cos θ_app = r cos θ_i, where r (typically greater than unity) is the roughness factor and θ_i is the intrinsic contact angle of the flat surface. On the other hand, Cassie and Baxter³⁴ described a drop resting on top of textures with air trapped underneath the drop and between the structures (often referred as a “fakir” drop^35,36). Defining the surface area fraction of the solid in contact with the drop as ϕ, then θ_app of the fakir drop can be expressed as

cos θ_app = −1 + ϕ(cos θ_i + 1) (1)

In the Cassie–Baxter (CB) regime, a drop attains θ_app higher than 150° and exhibits small contact angle hysteresis (CAH) i.e. higher mobility when compared to the Wenzel regime.

Using a micropillar gradient, Shastry et al.³⁷ have experimentally demonstrated that an additional energy by vibrating the surface was necessary to initiate drop motion due to CAH which needed to be overcome. In a follow-up work, Reyssat et al.³⁸ have reported a similar experiment and proposed a physical model based on a simple scaling law, which predicts drop velocity as a function of input vibrational energy as well as microtexture gradients. On the contrary, McHale et al.³⁹ have successfully demonstrated drop motion without any external forces on superhydrophobic gradient surfaces with extremely small CAH (<10°). Moreover, Moradi et al.⁴⁰ have numerically simulated spontaneous drop motion on texture gradients without external input.

Despite recent progress in manipulating drops, a scarcity of experimental evidence of drop motion on heterogeneous wettability still remains. For example, the effects of microstructures on the wetted surface may result in differential wettability and/or CAH which can be detrimental on drop mobility. Furthermore, the criteria for spontaneous drop motion on such surfaces with heterogeneous wettability are yet to be elucidated. In this contribution, we conducted a systematic analysis of the influence of differential surface texture patterns on drop mobility. To this end, we placed water drops at the boundary between two surfaces with different textures (different ϕ), resulting in a “contrast” of wettability. In turn, the wettability contrast led to drop motion which we followed with a high speed camera. Notably, the drops spontaneously moved toward the surfaces with larger ϕ (more hydrophilic) without any external force/vibration. Interestingly, the drops did not seem to either slide or roll, they rather walked in an oscillatory manner with a velocity proportional to the difference in surface area fractions Δϕ. Additionally, we have found that low CAH in the dewetting/rear surface was the necessary component for drop motion. We combined experimental observations with detailed surface energy analysis in order to rationalise our findings and provide a description of the physical mechanism underpinning drop motion. In particular, the drops were directed by energy minimisation, converting excess surface free energy into kinetic one and moving toward the surface with larger ϕ. Moreover, our energy analysis has elucidated the magnitude of the minimum excess free energy required to overcome CAH and initiate spontaneous drop motion. We believe this contribution to provide paramount information to inform the design of micro-structured surfaces in order to tailor drop motion.

Experimental

Surface preparation

We fabricated a number of 1 × 1 cm² surfaces comprising arrays of uniformly arranged square (cross-section 5 × 5, 10 × 10 and 20 × 20 μm²) and circular (diameter 10 μm) pillars, with spacing between pillars ranging from 5 to 80 μm. As a consequence, the surface area fraction varied from ϕ = 0.003–0.444. The pillars were fabricated on silicon wafers using photolithography and deep reactive ion etching, and then coated with a perfluorodecyltrichlorosilane (FDTS) monolayer by molecular vapour deposition, providing an intrinsic contact angle of θ_i = 114° ± 6.7° on a flat surface. The characteristic surface fraction (ϕ) and wetting characteristics (equilibrium (θ_app), advancing (θ_adv) and receding (θ_rec) contact angles) are listed in Table 1 for each surface fabricated. Here, each surface is named as S-j-k where S denotes the shape (Sq stands for square and Ci circular), j the lateral dimension or diameter and k the pillar spacing in micrometre, respectively. θ of each surface were close to those calculated by eqn (1), hence we assume our drops to be following the Cassie–Baxter or fakir wetting regime. Exemplary optical microscopic photos of Sq-10-20 and Ci-10-40, and 3D laser scanning microscopy for the boundary Sq-10-40/Sq-10-20 taken with an Olympus LEXT OLS4000 are presented in Fig. 1.

Table 1 List of surfaces with their surface area fractions, ϕ and equilibrium (θ_app), advancing (θ_adv) and receding (θ_rec) contact angles. Contact angles of each surface were measured five times and the mean values and the standard deviations are presented

Name	ϕ	θ app (deg)	θ adv (deg)	θ rec (deg)
Sq-5-5	0.250	148 ± 1.6	163 ± 0.2	116 ± 5.0
Sq-5-20	0.040	163 ± 0.5	171 ± 0.3	148 ± 0.5
Sq-5-40	0.012	167 ± 0.7	170 ± 0.6	160 ± 1.3
Sq-5-80	0.003	169 ± 0.8	169 ± 1.0	164 ± 1.8
Sq-10-5	0.444	151 ± 1.0	165 ± 2.1	118 ± 3.4
Sq-10-20	0.111	154 ± 0.8	171 ± 0.5	132 ± 2.1
Sq-10-40	0.040	164 ± 1.0	172 ± 1.6	147 ± 1.3
Sq-10-80	0.012	166 ± 0.5	170 ± 1.4	152 ± 1.2
Sq-20-20	0.250	150 ± 1.1	165 ± 2.3	123 ± 3.2
Sq-20-40	0.111	155 ± 0.9	169 ± 0.9	136 ± 1.9
Sq-20-80	0.040	163 ± 0.8	169 ± 1.0	145 ± 2.3
Ci-5-5	0.349	151 ± 1.3	168 ± 3.7	116 ± 2.8
Ci-5-20	0.087	158 ± 1.1	169 ± 0.6	138 ± 1.9
Ci-5-40	0.031	163 ± 2.5	170 ± 1.2	151 ± 1.8

---

Fig. 1 Photographs of (a) Sq-10-40 and (b) Sq-10-20, and (c) 3D scanned topography of the boundary between Sq-10-40 (left) and Sq-10-20 (right).

Experimental setup and procedures

The centre of 10 μL drops of distilled water were placed at the boundary between two surfaces with different ϕ. Drop deposition was carried out using a computer controlled dosing system (KRÜSS DSA100) which was connected to a syringe needle with a 0.51 mm outer diameter. Extra care was taken to deposit drops under the Cassie–Baxter regime. Drop motion was captured by a CCD camera (iDS UI-3060CP with a SONY 2.3 MP sensor) with a resolution and frequency of 6 μm per pixel and 250 Hz, respectively. Subsequently, we analysed the videos to trace the drop motion (position, displacement and velocity) as well as the temporal variations in drop shape using a custom-built Matlab code. Experiments were carried out under atmospheric conditions and repeated at least 10 times for each surface combination to establish reproducibility.

Results and discussion

Drop motion

As a systematic analysis, we examined eleven combinations of the surfaces listed in Table 1 to parametrise the differential surface area fraction Δϕ between 0.009 and 0.441. In all cases, the same trend in motion was observed. Thus, we present the representative case of the boundary between Sq-10-40 (ϕ = 0.040) and Sq-10-20 (ϕ = 0.111) (see Fig. S1, ESI† for the other cases) to comprehend drop behaviour. Fig. 2 shows the motion of a drop placed at the boundary (cyan dashed line). Initial time (t = 0 ms) was set to the frame at which the drop detached from the needle. Once detached, the drop spontaneously moved toward Sq-10-20, which exhibited denser pillars and hence slightly lower θ_app. To follow drop displacement, we track the front, rear and middle contact points, depicted with red, blue and green respectively. These points were plotted as a function of time in Fig. 3, where the non-monotonic drop motion becomes readily apparent. In fact, the drop oscillated vertically resulting in sequential wetting and dewetting events. Hence, Fig. 3 is divided in sequential wetting/dewetting events for clarity. During a wetting event, both sides of the drop spread forming a “pancake” shape, whereas in a dewetting event both sides retracted forming an “egg” shape. The drop advanced mainly during the dewetting event, due to an asymmetric retreat between the front and rear side of the drop. In particular, the rear side of the drop retreated significantly whereas the front one was mostly pinned. On the other hand, the drop spread rather evenly during the wetting event, with imperceptible contribution to the displacement. Similar drop motion has been reported previously; albeit attributed to an imposed vibration which provided the necessary energy to initiate movement.^37,38 In our system, the initial energy required for drop motion was provided from the deformation of the drop during deposition (see the first frame in Fig. 2), however. This deformation led to deviation from the equilibrium state, resulting in excess energy accumulation. At the moment of drop release, the drop shrank in an attempt to minimise its surface area, converting the excess surface free energy into kinetic energy. This will be further discussed in the energy analysis section.

Fig. 2 Sequential snapshots of a 10 μL water drop moving on the boundary between surfaces Sq-10-40 (ϕ = 0.040, left) and Sq-10-20 (ϕ = 0.111, right). Cyan dashed lines represent the boundary between the two surfaces. Red up-triangles, blue down-triangles and green crosses represent the front, rear and middle contact points, respectively.

Fig. 3 Evolution of each contact point (front, rear and middle) over time. The position of the boundary between Sq-10-40 (ϕ = 0.040) and Sq-10-20 (ϕ = 0.111) is set as x = 0 mm. Insets represent typical drop shape during wetting and dewetting events.

Drop velocity vs. Δϕ

Fig. 4 depicts the mean drop velocity (calculated from the mid tracking point) v, as a function of Δϕ, and fast and slow drops can be readily distinguished. The velocities of the faster drops ranged between 5–15 mm s⁻¹ and were related to Δϕ. On the other hand, the velocities of the slower drops, which are highlighted in the boxed area, ranged between 3–5 mm s⁻¹. Nonetheless, we can surmise at present (Fig. 4) the importance of Δϕ on the velocity of the drops, which can be associated with translation of vertical vibration into horizontal motion according to the wettability contrast. The disambiguity between the faster and the slower drops will be probed next.

Fig. 4 Drop velocity v, as a function of differential surface area fraction Δϕ, for a variety of surface combinations, denoted in legend (rear/front).

Effect of contact angle hysteresis

Contact angle hysteresis should be detrimental to drop motion as it results in a stronger pinning of the contact line and should be the underlying reason for the deviating cases in Fig. 4. However, CAH cannot be simply described in terms of ϕ.^41–43 Xu and Choi⁴² proposed as the criterion for a drop to be sticky or slippery the normalised maximal three-phase contact line, δ = pillar perimeter/pillar pitch (for a flat surface, δ = 1). The pinning force per unit length is defined as f_p = σ_LV(cos θ_rec − cos θ_app), where σ_LV denotes the surface tension of the liquid and is plotted as a function of δ in Fig. 5. f_p will be larger than that of a flat surface (dashed line), if δ > 1 and vice versa. f_p of Sq-10-20 (δ = 1.33), Sq-20-40 (δ = 1.33) and Ci-5-20 (δ = 1.05), which were the rear sides of the boxed data in Fig. 4, were found to be larger than the rest and the equivalent flat surface (f_p ∼ 10 mN m⁻¹). It is also noteworthy that drop motion was not instantaneous in these unusual cases, attributable to the stronger f_p retarding drop motion on these surfaces. Consequently, the velocity of the drops increased as a function of Δϕ, provided that the pinning force of the rear surface was sufficiently small (δ < 1).

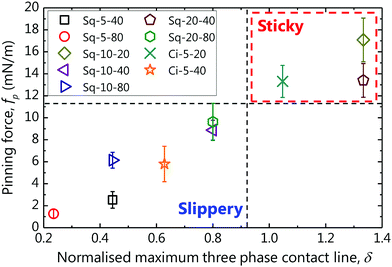Fig. 5 Pinning force f_p, vs. normalised maximal three phase contact line δ, for the rear surfaces. Vertical dashed line at δ = 1 distinguishes between sticky (δ > 1) and slippery (δ < 1) surfaces.

Energy analysis

Let us at this point attempt to elucidate the underlying mechanism of drop motion. An analysis of the surface free energy was carried out as drop motion on wettability (or interfacial energy) contrasts should be governed by energy minimisation. We consider a drop placed at the boundary between two surfaces, Sf A and Sf B with different surface area fractions, i.e. ϕ_A < ϕ_B. The surface free energy G of a drop in contact with a solid surface including the solid–vapour and solid–liquid interfacial tensions, denoted as σ_SV and σ_SL, respectively, can be generally expressed as:^44–46

G = σ_LVA_LV − (σ_SV − σ_SL)A_SL, (2)

where A_LV and A_SL are the liquid–vapour and solid–liquid interfacial areas, respectively. Approximating σ_SV − σ_SL in eqn (2) as σ_LV cos θ_i using Young's relation, yields:

G = σ_LV(A_LV − A_SL cos θ_i). (3)

In the Cassie–Baxter regime, A_LV = A_cap + (1 − ϕ)A_base and A_SL = ϕA_base, where A_cap denotes the surface area of the liquid cap exposed to vapour surroundings and A_base is the apparent base area of the liquid in contact with the pillars and trapped air. Hence, eqn (3) can be rewritten as G = σ_LV{A_cap + (1 − ϕ)A_base − ϕA_base cos θ_i}. Solving eqn (1) as cos θ_i and substituting leads to:^45,46

G = σ_LV(A_cap − A_base cos θ_app). (4)

In Fig. 6, we plot the evolution of G as a function of time for the exemplary case of Sq-10-40/Sq-10-20 (see left column in Fig. S2, ESI† for the rest of the cases). G was found to be maximal at the moment of drop deposition due to large surface deformation (initial state G_ini). Immediately after release, the drop on the wettability contrast shrank rapidly in order to minimise its energy (metastable state, G_meta ≈ 1.62 μJ). Then, the drop started moving toward Sq-10-20. This motion coincided with a minor reduction in the value of G reaching ca. 1.61 μJ around which it oscillated until the drop finally settled in Sq-10-20 (final state).

Fig. 6 Example of the evolution over time of the surface free energy of a drop placed at the boundary between Sq-10-40 (denoted as Sf A, ϕ_A = 0.040) and Sq-10-20 (denoted as Sf B, ϕ_B = 0.111). Insets are snapshots of the drop at each time. The experimental data points are fitted with the exponential decay function (blue line).

Drop motion may be explained by considering the dependence of G on θ_app in eqn (4). θ_app depends on ϕ as shown in Table 1, hence, a drop on a contrast Δϕ will move toward the surface with larger ϕ (lower θ_app) to minimise G. The oscillation may be attributed to shedding of excess free energy during motion and perhaps to the action of contact angle hysteresis (CAH). CAH pins the drop (pinning barrier), resulting in deformation prior to or oscillations during motion.⁴⁷ It is also worth noting that for every case studied, G was found to decay exponentially with time i.e. G(t) = G_plateau + G_inie^−αt as indicated with a blue curve in Fig. 6 (also in the left column of Fig. S2, ESI†). The constant α could perhaps be dependent on the drop size and properties as well as the wetting conditions since the energy variations were apparently related to the oscillatory behaviour of the drop.^48,49

We rationalise the underlying mechanism of drop motion and its spontaneity by calculating energy diagrams and summarizing them in four representative moments for each case studied. Fig. 7 depicts the energy diagram calculated for the exemplary Sq-10-40/Sq-10-20 (denoted as Sf A/Sf B, respectively) system. The energy diagrams for the rest of the cases are included in the right column of Fig. S2 in ESI.† In each diagram, the drop motion process is divided into four representative energy states: initial, metastable, CAH barrier and final. G_A and G_B denote the equilibrium G for a drop resting entirely on Sq-10-40 (Sf A) and Sq-10-20 (Sf B), respectively. We define the metastable energy G_meta to be G_meta = (G_A + G_B)/2 (assuming the drop is resting equally on both sides). G_CAH is the energy of the drop necessary to initiate motion. The G_CAH value should be equivalent to the energy stored in a drop maximally deformed due to CAH before it can move⁴⁷ and the calculation will be defined below. For a drop on a wettability contrast to move, the drop must have sufficient energy to overcome G_CAH; otherwise it should remain at the metastable state. In our experiments, the initial energy G_ini was provided to the drop during deposition via deformation, as shown in the first inset of Fig. 7, and was calculated using eqn (4). G_ini was found to be sufficiently larger than the peak of G_CAH, hence the drop on the wettability contrast, as in the second inset of Fig. 7, should move to the lowest energy state, G_B (red line). The third inset in Fig. 7 shows the final position of the drop in the experiment and corroborates our claim.

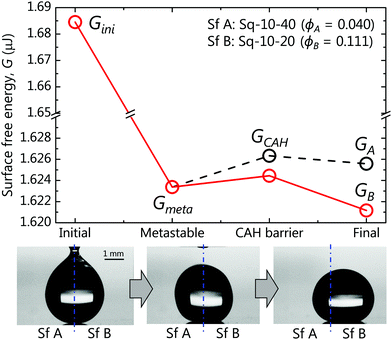Fig. 7 Energy states of the system consisting of Sq-10-40 (denoted as Sf A, ϕ_A = 0.040) and Sq-10-20 (denoted as Sf B, ϕ_B = 0.111).

We should note here that the shape of the drops both at equilibrium and during deformation is complex due to gravitational and CAH effects^47,50,51 and cannot be extracted directly from the images. Hence, we estimate A_cap and A_base for eqn (4) using the open source finite element method solver, Surface Evolver,⁵² which essentially predicts the three-dimensional shape of any drop based on the principle of energy minimisation. To account for the effect of CAH, we incorporated a friction-based algorithm proposed by Santos and White.⁵³ In particular, we simulated the shape of a composite pinned drop, comprising θ_adv in the front of the drop from Sf A and θ_rec in its rear from Sf B (or vice versa for a drop moving the opposite way). θ_adv and θ_rec were experimentally measured on each surface and presented in Table 1.

In Fig. 8, we schematically summarise the underlying mechanism of drop motion on wettability contrasts and the criterion for the direction. Assuming, a system that comprises Sf A and Sf B and ϕ_A < ϕ_B, then three possible energy states arise G_A > G_meta > G_B. Consequently, a drop placed at the wettability contrast will move in order to minimise its energy. As mentioned earlier, however, the drop must traverse the G_CAH peak. Therefore, G_ini ≥ G_CAH is required for drop motion to ensue. The direction of the motion ought to be toward the most energetically favourable state, G_B.

Fig. 8 Schematic illustration of proposed surface-energy-based mechanism suggesting the direction of motion for a drop at the boundary between two surfaces, Sf A and Sf B with ϕ_A < ϕ_B.

Conclusion

We have conducted a systematic analysis of the influence of surface wettability contrast on drop mobility. Millimetre-sized water drops were placed at the boundary between two surfaces with different surface area fractions ϕ, and hence different associated wettabilities. We observed spontaneous motion of the drop, with an oscillatory behaviour, toward the more hydrophilic (denser pillars) surfaces. Drop velocity increased (v ≈ 5–15 mm s⁻¹) as a function of differential surface area fraction (Δϕ = 0.009–0.441) as long as the surface on the rear side had sufficiently small contact angle hysteresis. Otherwise, the motion decelerated significantly regardless of Δϕ. We conducted energy analysis of the system and found the drop motion to be driven by minimisation of surface free energy. We then proposed a universal mechanism capable of predicting the criterion for spontaneous motion of drops on wettability contrasts. Our findings will inform the design of several future microfluidic devices used in applications such as chemical mixing or bio-sensing.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We gratefully acknowledge Dr Prashant Valluri of the University of Edinburgh for his suggestions for the energy analysis. The surface coatings used in this work were provided by MEMSstar Ltd. This work was supported by the Japan Society for the Promotion of Science (JSPS) KAKENHI Grant Number 17J05137.

References

1. S.-Y. Teh, R. Lin, L.-H. Hung and A. P. Lee, Lab Chip, 2008, 8, 198–220.
2. C.-G. Yang, Z.-R. Xu and J.-H. Wang, Trends Anal. Chem., 2010, 29, 141–157.
3. R. Seemann, M. Brinkmann, T. Pfohl and S. Herminghaus, Rep. Prog. Phys., 2012, 75, 016601.
4. J. L. Garcia-Cordero and Z. H. Fan, Lab Chip, 2017, 17, 2150–2166.
5. R. Blossey, Nat. Mater., 2003, 2, 301–306.
6. V. A. Ganesh, H. K. Raut, A. S. Nair and S. Ramakrishna, J. Mater. Chem., 2011, 21, 16304–16322.
7. S. Nishimoto and B. Bhushan, RSC Adv., 2013, 3, 671–690.
8. K. Golovin, D. H. Lee, J. M. Mabry and A. Tuteja, Angew. Chem., Int. Ed., 2013, 52, 13007–13011.
9. Y. Lu, S. Sathasivam, J. Song, C. R. Crick, C. J. Carmalt and I. P. Parkin, Science, 2015, 347, 1132–1135.
10. L. Cao, A. K. Jones, V. K. Sikka, J. Wu and D. Gao, Langmuir, 2009, 25, 12444–12448.
11. L. Mishchenko, B. Hatton, V. Bahadur, J. A. Taylor, T. Krupenkin and J. Aizenberg, ACS Nano, 2010, 4, 7699–7707.
12. P. Guo, Y. Zheng, M. Wen, C. Song, Y. Lin and L. Jiang, Adv. Mater., 2012, 24, 2642–2648.
13. J. Lv, Y. Song, L. Jiang and J. Wang, ACS Nano, 2014, 8, 3152–3169.
14. S. Daniel, M. K. Chaudhury and J. C. Chen, Science, 2001, 291, 633–636.
15. N. Miljkovic and E. N. Wang, MRS Bull., 2013, 38, 397–406.
16. D. Orejon, O. Shardt, P. R. Waghmare, N. S. Kumar Gunda, Y. Takata and S. K. Mitra, RSC Adv., 2016, 6, 36698–36704.
17. X. Qu, J. B. Boreyko, F. Liu, R. L. Agapov, N. V. Lavrik, S. T. Retterer, J. J. Feng, C. P. Collier and C.-H. Chen, Appl. Phys. Lett., 2015, 106, 221601.
18. F. Brochard, Langmuir, 1989, 5, 432–438.
19. R. S. Subramanian, N. Moumen and J. B. McLaughlin, Langmuir, 2005, 21, 11844–11849.
20. S. Lach, S. M. Yoon and B. A. Grzybowski, Chem. Soc. Rev., 2016, 45, 4766–4796.
21. M. K. Chaudhury and G. M. Whitesides, Science, 1992, 256, 1539–1541.
22. I. Lagzi, S. Soh, P. J. Wesson, K. P. Browne and B. A. Grzybowski, J. Am. Chem. Soc., 2010, 132, 1198–1199.
23. S. C. Hernández, C. J. C. Bennett, C. E. Junkermeier, S. D. Tsoi, F. J. Bezares, R. Stine, J. T. Robinson, E. H. Lock, D. R. Boris, B. D. Pate, J. D. Caldwell, T. L. Reinecke, P. E. Sheehan and S. G. Walton, ACS Nano, 2013, 7, 4746–4755.
24. Q. Liu and B. Xu, Langmuir, 2015, 31, 9070–9075.
25. C. Song, K. Kim, K. Lee and H. K. Pak, Appl. Phys. Lett., 2008, 93, 084102.
26. Y. Zhao, F. Liu and C.-H. Chen, Appl. Phys. Lett., 2011, 99, 104101.
27. G. Karapetsas, K. C. Sahu, K. Sefiane and O. K. Matar, Langmuir, 2014, 30, 4310–4321.
28. N. Bjelobrk, H.-L. Girard, S. Bengaluru Subramanyam, H.-M. Kwon, D. Quéré and K. K. Varanasi, Phys. Rev. Fluids, 2016, 1, 063902.
29. M. G. Pollack, A. D. Shenderov and R. B. Fair, Lab Chip, 2002, 2, 96–101.
30. S. K. Cho, H. Moon and C.-J. Kim, J. Microelectromech. Syst., 2003, 12, 70–80.
31. F. Mugele and J.-C. Baret, J. Phys.: Condens. Matter, 2005, 17, 705–774.
32. M.-C. Liu, J.-G. Wu, M.-F. Tsai, W.-S. Yu, P.-C. Lin, I.-C. Chiu, H.-A. Chin, I.-C. Cheng, Y.-C. Tung and J.-Z. Chen, RSC Adv., 2012, 2, 1639–1642.
33. R. N. Wenzel, Ind. Eng. Chem., 1936, 28, 988–994.
34. A. B. D. Cassie and S. Baxter, Trans. Faraday Soc., 1944, 40, 546–551.
35. L. Mahadevan, Nature, 2001, 411, 895–896.
36. D. Quéré, Nat. Mater., 2002, 1, 14–15.
37. A. Shastry, M. J. Case and K. F. Böhringer, Langmuir, 2006, 22, 6161–6167.
38. M. Reyssat, F. Pardo and D. Quéré, Europhys. Lett., 2009, 87, 36003.
39. G. McHale, S. J. Elliott, M. I. Newton and N. J. Shirtcliffe, in Contact Angle, Wettability and Adhesion, ed. K. L. Mittal, Koninklijke Brill NV, Leiden, 2009, vol. 6, pp. 219–233.
40. N. Moradi, F. Varnik and I. Steinbach, Europhys. Lett., 2010, 89, 26006.
41. M. Reyssat and D. Quéré, J. Phys. Chem. B, 2009, 113, 3906–3909.
42. W. Xu and C.-H. Choi, Phys. Rev. Lett., 2012, 109, 024504.
43. R. Raj, R. Enright, Y. Zhu, S. Adera and E. N. Wang, Langmuir, 2012, 28, 15777–15788.
44. M. E. R. Shanahan, Langmuir, 1995, 11, 1041–1043.
45. N. A. Patankar, Langmuir, 2003, 19, 1249–1253.
46. Y. Y. Yan, N. Gao and W. Barthlott, Adv. Colloid Interface Sci., 2011, 169, 80–105.
47. L. Gao and T. J. McCarthy, Langmuir, 2006, 22, 6234–6237.
48. S. Chandrasekhar, Proc. London Math. Soc., 1959, s3-9, 141–149.
49. T.-V. Nguyen, M.-D. Nguyen, H. Takahashi, K. Matsumoto and I. Shimoyama, Lab Chip, 2015, 15, 3670–3676.
50. C. W. Extrand and S. I. Moon, Langmuir, 2010, 26, 17090–17099.
51. J. Park, J. Park, H. Lim and H.-Y. Kim, Phys. Fluids, 2013, 25, 022102.
52. K. A. Brakke, Exp. Math., 1992, 1, 141–165.
53. M. J. Santos and J. A. White, Langmuir, 2011, 27, 14868–14875.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c8sm01762j

---