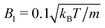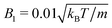Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Clustering of microswimmers: interplay of shape and hydrodynamics†
Mario
Theers
a,
Elmar
Westphal
b,
Kai
Qi
a,
Roland G.
Winkler
 a and
Gerhard
Gompper
a and
Gerhard
Gompper
 a
a
aTheoretical Soft Matter and Biophysics, Institute for Advanced Simulation and Institute of Complex Systems, Forschungszentrum Jülich, D-52425 Jülich, Germany. E-mail: r.winkler@fz-juelich.de; g.gompper@fz-juelich.de
bPeter Grünberg Institute and Jülich Centre for Neutron Science, Forschungszentrum Jülich, D-52425 Jülich, Germany. E-mail: e.westphal@fz-juelich.de
First published on 19th October 2018
Abstract
The spatiotemporal dynamics in systems of active self-propelled particles is controlled by the propulsion mechanism in combination with various direct interactions, such as steric repulsion and hydrodynamics. These direct interactions are typically anisotropic, and come in different “flavors”, such as spherical and elongated particle shapes, pusher and puller flow fields, etc. The combination of the various aspects is expected to lead to new emergent behavior. However, it is a priori not evident whether shape and hydrodynamics act synergistically or antagonistically to generate motility-induced clustering (MIC) and phase separation (MIPS). We employ a model of prolate spheroidal microswimmers—called squirmers—in quasi-two-dimensional confinement to address this issue by mesoscale hydrodynamic simulations. For comparison, non-hydrodynamic active Brownian particles (ABPs) are considered to elucidate the contribution of hydrodynamic interactions. For spherical particles, the comparison between ABPs and hydrodynamic-squirmer ensembles reveals a suppression of MIPS due to hydrodynamic interactions. Yet, our analysis shows that dynamic clusters exist, with a broad size distribution. The fundamental difference between ABPs and squirmers is attributed to an increased reorientation of squirmers by hydrodynamic torques during their collisions. In contrast, for elongated squirmers, hydrodynamics interactions enhance MIPS. The transition to a phase-separated state strongly depends on the nature of the swimmer's flow field—with an increased tendency toward MIPS for pullers, and a reduced tendency for pushers. Thus, hydrodynamic interactions show opposing effects on MIPS for spherical and elongated microswimmers, and details of the propulsion mechanism of biological microswimmers may be very important to determine their collective behavior.
1 Introduction
Motile bacteria at interfaces exhibit intriguing collective phenomena,1,2 such as cluster formation, observed for Myxococcus xanthus3 or Thiovulum majus,4 as well as swarming, swirling, raft formation,5–10 and the emergence of mesoscale turbulence,8,11,12 observed for E. coli13 or Bacillus subtilis.14 Similarly, experiments on self-phoretic artificial spherical microswimmers, such as Janus particles, self-propelled liquid droplets, and photo-activated colloids, exhibit cluster formation and phase separation despite their isotropic shape and purely repulsive interactions.15–21 The various active agents are propelled by different mechanisms and may exhibit different steric and propulsion-related interactions. Hence, it is a priori not evident which processes govern structure formation in the rather distinct systems. Unravelling the underlying universal features and discriminating them from specific aspects requires dedicated experimental and theoretical studies.Computer simulations of model systems, such as spherical active Brownian particles (ABPs), yield motility-induced clustering (MIC) and motility-induced phase separation (MIPS)20,22–27 in qualitative agreement with the above-mentioned experiments on synthetic self-phoretic particles. The intuitive explanation for the emergence of MIC and MIPS is a positive feedback between blocking of persistent particle motion by steric interactions, and an enhanced probability of collisions with further particles at sufficiently large concentrations and activities.21,28,29 However, in self-phoretic systems, the phoretic field has been shown to significantly contribute to clustering through field-induced attractive interactions.30,31
Cluster formation, swarming, and mesoscale turbulence of anisotropic objects such as bacteria are explained by steric interaction-induced alignment. Computer simulations of two-dimensional assemblies of rods suggest that the interplay of rod geometry, self-propulsion, and steric interaction suffices to facilitate aggregation into clusters3,32–34 and even leads to swarming and turbulence.12,13
Aside from steric, other interaction mechanisms between active particles are present, evidently and most prominently fluid-mediated interactions, since motile bacteria and phoretic microswimmers propel themselves via the embedding fluid. Hence, a crucial aspect regarding MIC and MIPS of microswimmers is the role of hydrodynamics. At equilibrium, hydrodynamic interactions (HI) solely affect the dynamics and not the structural properties of a system. Since active systems are intrinsically out of equilibrium, this does not necessarily apply, and the steady-state—and hence the formation of clusters—is strongly affected by hydrodynamics.28,35–38 Furthermore, the particular geometry of a microswimmer, such as the cell body and the flagellum or the flagella bundle of bacteria, may lead to a coupling of the orientational dynamics and fluid flow; such a coupling can lead to mesoscale turbulence.39,40
The phase behavior of active particles in the presence of hydrodynamic interactions has received much less attention than ABPs. In simulations, this is largely due to the substantial computational challenges posed by hydrodynamics. Specifically, the long-ranged flow field created by the swimmers has to be accounted for adequately. In experiments, HI are difficult to switch off, and therefore their contribution is hard to assess. In contrast, simulations can be performed with and without HI and the latter effect on MIPS can be analyzed, although with an increased numerical effort.
A frequently applied model for a self-propelled particle in the presence of a fluid is a squirmer35,41–46—a spheroidal colloid with a prescribed slip velocity on its surface. It was originally introduced to describe ciliated microswimmers such as Paramecia and Volvox. Nowadays, it is applied to a broad class of microswimmers, both biological as well as synthetic ones. A squirmer is typically characterized by two modes accounting for its swimming velocity and its active stress. The latter distinguishes between pushers (e.g., E. coli, sperm), pullers (e.g., Chlamydomonas), and neutral squirmers (e.g., Paramecium).46
In order to shed light onto the importance of hydrodynamics for structure formation in active systems, we perform mesoscale hydrodynamic simulations applying the multiparticle collision (MPC) dynamics approach, a particle-based hydrodynamic simulation method to solve the Navier–Stokes equations.47–49 Specifically, we consider squirmers confined in a thin slit, i.e., in a quasi-2D geometry. Here, we want to address and clarify several issues. On the one hand, we want to resolve the contradiction between ref. 35 and 28, which predict enhanced clustering of spherical squirmers or no MIPS in the presence of HI, respectively. On the other hand, we consider squirmers of prolate spheroidal shape. This is motivated by the different mechanisms of cluster formation for spherical and elongated particles (blocking vs. alignment). Thus, the effect of hydrodynamic interactions on the collective behavior of spherical swimmers can be qualitatively different as compared to swimmers with elongated shapes.
As an important result, we find no MIPS for spherical squirmers in the quasi-2D system, which is in agreement with ref. 28 and 38, but in contrast to ref. 35. We attribute the discrepancy to peculiarities of the compressible MPC fluid employed in ref. 35, which requires a suitable choice of the parameters for simulations of low-compressibility fluids. Hence, HI suppress cluster formation and MIPS of self-propelled spherical squirmers compared to ABPs. Interestingly, the opposite is true for spheroidal squirmers with sufficiently large aspect ratios, where we find a substantial enhancement of MIPS through HI. This applies for pushers, pullers, and neutral squirmers, as long as the force dipole is sufficiently weak. In the case of large force dipoles, pushers show the least tendency to phase separate, with even ABPs exhibiting stronger cluster formation. A density–aspect-ratio phase diagram for moderate force dipole strength shows most pronounced phase separation for pullers, followed by neutral squirmers, pushers, and finally ABPs. Thus, the effects of shape and hydrodynamics are highly non-additive, and act sometimes synergistically, and sometimes antagonistically.
The paper is structured as follows. Previous results of squirmer simulations of collective phenomena are briefly summarized in Section 2. Section 3 introduces the model for prolate squirmers. A comparison between MPC and ABP simulation results of spherical squirmers is presented in Section 4. Section 5 presents results for prolate spheroidal swimmers, and Section 6 discusses the various obtained aspects. Section 7 summarizes our results. Appendix A presents the simulation approach for the fluid (MPC) (A.1), the coupling of a squirmer with the fluid (A.2), and the simulation method for ABPs (A.3). Appendix B collects definitions relevant to rigid-body dynamics of ABPs, and Appendix C discusses technical aspects of fluid compressibility in particle-based simulations of squirmers.
2 Collective behavior of squirmers—brief summary of previous simulation studies
The dynamics of spheroidal squirmers in two dimensions (2D) and in a three-dimensional slit geometry (quasi-2D) has been studied and compared with ABPs in ref. 28 and 38, and ref. 35 and 50, respectively. In ref. 28, the squirmer dynamics is strictly two dimensional, but embedded in a 3D fluid. The shape of the squirmers is changed from infinitely long cylinders (perpendicular to the 2D plane), corresponding to 2D HI, to highly flattened cylinders with 3D HI. Independent of the cylinder length (and dimensionality of HI), the simulation studies show no evidence of phase separation, in contrast to comparable simulations of ABPs. The qualitatively different behavior is attributed to a faster decorrelation of the squirmer's swimming direction due to HI compared to the configuration-independent rotational diffusion of ABPs. The studies of ref. 38 emphasize the importance of near-field HI in the suppression of MIPS. However, clustering of the squirmers is observed as well as the formation of polar order for nearly neutral squirmers. Note that in both ref. 28 and 38, thermal fluctuations are neglected. Hence, there is no thermal rotational diffusion leading to a decorrelation of the squirmer's orientational motion. In the simulations of ref. 35 and 50, squirmers are confined in a narrow slit (quasi-2D), slightly wider than their diameter, which captures the geometry of experiments, where glass plates are used for confinement, and thermal fluctuations are taken into account. Here, the swimming direction is free to orient in three dimensions, and hydrodynamics is screened and decays as 1/ρ2 parallel to the confining surfaces in the slit center, where ρ is the radial distance from the squirmer.51 Most importantly, hydrodynamics is argued to enhance MIPS, in contrast to findings of ref. 28 and 38, and a phase diagram is presented in ref. 50.A quasi-2D setup is certainly less favorable for cluster formation of ABPs compared to a strict 2D system,24,52 since the swimmer's propulsion direction can point toward a wall, which reduces steric blocking and the lateral swim pressure.53–55 Thus, compared to strictly 2D ABP systems, ABPs in quasi-2D require higher Péclet numbers and packing fractions to form clusters, and those clusters exhibit a finite life time. Surface hydrodynamic interactions may lead to preferred squirmer orientations. Here, considerations based on far-field HI predict a parallel alignment of the propulsion direction for pushers and a normal orientation for pullers at a no-slip surface.56 Hence, quasi-2D confinement may result in a different behavior, and near-field effects (specifically with the confining walls) might be important for cluster formation as indicated by the studies of ref. 35 and 46.
For suspensions of athermal spherical squirmers in 3D, lattice-Boltzmann57 and force-coupling36 simulations have also found a pronounced polar order for pullers and neutral squirmers and clustering over a certain range of force-dipole strengths. However, no large-scale MIPS is observed. In contrast, ABPs in 3D clearly exhibit MIPS25–27 and large-scale collective motion.25 Moreover, simulations of 2D, quasi-2D, and 3D systems of attractive squirmers show a substantially enhanced cluster formation compared to purely repulsive squirmers.36,37 Also in such situations, hydrodynamics is found to reduce MIPS compared to ABPs.
So far, the influence of HI on MIPS has mainly been studied for spherical squirmers. In contrast, very little is known about the influence of HI on the structure and dynamics of elongated spheroidal squirmers confined in narrow slits. Here, the shape, squirmer–squirmer HI, and HI with the confining surfaces affect cluster formation and a possible MIC and MIPS.46
3 Model and simulation approach
We model a nonspherical squirmer as a prolate spheroidal rigid body with the prescribed surface velocity (cf.Fig. 1)46| usq = −B1(eζ·ez)(1 + βζ)eζ, | (1) |
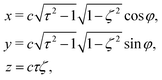 | (2) |
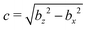 , −1 ≤ ζ ≤ 1, 1 ≤ τ < ∞, and 0 ≤ φ ≤ 2π. The advantage of the choice (1) for the slip velocity is that an analytical solution of the flow field can be obtained.46 Constant B1 in eqn (1) determines the amplitude of the slip velocity and is related to the self-propulsion velocity U0via46
, −1 ≤ ζ ≤ 1, 1 ≤ τ < ∞, and 0 ≤ φ ≤ 2π. The advantage of the choice (1) for the slip velocity is that an analytical solution of the flow field can be obtained.46 Constant B1 in eqn (1) determines the amplitude of the slip velocity and is related to the self-propulsion velocity U0via46| U0 = B1τ0(τ0 − (τ02 − 1)coth−1τ0), | (3) |
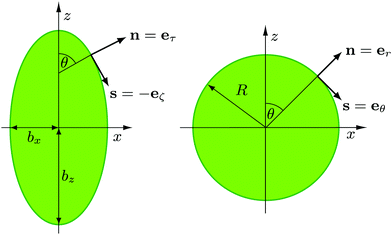 | ||
| Fig. 1 Illustration of normal and tangent vectors of a spheroidal (left) and spherical (right) squirmer. Self-propulsion along the body-fixed orientation vector e, here e = (0,0,1)T, is achieved by an axisymmetric prescribed surface velocity in the direction of the tangent vector s.46 | ||
We consider the collective dynamics of squirmers confined in a narrow slit of dimensions L × Ly × L (cf.Fig. 2), where the ratio of the squirmer minor axis and the width of the slit are 2bx/Ly = 6/7, i.e., we focus on a quasi-2D geometry.
The squirmers are embedded in a fluid, which we simulate by multiparticle collision (MPC) dynamics, a mesoscale hydrodynamics simulation approach.47–49 The details of the algorithm are described in Appendix A.1, and the implementation of the squirmer and the coupling with MPC in Appendix A.2.
For comparison, we perform simulations of active Brownian spheres and spheroids. The respective simulation approach is described in Appendix A.3.
4 Simulations—spherical squirmers
In the first step, we analyze the influence of HI on the phase behavior of spherical squirmers. The phase diagram for ABPs in two dimensions23,26,52 shows a pronounced regime of MIPS above a certain Péclet number and a broadening range of densities with increasing Péclet numbers. Here, we consider two activities for ABPs and squirmers, respectively, and various densities within the phase separated regime. In order to provide a convincing and comprehensive characterization, we discuss various structural properties.4.1 System setup and parameters
We consider two setups for the study of spherical swimmers, with different packing fractions and propulsion velocities. Common to both cases is the number of swimmers, Nsw = 196, the radius of the squirmer, R = 3a, the width of the slit, Ly = 7a, and the active-stress parameter, β ∈ {−1,0,1}.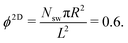 | (4) |
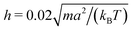 and the mean number of particles in a cell 〈Nc〉 = 80, which yields a fluid viscosity of
and the mean number of particles in a cell 〈Nc〉 = 80, which yields a fluid viscosity of 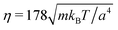 , as determined by independent simulations.62 The resulting Péclet number, which compares the time scale for rotational diffusion, 2DR (DR is the rotational diffusion coefficient), to the swimming time scale, 2R/U0, is
, as determined by independent simulations.62 The resulting Péclet number, which compares the time scale for rotational diffusion, 2DR (DR is the rotational diffusion coefficient), to the swimming time scale, 2R/U0, is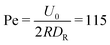 | (5) |
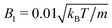 , and
, and 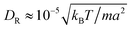 from simulations. The latter is approximately 20% larger than the theoretical value. The chosen value of 〈Nc〉 = 80 is large compared to typical MPC studies, and results in an increased computational effort. However, it leads to a high viscosity, hence, a low DR and a high Péclet number, a prerequisite to observe cluster formation in ABPs, as well as a low fluid compressibility. In ref. 63, a high Péclet number was achieved by a large B1 and hence U0. However, we find that such high values of B1 lead to fluid-density inhomogeneities and consequently simulation artifacts (see Appendix C). Complementary to the squirmer simulations with MPC, we perform ABP simulations with the same values for U0, DR, R, and Ly, but consider additionally the larger system size L = 192a in order to reduce finite-size effects.
from simulations. The latter is approximately 20% larger than the theoretical value. The chosen value of 〈Nc〉 = 80 is large compared to typical MPC studies, and results in an increased computational effort. However, it leads to a high viscosity, hence, a low DR and a high Péclet number, a prerequisite to observe cluster formation in ABPs, as well as a low fluid compressibility. In ref. 63, a high Péclet number was achieved by a large B1 and hence U0. However, we find that such high values of B1 lead to fluid-density inhomogeneities and consequently simulation artifacts (see Appendix C). Complementary to the squirmer simulations with MPC, we perform ABP simulations with the same values for U0, DR, R, and Ly, but consider additionally the larger system size L = 192a in order to reduce finite-size effects.
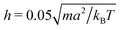 and 〈Nc〉 = 480 result in a high viscosity
and 〈Nc〉 = 480 result in a high viscosity 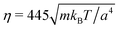 and, with
and, with 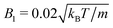 , the high Péclet number Pe = 575.
, the high Péclet number Pe = 575.
4.2 Results
Fig. 3 displays snapshots of structures of spherical ABPs and squirmers for the parameter Set 1. The ABP system exhibits strong clustering and a hexagonal order, whereas no large clusters and no pronounced order emerge for neutral squirmers. Hence, hydrodynamics strongly affects the aggregation behavior.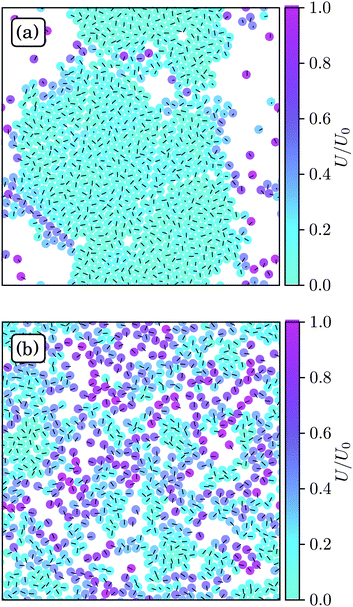 | ||
| Fig. 3 Snapshots of spherical squirmers at Pe = 115, the packing fraction ϕ2D = 0.6, and the simulation box length L = 192a. (a) Active Brownian particles exhibit MIPS and a local hexagonal order. (b) Neutral squirmers (β = 0) exhibit no long-range order and no MIPS. Note that the cluster in (a) partly dissolves in the course of time and a new system-spanning cluster is formed subsequently. Similarly, the clusters in (b) are unstable. See the ESI† for movies of the two cases (M1 and M2). | ||
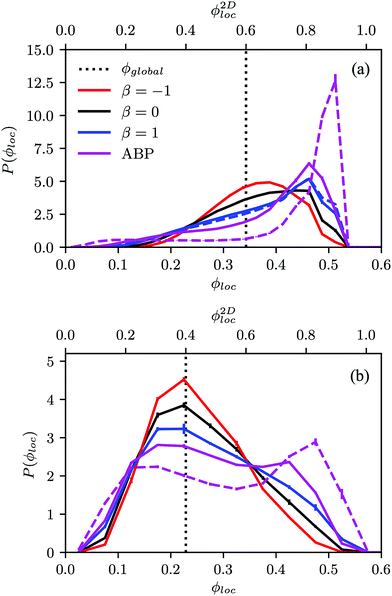
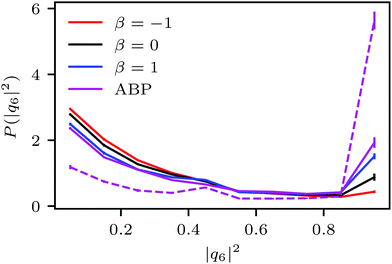
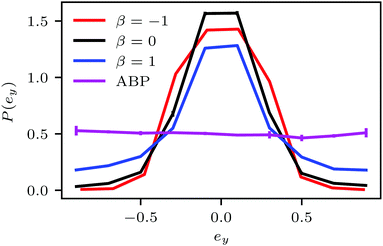
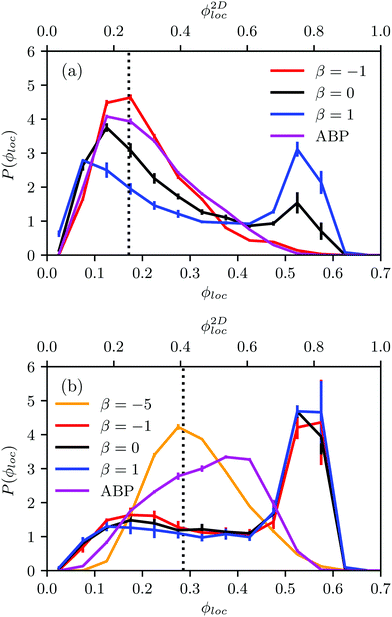
Fig. 4(a) shows distributions of local packing fractions for squirmers and ABPs at Pe = 115 (parameter set 1). We consider two system sizes for the ABPs and pullers (β = 1), namely L = 96a and L = 192a, to provide clear evidence of a possible MIPS. The ABP system exhibits pronounced peaks at the packing fractions ϕ2Dloc ≈ 0.8 (L/a = 96, solid) and ϕ2Dloc ≈ 0.85 (L/a = 192, dashed), respectively, close to the maximum value of ϕ2D = 0.907 of 2D hexagonal packing, and lower probabilities for dilute regions. The two curves reflect a strong system-size dependence, as is well-known for first-order phase transitions, because the system is affected by interfaces.65 Accordingly, and in agreement with previous simulations,22–24,52 our ABP system phase separates into a dense giant cluster comprising the vast majority of the ABPs (cf.Fig. 5) and a dilute gas-like region. In contrast, squirmers show a far less pronounced high-density region. Most remarkably, the distribution function P(ϕloc) is independent of the system size, as indicated in Fig. 4(a) for pullers, which we consider as an indication that squirmers exhibit no MIPS. The force dipole evidently strongly affects cluster formation as is reflected by the differences of the distribution functions. Therefore, pulling (β = 1) promotes the formation of larger clusters, whereas pushing (β = −1) is a disadvantage for cluster formation.
At the lower packing fraction ϕ2D = 0.4 and the high Péclet number Pe = 575 (parameter set 2) (Fig. 4(b)), ABPs exhibit a two-peak distribution, which becomes more pronounced with an increasing system size, and the peaks shift to smaller and larger concentrations, respectively, as expected for a first order phase transition, indicating a MIPS in the limit L→∞. For the squirmers, the maximum of the local density for pullers and neutral squirmers coincides with the global density ϕ2D = 0.4. However, for pullers a long tail toward higher local densities indicates the formation of large temporary clusters (MIC). Considering the higher packing fraction ϕ2D = 0.6 for Pe = 575, we find little differences in the density distributions of Fig. 4(a).
![[scr N, script letter N]](https://www.rsc.org/images/entities/char_e52d.gif) (n), which is defined as
(n), which is defined as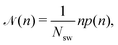 | (6) |
![[scr N, script letter N]](https://www.rsc.org/images/entities/char_e52d.gif) (n) is the average fraction of particles that are members of a cluster of size n, and p(n) is the number of clusters of size n. The distribution is normalized such that
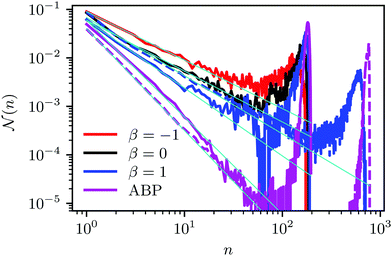
(n) is the average fraction of particles that are members of a cluster of size n, and p(n) is the number of clusters of size n. The distribution is normalized such that 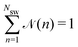 . We use a distance criterion to define a cluster: a swimmer belongs to a cluster, when its center-to-center distance to another swimmer of the cluster is within 1.02σ. As shown in Fig. 5, predominately smaller clusters are formed for squirmers. However, ABPs exhibit a peak for clusters comprising almost all swimmers, consistent with MIPS. This is particularly evident for the larger system size. With increasing system size, the probability for intermediate-size clusters drops significantly and
. We use a distance criterion to define a cluster: a swimmer belongs to a cluster, when its center-to-center distance to another swimmer of the cluster is within 1.02σ. As shown in Fig. 5, predominately smaller clusters are formed for squirmers. However, ABPs exhibit a peak for clusters comprising almost all swimmers, consistent with MIPS. This is particularly evident for the larger system size. With increasing system size, the probability for intermediate-size clusters drops significantly and ![[scr N, script letter N]](https://www.rsc.org/images/entities/char_e52d.gif) (n) is dominated by small and giant clusters. However, the initial power-law decay of
(n) is dominated by small and giant clusters. However, the initial power-law decay of ![[scr N, script letter N]](https://www.rsc.org/images/entities/char_e52d.gif) (n) changes only slightly from
(n) changes only slightly from ![[scr N, script letter N]](https://www.rsc.org/images/entities/char_e52d.gif) (n)ABP ∼ n−2.0 for L = 96a to
(n)ABP ∼ n−2.0 for L = 96a to ![[scr N, script letter N]](https://www.rsc.org/images/entities/char_e52d.gif) (n)ABP ∼ n−2.1 for L = 192a. For larger systems, we expect an even more pronounced giant cluster consistent with the appearance of MIPS.52 Compared to ABPs, squirmers exhibit a higher probability for medium-size clusters in the range 2 < n ≲ 150. The cluster-size distributions decay in a power-law manner for n ≲ 30, where, pushers exhibit the slowest decay with
(n)ABP ∼ n−2.1 for L = 192a. For larger systems, we expect an even more pronounced giant cluster consistent with the appearance of MIPS.52 Compared to ABPs, squirmers exhibit a higher probability for medium-size clusters in the range 2 < n ≲ 150. The cluster-size distributions decay in a power-law manner for n ≲ 30, where, pushers exhibit the slowest decay with ![[scr N, script letter N]](https://www.rsc.org/images/entities/char_e52d.gif) (n) ∼ n−1.0, and pullers the somewhat fastest decay
(n) ∼ n−1.0, and pullers the somewhat fastest decay ![[scr N, script letter N]](https://www.rsc.org/images/entities/char_e52d.gif) (n) ∼ n−1.4. This power-law decrease of
(n) ∼ n−1.4. This power-law decrease of ![[scr N, script letter N]](https://www.rsc.org/images/entities/char_e52d.gif) (n) is independent of the system size. The qualitative and quantitative behavior changes when the concentration is reduced (not shown). For ϕ2D = 0.4, all systems exhibit an initial power-law decay
(n) is independent of the system size. The qualitative and quantitative behavior changes when the concentration is reduced (not shown). For ϕ2D = 0.4, all systems exhibit an initial power-law decay ![[scr N, script letter N]](https://www.rsc.org/images/entities/char_e52d.gif) (n) ∼ n−1 and no system-spanning cluster appears. However, pushers and neutral squirmers show a stronger, non-power-law decay for large cluster sizes. Hence, there is a crossover from a power-law to a faster decay of the cluster-size distribution function with decreasing concentration for β ≤ 0. A similar behavior has been observed in ref. 37.
(n) ∼ n−1 and no system-spanning cluster appears. However, pushers and neutral squirmers show a stronger, non-power-law decay for large cluster sizes. Hence, there is a crossover from a power-law to a faster decay of the cluster-size distribution function with decreasing concentration for β ≤ 0. A similar behavior has been observed in ref. 37.
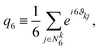 | (7) |
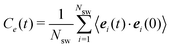 | (8) |
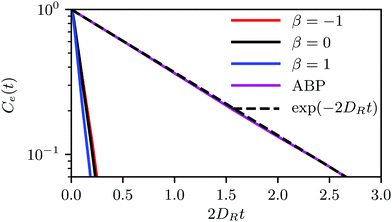
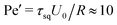 , a value, where no phase transition is expected even for ABPs. However, the differences in the tendency of the squirmers to form clusters (cf.Fig. 4(a)) indicate the importance of hydrodynamic interactions, which are not captured in the Péclet number calculated on the basis of the rotational diffusion coefficient at infinite dilution.
, a value, where no phase transition is expected even for ABPs. However, the differences in the tendency of the squirmers to form clusters (cf.Fig. 4(a)) indicate the importance of hydrodynamic interactions, which are not captured in the Péclet number calculated on the basis of the rotational diffusion coefficient at infinite dilution.
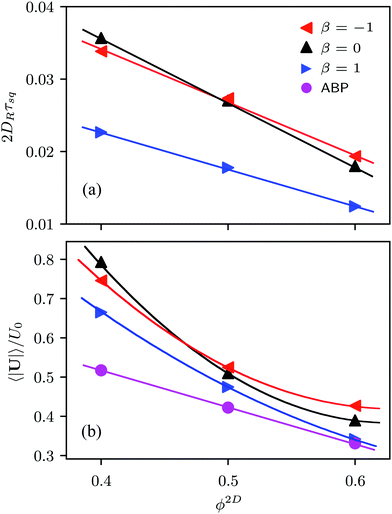
The relaxation time τsq depends on the squirmer concentration, as shown in Fig. 10(a) for Pe = 575. Compared to ABPs, the τsq of squirmers is reduced by orders of magnitude (factor 50–80) and decreases almost linearly in the considered range of concentrations (for Pe = 115, 2DRτsq ≈ 0.1 (cf.Fig. 9)). Naturally, τsq will increase in a nonlinear manner for ϕ2D → 0, because at ϕ2D = 0, 2DRτsq = 1. In addition, the average swimming velocity 〈|U|〉 decreases with increasing concentration, also for ABPs (cf.Fig. 10(b)). The velocity for ABPs seems to decrease linearly, whereas those of the various squirmers decline nonlinearly. A decreasing swimming velocity and relaxation time with increasing areal fraction have also been found in ref. 28 for strictly 2D systems.
5 Simulations—spheroidal squirmers
To elucidate the influence of HI on the phase behavior of spheroidal squirmers, we focus on the Péclet number Pe = 12 and packing fractions 0.4 ≤ ϕ2D ≤ 0.6. For this Péclet number and densities, spherical ABPs are far from a phase transition and in the fluid-like regime.52 The phase behavior of spheroidal ABPs depends on the aspect ratio; no systematic studies to obtain a phase diagram have been performed so far.5.1 System setup and parameters
We consider spheroidal squirmers with the minor axis bx = 3a and the aspect ratios bz/bx ∈ {1,1.5,2,3,4} in the quasi-2D geometry described above (see Fig. 2). We employ the MPC time step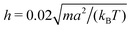 , rotation angle α = 130°, and the mean number of particles 〈Nc〉 = 10, which yields the fluid viscosity
, rotation angle α = 130°, and the mean number of particles 〈Nc〉 = 10, which yields the fluid viscosity 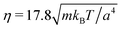 .
.
To investigate the collective behavior for different packing fractions ϕ = 4πNswbx2bz/3L2Ly, or equivalently area packing fractions ϕ2D = Nswπbxbz/L2, the length L of the simulation box is varied, while the number of swimmers is fixed at Nsw = 196 for bz/bx = 1 and Nsw = 200 for all other aspect ratios. We choose the values of the swimming mode 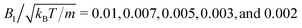 , which yields, with eqn (3), the Péclet number
, which yields, with eqn (3), the Péclet number
| Pe = U0/(2D⊥Rbz) = 12 | (9) |
5.2 Results
Fig. 11 illustrates structure formation for various aspect ratios. Although the Péclet number Pe = 12 is quite low, spheroidal squirmers clearly reveal clusters for all aspect ratios bx/bz ≥ 2. Therefore, a larger aspect ratio is beneficial for cluster formation. For spherical squirmers, no phase separation occurs at this Péclet number (Fig. 11(a)), consistent with the results of ref. 52. The anisotropic nature of the spheroids leads to shape-induced jamming and alignment, where alignment increases with increasing aspect ratio as is evident from the comparison of Fig. 11(b) and (d). | ||
| Fig. 11 Snapshots of the structure of neutral (β = 0) spheroidal squirmers for Pe = 12, the area packing fraction ϕ2D = 0.5, and the aspect ratios (a) bz/bx = 1, (b) 2, (c) 3, and (d) 4. See the ESI† for movies of the various cases (M3–M6). | ||
The probability distribution P(ϕloc) of the local packing fraction is displayed in Fig. 12. No phase separation occurs for ABPs and pushers (β = −1) at the concentration ϕ2Dloc = 0.3 (Fig. 12(a)); however, clusters appear for neutral squirmers (β = 0) and pullers (β = 1). At the higher concentration ϕ2Dloc = 0.5 (Fig. 12(b)), all squirmers with β = 0,±1 exhibit dense clusters. In contrast, spheroidal ABPs exhibit only a weak tendency to form clusters. This points toward a major role of hydrodynamics in cluster formation of elongated squirmers. Simulations of pushers with a strong active stress (β = −5) emphasize this aspect. Here, we find a clear maximum in P(ϕloc) at the average density and, hence, no MIPS. Near-field HI by the stronger flow field lead to a faster reorientation dynamics and, hence, a less pronounced order.
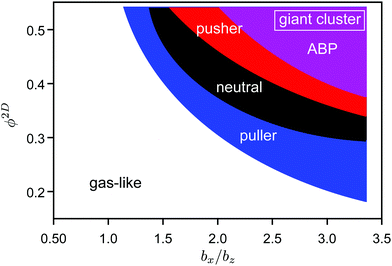 | ||
| Fig. 13 State diagram for squirmers and ABPs at Pe = 12. The blue, black, red, and purple areas indicate giant clusters for pullers (β = 1), neutrals (β = 0), pushers (β = 1), and active Brownian particles, respectively. Therefore clusters of pullers appear in all colored areas, clusters of neutral squirmers in the black, red, and purple area, etc. See the ESI† for individual state diagrams of the various swimmers. | ||
6 Discussion
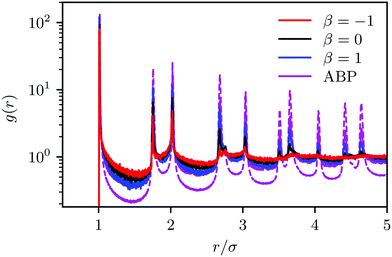
For spherical squirmers, the various structural quantities—distribution of local packing fraction, cluster-size distribution, pair correlation function, and probability distribution of hexagonal order parameter—reveal suppression of MIPS by hydrodynamic interactions over a wide-range of densities and Péclet numbers deep inside the MIPS parameter regime of ABPs. The distinct flow fields of pushers, pullers, and neutral squirmers influence the structural properties of the fluid, and MIC emerges, most pronounced for pullers and least for pushers. However, no phase separation occurs for packing fractions ϕ2D ≲ 0.6. We did not explore the high-density part of the phase diagram, where further phases and transitions might be expected. Interestingly, HI reduce finite-system-size effects as distribution functions for the local packing fraction and the cluster size are essentially independent of the system size.Our simulation results for spherical squirmers agree with certain aspects of previous studies, but disagree with others. In particular, the cluster-size distribution function has been analyzed in ref. 37 for the same squirmer model using the Lattice Boltzmann approach, but using a somewhat different simulation setup. Significantly larger systems with many more squirmers have been considered, and three-dimensional hydrodynamic interactions, but with squirmers confined in 2D at the density ϕ2D = 0.1. In agreement with our Fig. 5, in ref. 37 a power-law decay (p(n) ∼ n−2.0) for small cluster sizes (n ≲ 103) is obtained for pullers with 0 < β ≲ 1. For other β (β > 2 and β < 0), a stronger decay appears for n ≳ 10. This non-power-law decay is stronger than that observed in our simulations. Hence, at smaller concentrations we expect a stronger drop of the cluster distribution for β < 0 also in our quasi-2D system.
Our simulation results of spherical squirmers disagree qualitatively and quantitatively with the results of ref. 35 and 50, where comparable systems have been considered. We find that hydrodynamic interactions suppress cluster formation of squirmers, in contrast to ref. 35. According to ref. 50, the Péclet numbers of our neutral squirmers are deep in the phase-separated region of the phase diagram (Fig. 3 of ref. 50).70 However, we do not see any signature for phase separation, not even for neutral squirmers. Moreover, the distribution function of the bond order parameter differs significantly. For squirmers, we find the most pronounced local order for pullers, followed by neutral squirmers and the weakest order for pushers, in agreement with other studies.36–38 The studies of ref. 35 show the strongest cluster formation and local order for neutral squirmers, comparable to strictly 2D ABPs and more pronounced compared to ABPs in quasi-2D.
We suspect that the origin of the discrepancy between our results and those of ref. 35 and 50 is the different compressibilities of the employed MPC fluids. It is shown in Appendix C that the squirmer-induced fluid transport can cause strong MPC-fluid density inhomogeneities when squirmers are blocked, either by other squirmers or by a surface, at too strong propulsion velocities. A significant fluid-density modulation leads to a reduced propulsion efficiency and a reduced active pressure inside the cluster. As a consequence, propulsion of squirmers confined inside a cluster is effectively reduced, which leads to more stable clusters. By our choice of simulation parameters, we ensured that critical fluid density variations are avoided. Thus, the results of the simulation studies of ref. 35 and 50 are incompatible with ours; however, if (strong) compressibility effects would be considered as relevant, like fluids near a critical point, these studies are applicable.
In the case of spheroidal squirmers, HI strongly enhance phase separation even for Péclet numbers as low as Pe = 12 and densities, where spheroidal ABPs are deep inside the fluid state. Two aspects contribute to the hydrodynamic enhancement of cluster formation, namely near-field HI between squirmers, and between a squirmer and the confining walls.46 The effect of the active stress, β, is evident from the state diagram of Fig. 13. Our simulation studies of ref. 46 on the cooperative motion of two squirmers in a slit geometry already reveal a long-time stable configuration of two pullers, in which they swim together in a wedge-like conformation with a constant small angle. A similar configuration of neutral squirmers or pushers is far less stable and the squirmers scatter more strongly, which emphasizes the relevance of specificities in fluid interactions of the squirmers due to their close proximity, and in particular with the walls. Applying three-dimensional hydrodynamic interactions rather than no-slip boundary conditions to a still confined pair of pullers yields short cooperative motion only, emphasizing that surface hydrodynamics is extremely important.46 Hence, the seed for the cluster formation is the cooperative motion of two squirmers. Blockage by additional encountering squirmers further stabilizes the emerging cluster. The latter is reflected in the density dependence of the cluster formation.
7 Summary and conclusions
We have studied the collective dynamics of spherical and spheroidal squirmers confined in a narrow slit by mesoscale hydrodynamic simulations (MPC). To elucidate the role of hydrodynamic interactions, we have complemented the studies by simulations of spherical and spheroidal active Brownian particles.We find that hydrodynamics suppresses phase separation for spherical microswimmers, in contrast to ref. 35, but in accordance with ref. 28. We attribute the contradiction with ref. 35 to compressibility effects of the MPC fluid. In agreement with ref. 28, we confirm that a hydrodynamically enhanced reorientation of squirmers during swimmer–swimmer collisions implies an effectively lower Péclet number and, hence, a suppression of phase separation. However, the squirmers form short-lived clusters, MIC, over a broad range of cluster sizes. As already pointed out in ref. 38, near-field hydrodynamic interactions play a major role in cluster formation. This is reflected in the clear differences between pullers, neutral squirmers, and pushers.38 A strong near-field effect can be expected, since the multipole contributions to a swimmer's flow field decay quickly with distance parallel to the confining walls in a narrow channel.51
For anisotropic swimmers, alignment due to steric interactions is a key mechanism for MIC, while isotropic swimmers form clusters due to jamming and blocking. Our studies of elongated, prolate spheroidal squirmers yield hydrodynamically enhanced MIC compared to ABPs. This result is surprising at first glance. Based on our studies on the cooperative motion of pairs of confined elongated squirmers, we attribute this enhancement to near-field hydrodynamics and, most importantly, swimmer–surface hydrodynamic interactions, yet, the anisotropic shape leads to shape-induced phase separation for ABPs at considerably lower Péclet numbers than for spheres. This is related to differences in the clustering mechanisms of isotropic and anisotropic swimmers.
For both, spherical and spheroidal squirmers, the active stress parameter β correlates positively with cluster formation, i.e., pullers (β > 0) show the strongest tendency to form clusters, followed by neutral squirmers (β = 0), and pushers (β < 0). In fact, this is well consistent with our previous study of two squirmers in a narrow slit, which shows that cooperativity is most pronounced for pullers.46
Simulations of dumbbell swimmers71,72 in three dimensions have also been performed and hydrodynamically enhanced MIC has been observed.73 Since dumbbell swimmers are anisotropic, this finding is consistent with our results for spheroidal squirmers. However, we have to be careful with too general conclusions. As we demonstrated, MIC depends decisively on the hydrodynamic flow field, i.e., the details of the flow field matter. This is reflected by our results for very strong pushers (β = −5), which show a suppression of the phase separation.
The observed clustering of spheroidal squirmers is in contrast to the behavior of motile bacteria, e.g., E. coli, in suspensions, which display active turbulence.13 At the moment, there is no unambiguous understanding of the different behaviors and underlying mechanisms. Could the dependence on the Péclet number explain the differences? The rotational diffusion coefficient DeR = 0.057 s−1 of non-tumbling E. coli has been measured in ref. 74. With the swimming velocity Ue0 = 30 μs and the length 2bz ≈ 10μ, we obtain a Péclet number Pee ≈ 50. Our simulations show that such a Pe even further enhances clustering. There seems to be an additional relevant interaction in bacteria suspensions. Of course, it could be related to the structure of bacteria with the cell body and the flagella bundle,75 which forms a rather flexible structure. Depending on the body-bundle orientation, a bacterium exhibits a wobbling motion, which perturbs alignment and leads to a fast decay of orientational correlations of nearby swimmers.76 Furthermore, hydrodynamic interactions could be responsible; the propulsion of the bacterium with a rotating flagella bundle and a counterrotating cell body leads to a rotlet dipole.77 Such a flow field induces a circular motion on a planar surface77–80 and may also enhance the decorrelation of the orientational order. Another mechanism has been proposed in ref. 39 and 40. The particular geometry of a microswimmer, such as the inhomogeneous, elongated shape of bacteria, may lead to a coupling of the orientational dynamics and the fluid flow. This could be a mechanism for an enhanced rotational motion, and the emergence of mesoscale turbulence. Naturally, further mechanisms may exist, an example is a fore-aft asymmetry,81 which lead to the required enhanced reorientation dynamics, necessary for the suppression of MIPS and the maintenance of a dynamic state. Here, systematic studies are desirable to elucidate the relevance and importance of the various mechanisms and interactions.
Squirmers are highly idealized models of biological microswimmers, not only in terms of shape, but also in terms of the stationary, time-independent flow fields. The strong interplay between the shape and hydrodynamics, which is revealed by our simulations, indicates that the details of the cell shape and the propulsion pattern may play a much more important role in the collective dynamics of biological microswimmers than previously expected.
Conflicts of interest
There are no conflicts to declare.Appendix A: simulation approaches
A.1 Multiparticle collision dynamics (MPC)
In MPC,47–49 a fluid is represented by N point particles of mass m with continuous positions ri and velocities vi (i ∈ {1,…,N}). The particle dynamics proceeds in two steps—streaming and collision. During the streaming step of duration h (collision time), the particles move ballistically, i.e., their positions are updated according to| ri(t + h) = ri(t) + hvi(t). | (10) |
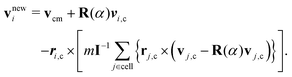 | (11) |
We measure lengths in units of the collision cell size a and time in units of 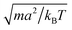 , where kB is the Boltzmann factor, which corresponds to the choice a = m = kBT = 1. The rotation angle is set to α = 130°. The viscosity η of the fluid can be tuned by changing the mean number of particles 〈Nc〉 in a cell or the time step h.62,83,87
, where kB is the Boltzmann factor, which corresponds to the choice a = m = kBT = 1. The rotation angle is set to α = 130°. The viscosity η of the fluid can be tuned by changing the mean number of particles 〈Nc〉 in a cell or the time step h.62,83,87
A.2 Boundary conditions and squirmer implementation
No-slip boundary conditions are implemented at the confining walls (cf.Fig. 2) using the bounce-back rule vi′(t) = −vi(t), where vi and vi′ are the velocity before and after the particle's collision with the wall, respectively. Additionally, spatially uniformly distributed phantom particles with Gaussian distributed velocity components are inserted into the walls and interact with fluid particles during the collision step.49,90 Parallel to the walls, periodic boundary conditions are applied.During the streaming step, a squirmer moves like a passive colloid according to rigid-body equations of motion. The equations of motion of the rotational degrees of freedom are solved by introducing quaternions46,67 (see also Appendix A.3). Interacting fluid particles experience the modified bounced back rule vi′ = −vi + 2vS, where vS is the squirmer's surface velocity at the point of contact. This surface velocity includes its translational and rotational velocity as well as its slip velocity usq (eqn (1)). The change of the fluid particle's linear and angular momentum is transferred to the squirmer, such that the total momenta are conserved. For the collision step, as for walls, spatially uniformly distributed phantom particles are generated inside the squirmer with Gaussian distributed velocity components, where their mean value is given by the rigid-body translational and rotational velocity plus the squirming velocity, and the variance is equal to kBT/m.45,46 After the collision step, the linear and angular momentum changes of all phantom particles are transferred to the squirmer. A more detailed description is provided in ref. 46. Repulsive forces and torques due to steric interactions between squirmers, and between a squirmer and a wall, during a streaming step are implemented as outlined in the appendix of ref. 46 (see also ref. 91).
A.3 Simulation algorithm for spheroidal active Brownian particles
For active Brownian particles, as for the hydrodynamic case, we solve the rigid-body equations of motion, but now in the presence of translational and rotational noise. The squirmer orientation is parameterized by a unit quaternion q = (q0,q1,q2,q3).67 The integration scheme for the overdamped dynamics of the center-of-mass R(t) and quaternion q(t) of the spheroid is92| R(t + h) = R(t) + μFh + U0eh, | (12) |
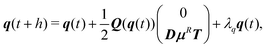 | (13) |
![[q with combining tilde]](https://www.rsc.org/images/entities/b_i_char_0071_0303.gif) and then determine λq such that
and then determine λq such that ![[q with combining tilde]](https://www.rsc.org/images/entities/b_i_char_0071_0303.gif) + λqq is normalized.92
+ λqq is normalized.92
The mobility matrix μ relates the applied force F to the resulting ABP velocity UviaU = μF, while the rotational mobility matrix μR relates the applied torque T to the resulting angular velocity ΩviaΩ = μRT. In the body-fixed frame, the respective mobility matrices are diagonal, with diagonal elements given by the inverse translational and rotational friction coefficients γx−1, γy−1, γz−1 and ξx−1, ξy−1, ξz−1, respectively. For a prolate spheroid γx = γy = γ⊥, γz = γ‖, ξx = ξy = ξ⊥, and ξz = ξ‖. The parallel and perpendicular friction coefficients are provided in Appendix B. For zero eccentricity, i.e., a sphere with bx = bz = R, we obtain γ‖ = γ⊥ = 6πηR and ξ‖ = ξ⊥ = 8πηR3.
In the body-fixed frame, the Cartesian components of the thermal force Fth are Gaussian distributed random numbers of zero mean and variance 2kBTγα/h (α ∈ {x,y,z}). The thermal torque Tth is generated similarly, but with variance 2kBTξα/h. The implementation of the repulsive forces and torques due to steric interactions between ABPs and between an ABP and a wall is described in the appendix of ref. 46.
Appendix B: rigid-body dynamics: quaternions
The rotation matrix D and the matrix Q introduced in eqn (13) are given by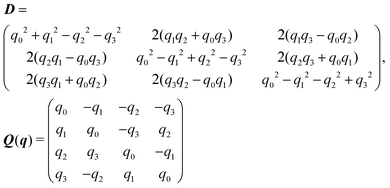 | (14) |
The translational and rotational friction coefficients of a spheroid are given by
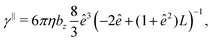 | (15) |
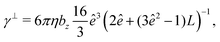 | (16) |
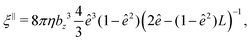 | (17) |
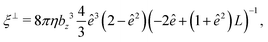 | (18) |
Appendix C: avoiding MPC simulation artifacts related to density inhomogeneities
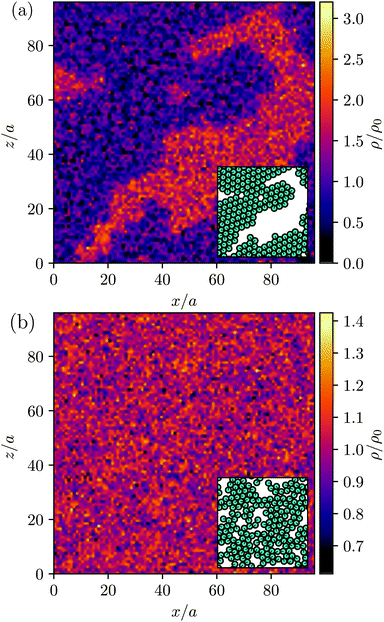
MPC is a compressible fluid and correspondingly strong density inhomogeneities can emerge for certain choices of MPC parameters. Fig. 14 provides an example of the fluid-particle density distribution for neutral spherical squirmers confined in a narrow slit (cf.Fig. 2). The squirmer density is ϕ2D = 0.6 and the Péclet number Pe = 115. However, the Péclet number is realized by different combinations of the MPC fluid and squirmer parameters. In Fig. 14(a), we set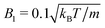 and 〈Nc〉 = 10, and in (b)
and 〈Nc〉 = 10, and in (b) 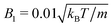 and 〈Nc〉 = 80. The latter gives a ten times larger viscosity. The other parameters are the same as defined in Appendix A.1 and Section 4.1.
and 〈Nc〉 = 80. The latter gives a ten times larger viscosity. The other parameters are the same as defined in Appendix A.1 and Section 4.1.
Fig. 14(a) shows large density inhomogeneities with dense (orange) and rarefied regions (purple). Therefore, the rarefied regions coincide with the area occupied by the large squirmer cluster (cf. inset of Fig. 14(a)). In contrast, the MPC fluid distribution in Fig. 14(b) is rather homogeneous aside from thermal fluctuations and no link to the squirmer distribution is evident. It seems that a pressure gradient is built up by active clustered squirmers by expelling the fluid from the cluster—an effect related to the compressibility of MPC. For density inhomogeneities as large as those in Fig. 14(a), MPC simulations do not describe incompressible fluids, since the viscosity of the MPC fluid depends linearly on density and, hence, depends strongly on the location.
The mechanism in a MPC fluid, which opposes the diminished density in the gaps between squirmers is fluid-particle diffusion. The ratio of time tdiff necessary for a MPC particle to diffuse over a swimmer diameter σ = 2R, compared to the time required for a MPC particle to be advected by the surface activity of a squirmer with velocity U0 over the same distance, yields the dimensionless pumping number
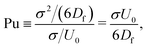 | (19) |
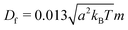 is the MPC-fluid diffusion coefficient. For small pumping number, Pu, we expect the density inhomogeneities to disappear, i.e., MPC fluid-particle diffusion is faster than activity-induced advection. The above choices of parameters yield the pumping numbers Pu = 5 (Fig. 14(a)) and Pu = 0.5 (Fig. 14(b)). Consistent with our expectation, the difference in the pumping number explains the appearing density modulations.
is the MPC-fluid diffusion coefficient. For small pumping number, Pu, we expect the density inhomogeneities to disappear, i.e., MPC fluid-particle diffusion is faster than activity-induced advection. The above choices of parameters yield the pumping numbers Pu = 5 (Fig. 14(a)) and Pu = 0.5 (Fig. 14(b)). Consistent with our expectation, the difference in the pumping number explains the appearing density modulations.
In terms of the Péclet number, Pu is given by Pu = σ2DRPe/6Df. Since Pe ≫ 1 for active systems, Pu < 1 requires σ2DR/6Df ≪ 1. Hence, the MPC parameters have to be chosen such that DR ≪ 1. Because DR ∼ 1/η, this is achieved for 〈Nc〉 ≫ 1. Such an increase in 〈Nc〉 leaves Df virtually unchanged, however, implies an increase in computational effort.
Acknowledgements
We thank A. Wysocki and R. Hornung for helpful discussions. The support of this work from the DFG priority program SPP 1726 “Microswimmers – from Single Particle Motion to Collective Behaviour” is gratefully acknowledged. We also acknowledge the partial financial support from the Bavarian Ministry of Economic Affairs, Energy and Technology within joint projects between Helmholtz institutes. In addition, the authors gratefully acknowledge the computing time granted for JARA-HPC on supercomputer JURECA at Forschungszentrum Jülich.References
- J. Elgeti, R. G. Winkler and G. Gompper, Rep. Prog. Phys., 2015, 78, 056601 CrossRef CAS PubMed.
- M. C. Marchetti, J. F. Joanny, S. Ramaswamy, T. B. Liverpool, J. Prost, M. Rao and R. A. Simha, Rev. Mod. Phys., 2013, 85, 1143 CrossRef CAS.
- F. Peruani, J. Starruß, V. Jakovljevic, L. Søgaard-Andersen, A. Deutsch and M. Bär, Phys. Rev. Lett., 2012, 108, 098102 CrossRef PubMed.
- A. P. Petroff, X.-L. Wu and A. Libchaber, Phys. Rev. Lett., 2015, 114, 158102 CrossRef PubMed.
- D. B. Kearns, Nat. Rev. Microbiol., 2010, 8, 634 CrossRef CAS PubMed.
- N. C. Darnton, L. Turner, S. Rojevsky and H. C. Berg, Biophys. J., 2010, 98, 2082 CrossRef CAS PubMed.
- X.-L. Wu and A. Libchaber, Phys. Rev. Lett., 2000, 84, 3017 CrossRef CAS PubMed.
- C. Dombrowski, L. Cisneros, S. Chatkaew, R. E. Goldstein and J. O. Kessler, Phys. Rev. Lett., 2004, 93, 098103 CrossRef PubMed.
- M. F. Copeland and D. B. Weibel, Soft Matter, 2009, 5, 1174 RSC.
- R. Zhang, L. Turner and H. C. Berg, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 288–290 CrossRef CAS PubMed.
- N. H. Mendelson, A. Bourque, K. Wilkening, K. R. Anderson and J. C. Watkins, J. Bacteriol., 1999, 181, 600 CAS.
- H. H. Wensink and H. Löwen, J. Phys.: Condens. Matter, 2012, 24, 460130 CrossRef PubMed.
- H. H. Wensink, J. Dunkel, S. Heidenreich, K. Drescher, R. E. Goldstein, H. Löwen and J. M. Yeomans, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 14308 CrossRef CAS PubMed.
- A. Sokolov and I. S. Aranson, Phys. Rev. Lett., 2012, 109, 248109 CrossRef PubMed.
- R. Golestanian, T. B. Liverpool and A. Ajdari, Phys. Rev. Lett., 2005, 94, 220801 CrossRef PubMed.
- I. Theurkauff, C. Cottin-Bizonne, J. Palacci, C. Ybert and L. Bocquet, Phys. Rev. Lett., 2012, 108, 268303 CrossRef CAS PubMed.
- S. Thutupalli, R. Seemann and S. Herminghaus, New J. Phys., 2011, 13, 073021 CrossRef.
- J. Palacci, S. Sacanna, A. P. Steinberg, D. J. Pine and P. M. Chaikin, Science, 2013, 339, 936 CrossRef CAS PubMed.
- I. Buttinoni, J. Bialké, F. Kümmel, H. Löwen, C. Bechinger and T. Speck, Phys. Rev. Lett., 2013, 110, 238301 CrossRef PubMed.
- M. C. Marchetti, Y. Fily, S. Henkes, A. Patch and D. Yllanes, Curr. Opin. Colloid Interface Sci., 2016, 21, 34 CrossRef CAS.
- C. Bechinger, R. Di Leonardo, H. Löwen, C. Reichhardt, G. Volpe and G. Volpe, Rev. Mod. Phys., 2016, 88, 045006 CrossRef.
- Y. Fily and M. C. Marchetti, Phys. Rev. Lett., 2012, 108, 235702 CrossRef PubMed.
- G. S. Redner, M. F. Hagan and A. Baskaran, Phys. Rev. Lett., 2013, 110, 055701 CrossRef PubMed.
- J. Bialké, T. Speck and H. Löwen, Phys. Rev. Lett., 2012, 108, 168301 CrossRef PubMed.
- A. Wysocki, R. G. Winkler and G. Gompper, EPL, 2014, 105, 48004 CrossRef.
- J. Stenhammar, D. Marenduzzo, R. J. Allen and M. E. Cates, Soft Matter, 2014, 10, 1489 RSC.
- A. Wysocki, R. G. Winkler and G. Gompper, New J. Phys., 2016, 18, 123030 CrossRef.
- R. Matas-Navarro, R. Golestanian, T. B. Liverpool and S. M. Fielding, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2014, 90, 032304 CrossRef PubMed.
- M. E. Cates and J. Tailleur, Annu. Rev. Condens. Matter Phys., 2015, 6, 219 CrossRef CAS.
- R. Golestanian, Phys. Rev. Lett., 2012, 108, 038303 CrossRef PubMed.
- O. Pohl and H. Stark, Phys. Rev. Lett., 2014, 112, 238303 CrossRef PubMed.
- F. Peruani, A. Deutsch and M. Bär, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2006, 74, 030904 CrossRef PubMed.
- Y. Yang, V. Marceau and G. Gompper, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2010, 82, 031904 CrossRef PubMed.
- M. Abkenar, K. Marx, T. Auth and G. Gompper, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2013, 88, 062314 CrossRef PubMed.
- A. Zöttl and H. Stark, Phys. Rev. Lett., 2014, 112, 118101 CrossRef PubMed.
- B. Delmotte, E. E. Keaveny, F. Plouraboué and E. Climent, J. Comput. Phys., 2015, 302, 524 CrossRef.
- F. Alarcón, C. Valeriani and I. Pagonabarraga, Soft Matter, 2017, 13, 814 RSC.
- N. Yoshinaga and T. B. Liverpool, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2017, 96, 020603 CrossRef PubMed.
- S. Heidenreich, J. Dunkel, S. H. L. Klapp and M. Bär, Phys. Rev. E, 2016, 94, 020601 CrossRef PubMed.
- H. Reinken, S. H. L. Klapp, M. Bär and S. Heidenreich, Phys. Rev. E, 2018, 97, 022613 CrossRef PubMed.
- M. J. Lighthill, Comm. Pure Appl. Math., 1952, 5, 109 CrossRef.
- J. R. Blake, J. Fluid Mech., 1971, 46, 199 CrossRef.
- T. Ishikawa and M. Hota, J. Exp. Biol., 2006, 209, 4452 CrossRef PubMed.
- I. Pagonabarraga and I. Llopis, Soft Matter, 2013, 9, 7174 RSC.
- I. O. Götze and G. Gompper, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2010, 82, 041921 CrossRef PubMed.
- M. Theers, E. Westphal, G. Gompper and R. G. Winkler, Soft Matter, 2016, 12, 7372 RSC.
- A. Malevanets and R. Kapral, J. Chem. Phys., 1999, 110, 8605 CrossRef CAS.
- R. Kapral, Adv. Chem. Phys., 2008, 140, 89 CrossRef CAS.
- G. Gompper, T. Ihle, D. M. Kroll and R. G. Winkler, Adv. Polym. Sci., 2009, 221, 1 CAS.
- J. Blaschke, M. Maurer, K. Menon, A. Zöttl and H. Stark, Soft Matter, 2016, 12, 9821 RSC.
- A. J. T. M. Mathijssen, A. Doostmohammadi, J. M. Yeomans and T. N. Shendruk, J. Fluid Mech., 2016, 806, 35 CrossRef.
- P. Digregorio, D. Levis, A. Suma, L. F. Cugliandolo, G. Gonnella and I. Pagonabarraga, Phys. Rev. Lett., 2018, 121, 098003 CrossRef PubMed.
- S. C. Takatori, W. Yan and J. F. Brady, Phys. Rev. Lett., 2014, 113, 028103 CrossRef CAS PubMed.
- S. C. Takatori and J. F. Brady, Soft Matter, 2015, 11, 7920 RSC.
- R. G. Winkler, A. Wysocki and G. Gompper, Soft Matter, 2015, 11, 6680 RSC.
- S. E. Spagnolie and E. Lauga, J. Fluid Mech., 2012, 700, 105 CrossRef.
- F. Alarcón and I. Pagonabarraga, J. Mol. Liq., 2013, 185, 56 CrossRef.
- S. R. Keller and T. Y. Wu, J. Fluid Mech., 1977, 80, 259 CrossRef.
- A. M. Leshansky, O. Kenneth, O. Gat and J. E. Avron, New J. Phys., 2007, 9, 145 CrossRef.
- K. Ishimoto and E. A. Gaffney, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2013, 88, 062702 CrossRef PubMed.
- T. Ishikawa, M. P. Simmonds and T. J. Pedley, J. Fluid Mech., 2006, 568, 119 CrossRef.
- M. Theers and R. G. Winkler, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2015, 91, 033309 CrossRef PubMed.
- A. Zöttl and H. Stark, Phys. Rev. Lett., 2012, 108, 218104 CrossRef PubMed.
- C. H. Rycroft, Chaos, 2009, 19, 041111 CrossRef PubMed.
- M. S. S. Challa, D. P. Landau and K. Binder, Phys. Rev. B: Condens. Matter Mater. Phys., 1986, 34, 1841 CrossRef CAS.
- J.-P. Hansen and I. R. McDonald, Theory of Simple Liquids, Academic Press, London, 1986 Search PubMed.
- M. P. Allen and D. J. Tildesley, Computer Simulation of Liquids, Clarendon Press, Oxford, 1987 Search PubMed.
- P. J. Steinhardt, D. R. Nelson and M. Ronchetti, Phys. Rev. B: Condens. Matter Mater. Phys., 1983, 28, 784 CrossRef CAS.
- P. Persson and G. Strang, SIAM Rev., 2004, 46, 329 CrossRef.
- Note that the definition of the Péclet number of ref. 50 is different; it is three times ours.
- A. Suma, G. Gonnella, G. Laghezza, A. Lamura, A. Mossa and L. F. Cugliandolo, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2014, 90, 052130 CrossRef PubMed.
- J. T. Siebert, J. Letz, T. Speck and P. Virnau, Soft Matter, 2017, 13, 1020 RSC.
- A. Furukawa, D. Marenduzzo and M. E. Cates, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2014, 90, 022303 CrossRef PubMed.
- K. Drescher, J. Dunkel, L. H. Cisneros, S. Ganguly and R. E. Goldstein, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 10940 CrossRef CAS PubMed.
- H. C. Berg, E. Coli in Motion, Springer, New York, 2004 Search PubMed.
- T. Eisenstecken, J. Hu and R. G. Winkler, Soft Matter, 2016, 12, 8316 RSC.
- J. Hu, A. Wysocki, R. G. Winkler and G. Gompper, Sci. Rep., 2015, 5, 9586 CrossRef PubMed.
- E. Lauga, W. R. DiLuzio, G. M. Whitesides and H. A. Stone, Biophys. J., 2006, 90, 400 CrossRef CAS PubMed.
- R. Di Leonardo, D. Dell'Arciprete, L. Angelani and V. Iebba, Phys. Rev. Lett., 2011, 106, 038101 CrossRef CAS PubMed.
- L. Lemelle, J.-F. Palierne, E. Chatre, C. Vaillant and C. Place, Soft Matter, 2013, 9, 9759 RSC.
- Q.-S. Chen, A. Patelli, H. Chaté, Y.-Q. Ma and X.-Q. Shi, Phys. Rev. E, 2017, 96, 020601 CrossRef PubMed.
- T. Ihle and D. M. Kroll, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2001, 63, 020201(R) CrossRef PubMed.
- H. Noguchi and G. Gompper, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2008, 78, 016706 CrossRef PubMed.
- M. Yang, M. Theers, J. Hu, G. Gompper, R. G. Winkler and M. Ripoll, Phys. Rev. E, 2015, 92, 013301 CrossRef PubMed.
- T. Ihle and D. M. Kroll, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2003, 67, 066705 CrossRef CAS PubMed.
- C.-C. Huang, R. G. Winkler, G. Sutmann and G. Gompper, Macromolecules, 2010, 43, 10107 CrossRef CAS.
- C.-C. Huang, A. Varghese, G. Gompper and R. G. Winkler, Phys. Rev. E, 2015, 91, 013310 CrossRef PubMed.
- T. Ihle, Phys. Chem. Chem. Phys., 2009, 11, 9667 RSC.
- C.-C. Huang, G. Gompper and R. G. Winkler, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2012, 86, 056711 CrossRef PubMed.
- A. Lamura, G. Gompper, T. Ihle and D. M. Kroll, Europhys. Lett., 2001, 56, 319–325 CrossRef CAS.
- L. Paramonov and S. N. Yaliraki, J. Chem. Phys., 2005, 123, 194111 CrossRef PubMed.
- I. M. Ilie, W. J. Briels and W. K. D. Otter, J. Chem. Phys., 2015, 142, 114103 CrossRef PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c8sm01390j |
| This journal is © The Royal Society of Chemistry 2018 |