Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Phase separation around a heated colloid in bulk and under confinement
Sutapa
Roy
 *ab and
Anna
Maciołek
*ab and
Anna
Maciołek
 c
c
aMax-Planck-Institut für Intelligente Systeme, Heisenbergstr. 3, 70569 Stuttgart, Germany. E-mail: sutapa@is.mpg.de
bIV. Institut für Theoretische Physik, Universität Stuttgart, Pfaffenwaldring 57, 70569 Stuttgart, Germany
cInstitute of Physical Chemistry, Polish Academy of Sciences, Kasprzaka 44/52, PL-01-224 Warsaw, Poland
First published on 19th September 2018
Abstract
We study the non-equilibrium coarsening dynamics of a binary liquid solvent around a colloidal particle in the presence of a time-dependent temperature gradient that emerges after a temperature quench of a suitable coated colloid surface. The solvent is maintained at its critical concentration and the colloid is fixed in space. The coarsening patterns near the surface are shown to be strongly dependent on the colloid surface adsorption properties and on the temperature evolution. The temperature gradient alters the morphology of the binary solvent near the surface of the colloid as compared to the coarsening proceeding at a constant temperature everywhere. We also present results for the evolution of coarsening in thin films with confining surfaces preferring one species of the binary liquid mixture over the other. Confinement leads to a faster phase segregation process and formation of a bridge connecting the colloid and both confining walls.
1 Introduction
Phase separation of binary mixtures induced by a temperature quench into the miscibility gap is a subject of continuous research activity driven by application perspectives, e.g., the buildup of nanostructured materials of well defined structure.1,2 In the latter context, the effects of surfaces and confinement on a coarsening process are of particular interest as they may be used to control the structure formation. If the surface has a preference for one of the two components of a binary mixture, the fluid structures emerging after the homogeneous temperature quench at a critical concentration are essentially distinct from those due to spinodal decomposition.3–5 This is because the adsorption of the preferred component at the surface affects the fluctuations of concentration away from the surface. In the presence of confinement, e.g., in thin films, the coarsening process becomes complex due to the interplay between finite-size and surface adsorption effects.5 Addition of colloidal particles to a binary liquid undergoing demixing via spinodal decomposition widens the possibility for controlling pattern formation. It has been demonstrated that colloidal particles significantly curtail coarsening6,7 and in the case of adsorptionwise neutral colloids can lead to the formation of interesting soft-solid materials, called ‘bijels’.7,8 By using Janus colloids, with a difference in adsorption preference between their two hemispheres, one can create regular lamellar structures.9,10Application of local temperature quenches instead of spatially homogeneous ones creates temperature gradients, which strongly couple to the local composition of a binary mixture and alter the mechanism of coarsening. For example, if such a quench propagates through space over time it may lead to macroscopic coarsening with patterns that are different from those seen in spatially homogeneous quenching.11 Local temperature quenches can be realized by direct laser heating11,12 of parts of binary liquid mixtures or by optical heating12,13 of the surface of suitably coated colloids suspended in such mixtures. One might think of using optically heated colloids for the buildup of soft solids, therefore, it is interesting to know how local is the phase separation around each colloid and how the coarsening process depends on the adsorption preference of the surface of a colloid. Here we address these problems by using numerical simulations. We focus on the early-stage of a coarsening process in which diffusive dynamics dominates. We are also interested in the coarsening mechanism around colloids which are not kept in bulk, but are confined between surfaces exhibiting an adsorption preference for one of the two components of a binary solvent. Such studies are relevant for typical experimental realizations in which the samples cells are in a slab geometry. The effects of such confinement on the early-time non-equilibrium process of concentration gradient formation around the colloid are difficult to foresee. What makes it particularly complicated is the presence of the temperature field coupled to the local concentration field.
Local quenches of a binary mixture as realized by optical heating of the surface of a suspended, suitably coated colloid bear particular relevance for experimental studies of moving Janus colloids.14–17 However, for these systems the transient dynamics of the binary solvent at early times has hardly been studied.18 In ref. 18, which we coauthored, both Janus and homogeneous spherical particles have been considered for off-critical compositions of a binary solvent. In the present paper we focus on a homogeneous colloid and the critical composition of the solvent, which are relevant for fabrication of bicontinuous structures such as bigels. In order to mimic different physical situations, we consider two types of boundary conditions for the temperature field at the boundary of the simulation box and compare the corresponding coarsening patterns. We also extend the model studied in ref. 18 in order to assess the role of the Soret effect for pattern formation. In ref. 12 it has been argued that taking into account this effect is necessary to reproduce in numerical simulations the essential spatial and temporal phenomena occurring after local heating of a polymer blend in the two phase region.
Our paper is organized as follows: in Section 2 we explain the phenomenological model considered and the numerical techniques used in our work. Section 3 presents our analytical results for the time-dependent temperature profiles for different boundary conditions. There, we also explain our numerical findings on the non-equilibrium dynamics of structure formation around a suspended colloidal particle under a temperature gradient. All results correspond to the critical concentration of the binary solvent and thermal quench inside the binodal region. Section 3 also contains results for phase separation around a colloid kept in confinement in a slab geometry. There, we provide a brief discussion on the influence of the Soret effect on the structure formation process. Finally Section 4 summarizes the paper with a brief perspective of future work.
2 Model
When a binary liquid mixture (with an upper critical point for demixing) is quenched instantaneously from a homogeneous state above Tc into the two-phase coexistence region below Tc, domains of like particles form and grow with time t. This is known as phase ordering dynamics.19,20 For a fluid at its critical concentration, the coarsening morphology is percolating and leads to spinodal decomposition which involves three distinct regimes: the early-time diffusive regime (a = 1/3),19 the viscous regime (a = 1),21 and the late-stage inertial regime (a = 2/3).22 Here, a is the exponent corresponding to a temporal power-law growth![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) (t) ∝ ta of the average domain size. The latter two regimes of this spinodal decomposition process are due to convective flow of material generated by hydrodynamic effects. In the present paper, as a first step towards the understanding of coarsening around the hot colloid, we focus solely on the diffusive dynamics.
(t) ∝ ta of the average domain size. The latter two regimes of this spinodal decomposition process are due to convective flow of material generated by hydrodynamic effects. In the present paper, as a first step towards the understanding of coarsening around the hot colloid, we focus solely on the diffusive dynamics.
A local temperature quench of the surface of a colloidal particle gives rise to a temperature front, which propagates away from the surface. This can be described by time-dependent temperature field T(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ,t). The temperature field couples strongly to the local concentration of a binary solvent. We introduce the order parameter (OP) field Ψ(
,t). The temperature field couples strongly to the local concentration of a binary solvent. We introduce the order parameter (OP) field Ψ(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ,t) as a difference Ψ(
,t) as a difference Ψ(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ,t) = cA(
,t) = cA(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ,t) − cB(
,t) − cB(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ,t) in the concentration of components A and B of a binary mixture, where cA,B = ρA,B/(ρA + ρA,B) = NA,B/N and ρA,B = NA,B/V are the local number densities. This OP is conjugated to the chemical potential difference μ = μA − μB between the chemical potentials of species A and B. For phase separation driven by diffusion, we assume that the time t evolution of both fields is governed by the Cahn–Hilliard–Cook (CHC) equation or Model B23 based on the Ginzburg–Landau free energy functional, in conjunction with the heat diffusion equation. The Ginzburg–Landau free energy functional of the solvent OP is given by
,t) in the concentration of components A and B of a binary mixture, where cA,B = ρA,B/(ρA + ρA,B) = NA,B/N and ρA,B = NA,B/V are the local number densities. This OP is conjugated to the chemical potential difference μ = μA − μB between the chemical potentials of species A and B. For phase separation driven by diffusion, we assume that the time t evolution of both fields is governed by the Cahn–Hilliard–Cook (CHC) equation or Model B23 based on the Ginzburg–Landau free energy functional, in conjunction with the heat diffusion equation. The Ginzburg–Landau free energy functional of the solvent OP is given by
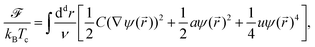 | (1) |
![[T with combining tilde]](https://www.rsc.org/images/entities/i_char_0054_0303.gif) (
(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ) =
) = ![[scr A, script letter A]](https://www.rsc.org/images/entities/char_e520.gif) (T(
(T(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ) − Tc)/Tc), where
) − Tc)/Tc), where ![[scr A, script letter A]](https://www.rsc.org/images/entities/char_e520.gif) is a constant number. Then using the continuity equation for the evolution of the OP, which is conserved, together with a generalized Fick's law
is a constant number. Then using the continuity equation for the evolution of the OP, which is conserved, together with a generalized Fick's law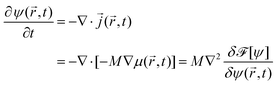 | (2) |
![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ,t), one obtains the modified CHC equation with a spatio-temporal temperature field
,t), one obtains the modified CHC equation with a spatio-temporal temperature field ![[T with combining tilde]](https://www.rsc.org/images/entities/i_char_0054_0303.gif) (
(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ,t)24
,t)24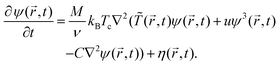 | (3) |
M > 0 is the diffusive mobility which is assumed to be spatially constant and independent of the local concentration. Assuming local equilibrium, the noise η(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ,t) conserving the OP obeys the following fluctuation–dissipation relation
,t) conserving the OP obeys the following fluctuation–dissipation relation
〈μ(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ,t)μ( ,t)μ(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ′, t′)〉 = −2(M/ν)kBT( ′, t′)〉 = −2(M/ν)kBT(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) )∇2δ( )∇2δ(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) − − ![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ′)δ(t − t′). ′)δ(t − t′). | (4) |
For the system at homogeneous temperature T, the correlation length (below Tc) and the characteristic time are given by 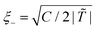 and t0 = 2ξ−2(T)/(Dm(T)|
and t0 = 2ξ−2(T)/(Dm(T)|![[T with combining tilde]](https://www.rsc.org/images/entities/i_char_0054_0303.gif) |), respectively, where Dm(T) = (M/ν)kBT is the interdiffusion constant of a binary solvent. We normalize the length, time and ψ by ξ−, t0, and
|), respectively, where Dm(T) = (M/ν)kBT is the interdiffusion constant of a binary solvent. We normalize the length, time and ψ by ξ−, t0, and 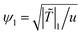 , where ψ1 corresponds to the concentration after phase separation, taken at the quench temperature T = T1 < Tc. We then obtain the dimensionless form of eqn (3)
, where ψ1 corresponds to the concentration after phase separation, taken at the quench temperature T = T1 < Tc. We then obtain the dimensionless form of eqn (3)
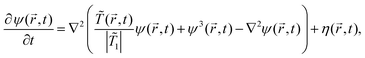 | (5) |
![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ,t) is expressed in units of η0 = ψ1/t0. After the colloid surface is cooled, because of heat flow the surrounding solvent temperature also changes with time. The time evolution of the temperature field is dictated by the heat diffusion equation
,t) is expressed in units of η0 = ψ1/t0. After the colloid surface is cooled, because of heat flow the surrounding solvent temperature also changes with time. The time evolution of the temperature field is dictated by the heat diffusion equation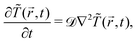 | (6) |
![[scr D, script letter D]](https://www.rsc.org/images/entities/char_e523.gif) = Dth/(|
= Dth/(|![[T with combining tilde]](https://www.rsc.org/images/entities/i_char_0054_0303.gif) 1|Dm) is the so-called Lewis number and Dth is the thermal diffusivity of the solvent. Eqn (5) and (6) were first considered in ref. 24 to study phase separation near a planar surface subjected to a temperature quench. The authors of ref. 25 derived a CHC equation starting from a master equation for a Kawasaki spin-exchange kinetic Ising model26 with a space-dependent temperature. They have obtained a more complex expression with additional terms involving coupling between ∇T and ∇ψ and higher order temperature derivatives.
1|Dm) is the so-called Lewis number and Dth is the thermal diffusivity of the solvent. Eqn (5) and (6) were first considered in ref. 24 to study phase separation near a planar surface subjected to a temperature quench. The authors of ref. 25 derived a CHC equation starting from a master equation for a Kawasaki spin-exchange kinetic Ising model26 with a space-dependent temperature. They have obtained a more complex expression with additional terms involving coupling between ∇T and ∇ψ and higher order temperature derivatives.
Here, we assume that a generalized force is proportional to the gradient of the chemical potential [−M∇μ(r,t)] (a generalized force proportional to the gradient of temperature is discussed in Section 3.4). This is because our theory is based on the Landau–Ginzburg free energy functional. However, one can use another thermodynamic potential functional which will lead to a different form of generalized force. For an equilibrium system the choice of independent thermodynamic fields and, hence, thermodynamic potentials is a matter of convenience (see e.g.ref. 27). Similar seems to apply to dynamics. In some cases the composition, the density and the energy density fields are used as the fundamental variables.28 In other cases, the entropy density rather than the energy density is employed. Non-thermal systems are discussed in ref. 29–31. In ref. 29 an extension of the Cahn–Halliard model of phase separations to such situations has been proposed and its mathematical properties have been studied. Onuki30 introduced a dynamic van der Waals theory based on the entropy functional, in which the generalized forces are proportional to ∇(μ(r,t)/T(r,t)) and to ∇(1/T(r,t)). Gonnella and co-authors31 extended this approach to fluid mixtures. It turns out that in near-critical solvents μ/T derived from the entropy functional as a function of the order parameter field ψ takes the same form as μ derived from the Landau–Ginzburg free energy functional. Hence, both approaches lead to the same dynamic equation (eqn (5)).
Eqn (5) and (6) have to be supplemented with appropriate boundary conditions (BC)32 at the colloid surface. One BC corresponds to no OP flux through the colloid surface
(![[n with combining circumflex]](https://www.rsc.org/images/entities/i_char_006e_0302.gif) ·∇μ( ·∇μ(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ,t))| ,t))|![[scr S, script letter S]](https://www.rsc.org/images/entities/char_e532.gif) = ( = (![[n with combining circumflex]](https://www.rsc.org/images/entities/i_char_006e_0302.gif) ·∇δ ·∇δ![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) [ψ]/δψ( [ψ]/δψ(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ,t)) ,t))![[scr S, script letter S]](https://www.rsc.org/images/entities/char_e532.gif) = 0, = 0, | (7) |
![[scr S, script letter S]](https://www.rsc.org/images/entities/char_e532.gif) and
and ![[n with combining circumflex]](https://www.rsc.org/images/entities/i_char_006e_0302.gif) refer to the colloid surface and the unit vector perpendicular to it and pointing into it, respectively. The other BC accounts for the adsorption preference of the colloid surface for one of the two components of the binary liquid mixture. This is done by considering a surface energy contribution33
refer to the colloid surface and the unit vector perpendicular to it and pointing into it, respectively. The other BC accounts for the adsorption preference of the colloid surface for one of the two components of the binary liquid mixture. This is done by considering a surface energy contribution33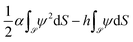 in addition to the bulk free energy
in addition to the bulk free energy ![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) . Here, α is a surface enrichment parameter and h is the symmetry breaking surface field. After suitable rescaling of α and h, this gives rise to the dimensionless static so-called Robin BC
. Here, α is a surface enrichment parameter and h is the symmetry breaking surface field. After suitable rescaling of α and h, this gives rise to the dimensionless static so-called Robin BC(![[n with combining circumflex]](https://www.rsc.org/images/entities/i_char_006e_0302.gif) ·∇ψ( ·∇ψ(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ) + αψ( ) + αψ(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ))| ))|![[scr S, script letter S]](https://www.rsc.org/images/entities/char_e532.gif) = h. = h. | (8) |
For the boundary condition associated with the temperature field we take
![[T with combining tilde]](https://www.rsc.org/images/entities/i_char_0054_0303.gif) ( (![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) )| )|![[scr S, script letter S]](https://www.rsc.org/images/entities/char_e532.gif) = = ![[T with combining tilde]](https://www.rsc.org/images/entities/i_char_0054_0303.gif) 1, 1, | (9) |
![[T with combining tilde]](https://www.rsc.org/images/entities/i_char_0054_0303.gif) 1; we assume no heat diffusion in the colloid.
1; we assume no heat diffusion in the colloid.
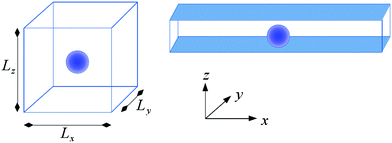
For the numerical setup a spherical colloid of radius R is placed at the center of a rectangular box of side lengths Lx, Ly and Lz (see Fig. 1). Outside the colloid, each grid point on a simple cubic lattice mesh refers to the binary solvent which is characterized by ψ(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ,t) and
,t) and ![[T with combining tilde]](https://www.rsc.org/images/entities/i_char_0054_0303.gif) (
(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ,t). The initial configuration is generated as follows: each solvent grid point is assigned an OP value which is chosen from a uniform random number distribution [−½
,t). The initial configuration is generated as follows: each solvent grid point is assigned an OP value which is chosen from a uniform random number distribution [−½![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ½] such that the spatially averaged OP is ψ0 = 0. This corresponds to the critical concentration of the binary solvent. The initial temperature values throughout the system are
½] such that the spatially averaged OP is ψ0 = 0. This corresponds to the critical concentration of the binary solvent. The initial temperature values throughout the system are ![[T with combining tilde]](https://www.rsc.org/images/entities/i_char_0054_0303.gif) i(
i(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ) = 1. At t = 0, the grid points corresponding to the colloid surface are quenched to a temperature
) = 1. At t = 0, the grid points corresponding to the colloid surface are quenched to a temperature ![[T with combining tilde]](https://www.rsc.org/images/entities/i_char_0054_0303.gif) 1 and (5) and (6) are solved numerically using the Euler34 method to obtain ψ(
1 and (5) and (6) are solved numerically using the Euler34 method to obtain ψ(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ,t) and
,t) and ![[T with combining tilde]](https://www.rsc.org/images/entities/i_char_0054_0303.gif) (
(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ,t). Periodic boundary conditions35 are imposed at the side walls of the cubic box. In order to implement the BC on a curved colloid surface a trilinear interpolation method36 has been used. All numerical results presented here correspond to a temperature quench inside the miscibility region of the equilibrium phase diagram T1 = −1 and they have been obtained using a numerical timestep dt = 0.001. The spatially averaged order parameter is maintained at its critical value ψ0 = 0. We consider homogeneous colloids with constant values of surface parameters α and h. The noise amplitude is taken to be 10−4. Typical values of the dimensional parameters used here are a0 = 0.2 nm, ξ−(T1) = 1.2 nm,
,t). Periodic boundary conditions35 are imposed at the side walls of the cubic box. In order to implement the BC on a curved colloid surface a trilinear interpolation method36 has been used. All numerical results presented here correspond to a temperature quench inside the miscibility region of the equilibrium phase diagram T1 = −1 and they have been obtained using a numerical timestep dt = 0.001. The spatially averaged order parameter is maintained at its critical value ψ0 = 0. We consider homogeneous colloids with constant values of surface parameters α and h. The noise amplitude is taken to be 10−4. Typical values of the dimensional parameters used here are a0 = 0.2 nm, ξ−(T1) = 1.2 nm, ![[scr A, script letter A]](https://www.rsc.org/images/entities/char_e520.gif) ≃ 46, t0 = 10−4 s, Dm = 10−13 m2 s−1 and Dth = 10−7 m2 s−1.
≃ 46, t0 = 10−4 s, Dm = 10−13 m2 s−1 and Dth = 10−7 m2 s−1.
Note that by construction, (6) does not ensure that at the outer edge of the cubic simulation box the temperature is maintained at its initial value ![[T with combining tilde]](https://www.rsc.org/images/entities/i_char_0054_0303.gif) i at all times. One of the possibilities is to keep the temperature at the boundary of the simulation box free with no heat flux through the outer edge of the simulation box:
i at all times. One of the possibilities is to keep the temperature at the boundary of the simulation box free with no heat flux through the outer edge of the simulation box:
∂![[T with combining tilde]](https://www.rsc.org/images/entities/i_char_0054_0303.gif) ( (![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ,t)/∂r|outer ,t)/∂r|outer![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) edge = 0. edge = 0. | (10) |
This may serve well to describe the early temperature evolution within small sample cells. In order to mimic experimental realizations in which a colloidal particle is placed in a macroscopically large cell, one can set the temperature at the outer edge of the simulation box
![[T with combining tilde]](https://www.rsc.org/images/entities/i_char_0054_0303.gif) ( (![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ,t)|outer ,t)|outer![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) edge = edge = ![[T with combining tilde]](https://www.rsc.org/images/entities/i_char_0054_0303.gif) i i | (11) |
In the present paper we consider both the free BC with no heat flux through the boundary and the BC given by eqn (11).
For the confined geometry, the spherical colloid is placed at the center of a rectangular box with side length Lz along the z-direction much smaller than the length along the other two directions: Lz ≪ Lx and Lx = Ly. The outer edges of the box along the x and y directions (see Fig. 1) bear a periodic boundary condition (PBC)35 and the top and bottom edges along the z direction hold the surface BC
(![[n with combining circumflex]](https://www.rsc.org/images/entities/i_char_006e_0302.gif) ·∇ψ( ·∇ψ(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ) + αsψ( ) + αsψ(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) )| )|![[scr S, script letter S]](https://www.rsc.org/images/entities/char_e532.gif) = h. = h. | (12) |
Both top and bottom surfaces prefer the same component of the binary solvent with the same strength. The top and bottom surfaces also hold the BC given by (7).
3 Results
3.1 Temperature profile
We have solved (6) with the BC on the surface of the colloid (9) and the initial condition![[T with combining tilde]](https://www.rsc.org/images/entities/i_char_0054_0303.gif) (
(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) , t = 0) =
, t = 0) = ![[T with combining tilde]](https://www.rsc.org/images/entities/i_char_0054_0303.gif) i analytically using spherical coordinates for R ≤ r ≤ L. For the BC given by eqn (10), the stationary state is
i analytically using spherical coordinates for R ≤ r ≤ L. For the BC given by eqn (10), the stationary state is ![[T with combining tilde]](https://www.rsc.org/images/entities/i_char_0054_0303.gif) frs(r) = −|
frs(r) = −|![[T with combining tilde]](https://www.rsc.org/images/entities/i_char_0054_0303.gif) 1|. It is approached according to
1|. It is approached according to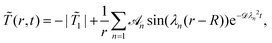 | (13) |
| tan(λn(L − R)) = λnL | (14) |
![[scr A, script letter A]](https://www.rsc.org/images/entities/char_e520.gif) n is given by
n is given by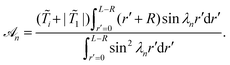 | (15) |
For the temperature at the outer boundary of the simulation box r = L fixed at the value ![[T with combining tilde]](https://www.rsc.org/images/entities/i_char_0054_0303.gif) (r = L,t) =
(r = L,t) = ![[T with combining tilde]](https://www.rsc.org/images/entities/i_char_0054_0303.gif) i we find
i we find
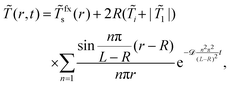 | (16) |
![[T with combining tilde]](https://www.rsc.org/images/entities/i_char_0054_0303.gif) fxs(r) is given by
fxs(r) is given by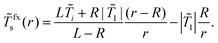 | (17) |
In Fig. 2 we compare the temperature profiles in the solvent evolving in time according to dynamical eqn (6) with two different BC: (i) no heat flux at the outer edge of the simulation box (10) and (ii) a fixed temperature at the edge of the simulation box (11). There, ![[T with combining tilde]](https://www.rsc.org/images/entities/i_char_0054_0303.gif) (
(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ,t) is plotted against the reduced radial distance r from the colloid centre in the midplane z = Lz/2 of the system at a fixed time t = 10 (for the no heat flux (i) BC we also show the temperature profile at the later time t = 200 – see below). The results in Fig. 2 correspond to Lz = Lx = Ly = 100, R = 10,
,t) is plotted against the reduced radial distance r from the colloid centre in the midplane z = Lz/2 of the system at a fixed time t = 10 (for the no heat flux (i) BC we also show the temperature profile at the later time t = 200 – see below). The results in Fig. 2 correspond to Lz = Lx = Ly = 100, R = 10, ![[T with combining tilde]](https://www.rsc.org/images/entities/i_char_0054_0303.gif) i = 1, and
i = 1, and ![[T with combining tilde]](https://www.rsc.org/images/entities/i_char_0054_0303.gif) 1 = −1. The shaded region is the colloid surface. For both types of BC the temperature at the surface of the colloid is maintained at the quench value
1 = −1. The shaded region is the colloid surface. For both types of BC the temperature at the surface of the colloid is maintained at the quench value ![[T with combining tilde]](https://www.rsc.org/images/entities/i_char_0054_0303.gif) 1 = −1 and with increasing distance from the colloid the temperature gradually increases towards its initial value. However, in the case of the fixed (ii) BC (circles),
1 = −1 and with increasing distance from the colloid the temperature gradually increases towards its initial value. However, in the case of the fixed (ii) BC (circles), ![[T with combining tilde]](https://www.rsc.org/images/entities/i_char_0054_0303.gif) (
(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ,t) far away from the colloid is exactly equal to
,t) far away from the colloid is exactly equal to ![[T with combining tilde]](https://www.rsc.org/images/entities/i_char_0054_0303.gif) i. On the other hand, for the no heat flux (i) BC (squares) the temperature away from the colloid is slightly lower than
i. On the other hand, for the no heat flux (i) BC (squares) the temperature away from the colloid is slightly lower than ![[T with combining tilde]](https://www.rsc.org/images/entities/i_char_0054_0303.gif) i. In Fig. 2 we also plot the analytical expressions of
i. In Fig. 2 we also plot the analytical expressions of ![[T with combining tilde]](https://www.rsc.org/images/entities/i_char_0054_0303.gif) (r,t) from (13) and (16), marked by the solid lines, with which our numerical data (symbols) for both agree very well. The slight discrepancy is due to the fact that the solution in (16) is obtained within spherical polar coordinates and the numerical results are obtained in a rectangular box and with a finite cubic grid. Note that a finer mesh will yield a much better match between the two. In the case of the no heat flux (i) BC the system continues to cool down until it reaches the stationary state with
(r,t) from (13) and (16), marked by the solid lines, with which our numerical data (symbols) for both agree very well. The slight discrepancy is due to the fact that the solution in (16) is obtained within spherical polar coordinates and the numerical results are obtained in a rectangular box and with a finite cubic grid. Note that a finer mesh will yield a much better match between the two. In the case of the no heat flux (i) BC the system continues to cool down until it reaches the stationary state with ![[T with combining tilde]](https://www.rsc.org/images/entities/i_char_0054_0303.gif) frs(r) = −|
frs(r) = −|![[T with combining tilde]](https://www.rsc.org/images/entities/i_char_0054_0303.gif) 1|. As can be inferred from the behavior of the temperature profile shown in Fig. 2, at time t = 200 this stationary state is not yet achieved.
1|. As can be inferred from the behavior of the temperature profile shown in Fig. 2, at time t = 200 this stationary state is not yet achieved.
3.2 Coarsening in the bulk
We first explore the effect of temperature evolution on the coarsening dynamics around the colloid in the bulk. Fig. 3 corresponds to the no heat flux (i) BC. There we plot the coarsening snapshots at three different times following a temperature quench of the colloid surface from![[T with combining tilde]](https://www.rsc.org/images/entities/i_char_0054_0303.gif) 0 = 1 to
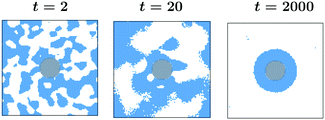
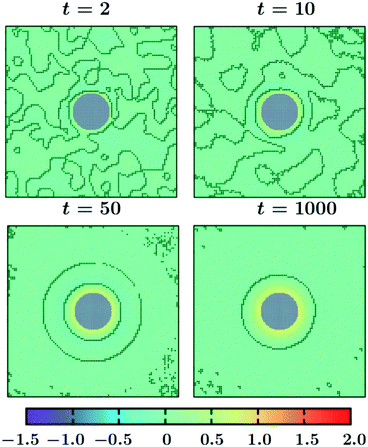
0 = 1 to ![[T with combining tilde]](https://www.rsc.org/images/entities/i_char_0054_0303.gif) 1 = −1. The results in Fig. 3 correspond to a colloid with a homogeneous surface with α = 0.5, and h = 1, i.e., preferring a phase with ψ > 0. The color code for the order parameter is provided in the figure, with the interface between the regions with ψ > 0 and ψ < 0 marked by black lines. Grey circle refers to the colloid. At very early time t = 2 only one thin surface layer is formed on the colloid, whereas in the bulk spinodal-like phase segregation has started which is clear from the contour lines. With increasing time, these surface patterns propagate into the bulk and more concentric rings form. Note that two neighbouring rings consist of opposite phases. The qualitative feature of this process is similar to the coarsening process under a temperature gradient for an off-critical concentration ψ0 = 0.1 and with α = 0.5, and h = 1 (see ref. 18). Once the layered patterns reach the boundaries of the simulation box, the layers start to break up (not shown here but similar to t = 1400 in Fig. 2(b) in ref. 18) due to an interplay of surface and bulk demixing. For larger systems we expect more rings to form, however, the qualitative features should stay the same.
1 = −1. The results in Fig. 3 correspond to a colloid with a homogeneous surface with α = 0.5, and h = 1, i.e., preferring a phase with ψ > 0. The color code for the order parameter is provided in the figure, with the interface between the regions with ψ > 0 and ψ < 0 marked by black lines. Grey circle refers to the colloid. At very early time t = 2 only one thin surface layer is formed on the colloid, whereas in the bulk spinodal-like phase segregation has started which is clear from the contour lines. With increasing time, these surface patterns propagate into the bulk and more concentric rings form. Note that two neighbouring rings consist of opposite phases. The qualitative feature of this process is similar to the coarsening process under a temperature gradient for an off-critical concentration ψ0 = 0.1 and with α = 0.5, and h = 1 (see ref. 18). Once the layered patterns reach the boundaries of the simulation box, the layers start to break up (not shown here but similar to t = 1400 in Fig. 2(b) in ref. 18) due to an interplay of surface and bulk demixing. For larger systems we expect more rings to form, however, the qualitative features should stay the same.
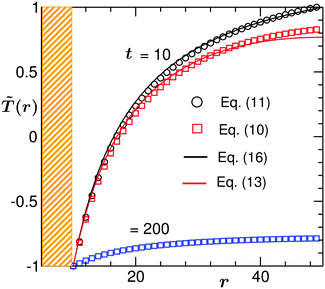 | ||
Fig. 2 Temperature profiles near a homogeneous colloid suspended in a binary solvent at time t = 10 following a temperature quench of the colloid surface from ![[T with combining tilde]](https://www.rsc.org/images/entities/i_char_0054_0303.gif) i = 1 to i = 1 to ![[T with combining tilde]](https://www.rsc.org/images/entities/i_char_0054_0303.gif) 1 = −1. The surrounding solvent cools due to heat flow from the colloid. r is the radial distance in the midplane from the colloid center. The shaded region denotes the colloid surface. The square and circle symbols correspond to the numerical data for the temperature evolution following eqn (6) with the BC given by eqn (10) and by eqn (11), respectively. In the case of the BC given by eqn (11), the temperature of the solvent far away from the colloid is always maintained at the initial temperature 1 = −1. The surrounding solvent cools due to heat flow from the colloid. r is the radial distance in the midplane from the colloid center. The shaded region denotes the colloid surface. The square and circle symbols correspond to the numerical data for the temperature evolution following eqn (6) with the BC given by eqn (10) and by eqn (11), respectively. In the case of the BC given by eqn (11), the temperature of the solvent far away from the colloid is always maintained at the initial temperature ![[T with combining tilde]](https://www.rsc.org/images/entities/i_char_0054_0303.gif) i = −1, whereas using the BC given by eqn (10) leads to lowering of the temperature far away from the colloid. For the latter case, at t = 200 the whole system is cooled down below the critical temperature and the temperature profile is close to the steady state one given by i = −1, whereas using the BC given by eqn (10) leads to lowering of the temperature far away from the colloid. For the latter case, at t = 200 the whole system is cooled down below the critical temperature and the temperature profile is close to the steady state one given by ![[T with combining tilde]](https://www.rsc.org/images/entities/i_char_0054_0303.gif) frs(r) = −| frs(r) = −|![[T with combining tilde]](https://www.rsc.org/images/entities/i_char_0054_0303.gif) 1|. The solid lines stand for the corresponding analytical predictions for 1|. The solid lines stand for the corresponding analytical predictions for ![[T with combining tilde]](https://www.rsc.org/images/entities/i_char_0054_0303.gif) (r,t) (see eqn (13) and (16)) with which the numerical data accord very well. For details of the numerical technique and analytical solutions, see the main text. Results correspond to L = 100, R = 10, and (r,t) (see eqn (13) and (16)) with which the numerical data accord very well. For details of the numerical technique and analytical solutions, see the main text. Results correspond to L = 100, R = 10, and ![[scr D, script letter D]](https://www.rsc.org/images/entities/char_e523.gif) = 50. = 50. | ||
In Fig. 4, we present snapshots of the order parameter evolution for the fixed (ii) BC. The surface patterns bear spherical symmetry like in Fig. 3. However, compared to Fig. 3 the ring-like layers in this case propagate over a much shorter distance from the colloid. Also, coarsening progresses much faster in this case. Thus, the different BCs for the temperature evolution (eqn (10) and (11)) do not change the qualitative features of the surface morphology, however, they alter the distance over which the surface patterns propagate.
In order to further quantify the order parameter morphology shown in Fig. 3 and 4, we calculate the two-point equal time correlation function defined as
| C(ζ = r − R,t) = 〈ψ(R,t)ψ(R + ζ,t)〉 − 〈ψ(R,t)〉〈ψ(R + ζ,t)〉 | (18) |
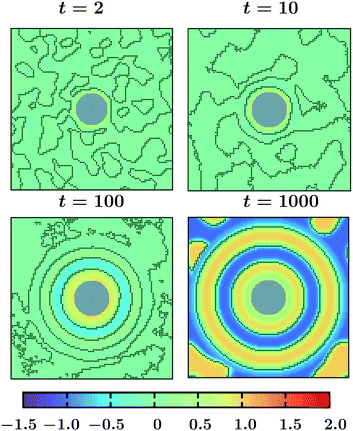 | ||
Fig. 3 Non-equilibrium coarsening of a binary solvent under a time-dependent temperature gradient around a colloid with preferential attraction to one of the two components of the binary mixture. Starting with a disordered initial configuration the colloid surface is cooled to ![[T with combining tilde]](https://www.rsc.org/images/entities/i_char_0054_0303.gif) 1 = −1 and the subsequent evolution of the order parameter and temperature fields is described by eqn (5) and (6), respectively. The BC for the temperature field at the outer edge of the simulation box is given by eqn (10). All snapshots are in the midplane z = Lz/2 of the system. The color code corresponds to different values of the order parameter with the black lines marking the contour lines and the grey circular region stands for the colloid. At early time, a spinodal-like decomposition in the bulk is present. With time, concentric circular surface rings form and they propagate into the bulk. Results correspond to L = 100, R = 10, 1 = −1 and the subsequent evolution of the order parameter and temperature fields is described by eqn (5) and (6), respectively. The BC for the temperature field at the outer edge of the simulation box is given by eqn (10). All snapshots are in the midplane z = Lz/2 of the system. The color code corresponds to different values of the order parameter with the black lines marking the contour lines and the grey circular region stands for the colloid. At early time, a spinodal-like decomposition in the bulk is present. With time, concentric circular surface rings form and they propagate into the bulk. Results correspond to L = 100, R = 10, ![[T with combining tilde]](https://www.rsc.org/images/entities/i_char_0054_0303.gif) 1 = −1, α = 0.5, and h = 1. 1 = −1, α = 0.5, and h = 1. | ||
 | ||
| Fig. 4 Same as Fig. 3, but for the temperature evolution with the BC at the outer edge of the simulation box given by eqn (11). In this case the ring-like surface patterns do not propagate much into the bulk and coarsening is much faster as compared to Fig. 3. | ||
In Fig. 5, C(ζ,t) for the case of the no flux (i) BC (corresponding to the snapshots shown in Fig. 3) is plotted vs. the rescaled distance (ζ + R)/R, at three times t. At very early times, the spatial decay of C(ζ,t) is rather fast. Upon increasing time it slows down, the first layer widens and C(ζ,t) develops multiple peaks, which correspond to the various surface layers. As observed, at t = 10 C(ζ,t) has one prominent minimum, indicative of one surface layer. However, at t = 200 C(ζ,t) exhibits damped oscillations which extend to the boundary of the system. The corresponding temperature profile is shown in Fig. 2. Although at time t = 200 the temperature in the whole sample is below the critical one, the pattern of phase separation is not that of a standard spinodal decomposition but remains ring-like (see Fig. 3).
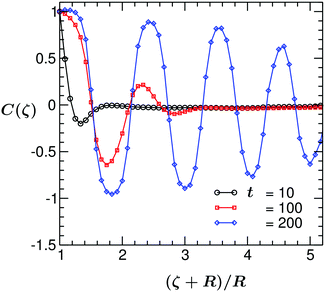 | ||
| Fig. 5 Plot of the two-point equal time correlation function C(ζ = r − R) of the binary solvent vs. the scaled distance (ζ + R)/R in the midplane of the system, at three different times. Results correspond to the coarsening mechanism with a temperature gradient following eqn (6) with no flux (i) BC eqn (10) and for a colloid with preferential attraction to one of the two components of the binary solvent. Each maximum/minimum in C(ζ,t) corresponds to one surface layer around the colloid. With increasing time the thickness of the surface layer increases. All system parameters are the same as in Fig. 3. | ||
This has to be compared with the behavior of the correlation function for the case of the fixed (ii) BC (corresponding to the snapshots shown in Fig. 4). In Fig. 6, we plot C(ζ,t) vs. the scaled distance (ζ + R)/R, at three different times. The qualitative trend of C(ζ,t) is similar to the one described above. However, one distinct feature is observed at very late times: for the fixed (ii) BC C(ζ,t) exhibits only two minima/maxima. This is due to the fact that for the fixed (ii) BC the temperature further away from the colloid stays always above Tc and the surface patterns can propagate over a much shorter distance from the colloid surface.
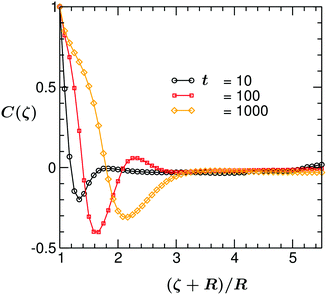 | ||
| Fig. 6 The same as in Fig. 5, but for the temperature evolution followed by eqn (6) with fixed (ii) BC eqn (11). At very late times, C(ζ,t) exhibits only two mimima/maxima. | ||
One factor that influences the early stage of the solvent coarsening is the size of the colloidal particle. This can be inferred from Fig. 7(a), which shows the early time t = 10 angularly averaged order parameter (OP) profile ψ(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ,t) in the midplane z = Lz/2 of the system for the (ii) BC. There, the results for three values of the colloid radius R are presented. In order to avoid finite-size effects on the domain size, the results presented in Fig. 7 correspond to different values of colloid radius R and system size L chosen such that the space available for domain formation, viz., L/2 − R is kept the same. We find that upon a roughly 3.3 fold increase of the colloid radius R, the value of the OP on the colloid surface ψ(0,t) increases monotonically by a factor of ca. 1.3. Concomitantly – and consistent with the conserved dynamics – the minimum of ψ(
,t) in the midplane z = Lz/2 of the system for the (ii) BC. There, the results for three values of the colloid radius R are presented. In order to avoid finite-size effects on the domain size, the results presented in Fig. 7 correspond to different values of colloid radius R and system size L chosen such that the space available for domain formation, viz., L/2 − R is kept the same. We find that upon a roughly 3.3 fold increase of the colloid radius R, the value of the OP on the colloid surface ψ(0,t) increases monotonically by a factor of ca. 1.3. Concomitantly – and consistent with the conserved dynamics – the minimum of ψ(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ,t) deepens by approximately the same factor. Note that the position of the minimum remains almost unchanged. This is because, at least at early times, it is determined by the wave vector characterizing the fastest growing mode.18 In Fig. 7(b), we also show the OP profiles at a late time t = 1000 when the systems almost reached the steady state. In this case, with increasing R by a factor of ca. 3.3, the value of the OP on the colloid surface increases by a factor of roughly 1.28.
,t) deepens by approximately the same factor. Note that the position of the minimum remains almost unchanged. This is because, at least at early times, it is determined by the wave vector characterizing the fastest growing mode.18 In Fig. 7(b), we also show the OP profiles at a late time t = 1000 when the systems almost reached the steady state. In this case, with increasing R by a factor of ca. 3.3, the value of the OP on the colloid surface increases by a factor of roughly 1.28.
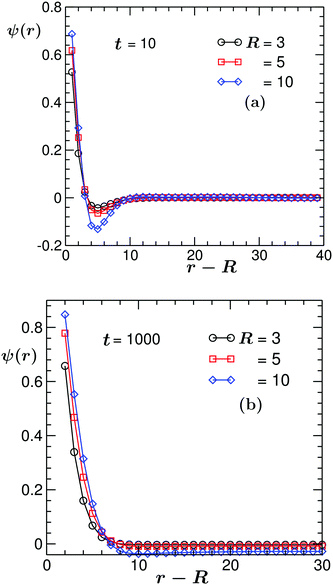 | ||
Fig. 7 Angularly averaged order parameter profile ψ(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ,t) vs. the distance (r − R) from the colloid surface at (a) an early time t = 10 of the coarsening process and (b) at a very late time t = 1000 when the system has almost reached the steady state. Different curves correspond to different colloid sizes. The temperature field evolves according to eqn (6) with fixed (ii) BC eqn (11). At both times, the value of the order parameter on the colloid surface increases with increasing radius R. ,t) vs. the distance (r − R) from the colloid surface at (a) an early time t = 10 of the coarsening process and (b) at a very late time t = 1000 when the system has almost reached the steady state. Different curves correspond to different colloid sizes. The temperature field evolves according to eqn (6) with fixed (ii) BC eqn (11). At both times, the value of the order parameter on the colloid surface increases with increasing radius R. | ||
It is instructive to compare the OP patterns evolving in the presence of a temperature gradient with those for an instantaneous quench, i.e., in the absence of any temperature gradient. The composition wave observed in the latter case (see Fig. 8) is distinctly different from the one in Fig. 3 and 4. For the chosen values of α and h, only one ‘ring’ forms and the spinodal-like patterns are more prevalent in the system. This observation is also in agreement with phase separation in polymer blends around fillers.37 Of course, with time the thickness of the surface ring around the colloid surface increases. However, the qualitative and quantitative features of the coarsening patterns are different. As one expects, the long time limit pattern for an instantaneous homogeneous quench is the same as in the system following a temperature quench of the colloid surface with the no flux (i) BC at the outer edge of the simulation box (the one in Fig. 3). This is because in the latter case the stationary temperature profile is constant and equal to ![[T with combining tilde]](https://www.rsc.org/images/entities/i_char_0054_0303.gif) 1 = −1 throughout the system. Accordingly, the solvent phase separates globally forming an interface around the colloid, while for the fixed (ii) BC there is always a temperature gradient present in the system and the solvent remains in a mixed phase far away from the colloid.
1 = −1 throughout the system. Accordingly, the solvent phase separates globally forming an interface around the colloid, while for the fixed (ii) BC there is always a temperature gradient present in the system and the solvent remains in a mixed phase far away from the colloid.
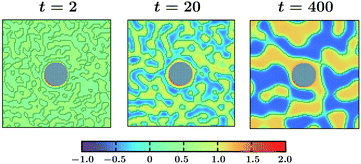 | ||
| Fig. 8 Coarsening patterns around a colloidal particle for an instantaneous quench, i.e., when both the colloid and the solvent are at the same constant temperature. Only one surface ring forms at early time. Spinodal-like patterns are more prominent, unlike in Fig. 4. | ||
Now, we focus on the influence of the surface properties of the colloid on the coarsening morphology in the presence of a temperature gradient, for ψ0 = 0. In Fig. 9, we present snapshots during the temperature-gradient induced coarsening around a neutral colloid, i.e., for α = 0 and h = 0. The temperature field obeys the fixed temperature (ii) BC. Since h = 0, the order OP values are much smaller as compared to Fig. 3 and 4. For the sake of clarity, in Fig. 9 we plot only the part of the solvent where ψ(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ,t) > 0 in blue color. The white part corresponds to the other phase ψ < 0. Clearly, starting from very early time the surface pattern is very different from the pattern for preferential attraction (see Fig. 3 and 4). While in the case of preferential attraction with ψ0 = 0 only one phase stays on the colloid surface at all times, for a neutral colloid both phases are present (see t = 2 and t = 20) until the system almost completely phase separates at t = 2000. Besides, the surface morphology for a neutral colloid is not spherically symmetric.
,t) > 0 in blue color. The white part corresponds to the other phase ψ < 0. Clearly, starting from very early time the surface pattern is very different from the pattern for preferential attraction (see Fig. 3 and 4). While in the case of preferential attraction with ψ0 = 0 only one phase stays on the colloid surface at all times, for a neutral colloid both phases are present (see t = 2 and t = 20) until the system almost completely phase separates at t = 2000. Besides, the surface morphology for a neutral colloid is not spherically symmetric.
In ref. 18 the solvent patterns around a neutral colloid during the coarsening process in the presence of a temperature gradient have been studied for the off-critical concentration ψ0 = 0.1. Comparing results from ref. 18 with the present ones, we can see qualitative differences: for the critical concentration of the solvent, both phases form on the surface of a neutral colloid and the surface morphology is not spherically symmetric whereas for an off-critical concentration, only one phase is present on the surface of the neutral colloid and the surface patterns are spherically symmetric. Solvent concentration thus strongly affects the surface morphology for a neutral colloid.
3.3 Confinement effects
In this section we investigate the effect of confinement on the non-equilibrium phase segregation dynamics around the colloid. This is highly relevant for experimental studies where typically sample cells are finite slabs. Fig. 10 depicts the temperature profile of the binary solvent around the colloid at time t = 10 following the temperature quench from![[T with combining tilde]](https://www.rsc.org/images/entities/i_char_0054_0303.gif) = 1 to
= 1 to ![[T with combining tilde]](https://www.rsc.org/images/entities/i_char_0054_0303.gif) 1 = −1 inside the binodal region. Results correspond to the cross-section in the x–z plane at y = Ly/2 with the confining walls at z = 0 and z = Lz. Both walls and the colloid prefer the same phase ψ > 0 of the binary solvent with the surface parameters α = 0.5 and h = 1. A strong temperature gradient is observed in Fig. 10. The temperature at the outer boundaries of the simulation box is maintained at
1 = −1 inside the binodal region. Results correspond to the cross-section in the x–z plane at y = Ly/2 with the confining walls at z = 0 and z = Lz. Both walls and the colloid prefer the same phase ψ > 0 of the binary solvent with the surface parameters α = 0.5 and h = 1. A strong temperature gradient is observed in Fig. 10. The temperature at the outer boundaries of the simulation box is maintained at ![[T with combining tilde]](https://www.rsc.org/images/entities/i_char_0054_0303.gif) = 1 according to eqn (11) whereas close to the colloid
= 1 according to eqn (11) whereas close to the colloid ![[T with combining tilde]](https://www.rsc.org/images/entities/i_char_0054_0303.gif) (
(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ) < 0. The spread of the region with negative temperature increases for larger colloids. The spatial gradient in the temperature field is clearly visible in Fig. 10.
) < 0. The spread of the region with negative temperature increases for larger colloids. The spatial gradient in the temperature field is clearly visible in Fig. 10.
The evolution of the OP for a thin slab with Lz = 20 and for a thick slab with Lz = 40 is shown in Fig. 11 and in Fig. 12, respectively. In both figures Lx = Ly = 100 and all other parameters are the same as in Fig. 10. The color indicates the value of the OP. As can be seen in Fig. 11, already at very early time t = 2 the surface layers form around the colloid as well as on the top and the bottom walls. These surface layers are all connected with each other, forming a bridge-like structure. Away from the confining surfaces exerting symmetry breaking BCs on the OP, the spinodal-like patterns are prominent. With increasing time the surface layers and the bridge get thicker and the bulk phase separation proceeds until a stationary state is achieved (see t = 100, which is close to the stationary state). Note that the coarsening process in this case is much faster as compared to that in the bulk. This is because of the presence of the walls which attract one species of the solvent favorably and thus speed up phase separation in the bulk. In the case of a thicker slab (see Fig. 12), at very early time t = 2 the surface layers form on the colloid and the top and bottom walls, like in Fig. 11. However, in this case, the wall surface layers are separated from the one on the colloid and no bridge formation occurs. With increasing time the surface layers get thicker (see t = 100) and the bulk phase separates. However, no thick bridge forms – even at very late time. Thus, coarsening of a solvent around the confined colloid depends strongly on the separation of the confining walls and this may have repercussion in multi-colloid dynamics as well. For example, a capillary interaction may lead to clustering phenomena.
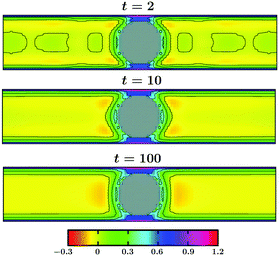 | ||
Fig. 11 Non-equilibrium order parameter evolution around a colloidal particle confined between two walls following a temperature quench from ![[T with combining tilde]](https://www.rsc.org/images/entities/i_char_0054_0303.gif) = 1 to = 1 to ![[T with combining tilde]](https://www.rsc.org/images/entities/i_char_0054_0303.gif) 1 = −1. All parameters are the same as in Fig. 10. Results correspond to a thin slab with Lz = 20 and Lx = Ly = 100. A bridge connecting the colloidal particle and both the top and bottom walls starts to form already at very early time. With increasing time this bridge and the thickness of the surface layers grow and spinodal-like phase separation proceeds in the bulk. 1 = −1. All parameters are the same as in Fig. 10. Results correspond to a thin slab with Lz = 20 and Lx = Ly = 100. A bridge connecting the colloidal particle and both the top and bottom walls starts to form already at very early time. With increasing time this bridge and the thickness of the surface layers grow and spinodal-like phase separation proceeds in the bulk. | ||
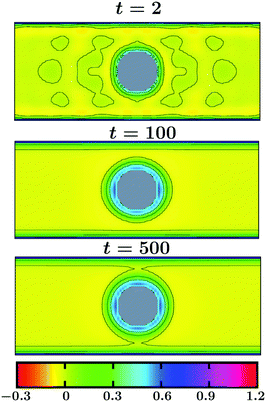 | ||
| Fig. 12 Same as in Fig. 11, but for a thicker slab with Lz = 40. At very early time the surface layers form around the colloidal particle as well as on the top and the bottom walls. As time increases, these surface layers get thicker and spinodal-like phase separation proceeds in the bulk. Note that no prominent bridge formation is observed unlike in Fig. 11. | ||
3.4 Soret term
In the present phenomenological approach, an effect of the inhomogeneous temperature field, the Ludwig–Soret effect, enters only through the OP flux due to the chemical potential gradient![[j with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006a_20d1.gif) ∝ −∇μ(r,t). However, following the Onsager's theory for irreversible processes, which provides phenomenological equations relating thermodynamic fluxes to the generalized forces −μ/T and 1/T,38 one can add to the OP flux
∝ −∇μ(r,t). However, following the Onsager's theory for irreversible processes, which provides phenomenological equations relating thermodynamic fluxes to the generalized forces −μ/T and 1/T,38 one can add to the OP flux ![[j with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006a_20d1.gif) a cross-term due to the temperature gradient with an independent coefficient related to the thermal diffusion coefficient
a cross-term due to the temperature gradient with an independent coefficient related to the thermal diffusion coefficient ![[scr D, script letter D]](https://www.rsc.org/images/entities/char_e523.gif) T.
T.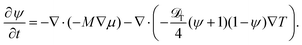 | (19) |
Here we assume that both M and ![[scr D, script letter D]](https://www.rsc.org/images/entities/char_e523.gif) T are constants. Upon rescaling and adding conserving noise eqn (19) reduces to
T are constants. Upon rescaling and adding conserving noise eqn (19) reduces to
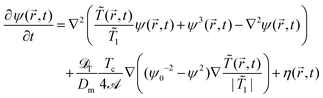 | (20) |
For a typical binary solvent away from phase transitions the ratio ![[scr D, script letter D]](https://www.rsc.org/images/entities/char_e523.gif) T/
T/![[scr D, script letter D]](https://www.rsc.org/images/entities/char_e523.gif) m, which is called the Soret coefficient, is of the order of ST ≃ 10−3 K−1. This means that for deep quenches the Ludwig–Soret contribution causes only a minor perturbation to the behavior of a system. Indeed, we have checked that for the values of the coefficient B = (
m, which is called the Soret coefficient, is of the order of ST ≃ 10−3 K−1. This means that for deep quenches the Ludwig–Soret contribution causes only a minor perturbation to the behavior of a system. Indeed, we have checked that for the values of the coefficient B = (![[scr D, script letter D]](https://www.rsc.org/images/entities/char_e523.gif) TTc)/(4Dm
TTc)/(4Dm![[scr A, script letter A]](https://www.rsc.org/images/entities/char_e520.gif) ) ranging from 0 (i.e., no Soret effect) to 0.5 and with ψ0 = 0 the changes in the OP profile and in the two-point equal time correlation function are minimal. Specifically, for the temperature field evolving according to eqn (6) with the fixed (ii) BC (eqn (11)), the OP value ψ(0,t = 10) on the colloid surface reduces from 0.7479 at B = 0 to 0.7385 for B = 0.5. The first minimum of both the OP and the normalized two-point equal time correlation function C(r) also slightly decreases with increasing B; for the OP it takes values −0.1862 for B = 0 and −0.2004 at B = 0.5 whereas for C(r) it reaches the value −0.4636 for B = 0 and −0.5230 for B = 0.5. We note that for the fixed temperature (ii) BC, the Soret term in the evolution equation eqn (20) for the OP breaks the conservation of the total OP. This is why the OP profile is slightly shifted towards negative values. This is not the case for the no flux (i) BC. Nevertheless, also for the latter BC the overall changes in the OP and in C(r) in the studied range of parameter B ≤ 0.5 are tiny.
) ranging from 0 (i.e., no Soret effect) to 0.5 and with ψ0 = 0 the changes in the OP profile and in the two-point equal time correlation function are minimal. Specifically, for the temperature field evolving according to eqn (6) with the fixed (ii) BC (eqn (11)), the OP value ψ(0,t = 10) on the colloid surface reduces from 0.7479 at B = 0 to 0.7385 for B = 0.5. The first minimum of both the OP and the normalized two-point equal time correlation function C(r) also slightly decreases with increasing B; for the OP it takes values −0.1862 for B = 0 and −0.2004 at B = 0.5 whereas for C(r) it reaches the value −0.4636 for B = 0 and −0.5230 for B = 0.5. We note that for the fixed temperature (ii) BC, the Soret term in the evolution equation eqn (20) for the OP breaks the conservation of the total OP. This is why the OP profile is slightly shifted towards negative values. This is not the case for the no flux (i) BC. Nevertheless, also for the latter BC the overall changes in the OP and in C(r) in the studied range of parameter B ≤ 0.5 are tiny.
The cross-term may become more important in the asymptotic critical regime close to Tc (here we refer to a recent review on the Soret effect39). This is because the interdiffusion constant Dm shows critical slowing down,40i.e., the increase of characteristic diffusion time ∝Dm upon approaching a critical point, whereas the thermal coefficient ![[scr D, script letter D]](https://www.rsc.org/images/entities/char_e523.gif) T does not. Specifically, in the asymptotic critical regime Dm ∝ |τ|−ν(1
T does not. Specifically, in the asymptotic critical regime Dm ∝ |τ|−ν(1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) +
+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ηz), where τ = (T − Tc)/Tc, ν ≃ 0.63 is the critical exponent of the bulk correlation length of the solvent, and ηz ≃ 0.063 is the critical exponent of the solvent viscosity. Because DT ≃ const, one has ST ∝ |τ|−ν(1
ηz), where τ = (T − Tc)/Tc, ν ≃ 0.63 is the critical exponent of the bulk correlation length of the solvent, and ηz ≃ 0.063 is the critical exponent of the solvent viscosity. Because DT ≃ const, one has ST ∝ |τ|−ν(1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) +
+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ηz). This means that for very shallow quenches the Soret term eqn (20) can be even dominant.
ηz). This means that for very shallow quenches the Soret term eqn (20) can be even dominant.
4 Summary and outlook
In summary, using numerical simulations and analytical theory we have studied the non-equilibrium early-time coarsening dynamics of a binary solvent around a suspended colloidal particle in the presence of a time-dependent temperature gradient. Following a sudden temperature quench of the colloid surface the surrounding solvent cools via heat diffusion. The ensuing order parameter field is solved using the modified Cahn–Hilliard–Cook equation which takes care of the coupling to a time-dependent temperature-field, in conjunction with the heat diffusion equation which dictates the temporal evolution of the temperature field. The colloid surface attraction preference to one of the two components of the binary mixture is modeled by considering a symmetry-breaking surface field. Two types of boundary conditions for the temperature field – mimicking different physical situations – have been considered and their influence on the non-equilibrium dynamics has been explored in detail. We have studied the coarsening process for different surface adsorption properties, concentrations of the solvent and temperature evolution conditions. Under the time-dependent temperature gradient and for a colloid with selective surface adsorption, upon a temperature quench spherical surface layers form close to the colloid, which with increasing time propagate into the bulk. Concomitantly, the thickness of the surface layer on the colloid increases with time. For a neutral colloid, i.e., without any surface adsorption preference, drastic changes in the coarsening morphology are observed. In the latter case, both phases prevail on the colloid surface whereas in the former case only one phase stays on the surface. Also, in the absence of preferential attraction the surface patterns are not spherically symmetric. These features of coarsening are reflected in the two-point equal time correlation function and the order parameter profiles. We have also provided a comparison with the coarsening phenomena occurring after an instantaneous quench, i.e., without any temperature gradient in the system. In the absence of the temperature gradient, the surface ring formation is much less pronounced as compared to the spinodal decomposition.Our study also presents results on the coarsening process around a confined colloid in the presence of two confining surfaces with a preference to the same component of the binary mixture. In this case, enriched surface layers form both on the colloid as well as on the walls which make coarsening much faster in the confined geometry. For thin films a liquid bridge forms connecting the colloidal particle and the confining walls. These results are particularly important for experimental realizations where typically a colloidal suspension is confined in a quasi-two-dimensional chamber. It will be interesting to study Janus particles in such geometries and the role of bridging for the mechanism of self-propulsion.
We note that the details of pattern evolution such as, e.g., the extension of the surface patterns depend crucially on the BCs of the temperature field imposed at the outer edge of the system. The type of the BCs for particular cases could be validated experimentally by comparing the coarsening morphologies. Qualitative features of our numerical results have been found in experiments with micron-sized colloids, which will be reported elsewhere. In future we will undertake an improvement of our phenomenological model to include heat flow across the colloidal particle, which will better mimic experimental situations, and to account for heat dissipation.
It is known that in the presence of an externally applied temperature gradient, colloidal particles in a solution undergo motion, which is known as thermophoresis. In our system, the particle itself generates the temperature gradient. However, even if we were able to account for the motion of a colloid (in our approach the particle is fixed in space), we would not expect any active motion. The reason lies in the particle homogeneity – one needs an asymmetric source that generates and maintains temperature and/or concentration gradients around the particle for self-propulsion to occur. This can be realized by using, e.g., Janus particles.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
The work by AM has been supported by the Polish National Science Center (Harmonia Grant No. 2015/18/M/ST3/00403). We thank Mihail N. Popescu for an inspiring discussion.References
- R. Akbarzadeh and A. M. Yousefi, J. Biomed. Mater. Res., Part B, 2014, 102, 1304 CrossRef PubMed
.
- E. Torino, R. Aruta, T. Sibillano, C. Giannini and P. A. Netti, Sci. Rep., 2016, 6, 32727 CrossRef PubMed
.
- S. K. Das, S. Puri, J. Horbach and K. Binder, Phys. Rev. Lett., 2006, 96, 016107 CrossRef PubMed
.
- S. Puri, J. Phys.: Condens. Matter, 2005, 17, R1 CrossRef
.
- K. Binder, S. Puri, S. K. Das and J. Hörbach, J. Stat. Phys., 2010, 138, 51–84 CrossRef
.
- H.-J. Chung, K. Ohno, T. Fukuda and R. J. Composto, Nano Lett., 2005, 5, 1878 CrossRef PubMed
.
- E. M. Herzig, K. A. White, A. B. Schofield, W. C. K. Poon and P. S. Clegg, Nat. Mater., 2007, 6, 966 CrossRef PubMed
.
- K. Stratford, R. Adhikari, I. Pagonabarraga, J.-C. Desplat and M. E. Cates, Science, 2005, 309, 2198 CrossRef PubMed
.
- A. Krekhov, V. Weith and W. Zimmermann, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2013, 88, 040302(R) CrossRef PubMed
.
- Y. Iwashita and Y. Kimura, Soft Matter, 2013, 9, 10694 RSC
.
- R. Kurita, Sci. Rep., 2017, 7, 6912 CrossRef PubMed
.
- W. Köhler, A. Krekhov and W. Zimmermann, Adv. Polym. Sci., 2007, 227, 145 CrossRef
.
- H.-R. Jiang, N. Yoshinaga and M. Sano, Phys. Rev. Lett., 2010, 105, 268302 CrossRef PubMed
.
- G. Volpe, I. Buttinoni, D. Vogt, H.-J. Kammerer and C. Bechinger, Soft Matter, 2011, 7, 8810 RSC
.
- I. Buttinoni, G. Volpe, F. Kümmel, G. Volpe and C. Bechinger, J. Phys.: Condens. Matter, 2012, 24, 284129 CrossRef PubMed
.
- J. R. Gomez-Solano, A. Blokhuis and C. Bechinger, Phys. Rev. Lett., 2016, 116, 138301 CrossRef PubMed
.
- J. R. Gomez-Solano, S. Samin, C. Lozano, P. Ruedas-Batuecas, R. van Roij and C. Bechinger, Sci. Rep., 2017, 7, 14891 CrossRef PubMed
.
- S. Roy, S. Dietrich and A. Maciolek, Phys. Rev. E, 2018, 97, 042603 CrossRef PubMed
.
- A. J. Bray, Adv. Phys., 1994, 43, 357 CrossRef
.
-
K. Binder, in Kinetics of Phase Transitions, ed. S. Puri and V. Wadhawan, CRC, Boca Raton, 2009, p. 62 Search PubMed
.
- E. D. Siggia, Phys. Rev. A: At., Mol., Opt. Phys., 1979, 20, 595 CrossRef
.
- H. Furukawa, Phys. Rev. A: At., Mol., Opt. Phys., 1987, 36, 2288 CrossRef
.
- P. C. Hohenberg and B. I. Halperin, Rev. Mod. Phys., 1977, 49, 435 CrossRef
.
- R. C. Ball and R. L. H. Essery, J. Phys.: Condens. Matter, 1990, 2, 10303 CrossRef
.
- P. K. Jaiswal, S. Puri and K. Binder, EPL, 2013, 103, 66003 CrossRef
.
-
K. Kawasaki, Phase Transition and Critical Phenomena, ed. C. Domb and M. S. Green, Academic Press, London, 1972, vol. 2 Search PubMed
.
- S. S. Leung and R. B. Griffiths, Phys. Rev. A: At., Mol., Opt. Phys., 1973, 8, 2670 CrossRef
.
- A. Onuki, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1997, 55, 403 CrossRef
.
- H. W. Alt and I. Pawlow, Phys. D, 1992, 59, 389 CrossRef
.
- A. Onuki, Phys. Rev. Lett., 2005, 94, 054501 CrossRef PubMed
.
- G. Gonnella, A. Lamura and A. Piscitelli, J. Phys. A: Math. Theor., 2008, 41, 105001 CrossRef
.
- H. W. Diehl and H. K. Janssen, Phys. Rev. A: At., Mol., Opt. Phys., 1992, 45, 7145 CrossRef
.
- H. W. Diehl, Int. J. Mod. Phys. B, 1997, 11, 3503 CrossRef
.
-
J. C. Butcher, Numerical methods for ordinary differential equations, Wiley, England, 2008 Search PubMed
.
-
M. P. Allen and D. J. Tildesley, Computer Simulations of Liquids, Clarendon, Oxford, 1987 Search PubMed
.
-
L. M. Surhone, M. T. Timpledon and S. F. Marseken, Trilinear Interpolation, Betascript Publishing, United States, 2010 Search PubMed
.
- B. P. Lee, J. F. Douglas and S. C. Glotzer, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1999, 60, 5812 CrossRef
.
- L. Onsager, Phys. Rev., 1931, 37, 405 CrossRef
.
- W. Köhler and K. Morozov, J. Non-Equilib. Thermodyn., 2016, 41, 151 Search PubMed
.
- P. C. Hohenberg and B. I. Halperin, Rev. Mod. Phys., 1977, 49, 435 CrossRef
.
| This journal is © The Royal Society of Chemistry 2018 |