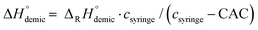Open Access Article
Open Access ArticleSweet surfactants: packing parameter-invariant amphiphiles as emulsifiers and capping agents for morphology control of inorganic particles†
Michael
Voggel
,
Rebecca M.
Meinusch
,
Vanessa
Siewert
,
Marius
Kunkel
,
Valentin
Wittmann
 * and
Sebastian
Polarz
* and
Sebastian
Polarz
 *
*
University of Konstanz, Department of Chemistry, Universitätsstraße 10, 78457 Konstanz, Germany. E-mail: valentin.wittmann@uni-konstanz.de; sebastian.polarz@uni-konstanz.de
First published on 22nd August 2018
Abstract
Surfactants are not only pivotal constituents in any biological organism in the form of phospholipids, they are also essential for numerous applications benefiting from a large, internal surface, such as in detergents, for emulsification purposes, phase transfer catalysis or even nanoparticle stabilization. A particularly interesting, green class of surfactants contains glycoside head groups. Considering the variability of glycosides, a large number of surfactant isomers become accessible. According to established models in surfactant science such as the packing parameter or the hydrophilic lipophilic balance (HLB), they do not differ from each other and should, thus, have similar properties. Here, we present the preparation of a systematic set of glycoside surfactants and in particular isomers. We investigate to which extent they differ in several key features such as critical aggregation concentration, thermodynamic parameters, etc. Analytical methods like isothermal titration calorimetry (ITC), tensiometry, dynamic light scattering (DLS), small angle-X-ray scattering (SAXS), transmission electron microscopy (TEM) and others were applied. It was found that glycosurfactant isomers vary in their emulsification properties by up to two orders of magnitude. Finally, we have investigated the role of the surfactants in a microemulsion-based technique for the generation of zinc oxide (ZnO) nanoparticles. We found that the choice of the carbohydrate head has a marked effect on the shape of the formed inorganic nanocrystals.
1 Introduction
The generic term ‘amphiphile’ refers to substances, which are compatible with media characterized by different polarity. Regarding their polarity, solvents are typically considered either hydrophilic (water, alcohols) or hydrophobic (oils). Because of their unique property, amphiphiles are used in numerous applications involving media of different polarity, for example as detergents, emulsifiers, phase-transfer agents or as stabilizing agents in nanoparticle synthesis. Their ability to undergo self-assembly is another fascinating feature of amphiphiles. Classical examples are the formation of micelles or liquid crystalline phases.Surfactants are one subclass among amphiphiles. They possess a well-defined molecular architecture, in which a hydrophilic head group is attached to a hydrophobic moiety, in most cases an alkyl chain. Surfactants can be further categorized according to their head group to be either ionic or non-ionic.1 While the number of cationic or anionic groups is relatively limited, a large variety of non-ionic head groups exists, and their choice profoundly affects the properties of the surfactant.2,3 Numerous non-ionic surfactants contain ethoxylates and oligo-ethylene glycol derivatives, respectively.
Surfactants with hydrophilic head groups cannot only be generated by de novo synthesis, they can also originate from the natural pool of organic compounds. For example, alkyl (poly)glycosides are surfactants produced at a large scale (>300![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 t/a) from sustainable resources, such as starch and fat.4 The obtained mixture of substances can vary in the number of carbohydrates, their anomeric configuration, and the degree of alkylation.5 The chemistry of these carbohydrate surfactants was already established by E. Fischer in 1911,6 and a comprehensive overview was given by Rybinski and Hill in 1998.7 The advantages of carbohydrate surfactants are manifold and include biodegradability, chirality and low toxicity. Due to these properties, they find numerous applications in detergents and cosmetics. In more specialized applications they have been successfully used for the extraction and crystallization of proteins or for transfection.8 Carbohydrate surfactants can also undergo self-assembly and form so-called niosomes, the synthetic analogues of liposomes.9 Due to their enhanced stability, niosomes have been successfully tested as biocompatible drug-delivery systems.10 The application of glycoside surfactants in enantioselective phase transfer catalysis is highly interesting, but is still less explored.11,12
000 t/a) from sustainable resources, such as starch and fat.4 The obtained mixture of substances can vary in the number of carbohydrates, their anomeric configuration, and the degree of alkylation.5 The chemistry of these carbohydrate surfactants was already established by E. Fischer in 1911,6 and a comprehensive overview was given by Rybinski and Hill in 1998.7 The advantages of carbohydrate surfactants are manifold and include biodegradability, chirality and low toxicity. Due to these properties, they find numerous applications in detergents and cosmetics. In more specialized applications they have been successfully used for the extraction and crystallization of proteins or for transfection.8 Carbohydrate surfactants can also undergo self-assembly and form so-called niosomes, the synthetic analogues of liposomes.9 Due to their enhanced stability, niosomes have been successfully tested as biocompatible drug-delivery systems.10 The application of glycoside surfactants in enantioselective phase transfer catalysis is highly interesting, but is still less explored.11,12
Further, carbohydrate-based surfactants are highly interesting from a fundamental perspective. The huge number of different carbohydrates and in particular the accessibility of various isomers makes sugar-based amphiphiles special.13 In contrast to other systems, one can apply subtle differences to the structure of the surfactant head group region while maintaining key surfactant parameters such as the packing parameter or the HLB value (see also Fig. 1).
The packing parameter P is a widely used concept, which was introduced by Israelachvili.14P describes the shape of a surfactant taking into account the volume of the hydrophobic chain (V0), the equilibrium area per molecule at the interface (Amin), and the length of the hydrophobic chain (l0); P = V0/(Amin·l0). Another concept, which is particularly useful for classifying non-ionic surfactants, is the hydrophilic–lipophilic balance (HLB) introduced by Griffin.15 The HLB value is proportional to the ratio of the molar mass of the hydrophilic moieties (Mh) of the surfactant and its total molecular mass (M); HLB = 20·(Mh/M). The HLB value can serve as first evidence, whether the surfactant might be appropriate for certain applications e.g. as oil-in-water emulsifier. A change of the surfactant structure normally results in a significant change of the packing and HLB parameters. Therefore, carbohydrate surfactants are ideal models for investigating, how even small changes in the surfactant structure can affect amphiphilic properties. Important work in this research field was done by Vill and coworkers.16–18 Their studies mainly focused on the determination of the thermotropic behavior (clearing points)16 and lyotropic phase diagrams obtained from polarization microscopy.17,18 In 2014, Lindhorst and coworkers investigated the micellization behavior of a series of octyl glycoside surfactants by applying isothermal titration calorimetry (ITC) and diffusion ordered NMR spectroscopy.19 They could show that the critical micelle concentration (CMC) value is influenced by the choice of carbohydrate and anomeric configuration.
Here, we present the investigation of a comprehensive, multidimensional library of glycoside surfactants (Fig. 1). In a systematic way, we studied the effect of different parameters, such as the nature of the tail and the head group. We investigated the effect of subtle variations of the head group including isomeric (glucose, galactose, mannose) or similar carbohydrates (xylose) as well as different anomeric configurations. Major effort has been put into the synthesis and isolation of surfactants in pure form. After thorough investigation of self-aggregation processes, we tested the use of the surfactants as emulsifiers. In a proof-of-concept experiment, we show that sugar-based surfactants can also function as capping agents influencing the morphology of inorganic zinc oxide nanoparticles grown in an emulsion-based method. This method was developed by us in the past,20–23 however, glycoside surfactants had not yet been used as emulsifiers.
2 Experimental
2.1 General methods
N-Iodosuccinimide was purchased from abcr; Span 20 and Triton X-100 were purchased from TCI chemicals; octyl α-D-glucopyranoside (GlcαC8), hexyl and octyl β-D-glucopyranoside (GlcβC6, GlcβC8), and hexyl β-D-maltoside (MalβC6) were purchased from Sigma Aldrich; octyl, decyl, and dodecyl β-D-maltoside (MalβC8, MalβC10, MalβC12) and dodecyl α-D-maltoside (MalαC12) were purchased from Carbosynth. Isopropyl β-D-1-thiogalactoside (IPTG) was purchased from Carbolution Chemicals. All solvents were distilled prior to use and if required, dried according to standard procedures. All reactions were monitored by TLC on silica gel 60 F254 (Merck) on aluminum sheets with detection by UV-light (λ = 254 nm). Additionally, a solution of Ce(SO4)2·4H2O (25 mM) and (NH4)6Mo7O24·4H2O (16 mM) in H2SO4 (10 wt%) followed by gentle heating was used for visualization. Preparative flash column chromatography (FC) was performed with silica 60 M (0.04–0.063 mm, Macherey-Nagel). NMR spectra were recorded at room temperature on Avance III 400 and Avance III 600 instruments from Bruker. Chemical shifts are reported in ppm relative to solvent signals (CDCl3: δH = 7.26, δC = 77.16; DMSO-d6: δH = 2.50, δC = 39.52). Signals were assigned by first order analysis and two-dimensional 1H,1H, 1H,13C and 1H,31P correlation spectroscopy (COSY, HSQC and HMBC). High-resolution electrospray ionization mass spectra (ESI-HRMS) were recorded on a Bruker micrOTOF II instrument.2.2 Synthesis
(a) Formation of the triflated alcohol. A solution of alkyl alcohol (1.5 equiv.) and 2,6-lutidine (2.25 equiv.) in dry CH2Cl2 (15 mL g−1 alcohol) was cooled to 0 °C and triflic anhydride (2.1 equiv.) was added dropwise. After 15 min, n-hexane (30 mL g−1 alcohol) was added and the reaction mixture was washed with ice cold 0.1 M KHSO4 solution, dried over Na2SO4 and concentrated under reduced pressure at 0 °C. The crude triflated alcohol was then immediately used without further purification.
(b) Anomeric O-alkylation24. A solution of the corresponding, previously prepared, 2,3,4,6-tetra-O-acetylhexose25,26 (1 equiv.) in dry dimethoxyethane (10 mL g−1) was cooled to 0 °C and sodium hydride (1.1 equiv., 60 wt% dispersion in mineral oil) was added portionwise. After gas evolution had ceased, the reaction mixture was cooled to −50 °C and the triflated alcohol, dissolved in dry dimethoxyethane (5 mL g−1 carbohydrate), was added and the reaction stirred overnight. The solvent was removed under reduced pressure and the remaining syrup was redissolved in ethyl acetate and washed with brine, dried over Na2SO4 and the solvent was evaporated. The crude product was purified by FC (petroleum ether/ethyl acetate) yielding the acetylated alkyl α- and β-D-gluco- and -mannopyranosides.
(c) Deprotection (Zemplén-protocol)27. The acetylated alkyl glucopyranoside or alkyl mannopyranoside was dissolved in dry MeOH (19 mL g−1) and NaOMe (0.2 equiv., 0.5 M solution in MeOH) was added and stirred for 1 h. The reaction mixture was treated with Amberlite IR-120 ion exchange resin (H+-form), filtered over celite and the solvent evaporated yielding the alkyl glucopyranoside or alkyl mannopyranoside (for details, yields, and product characterization see ESI†).
(6-Hydroxyhexyl)-triphenylphosphonium bromide. 6-Bromohexan-1-ol32 (20.0 g, 110.4 mmol) was dissolved in dry acetonitrile (250 mL) and triphenylphosphine (30.4 g, 116 mmol) was added. The reaction mixture was heated to reflux for 24 h. Afterwards, the mixture was concentrated under reduced pressure and the residue redissolved in dry CH2Cl2, precipitated by addition of diethyl ether and freezing to −196 °C (to achieve full precipitation). After thawing, the supernatant was decanted. This procedure was repeated two times to ensure removal of excess triphenylphosphine. Remaining solvent was removed under reduced pressure to yield the phosphonium salt as white solid (43.9 g, 90%). 1H NMR (400 MHz, CDCl3): δ = 7.81–7.66 (m, 15 H, Ph), 3.68–3.61 (m, 2 H, H-1), 3.56 (t, J = 5.4 Hz, 2 H, H-6), 2.60 (s, 1 H, OH), 1.64 (s, 4 H, H-2, H-3), 1.49–1.42 (m, 4 H, H-4, H-5); 31P NMR (162 MHz, CDCl3): δ = 24.36 (s).
(Z)-Dodec-6-en-1-ol (3). NaH (60 wt% dispersion in mineral oil, 7.81 g, 195.5 mmol) was washed two times with dry n-hexane in order to remove the mineral oil. Then, dry DMSO (72 mL) was added and carefully heated to 75 °C until gas-evolution had ceased. The reaction mixture was diluted with dry THF (30 mL) and cooled to 0 °C. To the cooled mixture the phosphonium salt (43.3 g, 97.8 mmol), dissolved in dry DMSO (50 mL, 40 °C), was slowly added and stirred for 45 min. Subsequently, freshly distilled n-hexanal (12 mL, 97.7 mmol) was added dropwise and stirred for 20 min. Afterwards, the reaction mixture was poured on ice water and extracted with diethyl ether. After removal of the solvents, the residue was extracted with n-hexane. The combined extracts were washed with water, dried over MgSO4 and the solvent evaporated. The crude product was purified via FC (petroleum ether/ethyl acetate 30
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) to yield 7.5 g (42%) of the alcohol (E
1) to yield 7.5 g (42%) of the alcohol (E![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Z = 1
Z = 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10) as colorless oil. Rf = 0.28 (petroleum ether/ethyl acetate 5
10) as colorless oil. Rf = 0.28 (petroleum ether/ethyl acetate 5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1); 1H NMR of Z-product (400 MHz, CDCl3): δ = 5.40–5.31 (m, 2 H, H-6, H-7), 3.63 (t, J = 6.6 Hz, 2 H, H-1), 2.06–1.96 (m, 4 H, H-5, H-8), 1.61–1.54 (m, 2 H, H-2) 1.39–1.24 (m, 10 H, H-4, H-9, H-3, H-11, H-10), 0.88 (t, J = 7.2 Hz, 3 H, H-12); 13C NMR (101 MHz, CDCl3): δ = 130.3 (C-6/7), 129.7 (C-6/7), 63.2 (C-1), 32.9 (C-2), 31.7 (C-10), 29.7 (C-9), 29.6 (C-4), 27.3 (C-5/8), 27.3 (C-5/8), 25.6 (C-3), 22.7 (C-11), 14.2 (C-12).
1); 1H NMR of Z-product (400 MHz, CDCl3): δ = 5.40–5.31 (m, 2 H, H-6, H-7), 3.63 (t, J = 6.6 Hz, 2 H, H-1), 2.06–1.96 (m, 4 H, H-5, H-8), 1.61–1.54 (m, 2 H, H-2) 1.39–1.24 (m, 10 H, H-4, H-9, H-3, H-11, H-10), 0.88 (t, J = 7.2 Hz, 3 H, H-12); 13C NMR (101 MHz, CDCl3): δ = 130.3 (C-6/7), 129.7 (C-6/7), 63.2 (C-1), 32.9 (C-2), 31.7 (C-10), 29.7 (C-9), 29.6 (C-4), 27.3 (C-5/8), 27.3 (C-5/8), 25.6 (C-3), 22.7 (C-11), 14.2 (C-12).
(Z)-Dodec-6-enyl 2,3,4,6-tetra-O-acetyl-α/β-D-mannopyranoside (4α,4β). First, the triflated alcohol (21.82 mmol) was synthesized as described in 2.2.1. 2,3,4,6-Tetra-O-acetyl-D-mannopyranose (1, 5.06 g, 14.55 mmol) was dissolved in dry dimethoxyethane (80 mL) and cooled to 0 °C. NaH (60 wt% dispersion in mineral oil, 615 mg, 16 mmol) was added and after 10 min the triflated alcohol, dissolved in dimethoxyethane (20 mL), was added dropwise and the reaction stirred overnight. After removing solvent under reduced pressure, the residue was dissolved in ethyl acetate, washed with water and dried over Na2SO4. The solvent was evaporated and the crude product was purified by FC (petroleum ether/ethyl acetate = 10
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 to 6
1 to 6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) to yield the pure α-product 4α (3.26 g, 44%) and the β-product 4β (500 mg, 7%) as slightly yellow solids. Rf(4α) = 0.49 (petroleum ether/ethyl acetate 3
1) to yield the pure α-product 4α (3.26 g, 44%) and the β-product 4β (500 mg, 7%) as slightly yellow solids. Rf(4α) = 0.49 (petroleum ether/ethyl acetate 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1); Rf(4β) = 0.38 (petroleum ether/ethyl acetate 3
1); Rf(4β) = 0.38 (petroleum ether/ethyl acetate 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1); 1H NMR of 4α (400 MHz, CDCl3): δ = 5.41–5.32 (m, 3 H, H-3, H-12, H-13), 5.27 (t, J = 10.0 Hz, 1 H, H-4), 5.23 (dd, J = 3.3 Hz, 2.5 Hz, 1 H, H-2), 4.80 (d, J = 1.3 Hz, 1 H, H-1), 4.28 (dd, J = 12.3 Hz, 5.4 Hz, 1 H, H-6a), 4.10 (dd, J = 12.2 Hz, 2.3 Hz, 1 H, H-6b), 3.98 (ddd, J = 12.3 Hz, 5.3 Hz, 2.3 Hz, 1 H, H-5), 3.67 (dt, J = 9.6 Hz, 6.9 Hz, 1 H, H-7a), 3.45 (dt, J = 9.6 Hz, 6.6 Hz, 1 H, H-7b), 2.15 (s, 3 H, Ac-2), 2.10 (s, 3 H, Ac-6), 2.04 (s, 3 H, Ac-4), 2.03 (m, 4 H, H-11, H-14), 1.99 (s, 3H, Ac-3), 1.61 (m, 2 H, H-8), 1.41–1.22 (m, 10 H, H-9, H-10, H-15, H-16, H-17), 0.89 (t, J = 6.8 Hz, 3 H, H-18); 13C NMR of 4α (101 MHz, CDCl3): δ = 170.7 (Ac-6), 170.1 (Ac-2), 169.9 (Ac-3), 169.8 (Ac-4), 130.3 (C-12/13), 129.4 (C-12/13), 97.6 (C-1), 69.8 (C-2), 69.2 (C-3), 68.5 (C-5/7), 68.4 (C-5/7), 66.3 (C-4), 62.6 (C-6), 31.5 (C-16), 29.5 (C-9/10/15), 29.4 (C-9/10/15), 29.2 (C-8), 27.2 (C-11/14), 27.1 (C-11/14), 25.7 (C-9/10/15), 22.6 (C-17), 20.9 (C-Ac), 20.8 (C-Ac), 20.71 (C-Ac), 20.70 (C-Ac), 14.1 (C-18); ESI-HRMS: calcd for C26H42O10Na [M + Na]+, 537.2669; found, 537.2762.
1); 1H NMR of 4α (400 MHz, CDCl3): δ = 5.41–5.32 (m, 3 H, H-3, H-12, H-13), 5.27 (t, J = 10.0 Hz, 1 H, H-4), 5.23 (dd, J = 3.3 Hz, 2.5 Hz, 1 H, H-2), 4.80 (d, J = 1.3 Hz, 1 H, H-1), 4.28 (dd, J = 12.3 Hz, 5.4 Hz, 1 H, H-6a), 4.10 (dd, J = 12.2 Hz, 2.3 Hz, 1 H, H-6b), 3.98 (ddd, J = 12.3 Hz, 5.3 Hz, 2.3 Hz, 1 H, H-5), 3.67 (dt, J = 9.6 Hz, 6.9 Hz, 1 H, H-7a), 3.45 (dt, J = 9.6 Hz, 6.6 Hz, 1 H, H-7b), 2.15 (s, 3 H, Ac-2), 2.10 (s, 3 H, Ac-6), 2.04 (s, 3 H, Ac-4), 2.03 (m, 4 H, H-11, H-14), 1.99 (s, 3H, Ac-3), 1.61 (m, 2 H, H-8), 1.41–1.22 (m, 10 H, H-9, H-10, H-15, H-16, H-17), 0.89 (t, J = 6.8 Hz, 3 H, H-18); 13C NMR of 4α (101 MHz, CDCl3): δ = 170.7 (Ac-6), 170.1 (Ac-2), 169.9 (Ac-3), 169.8 (Ac-4), 130.3 (C-12/13), 129.4 (C-12/13), 97.6 (C-1), 69.8 (C-2), 69.2 (C-3), 68.5 (C-5/7), 68.4 (C-5/7), 66.3 (C-4), 62.6 (C-6), 31.5 (C-16), 29.5 (C-9/10/15), 29.4 (C-9/10/15), 29.2 (C-8), 27.2 (C-11/14), 27.1 (C-11/14), 25.7 (C-9/10/15), 22.6 (C-17), 20.9 (C-Ac), 20.8 (C-Ac), 20.71 (C-Ac), 20.70 (C-Ac), 14.1 (C-18); ESI-HRMS: calcd for C26H42O10Na [M + Na]+, 537.2669; found, 537.2762.
1H NMR of 4β (400 MHz, CDCl3): δ = 5.47 (dd, J = 3.2 Hz, 0.8 Hz, 1 H, H-2), 5.34 (m, 2 H, H-12, H-13), 5.25 (t, J = 9.9 Hz, 1 H, H-4), 5.05 (dd, J = 9.9 Hz, 3.2 Hz, 1 H, H-3), 4.62 (d, J = 0.9 Hz, 1 H, H-1), 4.30 (dd, J = 12.2 Hz, 5.6 Hz, 1 H, H-6a), 4.15 (dd, J = 12.2 Hz, 4.2 Hz, 1 H, H-6b), 3.86 (dt, J = 9.4 Hz, 6.7 Hz, 1 H, H-7a), 3.66 (ddd, J = 9.9 Hz, 5.6 Hz, 4.2 Hz, 1 H, H-5), 3.49 (dt, J = 9.4 Hz, 6.9 Hz, 1 H, H-7b), 2.18 (s, 3 H, Ac-2), 2.09 (s, 3 H, Ac-6), 2.04 (s, 3 H, Ac-4), 2.01 (m, 4 H, H-11, H-14), 1.99 (s, 3 H, Ac-3), 1.59 (m, 2 H, H-8), 1.38–1.23 (m, 10 H, H-9, H-10, H-15, H-16, H-17), 0.88 (t, J = 6.8 Hz, 1 H, H-18); 13C NMR of 4β (101 MHz, CDCl3): δ = 170.9 (Ac-6), 170.6 (Ac-2), 170.2 (Ac-3), 169.7 (Ac-4), 130.3 (C-12/13), 129.6 (C-12/13), 98.9 (C-1), 72.6 (C-5), 71.3 (C-3), 70.6 (C-7), 69.0 (C-2), 66.4 (C-4), 62.8 (C-6), 31.7 (C-16), 29.60 (C-9/10/15), 29.56 (C-9/10/15), 29.4 (C-8), 27.3 (C-11/14), 27.2 (C-11/14), 25.7 (C-9/10/15), 22.7 (C-17), 21.0 (C-Ac), 20.9 (C-Ac), 20.85 (C-Ac), 20.7 (C-Ac), 14.2 (C-18); ESI-HRMS: calcd for C26H42O10Na [M + Na]+, 537.2669; found, 537.2672.
(Z)-Dodec-6-enyl α-D-mannopyranoside (ManαCuns12). (Z)-Dodec-6-enyl 2,3,4,6-tetra-O-acetyl-α-D-mannopyranoside (4α, 3.26 g, 6.34 mmol) was deprotected following the general procedure described in Section 2.2.1 to yield ManαCuns12 as yellow solid (2.16 g, 98%). Rf = 0.41 (CH2Cl2/MeOH 5
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1); 1H NMR (400 MHz, DMSO-d6): δ = 5.33 (m, 2 H, H-12, H-13), 4.67 (d, J = 5.3 Hz, 1 H, OH-4), 4.64 (d, J = 4.6 Hz, 1 H, OH-2), 4.57 (d, J = 1.4 Hz, 1 H, H-1), 4.50 (d, J = 5.9 Hz, 1 H, OH-3), 4.39 (d, J = 5.89 Hz, 1 H, OH-6), 3.67–3.60 (m, 1 H, H-6a), 3.60–3.54 (m, 2 H, H-2, H-7a), 3.47–3.40 (m, 2 H, H-3, H-6), 3.40–3.34 (m, 1 H, H-4), 3.30–3.24 (m, 2 H, H-5, H-7b), 2.07–1.88 (m, 4 H, H-11, H-14), 1.55–1.43 (m, 2 H, H-8), 1.38–1.19 (m, 10 H, H-9, H-10, H-15, H-16, H-17), 0.86 (t, J = 6.8 Hz, 3 H, H-18); 13C NMR (101 MHz, DMSO-d6): δ = 129.7 (C-12/13), 129.5 (C-12/13), 99.7 (C-1), 73.9 (C-5), 71.0 (C-3), 70.4 (C-2), 67.0 (C-4), 66.2 (C-7), 61.3 (C-6), 30.8 (C-16), 28.93 (C-9/10/15), 28.87 (C-9/10/15), 28.8 (C-8), 26.58 (C-11/14), 26.55 (C-11/14), 25.4 (C-9/10/15), 21.9 (C-17), 13.9 (C-18); ESI-HRMS: calcd for C18H34O6Na [M + Na]+, 369.2246; found, 369.2208.
1); 1H NMR (400 MHz, DMSO-d6): δ = 5.33 (m, 2 H, H-12, H-13), 4.67 (d, J = 5.3 Hz, 1 H, OH-4), 4.64 (d, J = 4.6 Hz, 1 H, OH-2), 4.57 (d, J = 1.4 Hz, 1 H, H-1), 4.50 (d, J = 5.9 Hz, 1 H, OH-3), 4.39 (d, J = 5.89 Hz, 1 H, OH-6), 3.67–3.60 (m, 1 H, H-6a), 3.60–3.54 (m, 2 H, H-2, H-7a), 3.47–3.40 (m, 2 H, H-3, H-6), 3.40–3.34 (m, 1 H, H-4), 3.30–3.24 (m, 2 H, H-5, H-7b), 2.07–1.88 (m, 4 H, H-11, H-14), 1.55–1.43 (m, 2 H, H-8), 1.38–1.19 (m, 10 H, H-9, H-10, H-15, H-16, H-17), 0.86 (t, J = 6.8 Hz, 3 H, H-18); 13C NMR (101 MHz, DMSO-d6): δ = 129.7 (C-12/13), 129.5 (C-12/13), 99.7 (C-1), 73.9 (C-5), 71.0 (C-3), 70.4 (C-2), 67.0 (C-4), 66.2 (C-7), 61.3 (C-6), 30.8 (C-16), 28.93 (C-9/10/15), 28.87 (C-9/10/15), 28.8 (C-8), 26.58 (C-11/14), 26.55 (C-11/14), 25.4 (C-9/10/15), 21.9 (C-17), 13.9 (C-18); ESI-HRMS: calcd for C18H34O6Na [M + Na]+, 369.2246; found, 369.2208.
(Z)-Dodec-6-enyl β-D-mannopyranoside (ManβCuns12). (Z)-Dodec-6-enyl 2,3,4,6-tetra-O-acetyl-β-D-mannopyranoside (4β, 498 mg, 0.97 mmol) was deprotected following the general procedure described in Section 2.2.1 to yield ManβCuns12 as yellow solid (322 mg, 96%). Rf = 0.43 (CH2Cl2/MeOH 5
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1); 1H NMR (400 MHz, DMSO-d6): δ [ppm] = 5.39–5.29 (m, 2 H, H-12, H-13), 4.69 (d, J = 4.9 Hz, 1 H, OH-4), 4.49 (d, J = 5.9 Hz, 1 H, OH-3), 4.39 (t, J = 5.9 Hz, 1 H, OH-6), 4.33 (s, 1 H, H-1), 4.23 (d, J = 5.0 Hz, 1 H, OH-2), 3.75 (dt, J = 9.8 Hz, 7.2 Hz, 1 H, H-7a), 3.71–3.63 (m, 1 H, H-6a), 3.63–3.58 (m, 1 H, H-2), 3.48–3.36 (m, 2 H, H-6b, H7-b), 3.29–3.19 (m, 2 H, H-4, H-3), 3.04–2.97 (m, 1 H, H-5), 2.07–1.88 (m, 4 H, H-11, H-14), 1.56–1.45 (m, 2 H, H-8), 1.37–1.39 (m, 10 H, H-9, H-10, H-15, H-16, H-17), 0.86 (t, J = 6.8 Hz, 3 H, H-18); 13C NMR (101 MHz, DMSO-d6): δ = 129.7 (C-12/13), 129.6 (C-12/13), 100.2 (C-1), 77.5 (C-5), 73.7 (C-3), 70.6 (C-2), 68.3 (C-7), 67.2 (C-4), 61.4 (C-6), 30.8 (C-16), 29.1 (C-9/10/15), 29.0 (C-9/10/15), 28.8 (C-8), 26.61 (C-11/14), 26.56 (C-11/14), 25.2 (C-9/10/15) 21.9 (C-17), 13.9 (C-18); ESI-HRMS: calcd for C18H34O6Na [M + Na]+, 369.2246; found, 369.2307.
1); 1H NMR (400 MHz, DMSO-d6): δ [ppm] = 5.39–5.29 (m, 2 H, H-12, H-13), 4.69 (d, J = 4.9 Hz, 1 H, OH-4), 4.49 (d, J = 5.9 Hz, 1 H, OH-3), 4.39 (t, J = 5.9 Hz, 1 H, OH-6), 4.33 (s, 1 H, H-1), 4.23 (d, J = 5.0 Hz, 1 H, OH-2), 3.75 (dt, J = 9.8 Hz, 7.2 Hz, 1 H, H-7a), 3.71–3.63 (m, 1 H, H-6a), 3.63–3.58 (m, 1 H, H-2), 3.48–3.36 (m, 2 H, H-6b, H7-b), 3.29–3.19 (m, 2 H, H-4, H-3), 3.04–2.97 (m, 1 H, H-5), 2.07–1.88 (m, 4 H, H-11, H-14), 1.56–1.45 (m, 2 H, H-8), 1.37–1.39 (m, 10 H, H-9, H-10, H-15, H-16, H-17), 0.86 (t, J = 6.8 Hz, 3 H, H-18); 13C NMR (101 MHz, DMSO-d6): δ = 129.7 (C-12/13), 129.6 (C-12/13), 100.2 (C-1), 77.5 (C-5), 73.7 (C-3), 70.6 (C-2), 68.3 (C-7), 67.2 (C-4), 61.4 (C-6), 30.8 (C-16), 29.1 (C-9/10/15), 29.0 (C-9/10/15), 28.8 (C-8), 26.61 (C-11/14), 26.56 (C-11/14), 25.2 (C-9/10/15) 21.9 (C-17), 13.9 (C-18); ESI-HRMS: calcd for C18H34O6Na [M + Na]+, 369.2246; found, 369.2307.
(Z)-Dodec-6-enyl 2,3,4,6-tetra-O-acetyl-α/β-D-galactopyranoside (5α,5β). First, the triflated alcohol (1.5 equiv.) was synthesized as described in Section 2.2.1. 2,3,4,6-Tetra-O-acetyl-D-galactopyranose (2, 1.26 g, 3.62 mmol) was dissolved in dry dimethoxyethane (20 mL) and cooled to −50 °C. NaH (60 wt% dispersion in mineral oil, 159.3 mg, 3.98 mmol) was added. After 10 min, the triflated alcohol, dissolved in dimethoxyethane (20 mL), was added dropwise and the reaction stirred overnight. After removing the solvent under reduced pressure, the residue was dissolved in ethyl acetate, washed with water and dried over Na2SO4. The solvent was evaporated and the crude product was purified by FC (petroleum ether/ethyl acetate = 10
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 to 6
1 to 6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) to yield the pure α-product 5α (244 mg, 13%) and the β-product 5β (1.17 g, 63%) as white solids. Rf(5α) = 0.20 (petroleum ether/ethyl acetate 5
1) to yield the pure α-product 5α (244 mg, 13%) and the β-product 5β (1.17 g, 63%) as white solids. Rf(5α) = 0.20 (petroleum ether/ethyl acetate 5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1); Rf(5β) = 0.14 (petroleum ether/ethyl acetate 5
1); Rf(5β) = 0.14 (petroleum ether/ethyl acetate 5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1); 1H NMR of 5α (400 MHz, CDCl3): δ = 5.46–5.45 (dd, J = 3.4 Hz, 1.2 Hz, 1 H, H-4), 5.40–5.30 (m, 3 H, H-2, H-12, H-13), 5.12–5.09 (m, 2 H, H-3, H-1), 4.22 (dt, J = 6.3 Hz, 1.2 Hz, 1 H, H-5), 4.09 (ddd, J = 6.3 Hz, 3.2 Hz, 2.3 Hz, 2 H, H-6), 3.68 (dt, J = 9.9 Hz, 6.5 Hz, 1 H, H-7a), 3.42 (dt, J = 9.9 Hz, 6.5 Hz, 1 H, H-7b), 2.14 (s, 3 H, Ac-4), 2.07 (s, 3 H, Ac-3), 2.04 (s, 3 H, Ac-6), 2.02 (m, 4-H, H-11, H-14), 1.98 (s, 3 H, Ac-2), 1.61–1.57 (m, 2 H, H-8), 1.38–1.27 (m, 10 H, H-10, H-15, H-9, H-17, H-16), 0.88 (d, J = 13.2 Hz, 3 H, H-18); 13C NMR of 5α (101 MHz, CDCl3): δ = 170.6 (Ac-3), 170.5 (Ac-6), 170.4 (Ac-4), 170.2 (Ac-2), 130.4 (C-12/13), 129.5 (C-12/13), 96.3 (C-1), 68.8 (C-7), 68.4 (C-3), 68.3 (C-4), 67.9 (C-2), 66.3 (C-5), 62.0 (C-6), 32.7 (C-16), 31.7 (C-9/10/15), 29.6 (C-9/10/15), 29.4 (C-8), 27.4 (C-11/14), 27.3 (C-11/14), 25.9 (C-9/10/15), 22.7 (C-17), 20.9 (Ac-3), 20.84 (Ac-6), 20.82 (Ac-4), 20.80 (Ac-2), 14.2 (C-18); ESI-HRMS: calcd for C26H42O10Na [M + Na]+, 537.2669; found, 537.2742.
1); 1H NMR of 5α (400 MHz, CDCl3): δ = 5.46–5.45 (dd, J = 3.4 Hz, 1.2 Hz, 1 H, H-4), 5.40–5.30 (m, 3 H, H-2, H-12, H-13), 5.12–5.09 (m, 2 H, H-3, H-1), 4.22 (dt, J = 6.3 Hz, 1.2 Hz, 1 H, H-5), 4.09 (ddd, J = 6.3 Hz, 3.2 Hz, 2.3 Hz, 2 H, H-6), 3.68 (dt, J = 9.9 Hz, 6.5 Hz, 1 H, H-7a), 3.42 (dt, J = 9.9 Hz, 6.5 Hz, 1 H, H-7b), 2.14 (s, 3 H, Ac-4), 2.07 (s, 3 H, Ac-3), 2.04 (s, 3 H, Ac-6), 2.02 (m, 4-H, H-11, H-14), 1.98 (s, 3 H, Ac-2), 1.61–1.57 (m, 2 H, H-8), 1.38–1.27 (m, 10 H, H-10, H-15, H-9, H-17, H-16), 0.88 (d, J = 13.2 Hz, 3 H, H-18); 13C NMR of 5α (101 MHz, CDCl3): δ = 170.6 (Ac-3), 170.5 (Ac-6), 170.4 (Ac-4), 170.2 (Ac-2), 130.4 (C-12/13), 129.5 (C-12/13), 96.3 (C-1), 68.8 (C-7), 68.4 (C-3), 68.3 (C-4), 67.9 (C-2), 66.3 (C-5), 62.0 (C-6), 32.7 (C-16), 31.7 (C-9/10/15), 29.6 (C-9/10/15), 29.4 (C-8), 27.4 (C-11/14), 27.3 (C-11/14), 25.9 (C-9/10/15), 22.7 (C-17), 20.9 (Ac-3), 20.84 (Ac-6), 20.82 (Ac-4), 20.80 (Ac-2), 14.2 (C-18); ESI-HRMS: calcd for C26H42O10Na [M + Na]+, 537.2669; found, 537.2742.
1H NMR of 5β (400 MHz, CDCl3): δ = 5.38 (dd, J = 3.5 Hz, 1.0 Hz, 1 H, H-4), 5.36–5.29 (m, 2 H, H-12, H-13), 5.20 (dd, J = 10.5 Hz, 8.0 Hz, 1 H, H-2), 5.01 (dd, J = 10.5 Hz, 3.5 Hz, 1 H, H-3), 4.45 (d, J = 8.0 Hz, 1 H, H-1), 4.20–4.10 (m, 2 H, H-6), 3.91–3.85 (m, 2 H, H-5, H-7a), 3.46 (dt, J = 9.7 Hz, 7.0 Hz, 1 H, H-7b), 2.14 (s, 3 H, Ac-4), 2.04 (m, 6 H, Ac-2, Ac-6), 2.01 (m, 4 H, H-11, H-14), 1.98 (s, 3 H, Ac-3) 1.64–1.55 (m, 2 H, H-8), 1.35–1.25 (m, 10 H, H-9, H-10, H-15, H-16, H-17), 0.88 (t, J = 6.9 Hz, 3 H, H-18); 13C NMR of 5β (101 MHz, CDCl3): δ = 170.5 (Ac-6), 170.4 (Ac-4), 170.3 (Ac-3), 169.5 (Ac-2), 130.4 (C-12/13), 129.6 (C-12/13), 101.5 (C-1), 71.1 (C-3), 70.7 (C-5), 70.3 (C-7), 69.1 (C-2), 67.2 (C-4), 61.4 (C-6), 31.7 (C-16), 29.6 (C-8), 29.55 (C-10), 29.48 (C-15), 27.3 (C-11/14), 27.3 (C-11/14), 25.6 (C-9), 22.7 (C-17), 21.2 (Ac-4), 20.9 (Ac-2), 20.8 (Ac-6), 20.7 (Ac-3), 14.2 (C-18); ESI-HRMS: calcd for C26H42O10Na [M + Na]+, 537.2669; found, 537.2761.
(Z)-Dodec-6-enyl α-D-galactopyranoside (GalαCuns12). (Z)-Dodec-6-enyl 2,3,4,6-tetra-O-acetyl-α-D-galactopyranoside (5α, 234 mg, 0.455 mmol) was deprotected following the general procedure described in Section 2.2.1 to yield GalαCuns12 as white solid (194 mg, 94%). Rf = 0.28 (CH2Cl2/MeOH 10
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1); 1H NMR (400 MHz, DMSO-d6): δ = 5.39–5.29 (m, 2 H, H-12, H-13), 4.61 (d, J = 3.5 Hz, 1 H, H-1), 4.50–4.48 (m, 2 H, OH-6, OH-3), 4.35 (d, J = 6.3 Hz, 1 H, OH-2), 4.31 (d, J = 4.3 Hz, 1 H, OH-4), 3.69 (t, J = 3.1 Hz, 1 H, H-4), 3.59–3.47 (m, 5 H, H-7a, H-2, H-5, H-3, H-6a), 3.45–3.39 (m, 1 H, H-6b), 3.29–3.27 (m, 1 H, H-7b), 1.99–1.96 (m, 4 H, H-11, H-14), 1.53–1.50 (m, 2 H, H-8), 1.24–1.25 (m, 12 H, H-9, H-10, H-15, H-16, H-17), 0.86 (t, J = 6.7 Hz, 3 H, H-18); 13C NMR (101 MHz, DMSO-d6): δ = 129.7 (C-12/13), 129.6 (C-12/13), 98.8 (C-1), 71.1 (C-2/3/5), 69.6 (C-4), 68.9 (C-2/3/5), 68.4 (C-2/3/5), 66.8 (C-7), 60.6 (C-6), 30.8 (C-16/17), 29.0 (C-8), 28.8 (C-9/10/15), 26.6 (C-11/14), 26.55 (C-11/14), 25.4 (C-9/10/15), 21.9 (C-16/17), 13.9 (C-18); ESI-HRMS: calcd for C18H34O6Na [M + Na]+, 369.2246; found, 369.2226.
1); 1H NMR (400 MHz, DMSO-d6): δ = 5.39–5.29 (m, 2 H, H-12, H-13), 4.61 (d, J = 3.5 Hz, 1 H, H-1), 4.50–4.48 (m, 2 H, OH-6, OH-3), 4.35 (d, J = 6.3 Hz, 1 H, OH-2), 4.31 (d, J = 4.3 Hz, 1 H, OH-4), 3.69 (t, J = 3.1 Hz, 1 H, H-4), 3.59–3.47 (m, 5 H, H-7a, H-2, H-5, H-3, H-6a), 3.45–3.39 (m, 1 H, H-6b), 3.29–3.27 (m, 1 H, H-7b), 1.99–1.96 (m, 4 H, H-11, H-14), 1.53–1.50 (m, 2 H, H-8), 1.24–1.25 (m, 12 H, H-9, H-10, H-15, H-16, H-17), 0.86 (t, J = 6.7 Hz, 3 H, H-18); 13C NMR (101 MHz, DMSO-d6): δ = 129.7 (C-12/13), 129.6 (C-12/13), 98.8 (C-1), 71.1 (C-2/3/5), 69.6 (C-4), 68.9 (C-2/3/5), 68.4 (C-2/3/5), 66.8 (C-7), 60.6 (C-6), 30.8 (C-16/17), 29.0 (C-8), 28.8 (C-9/10/15), 26.6 (C-11/14), 26.55 (C-11/14), 25.4 (C-9/10/15), 21.9 (C-16/17), 13.9 (C-18); ESI-HRMS: calcd for C18H34O6Na [M + Na]+, 369.2246; found, 369.2226.
(Z)-Dodec-6-enyl β-D-galactopyranoside (GalβCuns12). (Z)-Dodec-6-enyl 2,3,4,6-tetra-O-acetyl-β-D-galactopyranoside (5β, 1.17 g, 2.28 mmol) was deprotected following the general procedure described in Section 2.2.1 to yield GalβCuns12 as white solid (831 mg, 92%). Rf = 0.53 (CH2Cl2/MeOH 5
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1); 1H NMR (400 MHz, DMSO-d6): δ = 5.39–5.29 (m, 2 H, H-12, H-13), 4.75 (d, J = 4.0 Hz, 1 H, OH-2), 4.64 (s, 1 H, OH-3), 4.52 (t, J = 5.6 Hz, 1 H, OH-6), 4.30 (d, J = 4.5 Hz, 1 H, OH-4), 4.04 (d, J = 7.3 Hz, 1 H, H-1), 3.71 (dt, J = 9.6 Hz, 6.8 Hz, 1 H, H-7a), 3.62 (s, 1 H, H-4), 3.55–3.44 (m, 2 H, H-6), 3.39 (dt, J = 9.5 Hz, 6.7 Hz, 1 H, H-7b), 3.30–3.28 (m, 1 H, H-5), 3.26–3.24 (m, 2 H, H-2, H-3), 2.01–1.96 (m, 4 H, H-11, H-14), 1.53–1.50 (m, 2 H, H-8), 1.32–1.23 (m, 12 H, H-9, H-10, H-15, H-16, H-17), 0.86 (t, J = 6.6 Hz, 3 H, H-18); 13C NMR (101 MHz, DMSO-d6): δ = 129.64 (C-12/13), 129.56 (C-12/13), 103.5 (C-1), 75.1 (C-5), 73.5 (C-2/3), 70.5 (C-2/3), 68.4 (C-7), 68.1 (C-4), 60.4 (C-6), 30.8 (C-16/17), 29.2 (C-9/10/15), 29.0 (C-9/10/15), 28.8 (C-8), 26.6 (C-11/14), 26.55 (C-11/14), 25.2 (C-9/10/15), 21.9 (C-16/17), 13.9 (C-18); ESI-HRMS: calcd for C18H34O6Na [M + Na]+, 369.2246; found, 369.2250.
1); 1H NMR (400 MHz, DMSO-d6): δ = 5.39–5.29 (m, 2 H, H-12, H-13), 4.75 (d, J = 4.0 Hz, 1 H, OH-2), 4.64 (s, 1 H, OH-3), 4.52 (t, J = 5.6 Hz, 1 H, OH-6), 4.30 (d, J = 4.5 Hz, 1 H, OH-4), 4.04 (d, J = 7.3 Hz, 1 H, H-1), 3.71 (dt, J = 9.6 Hz, 6.8 Hz, 1 H, H-7a), 3.62 (s, 1 H, H-4), 3.55–3.44 (m, 2 H, H-6), 3.39 (dt, J = 9.5 Hz, 6.7 Hz, 1 H, H-7b), 3.30–3.28 (m, 1 H, H-5), 3.26–3.24 (m, 2 H, H-2, H-3), 2.01–1.96 (m, 4 H, H-11, H-14), 1.53–1.50 (m, 2 H, H-8), 1.32–1.23 (m, 12 H, H-9, H-10, H-15, H-16, H-17), 0.86 (t, J = 6.6 Hz, 3 H, H-18); 13C NMR (101 MHz, DMSO-d6): δ = 129.64 (C-12/13), 129.56 (C-12/13), 103.5 (C-1), 75.1 (C-5), 73.5 (C-2/3), 70.5 (C-2/3), 68.4 (C-7), 68.1 (C-4), 60.4 (C-6), 30.8 (C-16/17), 29.2 (C-9/10/15), 29.0 (C-9/10/15), 28.8 (C-8), 26.6 (C-11/14), 26.55 (C-11/14), 25.2 (C-9/10/15), 21.9 (C-16/17), 13.9 (C-18); ESI-HRMS: calcd for C18H34O6Na [M + Na]+, 369.2246; found, 369.2250.
2.3 Analytical techniques
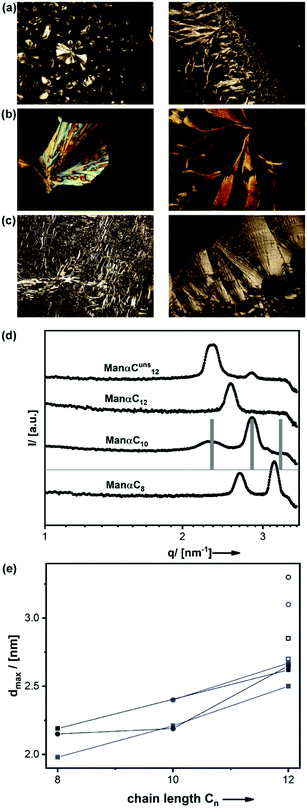
 ), enthalpy (
), enthalpy ( ) and entropy (ΔS°) of the demicellation process were calculated based on the phase separation model using the following equations19,33 (with molar fraction CAC′, observed reaction enthalpy ΔRH° and the concentration of injected surfactant solution csyringe):
) and entropy (ΔS°) of the demicellation process were calculated based on the phase separation model using the following equations19,33 (with molar fraction CAC′, observed reaction enthalpy ΔRH° and the concentration of injected surfactant solution csyringe):For determination of CAC > 100 mM, a diluted solution of the surfactant (approx. 0.5-fold CAC) was placed in the sample cell, in which and a concentrated surfactant solution (approx. 2.5–3-fold CAC) was titrated. Due to the smaller concentration window, multiple titration cycles were performed consecutively while removing the supernatant solution after each cycle. Each data set was processed as described before, plotted in Origin 2018, and the combined titrations were fitted with a sigmoidal function.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) c) was used to calculate the surface excess concentration Γmax and the minimum molecular area occupied Amin by34
c) was used to calculate the surface excess concentration Γmax and the minimum molecular area occupied Amin by34Γmax = −(2.303RT)−1·(dγ/d![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) c) c) |
| Amin = (NA·Γmax)−1 |
3 Results and discussion
3.1 Library of glycosurfactants
Fig. 1 gives an overview of the glycosurfactants used in our studies. We included compounds with mono-hexose-type head groups ranging from the well-known glucose surfactants over galactose and mannose to xylose derivatives. Compounds with the same length of the saturated hydrophobic side chain are either true isomers (for glucose, galactose, and mannose) or at least very similar (xylose differs from glucose only by a missing hydroxymethyl group). Therefore, these amphiphiles formally do not differ in their packing parameter P or HLB value. The same is true, if the anomeric configuration (α,β) is varied. A significant change in the head group region is realized for the surfactants containing the disaccharide maltose. A variation of the hydrocarbon chain length will obviously affect P and HLB. Beside surfactants with a saturated alkyl chain, we also included novel galactoside and mannoside surfactants with an unsaturated chain. This structural variation can also be regarded as almost P and HLB invariant.3.2 Synthesis of glycosurfactants
Except for some glycosurfactants that were commercially available, the members of the library were synthesized either by anomeric O-alkylation (Glcα/βC12, Galα/βCuns12, Manα/βCn, Manα/βCuns12), by NIS-promoted glycosylation of thiogalactoside 6 (Galα/βCn), or by Lewis-acid catalyzed glycosylation of peracetylated xylose 7 (Xylα/βC12) as shown in Fig. 2. For the synthesis of Galα/βCuns12 and Manα/βCuns12 by anomeric O-alkylation, (Z)-dodec-6-en-1-ol (3) was triflated using triflic anhydride and then reacted with 2,3,4,6-tetra-O-acetylated mannose 1 or galactose 2 and sodium hydride to obtain the glycosides 4 and 5, respectively, as mixtures of anomers (Fig. 2a). The anomers could be separated by flash chromatography to obtain 4α (44%), 4β (7%), 5α (13%), and 5β (63%). Subsequent deacetylation under Zémplen conditions gave the unsaturated glycosurfactants in high yields. Being stereoisomers, all four compounds lead to identical high-resolution mass spectra (Fig. 2b).For the synthesis of the saturated galactosides, we reacted benzylated thiogalactoside 6, which is conveniently obtained from commercially available IPTG in one step, with the respective alcohol in presence of NIS. After separation of the anomers by flash chromatography and debenzylation, pure glycosurfactants were obtained. For the synthesis of Xylα/βC12, peracetylated xylose 7 was activated with BF3 etherate and reacted with dodecanol. Interestingly, this reaction gave high amounts of the α-anomer despite the presence of the neighboring group-active acetyl group in the 2-position. Zémplen deacetylation gave the xylose surfactants.
All new compounds were fully characterized by 1H and 13C NMR spectroscopy as well as ESI-HRMS. The anomeric configuration was determined from the 3JH-1,H-2 coupling constants for all glucosides, galactosides, and xylosides. For the mannosides, we relied on heteronuclear 1JC-1,H-1 coupling constants that were obtained from non-decoupled 1H,13C HSQC spectra. Exemplarily, the values for Manα/βCuns12 are 170 Hz (α-anomer) and 155 Hz (β-anomer) which is in agreement with reported values for mannosides.35
3.3 Surfactant properties
To get a first impression of similarities and differences between the surfactants, we generated optimized molecular structures with electrostatic potential mapping of the surfactants (cf.Fig. 1). It is obvious that the packing parameter and the HLB value are mainly influenced by two factors: the number of hexose units in the head group (HLBGlcβC12 = 10.3 → HLBMalβC12 = 13.3) and the length of the hydrophobic chain (HLBGlcβC6 = 13.6 → HLBGlcβC10 = 11.2). Considering the situation for different isomers of the surfactants, the HLB value and also the packing parameter will remain similar. The incorporation of a double bond should also only slightly influence these parameters. Therefore, we expected the surfactants with maltose head groups to behave differently than the monosaccharide derivatives, in agreement to literature.36 It seems that the anomeric configuration also has a noticeable effect because at least for our calculations the molecular structures are different when comparing the α- and the β-form (for an example see Fig. 1a). The latter expectation is also in line with the literature.19 To further study these hypotheses and findings, we systematically checked the key properties of the surfactants of our library.Although the assignment of a microstructure from POLMIC textures is often difficult, it becomes visible that the change of the head group Man→Gal (a,b), the anomeric configuration α→β (a,b,c), and also the shape of the tail C12→Cuns12 (b,c) influence the structure of the LLCs. More information about the microstructure of the LLCs phases are obtained by small angle X-ray scattering (SAXS, see Fig. ESI-1, ESI†). For better reproducibility, all samples were equilibrated in air after being dried from aqueous solution. All samples show a distinct SAXS pattern containing 1–3 signals. With increasing length of the hydrocarbon chain the surfactant size increases. A shift of the LLC lattice planes to larger distances and, according to Braggs law, a shift of the diffraction signals to lower scattering vectors q would be expected. This is exactly what we can extract as qualitative result from Fig. 3d and e.
For the saturated surfactants the lattice distance corresponding to the most intensive signal (dmax) linearly depends on the length of the hydrocarbon chain. Comparing a surfactant containing an unsaturated tail with the saturated counterpart, it is seen that the dmax value for ManαC12 is 0.2 nm smaller than dmax(ManαCuns12) = 2.7 nm. This effect can be explained by the influence of the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C bond, which hampers an ordered arrangement of the carbohydrate chain and leads to an increased lattice spacing. Furthermore, the latter value corresponds well to the double of the molecular length of ManCuns12. A distance resembling twice the molecular length is expected for almost any LLC-phase. In comparison, the ManβCn compounds exhibit dmax values, which are approx. 0.2 nm larger, which can be attributed to the more linear arrangement of head group and tail of the β-linked surfactants. The head group has an influence as well, and it seems that the LLC phases of galactosides are slightly larger than for the mannosides. In combination, one can shift dmax(ManαC12) = 2.5 nm to dmax(ManβCuns12) = 3.3 nm (Fig. 3e), although P is almost constant for these two surfactants.
C bond, which hampers an ordered arrangement of the carbohydrate chain and leads to an increased lattice spacing. Furthermore, the latter value corresponds well to the double of the molecular length of ManCuns12. A distance resembling twice the molecular length is expected for almost any LLC-phase. In comparison, the ManβCn compounds exhibit dmax values, which are approx. 0.2 nm larger, which can be attributed to the more linear arrangement of head group and tail of the β-linked surfactants. The head group has an influence as well, and it seems that the LLC phases of galactosides are slightly larger than for the mannosides. In combination, one can shift dmax(ManαC12) = 2.5 nm to dmax(ManβCuns12) = 3.3 nm (Fig. 3e), although P is almost constant for these two surfactants.
The precise assignment of a supramolecular structure is difficult, if only a limited number of diffraction signals is available as in the current case, and one cannot exclude that mixtures of different phases occur. However, a satisfactory agreement was found to the pattern created by a so-called ordered bicontinuous double diamond phase (OBDD, space group Pn3m) with a lattice constant of a = 3.831 nm for ManαC10 as shown in Fig. 3d. The OBDD structure itself has been found rarely in general,37,38 and to the best of our knowledge it has not been reported for a carbohydrate-based surfactant. OBDD is a complex structure formed by the interpenetration of two diamondoid networks. It is interesting to note that researchers recently have discussed the correlation between such structures and chirality.39
Fig. 4a exemplarily shows the integrated ITC curve for one measurement of the novel unsaturated surfactant GalβCuns12. Each ITC measurement was repeated several times yielding consistent data. The ITC curves of other surfactants involved in the current study are given in Fig. ESI-2 (ESI†). For GalβCuns12, an aggregation point at a concentration of c = 1.12 ± 0.08 mM becomes visible, which corresponds to the CAC of this surfactant. In an ITC experiment, concentrated solutions of surfactants were titrated into water. With this technique, the heat that is produced during titration is detected. From this, thermodynamic values for the de-aggregation process upon dilution can be directly derived. Assuming reversible processes, which is typically the case for soft-matter interactions, the thermodynamic functions for aggregation and de-aggregation are equitable, but with opposite sign. For GalβCuns12 we obtained ΔGag = −26.35 kJ mol−1 and ΔHag = 2.40 kJ mol−1.
 | ||
| Fig. 4 (a) Integrated ITC curve and (b) tensiometry curve of GalβCuns12 in water. (c) Integrated ITC curve and (d) tensiometry curve of GalβC8 in water. | ||
Concentration-dependent surface tension (γ) was also used as additional technique to determine the CAC (see Fig. 4b for GalβCuns12 and Fig. ESI-3, ESI† for the other surfactants samples). The γ–c curve of GalβCuns12 exhibits features, which are characteristic for surfactants. With increasing concentration, more and more molecules get located at the water–air interface. Consequently, γ decreases until the interface is fully occupied. At this point aggregation in solution takes place, and the slope of the γ–c changes. The CAC was determined as 1.05 mM from the tensiometry data (Fig. 4b), which is in good agreement with the ITC measurements. The value for surface tension reached at this transition (γmin) is 28.3 mN m−1, which is at the lowest end for surfactants with alkyl side chains and non-ionic head groups.40,41
From DLS measurements at three different concentrations, we obtained particle size distribution curves which are shown in Fig. 5a. Below the CAC, as expected, the scattering intensity is very low and there are barely any aggregates observable. At c = CAC, significant scattering, originating from objects 25 nm in diameter, can be observed. Upon raising the concentration the aggregate size increases (Dh = 60 nm). The latter findings can be confirmed by transmission electron microscopy under cryogenic conditions taken from GalβCuns12 dispersions at c = CAC and 3 × CAC (Fig. 5c and d). At c = CAC a large number of particles with a diameter of ≈25–30 nm is visible. The size of the particles (100–300 nm) has increased significantly at c = 3 × CAC. The dimension of a conventional, spherical micelle would be of the order of 2-times the diameter of the surfactant (2 × 1.8 nm ≈ 3.6 nm). The observed aggregates are obviously much larger. It has been reported in the literature,42 that sugar-based surfactants have a high tendency for the formation of non-equilibrium aggregates in water.
The same set of data was acquired for all other compounds of the series shown in Fig. 1 (refer to the ESI†). As example with a shorter chain, the data for surfactant GalβC8 is shown in Fig. 4c, d and 5b. Because the length of the hydrocarbon chain affects the packing parameter and the HLB value, a significant change of the surfactant parameters is expected for GalβC8, and this is exactly what we found. DLS measurements revealed small aggregate sizes of 4.4 nm only slightly rising at higher concentrations, which suggests the presence of micelles. In addition, ITC and tensiometry data are in agreement. We could confirm that the used methods resulted in reliable data about the surfactants’ behavior, giving the possibility to analyze the data for systematic correlations.
The dependencies on the hydrocarbon chain length is the most obvious correlation, as indicated in the last paragraph. The most influenced factor is the CAC as seen from Fig. 6a. For aggregate formation of glycoside surfactants with Cn = 6, high concentrations (>100 mM) are required. Doubling of the chain length (Cn = 12) leads to a decrease of CAC by two orders of magnitude. This effect found for our carbohydrate surfactants is stronger compared to classical ionic surfactants such as sodium alkyl sulfates (e.g. sodium dodecyl sulphate, SDS), where an increase of only one order of magnitude comparing C6 with C12 tailed surfactants is found.43,44 Because the monosaccharide-surfactants with longer alkyl chains showed reduced solubility in water, it was not possible to determine the CAC for a chain-length >8 and >10, respectively.42 However, the solubility increased for the novel surfactants containing the unsaturated C12 carbon chain. We found that their CAC values lie above the line for the extrapolation to n = 12 of the respective saturated compounds. Again, as for the lyotropic liquid crystals described before, the presence of the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C double bond has a remarkable effect. This may arise from an unfavorable conformation of the hydrocarbon chain, which is beneficial for a better solubility.
C double bond has a remarkable effect. This may arise from an unfavorable conformation of the hydrocarbon chain, which is beneficial for a better solubility.
For the thermodynamic data, some distinct trends can be identified. The free enthalpy of aggregation ΔGag depends almost linearly on Cn (Fig. 6b). Considering the ΔHag values, which are slightly positive, it was found that the aggregation of the surfactants in water is predominantly entropy-driven. This effect was assigned in surfactant chemistry to the so-called hydrophobic effect.45 Because water molecules cannot solvate the hydrophobic chain of the surfactant, they have to adopt an entropically unfavorable state for a single surfactant molecule in solution. When aggregates like micelles form, these water molecules are released gaining entropy. Thus, it is expected that the influence of entropy increases with longer alkyl chains, which is also in agreement with our data. The decrease of ΔHag with increasing Cn indicates, that the overall interaction becomes less repulsive, which can be explained by the increasing van der Waals interaction between the extended hydrocarbon chains. Comparing surfactants of the same chain length (e.g. C8) but with different head groups reveals that the ΔHag values differ from each other, which is a sign for the strong influence of different head groups.
Regarding the aggregate size, a general trend exists as well. Here, on can distinguish between the cases, where micellar aggregates are formed, and those with formation of larger aggregates (Fig. 6c). Because the diameter of a spherical micelle equals in good approximation twice the length of a surfactant, the observed increase with longer hydrophobic chain is expected. The size of aggregates, which are much larger than micelles, qualitatively increases with longer alkyl chains as well. The transition from micelles to larger aggregates is influenced by the head group. Maltoside surfactants remain in the micellar state even for a long alkyl chain such as C12. In the case of galactoside- or mannoside surfactants, the transition occurs already for C8 and C10 chains, respectively, as indicated by the dashed lines in Fig. 6c. It can also be seen, that the anomeric configuration has a strong impact. For the galactose- as well as the glucose-based surfactants there is a remarkable difference in aggregate size for the α-form compared to the β-form indicated by the arrows in Fig. 6c.
The influence of the head group can be evaluated in further depth by taking a closer look at the tensiometry data. By calculating the maximum surface excess concentration Γexc, the minimum molecular area of the surfactant occupied at the air–water interface Amin can be determined. Although the molecular mass of the head group is the same or very similar (in the case of xylose) in the cases presented in Fig. 7, the mannoside head groups occupy a significantly higher surface area than the xyloside head groups. It can be understood that the surface tension reached at c > CAC (γmin) is smaller for smaller values of Amin, because the alkyl chains can pack denser at the air–water interface.
The anomeric conformation should also influence the way the surfactants pack at the air–water interface (see also Fig. 1). Therefore, it is not surprising that α- and β-forms differ, if all other parameters are kept constant. This effect can arise from the “molecular kink” introduced in the α-form, which leads to an increase in Amin. However, it is not expected that the alkyl chains pack denser as indicated by the lower γmin values.
Fig. 8d shows the emulsification behavior of the novel surfactants ManαCuns12 and GalαCuns12 in comparison to their saturated counterpart. It is noticeable that the saturated and unsaturated surfactants of the same head group exhibit nearly identical stabilization capabilities. This suggests that the unsaturated surfactants are promising substitutes (higher solubility, but similar emulsification behavior) for the saturated surfactants. However, it is obvious that the choice of headgroup greatly impacts the performance of the surfactant (see also Fig. 8f). For better comparison, we seek to parameterize the time dependent curves.
One parameter obviously is the remaining volume of the emulsion at t = 250 h. The demixing process was fitted by a mono-exponential decay (Vem,rel ∝ exp(−t/k)), and k was used as parameter for the description of the emulsions stability as well. Thus, high k values characterize a stable emulsion, which demixes slowly. Fig. 8e shows the two described parameters for a series of surfactants differing in hydrocarbon chain length Cn. Please note the logarithmic scale of the y-axis, indicating there are huge differences in how fast the emulsions destabilize. There is no uniform trend, however, a chain length of n > 8 seems to be beneficial for the performance as emulsifier, which is reasonable, because the HLB value decreases in this direction. In contrast to the properties discussed before, there are only minor differences observed regarding a change in the anomeric configuration or regarding the presence of an unsaturated side chain. The overall best emulsifiers from our library were found to be ManαC10, ManαC12 and ManαCuns12, which exhibited nearly identical emulsifier properties. Surfactants with the same Cn have the same HLB value and should, thus, also perform equally as emulsifiers. This statement is wrong as seen from Fig. 8f for n = 12. Here, the head group has a huge influence on the stability of the emulsion. However, giving a universal explanation for these differences proves difficult, as many factors have to be taken into account for such complex, ternary systems (ratio of surfactant, water and hydrocarbon, polarity of the latter). However, from our experiments, we can deduce, that the rather small differences between our surfactants, introduced by change of the anomeric configuration and/or epimerisation of distinct OH-moieties in the carbohydrate headgroup, can impact their performance to the same degree as changing the size/polarity of the headgroup or changing the length of the hydrophobic moiety.
Water in cyclohexane emulsions were prepared with either MalβC12 or GalαC12. The ZnO precursor was then added (for detailed procedure refer to the experimental part). From the reaction, a white dispersion is obtained. After removal of solvent, powder X-ray diffraction (PXRD) was conducted. The resulting patterns (Fig. 9b) clearly show that in both cases ZnO with Wurtzite structure was obtained. Other crystalline phases are not present, and there are no marked differences by comparing the samples prepared using the two surfactants. Transmission electron microscopy (TEM) measurements show that the samples are morphologically different as shown in Fig. 9c, d and Fig. ESI-5 (ESI†). The use of MalβC12 led to the formation of particles with a shape resembling a rugby ball. As interesting as this shape may seem, it actually represents nanoparticles in the so-called Wulff form. The Wulff form is the shape a crystal adopts solely on the intrinsic stability of its facets.51 Therefore, it can be concluded, that the energy of surfaces terminating the crystal was not influenced by MalβC12 during growth. This result indicates that the maltose head group does not specifically interact with the ZnO crystal. The ZnO particle shape found for GalαC12 is much different from the Wulff form. The particles have a rhombus-like shape with the edges forming angles of 120° and 60°, respectively (see Fig. ESI-5, ESI†). Therefore, we assume the shape proposed in Fig. 9a. This is in agreement with the good fit of the measured atomic plane distance (2.8 Å) to the literature value for the (100) plane (2.81 Å). In addition to a restriction of growth in crystallographic c-direction, GalαC12 seems to stabilize the (100) and the (010) facets. Particles with crystallographic a,b-direction as main directions of growth are not unusual.52,53 However, these particles do typically represent hexagonal plates or variants of it. The more rod-like morphology in combination to this particular crystallographic orientation is unusual to the best of our knowledge. Based on these first promising findings we will further investigate the potential of our surfactant library for nanoparticle synthesis.
4 Conclusions
In this work, we presented a library of well-defined glyco-surfactants. Besides known, saturated alkyl-glycosides, we could successfully introduce a novel class of glycosurfactants bearing an internally unsaturated alkyl chain. From our library's compounds, we could investigate the influence of alkyl chain length/structure, carbohydrate moiety and anomeric configuration on the properties of the surfactants. From our data, we can conclude that the chain length influences the parameters of the surfactants (dH, CAC, thermodynamic parameters) as expected. The novel unsaturated surfactants show a differing behavior, which arises from a bent shape of the alkyl chains. We could also find significant differences for changes in the head group. The sugar moiety as well as the anomeric configuration led to different CACs and also greatly impacted the emulsification capabilities of the surfactants. The most important take-home message of our study is, although invariant in packing parameter and HLB value, surfactant isomers do vary significantly in almost all key properties.Two promising surfactants were then, as proof-of-principle, tested as capping agents for the generation of anisotropic ZnO nanocrystals. We could show that subtle changes in the carbohydrate head group can indeed induce changes in nanoparticle growth. With these findings, we will now further explore the potential of glycosurfactants for the synthesis of defined, anisotropic nanoparticles.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
The project was supported by the Deutsche Forschungsgemeinschaft (collaborative research center SFB 1214, project A1). R. M. M. acknowledges a PhD fellowship from the Konstanz Research School Chemical Biology. M. K. was funded by an ERC consolidator grant (ISURF, project 614606). We thank A. Friemel and U. Haunz for their assistance with NMR spectroscopy and M. Krumova for Cryo-TEM support.Notes and references
- Non-Ionic Surfactants, ed. P. L. Wendt and D. Hoysted, Nova Science Publishers, Inc., 2010 Search PubMed.
- L. J. Chen, S. Y. Lin, C. C. Huang and E. M. Chen, Colloids Surf., A, 1998, 135, 175–181 CrossRef.
- J. Eastoe and J. S. Dalton, Adv. Colloid Interface Sci., 2000, 85, 103–144 CrossRef PubMed.
- P. K. Vemula and G. John, Acc. Chem. Res., 2008, 41, 769–782 CrossRef PubMed.
- J. D. Desai and I. M. Banat, Microbiol. Mol. Biol. Rev., 1997, 61, 47–64 Search PubMed.
- E. Fischer and B. Helferich, Justus Liebigs Ann. Chem., 1911, 383, 68–91 CrossRef.
- W. von Rybinski and K. Hill, Angew. Chem., Int. Ed., 1998, 37, 1328–1345 CrossRef PubMed.
- D. Blunk, P. Bierganns, N. Bongartz, R. Tessendorf and C. Stubenrauch, New J. Chem., 2006, 30, 1705–1717 RSC.
- H. Abdelkader, A. W. G. Alani and R. G. Alany, Drug Delivery, 2014, 21, 87–100 CrossRef PubMed.
- R. Rajera, K. Nagpal, S. K. Singh and D. N. Mishra, Biol. Pharm. Bull., 2011, 34, 945–953 CrossRef.
- M. Beller, J. G. E. Krauter, A. Zapf and S. Bogdanovic, Catal. Today, 1999, 48, 279–290 CrossRef.
- M. Hager and K. Holmberg, Tetrahedron Lett., 2000, 41, 1245–1248 CrossRef.
- Y. Y. Luk and N. L. Abbott, Curr. Opin. Colloid Interface Sci., 2002, 7, 267–275 CrossRef.
- J. N. Israelachvili, D. J. Mitchell and B. W. Ninham, J. Chem. Soc., Faraday Trans. 2, 1976, 72, 1525–1568 RSC.
- W. C. Griffin, J. Soc. Cosmet. Chem., 1954, 5, 249–256 Search PubMed.
- V. Vill, T. Bocker, J. Thiem and F. Fischer, Liq. Cryst., 1989, 6, 349–356 CrossRef.
- P. Sakya, J. M. Seddon and V. Vill, Liq. Cryst., 1997, 23, 409–424 CrossRef.
- V. Vill and R. Hashim, Curr. Opin. Colloid Interface Sci., 2002, 7, 395–409 CrossRef.
- J. Schmidt-Lassen and T. K. Lindhorst, MedChemComm, 2014, 5, 1218–1226 RSC.
- C. Lizandara-Pueyo, S. Siroky, M. R. Wagner, A. Hoffmann, J. S. Reparaz, M. Lehmann and S. Polarz, Adv. Funct. Mater., 2011, 21, 295–304 CrossRef.
- C. Lizandara-Pueyo, S. Dilger, M. R. Wagner, M. Gerigk, A. Hoffmann and S. Polarz, CrystEngComm, 2014, 16, 1525–1531 RSC.
- M. Gerigk, P. Ehrenreich, M. R. Wagner, I. Wimmer, J. S. Reparaz, C. M. S. Torres, L. Schmidt-Mende and S. Polarz, Nanoscale, 2015, 7, 16969–16982 RSC.
- M. Gerigk, J. Bahner, T. Kollek, S. Helfrich, R. Rosenberg, H. Cölfen and S. Polarz, Part. Part. Syst. Charact., 2017, 34, 1600215 CrossRef.
- W. Klotz and R. R. Schmidt, J. Carbohydr. Chem., 1994, 13, 1093–1101 CrossRef.
- T. Ren and D. Liu, Tetrahedron Lett., 1999, 40, 7621–7625 CrossRef.
- J. Zhang and P. Kováč, J. Carbohydr. Chem., 1999, 18, 461–469 CrossRef.
- G. Zemplén and E. Pacsu, Ber. Dtsch. Chem. Ges., 1929, 62, 1613–1614 CrossRef.
- Y. Du, M. Zhang, F. Yang and G. Gu, J. Chem. Soc., Perkin Trans. 1, 2001, 3122–3127 RSC.
- J. Ohlsson and G. Magnusson, Carbohydr. Res., 2000, 329, 49–55 CrossRef PubMed.
- R. Lopez and A. Fernandez-Mayoralas, J. Org. Chem., 1994, 59, 737–745 CrossRef.
- M. Horiike and C. Hirano, Agric. Biol. Chem., 1980, 44, 2229–2230 Search PubMed.
- J. M. Chong, M. A. Heuft and P. Rabbat, J. Org. Chem., 2000, 65, 5837–5838 CrossRef PubMed.
- S. Paula, W. Sues, J. Tuchtenhagen and A. Blume, J. Phys. Chem., 1995, 99, 11742–11751 CrossRef.
- G. Chen, Z. Li, L. Chen, S. Ji and W. Shen, J. Dispersion Sci. Technol., 2017, 38, 506–514 CrossRef.
- K. Bock and C. Pedersen, J. Chem. Soc., Perkin Trans. 2, 1974, 293–297 RSC.
- G. Milkereit, V. M. Garamus, K. Veermans, R. Willumeit and V. Vill, J. Colloid Interface Sci., 2005, 284, 704–713 CrossRef PubMed.
- E. L. Thomas, D. B. Alward, D. J. Kinning, D. C. Martin, D. L. Handlin and L. J. Fetters, Macromolecules, 1986, 19, 2197–2202 CrossRef.
- C. Y. Chu, X. Jiang, H. Jinnai, R. Y. Pei, W. F. Lin, J. C. Tsai and H. L. Chen, Soft Matter, 2015, 11, 1871–1876 RSC.
- C. Dressel, F. Liu, M. Prehm, X. B. Zeng, G. Ungar and C. Tschierske, Angew. Chem., Int. Ed., 2014, 53, 13115–13120 CrossRef PubMed.
- N. M. Kovalchuk, A. Trybala, V. Starov, O. Matar and N. Ivanova, Adv. Colloid Interface Sci., 2014, 210, 65–71 CrossRef PubMed.
- W. H. Ansari, N. Fatma, M. Panda and D. Kabir-ud, Soft Matter, 2013, 9, 1478–1487 RSC.
- H. L. Lu, I. Pezron, T. Gaudin and A. Drelich, Colloids Surf., A, 2018, 540, 10 CrossRef.
- A. M. Tedeschi, E. Busi, L. Paduano, R. Basosi and G. D'Errico, Phys. Chem. Chem. Phys., 2003, 5, 5077–5083 RSC.
- F. A. Alejandra and B. D. Carlos, Helv. Chim. Acta, 2007, 90, 1141–1151 CrossRef.
- P. Alexandridis, J. F. Holzwarth and T. A. Hatton, Macromolecules, 1994, 27, 2414–2425 CrossRef.
- M. A. Malik, M. Y. Wani and M. A. Hashim, Arabian J. Chem., 2012, 5, 397–417 CrossRef.
- A. K. Ganguli, A. Ganguly and S. Vaidya, Chem. Soc. Rev., 2010, 39, 474–485 RSC.
- S. de Oliveira Honse, K. Kashefi, R. M. Charin, F. W. Tavares, J. C. Pinto and M. Nele, Colloids Surf., A, 2018, 538, 565–573 CrossRef.
- C. Lizandara-Pueyo, M. W. E. van den Berg, A. De Toni, T. Goes and S. Polarz, J. Am. Chem. Soc., 2008, 130, 16601–16610 CrossRef PubMed.
- C. Lizandara-Pueyo, M. C. Morant-Minana, M. Wessig, M. Krumm, S. Mecking and S. Polarz, RSC Adv., 2012, 2, 5298–5306 RSC.
- S. Polarz, Adv. Funct. Mater., 2011, 21, 3214–3230 CrossRef.
- Z. R. R. Tian, J. A. Voigt, J. Liu, B. McKenzie, M. J. McDermott, M. A. Rodriguez, H. Konishi and H. F. Xu, Nat. Mater., 2003, 2, 821–826 CrossRef PubMed.
- C. H. Ye, Y. Bando, G. Z. Shen and D. Golberg, J. Phys. Chem. B, 2006, 110, 15146–15151 CrossRef PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Additional information on synthetic procedures and molecular characterization data; additional data on surfactant self-assembly Fig. ESI-1–4. See DOI: 10.1039/c8sm01091a |
| This journal is © The Royal Society of Chemistry 2018 |