DOI:
10.1039/C8SM00919H
(Paper)
Soft Matter, 2018,
14, 6001-6012
Characterisation of protein aggregation with the Smoluchowski coagulation approach for use in biopharmaceuticals
Received
4th May 2018
, Accepted 6th June 2018
First published on 4th July 2018
Abstract
Protein aggregation is a field of increasing importance in the biopharmaceutical industry. Aggregated particles decrease the effectiveness of the drug and are associated with other risks, such as increased immunogenicity. This article explores the possibility of using the Smoluchowski coagulation equation and similar models in the prediction of aggregate-particle formation. Three different monoclonal antibodies, exhibiting different aggregation pathways, are analysed. Experimental data are complemented with aggregation dynamics calculated by a coagulation model. Different processes are implemented in the coagulation equation approach, needed to cover the actual phenomena observed in the aggregation of biopharmaceuticals, such as the initial conformational change of the native monomer and reversibility of smaller oligomers. When describing the formation of larger particles, the effect of different aggregation kernel parameters on the corresponding particle size distribution is studied. A significant impact of the aggregate fractal nature on overall particle size distribution is also analysed. More generally, this work is aimed to establish a mesoscopic phenomenological approach for characterisation of protein aggregation phenomena in the context of biopharmaceuticals, capable of covering various aggregate size scales from nanometres to micrometres and reach large time-scales, up to years, as needed for drug development.
1 Introduction
The rapid development of biopharmaceuticals in recent years has opened up new fields of research concerning protein aggregation and degradation.1,2 Biopharmaceuticals are therapeutic proteins for use in medical treatment of various conditions such as rheumatoid arthritis,3 Crohn's disease,4 breast cancer,5 psoriasis6 and others. They are extracted from or synthesized in biological sources—microbes, animals, plants or humans. They are globular proteins, with specific spatial conformations which enable them to perform their biological functions. Proteins in biopharmaceuticals are often susceptible to aggregation, which is formation of particles or aggregates containing up to several thousand interconnected protein subunits. Non-native irreversible aggregation of proteins affects multiple steps in the production, including expression, purification, freezing, transportation and long-term storage.7–9 Aggregated particles are unable to perform biological functions of native protein. What is more, they can trigger an immune response in the patient, resulting in rejection of the drug. The identification of underlying causes and mechanisms that drive protein aggregation is thus of crucial importance not only for the biopharmaceutical industry, but, more importantly, for the welfare of patients.
The conformational as well as colloidal stability of the proteins and consequently their biological functions depend on various solution properties, including pH, temperature and presence of other molecules in the solution, such as salts and sugars.10–13 Even small changes in these environmental conditions greatly affect the long-term stability and efficacy of the drug via their impact on hydrophobic interactions, electrostatic interactions, van der Waals forces and other contributions to the total intra- and inter-molecular potential.
Protein aggregation is a process which spans multiple size scales, from the nanometre scale of individual protein macromolecules to the visible particles, comprised of millions of these elementary building blocks. Different methods must be employed to detect aggregates in different size ranges. Size exclusion chromatography (SEC) is used to separate the smallest oligomers. Larger particles (>100 nm) can be measured with resonant mass measurements (RMM). The largest particles (>1 μm) are detected by micro-flow imaging (MFI). Because the number of visible aggregates is small, large volumes of samples have to be analysed to measure their concentration, but such an amount of material is usually not readily available in the early development phase. On the other hand, large particles in biopharmaceuticals are the most immunogenic14,15 and also prohibited by European Pharmacopoeia (EP) and United States Pharmacopeia (USP). The prediction of their formation under different conditions would greatly contribute to development of the final drug product formulation. A tool that could describe their assembly from the native protein monomers and predict their concentration would therefore be a valuable addition to the biopharmaceutical industry.
The Smoluchowski coagulation model is a population balance equation.16,17 It is a deterministic mean field model which describes the time evolution of the number density of particles as they coagulate based on the mass action law. Its basic principle has been applied to polymerization, coagulation of aerosols and flocculation. Recently, application of the same kinetics to biopharmaceuticals has been proven successful by the ground-breaking work of Arosio and Nicoud et al.18–22 Aggregation of human immunoglobulin G under severe stress conditions has been described in terms of population balance modelling, identifying dominant molecular mechanisms based on bulk aggregation measurements of smaller oligomers under various stress conditions, such as exposure to acid23,24 and severe temperature. The effect of various excipients and conditions on the model parameters was also studied. The connection between bulk measurements of stability parameters and microscopic mechanisms25,26 is also crucial in establishing a viable model for prediction of protein aggregation at the mesoscale. In addition to the bulk, surfaces and interfaces are also notorious for particle formation and adhesion,27,28 but are out of scope of mean field models such as the Smoluchowski equation. However, when left undisturbed, contribution of interfaces to aggregation is significantly reduced.29,30 Therefore, when talking about product shelf-life, the bulk aggregation model is a reasonable approach.
In this article, we study the aggregation dynamics of three IgG 1 monoclonal antibodies. These proteins exhibit different aggregation pathways, covering the common processes observed in biopharmaceuticals. Two monoclonal antibodies were subjected to elevated temperature conditions, and the third was used to study the reversibility of smaller oligomers after dilution. For elevated temperature, 40 °C was used because it is much lower than the denaturation temperature of both antibodies under specified conditions (data not shown). The results are therefore representative of long-term stability of biopharmaceuticals. Experimental data were interpreted with the Smoluchowski coagulation equation as a model for protein aggregation at all size scales from smaller oligomers to visible particles, consisting of hundreds of thousands of protein monomers. Implementation of size binning,31,32 described in the following chapter, was crucial for achieving such particle sizes. The system of equations was also modified to describe some additional phenomena, besides simple coagulation, that have been observed33 in the aggregation of biopharmaceuticals. The additional phenomena include a conformational change of the native protein state as the first step of aggregation and reversibility of smaller oligomers. A computational model based on a Runge–Kutta integrator was used to solve the differential equations. First, we explain basic aggregation mechanisms and parameters that can be deduced from measurements of smaller oligomers. Later, we move on to the formation of mesoscopic and microscopic particles and explore the effect of physical parameters, like Fuchs stability ratio and aggregate fractal dimension, on the corresponding aggregation dynamics. But the benefits of such a model go far beyond simple explanatory purposes. By further understanding the link between actual solution properties, such as temperature and pH, and the model parameters, the model could be used to predict the formation of particles of various sizes, from oligomers at the nanometre scale to larger, more immunogenic particles.
2 Experimental section
2.1 Sample preparation
Three monoclonal IgG1s (mAb 1, mAb 2 and mAb 3, isoelectric points between pH 8 and pH 9) were provided by Lek biopharmaceutical site in Mengeš. Mab 1 was provided in 25 mM citrate buffer at pH 6.5. It was concentrated (Amicon Ultra centrifuge filter unit, 50 kDa MWCO) and then diluted with 25 mM citrate buffer and sucrose (Sigma) to produce 6 formulations at 1, 10 and 50 mg ml−1 with and without 200 mM sucrose. The formulations were aliquoted (volume of 1.7 ml) into Sarstedt Micro tubes, 2 ml, PP, and incubated at 40 °C. SEC, RMM and MFI measurements were performed every week for 2 months. Prior to MFI and resonant mass measurements, the samples were degassed at 940 mbar for 20 min and homogenised (rotated 10 times). Mab 2 was provided in histidine buffer at pH 6. The buffer was exchanged to 20 mM sodium citrate (Citric acid, Merck), pH 7. Six samples with concentrations from 10 mg ml−1 to 60 mg ml−1 were prepared and aliquoted into Nunc 0.5 ml cryobank vials and incubated at 40 °C. SEC measurements were performed before incubation and after one and two months of incubation. MAb 3 was provided in phosphate buffer at a concentration of 63 mg ml−1. The protein sample was unstressed with the exception of freezing after purification and thawing before the experiment. All of the aggregates were already present at the start of the experiment. The thawed sample was stored at 5 °C for a month to reach an equilibrium state, and then diluted to 1 mg ml−1 with purified water and stored back at 5 °C. SEC measurements were performed several times in the course of next week.
2.2 Size exclusion chromatography
Samples were analysed at 40 °C on a Waters ACQUITY UPLC System with a SEC column (200 Å pore size, 1.7 μm bead size and 4.6 mm × 150 mm column dimensions). The sample load was 0.75 μl. The mobile phase (50 mM sodium dihydrogen phosphate and 400 mM sodium perchlorate, pH 6.0) flow rate was 0.4 ml min−1 with a total run time of 5 min. If necessary, samples were diluted to 1 mg ml−1 in 150 mM sodium phosphate, pH 7, and held at 2–8 °C in the autosampler prior to injection. The data were analysed with Empower 3 software. A standard (IgG at 1 mg ml−1) with a known amount of aggregates was loaded prior to and after each set of measurements to ensure the comparability of results during the course of the experiment. The variability of the relative aggregate content measurement (aggregates/monomer) at the described column loading was estimated to be 0.1% (absolute value). SEC total protein mass recovery was within the measurement error for all tested formulations before and after stress.
2.3 Resonant mass measurements
An Archimedes system (Affinity Biosensors) controlled by ParticleLab version 1.20 software was used. The system was flushed with purified water and the fluidic channels were unclogged with built-in operations (software option “sneeze”) before each measurement. The sample solution was then loaded for 30 s. Limit of detection was determined in the automatic LOD mode. Samples of 150 nl were analysed. The particles were assumed to be globular with a protein density of 1.32 g ml−1 for particle size estimation.
2.4 Micro-flow imaging
A Micro-Flow Imaging system (MFI5100, ProteinSimple), equipped with a silane-coated flow cell (400 μm, 1.6 mm) and controlled by the MFI View System software version 2, was used. The system was flushed with 5 ml of purified water before each measurement. The background was zeroed by flowing UPW. 0.7 ml samples were analysed at a flow rate of 0.2 ml min−1 and a camera shot rate of 3 flashes per second, with an additional 0.7 ml of prerun volume. The equivalent circle diameter (ECD) was calculated and used as a measure of particle size.
2.5 Theoretical model
The Smoluchowski coagulation model is a deterministic mean field set of equations which describes the kinetics of the process of binary aggregation.16 It assumes that the system is composed of a large number of identical indivisible primary particles (monomers). These monomers irreversibly bind and form larger particles. Denoting an aggregate Ai composed of i primary particles, the processes in such a system can be represented byThe concentration (number density) of particles Ai at a time t is represented by variables ni(t), the concentrations being averaged over some spatial domain.
The rate of aggregation is assumed to be directly proportional to the concentrations of coagulating particles and to the constant of proportionality, known as a rate constant. Such construction also inherently assumes that there are no spatial correlations in the vessel and that two clusters of any size can coalesce. If the process from eqn (1) occurs with a rate constant ki,j, these assumptions yield in principle an infinitely sized system of differential equations describing irreversible aggregation across the whole size range of particles:
| |  | (2) |
The rate constants
kij are referred to collectively as the aggregation kernel. The kernel is a matrix, which is also infinite in size. In practice, it is cut off at a large enough
i and
j so that it does not affect the relevant results. In the model, we have used the following kernels:
| |  | (4) |
| |  | (5) |
The first kernel,
kc, is the simplest with all of its matrix elements set to a constant value. The equation with this kernel even has an analytical solution,
16 and it represents a system where all the particles can interact with the same probability, but does not account for their diffusivity or reaction cross-section. The second kernel,
kmono, only allows the interaction between two particles if one of them is a monomer. The system described by this kernel undergoes a simple monomer addition process where monomers are added one by one to larger particles. When the supply of monomers is depleted, the aggregation process stops. The third kernel (also shown in
Fig. 1),
kRLCA, corresponds to diffusion/reaction limited cluster aggregation. Brownian motion of particles in a solution is assumed; temperature
T and viscosity
η are the parameters of the kernel. Parameter
df is the fractal dimension of the clusters and describes the scaling of particle size with the number of its building blocks. The fractal dimension of a globular particle is
df = 3—however, polymers in a good solvent exhibit a fractal dimension of
df = 5/3. On contact, the particles coalesce with a finite probability, described by the Fuchs stability ratio
W and the exponent of the product kernel
γ. The Fuchs ratio can be computed from the total interaction potential between the primary particles, but is usually determined from the fit due to the complexity of protein–protein interactions.
22 The parameter
γ describes the sticking probability for two colliding aggregates and is proportional to the total number of primary particle interactions upon their contact. Since the number of primary particles located on the external surface of a fractal aggregate scales as
i1−1/df,
γ can be roughly estimated as
although various alternative approximations exist.
34 The model can be further simplified by defining the characteristic time of aggregation,
| |  | (7) |
where
n0 is an arbitrarily chosen concentration, and unless otherwise stated (when samples of different concentrations are compared), the initial native monomer concentration. For simpler comparison between kernels, the constants from
kcij and
kmonoij are also set to

, which makes
kc11 =
kmono11 =
kRLCA11.
 |
| | Fig. 1 A schematic representation of the mechanisms of protein aggregation. (a) Unimolecular conformational change from the native state N into the aggregation prone state A1, described by eqn (8) and (9), resulting in first order kinetics. (b) Bimolecular coagulation of monomers, resulting in second order kinetics, and the reversibility of smaller oligomers, described by eqn (12). (c) Basic Smoluchowski aggregation process described by eqn (2). On the right, the reaction limited cluster aggregation from eqn (5) is represented by two matrices, with parameters γ = 0 (top) and γ = 0.3 (bottom). | |
In biopharmaceuticals, other mechanisms besides simple coagulation as covered by eqn (2) are also present. The first one implemented in our model is the initial irreversible conformational change of the native monomer as the first step of aggregation. This step represents spontaneous protein unfolding and subsequent misfolding, so its hydrophobic surfaces remain partially exposed. By denoting the native monomer Mnat (corresponding concentration nnat), its aggregation prone conformational isomer with A1 (corresponding concentration n1), and the corresponding rate constant ![[k with combining tilde]](https://www.rsc.org/images/entities/i_char_006b_0303.gif) , eqn (2) can be expanded by
, eqn (2) can be expanded by
| |  | (8) |
| |  | (9) |
| |  | (10) |
The native monomer is in this case not directly included in the process of aggregation described by
eqn (2)—only through the intermediate state A
1.
The second relevant mechanism is the reversibility of smaller oligomers (in the literature dimers, trimers, tetramers), while larger particles are reported to be irreversible. In order to incorporate the reversibility of dimers, the Smoluchowski approach needs to be generalised. In the system eqn (2), which describes irreversible aggregation, the reversibility is incorporated with addition of elements describing fragmentation to the first equations in the system:
| |  | (11) |
| |  | (12) |
In principle, the dimer A
2 could break apart into either M
nat or A
1, according to our previous expansion. For simplicity, this model was only used with the original Smoluchowski model without
eqn (8) to show the basic effect of this process on the concentration distribution of the particles. All of the processes listed above are schematically shown in
Fig. 1. In principle, a combination of all these processes contributes to protein aggregation.
2.6 Model implementation
In biopharmaceuticals, the size range of aggregates spans many orders of magnitude. The largest particles are aggregates built from thousands, even millions, of individual protein molecules. To accurately simulate the dynamics up to the particle of size An, a system consisting of n differential equations with approximately n terms each has to be solved in every time step, yielding a time complexity of O(n2). The sectional or size-binning approach is therefore usually advocated for solving problems where the number of building blocks in individual particles spans multiple orders of magnitude.31,32 Our implementation of the sectional approach uses nmax = 33 bins with particles consisting of an average number of building blocks in each bin 1, 2, 4, 8,…,2nmax, meaning that particles of sizes 1, 2, 3–5, 5–10,… are binned together, with the value 2n in the centre of each bin. The number distribution in each size bin is assumed to be constant and the kernel is also approximated by a constant for each bin.
The goal of this work is to demonstrate primarily how the main dynamic traits of the system are affected by different parameters; therefore, the size-binning can be quite coarse. However, for a full quantitative link to actual aggregation data, the implemented size-binning method would most likely have to be improved. An arbitrary number of bins can be chosen and subsequent precision obtained.32
3 Results and discussion
3.1 Smaller oligomers
The major important information when designing pathways to control the aggregation is to determine the order of aggregation kinetics (first, second). This order can be used to determine whether the initial conformational change, described by eqn (8), is necessary for the subsequent aggregation (unimolecular process). If it is, the aggregation follows first order reaction kinetics and the relative aggregation rate does not depend on protein concentration in the sample. In this case, the protein can be stored at high concentration without accelerating the aggregation process, which in the biopharmaceutical context is very important when selecting the final protein concentration in the drug product. Differently, if the aggregation kinetics follows second (bimolecular process) or mixed order, then a minimum concentration should be chosen, depending on the route of administration and other factors. Fig. 2 shows exemplary SEC aggregation measurements of mAb 1 formulations which contain sucrose. The formulations containing only buffer are similar and not shown.
 |
| | Fig. 2 Experimental measurements of relative aggregate content for mAb 1 formulations containing 200 mM sucrose. The error bars represent the estimated SEC measurement error. | |
The order of such measurements can be derived from eqn (2) and (8). Assuming a sample of native protein monomers at t = 0 where the concentration of aggregates can be neglected, as is the case with biopharmaceuticals at the beginning of their shelf-life, these equations can be simplified to
| |  | (13) |
and
| |  | (14) |
respectively. When measuring the concentration of the native monomer protein molecules in the sample, we can introduce the initial relative rate of monomer loss through aggregation as
| |  | (15) |
If the initial step of aggregation in the sample follows the basic bimolecular Smoluchowski process,
R is a linear function of concentration, whereas if the unimolecular conformational change is the rate limiting process,
R is a constant. By observing the rate dependence as a function of initial concentration the order of aggregation kinetics can be directly distinguished as shown in
Fig. 3. What is more, the corresponding kernel elements
k11 and
![[k with combining tilde]](https://www.rsc.org/images/entities/i_char_006b_0303.gif)
can be readily determined from the graph. Both unimolecular and bimolecular processes are present in formulations with and without sucrose. Sucrose is expected to inhibit the initial conformational change
via the preferential exclusion from the surface and the corresponding increase in protein conformational stability. This also slightly decreases protein solubility, potentially resulting in a faster bimolecular aggregation. At the tested sucrose concentration, however, both effects are negligible.
 |
| | Fig. 3 Identification of the reaction order of aggregation. (a) Model results for the initial relative rate of monomer loss through aggregation R from eqn (15) as a function of initial native monomer concentration for different processes. The rate R is a linear function (through zero) in the case of a bimolecular process (second order) and a constant in the case of conformational change to intermediate state (first order). (b) Experimentally determined aggregation rates (slopes from Fig. 2) for all mAb 1 formulations. The initial kernel elements k11 and ![[k with combining tilde]](https://www.rsc.org/images/entities/i_char_006b_0303.gif) can be easily read from the graph (slope and intercept, respectively). can be easily read from the graph (slope and intercept, respectively). | |
A rather experimental challenge in the determination of monomer concentration in samples which follow the first order aggregation rate is the distinction between the native monomer Mnat and its aggregation prone conformational isomer A1. The two are likely not discernible based on their size and molecular weight alone, for example by techniques like SEC. In this case, the measured monomer concentration is the sum of both species. The relative differences in the modelled signal are shown in Fig. 4. The monomer concentration curve has a distinct sigmoidal shape, which depends on the ratio of both contributions to A1 isomer dynamics from eqn (9), namely the rate of formation ![[k with combining tilde]](https://www.rsc.org/images/entities/i_char_006b_0303.gif) nnat and the rate of elimination through aggregation k11n12. If the conformational change is much slower compared to the subsequent coagulation, the concentration of the intermediate state A1 is negligible throughout the aggregation process and the measured concentration time dependence is purely exponential. If the subsequent coagulation is the rate limiting step, the sigmoidal curve is much more prominent. Because the conformational change is a unimolecular process and coagulation is a binary process, this ratio is also affected by protein concentration, as also described by Nicoud et al.22 The resulting sigmoidal shape of the monomer concentration and the apparent lag time in the concentration evolution of conformational isomers and dimers display a power-law dependence on concentration. But the power law is not only valid for a broad range of concentrations, as shown in Fig. 4b, but also for different parameters
nnat and the rate of elimination through aggregation k11n12. If the conformational change is much slower compared to the subsequent coagulation, the concentration of the intermediate state A1 is negligible throughout the aggregation process and the measured concentration time dependence is purely exponential. If the subsequent coagulation is the rate limiting step, the sigmoidal curve is much more prominent. Because the conformational change is a unimolecular process and coagulation is a binary process, this ratio is also affected by protein concentration, as also described by Nicoud et al.22 The resulting sigmoidal shape of the monomer concentration and the apparent lag time in the concentration evolution of conformational isomers and dimers display a power-law dependence on concentration. But the power law is not only valid for a broad range of concentrations, as shown in Fig. 4b, but also for different parameters ![[k with combining tilde]](https://www.rsc.org/images/entities/i_char_006b_0303.gif) and k11, since the relative lag time depends only on the ratio
and k11, since the relative lag time depends only on the ratio ![[k with combining tilde]](https://www.rsc.org/images/entities/i_char_006b_0303.gif) nnat/k11. Special care should be taken not to confuse such measurements with a lag phase, which is common in amyloid fibrillation of peptides and smaller proteins in very small volumes,35 but has been attributed to stochastic processes.
nnat/k11. Special care should be taken not to confuse such measurements with a lag phase, which is common in amyloid fibrillation of peptides and smaller proteins in very small volumes,35 but has been attributed to stochastic processes.
 |
| | Fig. 4 Modelled protein aggregation dynamics as can be determined by SEC measurements of monomers and dimers. (a) Monomer and dimer concentration as a function of time. The monomer peak is the sum of the native and the intermediate state and its time dependence exhibits a distinct sigmoidal shape. (b and c) Lag time, and relative maximum of A1 particles  —the parameters of the intermediate state concentration curve, which define the sigmoidal shape of the measured sum—as a function of initial native monomer concentration. The relative maximum concentration of the intermediate state is decreased with increasing initial native monomer concentration and it appears earlier in the aggregation process. This lag time has a distinct power-law dependence on the starting protein concentration, as seen in (b), with lag time ∝ n0−0.45. —the parameters of the intermediate state concentration curve, which define the sigmoidal shape of the measured sum—as a function of initial native monomer concentration. The relative maximum concentration of the intermediate state is decreased with increasing initial native monomer concentration and it appears earlier in the aggregation process. This lag time has a distinct power-law dependence on the starting protein concentration, as seen in (b), with lag time ∝ n0−0.45. | |
An experimental example of the described phenomenon is shown in Fig. 5, which shows aggregation measurements of mAb 2 (citrate buffer, pH 7) at concentrations ranging from 10 mg ml−1 to 60 mg ml−1. The aggregation of this protein under the specified conditions is mostly unimolecular with a distinct apparent lag time at lower concentrations. The model is fitted to the data, with the model parameters displayed on the chart. The fitted data represent total aggregate concentrations, so the emphasis is on native monomer conformational change (![[k with combining tilde]](https://www.rsc.org/images/entities/i_char_006b_0303.gif) ) and the subsequent interaction between such monomers (k11). Interactions between dimers and larger species are less important when considering the total aggregate content; therefore, the simplest kernel kc is used. By using this kernel, we also avoid overparametrising our system with low impact parameters such as fractal dimension and sticking probability. In addition to the measured initial aggregate concentration, the model assumes a 2.5% content of conformationally compromised monomers at t0. The Fuchs stability ratio W for interaction between conformationally compromised monomers (among themselves and other aggregates) can also be estimated from the fit. The value (∼109) is many orders of magnitude larger than the estimated electrostatic contribution (W ≈ 1), which is in line with previous findings about protein–protein interactions.20 This large value indicates the presence of a high energy barrier that particles must overcome before colliding, which reduces the collision efficiency and thus delays the aggregation process with respect to diffusion-limited conditions. The reported value is several orders of magnitude larger still than those reported previously (∼107), which can be attributed to denaturation temperature of the proteins with respect to the stress conditions. Under moderate stress conditions of this study (40 °C), only minor conformational changes are expected, while previously reported values correspond to 70 °C, where all the proteins are partially or completely unfolded and thus much more reactive.
) and the subsequent interaction between such monomers (k11). Interactions between dimers and larger species are less important when considering the total aggregate content; therefore, the simplest kernel kc is used. By using this kernel, we also avoid overparametrising our system with low impact parameters such as fractal dimension and sticking probability. In addition to the measured initial aggregate concentration, the model assumes a 2.5% content of conformationally compromised monomers at t0. The Fuchs stability ratio W for interaction between conformationally compromised monomers (among themselves and other aggregates) can also be estimated from the fit. The value (∼109) is many orders of magnitude larger than the estimated electrostatic contribution (W ≈ 1), which is in line with previous findings about protein–protein interactions.20 This large value indicates the presence of a high energy barrier that particles must overcome before colliding, which reduces the collision efficiency and thus delays the aggregation process with respect to diffusion-limited conditions. The reported value is several orders of magnitude larger still than those reported previously (∼107), which can be attributed to denaturation temperature of the proteins with respect to the stress conditions. Under moderate stress conditions of this study (40 °C), only minor conformational changes are expected, while previously reported values correspond to 70 °C, where all the proteins are partially or completely unfolded and thus much more reactive.
 |
| | Fig. 5 Experimental characterisation of unimolecular aggregation of mAb 2. Relative SEC aggregate content measurements are overlaid with a fitted model (dotted lines), with the model parameters displayed. The model assumes a purely unimolecular first aggregation step. | |
The second phenomenon relevant in the study of protein aggregation is the reversibility of smaller oligomers, such as dimers and trimers. We have modelled this step with the expansion of the basic Smoluchowski model, as described in eqn (11) and (12). The best way to determine the extent of reversibility of smaller oligomers is through dilution. Assuming that the initial native monomer n0 concentration in a sample is much larger than the initial concentration of the dimer n20 and that the content of all larger particles is negligible (nnat ≫ n20 ≫ ni0, i > 2), as is often the case with unstressed or mildly stressed samples, a stable dimer/monomer ratio  can be obtained by solving eqn (11) in equilibrium state,
can be obtained by solving eqn (11) in equilibrium state,  :
:
| | 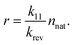 | (16) |
By performing a dilution of a sample, we diminish both
n2 and
nnat by a dilution factor
f and we get
| |  | (17) |
where
r0 is the initial ratio and
rd is the ratio after dilution. The time dependence of this ratio immediately after dilution can be obtained by solving
eqn (12):
| |  | (18) |
In the limit of
t → ∞,
eqn (18) reduces to
eqn (16). The ratio should be measured several times over the course of hours or days after dilution (
e.g. by size exclusion). If the equilibrium value differs from the one obtained from
eqn (17), it is likely that two or more species of dimers are present, at least one of which is irreversible.
Fig. 6 shows the experimental results and a schematic interpretation of such a dilution experiment using mAb 3. The measurements are performed by SEC. Besides the monomer peak, only one more peak is present, assumed to correspond to dimers according to the column calibration curve. The sample was diluted from 60 mg ml
−1 to 1 mg ml
−1. The dimer concentration fell from the initial 1.6% and stabilised at 1.1% after a week at 5 °C. An excellent fit of
eqn (18) to the size exclusion data suggests that only a third of all mAb 3 dimers are reversible.
 |
| | Fig. 6 Experimental determination of mAb 3 dimer reversibility. (a) Dimer/monomer concentration and a fit of eqn (18) – solid line. The dotted line corresponds to the estimated irreversible dimer content. (b) A schematic interpretation of monomer/dimer dynamics after dilution. If the ratio r after dilution remains much higher than 1/f of the starting ratio when equilibrium is achieved, an irreversible dimer species is most likely present in the sample. | |
Even though mAb 3 solution contains reversible dimers, this is not the crucial step in aggregation, with the majority of dimers irreversible and thus already subjected to the classical irreversible process described by eqn (2). The other two monoclonal antibodies exhibit no reversibility (data not shown). Characterisation of reversibility as presented, however, is important when designing stability studies, where dilutions and buffer exchanges are present during sample preparation as well as after stress conditions prior to measurement of aggregation. Data interpretation as presented in Fig. 6 is intended to meet the requirements of such scenarios.
3.2 Towards visible particles
The results for smaller aggregates were mostly obtained, or at least approximated, by analytical means. The advantage of the model is that it can also give results for much larger particles, which can regularly be found in biopharmaceutical samples (Fig. 7), comprised of thousands, if not millions, of individual protein monomers. While smaller aggregates covered in the previous section are mostly characterised by size exclusion measurements, the methods of choice for detection of such larger particles are resonant mass measurements and flow imaging microscopy. Fig. 7 shows the aggregation process not only on the scale of individual monomers, but also much larger particles. As we have shown, the evolution of distribution of smaller oligomers mostly depends on elementary processes involving the protein monomers, which can in turn be deduced from the measurements of their concentration. The ensuing distribution of larger particles, however, also depends heavily on the fractal nature of the clusters and the parameter γ, which govern the cluster–cluster aggregation, rather than simple monomer addition.
 |
| | Fig. 7 Model dynamics of differently sized aggregates and their ensuing size distribution. (a) Concentration of larger particles as a function of time. (b) Distribution of particles by size at different time points. The size is estimated by using the fractal dimension of df = 5/3 and monomer size of 10 nm. Different methods used to measure the particle concentration are also suggested, with the example chromatogram for SEC measurements and pictures of actual aggregates taken by flow imaging microscopy. | |
In this section, the concentration distributions of larger particles, rather than their time dependencies, are presented. Fig. 7 shows a model distribution of concentrations ni across the whole size range at time points when 5%, 20% and 50% of the native monomers are depleted. The y axes show the number of building blocks as well as the approximate size of the particles. The monomer size was assumed to be 10 nm. The central parameter in relating the particle size with the number of primary particles (monomers) is the fractal dimension of the aggregate, which determines how the particle size scales with the number of its building blocks, described by the equation
where
D is the characteristic size of the particle and
n is the number of its building blocks. Even though the proteins themselves are globular (
df = 3), the structures formed
via their coagulation are not necessarily so. If large particles with protein monomers as building blocks behave as polymers, their fractal dimension is
df = 5/3. A fractal dimension of anywhere between 1.5 and 2.6 has been reported for protein aggregates of various sizes, formed under different conditions.
19–24 Note that even a small difference in the estimation of fractal dimension brings rather major differences in the particle size. For example, a globular aggregate built from 1 million primary particles of size 10 nm measures 1 μm in size, while the same aggregate behaving as a polymer chain is forty times larger, at 40 μm.
While physically counting the individual protein monomers in an aggregate is impossible, their number can be estimated by measuring the weight of the aggregate. The fractal dimension of aggregates can therefore be estimated by measuring their weights and sizes with a combination of different methods, for example by resonant mass detection in combination with flow imaging for larger particles or size exclusion chromatography coupled with dynamic (size) and static (weight) light scattering for smaller aggregates. Alternatively, the fractal dimension can be determined from the power-law regime of the average structure factor, also determined by scattering measurements.36
Fig. 8 shows the effect of different kernel types and parameters, including fractal dimension, on the particle size distribution. All of the distributions in the figure are shown at a time point when 5% of the monomer is depleted. Also shown in the figure is a comparison of different kernels. In contrast to smaller particles, the concentration distribution of larger particles depends strongly on the structure of the kernel. The simple monomer addition kernel is the only presented kernel where aggregation is cut off when the monomers are depleted, producing a final distribution of particles, while aggregation governed by other kernels in principle ultimately produces a single particle containing all of the aggregating material. But even in the beginning stages of aggregation, the particle sizes stemming from the simple monomer addition kernel are significantly smaller than from kernels that include cluster–cluster aggregation. If present, the cluster–cluster aggregation thus governs the formation of larger particles. The most suitable general kernel including all the basic physical processes is the RLCA kernel, so some effects of its parameters on the particle distribution are also shown. The parameter γ in particular has a great effect on the formation of larger particles. This parameter can be roughly estimated from the fractal dimension df with the help of eqn (6), which would put a realistic value of γ somewhere between 0.3 and 0.7. A broader range of values (0 to 1) is shown here for presentation purposes. First and second order aggregation, already compared in Fig. 3, are again revised. The aggregation following first order produced much smaller particles, but mainly because by the time 5% of the native monomer is depleted, most of this deficit is still trapped in the intermediate state—different aggregation parameter ![[k with combining tilde]](https://www.rsc.org/images/entities/i_char_006b_0303.gif) might yield different results, as presented later.
might yield different results, as presented later.
 |
| | Fig. 8 Effect of different kernel types and parameters on the modelled particle size distribution. (a) Effect of the aggregate fractal dimension (kernel used kc). (b) Comparison of kernel types—reaction limited cluster aggregation kernel, constant kernel, simple polymerisation kernel. (c) Effect of parameter γ in a RLCA kernel. (d) Binary aggregation versus aggregation via a unimolecular process from eqn (8). | |
The calculated distribution of particle sizes can also be used to estimate the size of the largest particle that one could observe in a given sample. By declaring ns as the concentration at which a single particle is present in our volume of sample, the size of the largest particle in the sample can be estimated from the distribution of particle sizes. Defining is as the particle size beyond which only a single particle is likely to be larger, we get
| |  | (20) |
By treating
i as a continuous variable,
eqn (20) can be rewritten as
| |  | (21) |
Let us now consider a typical biopharmaceutical sample with a volume of
V = 1 ml, a protein (mass of the native monomer) concentration of
c = 1 mg ml
−1 and a monomer weight of
m = 150 kDa or approximately 3 × 10
−16 mg. These data can be used to determine the
ns for our model:
| |  | (22) |
With the integral value defined, we can now use
eqn (21) to estimate the size of the largest particle. Because we cannot calculate an infinite number of different concentrations in a numerical computation, the summation is cut off at a large enough value of
imax so that the contributions of all larger particles can be neglected. In our case of 33 bins, that is approximately
imax ≈ 2
32 ≈ 10
10. In practice, the numerical integration of
eqn (21) is done by summation of the numerically calculated particle distribution values from
imax backwards until the value of the sum surpasses
ns, and the corresponding
i is declared
is. The particle size corresponding to
is is declared as the maximum particle size in the sample.
Fig. 9 shows the estimated maximum sizes of fractal aggregates in a typical biopharmaceutical sample when 5% of the monomer is depleted. The conformational change with the reaction rate of
![[k with combining tilde]](https://www.rsc.org/images/entities/i_char_006b_0303.gif)
is the rate limiting step of aggregation. The reaction rate of this conformational change leading to native monomer loss can be compared to the rate of subsequent aggregation with the ratio
K, which we define as
| |  | (23) |
Values of
K smaller than 1 effectively speed up the aggregation of larger particles compared to the native monomer loss, leading to the formation of larger aggregates. For comparison,
K ≈ 0.001 for mAb 2, as shown in
Fig. 5. Relation
equation (6) is also applied, correlating the sticking probability of aggregates with the number of primary particles on their surface. We can see that the fractal nature of the aggregates has a significant impact on aggregation dynamics. Aggregates with a smaller fractal dimension are physically larger, but are comprised of a smaller number of primary particles due to their decreased reactivity. This decrease is a result of a lesser number of the aggregates’ primary particles that come into contact upon their collision. Denser aggregates with a larger fractal dimension are smaller but coalesce more readily upon collision, resulting in a larger number of primary particles—
i.e. heavier aggregates. We can influence the aggregates’ fractal dimension by factors such as pH and ionic strength,
20–22 giving us an attractive possibility of optimizing either the size or the weight of the aggregates
via their fractal dimension. The same factors, however, also influence other parameters such as the Fuchs stability ratio and the rate of native monomer degradation
![[k with combining tilde]](https://www.rsc.org/images/entities/i_char_006b_0303.gif) via
via their impact on the particle potential and conformational stability. A comprehensive case-by-case study of such impacts should therefore be performed to optimise the formulation according to the model parameters.
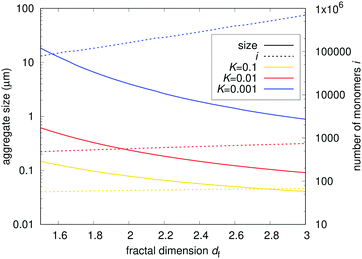 |
| | Fig. 9 Estimated maximum sizes of fractal aggregates in a typical biopharmaceutical sample. The solid lines represent the physical size of aggregates in μm. The dashed lines represent the number of primary particles comprising the aggregates. The results for different ratios between unimolecular and subsequent bimolecular process rates K are shown. The fractal nature of the aggregates has a significant impact on aggregation dynamics. | |
An example of combined experimental data of particle size distribution is shown in Fig. 10. Size exclusion chromatography, resonant mass measurements and micro-flow imaging data are shown together in a size distribution representation directly comparable to numerical results in Fig. 8. However, with the measured particle sizes approaching 100 μm, the mean field Smoluchowski approach is not suitable anymore. Sedimentation becomes an issue with particles exceeding the size of approximately 1 μm (data not shown), causing a selective increase in the concentration of larger particles near the bottom of the vial. Larger particles therefore coalesce more rapidly because of sedimentation, leading to an underestimation in the calculated particle size as shown in Fig. 9. Both vial shape and sample volume should be taken into account when adjusting the basic Smoluchowski equation to include this phenomenon. Adhesion of particles to the bottom of the vial is also a factor, even more so for larger particles due to their low concentration. Proteins are surface active molecules that are known to coat hydrophobic interfaces such as vial walls, which also has an effect on aggregation. Therefore, fitting the data with a numerically calculated size distribution based on the mean field approach could return misleading parameter values. Another issue is the measurement gap in the sub-micron range, where the mean field model would still be suitable. Additional experimental methods, such as field flow fractionation,37 could help in the characterisation of particles in this range for a quantitative fit.
 |
| | Fig. 10 Combined experimental data for mAb 1 at the highest concentration. Particle size distribution,  , where D is the estimated particle size, is plotted as a function of size. (a) Evolution of size distribution in a buffer only formulation. (b) Evolution of size distribution in a formulation containing sucrose. For size exclusion measurements, the monomer size is assumed to be 10 nm. The aggregates (mostly dimers) are grouped together with a size estimation of 15 nm. The sizes from resonant mass measurements are calculated using df = 3. For micro-flow imaging, the estimated circular diameter (ECD) is taken as a size estimate. , where D is the estimated particle size, is plotted as a function of size. (a) Evolution of size distribution in a buffer only formulation. (b) Evolution of size distribution in a formulation containing sucrose. For size exclusion measurements, the monomer size is assumed to be 10 nm. The aggregates (mostly dimers) are grouped together with a size estimation of 15 nm. The sizes from resonant mass measurements are calculated using df = 3. For micro-flow imaging, the estimated circular diameter (ECD) is taken as a size estimate. | |
Even with these deficiencies, some qualitative conclusions can still be drawn. The addition of sucrose does not prevent the formation of smaller aggregates, detected by SEC, but causes a dramatic decrease in the formation of micron-sized and larger particles. Sucrose therefore does not have an effect on the smaller aggregation kernel elements, but either severely decreases the kernel elements describing the formation of larger particles through increased Fuchs stability ratio, or increases the fractal dimension of aggregates through preferential exclusion from the surface, resulting in more compact aggregates. The latter would result in smaller aggregates with more mass, as implied by Fig. 9. Since the resonant mass measurements, which are not affected by the fractal nature of the aggregates, do not show such an increase in the sucrose formulation, the first mechanism is more likely. The underlying cause of this mechanism is yet to be explored.
To generalise, the problem of protein aggregation is being tackled on multiple size scales.18,38 Most of the recent modelling has been done at the molecular level, simulating the protein molecule itself and its interaction with the solvent and environment.39,40 In such simulations, atomistic resolution and coarse grained modelling are combined to identify various regions prone to post-translational modifications and subsequent aggregation and degradation. At the state-of-the art, the aggregation mechanisms at the smallest scale are a true top-level modelling challenge, from both fundamental perspectives and top-level hardware and software infrastructure needed for such studies. For example, folding and unfolding of large multi-domain proteins, such as monoclonal antibodies, is indeed a complex process and one which is still poorly understood. Our approach, on the other hand, is more phenomenological in nature, offering a complementary view of the problem. An initial set of experimental data is needed to determine the model parameters, which can then be used to predict the formation of aggregates at time and size scales relevant in the biopharmaceutical industry. This article helps to close the gap between molecular processes and actual aggregation measurements in bulk solution, with an emphasis on biopharmaceutical development.
4 Conclusions
This study explores protein aggregation dynamics from the distinct perspective of biopharmaceutical design. Experimental data from three different mAbs are presented and complemented with a coagulation model based on the modified Smoluchowski coagulation equation. We show the difference between first order and second order aggregation kinetics and show a way to determine which of the two is the dominant process in the investigated sample. In the case of first order kinetics, where a conformational change of the native monomer form drives the subsequent aggregation, the widely used measurement techniques, such as SEC, may not be able to distinguish between both conformational isomers. In this case, the measured aggregate concentration at lower protein concentration exhibits an apparent lag time, which decreases with increasing concentration, following a distinct power law. A model was fitted to the data and the fitted model parameters were compared to previously reported values. Characterisation of oligomer reversibility with dilution is also discussed. Next, we show that the values of the aggregation kernel beyond the first few elements notably affect the concentration distribution of larger aggregates. The effect of fractal nature of the aggregates on the aggregation dynamics is explored. The maximum size of an aggregated particle in a typical biopharmaceutical sample is estimated by integration of the numerically calculated particle distribution, showing how an implementation of such a model could directly impact early drug development. Based on experimental data, drawbacks regarding the mean field approach with sedimenting particles are also discussed. Finally, this work is a contribution towards modelling and interpreting experimental measurements of protein aggregation at the mesoscale, with aggregate scales measuring from nanometres to microns and time scales relevant for shelf life of therapeutics, with an emphasis on biopharmaceutical development.
Conflicts of interest
There are no conflicts to declare.
Acknowledgements
Authors acknowledge funding from Lek d.d., part of Novartis, under contract BIO17/2016 and from Slovenian Research Agency ARRS grants P1-0099, J1-7300 and L1-8135.
References
- R. R. Kopito, Trends Cell Biol., 2016, 26, 559–560 CrossRef PubMed
 .
.
- P. J. Carter, Nat. Rev. Immunol., 2006, 6, 343–357 CrossRef PubMed
 .
.
- J. C. Edwards, L. Szczepanski, J. Szechinski, A. Filipowicz-Sosnowska, P. Emery, D. R. Close, R. M. Stevens and T. Shaw, N. Engl. J. Med., 2004, 350, 2572–2581 CrossRef PubMed
 .
.
- S. M. Wilhelm and B. L. Love, Clinical Pharmacist, 2017, 9 DOI:10.1211/CP.2017.20202316
 .
.
- J. Baselga, J. Cortes, S.-B. Kim, S.-A. Im, R. Hegg, Y.-H. Im, L. Roman, J. L. Pedrini, T. Pienkowski, A. Knott, E. Clark, M. C. Benyunes, G. Ross and S. M. Swain, N. Engl. J. Med., 2012, 366, 109–119 CrossRef PubMed
 .
.
- W. Tausend, C. Downing and S. Tyring, J. Cutaneous Med. Surg., 2014, 18, 156–169 Search PubMed
 .
.
- M. Vazquez-Rey and D. A. Lang, Biotechnol. Bioeng., 2011, 108, 1494–1508 CrossRef PubMed
 .
.
- C. J. Roberts, T. K. Das and E. Sahin, Int. J. Pharm., 2011, 418, 318–333 CrossRef PubMed
 .
.
- T. Skamris, T. Xinsheng, M. Thorolfsson, H. S. Karkov, H. B. Rassmusen, A. E. Langkilde and B. Vestergaard, Pharm. Res., 2015, 33, 716–728 CrossRef PubMed
 .
.
- E. Y. Chi, S. Krishnan, T. W. Randolph and J. F. Carpenter, Pharm. Res., 2003, 20, 1325–1334 CrossRef
 .
.
- S. Mossallatpour and A. Ghahghaei, Biomacromolecular Journal, 2015, 1, 58–68 Search PubMed
 .
.
- D. Roberts, R. Keeling, M. Tracka, C. F. v. d. Walle, S. Uddin, J. Warwicker and R. Curtis, Mol. Pharmaceutics, 2014, 11, 2475–2489 CrossRef PubMed
 .
.
- M. Stranz and E. S. Kastango, Int. J. Pharm. Compd., 2002, 6, 216–220 Search PubMed
 .
.
- A. S. Rosenberg, AAPS J., 2006, 8, E501–E507 CrossRef PubMed
 .
.
- J. F. Carpenter, T. W. Randolph, W. Jiskoot, D. J. A. Crommelin, C. R. Middaugh, G. Winter, Y.-X. Fan, S. Kirshner, D. Verthelyi, S. Kozlowski, K. A. Clouse, P. G. Swann, A. Rosenberg and B. Cherney, J. Pharm. Sci., 2008, 98, 1201–1205 CrossRef PubMed
 .
.
- J. A. Wattis, Phys. D, 2006, 222, 1–20 CrossRef
 .
.
- I. Kryven, S. Lazzari and G. Storti, Macromol. Theory Simul., 2014, 23, 170–181 CrossRef
 .
.
- L. Nicoud, M. Owczarz, P. Arosio, M. Lattuada and M. Morbidelli, Biotechnol. J., 2015, 10, 367–378 CrossRef PubMed
 .
.
- P. Arosio, S. Rima, M. Lattuada and M. Morbidelli, J. Phys. Chem. B, 2012, 116, 7066–7075 CrossRef PubMed
 .
.
- L. Nicoud, P. Arosio, M. Sozo, A. Yates, E. Norrant and M. Morbidelli, J. Phys. Chem. B, 2014, 118, 10595–10606 CrossRef PubMed
 .
.
- L. Nicoud, M. Sozo, P. Arosio, A. Yates, E. Norrant and M. Morbidelli, J. Phys. Chem. B, 2014, 118, 11921–11930 CrossRef PubMed
 .
.
- L. Nicoud, J. Jagielski, D. Pfister, S. Lazzari, J. Massant, M. Lattuada and M. Morbidelli, J. Phys. Chem. B, 2016, 120, 3267–3280 CrossRef PubMed
 .
.
- H. Imamura and S. Honda, J. Phys. Chem. B, 2016, 120, 9581–9589 CrossRef PubMed
 .
.
- H. Imamura, A. Sasaki and S. Honda, J. Phys. Chem. B, 2017, 121, 8085–8093 CrossRef PubMed
 .
.
- M. A. Blanco, E. Sahin, A. S. Robinson and C. J. Roberts, J. Phys. Chem. B, 2013, 117, 16013–16028 CrossRef PubMed
 .
.
- G. V. Barnett, V. I. Razinkov, B. A. Kerwin, T. M. Laue, A. H. Woodka, P. D. Butler, T. Perevozchikova and C. J. Roberts, J. Phys. Chem. B, 2015, 119, 5793–5804 CrossRef PubMed
 .
.
- M. L. Fleischman, J. Chung, E. P. Paul and R. A. Lewus, J. Pharm. Sci., 2017, 106, 994–1000 CrossRef PubMed
 .
.
- E. Koepf, R. Schroeder, G. Brezesinski and W. Friess, Eur. J. Pharm. Biopharm., 2017, 119, 396–407 CrossRef PubMed
 .
.
- S. Rudiuk, L. Cohen-Tannoudji, S. Huille and C. Tribet, Soft Matter, 2012, 8, 2651–2661 RSC
 .
.
- S. B. Mehta, L. Rachael, J. S. Bee, T. W. Randolph and J. F. Carpenter, J. Pharm. Sci., 2015, 104, 1282–1290 CrossRef PubMed
 .
.
- D. M. Stratton, J. Gans and E. Williams, J. Comput. Phys., 1994, 112, 364–369 CrossRef
 .
.
- E. Debry and B. Sportisse, Appl. Numer. Math., 2007, 57, 1008–1020 CrossRef
 .
.
- C. J. Roberts, Trends Biotechnol., 2014, 32, 372–380 CrossRef PubMed
 .
.
- A. Schmitt, G. Odriozola, A. Moncho-Jorda, J. Callejas-Fernandez, R. Martinez-Garcia and R. Hidalgo-Alvarez, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 2000, 62, 8335–8343 CrossRef
 .
.
- P. Arosio, T. P. J. Knowles and S. Linse, Phys. Chem. Chem. Phys., 2015, 17, 7606–7618 RSC
 .
.
- M. Lattuada, H. Wu, A. Hasmy and M. Morbidelli, Langmuir, 2003, 19, 6312–6316 CrossRef
 .
.
- S. Cao, J. Pollastrini and Y. Jiang, Curr. Pharm. Biotechnol., 2009, 10, 382–390 Search PubMed
 .
.
- A. Morriss-Andrews and J. E. Shea, Annu. Rev. Phys. Chem., 2015, 66, 643–666 CrossRef PubMed
 .
.
- C. Wu and J.-E. Shea, Curr. Opin. Struct. Biol., 2011, 21, 209–220 CrossRef PubMed
 .
.
- A. Morriss-Andrews and J.-E. Shea, J. Phys. Chem. Lett., 2014, 5, 1899–1908 CrossRef PubMed
 .
.
|
| This journal is © The Royal Society of Chemistry 2018 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article *ac
*ac




 , which makes kc11 = kmono11 = kRLCA11.
, which makes kc11 = kmono11 = kRLCA11.

![[k with combining tilde]](https://www.rsc.org/images/entities/i_char_006b_0303.gif) , eqn (2) can be expanded by
, eqn (2) can be expanded by








![[k with combining tilde]](https://www.rsc.org/images/entities/i_char_006b_0303.gif) can be readily determined from the graph. Both unimolecular and bimolecular processes are present in formulations with and without sucrose. Sucrose is expected to inhibit the initial conformational change via the preferential exclusion from the surface and the corresponding increase in protein conformational stability. This also slightly decreases protein solubility, potentially resulting in a faster bimolecular aggregation. At the tested sucrose concentration, however, both effects are negligible.
can be readily determined from the graph. Both unimolecular and bimolecular processes are present in formulations with and without sucrose. Sucrose is expected to inhibit the initial conformational change via the preferential exclusion from the surface and the corresponding increase in protein conformational stability. This also slightly decreases protein solubility, potentially resulting in a faster bimolecular aggregation. At the tested sucrose concentration, however, both effects are negligible.

![[k with combining tilde]](https://www.rsc.org/images/entities/i_char_006b_0303.gif) can be easily read from the graph (slope and intercept, respectively).
can be easily read from the graph (slope and intercept, respectively).![[k with combining tilde]](https://www.rsc.org/images/entities/i_char_006b_0303.gif) nnat and the rate of elimination through aggregation k11n12. If the conformational change is much slower compared to the subsequent coagulation, the concentration of the intermediate state A1 is negligible throughout the aggregation process and the measured concentration time dependence is purely exponential. If the subsequent coagulation is the rate limiting step, the sigmoidal curve is much more prominent. Because the conformational change is a unimolecular process and coagulation is a binary process, this ratio is also affected by protein concentration, as also described by Nicoud et al.22 The resulting sigmoidal shape of the monomer concentration and the apparent lag time in the concentration evolution of conformational isomers and dimers display a power-law dependence on concentration. But the power law is not only valid for a broad range of concentrations, as shown in Fig. 4b, but also for different parameters
nnat and the rate of elimination through aggregation k11n12. If the conformational change is much slower compared to the subsequent coagulation, the concentration of the intermediate state A1 is negligible throughout the aggregation process and the measured concentration time dependence is purely exponential. If the subsequent coagulation is the rate limiting step, the sigmoidal curve is much more prominent. Because the conformational change is a unimolecular process and coagulation is a binary process, this ratio is also affected by protein concentration, as also described by Nicoud et al.22 The resulting sigmoidal shape of the monomer concentration and the apparent lag time in the concentration evolution of conformational isomers and dimers display a power-law dependence on concentration. But the power law is not only valid for a broad range of concentrations, as shown in Fig. 4b, but also for different parameters ![[k with combining tilde]](https://www.rsc.org/images/entities/i_char_006b_0303.gif) and k11, since the relative lag time depends only on the ratio
and k11, since the relative lag time depends only on the ratio ![[k with combining tilde]](https://www.rsc.org/images/entities/i_char_006b_0303.gif) nnat/k11. Special care should be taken not to confuse such measurements with a lag phase, which is common in amyloid fibrillation of peptides and smaller proteins in very small volumes,35 but has been attributed to stochastic processes.
nnat/k11. Special care should be taken not to confuse such measurements with a lag phase, which is common in amyloid fibrillation of peptides and smaller proteins in very small volumes,35 but has been attributed to stochastic processes.![[k with combining tilde]](https://www.rsc.org/images/entities/i_char_006b_0303.gif) ) and the subsequent interaction between such monomers (k11). Interactions between dimers and larger species are less important when considering the total aggregate content; therefore, the simplest kernel kc is used. By using this kernel, we also avoid overparametrising our system with low impact parameters such as fractal dimension and sticking probability. In addition to the measured initial aggregate concentration, the model assumes a 2.5% content of conformationally compromised monomers at t0. The Fuchs stability ratio W for interaction between conformationally compromised monomers (among themselves and other aggregates) can also be estimated from the fit. The value (∼109) is many orders of magnitude larger than the estimated electrostatic contribution (W ≈ 1), which is in line with previous findings about protein–protein interactions.20 This large value indicates the presence of a high energy barrier that particles must overcome before colliding, which reduces the collision efficiency and thus delays the aggregation process with respect to diffusion-limited conditions. The reported value is several orders of magnitude larger still than those reported previously (∼107), which can be attributed to denaturation temperature of the proteins with respect to the stress conditions. Under moderate stress conditions of this study (40 °C), only minor conformational changes are expected, while previously reported values correspond to 70 °C, where all the proteins are partially or completely unfolded and thus much more reactive.
) and the subsequent interaction between such monomers (k11). Interactions between dimers and larger species are less important when considering the total aggregate content; therefore, the simplest kernel kc is used. By using this kernel, we also avoid overparametrising our system with low impact parameters such as fractal dimension and sticking probability. In addition to the measured initial aggregate concentration, the model assumes a 2.5% content of conformationally compromised monomers at t0. The Fuchs stability ratio W for interaction between conformationally compromised monomers (among themselves and other aggregates) can also be estimated from the fit. The value (∼109) is many orders of magnitude larger than the estimated electrostatic contribution (W ≈ 1), which is in line with previous findings about protein–protein interactions.20 This large value indicates the presence of a high energy barrier that particles must overcome before colliding, which reduces the collision efficiency and thus delays the aggregation process with respect to diffusion-limited conditions. The reported value is several orders of magnitude larger still than those reported previously (∼107), which can be attributed to denaturation temperature of the proteins with respect to the stress conditions. Under moderate stress conditions of this study (40 °C), only minor conformational changes are expected, while previously reported values correspond to 70 °C, where all the proteins are partially or completely unfolded and thus much more reactive. can be obtained by solving eqn (11) in equilibrium state,
can be obtained by solving eqn (11) in equilibrium state,  :
: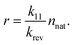



![[k with combining tilde]](https://www.rsc.org/images/entities/i_char_006b_0303.gif) might yield different results, as presented later.
might yield different results, as presented later.



![[k with combining tilde]](https://www.rsc.org/images/entities/i_char_006b_0303.gif) is the rate limiting step of aggregation. The reaction rate of this conformational change leading to native monomer loss can be compared to the rate of subsequent aggregation with the ratio K, which we define as
is the rate limiting step of aggregation. The reaction rate of this conformational change leading to native monomer loss can be compared to the rate of subsequent aggregation with the ratio K, which we define as
![[k with combining tilde]](https://www.rsc.org/images/entities/i_char_006b_0303.gif) via their impact on the particle potential and conformational stability. A comprehensive case-by-case study of such impacts should therefore be performed to optimise the formulation according to the model parameters.
via their impact on the particle potential and conformational stability. A comprehensive case-by-case study of such impacts should therefore be performed to optimise the formulation according to the model parameters.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.







