Particle-covered drops in electric fields: drop deformation and surface particle organization

Abstract

Drops covered by adsorbed particles are a prominent research topic because they hold promise for a variety of practical applications. Unlocking the enormous potential of particle-laden drops in new material fabrication, for instance, requires understanding how surface particles affect the electrical and deformation properties of drops, as well as developing new routes for particle manipulation at the interface of drops. In this study, we utilized electric fields to experimentally investigate the mechanics of particle-covered silicone oil drops suspended in castor oil, as well as particle assembly at drop surfaces. We used particles with electrical conductivities ranging from insulating polystyrene to highly conductive silver. When subjected to electric fields, drops can change shape, rotate, or break apart. In the first part of this work, we demonstrate how the deformation magnitude and shape of drops, as well as their electrical properties, are affected by electric field strength, particle size, conductivity, and coverage. We also discuss the role of electrohydrodynamic flows on drop deformation. In the second part, we present the electric field-directed assembly and organization of particles at drop surfaces. In this regard, we studied various parameters in detail, including electric field strength, particle size, coverage, and electrical conductivity. Finally, we present a novel method for controlling the local particle coverage and packing of particles on drop surfaces by simply tuning the frequency of the applied electric field. This approach is expected to find uses in optical materials and applications.

---

1 Introduction

Drops covered by micro- and nanoparticles have recently received considerable research interest.^1–4 This is because they are promising for a variety of practical applications, such as in food technology,⁵ the oil industry,⁶ biofuel processing,⁷ and for improving pharmaceutical products.⁸ Moreover, such drops possess characteristics that make them useful as experimental model systems for studying, for example, particle effects on interfacial tension,⁹ particle crystal growth and ordering or particle layer buckling on curved interfaces,^10–13 particle assembly and rearrangement on drop surfaces,^14,15 and particle detachment from drops.¹⁶ Particle-covered drops can additionally be employed for fabricating porous structures,¹⁷ granular or colloidal capsules of different mechanical properties, morphologies, or shapes,^18,19 and adaptive structures.²⁰ In this context, broadening knowledge of particle-covered drop stability, deformation, and surface particle manipulation is essential to further developing the abovementioned research areas.

The deformation of drops can be induced and investigated using various experimental tools, including atomic force microscopes,^21,22 microfluidic devices,^23–25 and by utilizing mechanical shearing^26,27 or electric fields.^28–32 For manipulating particles at drop surfaces or in the bulk of a drop, there are many physical or chemical approaches, such as pH-controlled particle assembly,³³ acoustic wave-induced bulk and surface particle convection,³⁴ magnetic field-directed particle assembly,³⁵ and electric field-assisted particle arrangements.³⁶

In this work, we explore the possibilities of employing electric fields as a contactless method for both drop deformation and the manipulation of particles at drop interfaces. In our experiments, no mechanical shearing or microfluidic flow was required to induce drop deformation, and the electric stresses imposed on the drops were axisymmetric. For that reason, the studied drops were stationary in the sample cell, which facilitated the experimental observation of the drops.

Particle organization at the surface of drops is achievable by various electric field phenomena. Electric fields can manipulate particles by exerting forces that are acting on them either directly, e.g. through particle motion via dipolar forces, or indirectly, e.g. by particle convection through electric field-induced liquid flows. Electrohydrodynamic (EHD) liquid flows,^37,38 dipolar interactions,³⁹ dielectrophoresis (DEP),^40,41 electro-statics,³⁶ or electrocoalescence¹⁹ can be utilized to transport, assemble, or sort particles at drop interfaces. Removing particles from a drop is also possible through tip-streaming mechanisms⁴² and strong EHD flows.¹⁴ The applicability of the abovementioned approaches depends on the electric properties of both the particles and the liquids. For example, the dielectrophoretic force (force exerted on an object subjected to a non-uniform electric field) acting on drop surface particles is very small (and cannot be used to manipulate particles) when the dielectric properties of those particles are similar to those of the drop and surrounding liquid.⁴¹

We performed experiments on silicone oil drops suspended in castor oil (weakly conductive liquids) that were covered by microparticles with a broad spectrum of electrical conductivities and subjected to uniform electric fields. We present our investigations and conclusions on drop deformation and stability affected by the applied electric field strength, surface particle size, and electrical properties (Section 3.1); as well as surface particle coverage (Section 3.2). Moreover, we show how surface particles can be assembled and structured at drop interfaces (Section 3.3). In addition, we demonstrate an approach for actively controlling local particle coverage and packing at drop interfaces (Section 3.4). Before investigating particle-covered drops, let us first discuss the behaviour of a corresponding and simplified system, namely, a particle-free silicone oil drop formed in castor oil and subjected to electric fields.

1.1 Behaviour of particle-free silicone oil drops in electric fields

The electric conductivity and dielectric constant of a silicone oil drop is smaller than those of the surrounding castor oil. When subjected to a direct current (DC) electric field, free charges (ionic impurities) in the oils accumulate at the drop interface. This results in the formation of a drop dipole moment directed in the opposite direction of the electric field. The action of the applied DC electric field on the free charges at the silicone oil drop yields electric stresses. At the electric poles of the drop (surface areas closest to the electrodes), electric stress has only a normal component that is balanced by capillary forces and the pressure difference across the drop interface. There are no free charges at the electric equator of the drop, and thus there is no electric stress at this area of the drop. Everywhere else at the drop interface, electric stress has two components: normal and tangential to the drop interface. As a result of normal electric stress, the drop is compressed along the electric field direction, obtaining (within a second) an oblate shape. Tangential electric stress induces electrohydrodynamic flows at the drop interface that shear the liquids inside and outside the drop. In general, the direction of these EHD flows depends on the free charge distribution at the drop interface. In the case of a silicone oil drop suspended in castor oil, the EHD flows at the drop surface are directed from the drop poles to the drop equator (for more details, see ref. 43). As long as the applied electric field strength is weak (typically <200 V mm⁻¹), the induced EHD liquid flows can be used to convect and eventually assemble surface particles, as we discuss later in this section. At strong DC electric fields, weakly-conductive drops may undergo electrorotation^44–46 or break apart.⁴⁷

The accumulation of free charges at the interface of a drop requires finite time. For the drop system studied here, the time for free charges to build up at the drop interface (the Maxwell–Wagner relaxation time)⁴³ was ∼1 s. Therefore, when applying alternating current (AC) electric fields with sufficiently high frequencies, the electric field changes direction so quickly that no free charges accumulate at the drop interface. Experimentally, we observed no EHD flows for electric field frequencies above 100 Hz. At such electric field conditions, the drop behaves as a dielectric drop, i.e. there are only polarization charges present and no free charges. The dipole moment of the drop is now in the same direction as the applied electric field, unlike the situation when a DC field is applied. Accordingly, the drop stretches along the electric field direction, acquiring a prolate shape, and no EHD flows are present. Drop deformation is defined as D = (d_‖ − d_⊥)/(d_‖ + d_⊥), where d_‖ and d_⊥ are the drop axes parallel and perpendicular to the electric field direction, respectively. For small deformations, the drop deformation scales as E² for both DC and AC electric fields.⁴³

1.2 Behaviour of particle-covered silicone oil drops in electric fields

Adding particles to the drop surface may alter drop behaviour and characteristics in electric fields. The deformation,^48–50 mechanics,^32,51,52 relaxation,²⁶ or rotation⁵³ of particle-covered drops can differ from those of a pure drop. The surface particle's size, concentration, and electrical properties can influence the properties of the drop. The deformation of a pure silicone oil drop subjected to a DC electric field is affected by the amount of free charges built up at its interface. The addition of particles may influence the free charge accumulation and lead to an increase of the drop deformation in either direction (oblate or prolate configurations) or decrease the drop deformation magnitude. Furthermore, the addition of particles may also affect the magnitude of EHD flows, change drop conductivity, or influence drop stability. We describe these situations in the first part of this work.

1.3 Assembly of surface particles and their active structuring

Previous work showed that non-conductive (polymeric) particles assemble at the drop equator in the form of a ribbon via EHD flows, whereas for the same silicone oil–castor oil system, conductive (silver-coated) particles formed longitudinal particle chains via dipolar interactions.²⁰ Particles that are similar except for their dielectric properties may be transported either to the electric poles or electric equator of the drop by dielectrophoretics.⁴² These examples demonstrate the importance of the electrical properties of surface particles for particle assembly. Besides their electrical properties, we also investigated the influence of particle coverage and particle size on their organization at drop interfaces.

The family of electrokinetic phenomena offers different types of mechanisms that also enable the formation of active materials. Previous work demonstrated that controlling electric field strength made it possible to actively structure and redistribute non-ohmic (i.e. having a non-linear relationship between the electric current and the voltage) clay mineral particles at the drop interface.²⁰ In the current study, we expanded the structuring to ohmic conductive particles. By utilizing the knowledge gained from the experiments presented in the first parts of this paper, we were able to actively structure conductive particles and to locally change their concentration and packing. Such smart material is easily controlled by tuning the electric field frequency, enabling the switching between two physical mechanisms: particle–particle dipolar interactions and EHD flows.

2 Materials and methods

2.1 Experimental set-up

Fig. 1 shows a schematic illustration of the set-up used in the experiments. The set-up consisted of a sample cell placed on a mechanical x–y–z translational stage, a signal generator (SDG1025, Sigilent), a high-voltage bipolar amplifier (10HVA24-BP1, HVP), two digital microscopes (AM7115MZTL, DINO-LITE) for front and side viewing (perpendicular and parallel to the electric field direction), and a PC for recording movies and images. The sample cell was made of glass with two of the inside walls coated with conductive indium tin oxide (ITO) constituting electrodes. A high-voltage signal was provided to the sample cell via two crocodile clips attached to the ITO-coated glass electrodes. The AC electrical signals used in the experiments presented in Section 3.4 were square-shaped and bipolar, and the provided signal values were root-mean-square values.

Fig. 1 (a) A schematic illustration of the set-up used in all experiments. The set-up consisted of a sample cell placed on a mechanical x–y–z translational stage, two digital microscopes for front and side viewing (perpendicular and parallel to the electric field direction), a signal generator, and a voltage amplifier for generating high-voltage bipolar signals provided to the cell via two crocodile clips. (b) The sample cell was made of glass with two of the walls coated with electrically-conductive ITO layers. The transparent ITO-covered glass electrodes allowed for observation in a direction along the electric field. Drops with or without particles were made using a mechanical pipette.

2.2 Oils and particles

The sample cell was filled with castor oil (83912, Sigma-Aldrich, density of ∼0.96 g cm⁻³ at 25 °C, electrical conductivity of ∼50–100 pS m⁻¹, relative permittivity ∼4.7, and viscosity of ∼700 mPa s at 25 °C). Silicone oil (6678.1000, Rhodorsil Oils 47, density of ∼0.96 g cm⁻³ at 25 °C, electrical conductivity of ∼5–10 pS m⁻¹, relative permittivity ∼2.8, and viscosity of ∼50 mPa s at 25 °C) drops with or without particles were made in castor oil using a mechanical pipette, as presented in Fig. 1b. Particles in the bulk of the silicone oil drops were brought to the drop interface by applying a DC electric field and/or by particle sedimentation.

Different particle materials were used in the experiments, including conductive silver-coated hollow glass microspheres (M-40-0.67 and M-60-0.17, with an average size of 15 μm and 55 μm, both with electrical conductivities of ∼10⁷ S m⁻¹, purchased from Cospheric LLC) and polystyrene (PS) particles with an average size of ∼40 μm (Dynoseeds TS40 6317, electrical conductivity of ∼10⁻¹¹ S m⁻¹, density of ∼1.05 g cm⁻³, purchased from Microbeads AS, Norway). The pristine PS particles were chemically treated (sulfonated, as described by Mikkelsen et al.⁵⁴) to increase their electrical conductivities to ∼5 × 10⁻⁹ S m⁻¹. The PS particles were labelled PS0, PS16, and PS32, where the numbers refer to the sulfonation reaction time in minutes.

2.3 PIV experiments

The flowlines around drops were traced using particle image velocimetry (PIV). Fluorescent PE particles (UVPMS-BY2-1.00, size of ∼35 μm, Cospheric LLC) were dispersed in castor oil (0.3% by weight) and poured in the sample cell. A 500 μm thin sheet of particles was selected by focusing a 532 nm laser light (COM-09906-5 mW, SparkFun Electronics) from above the sample cell through a laser line generator lens (Powell lens), as presented in Fig. S1 (ESI†). Silicone oil drops with or without surface particles were created in the castor oil using a mechanical pipette and brought to the drop interface, as explained above. During the experiments, the laser sheet was always aligned in the middle of the drop and oriented along the electric field direction and perpendicular to the view direction of the microscope. Movies (5 fps) were recorded for each experiment with a 1920 × 1080 pixel resolution (1 pixel ∼ 6.2 μm). 25 sequential frames were then compared and analysed using PIVlab (v.1.41, Matlab toolbox application),⁵⁵ yielding flow velocities for each interrogation area (the frames were split into a number of interrogation areas of size 64 × 64 pixels, which were then individually cross-correlated with the previous frame to obtain displacement vectors). Matlab (v.R2017b, MathWorks) was then used to plot the flow velocities, while Adobe Photoshop CC2018 (v.19.0, Adobe Systems) was utilized to create masks and add images of the analysed drops on top of the flow velocity figures.

3 Results

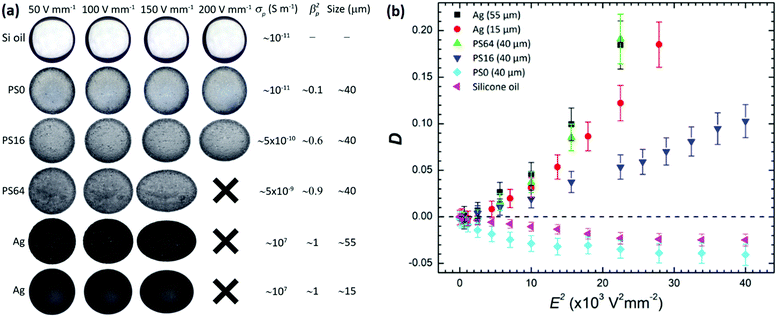
3.1 Electric field-induced deformation of Pickering drops

Initially, we investigated how the deformation of Pickering drops (drops fully covered by particles) is influenced by the strength of an applied DC electric field, as well as the size and electrical conductivity of surface particles. Silicone oil drops (size ∼2 mm) covered by particles were formed in castor oil and subjected to DC electric fields ranging from 0 to 200 V mm⁻¹. Fig. 2a presents images of five silicone oil drops covered by particles with electrical conductivities ranging from 10⁻¹¹ to 10⁷ S m⁻¹ and sizes between 15 and 55 μm. The drops were densely covered by particles (we estimated the particle coverage to be around 0.8, which is close to the maximum theoretical packing fraction).⁵⁶ As a reference, the deformation of a pure silicone oil drop is also included. Note that all drops were spherical before the application of electric fields, indicating that there was no particle jamming. This is important because the rigidity of jammed elastic shells increases with asphericity, and higher rigidity makes the particle-covered drop more difficult (requiring higher electric stress) to deform.⁵⁷

Fig. 2 (a) Electric field-induced deformation of silicone oil drops covered by particles with different electrical properties and sizes. The size of the drops was 2 mm and the electric field was applied in the horizontal direction. The deformation of a pure silicone drop is also included as a reference. Values of the electrical conductivity of the particles (σ_p), the conductivity mismatch between particles and castor oil (β_p = (σ_p − σ_ex)/(σ_p + 2σ_ex)), and the size of the particles are provided. The crosses indicate drop breakup. (b) Steady-state deformation versus applied electric field squared for the drops imaged in (a).

Fig. 2b presents quantitative data on drop deformation versus the applied electric field strength for the drops imaged in Fig. 2a. The particle-free silicone oil drop (pink triangles) and the drop covered by non-conductive PS0 particles (cyan diamonds) deformed into oblate shapes (compressed in the direction of the electric field). That is because the free charges accumulated at the drop surfaces created a drop dipole moment oriented in the opposite direction of the electric field. However, the steady state deformation of the PS0-covered drop was slightly larger than that of the particle-free silicone oil drop.

Supported by our previous work, we propose two origins for the increased drop deformation. First, the insulating particles reduced the electrical conductivity of the drop interface, allowing more free charges from the oils to accumulate on the drop interface, hence increasing the electric stress on the drop. Second, the induced EHD flows were greatly diminished or absent when the drop was covered by particles.³² EHD flows have been reported to weaken the steady-state deformation of particle-free drops by removing free charges from the drop interface by convection, thus decreasing the charge accumulation at drop surfaces (and the electric stress acting on the drops).⁵⁸

We decided to perform experiments to study the effect of particle coverage on EHD flows (their patterns and strengths). Fig. 3 presents the results of PIV experiments performed on silicone oil drops with PS0 surface particles at different particle coverages subjected to a DC electric field of 170 V mm⁻¹. The results from the PIV experiments confirm that the induced EHD flows at drop interfaces are indeed reduced by surface particles. When the particle coverage was increased from 0 (particle-free drop) to around 0.8 (drop fully covered by particles), the maximum EHD flow velocity around the drop decreased from 150 to nearly 0 μm s⁻¹, verifying that EHD flows surrounding a silicone oil drop in castor oil are suppressed when the drop is fully covered by particles. Moreover, Fig. 3b and c shows that EHD flows exist near the particle-free regions of the drop, and that these flows are asymmetric, i.e. the flow magnitude is stronger at the drop sides where there are less particles. The particle layer gives the drop surface shear elasticity (it behaves like an elastic sheet), which immobilizes the drop surface and greatly suppresses the EHD flows around particle-covered areas at the drop interface.^59,60

Fig. 3 (a–d) PIV images of (a) a particle-free silicone oil drop and silicone oil drops covered by non-modified PS particles with particle coverages (b) ∼0.2, (c) ∼0.48, and (d) ∼0.81. The drops were subjected to a DC electric field of 170 V mm⁻¹ (in the horizontal direction), yielding steady-state drop deformations of (a) −0.023, (b) −0.026, (c) −0.028, and (d) −0.04. All drops had diameters equal to 2 mm and the scale bar is 1 mm. The asymmetry of the flow fields in (a–c) was caused by downward drop sedimentation, drop motion towards one of the electrodes, and, in (b and c), by non-uniform particle distribution. The masks in the middle of the flow fields are figures created from images of the drops used in the experiments.

We found that silicone oil drops behaved as conductive drops and stretched in the direction of the applied electric field (prolate deformation) when they were fully covered by particles that were more conductive than both oils. In fact, the results presented in Fig. 2b are in accordance with previous work on the deformation of conducting drops.⁴⁷ In DC electric fields, drops behaving as conductors acquire a free charge distribution that sets up a drop dipole moment oriented in the same direction as the electric field, i.e. the dipole moment of these drops is oriented in the opposite direction to the dipole moment of the pure silicone oil drop (or the drops covered by PS0 particles).⁶¹ Accordingly, the electric stress at the drop surface deforms the conductive drop to a prolate shape. The next section presents more about drop stretching and our study of the influence of particle coverage on drop deformation.

3.2 Influence of particle coverage on drop deformations

Fig. 4a presents images of silicone oil drops covered by five types of particles (the same particles shown in Fig. 2) with different particle coverages. The drops were subjected to a DC electric field of 170 V mm⁻¹. Fig. 4b displays quantitative data on drop deformation against particle coverage (φ) for the drops imaged in Fig. 4a.

Fig. 4 (a) Electric field-induced deformation of silicone oil drops covered by non-modified and modified PS particles (40 μm) and silver coated glass spheres (15 and 55 μm). The size of the drops was 2 mm, and the direction of the applied 170 V mm⁻¹ DC electric field was horizontal. (b) Steady-state deformation of silicone oil drops as a function of particle coverage (φ ranges from 0–0.85) the images in (a) correspond to respective data points in (b), and the crosses in (a) indicate drop breakup.

We found that the drops covered by PS0 particles compressed more (higher negative values of deformation, cyan diamonds in Fig. 4b) when the particle coverage value increased. The drops covered by other particles became less compressed by increasing the particle coverage, and at certain particle coverage the deformation changed from oblate to prolate. Such a drop deformation transition occurred at lower particle coverage values for drops covered by more conducting particles (e.g. compare PS16 and PS64 in Fig. 4b), or by bigger particles (compare the drops covered by 55 μm vs. 15 μm Ag-coated glass spheres displayed in the bottom rows in Fig. 4a).

We observed that the particles formed chains when the particles at the drop interface were more conductive than the drop fluid (all particles except PS0). In addition to particle conductivity, chain formation also depends on particle size and particle coverage. The drop oblate–prolate transition occurs when the surface particles form chains spanning from drop pole to pole. The particle chains affect drop deformation by altering the build-up of free charges at the drop surface, owing to the faster conduction of charges through the chains compared to through the drop fluid. This also influences the EHD flows, as supported by the results in Fig. 5. The figure displays PIV images of silicone oil drops with and without PS64 particles subjected to a DC electric field of 170 V mm⁻¹. The figure shows that for a silicone oil drop covered with particles (PS64) that are more conductive than the drop and exterior oil, low particle coverage (φ ∼ 0.13–0.17) is sufficient to form pole–pole particle chains and suppress EHD flows (maximum flow velocity goes from 150 μm s⁻¹ to almost zero, as shown in Fig. 5a and d, respectively). Furthermore, Fig. 5b and c demonstrate the influence of particle chain distribution on the EHD flow fields, i.e. EHD flows may exist outside drop domains that are free of particle chains, whereas flows near drop regions with particles are very weak. The EHD flows weaken due to the fast conduction of charges through particle chains at the drop surface. The particle chains redistribute the free charges at the drop interface until the electric field component, which is parallel to the drop surface, becomes zero. In a steady state, the area of the drop containing conductive particles behaves as a conductor, i.e. the electric field has only a component perpendicular to the drop interface (because the electric field lines outside the drop are perpendicular to the drop surface and zero inside).⁶²

Fig. 5 PIV images of (a) a particle-free silicone oil drop and silicone oil drops covered by modified PS particles (PS64) with particle coverages: (b) ∼0.08, (c) ∼0.13, and (d) ∼0.17. The drops were subjected to a DC electric field of 170 V mm⁻¹ (in the horizontal direction), yielding drop steady-state deformations of (a) −0.023, (b) −0.023, (c) −0.013, and (d) 0.07. All drops had diameters equal to 2 mm with a scale bar of 1 mm. The asymmetry of the flow fields in (a) was caused by downward drop sedimentation, drop motion towards one of the electrodes, and, in (b and c), by non-uniform particle distribution. The masks in the middle of the flow fields are figures created from real images of the drops used in the experiments.

We also found that the magnitude of prolate deformation consistently increased with particle coverage, conductivity, and size (see Fig. 4b). For instance, at the same particle coverage, drops covered by PS64 particles of size 40 μm deformed less than drops covered by Ag-coated glass spheres that were slightly more conductive and larger. Moreover, drops covered by PS64 particles exhibited larger prolate deformations compared to drops covered by smaller, though more conductive, Ag particles.

3.3 Particle structuring at drop interfaces

Fig. 4a shows that at low particle coverages (φ ∼ 0.1), all types of particles were transported towards the drop equator by EHD convective flows. However, only the PS0 particles formed a compacted particle ribbon. All other particles structured into chains because of particle–particle dipolar interactions. The dipolar force between particles (all types except PS0) was strong enough to resist the present EHD flows, and to eventually form dipolar chains along the electric field lines. For a particle with radius R subjected to a DC electric field of strength E₀, the dipolar force F_D (between two particles) is given by the equation:⁶³F_D = 24πε₀ε_exR⁶E₀²β_p²/(2R + s)⁴, where ε₀ is the vacuum permittivity, ε_ex the dielectric constant of the exterior fluid, β_p = (σ_p − σ_ex)/(σ_p + 2σ_ex) is the particle's Clausius–Mossotti factor, σ_p and σ_ex are the conductivities of the particles and the exterior fluid, respectively, and s is the edge-to-edge separation distance between particles. Note that the abovementioned dipolar force equation is valid for a two-phase system. Here, we studied a three-phase system. However, because the surface particles on the drops had higher affinity to the surrounding castor oil (i.e., a larger part of each particle was immersed in castor oil), it was justifiable to consider the system a two-phase system and employ the simplified dipolar force equation.

The dipolar force between two PS16 particles is around six times larger than the dipolar force between two non-modified PS0 particles (β_p,PS16²/β_p,PS0² ≈ 6), even though the difference in conductivity is small, i.e. PS16 particles are two times more conductive than the PS0 particles. Particles that are more conductive than the PS16 particles form longer chains, owing to the increased dipolar force. Interestingly, although the Ag-coated glass spheres used in these experiments were 15 orders of magnitude more conductive than the PS64 particles, the dipolar force between a pair of Ag-coated glass spheres was comparable to that of a pair of PS64 particles (of similar size) (β_p,Ag²/β_p,PS64² ≈ 1.1).

Furthermore, for drops with high particle coverage subjected to a DC electric field of 170 V mm⁻¹, we observed that the surface particles (all types except PS0) concentrated at the drop poles (Fig. 4a). We propose that the particle concentration at the drop poles was caused by electrorheological chaining, where the formed chains grew towards the drop poles due to their locally-strong electric fields (the increased curvature resulted in a higher free charge density at the drop poles). Dielectrophoresis (forces acting on a particle when the electric field is non-uniform) could also be a possible explanation for the observed particle accumulation. Other researchers have demonstrated that surface particles can be transported towards drop poles and agglomerate there via dielectrophoresis.^15,42 However, according to our theoretical calculations, this could not have been the case here. We found that for all the different particles utilized in the experiments (except PS0), the dielectrophoretic (DEP) force on the particles was directed towards the drop equator rather than towards the drop poles. The term β′β(2 + β) in the equation for the DEP force determines the force direction.⁶⁴ Here β′ = (σ_p − σ_ex)/(σ_p + 2σ_ex) is the particle's Clausius–Mossotti factor, β = (σ_in − σ_ex)/(σ_in + 2σ_ex) is the drop's Clausius–Mossotti factor, and σ_p, σ_in, and σ_ex are the conductivities of the particles, drop fluid, and surrounding fluid, respectively. For all the drops except those covered by PS0, β′β(2 + β) < 0, indicating that any DEP force acting on the surface particles would move them towards the drop equator.⁶⁴

We validated the direction of the DEP force on the particles experimentally by forming a silicone oil drop covered by 15 μm silver-coated spheres and a silicone oil drop covered by PS0 particles. The particle coverages were low, and the drops were exposed to an AC electric field at 200 Hz and 300 V mm⁻¹. A DC electric field could not be used in this experiment because the induced EHD flows would have dominated the DEP force experienced by the particles (flow velocity ratio ν_EHD/ν_DEP ≈ 10³). As explained in the Introduction section, when an AC electric field at such a high frequency (200 Hz) is applied, the electric field changes direction too fast for free charges in the oils to accumulate at the drop interface and for EHD flows to be induced. In the absence of EHD flows, it is possible to observe particle movement by DEP. Note that for an AC electric field, the previously-described Clausius–Mossotti terms used in the equation to determine the DEP force direction change. The conductivities are replaced by permittivity terms, yielding: β_AC′ = (ε_p − ε_ex)/(ε_p + 2ε_ex) and β_AC = (ε_in − ε_ex)/(ε_in + 2ε_ex), where ε_p, ε_in, and ε_ex are the permittivities of the particles, drop fluid, and surrounding fluid, respectively.⁶⁵ For the fluids and particles used in this work, we calculated that the direction of the DEP force acting on the surface particles is the same whether the applied electric field is DC or AC. For all the particle-covered drops except those covered by PS0, β_AC′β_AC(2 + β_AC) < 0, indicating that the DEP force brings the particles to the drop equator. This was confirmed experimentally: when the AC electric field was turned on, the silver particles moved towards the drop equator and formed chains, whereas at the surface of the other drop, the PS0 particles translated much more slowly towards the drop poles. The PS0 particles also served as tracing particles, proving that there were no EHD flows present while the electric field of frequency 200 Hz was applied. Movie S1 (ESI†) presents the results of these experiments. Based on these results, we excluded the possibility of DEP interactions causing particle agglomeration at drop poles. Note that the silicone oil drops stretched (prolate deformation) in the direction of the applied AC electric field. That is because there were no free charges present, and the resulting drop dipole moment polarized by the electric field was oriented in the same direction as the electric field.⁶⁶

3.4 Manipulating interfacial particles by EHD flows and dipolar interactions

In this section, we demonstrate the possibilities of particle manipulation at drop interfaces by employing EHD flows and particle dipolar interactions. We utilize the knowledge gained from the previous sections about the influence of the particles’ properties, their coverage, and the electric field strength on the magnitude of EHD flows and drop deformation.

During the experiments and for all particles (except PS0), we observed that the growth of particle chains started from the drop equator and extended towards the drop poles (see Movie S1, ESI†), irrespective of the electric field frequency used (within the studied frequency range, i.e. from 0 to 1 kHz). The more particles present at the drop interface, the longer the chains became (until the particles started to agglomerate at the drop poles at high particle coverages).

We took advantage of this observation to create an adaptive structure in which particle packing, coverage, and structuring were easily controlled by only changing the frequency of the applied electric field. Fig. 6 shows a silicone oil drop (size of ∼3 mm) formed in castor oil and covered by 15 μm Ag-coated glass spheres (φ ∼ 0.15). The drop was subjected to an electric field of 170 V mm⁻¹ and viewed parallel (Fig. 6a and b) and perpendicular (Fig. 6c and d) to the electric field direction. When a DC electric field was applied, the particles formed chains via particle–particle dipolar interactions. However, the growth of the chains was limited (and thus also their lengths) by the induced EHD flows, i.e. the chains were not rigid enough to withstand the strain imposed by the EHD flows, and the electric poles of the drop became particle-free (Fig. 6a and c). As demonstrated in Movie S2 (ESI†), the EHD flows bend the ends of the particle chains, and sometimes even break and push the chains back towards the drop's electric equator (as indicated by the red arrows in Fig. 6a and c). To disable the EHD flows and allow the particle chains to grow towards the drop poles, we simply increased the electric field frequency to a value far above the critical frequency for EHD flow induction. As demonstrated in Fig. S2 (ESI†), a frequency of 200 Hz satisfies this condition. After changing the frequency from 0 to 200 Hz, the particles redistributed at the surface of the drop and locally changed the particle coverage, i.e. both drop poles were densely covered by particles at the cost of the particle coverage around the equatorial area. The direction of particle transport is indicated by the red arrows in Fig. 6b and d. After the frequency of the AC electric field was decreased from 200 to 0 Hz, EHD flows were induced (free charges had sufficient time to accumulate at the drop interface) to transport the particles located at the drop electric poles back to the drop electric equator.

Fig. 6 (a–d) Actively arranging surface-adsorbed conductive particles by switching the electric field frequency from 0 Hz (EHD flow regime) to 200 Hz (particle dipolar interaction regime). A silicone oil drop with diameter ∼3 mm is viewed (a and b) along and (c and d) perpendicular to the electric field direction, as indicated by the symbols. Ag-coated glass microspheres with mean diameters of ∼20 μm were used in this experiment, in which E = 200 V mm⁻¹ was fixed. The structuring process is reversible, and the switching between two particle conformations occurred in seconds, as shown in Movie S2 (ESI†).

For the current drop-particle system, the whole structuring process is reversible, as demonstrated in Movie S2 (ESI†). However, it is worth mentioning that the reversibility and feasibility of the approach depend on particle size, material, and concentration. When the experiment shown in Fig. 6 was repeated for drops covered by larger particles of the same type (55 μm silver-coated microspheres, φ ∼ 0.1), the process was irreversible, i.e. the particle-covered drop remained prolately deformed when the electric field was changed from AC to DC. The dipolar force between surface particles on a drop is proportional to the particle radius squared. As a consequence, the dipolar force between 55 μm sized particles is significantly larger compared to the force between 15 μm particles, considerably increasing the chain stiffness. The increased dipolar force between the 55 μm particles was sufficiently strong to keep the particles in the chain structures together by resisting the EHD shear stress induced at the drop surface when the applied electric field changed from AC to DC. Note that the surface particle rearrangement was accompanied with changes in the drop shape (compare Fig. 6c and d), and that the timescale for switching between the two particle conformations was on the order of seconds.

4 Conclusions and discussions

In conclusion, we studied both the behaviour of particle-covered drops and particle organization at drop interfaces by employing external electric fields. Here, we discuss our results and the underlying mechanisms, especially how particles on drop interfaces affect drop deformation, EHD flows, and particle structuring.

4.1 Surface particles and their effect on drop deformation

We found, that, besides the applied electric field strength, the particle material, particle coverage and size affect the deformation and electrical properties of silicone oil drops when subjected to electric fields. Our experiments show that the addition of particles to drop surfaces enhances the deformation magnitude of the drops, suppresses EHD flows, and alters drop shapes. For example, by adding conductive particles to the surface of a silicone oil (which is weakly-conductive), the drop geometry changes from oblate to prolate (from compressed to stretched in the direction of the electric field). Particles adsorbed at a drop interface may alter the surface tension, interfacial viscosity, or electric properties (conductivity and permittivity) of the drop.^32,53 Because the surface tension works against drop compression or stretching (trying to make the drop spherical and reduce the energy of the system), a change in surface tension can affect the deformation magnitude, but does not determine whether the drop is prolate or oblate. Besides, as observed in previous experiments on particle-covered silicone oil drops in castor oil, adding particles to the drop surfaces has an insignificant effect on the surface tension of the drops, and thus also a negligible effect on the deformation magnitude of such drops.³²

Similarly, an increase of the effective interfacial viscosity (expected after adding particles to the liquid interface)⁶⁷ affects only the magnitude of the drop deformation⁴³ and cannot cause the oblate-to-prolate shape transition. We therefore attribute the oblate–prolate deformation transition to changes in the electric properties of the drop interface. In the case of a silicone oil drop in castor oil, adding particles to the drop interface that are more conductive than the silicone and castor oil reverses the free charge distribution. The dipole moment of the drop (formed by free charges at the surface) changes direction from opposite of to similar to the electric field direction.

4.2 Suppression of EHD flows

Qualitative results from previous studies suggest that if the interfacial viscosity of a particle-covered silicone oil drop in castor oil is sufficiently large (high particle coverage), the particle layer can suppress electric field-induced EHD flows.^32,53 In this research, we performed both qualitative (e.g. presence and direction) and quantitative (flow magnitude) studies on EHD flows. Our experiments show that the addition of surface particles on a silicone oil drop in castor oil leads to a reduction of the electric field-induced EHD flow velocities around the drop, irrespective of the electrical conductivity of the surface particles. A monolayer of packed particles at a liquid interface behaves like an elastic sheet that can support stresses and strain.^59,60 For that reason, the shear elasticity of the particle layer immobilizes the drop interface and suppresses the EHD flows. However, the electrical properties of the surface particles do determine the critical particle concentration at which EHD flows are suppressed, as is explicitly shown in Fig. 3 and 5. Particles at the drop surface can form particle chains via dipole–dipole interactions (due to particle polarization), where the force between the particles depends on parameters such as particle size, electrical conductivity (for DC fields), and permittivity (for AC fields).⁶³ The presence of conductive particle chains affects the distribution of free charges at the drop interface by conducting charges faster through the particle chains than through the silicone oil drop (which is weakly conductive). If the concentration of particle chains at the drop surface is high, the drop behaves as a conductive drop with no electric stress component acting parallel to the drop interface.

4.3 Particle organization at drop surfaces

We also observed that particles at drop surfaces subjected to a constant DC electric field exhibit different structuring depending on their electrical properties and coverage. For instance, at the same low particle coverage, insulating surface particles assemble at the equator of silicone oil drops, forming ribbon-like structures composed of densely-packed particles, while silver-coated particles form short chains aligned with the electric field. We conclude that particle structuring is determined by the competition between EHD flows and particle–particle dipolar interactions. When the dipolar interactions between particles are strong, the particles can form long chains that cannot be broken by the EHD flows. Additionally, if the particle concentration is high, the chains can span the whole drop and particles concentrate at the drop poles. When the dipolar interactions between particles are weak, the EHD flows can be utilized to structure particles at drop poles or at the drop equator, depending on the electric properties of the drop and surrounding fluid.²⁰ For the system studied in our research (silicone oil drop in castor oil), the EHD flows were directed from drop poles to drop equator.

4.4 Method for manipulating conductive particles at drop surfaces

Furthermore, we present a novel method for manipulating conductive particles at drop surfaces. By applying an AC electric field and tuning the frequency, we actively structured surface particles and locally changed their concentration and packing. The adaptive particle structure is organized by dipolar interactions and EHD flows. When the frequency of the applied electric field is high, the particles form long chains via dipolar interactions and concentrate at the drop poles. Switching the electric field to DC induces EHD flows that move the particles from the drop poles towards the drop equator. The method resembles the pupil effect reported by Dommersnes et al.,²⁰ where the strength of the applied DC electric field was used to control the coverage of clay particles at a drop surface. The new method presented in this article is not limited to clay particles, it also allows for using surface particles of different conductive materials. A subtle point is that the size of particles and their concentrations must be chosen so that the dipolar forces are strong enough to assemble particles at drop poles under electric fields at high frequencies, and weak enough to allow for the formed chains to be broken by EHD flows at DC electric fields. It is worth pointing out that by reducing the viscosity of the liquids, the time for actively stretching the particle chains can be as small as micro-seconds, just by reducing the viscosity of the liquids to that of water. The electrical conductivities of the oils could also be tuned (e.g. by adding inorganic salts) to speed up this process. Another note is that from the frequency tuning experiments (demonstrated in Movie S2, ESI†), we learn that it is possible to control the packing density and likely also the characteristic periodicity between the particle chains. We envisage the possibility to further investigate these effects in respect to optical materials and applications.

4.5 Outlook

We believe the findings of this work are important for developing advanced structures, such as patchy microcapsules. With a myriad of applications ranging from energy storage to the encapsulation of an extensive range of materials, homogenous and patchy microcapsules have received considerable research interest in this decade. It has been reported that the target microencapsulated product will be worth around $9.25 billion by 2020.⁶⁸ To succeed in implementing these microcapsules, we need to precisely control the mechanical stability and structural properties of their shells.

Author contributions

Z. R. and A. M. initiated the project and designed all the experiments. F. K. E. and K. J. M. contributed to the design of the PIV measurements. A. M. and K. K. performed the experiments on drop deformation and contributed to data analysis and presentation. A. M., K. K., F. K. E., and K. J. M. performed the experiments on tracing EHD flows and contributed to data analysis and presentation. Z. R. and K. K. conducted the experiments on particle manipulation and contributed to data analysis and presentation. All authors took part in discussions on the finalization of the manuscript. A. M. and Z. R. authored the paper. A. M. administered the submission and the review process.

Conflicts of interest

There are no conflicts of interest to declare.

Acknowledgements

A. M. acknowledges financial support from the European Union's Horizon 2020 research and innovation framework programme under the M. Skłodowska-Curie grant agreement no. 752896. Z. R. and K. K. were supported by the Polish National Science Centre through OPUS programme (2015/19/B/ST3/03055). The contributions from K. J. M. and F. K. E. were supported by the Research Council of Norway through its Centres of Excellence funding scheme, project number 262644 (PoreLab). The authors thank Prof. Eirik Grude Flekkøy and Prof. Tomasz Hornowski for a careful reading of the manuscript and useful feedback.

References

1. A. Maestro, E. Santini, D. Zabiegaj, S. Llamas, F. Ravera, L. Liggieri, F. Ortega, R. G. Rubio and E. Guzman, Adv. Condens. Matter Phys., 2015, 17.
2. T. Bollhorst, K. Rezwan and M. Maas, Chem. Soc. Rev., 2017, 46, 2091–2126.
3. R. Urbas, R. Milošević, N. Kašiković, Ž. Pavlović and U. S. Elesini, Iran. Polym. J., 2017, 26, 541–561.
4. T. Brugarolas, F. Tu and D. Lee, Soft Matter, 2013, 9, 9046–9058.
5. E. Dickinson, Curr. Opin. Colloid Interface Sci., 2010, 15, 40–49.
6. B. Peng, L. Zhang, J. Luo, P. Wang, B. Ding, M. Zeng and Z. Cheng, RSC Adv., 2017, 7, 32246–32254.
7. S. Drexler, J. Faria, M. P. Ruiz, J. H. Harwell and D. E. Resasco, Energy Fuels, 2012, 26, 2231–2241.
8. M. H. Asfour, H. Elmotasem, D. M. Mostafa and A. A. A. Salama, Int. J. Pharm., 2017, 534, 325–338.
9. N. G. Vilkova and A. V. Nushtaeva, Mendeleev Commun., 2013, 23, 155–156.
10. W. T. M. Irvine, V. Vitelli and P. M. Chaikin, Nature, 2010, 468, 947–951.
11. V. N. Manoharan, Science, 2015, 349, 942.
12. F. Sicard and A. Striolo, Nanoscale, 2017, 9, 8567–8572.
13. J. Hegemann, S. Knoche, S. Egger, M. Kott, S. Demand, A. Unverfehrt, H. Rehage and J. Kierfeld, J. Colloid Interface Sci., 2018, 513, 549–565.
14. Z. Rozynek, M. Kaczmarek-Klinowska and A. Magdziarz, Materials, 2016, 9, 679.
15. E. Amah, K. Shah, I. Fischer and P. Singh, Soft Matter, 2016, 12, 1663–1673.
16. R. Ettelaie and S. V. Lishchuk, Soft Matter, 2015, 11, 4251–4265.
17. V. O. Ikem, A. Menner, T. S. Horozov and A. Bismarck, Adv. Mater., 2010, 22, 3588.
18. Z. Rozynek and A. Józefczak, Eur. Phys. J. B, 2016, 225, 741–756.
19. Z. Rozynek, A. Mikkelsen, P. Dommersnes and J. O. Fossum, Nat. Commun., 2014, 5, 3945.
20. P. Dommersnes, Z. Rozynek, A. Mikkelsen, R. Castberg, K. Kjerstad, K. Hersvik and J. O. Fossum, Nat. Commun., 2013, 4, 2066.
21. S. Y. Tan, R. F. Tabor, L. Ong, G. W. Stevens and R. R. Dagastine, Soft Matter, 2012, 8, 3112–3121.
22. J. K. Ferri, P. Carl, N. Gorevski, T. P. Russell, Q. Wang, A. Boker and A. Fery, Soft Matter, 2008, 4, 2259–2266.
23. M. K. Mulligan and J. P. Rothstein, Langmuir, 2011, 27, 9760–9768.
24. S. She, C. Xu, X. Yin, W. Tong and C. Gao, Langmuir, 2012, 28, 5010–5016.
25. D. F. do Nascimento, J. A. Avendano, A. Mehl, M. J. B. Moura, M. S. Carvalho and W. J. Duncanson, Sci. Rep., 2017, 7, 11898.
26. L. Bécu and L. Benyahia, Langmuir, 2009, 25, 6678–6682.
27. I. Koleva and H. Rehage, Soft Matter, 2012, 8, 3681–3693.
28. J. W. Ha and S. M. Yang, Phys. Fluids, 2000, 12, 1671–1684.
29. M. Ouriemi and P. M. Vlahovska, J. Fluid Mech., 2014, 751, 106–120.
30. R. B. Karyappa, S. D. Deshmukh and R. M. Thaokar, Phys. Fluids, 2014, 26, 122108.
31. M. Ouriemi and P. M. Vlahovska, Langmuir, 2015, 31, 6298–6305.
32. A. Mikkelsen, P. Dommersnes, Z. Rozynek, A. Gholamipour-Shirazi, M. d. S. Carvalho and J. O. Fossum, Materials, 2017, 10, 436.
33. C. Huang, Z. Sun, M. Cui, F. Liu, B. A. Helms and T. P. Russell, Adv. Mater., 2016, 28, 6612–6618.
34. M. Alghane, Y. Q. Fu, B. X. Chen, Y. Li, M. P. Y. Desmulliez and A. J. Walton, Jpn. J. Appl. Phys., 2011, 109, 114901.
35. Q. Xie, G. B. Davies and J. Harting, ACS Nano, 2017, 11, 11232–11239.
36. M. Li and D. Li, J. Nanopart. Res., 2016, 18, 120.
37. Z. Rozynek, P. Dommersnes, A. Mikkelsen, L. Michels and J. O. Fossum, Eur. Phys. J.-Spec. Top., 2014, 223, 1859–1867.
38. Z. Rozynek, R. Bielas and A. Józefczak, Soft Matter, 2018 10.1039/C8SM00671G.
39. P. Sheng and W. Wen, Annu. Rev. Fluid Mech., 2012, 44, 143–174.
40. E. Amah, K. Shah, I. Fischer and P. Singh, Soft Matter, 2016, 12, 1663–1673.
41. S. Nudurupati, M. Janjua, N. Aubry and P. Singh, Electrophoresis, 2008, 29, 1164–1172.
42. S. Nudurupati, M. Janjua, P. Singh and N. Aubry, Soft Matter, 2010, 6, 1157–1169.
43. G. Taylor, Philos. Trans. R. Soc., A, 1966, 291, 159–166.
44. P. F. Salipante and P. M. Vlahovska, Phys. Fluids, 2010, 22, 112110.
45. D. Das and D. Saintillan, J. Fluid Mech., 2017, 829, 127–152.
46. P. Dommersnes, A. Mikkelsen and J. O. Fossum, Eur. Phys. J.-Spec. Top., 2016, 225, 699–706.
47. Rahul B. Karyappa, Shivraj D. Deshmukh and Rochish M. Thaokar, J. Fluid Mech., 2014, 754, 550–589.
48. R. B. Karyappa, S. D. Deshmukh and R. M. Thaokar, Phys. Fluids, 2014, 26, 122108.
49. A. Mikkelsen, Z. Rozynek, K. Khobaib, P. Dommersnes and J. O. Fossum, Colloids Surf., A, 2017, 532, 252–256.
50. M. Ouriemi and P. M. Vlahovska, J. Fluid Mech., 2014, 751, 106–120.
51. A. Mikkelsen, P. Dommersnes and J. O. Fossum, Rev. Cubana Fis., 2016, 33, 47–49.
52. M. M. Cui, T. Emrick and T. P. Russell, Science, 2013, 342, 460–463.
53. M. Ouriemi and P. M. Vlahovska, Langmuir, 2015, 31, 6298–6305.
54. A. Mikkelsen, J. Wojciechowski, M. Rajňák, J. Kurimský, K. Khobaib, A. Kertmen and Z. Rozynek, Materials, 2017, 10, 329.
55. W. Thielicke and E. Stamhuis, J. Open Res. Software, 2014, 2, e30.
56. N. Estrada, Phys. Rev. E, 2016, 94, 062903.
57. A. Lazarus, H. C. B. Florijn and P. M. Reis, Phys. Rev. Lett., 2012, 109, 144301.
58. J. A. Lanauze, L. M. Walker and A. S. Khair, J. Fluid Mech., 2015, 774, 245–266.
59. D. Vella, P. Aussillous and L. Mahadevan, Europhys. Lett., 2004, 68, 212–218.
60. P. Erni, H. A. Jerri, K. Wong and A. Parker, Soft Matter, 2012, 8, 6958–6967.
61. R. Allan and S. Mason, Proc. R. Soc. London, Ser. A, 1962, 267, 45–61.
62. W. B. Smythe, Static and dynamic electricity, Hemisphere Publishing, 79 Madison Avenue, New York, NY10016, USA, 1988.
63. L. C. Davis, Jpn. J. Appl. Phys., 1992, 72, 1334–1340.
64. S. Nudurupati, M. Janjua, P. Singh and N. Aubry, ASME Dyn. Syst. Control Conf., Proc., 2009, 10, 159–167.
65. X.-D. Pan and G. H. McKinley, J. Colloid Interface Sci., 1997, 195, 101–113.
66. S. Torza, R. Cox and S. Mason, Philos. Trans. R. Soc., A, 1971, 269, 295–319.
67. S. Lishchuk and I. Halliday, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2009, 80, 016306.
68. Zion-Research, Microencapsulation Market for Pharmaceuticals, Household Products, Agrochemicals, Food Additives and Other Applications: Global Industry Perspective, Comprehensive Analysis, Size, Share, Growth, Segment, Trends and Forecast, 2014–2020, Market Research Store, 2016.

---

Footnotes

† Electronic supplementary information (ESI) available: Two supplementary movies. See DOI: 10.1039/c8sm00915e

‡ These authors contributed equally to this work.

---