 Open Access Article
Open Access ArticleThe detailed acoustic signature of a micro-confined cavitation bubble
Chiara
Scognamiglio
 *ab,
Francesco
Magaletti
a,
Yaroslava
Izmaylov
b,
Mirko
Gallo
a,
Carlo Massimo
Casciola
a and
Xavier
Noblin
*ab,
Francesco
Magaletti
a,
Yaroslava
Izmaylov
b,
Mirko
Gallo
a,
Carlo Massimo
Casciola
a and
Xavier
Noblin
 b
b
aDipartimento di Ingegneria Meccanica e Aerospaziale, Università di Roma La Sapienza, Via Eudossiana 18, 00184 Roma, Italy. E-mail: chiara.scognamiglio@uniroma1.it
bUniversité Côte d'Azur, CNRS, UMR7010, Institut de Physique de Nice, Parc Valrose, 06108 Nice Cedex 2, France
First published on 12th September 2018
Abstract
Numerous scenarios exist for a cavitation bubble growing in a liquid. We focus here on cavitation phenomena within water under static tension in a confined environment. Drawing inspiration from the natural materials in plants, we design a novel experimental setup where a micrometric volume of water is confined by a hydrogel-based material. We show that, submerging the sample in a hypertonic solution, the water within the cavity is placed under tension and the acoustic emission produced by the resulting bubble nucleation is precisely detected. This new experimental procedure is able to strongly reduce the acoustic reflections occurring at the hydrogel/air interface with more classical techniques. We also propose a mathematical model to characterise the pressure wave emitted in order to correctly take into account the dissipation effect induced by the visco-elastic behaviour of the confining hydrogel. Both bubble resonant frequency and damping are captured by the model and quantitatively match the values found in the experiments.
1 Introduction
Water can exist in a liquid state under highly tensile stress (negative pressure) and eventually relax its metastable state by nucleation of vapour cavities, a process dubbed cavitation.1,2Cavitation begun to be a hot topic in the field of hydraulic and marine engineering since bubbles collapse was found to be a serious cause of materials damage.3,4 Bubbles implosion causes the release of a big amount of energy in small spatial spots and in short time with high velocities, pressures, and temperatures involved in the process.5 Decades ago, other important effects occurring along with bubbles collapse have been studied, i.e. jet formation, shock waves and light emission (sonoluminescence).6 The rich dynamics of bubbles in a liquid continued to be gradually revealed, shining light on fascinating and unexpected features that have rendered cavitation a desirable phenomenon in several applications, i.e. drug delivery5,7–10 or sonochemical reactors.11,12 In most of the cases, the fate of a cavitation bubble is to collapse as the pressure of the surrounding liquid comes back to positive values. When the liquid is stretched quasi-statically, the size of the nucleated vapour bubble depends on the initial tension and liquid volume.13 M. Berthelot was the first investigator of statically stretched water. In 1850, he placed water in tension and observed cavitation using capillary tubes where liquid was isochorically cooled down.14
It is well known that cavitation also takes place in natural systems, i.e. in ferns sporangia15,16 or in the xylem – the fluidic network of ascending sap in a tree.17 When a tree undergoes a prolonged drought, water pressure in the xylem becomes negative and cavitation may take place. Bubble appearance, growth and conduit clogging, a process called embolism, eventually lead to the tree death. As a central topic for botanists, tree dehydration has been extensively studied through the acoustic emissions generated by the bubbles in the xylem. A common and non-invasive technique is recording the acoustic signals through transducers in direct contact with the intact wood.18,19 Such investigations revealed a strong correlation between acoustic emission and xylem drying.20,21 However, waveforms were not studied in detail22 and the bubbles which are the source of acoustic energy were hardly identified.23
In fern sporangia, cavitation occurs within a beam-like structure, the annulus, triggering a catapult which launches the spores as fast projectiles at long distances.24,25 In 1990, K. T. Ritman and J. A. Milburn acoustically detected cavitation in the fern annulus. They quantified the number of acoustic emissions during spores ejection and revealed their ultrasonic nature. However, also in this case, acoustic signals could not be characterised quantitatively in terms of, e.g., waveform, duration, frequency.26
An experimental set-up recently proposed offers the possibility to investigate confined cavitation in bio-mimetic structures.27,28 As a crucial improvement over natural settings, the synthetic configuration includes an optical access for cavitation bubble visualisation. The device consists of micrometric cells filled with water encapsulated in a synthetic rigid hydrogel. When the micro device is placed in a sub-saturated vapour environment, water evaporates from the external surface driven by the chemical potential difference establishing a flow from the inner cells toward the exterior. Therefore, liquid density and pressure reduce within the cells until a stretch threshold is reached: water finally breaks, a bubble appears and grows. With this method, fast oscillations of bubble volume were optically observed in spherical enclosures of water.13 Interesting hydrodynamic phenomena were identified by sampling at a frame rate of 0.2 MHz, described as formation, fragmentation and ripening of a toroidal bubble. Acoustic emissions generated in hydrogel-encapsulated wood were detected and their acoustic energy quantified.29 Still, the detailed acoustic emission of a bubble has not been revealed, not even in synthetic devices. Indeed, only the frequency and the acoustic energy were measured without identifying the exact waveform or quantifying the characteristic attenuation time of the acoustic emission.
In the context of cavitation – a rich phenomenology which includes a large variety of aspects – the present paper analyses in detail the acoustic emission emitted by a cavitation bubble nucleated in a micro-confined liquid, adopting a combined experimental and theoretical approach. To start with, cubic-shaped enclosures of water were realised in hydrogel inspired by the structure of fern sporangia.25 The original idea was to detect the bubble acoustic emissions after partial drying of the sample in sub-saturated air, much like the set-up just described. However, after a preliminary measurement campaign, it turned out that the signal was unavoidably contaminated by reflections. Reflections presumably occurred at the hydrogel/air interface due to impedance mismatch between the two phases, with the result of substantially biasing the signal and hampering the subsequent acoustic analysis. In order to prevent the undesired reflections, a new experimental procedure was devised to detect the actual emission of the confined bubbles. The basic idea consists in immerging the same hydrogel device in an environment at the same time capable of extracting water, thereby inducing cavitation, and preventing/minimizing acoustic reflections. With this purpose, the samples, soaked with water, were immersed in a salt solution to induce an osmotic outflow and drive the hydrogel dehydration. The bubble acoustic signature could then be acquired with no spurious reflections thanks to the good match of the acoustic impedance between hydrogel and solution. With this new approach, the acoustic parameters were characterised for the first time as a function of the enclosure volume. Experiments are complemented with a theoretical approach along the lines described in the paper of Drysdale et al.30 that predicts resonant frequency and damping rate of an oscillating bubble in a liquid confined by an elastic solid. Here the model is extended to take into account the viscoelastic behaviour of the enclosures, a crucial aspect in view of correctly explaining the experimental results.
The proposed method paves the way for investigating other artificial or biological systems where a porous media encloses a liquid, e.g. to help explaining the mechanism of embolism and dryness in trees.17,19,29,31 It could also be exploited to understand how cavitation bubbles trigger that wonderfully efficient ultra-fast catapult in ferns sporangia.25 Finally, it can inspire low-cost and efficient biomimetic devices where osmosis is used as the only driving-force.27,32–34
2 Experiments
An original experimental method was developed in order to observe bubbles nucleation in hydrogel cavities and detect their acoustic signature. Taking inspiration from the cells of the sporangium annulus in ferns, we encapsulated water in a cubic micrometric cavity of volume Vc and side Lc, surrounded by methacrylic acid (MAA) hydrogel, Fig. 1A. Contrarily to the natural structure,25 here cavities are purposely separated by a large distance dc (dc ≫ Lc). In this way, bubbles interaction is prevented and ultrasounds emitted by single independent bubbles can be investigated. | ||
| Fig. 1 (A) Scheme of the hydrogel device (not to scale). It is made of cubic cavities, with size Lc, confined by hydrogel: the central one encloses a bubble, just nucleated, with water at atmospheric pressure while the other two contain liquid still at negative pressure that pulls inward and bends the hydrogel walls. (B) Experimental set-up scheme (traditional method). The device is in contact with air and water evaporates from the bottom while the top surface is covered by an ophthalmic gel film to enhance the transmitted signal. A film of mylar is placed above the device in order to reflect the light coming from halogen lamp and passing through the microscope objective placed below the device. The magnified image-forming light will be then directed to the camera system by a splitter cube. (C) Experimental set-up scheme (new method): a tank in polydimethylsiloxane (PDMS) is used to contain the calcium chloride solution where the hydrogel sample is submerged. The optical set-up is still the one described in (B). (D) Profile of the osmotic pressure as a function of the CaCl2 solution obtained fitting the points presented in the book of J. Milburn35 for perfect osmotic membrane; the orange circle represents the osmotic pressure Π associated with the molarity chosen (CCaCl2 = 2.5). | ||
2.1 Sample preparation
To prepare the hydrogel samples, we first fabricated the micrometric pits using a photoresist SU8-2075 on a silicon wafer. The elastomeric stamp is obtained by moulding the photoresist in PDMS. We cured it for 2 hours at 95 °C to favour its reticulation. The PDMS was then peeled off from the photoresist, ready to be used as a stamp for the hydrogel. The hydrogel solution was prepared following the formulation of Wheeler and Stroock:28 16 vol% (hydroxyethyl)methacrylate (HEMA), 50 vol% methacrylic acid (MAA), 6 vol% ethylene glycol dimethylacrylate (EGDMA) and 28 vol% of deionized water. Then, 1 vol% of photoinitiator was added (36.5 w% 2,2-dimethoxy-2-phenylacetophenone (DMAP) with 63.5 w% vinyl-2-pyrrolidone (nVp)). We poured the solution on the PDMS stamp and we partially reticulated it under UV. After peeling off the patterned hydrogel layer from the PDMS, we placed on the top of it a 200 μm-thick hydrogel layer in order to close the cubic cavities. A further exposure under the UV lamp was performed to ensure a complete reticulation and a solid bonding of the two hydrogel pieces. The final dimensions of the device are about 1 cm × 2 cm × 400 μm and the sample contains around 20 independent cavities, Fig. 1A. At last, we immersed the sample into deionized water at 80 °C for 48 hours to fill completely the hydrogel pores and the cavities.2.2 Optical and acoustic set-up
The method proposed by Wheeler and Stroock to study bubble nucleation in such hydrogels devices consists in placing the fully hydrated sample in dry air or in humidity controlled environment to induce water evaporation.28 That approaches was originally conceived for bubble dynamics optical investigation as used in ref. 13 and 36. Coupling it with acoustic analysis entails complications, namely a good impedance adaptation between the hydrogel and the hydrophone has to be ensured in order to receive sufficiently intense and reflections-free signals. At the same time, light reflected from the device and directed towards the camera has to be intense enough to perform imaging. To comply with these restrictions, we take two different paths: (i) one, used traditionally since the work of T. Wheeler and A. Stroock,27 is based on the evaporation method, (ii) the other relies on a brand new procedure.In the first case, hydrogel tensile stress that leads to cavitation is induced by water evaporation from the bottom surface of the sample since an ophthalmic gel film is spread on the top surface to increase the signal transmitted to the hydrophone (the set-up is shown in Fig. 1B). Here, the drawback is that acoustic reflections from the hydrogel–air interface at the bottom of the device are significant due to the large impedance mismatch. As a consequence, the original signal emitted by the bubble may be strongly perturbed.
The alternative method we propose here employs a concentrated hypertonic solutions where the sample is submerged. In this case hydrogel dehydration is driven by the salt concentration difference with the advantage that the impedances of soaked hydrogel and solution are nearly exactly matched thereby minimising acoustic reflections. A scheme of the set-up is represented in Fig. 1C. The device is placed in a cylindrical PDMS tank filled with salt solution. The hydrophone (HNR-0500 Onda) is vertically inserted in the tank with its tip 5 mm away from the sample – optimal distance in order to receive high-intensity signals and well delayed reflections between the acoustic source (the bubble) and the receiver (the hydrophone tip). In this way, also the acoustic reflections from the bottom surface of the hydrogel are minimised.
We used a hypertonic solution of calcium chloride (CaCl2). Although flow of salt ions in and out the device cannot be excluded, their possible presence inside the cavities is found not to alter the phenomena of our present interest. In fact, under repeated use, the samples always reproduced the same cavitation parameters, i.e. nucleation time and detected acoustic signature.
Since the hydrogel pores are so small as to prevent ions diffusion into hydrogel, the process of dehydration that drives the pressure decrease and eventually leads to cavitation can be understood by modelling the hydrogel layer that separates the cavity from the solution as a semipermeable membrane. Following classical notions of non-equilibrium thermodynamics,37 the flux j of water out of the device is proportional to salt mass fraction and pressure jump across the hydrogel, j ∝ (∂μ/∂Y)ΔY + (∂μ/∂p)Δp, where Y is the salt mass fraction, p the pressure, μ(Y,p,T0) the chemical potential with T0 the temperature assumed constant and Δ denotes the jump across the layer. In general, for real solutions in presence of dissolved ions, the explicit expression for the chemical potential is too cumbersome to be reported here. The crucial aspect is that the chemical potential depends on pressure,  , where vm is the molar volume of the liquid. By definition, in equilibrium conditions the flux vanishes due to chemical potential equalisation, μ(Y,ps,T0) = μ(0,pl,T0). According to this equation a pressure difference, the osmotic pressure Π > 0, is build up between external solution and water in the cavity such that ps = pl + Π, i.e. the pressure pl in the cavity decreases with respect to the external pressure ps of the solution. The higher the salt concentration difference, the higher the osmotic pressure as shown in the experimental curve of Fig. 1D for perfect osmotic membranes. Considering salt solution at atmospheric pressure (ps = 0.1 MPa) and stretched water (for instance pl < −1 MPa), one can approximate the osmotic pressure to water tension: Π ≃ −pl.
, where vm is the molar volume of the liquid. By definition, in equilibrium conditions the flux vanishes due to chemical potential equalisation, μ(Y,ps,T0) = μ(0,pl,T0). According to this equation a pressure difference, the osmotic pressure Π > 0, is build up between external solution and water in the cavity such that ps = pl + Π, i.e. the pressure pl in the cavity decreases with respect to the external pressure ps of the solution. The higher the salt concentration difference, the higher the osmotic pressure as shown in the experimental curve of Fig. 1D for perfect osmotic membranes. Considering salt solution at atmospheric pressure (ps = 0.1 MPa) and stretched water (for instance pl < −1 MPa), one can approximate the osmotic pressure to water tension: Π ≃ −pl.
A precise characterisation of the hydrogel behaviour in the presence of a hypertonic solution goes beyond the purpose of the present work and will be addressed in a future study. Here, assuming a perfect osmotic membrane, we estimate cavitation probability in hydrogel cavities as a function of the solution molarity with the aim of identifying the salt concentration above which cavitation (almost) certainly occurs. In the protocol used in the actual experiments, the same sample was immersed in salt solution at seven different molar concentrations. By means of a camera, we recorded the dehydration process and counted cavitation events occurred in the sample after the chemical potential equilibrates. Between two realisations, the hydrogel was placed in DI water for 24 hours at 80 °C to re-hydrate. The same procedure was repeated for four samples having different cavity volume. The resulting cavitation probability profile, defined as the ratio of cavitated enclosures out of the total number of enclosures in the device, is shown in Fig. 2 as a function of the CaCl2 molarity. The curve exhibits a transition for molar concentrations around 2 M over a range of pressure, see the pressure scale reported on top of the plot. The threshold pressure in the stretched liquid, pl, defined as the pressure corresponding to a cavitation probability of 50%, depends on the confinement size. Averaging over the confinement size results in the grey curve shown in Fig. 2, where pl can be estimated to be around −21 MPa (1.8 M) by using the experimental curve given in ref. 35. In a previous study,28 where hydrogel samples were equilibrated in subsaturated air following the traditional approach, the cavitation threshold was −22 MPa showing that the two methods substantially provide coherent results. Interestingly such cavitation threshold, much smaller than found for ultra-pure water inclusions in quartz,38 is well explained by a recent model which takes into account the presence of dissolved gas in the liquid.39 The fact that the threshold we observe with the present device substantially matches that found by ref. 28 leads to the conclusion that salt ions, if present within the sample, do not alter the cavitation pressure pl within the experimental accuracy. Relying on the curves reported in Fig. 2, we chose to soak the samples in a 2.5 M solution in order to have certain occurrence of cavitation. It is worth noting that in these conditions the induced equilibrium osmotic pressure is around 35 MPa, beyond the water limit strength expected of hydrogel systems, hence the bubble could appear before the chemical equilibrium between salt solution and hydrogel water is reached (see Fig. 2).
Whatever the technique used to induce cavitation, either evaporation in air or osmotic pressure de-hydration in salt solution, the sample is placed on an inverted microscope (Zeiss Axiovert 200 M) and observed using a 2.5× objective. The light from a halogen lamp passes through the objective, hits the device and reflects back to the objective on a surface placed above the hydrogel device acting as a mirror, sketches in panels (B) and (C) of Fig. 1. The cavity image-forming light is then directed to the high-speed camera (phantom v711) working at 100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 fps. In this way, the moment the bubble appears can be identified with a temporal resolution of 10 μs. Since such resolution is insufficient to reveal the fast dynamics of the bubble during acoustic emission, the images are used to check that the source of the acoustic signal is the appearance of a bubble. The hydrophone, with tips centered in the camera, detects the pressure waves emitted from the observed cavities. The hydrophone is connected through a preamplifier and a differential amplifier to the oscilloscope (picoscope 3000 Series) that records data for 1 s with an acquisition rate of 62.5 MHz. Once a bubble appears, a trigger from a manually operated function generator is simultaneously sent to both camera and hydrophone in order to download all the images and pressure data recorded for one entire second before the trigger.
000 fps. In this way, the moment the bubble appears can be identified with a temporal resolution of 10 μs. Since such resolution is insufficient to reveal the fast dynamics of the bubble during acoustic emission, the images are used to check that the source of the acoustic signal is the appearance of a bubble. The hydrophone, with tips centered in the camera, detects the pressure waves emitted from the observed cavities. The hydrophone is connected through a preamplifier and a differential amplifier to the oscilloscope (picoscope 3000 Series) that records data for 1 s with an acquisition rate of 62.5 MHz. Once a bubble appears, a trigger from a manually operated function generator is simultaneously sent to both camera and hydrophone in order to download all the images and pressure data recorded for one entire second before the trigger.
3 Mathematical modelling
The oscillation of a vapor bubble in a confined space can be mathematically described following the work of Drysdale et al.30 The authors studied the problem under the approximation of spherical symmetry, considering an oscillating vapor bubble immersed in a viscous liquid inside a cavity. In the original work, material surrounding the cavity is assumed to be an elastic solid. As it will be shown later, this assumption needs to be relaxed to reproduce the present experimental results with sufficient accuracy. The response of the compressible liquid can be described by the linearized Navier–Stokes equation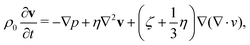 | (1) |
 | (2) |
 | (3) |
 | (4) |
 | (5) |
A purely elastic material cannot reproduce the high damping observed in our experiments with hydrogel. Hence a visco-elastic description based on a generalized Kelvin–Voigt model is proposed to incorporate both Hookean elasticity and Newtonian viscosity.40 The stress in the one-dimensional model
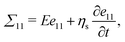 | (6) |
![[u with combining dot above]](https://www.rsc.org/images/entities/b_char_0075_0307.gif) s + ∇
s + ∇![[u with combining dot above]](https://www.rsc.org/images/entities/b_char_0075_0307.gif) Ts) = 1/2(∇vs + ∇vTs)
Ts) = 1/2(∇vs + ∇vTs) | (7) |
 | (8) |
Exploiting again the spherical symmetry, the solid velocity is us = ∇ϕs and the momentum equation for an oscillatory time dependence reduces to the Helmholtz equation
| ∇2ϕs + ks2ϕs = 0, | (9) |
 | (10) |
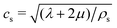 the speed of the pressure waves in the solid. Hereafter, because of the purely radial structure of the model, we will refer to the single effective viscosity coefficient
the speed of the pressure waves in the solid. Hereafter, because of the purely radial structure of the model, we will refer to the single effective viscosity coefficient ![[small eta, Greek, tilde]](https://www.rsc.org/images/entities/char_e110.gif) s = ζs − 4/3ηs.
s = ζs − 4/3ηs.
Since no incoming wave is present, the relevant solution of eqn (9) reads
 | (11) |
σrr = 0, at![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) r = Rb, r = Rb, | (12) |
| v = vs, at r = Rc, | (13) |
σrr = ∑rr, at![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) r = Rc, r = Rc, | (14) |
 | (15) |
 . The viscous dissipation of the hydrogel which accounts for most of the bubble oscillations attenuation is included in the expression for ks. The nonlinear eqn (15) is numerically solved by iteration. The model formulated above considers a single bubble in the liquid. It should be stressed that in the actual experiment the vapour phase may consist of a cloud of daughter bubbles formed out of the fragmentation of a parent one.36 A simple back of the envelope calculation shows that the relevant free energy is dominated by the compressibility of the system (e.g. liquid and hydrogel), the contribution arising from the bubble surface tension being orders of magnitude smaller. For a given vapour volume, the surface tension free energy scales with the cubic root of the number of daughter bubbles in the cloud and becomes comparable with the compressibility only if the number of bubbles is incredibly large (order of 1015). Such a large number is unphysical, since the corresponding volume would be much smaller that the critical bubble. In these conditions, we expect that a model using a single bubble is able to capture the acoustic properties of the actual system.
. The viscous dissipation of the hydrogel which accounts for most of the bubble oscillations attenuation is included in the expression for ks. The nonlinear eqn (15) is numerically solved by iteration. The model formulated above considers a single bubble in the liquid. It should be stressed that in the actual experiment the vapour phase may consist of a cloud of daughter bubbles formed out of the fragmentation of a parent one.36 A simple back of the envelope calculation shows that the relevant free energy is dominated by the compressibility of the system (e.g. liquid and hydrogel), the contribution arising from the bubble surface tension being orders of magnitude smaller. For a given vapour volume, the surface tension free energy scales with the cubic root of the number of daughter bubbles in the cloud and becomes comparable with the compressibility only if the number of bubbles is incredibly large (order of 1015). Such a large number is unphysical, since the corresponding volume would be much smaller that the critical bubble. In these conditions, we expect that a model using a single bubble is able to capture the acoustic properties of the actual system.
4 Results
4.1 Comparison of the two methods
Cavitation bubbles were observed with the camera and their location was found to be at the hydrogel wall, most often at the corners, suggesting their nucleation follows a heterogeneous process, as expected from nucleation theory. For each cavitation event, the hydrophone detected a pressure wave. Examples of acoustic emissions for both methods discussed in Section 2 are shown in Fig. 3 and 4. | ||
| Fig. 4 Acoustic signals captured with the proposed method. On the left column: Pressure waves emitted by a bubble nucleated in three cubic cavities with size Lc = 100–50–30 μm from top to bottom, respectively (blue dots); curves (in solid green line) obtained by substituting in eqn (16), ω0 and τ, found by fitting the frequency-domain signals (17). On the right column: Power spectra density (light blue filled squares), fitted with eqn (17) (solid red line). | ||
When using the traditional method relying on water evaporation, the signals received by the hydrophone clearly presents reflections, Fig. 3. On the contrary, the acoustic trace acquired with the new set-up based on the use of hypertonic solutions is much cleaner, Fig. 4.
Apparently, acoustic reflections, though hindering the evaluation of the damping coefficient 1/τ, do not affect the resonance frequency ω0. In fact, the development of the new method was fostered by the need of matching the impedance at the hydrogel-external environment interface in order to prevent/reduce reflections and precisely estimate the pressure wave attenuation. We thus assume that the signal received by the hydrophone in the new conditions, Fig. 4, is the actual signature of the bubble. Consistently, the reflection-affected signal can be reconstructed by artificially superimposing a reflected wave to the putatively reflection-free signal captured from new set-up. Due to the large density and sound speed difference between the two media which produces the high impedance mismatch, the incident wave reflects at the boundary with a (negative) unitary reflection coefficient R = Ar(ω)/Ai(ω) ≡ −1, Ai(ω)exp[ıω(t − xint/c)] + Ar(ω)exp[ıω(t + xint/c)] = 0, where xint is the location of the interface and Ar/i are the Fourier components of reflected and incident signal, respectively. Hence, the signal detected at the hydrophone in presence of reflections will have the form pph = pbubble(t) − pbubble(t + τdelay) where pbubble(t) is the actual bubble signature. In this conceptual model the free parameter is the time delay τdelay, related to the distance travelled by the reflected pressure wave. Using the reflection-free signal measured from the new set-up as pbubble(t), a best fit to the data of Fig. 3 provides τdelay = 190 ns. The fit (red solid line) reasonably matches the experimental data (grey symbols) in Fig. 3. Consistently, the estimated time delay is found to correspond to the distance the wave is expected to travel at the hydrogel sound speed (chydr = 2248 m s−1) from source to interface and back (see the scheme in Fig. 3), which is twice the hydrogel wall thickness (h ≃ 200 μm).
4.2 The resonant frequency and the attenuation time
In the following, we shall focus on the hydrogel-salt solution set-up. The three acoustic signals of Fig. 4, both in time- (left part) and frequency-domain (right part), are captured from bubbles nucleating in cavities with different size Lc ≃ 100, 50, 30 μm, respectively. They exhibit high amplitude oscillations with frequency in the range of MHz that are rapidly-damped within few cycles (see for comparison the data shown in ref. 36 concerning the bubble volume oscillations). During damping, the pressure may be described bypbubble(t) = P0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos(ω0t + ϕ)exp(−t/τ), cos(ω0t + ϕ)exp(−t/τ), | (16) |
 | (17) |
The fit of each data set using eqn (17) (see right part of Fig. 4) yields the estimate for the attenuation time τ and the resonant frequency f0 = ω0/(2π). The values found are then substituted in eqn (16) and the resulting curves are compared with the experimental time signals in Fig. 4. The same analysis is carried out for all the signals received by the hydrophone, leading to the characterisation of the resonant frequency and attenuation time as a function of the cavity volume Vc (see Fig. 5). In Fig. 5, the blue symbols denote the frequency f0 plotted versus the cavity effective radius  , the latter being measured by visualisation of the cavity just before bubble nucleation. As expected, the frequency increases with confinement. Indeed, a smaller cavity enhances the overall system rigidity, causing an increase in frequency. In the same figure the attenuation constant τ is plotted with red symbols. The bigger the liquid volume, the smaller the damping. The blue and red lines correspond to the theoretical curves for f0 and τ, respectively, that follow from the model described in Section 3. They are obtained by solving eqn (15) for the complex pulsation ω = ω0 + ı1/τ. We adopt the following values for the relevant parameters in the model: ρ0 = 994 kg m−3, c = 1484 m s−1, ρs = 1274 kg m−3, cs = 2248 m s−1.
, the latter being measured by visualisation of the cavity just before bubble nucleation. As expected, the frequency increases with confinement. Indeed, a smaller cavity enhances the overall system rigidity, causing an increase in frequency. In the same figure the attenuation constant τ is plotted with red symbols. The bigger the liquid volume, the smaller the damping. The blue and red lines correspond to the theoretical curves for f0 and τ, respectively, that follow from the model described in Section 3. They are obtained by solving eqn (15) for the complex pulsation ω = ω0 + ı1/τ. We adopt the following values for the relevant parameters in the model: ρ0 = 994 kg m−3, c = 1484 m s−1, ρs = 1274 kg m−3, cs = 2248 m s−1.
 | ||
Fig. 5 In blue: pressure wave frequency f0 emitted by the bubble as a function of the hydrogel cavity effective radius Reff. The blue squares indicate the experimental measurements while the blue lines represent the solution obtained through eqn (15): the solid curve with ![[small eta, Greek, tilde]](https://www.rsc.org/images/entities/char_e110.gif) s = 93 Pa s and Eadj, the dashed line with s = 93 Pa s and Eadj, the dashed line with ![[small eta, Greek, tilde]](https://www.rsc.org/images/entities/char_e110.gif) s = 108 Pa s and Emeas. In red: attenuation time τ as a function of the effective radius Reff. The symbols represent experimental points and the two curves, indistinguishable on the scale of the plot, are obtained by solving eqn (15). The frequency obtained with the original model proposed by Drysdale et al. is plotted in dotted black line. s = 108 Pa s and Emeas. In red: attenuation time τ as a function of the effective radius Reff. The symbols represent experimental points and the two curves, indistinguishable on the scale of the plot, are obtained by solving eqn (15). The frequency obtained with the original model proposed by Drysdale et al. is plotted in dotted black line. | ||
Eqn (15) is first solved using the Young modulus experimentally measured by performing tests on hydrogel samples with different geometries (Emeas = 1.4 GPa). The Lamé coefficients of the hydrogel are evaluated as λ = ρscs2 − 2μ with the shear modulus μ obtained by solving the relation Eμ/(9μ − 3E) = ρscs2 − 4μ/3. The hydrogel effective viscosity ![[small eta, Greek, tilde]](https://www.rsc.org/images/entities/char_e110.gif) s is treated as a free parameter to tune the theoretical model with the experimental results. By the least mean squares method, minimizing the error on the attenuation time, we found
s is treated as a free parameter to tune the theoretical model with the experimental results. By the least mean squares method, minimizing the error on the attenuation time, we found ![[small eta, Greek, tilde]](https://www.rsc.org/images/entities/char_e110.gif) s = 108 Pa s. Notwithstanding the strong assumption of spherical confinement, the theoretical curves of frequency and attenuation time obtained by such procedure can be made to accurately agree with the experimental results (dashed blue and red lines in the figure, with the red one perfectly superimposed to the corresponding red solid line, to be discussed below). Clearly the accuracy increases by increasing the flexibility of the model, i.e. leaving the hydrogel Young modulus as an additional free parameter. Assuming vanishing hydrogel viscosity,
s = 108 Pa s. Notwithstanding the strong assumption of spherical confinement, the theoretical curves of frequency and attenuation time obtained by such procedure can be made to accurately agree with the experimental results (dashed blue and red lines in the figure, with the red one perfectly superimposed to the corresponding red solid line, to be discussed below). Clearly the accuracy increases by increasing the flexibility of the model, i.e. leaving the hydrogel Young modulus as an additional free parameter. Assuming vanishing hydrogel viscosity, ![[small eta, Greek, tilde]](https://www.rsc.org/images/entities/char_e110.gif) s = 0, a least mean square fit of the frequency leads to Eadj = 1.61 GPa, within 10% of the measured value. If, on the other hand, the hydrogel viscosity is determined by also fitting the attenuation time, the optimal result is found to be
s = 0, a least mean square fit of the frequency leads to Eadj = 1.61 GPa, within 10% of the measured value. If, on the other hand, the hydrogel viscosity is determined by also fitting the attenuation time, the optimal result is found to be ![[small eta, Greek, tilde]](https://www.rsc.org/images/entities/char_e110.gif) s = 93 Pa s. The new curves, plotted in Fig. 5 with solid lines, exhibit indeed a better match with the experimental results. In particular the frequency overlaps the experimental data while the mismatch on the attenuation, significant for the smaller cavities, Reff ∼ 18 μm, still persists. Noteworthy, the improvement over the original model of Drysdale et al. due to the inclusion of the hydrogel viscous response is substantial.
s = 93 Pa s. The new curves, plotted in Fig. 5 with solid lines, exhibit indeed a better match with the experimental results. In particular the frequency overlaps the experimental data while the mismatch on the attenuation, significant for the smaller cavities, Reff ∼ 18 μm, still persists. Noteworthy, the improvement over the original model of Drysdale et al. due to the inclusion of the hydrogel viscous response is substantial.
5 Conclusions
In the context of a bubble appearing in a confined environment, we experimentally studied the emitted acoustic signal arising from its dynamics. The method proposed, based on the osmotic process, has several advantages. It allowed to dehydrate the hydrogel placing water within the cavity under tension. The negative pressure reached by water in the cavity can be easily set by tuning the solution molarity. We showed that for a 2.5 M calcium chloride solution, the liquid pressure pl is around −35 MPa and bubbles certainly appear. Moreover the cavitation threshold estimated is consistent with the one measured in a previous study28 for samples in contact with subsaturated air (pl = −22 MPa). Samples were employed several times, resisting cycles of dehydration in salt solution and hydration in water and yielding reproducible results. Once cavitation occurred in a hydrogel cavity, the detailed acoustic signature of a confined bubble was detected with high accuracy. Indeed, the impedance-mismatched boundaries (hydrogel/air), possible sources of acoustic perturbations, were replaced with well-matched interfaces (hydrogel/solution) resulting in an effective minimisation of acoustic reflections. The bubble resonant frequency is found to be of the order of MHz, in agreement with the volume oscillations frequency optically detected by O. Vincent et al. in ref. 36. The attenuation time, previously unavailable, was quantified, being of the order of a microsecond. Both acoustic parameters of the bubble acoustic emission were characterised as a function of the confinement volume. The proposed theoretical model quantitatively captures the experimental data. In particular, the embedding of visco-elastic effects in the description of the hydrogel motion was crucial to obtain the correct attenuation time of the acoustic emission thereby confirming the overall validity of the model. Submerging a tree xylem slice or a hydrogel bioinspired replica in a hypertonic solution, the phenomenon of embolism in trees could be followed detecting the true signal emitted by the bubble throughout all the steps of nucleation and possibly capturing other dynamic events optically observed with poor time and space resolution, i.e. bubble break-up, coalescence or penetration through pit membranes between adjacent vessels. Finally, the unprecedented time-resolved acoustic emissions we have characterised represent a fundamental preliminary study to understand the complex acoustic phenomena resulting from the interaction of bubbles placed in periodic poroelastic structures like fern sporangia. In principle, the device here conceived could also be used for the investigation of the physical properties of water under tension.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The research leading to these results has received funding from the European Research Council under the European Union's Seventh Framework Programme (FP7/2007-2013)/ERC Grant agreement no. [339446] and the Agence Nationale de la Recherche through a young researcher contract: “CAVISOFT, ANR-2010-JCJC-0407 01”.References
- D. Trevena, Contemp. Phys., 1967, 8, 185–195 CrossRef
.
-
P. G. Debenedetti, Metastable liquids: concepts and principles, Princeton University Press, 1996 Search PubMed
.
- R. E. Arndt, Annu. Rev. Fluid Mech., 1981, 13, 273–326 CrossRef
.
- A. Acosta and B. Parkin, J. Ship Res., 1975, 19, 193–205 Search PubMed
.
-
C. E. Brennen, Cavitation and bubble dynamics, Cambridge University Press, 2013 Search PubMed
.
- W. Lauterborn and H. Bolle, J. Fluid Mech., 1975, 72, 391–399 CrossRef
.
- A. J. Coleman, J. E. Saunders, L. A. Crum and M. Dyson, Ultrasound Med. Biol., 1987, 13, 69–76 CrossRef PubMed
.
- G. Ter Haar, Prog. Biophys. Mol. Biol., 2007, 93, 111–129 CrossRef PubMed
.
- P. R. Gogate and A. M. Kabadi, Biochem. Eng. J., 2009, 44, 60–72 CrossRef
.
- C. C. Coussios and R. A. Roy, Annu. Rev. Fluid Mech., 2008, 40, 395–420 CrossRef
.
- T. Mason, E. Joyce, S. Phull and J. Lorimer, Ultrason. Sonochem., 2003, 10, 319–323 CrossRef PubMed
.
- V. Saez, A. Fras-Ferrer, J. Iniesta, J. González-Garca, A. Aldaz and E. Riera, Ultrason. Sonochem., 2005, 12, 59–65 CrossRef PubMed
.
- O. Vincent, P. Marmottant, P. A. Quinto-Su and C.-D. Ohl, Phys. Rev. Lett., 2012, 108, 184502 CrossRef PubMed
.
- M. Berthelot, Ann. Chim. Phys., 1850, 30, 232–237 Search PubMed
.
- O. Renner, Jahrb. Wiss. Bot., 1915, 56, 647 Search PubMed
.
- A. Ursprung, Ber. Dtsch. Bot. Ges., 1915, 33, 153 Search PubMed
.
-
M. T. Tyree and M. H. Zimmermann, Xylem structure and the ascent of sap, Springer Science & Business Media, 2013 Search PubMed
.
- J. A. Milburn and R. Johnson, Planta, 1966, 69, 43–52 CrossRef PubMed
.
- M. T. Tyree and J. S. Sperry, Annu. Rev. Plant Biol., 1989, 40, 19–36 CrossRef
.
- J. A. Milburn, Planta, 1973, 112, 333–342 CrossRef PubMed
.
- D. M. Johnson, F. C. Meinzer, D. R. Woodruff and K. A. McCulloh, Plant, Cell Environ., 2009, 32, 828–836 CrossRef PubMed
.
- S. Rosner, A. Klein, R. Wimmer and B. Karlsson, New Phytol., 2006, 171, 105–116 CrossRef PubMed
.
- M. T. Tyree and M. A. Dixon, Plant Physiol., 1983, 72, 1094–1099 CrossRef PubMed
.
- X. Noblin, N. Rojas, J. Westbrook, C. Llorens, M. Argentina and J. Dumais, Science, 2012, 335, 1322 CrossRef PubMed
.
- C. Llorens, M. Argentina, N. Rojas, J. Westbrook, J. Dumais and X. Noblin, J. R. Soc., Interface, 2016, 13, 20150930 CrossRef PubMed
.
- K. Ritman and J. A. Milburn, J. Exp. Bot., 1990, 41, 1157–1160 CrossRef
.
- T. D. Wheeler and A. D. Stroock, Nature, 2008, 455, 208–212 CrossRef PubMed
.
- T. D. Wheeler and A. D. Stroock, Langmuir, 2009, 25, 7609–7622 CrossRef PubMed
.
- A. Ponomarenko, O. Vincent, A. Pietriga, H. Cochard, E. Badel and P. Marmottant, J. R. Soc., Interface, 2014, 11, 20140480 CrossRef PubMed
.
- C. Drysdale, A. A. Doinikov and P. Marmottant, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2017, 95, 053104 CrossRef PubMed
.
- A. D. Stroock, V. V. Pagay, M. A. Zwieniecki and N. Michele Holbrook, Annu. Rev. Fluid Mech., 2014, 46, 615–642 CrossRef
.
- C. S. Effenhauser, H. Harttig and P. Krämer, Biomed. Microdevices, 2002, 4, 27–32 CrossRef
.
- Y.-X. Guan, Z.-R. Xu, J. Dai and Z.-L. Fang, Talanta, 2006, 68, 1384–1389 CrossRef PubMed
.
- Z.-R. Xu, C.-H. Zhong, Y.-X. Guan, X.-W. Chen, J.-H. Wang and Z.-L. Fang, Lab Chip, 2008, 8, 1658–1663 RSC
.
-
J. A. Milburn, et al., Water flow in plants, Longman Inc., 1979 Search PubMed
.
- O. Vincent, P. Marmottant, S. R. Gonzalez-Avila, K. Ando and C.-D. Ohl, Soft Matter, 2014, 10, 1455–1461 RSC
.
- S. R. De Groot and P. Mazur, Non-equilibrium thermodynamics, Courier Corporation, 2013.
- M. E. M. Azouzi, C. Ramboz, J.-F. Lenain and F. Caupin, Nat. Phys., 2013, 9, 38–41 Search PubMed
.
- O. Vincent and P. Marmottant, J. Fluid Mech., 2017, 827, 194–224 Search PubMed
.
- A. Barzkar and H. Adibi, Math. Probl. Eng., 2015, 789238 Search PubMed
.
| This journal is © The Royal Society of Chemistry 2018 |


