 Open Access Article
Open Access ArticleThermal processing of thermogelling nanoemulsions as a route to tune material properties†
Li-Chiun
Cheng
 ,
P. Douglas
Godfrin
,
P. Douglas
Godfrin
 ,
James W.
Swan
,
James W.
Swan
 and
Patrick S.
Doyle
and
Patrick S.
Doyle
 *
*
Department of Chemical Engineering, Massachusetts Institute of Technology, Cambridge, MA 02139, USA. E-mail: pdoyle@mit.edu
First published on 20th June 2018
Abstract
Many soft matter systems have properties which depend on their processing history. It is generally accepted that material properties can be finely tuned by carefully directing self-assembly. However, for gelling colloidal systems, it is difficult to characterize such path-dependent effects since the colloidal attraction is often provided by adding another component to the system such as salts or depletants. Therefore, studies of and an understanding of the role of processing on the material properties of attractive colloidal systems are largely lacking. In this work, we systematically studied how processing greatly influences the properties and the microstructures of model attractive colloidal systems. We perform experiments using a thermogelling nanoemulsion as a model system where the isotropic attraction can be precisely tuned via the temperature. The effects of processing conditions on gel formation and properties is tested by performing well-designed sequential temperature jumps. By properly controlling the thermal history, we demonstrate that properties of colloidal gels can be beyond the limit set by direct quenching, which has been a major focus in literature, and that otherwise slow aging of the system associated with a decrease in elasticity can be prevented. Our results provide new experimental evidence of path-dependent rheology and associated microstructures in attractive colloidal systems and provide guidance to future applications in manufacturing complex colloid-based materials.
Introduction
Properties of many materials are affected by how they are processed. Perhaps the oldest and most common example is metal forging: after the metal is shaped into the desired geometry, it is subsequently heated and maintained at an elevated temperature, and then cooled (quenched) to achieve the final state. This intermediate step, known as thermal annealing, allows the metallic atoms to relocate themselves and form specific microstructures. By manipulating time and temperature, annealing can effectively alter mechanical properties of the metallic materials, such as ductility and toughness.1,2 Such thermal treatments can be also used in glasses or ceramic materials to remove internal stresses and prevent material failure.1 In modern technology, thermal annealing is also important in semiconductor manufacturing. Thermal treatment significantly improves the electric,3 optical,4,5 magnetic6 and mechanical properties.7 Annealing can be also applied to graphene-based materials to improve mechanical strength and electric conductivity due to improved atomic ordering.8In addition to hard condensed matter, (thermal) processing can also be applied to soft matter. Kim et al. found that poly(isoprene)-b-poly(lactide) copolymer melts can form aperiodic quasicrystalline states that are commonly found in metal alloys.9 By rapidly quenching the copolymer melt from the disordered state using liquid nitrogen, then reheating it to T < TODT (where TODT is the order–disorder transition temperature), the self-assembled polymer micelles can form hexagonal C14 and cubic C15 Laves phases. She et al. studied the self-assembly of polystyrene-b-poly(L-lactide) copolymer thin films grafted on silicon wafers.10 By thermally annealing the polymer film, large-scale perpendicular cylinder structures could be obtained. Moreover, such alignment of block copolymer films can also be controlled via an electric field. Olszowka et al. applied an in-plane electric field to process a triblock copolymer thin film composed of polystyrene-b-poly(2-hydroxyethyl methacrylate)-b-poly(methyl methacrylate) copolymer.11 A highly ordered stripe pattern perpendicular to the film plane could be achieved. Lu et al. studied how thermal processing controls polyamide 66/clay nanocomposite crystals.12 By carefully controlling the thermal history (melt, slow cooling, annealing), high crystallinity could be obtained.
There have been relatively few experimental studies examining how processing via temporal modulation of inter-particle interactions affects the material properties of gelling colloidal suspensions. A promising approach is to use electric13 and magnetic fields14,15 to direct self-assembly. In such systems, the external fields induce polarization that results in anisotropic inter-particle dipole–dipole interactions. The advantage of using such fields is that the interaction can be temporally modulated and is reversible, such that annealing strategies (e.g. AC electric fields or toggled magnetic fields) can be implemented to achieve equilibrium crystalline structures. However, the induced dipole–dipole interaction scales with the particle volume and becomes weak when the particles approach the nanoscale.16 Wagner and coworkers studied the properties of octadecyl-coated silica nanoparticles (which gel when the system is cooled) subject to different thermal histories.17,18 However, they found the rheological response of the system was independent of its thermal history. Sherman et al. employed simulations to study the self-assembly of nanoparticles under a toggled depletion attraction.19,20 Interestingly, by using time-dependent, periodically toggled attractions, particles could self-assemble into well-ordered crystalline structures without kinetic trapping in a disordered state. However, it is difficult to experimentally implement time varying colloidal interactions in gelling systems which rely on the addition of a third component (such as depletants or salts) as a means to vary inter-particle interactions. Recently, our group has developed a thermally gelling oil-in-water nanoemulsion consisting of surfactant stabilized, nano-sized polydimethylsiloxane droplets suspended in a poly(ethylene glycol)diacrylate (PEGDA) aqueous continuous phase.21 At elevated temperatures, the hydrophobic end groups of the PEGDA partition into the oil/water interface and bridge droplets, which results in isotropic attractive interactions that can be temporally tuned “at will” without adding another component. Initial work22 has shown that different heating rates result in different rheological responses, though thermal processing as a means to tune microstructure and mechanics has not been studied. We have also developed a technique that enables us to directly visualize the gel microstructure at any state using confocal microscopy,22–24 allowing us to study how processing controls the gel structures. Additionally, the major changes in the macroscopic (rheological) properties and microstructure of the nanoemulsion can be captured within ΔT = 30 to 40 °C (from room temperature to T = 50–60 °C).24,25 Such advantages make this nanoemulsion a suitable model system to understand how thermal processing affects the behavior of colloidal gels with quantifiable experimental evidence.
In this work, we experimentally investigate sequential thermal processing of thermogelling nanoemulsions as a means to control material properties. We use rheological properties and real-space microstructural correlations as our canonical metrics to characterize the material behaviors. By changing thermal processing routes, we show that properties of colloidal gels can be beyond the limit set by direct quenching. For example, under certain thermal processing conditions, the gel strength of the nanoemulsion can increase by 47% compared to a step-jump in temperature, and the thermal processing can effectively prevent a decrease in gel strength due to slow relaxation resulting from directly quenching the system at high temperatures. The path-dependent properties of our attractive colloidal systems motivate the concept that one should think beyond just varying chemical composition as a means to control material properties and should expand to consider processing as an equally important parameter. Indeed, several works have shown that even a single material system shows diverse structures and complex properties by carefully directing the self-assembly.26–28 In addition to being model colloidal systems, nanoemulsions are widely used in applications such as food products, cosmetics, pharmaceuticals, and enhanced oil recovery for which the ability to engineer material properties through processing conditions is desirable.29
Results and discussions
Thermally responsive nanoemulsions
Self-assembly of the nano-sized polydimethylsiloxane (PDMS) droplets is driven by molecular-scale poly(ethylene glycol)diacrylate (PEGDA) bridging at elevated temperatures, as shown in Fig. 1a. The oil-in-water nanoemulsions were prepared using high-pressure homogenization, which allows easy preparation of large quantities of emulsions with a range of droplet sizes (Fig. S1, ESI†). The canonical nanoemulsion formulation used in this work contains PDMS droplets (droplet diameter 2a = 37 nm) of volume fraction = 0.15 suspended in the aqueous continuous phase consisting of PEGDA of volume fraction 0.33 and sodium dodecyl sulfate (SDS) of concentration 0.175 M. For this formulation, the changes in rheology and microstructure of the nanoemulsion throughout the gelation process can be captured within ΔT = 30 °C (Fig. 1c and d, from T = 20.0 to 50.0 °C).At room temperature (20.0 °C), the droplets are well dispersed in the continuous phase due to the electrostatic repulsion provided by SDS on the droplet surface and small Peclet number (Pe = πD4Δρg/12kBT ∼ 10−7, where D is the droplet diameter, Δρ is the density difference between the oil and continuous phase, g is gravitational acceleration, kB is the Boltzmann constant and T is absolute temperature) of the nano-sized droplets.29 Accordingly, the nanoemulsion has a liquid-like behavior, which can been seen from direct observation (Fig. 1b) and the rheological response (Fig. 1c). As temperature rises, the hydrophobic end groups of PEGDA partition into the oil/water interface and form inter-droplet bridging. The gelation results in the increase of viscoelastic moduli (Fig. 1c), and ultimately gives a sample-spanning gel network and solid-like behavior of the sample.
One-step temperature jump rheology
We first investigated the sample with a single temperature jump (from T = 20.0 °C to a higher temperature). The one-step temperature jump can be viewed as directly quenching the nanoemulsion to a certain state, which is analogous to the formation of depletion gels by addition of small molecule depletants into a colloidal suspension. Although this simple quenching mechanism (i.e. one-step temperature jump) has been studied in our prior work,22,24 we will describe new insights in the following section which will guide our subsequent thermal processing.Fig. 1c shows the results of small amplitude oscillatory shear (SAOS) rheological responses of the nanoemulsion at various temperatures throughout gelation from T = 20.0 to 50.0 °C. The figure records the measurements just after the samples reach the target temperature (see Fig. S2, ESI† for complete response including the initial temperature increasing stage). The length of measurement was chosen to be 20 minutes which is long enough to capture the major changes in rheology and microstructure at the selected temperatures (Fig. 1c and d). At T = 20 °C, both moduli remain nearly constant and the loss modulus G′′ (measuring viscous dissipation) is larger than storage modulus G′ (measuring elasticity) throughout the measurement. This liquid-like behavior holds when the temperature is increased up to 30.0 °C (Fig. S2, ESI†).
The moduli significantly increase when the temperature is raised to 32.5 °C. As time proceeds, G′ ≈ G′′ and both moduli continue growing throughout the measurement. The frequency sweep measurement further confirms T = 32.5 °C is the gelation temperature where G′(ω) and G′′(ω) are parallel on the frequency spectrum (after the sample is held at 32.5 °C for 10 min, Fig. S3, ESI†), according to the classic Chambon–Winter criterion.30,31 When further increasing the temperature, the moduli grow dramatically with G′ > G′′ by over one order of magnitude. At T = 40.0 °C, the elastic modulus G′ is larger than that at T = 32.5 °C by nearly two orders of magnitude, though G′ and G′′ continue to increase in time. Fig. S4 (ESI†) shows a long-time characterization (up to 50 min) at 32.5 °C where changes in microstructures and the rheological response can be easily observed. The result shows the gelled system will eventually reach a pseudo-steady state as time proceeds. Above T = 40 °C, the moduli reach a plateau, and the increase in the moduli with respect to temperature is limited (Fig. S3, ESI†). At such high temperatures, G′ and G′′ are nearly constant on the frequency spectrum (Fig. S3, ESI†).
Hierarchal microstructures
We captured high-resolution images of nanoemulsion microstructures at various states using confocal microscopy. We labeled the oil droplets with a red, lipophilic dye (PKH26). Crosslinking the PEGDA in the continuous phase locks the self-assembled droplets in place at various states, and allows us to directly visualize the internal structures of the nanoemulsion gel at room temperature. Previous work has shown that the addition of small amounts of these chemicals has negligible influence on the nanoemulsion rheology and microstructure.22 Readers interested in investigation of the fractal dimensions are referred to previous work by our group.25Fig. 1d shows the microstructures at different temperatures and various times, t. The times were chosen to be 2, 5, 10 and 20 minutes in order to capture the major rheological changes. Interestingly, at T = 32.5 °C large strands coexist with clusters (see Fig. S2, ESI† for the discussion that these clusters are not stress-bearing structures). As time proceeds, strands increase in number and size, and fewer clusters are present (see Fig. S4, ESI† for long-time characterization). These microstructural trends are consistent with the rheology in Fig. 1c, where G′ and G′′ increase in time, since the larger strands are believed to be responsible for the viscoelastic response.24
In order to quantitatively study the microstructures in Fig. 1d, we measured correlation lengths from scattering plots. The raw confocal images were first processed via fast Fourier transform (FFT) using image processing software ImageJ. We then calculated the radially averaged light intensity, I(q), of the FFT images, where q is the wave vector (see Fig. S5, ESI† for an example of extracting correlation length).23,32 A representative scattering spectrum is shown in Fig. 2a. We can define three correlation lengths (LC = 2π/q) at T = 32.5 °C: primary correlation length (LC,1) from the primary peak, secondary correlation length (LC,2) from the secondary peak and tertiary correlation length (LC,3) from the inflection point. The calculated results are listed in Table 1.
| Temperature (°C) | Time (min) | G′ (Pa) | L C,1 (μm) | L C,2 (μm) | L C,3 (μm) |
|---|---|---|---|---|---|
| 32.5 | 2 | 0.635 | 23.3 ± 10.1 | 1.38 ± 0.07 | 1.15 ± 0.05 |
| 5 | 0.895 | 15.9 ± 11.6 | 1.46 ± 0.08 | 1.17 ± 0.09 | |
| 10 | 1.628 | 8.49 ± 2.01 | 1.71 ± 0.12 | 1.18 ± 0.04 | |
| 20 | 3.254 | 6.42 ± 1.80 | 1.86 ± 0.11 | 1.17 ± 0.05 | |
| 40.0 | 2 | 151.9 | 3.90 ± 0.24 | — | 1.10 ± 0.11 |
| 5 | 192.2 | 3.88 ± 0.47 | — | 1.01 ± 0.06 | |
| 10 | 216.8 | 3.32 ± 0.19 | — | 0.87 ± 0.05 | |
| 20 | 258.9 | 3.34 ± 0.15 | — | 0.86 ± 0.03 | |
| 50.0 | 2 | 445.3 | 2.30 ± 0.14 | — | 0.64 ± 0.03 |
| 5 | 463.4 | 2.42 ± 0.21 | — | 0.63 ± 0.01 | |
| 10 | 461.4 | 2.50 ± 0.19 | — | 0.65 ± 0.01 | |
| 20 | 428.8 | 2.44 ± 0.10 | — | 0.73 ± 0.03 | |
The physical meaning of three correlation lengths is elucidated in Fig. 2b–d. LC,1 extracted from the strongest scattering intensity corresponds to the averaged distance of the droplet-rich domains separated by the droplet-poor domains, shown as Fig. 2b. This primary correlation length (calculated as 2π/qmax, where qmax is the wave vector corresponding to the strongest intensity) has been investigated in previous work.22,33 On the other hand, LC,2 and LC,3 have not been reported before. LC,2 corresponds to the correlation length of the clusters suspended in the continuous phase, as shown in the Fig. 2c, which is further confirmed by calculating the LC of cropped images where only the freely suspended clusters are considered (Fig. S6, ESI†). Therefore, it is not surprising that LC,2 is absent at T = 40.0 and 50.0 °C since no coexisting clusters are observed (Fig. 1d). The tertiary correlation length (LC,3) is at a smaller length scale (i.e. larger q), suggesting a ‘secondary’ structure inside the droplet-rich domains, as represented in Fig. 2d. This is also validated by analyzing the intensity profile just within the droplet-rich domain shown in Fig. S6 (ESI†).
These secondary length scales (LC,1 and LC,3) are a manifestation of a hierarchical structure (see Fig. S7, ESI† for two-stage yielding which also suggests a hierarchical network), which was not analyzed in our earlier publication. Such hierarchy has been found in a depletion gel by Lu et al.34 where they found that after introducing depletants into a colloidal suspension, the colloids first form clusters, then form a spanning gel network, which is then arrested. Moreover, Schurtenberger and coworkers also found ‘multiple steps’ in depletion gel formation using simulations and showed that the higher order gel structures are built on ‘meta-particles’ composed of few particles.35 Interestingly, in their work, a scattering spectrum showing multi-stages was also reported, similar to Fig. 2a in this work.
At T = 32.5 °C, LC,3 remains nearly constant as time proceeds as shown in Table 1, and LC,3 ≈ 1.17 μm is consistent with the micron-sized clusters seen in Fig. 1d and Fig. S6a (ESI†). Additionally, at later times, more and thicker strands are formed while fewer freely suspended clusters are present (see Fig. S8, ESI† for the changes in the scattered intensity spectrum). Therefore, it is reasonable to postulate that the strands are formed from the aggregation of clusters (as supported by data in Fig. S4, ESI†), which is consistent with what has been described in the literature for other systems.34–36 The proposed mechanism is shown in Fig. 2e. Upon increasing the temperature, droplets aggregate and form clusters, and the clusters serve as ‘building blocks’ which then self-assemble and span the macroscopic sample. The decrease in LC,1 correlates with an increase in strands as time proceeds. As reported in Table 1, at T = 32.5 °C LC,1 decreases with time, which is consistent with the qualitative observation in Fig. 1d where the strands increase in number.
At T = 40.0 and 50.0 °C, we were not able to capture the aggregation of such building blocks since the assembly dynamics are faster at these higher temperatures. However, we can still observe changes in LC,3. At T = 50 °C, LC,3 remains constant for the first 10 min, and the sample maintains a nearly constant elastic modulus. The decreasing G′ and increasing LC,3 at longer times will be discussed in detail in the next section and compared with the thermally processed samples. At T = 40 °C, LC,3 decreases as time proceeds, which suggests the clusters still can re-assemble themselves even after they aggregate into a network. This reconstruction is reasonable because the characteristic diffusion time for 1 μm clusters is roughly 5 seconds, which suggests rearrangement over the rheological timescale is likely even after the bridging is formed. At such moderate temperature, the attraction is also weak enough not to induce strong dynamical arrest, such as what is seen at T = 50 °C.
Two-step thermal processing
The thermal processing demonstration in this work was conducted at T = 32.5, 40.0 and 50.0 °C. After the pre-shear (conditioning step) at T = 20.0 °C, the sample was first brought to T1 = 32.5 or 40.0 °C. After holding at T1 for thold = 2, 5 or 10 min, the temperature was then jumped to T2 = 40.0 or 50.0 °C. Therefore, a total of nine processing histories were explored: three sets of progressive temperature jumps (T1 to T2: 32.5 to 40.0 °C, 32.5 to 50.0 °C and 40.0 to 50.0 °C) with three different thold at each corresponding T1. The total measurement time was kept constant at 20 min for consistency with the one-step temperature jump experiments.Fig. 3 shows the results of the rheological responses of the thermally processed samples (see Fig. S9, ESI† for the temperature history). Both moduli, G′ and G′′, show the same trend under thermal processing, and only G′ is plotted here for discussion (G′′ can be found in Fig. S10, ESI†). The results from the one-step temperature jump are also plotted for comparison. Fig. 3a shows the rheology of thermal processing between T = 32.5 to 40.0 °C. Comparing with one-step jump at T = 40.0 °C, holding at 32.5 °C hinders the development of the gel strength, and a smaller modulus is obtained when remaining at 32.5 °C longer. Additionally, similar to the one-step jump at T = 40.0 °C, the moduli of processed samples are still increasing at the end of the measurement, suggesting that the gel is not fully arrested. The shape and the trend of the curves suggest the possibility of a master curve by rescaling the time. The rescaled data is shown in Fig. 3b, in which time has been rescaled to be zero when the temperature reaches T2. All processed samples collapse onto a master curve, suggesting the microstructures are self-similar, while the one-step jump sample is slightly above the master curve.
 | ||
| Fig. 3 Temporal elastic modulus, G′, of the nanoemulsion undergoing two-step temperature jump with (a) to (b) 32.5 to 40.0 °C, (c) to (d) 32.5 to 50.0 °C and (e) to (f) 40.0 to 50.0 °C. (a, c and e) Record the raw measurements. (b, d and f) Plot the G′ versus rescaled time. Rescaled time is equal to t − thold − tramp where tramp is the time needed for the temperature to adjust from T1 to T2 (limited by the Peltier plate). Typical values of tramp are 45–55 seconds (see Fig. S6, ESI† for details). | ||
To investigate the microstructure of the processed sample as well as the structural self-similarity, we also performed confocal microscopy to visualize the microstructures. We used the Peltier plate equipped on the rheometer to make sure the imaging samples underwent exactly the same temperature history as the samples used for rheological measurements. We then focused on the microstructures after the thermal processing was complete (i.e. the microstructures at t = 20 min). The imaging results and the corresponding analyses for all thermal processed samples are shown in Fig. 4 and Table 2, respectively. The elastic moduli are also listed in Fig. 4. For convenience in later discussion, the correlation length of a one-step jump to temperature T will be denoted as LTC.
| Temperature (°C) | t hold (min) | G′ (Pa) | L C,1 (μm) | L C,2 (μm) | L C,3 (μm) |
|---|---|---|---|---|---|
| 32.5 to 40.0 | 2 | 240.1 | 5.46 ± 0.61 | 1.48 ± 0.06 | 0.97 ± 0.04 |
| 5 | 214.7 | 5.19 ± 0.50 | 1.41 ± 0.10 | 0.97 ± 0.04 | |
| 10 | 195.5 | 5.17 ± 0.52 | 1.53 ± 0.07 | 1.00 ± 0.05 | |
| 32.5 to 50.0 | 2 | 470.6 | 5.42 ± 0.68 | 1.41 ± 0.10 | 0.85 ± 0.02 |
| 5 | 474.4 | 5.65 ± 0.92 | 1.40 ± 0.09 | 0.84 ± 0.02 | |
| 10 | 485.5 | 5.64 ± 0.61 | 1.45 ± 0.06 | 0.88 ± 0.05 | |
| 40.0 to 50.0 | 2 | 610.4 | 3.06 ± 0.18 | — | 0.79 ± 0.04 |
| 5 | 660.8 | 3.01 ± 0.21 | — | 0.77 ± 0.01 | |
| 10 | 662.3 | 3.08 ± 0.34 | — | 0.72 ± 0.02 | |
Fig. 4a–c show the microstructures of the processed samples from T = 32.5 to 40.0 °C with different holding times. Surprisingly, the microstructures are significantly different from both nanoemulsions with direct holding at T = 32.5 °C and T = 40.0 °C. For the processed samples, the internal structures fall between T = 32.5 °C and T = 40.0 °C, which is further confirmed by the LC,1 of the processed sample, which falls between L32.5C,1 and L40.0C,1, and a similar trend for LC,3. On the other hand, comparing amongst the thermally processed samples, LC,1 slightly decreases with longer holding time (but this change is insignificant if the standard deviation is considered), and LC,3 remains nearly constant. The nearly unchanged LC,1 and LC,3 suggest the difference in final moduli (after 20 min) after different holding times might result from either a smaller length scale that cannot be clearly resolved in our current microscopy setup (due to the resolution limit) or the number density of gel strands formed by residual clusters in solution (that is difficult to quantify from individual microscopy images). However, the self-similar structures of the samples explain the superposition behavior in Fig. 3b.
Interestingly, here we also observed an additional inflection point from the intensity spectrum, similar to the secondary peak in the one-step temperature jump at T = 32.5 °C. The LC,2 in the processed samples results from the microstructure associated with finer, cluster-like structures, as highlighted in the inset of Fig. 4e. We believe this smaller structure is a remnant of the freely suspended clusters from 32.5 °C, which can be found in the processed samples jumping from T = 32.5 to 40.0 °C and T = 32.5 to 50.0 °C, while no signal is found for T = 40.0 to 50.0 °C. Note that even though there are only two correlation lengths that can be determined from processed samples from T = 40.0 to 50 °C, we still use LC,1 and LC,3 for consistency with other samples.
Fig. 3c shows the rheological response of the processed samples from T = 32.5 to 50.0 °C. Interestingly, the processed samples possess similar moduli as the sample with one-step temperature jump at T = 50.0 °C, while they have significantly different microstructures, as shown in Fig. 4d–f and Table 2. Again, the processed samples show intermediate values of LC,1 and LC,3 (i.e.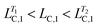 and
and 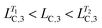 ), and the moduli collapse onto a master curve shown in Fig. 3d. By comparing among the processed samples, LC,1 and LC,3 still remain nearly constant, and the moduli are also relatively insensitive to the holding time, as observed when processing from T = 32.5 to 40.0 °C. The relative insensitivity is reasonable since a stronger attraction is induced at T = 50.0 °C, where the structure is dynamically arrested. Readers interested in an estimation of attractive potential energy are referred to the previous work by our group.21 This stronger attraction can be also qualitatively observed in Fig. 4 where the cluster associated microstructures (LC,2, signifying the remanence of the clusters from 32.5 °C) can be more easily seen in the T = 32.5 to 50.0 °C sample due to dynamic arrest, compared to the T = 32.5 to 40.0 °C. Additionally, by observing LC,3 (manifestation of the aggregated cluster with the droplet-rich domains), LC,3 of the T = 32.5 to 50.0 °C sample is smaller than that of T = 32.5 to 40.0 °C. Indeed, LC,3 is gradually reduced from the one-step jump at 32.5 °C (LC,3 ≈ 1.2 μm) to the two-step jump (LC,3 ≈ 1.0 μm for 32.5 to 40.0 °C and LC,3 ≈ 0.85 μm for 32.5 to 50.0 °C). The decrease in LC,3 suggests the aggregated clusters become tighter during the temperature jump.
), and the moduli collapse onto a master curve shown in Fig. 3d. By comparing among the processed samples, LC,1 and LC,3 still remain nearly constant, and the moduli are also relatively insensitive to the holding time, as observed when processing from T = 32.5 to 40.0 °C. The relative insensitivity is reasonable since a stronger attraction is induced at T = 50.0 °C, where the structure is dynamically arrested. Readers interested in an estimation of attractive potential energy are referred to the previous work by our group.21 This stronger attraction can be also qualitatively observed in Fig. 4 where the cluster associated microstructures (LC,2, signifying the remanence of the clusters from 32.5 °C) can be more easily seen in the T = 32.5 to 50.0 °C sample due to dynamic arrest, compared to the T = 32.5 to 40.0 °C. Additionally, by observing LC,3 (manifestation of the aggregated cluster with the droplet-rich domains), LC,3 of the T = 32.5 to 50.0 °C sample is smaller than that of T = 32.5 to 40.0 °C. Indeed, LC,3 is gradually reduced from the one-step jump at 32.5 °C (LC,3 ≈ 1.2 μm) to the two-step jump (LC,3 ≈ 1.0 μm for 32.5 to 40.0 °C and LC,3 ≈ 0.85 μm for 32.5 to 50.0 °C). The decrease in LC,3 suggests the aggregated clusters become tighter during the temperature jump.
Fig. 3e shows the rheological response of the processed samples from T = 40.0 to 50.0 °C. Interestingly, the modulus can be increased by 36 to 47%, depending on the holding time. The processed samples again have intermediate values of LC,1 and LC,3 (i.e.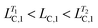 and
and  ), while LC,2 is absent since there are no freely suspended clusters at T = 40.0 °C. However, from Table 2, G′ with thold = 2 min is unexpectedly smaller than G′ with thold = 5 and 10 min, since LC,1 and LC,3 remain nearly constant across different holding times. This difference in G′ is reproducible when repeating the measurement (Fig. S11, ESI†). We hypothesize the difference in moduli might result from a smaller length scale that cannot be captured in our current microscopy setup. However, despite the slight difference, the processed samples do show the same trend that G′ is larger than that of the one-step jump sample at T = 50.0 °C.
), while LC,2 is absent since there are no freely suspended clusters at T = 40.0 °C. However, from Table 2, G′ with thold = 2 min is unexpectedly smaller than G′ with thold = 5 and 10 min, since LC,1 and LC,3 remain nearly constant across different holding times. This difference in G′ is reproducible when repeating the measurement (Fig. S11, ESI†). We hypothesize the difference in moduli might result from a smaller length scale that cannot be captured in our current microscopy setup. However, despite the slight difference, the processed samples do show the same trend that G′ is larger than that of the one-step jump sample at T = 50.0 °C.
In addition to the increase in moduli (see Fig. S10 for G′′, ESI†), we also note that thermal processing can prevent the gel from aging, which can be seen for the one-step jump to T = 50.0 °C. As shown in Fig. 3e, G′ starts to decrease after t ≈ 10 min (black dots). We hypothesize that such aging is due to a slow structural relaxation because the nanoemulsion is directly and deeply quenched to a non-equilibrium state.37 This age-dependent viscoelasticity associated with an internal stress relaxation in out-of-equilibrium systems has also been observed in depletion gels38 and actin/fascin bundle networks.39 To test our hypothesis, we performed a SAOS + LAOS measurement. If the relaxation is responsible for aging and the associated decrease in G′, yielding (by using LAOS) the gel should facilitate such relaxation and achieve the same final state. The results are shown in Fig. 5. The blue data shows the aging behavior of the nanoemulsion gel and the modulus eventually reached a plateau after ≈6000 s using only SAOS. On the other hand, in the black data we used LAOS to yield the gel for 30 s at t = 600 s and the modulus still reached the same plateau as seen in the long time SAOS experiment, but the entire process only took ≈1000 s. It thus takes approximately one-sixth the amount of time for the measurement with yielding to reach the final state. Additionally, similar to T = 40.0 to 50.0 °C processing (Fig. 3e), the samples processed from T = 32.5 to 50.0 °C also show that the decrease in G′ can be effectively reduced by thermal processing, which is highlighted by the inset in Fig. 5 (this is not easily observed in Fig. 3c due to the scale of the y-axis).
 | ||
| Fig. 5 Temporal decrease in G′ due to the slow relaxation when the nanoemulsion is directly quenched at T = 50.0 °C (blue). Yielding the nanoemulsion can effectively reduce the time needed to reach the final state (black). The yielding step is performed using LAOS with a strain = 15% at a frequency = 20 rad s−1. Inset plot highlights the thermal processing sample from T = 32.5 to 50.0 °C (which is difficult to notice in Fig. 3 due to the scale of the y-axis) can also prevent the decrease in modulus as processing from T = 40.0 to 50.0 °C. | ||
Fig. 6 summarizes how the gel strength (G′) and the microstructure (LC,1) can be controlled via thermal processing. The black dots are the results of the traditional direct quenching (single temperature jump) of the nanoemulsion gel—G′ increases as LC,1 decreases. This inverse relation of G′ to LC,1 has been reported in prior studies.33,40 On the other hand, with more complex thermal processing, properties beyond the limit set by direct quenching (indicated by the black dashed line) can be accessed. For example, with two-step processing we can maintain the same gel strength (e.g. G′ ≈ 450 Pa), but create much more open microstructures (more than doubling of LC,1 to ≈5.5 μm). We can also have gels with the same LC,1 (≈ 5.5 μm) but with different G′ (≈200 to 480 Pa). Additionally, two-step thermal processing can increase the gel strength beyond that attainable by directly quenching the system with a strong attraction potential. Overall, we find that thermal processing allows us to access states above the dashed line depicted for the one-step temperature jumps.
The properties of the nanoemulsion gels are highly dependent on how they reach the final state, even though the same final temperature is reached. The gels have significantly different rheology and microstructures depending on their thermal history, and these properties can be beyond the limit set by direct quenching, which has been a major focus in literature. We postulate that when undergoing thermal processing from T1 to T2, the system has a memory of the structures at T1 and reconstructs these intermediate structures when switched to T2. This postulate is consistent with the observation that the cluster-associated structures (LC,2) are found in processed samples from T = 32.5 to 40.0 °C and from T = 32.5 to 50.0 °C, which indicates the remanence of the clusters from 32.5 °C. A holding step at T1 seems to be similar to thermal annealing. Thermal annealing is often used as an additional step in material manufacturing processes that allows a system to reach the global free energy minimum without being kinetically trapped. It is therefore often used in order to create a regular order on a molecular scale and to improve and control the macroscopic properties.1 However, contrary to the results of thermal annealing, colloidal gel systems are often associated with a kinetically arrested disordered state, such as percolation18 or spinodal decomposition,34 whereas the global energy minimum corresponds to the bulk phase separation.29,41 Moreover, our thermal processing results are relatively insensitive to the length of time holding at T1, and the thermal processing does not facilitate a regular pattern of colloidal order. Both behaviors are contrary to what has been reported in the literature, where the properties of the material are strongly dependent on the annealing time.10,11 Future work using simulations will help elucidate the mechanism on the nanometer scale (i.e. single droplet) and the droplet diffusive time scale (droplet diffusive time ≈ a2/D = 6πηa3/kBT ∼ 10−4 s, where a is the droplet diameter, D is the droplet diffusivity, η is the viscosity of the continuous phase kB is the Boltzmann constant and T is absolute temperature). We will study both dynamics and mechanisms of the effect of thermal processing and the evolution of the microstructures, which will bring more insights into the spatial and temporal evolution of the system, as experimentally demonstrated in this work.
Conclusion
We have demonstrated that thermal processing conditions can be used to tune both the mechanical and structural properties of a thermally gelling nanoemulsion suspension. Under certain thermal processing conditions, the gel strength can be increased up to 47% compared to a single temperature jump. Additionally, the thermal processing can effectively prevent a decrease in gel strength due to a slow relaxation. By combining the results from one-step and two-step temperature jumps, properties of gels can be beyond the limit set by direct quenching, which has been a major focus in literature. We have also shown that the nanoemulsion gel is a hierarchical structure comprised of multiple length scales which are in turn related to the rheological properties. Our results suggest that the mechanistic reason for such control is that the system sequentially forms hierarchical microstructures and dynamic tuning of the droplet interactions through temperature can influence the trajectory taken through phase-space. Our work also provides new experimental evidence which relates the path-dependent rheological properties to associated microstructures in attractive colloidal systems. Future work using simulations will help validate the postulated mechanisms and role of hierarchical assembly. Concepts from our work could be applied to other attractive colloidal systems which can improve the understanding of such systems, and can be utilized in colloid-based material design. Translation of model systems to products requires the development of industrial processes. Here we demonstrated that the process itself is an important tool to be leveraged to tune material properties.Materials and methods
Materials
Sodium dodecyl sulfate (SDS), poly(ethylene glycol)diacrylate (PEGDA, Mn = 700 g mol−1), silicone oil (polydimethylsiloxane, PDMS, viscosity = 5 cSt at 25 °C), lipophilic dye PKH26 (excitation and emission wavelengths λex/λem = 551/567 nm) and photoinitiator 2-hydroxy-2-methylpropiophenone (Darocur 1173) were purchased from Sigma-Aldrich. All chemicals were used without further purification.Synthesis of nanoemulsions
The nanoemulsion system studied in this work was composed of a disperse phase PDMS of volume fraction = 0.15, an aqueous continuous phase consisting of PEGDA of volume fraction = 0.33, SDS of concentration = 0.175 M and deionized water.The nanoemulsions were synthesized by the following procedure. First, a pre-emulsion was prepared by adding PDMS to the aqueous continuous phase composed of PEGDA and SDS using magnetic stirring with a speed of 700 rpm. Stirring was maintained for 20 min or until no macroscopic phase separation was observed. A high-pressure homogenizer (EmulsiFlex-C3, Avestin) was used to process the pre-emulsion into the corresponding nanoemulsion. The homogenization was conducted at a pressure of 18 kpsi for 14 passes. The emulsion was cooled to 4 °C between each pass and the final nanoemulsion was stored at 4 °C until further use.
The size of PDMS droplets was monitored using dynamic light scattering (90Plus PALS, Brookhaven Instruments). Fig. S1 (ESI†) shows the evolution of droplet size after each pass. The droplet size was measured by diluting the oil volume fraction of the emulsion from 0.15 to 0.002 using an aqueous diluting agent consisting of PEGDA with volume fraction = 0.33. It has been reported previously that dilution using this diluent does not affect the droplet size and polydispersity.21 The nanoemulsion suspension used in this work has a droplet size equal to 37 nm with polydispersity equal to 0.187.
Rheology
Rheological characterization was performed by using a stress-controlled rheometer (ARG2, TA instrument) equipped with a 2° 60 mm aluminum upper-cone and a temperature-controlled Peltier lower-plate. For each measurement, the nanoemulsion was loaded onto the Peltier plate at 20 °C. A wetted solvent trap was used and a few drops of deionized water were added on top of the cone to control the evaporation. Before each measurement, a preshear step with a constant rotation at a rate of 20 rad s−1 for 30 seconds followed by a 90 seconds period where the sample remained quiescent at T = 20 °C, was performed. Thermal processing measurements (one-step and two-step jumping) were carried out at an oscillatory frequency = 20 rad s−1 with strain = 0.1%. The speed of temperature increase was set to be the maximum rate that the rheometer was able to achieve. Fig. S2b (ESI†) shows the actual temperature history during the measurement. Large amplitude oscillatory shear (LAOS) at an oscillatory frequency = 20 rad s−1 with strain = 15% was performed to yield the nanoemulsion at 50 °C for the gel aging (Fig. 5). LAOS was applied at t = 600 s for 30 seconds. Freshly loaded nanoemulsions were used for each measurement.Confocal microscopy
Direct visualization of the gel microstructures was carried out by using a confocal laser scanning microscope (LSM 700, Zeiss) quipped with a 63× oil-immersion objective (numerical aperture = 1.4). Samples for imaging were prepared as follows. First, the nanoemulsion was mixed with 1 vol% fluorescent dye and 1 vol% photoinitiator. It has been shown previously that the addition of this small amount of chemicals does not affect the microstructures.22 Subsequently, 150 μL of the mixture was loaded into a glass chamber (Lab-Tek™ #155411, Thermo Fisher Scientific). Pipetting samples into glass chambers for microscopy mimics the preshear step on the rheometer. Then, the sample-loaded glass chamber was put onto the Peltier plate on the rheometer at 20 °C for 90 seconds, and the sample underwent the same thermal history as during the rheological characterization. The time scale of the heat transfer from the Peltier plate to the sample through the glass is negligible. The thickness of the glass microscope slide is 0.15 mm according to the vendor. The thermal diffusivity of the glass slide is about 0.55 mm2 s−1.42 Therefore, The diffusive time scale is 0.152/0.55 = 0.04 s, which is negligible compared to the experimental time scale. After thermal processing, the sample was exposed to UV-light (λ = 365 nm) for 50 seconds. The crosslinking of the PEGDA in the continuous phase locks the pristine microstructure in place, which allows one to directly visualize the gel structure at room temperature using confocal microscopy.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This research was primarily supported by NSF through the Massachusetts Institute of Technology Materials Research Science and Engineering Center DMR – 1419807. L.-C. Cheng was supported in part by a scholarship from Think Global Education Trust (Taiwan). The authors thank G. H. McKinley and L. Chen for insightful discussions.References
- W. D. Callister and D. G. Rethwisch, Materials science and engineering: An Introduction, John Wiley and Sons, 9th edn, 2013 Search PubMed.
- M. Chen, Annu. Rev. Mater. Res., 2008, 38, 445–469 CrossRef.
- S. Nakamura, T. Mukai, M. Senoh and N. Iwasa, Jpn. J. Appl. Phys., 1992, 31, 139–142 CrossRef.
- S. Malik, C. Roberts, R. Murray and M. Pate, Appl. Phys. Lett., 1997, 71, 1987–1989 CrossRef.
- T. Kitatani, K. Nakahara, M. Kondow, K. Uomi and T. Tanaka, J. Cryst. Growth, 2000, 209, 345–349 CrossRef.
- W. Prellier, A. Fouchet and B. Mercey, J. Phys.: Condens. Matter, 2003, 15, 1583–1601 CrossRef.
- G. Ziegler, J. Heinrich and G. Wötting, J. Mater. Sci., 1987, 22, 3041–3086 CrossRef.
- H. Chen, M. B. Müller, K. J. Gilmore, G. G. Wallace and D. Li, Adv. Mater., 2008, 20, 3557–3561 CrossRef.
- K. Kim, M. W. Schulze, A. Arora, R. M. Lewis III, M. A. Hillmyer, K. D. Dorfman and F. S. Bates, Science, 2017, 356, 520–523 CrossRef PubMed.
- M.-S. She, T.-Y. Lo and R.-M. Ho, ACS Nano, 2013, 7, 2000–2011 CrossRef PubMed.
- V. Olszowka, M. Hund, V. Kuntermann, S. Scherdel, L. Tsarkova and A. Böker, ACS Nano, 2009, 3, 1091–1096 CrossRef PubMed.
- Y. Lu, Y. Zhang, G. Zhang, M. Yang, S. Yan and D. Shen, Polymer, 2004, 45, 8999–9009 CrossRef.
- S. O. Lumsdon, E. W. Kaler and O. D. Velev, Langmuir, 2004, 20, 2108–2116 CrossRef PubMed.
- J. W. Swan, P. A. Vasquez, P. A. Whitson, E. M. Fincke, K. Wakata, S. H. Magnus, F. D. Winne, M. R. Barratt, J. H. Agui, R. D. Green, N. R. Hall, D. Y. Bohman, C. T. Bunnell, A. P. Gast and E. M. Furst, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 16023–16028 CrossRef PubMed.
- J. W. Swan, J. L. Bauer, Y. Liu and E. M. Furst, Soft Matter, 2014, 10, 1102–1109 RSC.
- M. Grzelczak, J. Vermant, E. M. Furst and L. M. Liz-Marzán, ACS Nano, 2010, 4, 3591–3605 CrossRef PubMed.
- M. B. Gordon, C. J. Kloxin and N. J. Wagner, J. Rheol., 2017, 61, 23–34 CrossRef.
- A. P. R. Eberle, R. Castañeda-Priego, J. M. Kim and N. J. Wagner, Langmuir, 2012, 28, 1866–1878 CrossRef PubMed.
- Z. M. Sherman, H. Rosenthal and J. W. Swan, Langmuir, 2018, 34, 1029–1041 CrossRef PubMed.
- Z. M. Sherman and J. W. Swan, ACS Nano, 2016, 10, 5260–5271 CrossRef PubMed.
- M. E. Helgeson, S. E. Moran, H. Z. An and P. S. Doyle, Nat. Mater., 2012, 11, 344–352 CrossRef PubMed.
- L. C. Hsiao and P. S. Doyle, Soft Matter, 2015, 11, 8426–8431 RSC.
- L. C. Hsiao, A. Z. M. Badruddoza, L.-C. Cheng and P. S. Doyle, Soft Matter, 2017, 13, 921–929 RSC.
- L.-C. Cheng, L. C. Hsiao and P. S. Doyle, Soft Matter, 2017, 13, 6606–6619 RSC.
- M. E. Helgeson, Y. Gao, S. E. Moran, J. Lee, M. Godfrin, A. Tripathi, A. Bose and P. S. Doyle, Soft Matter, 2014, 10, 3122–3133 RSC.
- E. Wetterskog, C. Jonasson, D.-M. Smilgies, V. Schaller, C. Johansson and P. Svedlindh, ACS Nano, 2018, 12, 1403–1412 CrossRef PubMed.
- C. Yilmaz, A. Sirman, A. Halder and A. Busnaina, ACS Nano, 2017, 11, 7679–7689 CrossRef PubMed.
- L. Lin, X. Peng, M. Wang, L. Scarabelli, Z. Mao, L. M. Liz-Marzán, M. F. Becker and Y. Zheng, ACS Nano, 2016, 10, 9659–9668 CrossRef PubMed.
- A. Gupta, H. B. Eral, T. A. Hatton and P. S. Doyle, Soft Matter, 2016, 12, 2826–2841 RSC.
- H. H. Winter and F. Chambon, J. Rheol., 1986, 30, 367–382 CrossRef.
- F. Chambon and H. H. Winter, J. Rheol., 1987, 31, 683–697 CrossRef.
- S. Wassén, N. Lorén, K. van Bemmel, E. Schuster, E. Rondeau and A.-M. Hermansson, Soft Matter, 2013, 9, 2738–2749 RSC.
- Y. Gao, J. Kim and M. E. Helgeson, Soft Matter, 2015, 11, 6360–6370 RSC.
- P. J. Lu, E. Zaccarelli, F. Ciulla, A. B. Schofield, F. Sciortino and D. A. Weitz, Nature, 2008, 453, 499–503 CrossRef PubMed.
- T. Gibaud, N. Mahmoudi, J. Oberdisse, P. Lindner, J. S. Pedersen, C. L. P. Oliveira, A. Stradner and P. Schurtenberger, Faraday Discuss., 2012, 158, 267 RSC.
- P. J. Lu and D. A. Weitz, Annu. Rev. Condens. Matter Phys., 2013, 4, 217–233 CrossRef.
- L. Cipelletti and L. Ramos, Curr. Opin. Colloid Interface Sci., 2002, 7, 228–234 CrossRef.
- L. Ramos and L. Cipelletti, Phys. Rev. Lett., 2001, 87, 245503 CrossRef PubMed.
- O. Lieleg, J. Kayser, G. Brambilla, L. Cipelletti and A. R. Bausch, Nat. Mater., 2011, 10, 236–242 CrossRef PubMed.
- R. N. Zia, B. J. Landrum and W. B. Russel, J. Rheol., 2014, 58, 1121–1157 CrossRef.
- M. E. Helgeson, Curr. Opin. Colloid Interface Sci., 2016, 25, 39–50 CrossRef.
- H. Mehling, G. Hautzinger, O. Nilsson, J. Fricke, R. Hofmann and O. Hahn, Int. J. Thermophys., 1998, 19, 941–949 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c8sm00814k |
| This journal is © The Royal Society of Chemistry 2018 |




