Open Access Article
Open Access ArticleIdeal reversible polymer networks
German Alberto
Parada
 ab and
Xuanhe
Zhao
ab and
Xuanhe
Zhao
 *bc
*bc
aDept. of Chemical Engineering, MIT, 77 Massachusetts Ave., Cambridge, MA, USA
bSoft Active Materials Laboratory, Dept. of Mechanical Engineering, MIT, 77 Massachusetts Ave., Cambridge, MA, USA. E-mail: zhaox@mit.edu
cDept. of Civil and Environmental Engineering, MIT, 77 Massachusetts Ave., Cambridge, MA, USA
First published on 15th May 2018
Abstract
In this article we introduce the concept of ideal reversible polymer networks, which have well-controlled polymer network structures similar to ideal covalent polymer networks but exhibit viscoelastic behaviors due to the presence of reversible crosslinks. We first present a theory to describe the mechanical properties of ideal reversible polymer networks. Because short polymer chains of equal length are used to construct the network, there are no chain entanglements and the chains’ Rouse relaxation time is much shorter than the reversible crosslinks’ characteristic time. Therefore, the ideal reversible polymer network behaves as a single Maxwell element of a spring and a dashpot in series, with the instantaneous shear modulus and relaxation time determined by the concentration of elastically-active chains and the dynamics of reversible crosslinks, respectively. The theory provides general methods to (i) independently control the instantaneous shear modulus and relaxation time of the networks, and to (ii) quantitatively measure kinetic parameters of the reversible crosslinks, including reaction rates and activation energies, from macroscopic viscoelastic measurements. To validate the proposed theory and methods, we synthesized and characterized the mechanical properties of a hydrogel composed of 4-arm polyethylene glycol (PEG) polymers end-functionalized with reversible crosslinks. All the experiments conducted by varying pH, temperature and polymer concentration were consistent with the predictions of our proposed theory and methods for ideal reversible polymer networks.
Introduction
While most crosslinked polymer networks are heterogeneous and lack controlled structure, ideal covalent polymer networks have been recently reported. The ideal covalent networks feature well-defined lengths of polymer chains, crosslink functionalities and network architectures.7,8 To fabricate such networks, multi-arm (3 or 4-arm, typically) end-functionalized macromers of low molecular weight are mixed near the overlap concentration and crosslinked via a reaction of the end groups (Fig. 1a). These ideal covalent polymer networks not only provide powerful tools to study structure–property relationships of crosslinked polymers but also give elastomers and gels with well-controlled mechanical properties such as elasticity,9–11 mesh size, stretchability1,2,10,12,13 and fracture toughness.14 But due to the permanent nature of the crosslinks, these network do not exhibit any viscoelasticity. To obtain viscoelastic properties, reversible crosslinks can be introduced.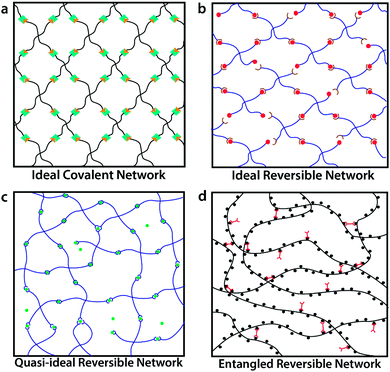 | ||
| Fig. 1 Schematics of (a) ideal covalent polymer network, featuring well-controlled network structure and permanent crosslinks;1,2 (b) the proposed ideal reversible polymer network, featuring well-controlled network structure and reversible crosslinks; (c) quasi-ideal reversible polymer network,3,4 with reversible crosslinks but possibility of local defects and loops; and (d) entangled reversible polymer network,5,6 with reversible crosslinks and chain entanglements. | ||
Reversible crosslinking motifs, which include dynamic covalent bonds, metal–ligand coordination, hydrogen bonding domains, electrostatic and hydrophobic interactions, and host–guest domains,15–18 have been extensively studied to design materials featuring self-healing properties,19,20 controlled stress–relaxations,21,22 bio-inspired adhesive behavior,3,23 and high fracture toughness.24 Existing studies on reversible crosslinks are mostly based on measurements and modeling of single molecules,25,26 reversible crosslinks on membranes27,28 or reversible crosslinks in random polymer networks.3,5,29–32 Well-controlled polymer networks containing reversible crosslinks (as shown in Fig. 1b) could facilitate better understanding of the reversible crosslinks themselves, and provide better controls over the physical properties of resultant networks. However, such well-controlled polymer networks with reversible crosslinks have rarely been synthesized or studied.33–35 Non-ideal networks are ubiquitous in the literature. For instance, researchers at the Holten-Andersen group have used 4-arm polyethylene glycol (PEG) containing metal–ligand coordination moieties (pyridine and catechol) at the chain ends.23,36,37 Upon the addition of metal ions, the PEG molecules are crosslinked to generate quasi-ideal reversible polymer networks with locally uncontrolled structures due to self-crosslinking between arms of the same macromer and crosslinking of more than two arms on the same metal ion (shown in Fig. 1c). As another example, researchers at the Craig group have synthesized and characterized dimethyl sulfoxide-based poly-4-vinylpyridine (PVP) networks crosslinked by small pincer-like bifunctional molecules with metal–ligand groups at the ends. Given the high molecular weight of PVP used, these networks contain chain entanglements (shown in Fig. 1d).5,6,38
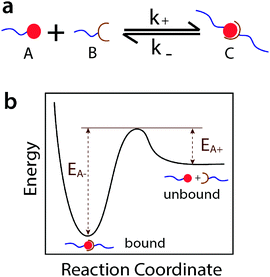
In this article we introduce the concept of ideal reversible polymer networks, which have well-controlled polymer network architectures similar to their covalent counterparts but feature reversible crosslinks (Fig. 1b). Unlike the entangled and quasi-ideal networks,3,39–41 there are no entanglements, other topological defects or point defects (crosslinks with different functionality) in these ideal reversible networks. Moreover, the networks exhibit time-dependent mechanical properties (i.e. viscoelasticity), due to the association and dissociation of the reversible crosslinks in them. We formulate a theoretical framework to quantitatively correlate the viscoelastic responses with the network architecture and properties of the reversible crosslinks. In this theory, the ideal reversible polymer networks are constituted of small end-functionalized 4-arm macromers near the overlap concentration, of which half are functionalized with group A and half with group B. All arms of the macromers are non-entangled (below critical entanglement molecular weight) and of equal length. Functional groups A and B are complementary and can form reversible crosslinks with each other but not with themselves. At equilibrium, a pair of complementary groups can be either at the unbound state (A + B) or the bound state C, which corresponds to a crosslink in the network (Fig. 2a).28 In the current theory, we use the Bell model28 to characterize the association and dissociation of the complementary reversible crosslinks. The theory can also be extended to incorporate other models for dynamics of reversible crosslinks such as the Evans model.42,43
Consequently, the theory gives that the ideal reversible polymer networks possess the following time-dependent mechanical properties: (i) their viscoelasticity resembles a single Maxwell element with a spring and a dashpot in series, (ii) the equilibrium concentration of bound reversible crosslinks determines the instantaneous shear modulus of the Maxwell element, and (iii) the time scale for dissociation of the crosslinks determines the relaxation time of the Maxwell element. Only a single relaxation time is expected for the ideal reversible networks due to the absence of intra-chain or inter-chain entanglements (low molecular weight macromers near the overlap concentration), and the fact that any Rouse relaxation process will occur much faster than the dissociation of reversible crosslinks.
Based on this theory, we further develop a set of general methods: (i) to independently control the instantaneous shear modulus and relaxation time of ideal reversible networks by independently varying the equilibrium concentration of crosslinks and dissociation time, respectively; and (ii) to quantitatively derive the kinetic parameters of the reversible crosslinks including reaction rates and activation energies from macroscopic measurements of viscoelastic properties of the ideal reversible polymer networks.
In order to validate the theory and methods proposed, we synthesized and characterized a hydrogel composed of 4-arm polyethylene glycol polymers end-functionalized with 3-fluorophenylboronic acid groups (i.e., group A) and diol groups (i.e., group B), respectively.33 The phenylboronic acid–diol reversible reaction is sensitive to pH and temperature, which can be varied to tune the kinetics of the reversible reaction.44–47 The 4-arm macromers with two different end-groups were mixed at equimolar ratio to form polymer networks around the overlap concentration of the macromers. The hydrogels were subjected to stress relaxation and small amplitude oscillatory shear tests in a rheometer to characterize its mechanical responses. All tests yielded viscoelastic behaviors of the reversible network equivalent to a Maxwell element, as predicted by the theory. The proposed method to independently control viscoelastic properties of ideal polymer networks were also validated experimentally. The concentrations of macromers were changed to control instantaneous shear modulus, while temperature and pH were varied to control both instantaneous shear modulus and relaxation time. The resultant changes of the network's viscoelastic properties quantitatively followed our theory's prediction. We further calculated the kinetic parameters of reversible crosslinks including reaction rates and activation energies from experimentally measured viscoelastic properties of the networks. The resultant values were consistent with previously-reported values.
Through a combination of theory and experiments, the current work not only lays the theoretical foundation for ideal reversible polymer network but also provide simple yet general methods to quantitatively control viscoelasticity of polymer networks (without the involvement of entanglements) and to measure kinetic properties of reversible crosslinks based on macroscopic mechanical properties. While reversible crosslinks have been widely used in the design of hydrogels with extraordinary mechanical properties24,48–51 and hydrogel-based biomedical devices,52–55 we expect the current work will provide better understanding and control of reversible crosslinks and polymer networks.3,11,36,56–61 In addition, the current study may shed light on how reversible polymer networks are controlled in biological systems.15,17,21,62,63
Theory of ideal reversible polymer networks
Kinetics of reversible crosslinks
The overall association and dissociation of two complementary functional groups (schematically illustrated in Fig. 2a) can be expressed as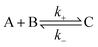 | (1) |
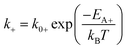 | (2a) |
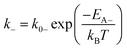 | (2b) |
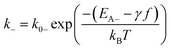 | (3) |
Concentration of reversible crosslinks at equilibrium
Let NA and NB be the number of functional groups A and B (at unbound and bound states) per unit volume of the polymer network, respectively; and NC the number of crosslinks (bound state) per unit volume of the polymer network. NA, NB and NC are also the concentrations of the corresponding functional groups and crosslinks. The formation of the crosslinks is assumed to follow the following kinetic equation,28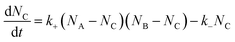 | (4) |
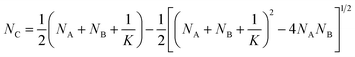 | (5) |
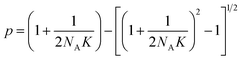 | (6) |
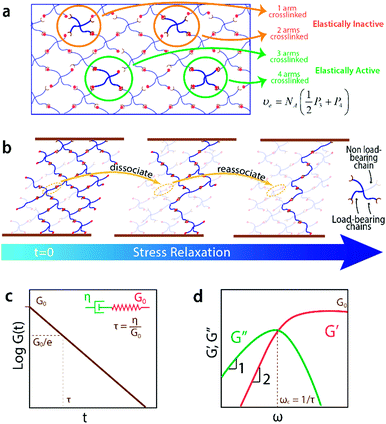
Concentration of elastically-active chains at equilibrium
The formation of a crosslink does not guarantee the formation of an elastically-active chain in the ideal reversible polymer network as illustrated in Fig. 3a. If only one arm of the macromer is crosslinked to the network, this macromer is a dangling end and does not contribute to the network's elasticity. If two arms are crosslinked to the network, the macromer will either act as a loop or a bridging chain, neither of which contribute to the network's elasticity. Only when 3 or 4 arms are crosslinked to the network the macromer will become elastically-active and contribute to the network's elasticity. The probabilities for a macromers to have three (P3) or four (P4) arms crosslinked to the infinite network are functions of the conversion p66| P3 = 4Pout(1 − Pout)3 | (7a) |
| P4 = (1 − Pout)4 | (7b) |
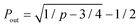 is the probability for a crosslink to lead to a dangling chain.66 Since it is not possible to achieve a percolated network when Pout is equal or greater than one, there is a threshold for the minimum value of conversion pmin = 1/3 under which it is not possible to form a network. From eqn (6), we can further derive the condition to form a percolated network as NAK > 0.75.
is the probability for a crosslink to lead to a dangling chain.66 Since it is not possible to achieve a percolated network when Pout is equal or greater than one, there is a threshold for the minimum value of conversion pmin = 1/3 under which it is not possible to form a network. From eqn (6), we can further derive the condition to form a percolated network as NAK > 0.75.
The concentration of elastically-active chains at equilibrium, υe, is then given by a weighted sum of the concentrations of macromers with 3 and 4 crosslinked arms. Specifically, macromers with 4 crosslinked arms contribute 4 elastically-active chains (one per arm) while those macromers with 3 crosslinked arms contribute 1.5 elastically-active chains (one half per arm), as described by Langley and Polmanteer.66,67
Therefore υe can be expressed as
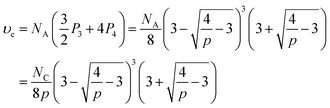 | (8) |
Concentration of loading-bearing chains during stress relaxation test
Let's imagine we carry out a stress relaxation test on the ideal reversible polymer network by applying a constant shear strain of small magnitudeεon the network beginning at time t = 0 and measuring the resulting shear stress σ(t) over time. The stress–relaxation shear modulus of the network is defined as,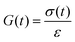 | (9) |
| G0 = υekBT | (10) |
| G(t) = υloadekBT | (11) |
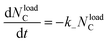 | (12) |
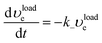 | (13) |
Maxwell model of ideal reversible polymer networks
By solving eqn (13) with the initial condition υloade(t = 0) = υe, we can calculate the evolution of the concentration of load-bearing chains in an ideal reversible polymer network during stress relaxation test asυloade(t) = υe![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−k−t) exp(−k−t) | (14) |
G(t) = υekBT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−k−t) exp(−k−t) | (15) |
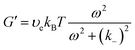 | (16a) |
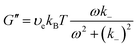 | (16b) |
Methods to control instantaneous shear modulus and relaxation time
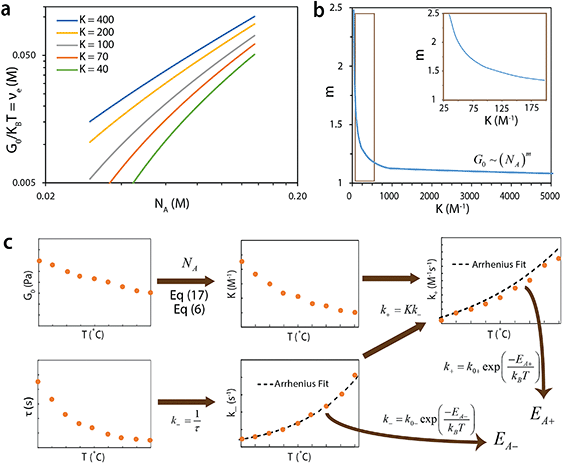
The developed theory provides guidelines to tune the instantaneous shear modulus G0 and the relaxation time τ of an ideal reversible polymer network independently, as G0 and τ arise from different physical mechanisms. Here we outline a set of methods to independently control instantaneous shear modulus and relaxation time.The instantaneous shear modulus of the network is solely controlled by the equilibrium concentration of elastically-active chains υe. By combining eqn (6), (8) and (11), it is possible to obtain an explicit but complex expression relating υe to the equilibrium constant K and concentration of functional group A, NA,
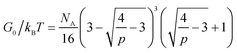 | (17) |
| G0 ∼ (NA)m | (18) |
Method 1 to control G0: with fixed macromer concentration, one can change the functional groups A and B on the macromers or the conditions of the network (e.g., temperature, pH) to change the equilibrium constant K and thus vary both the scaling component m and instantaneous shear modulus G0. Note that this method will also vary the relaxation time of the network, which will be discussed in the next section of the paper.
Method 2 to control G0: with fixed equilibrium constant K, one can directly vary the macromer concentration near the overlap concentration to tune G0. This strategy will not vary the relaxation time of the network. However, the range of tunable G0 is relatively limited in this strategy since the macromer concentration needs to be around overlap concentration.
Method 3 to control G0: for a fixed equilibrium constant K, one can change the molecular weight of the macromer M while maintaining the macromers at the overlap concentration. The pervaded volume of a macromer V scales with the macromer molecular weight by V ∝ M3υ, where υ is a scaling exponent that depends on the solvent quality. The value of υ is approximately 0.6 for polymers in a good solvent, such as PEG in aqueous solution.69 Furthermore, at the overlap concentration, the macromer concentration and macromer pervaded volume scales as NA ∝ V−1. Therefore, we can obtain a scaling between instantaneous shear modulus G0 and macromer molecular weight M at the overlap concentration,
| G0 ∼ M−3υm | (19) |
Compared with Method 2, this method can give a larger tunable range for G0, since the molecular weight of the macromers can varied significantly (up to the entanglement molecular weight). Furthermore, similar to method 2, changing M will not vary the relaxation time of the network.
From the theory section, the relaxation time τ for the reversible network is only determined by the dissociation rate of the reversible crosslink, k−. Therefore, we can use the following strategy to tune τ. One can change the functional groups A and B or the network conditions (e.g., temperature, pH) to vary k− and thus vary τ, since τ = 1/k−. It is important to note that adjusting k− will change K, so the scaling component m and instantaneous shear modulus G0 will also change. Therefore, to maintain G0 constant while tuning τ, it is necessary to vary the macromer concentration and/or molecular weight accordingly.
The methods to control G0 and τ introduced here are general for all ideal reversible network regardless of the reversible bond type used. For quasi-ideal and entangled networks, such as those systems used in past literature,3,4,31,32,36,56,58,59 the methods will be applicable in a qualitative way only.
Method to measure kinetic parameters of reversible crosslink from macroscale mechanical tests
The theory of ideal reversible network further allows one to quantitatively measure the kinetic parameters of reversible crosslink including association and dissociation rates (k+, k−) and activation energies for forward and reverse reactions (EA+, EA−) from macroscale mechanical tests of the network (i.e. G0 and τ data).For a given ideal reversible polymer network in an aqueous environment, the macromer concentration NA/2 and network parameters such as temperature T are known. From the stress relaxation test or the small-amplitude oscillatory shear test, we can measure G0 and τ at various temperatures. From the measured τ, we can calculate the dissociation rate k− = 1/τ at various temperatures. Then, by fitting eqn (2b) to the curve of k−vs. T, we can obtain the activation energy for reverse reaction EA−.
On the other hand, from the macromer concentration we can determine NA. This can be used with G0 values at various temperatures to calculate K at the corresponding temperatures through eqn (6) and (17). Since k− at various temperatures are known, we can calculate the corresponding association rates k+ = Kk−. Thereafter, by fitting eqn (2a) to the curve of k+vs. T, we can obtain activation energy for forward reaction EA+.
Materials and methods
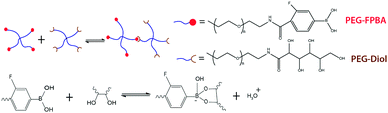
To validate the theory of ideal reversible polymer network and the consequent methods to tune and measure properties of the network, we have selected, synthesized and studied a model hydrogel system.In this work, we chose a 4-arm PEG-based reversible hydrogel system analogous to the 4-arm PEG-based ideal covalent networks developed by Sakai, Shibayama and colleagues.1,2,9,10 These networks contained very low amounts of entanglements and defects since the macromers behave as space-filling blobs that form a regular percolated network around the overlap concentration.1 To implement reversible crosslinking, we introduced 3-fluorophenylboronic acid functional groups (i.e., A group) and diol functional groups (i.e., B group) to the PEG macromers (Fig. 5). The dynamic covalent phenylboronic acid–diol chemistry was selected due to ease of synthesis, detailed molecular understanding of bonding kinetics and ability to tune the bonding kinetics by changing pH, temperature or the substituents on the phenyl ring.44–47,70 While this reaction was not strictly bimolecular, we used the conditional (or effective) formation constant framework to account for the effects of pH on the reversible reaction.46 Then, the reversible crosslinking could be described as a single reaction with unique equilibrium constant, forward and reverse rate constants (K, k+ and k−, respectively) at a fixed pH.
The functionalized PEG components were synthesized following the protocol published by Yesilyurt et al.33 Briefly, amino-terminated 4-arm PEG (5k or 10k, Jenkem Technologies) was conjugated to either D-gluconolactone or 4-carboxy-3-fluorophenylboronic acid (Sigma). The purified PEG-Diol and PEG-FPBA products were freeze-dried and stored at −20 °C until use. Separate PEG-Diol and PEG-FPBA solutions (with concentrations ranging from 15 to 25 mM) were made in 1× PBS buffer (pH 7.5, adjusted with 1 M NaOH). Additional amounts of 0.1 M NaOH were added to each solution to control the final pH of the hydrogel. The final pH was estimated using the Henderson–Hasselbalch equation with knowledge FBPA's pKa (7.2).33 The hydrogels were synthesized by mixing equal amounts of the PEG macromer solutions.
The mechanical properties of the model hydrogels were measured with a controlled stress rheometer AR-G2 (TA Instruments, New Castles, DE) fitted with a Peltier plate and a 20 mm 4° steel cone fixture. The PEG-Diol and PEG-FPBA solutions (100 μL of each) were directly mixed in the rheometer bottom plate and a solvent trap was used to prevent dehydration. The samples were equilibrated for 5 min prior to testing. The linear viscoelasticity region was determined by oscillatory strain amplitude sweeps at 1 Hz. This region extended up to 20% strain. Oscillatory frequency sweeps were conducted at 2% strain amplitude in the 0.1–100 rad s−1 range, 10 points per decade. Stress relaxation tests were carried out for 3 or 6 minutes at a constant strain of 10%. Analysis and fitting of the data was carried out using built-in non-linear fitting algorithms in OriginPro 8.5, and plotting was done with Microsoft Excel.
Results and discussion
To validate the theory of ideal reversible polymer networks, we carried out a set of stress relaxation and small-amplitude oscillatory shear tests on reversibly crosslinked 4-arm PEG networks at various temperatures (from 5 °C to 45 °C) and pH values (from 6.9 to 8.1). The molecular weight of the macromers was 5000 g mol−1 and they were at a total concentration of 15 mM in aqueous solution.The relaxation shear moduli G(t) measured for hydrogels at pH of 7.20 and various temperatures as functions of time t was plotted in Fig. 6a (on a semi-log plot). The curves indicated that the 4-arm PEG reversible network at each temperature indeed behaved as a Maxwell element with a defined instantaneous shear modulus and a single relaxation time, as demonstrated by the single slope.
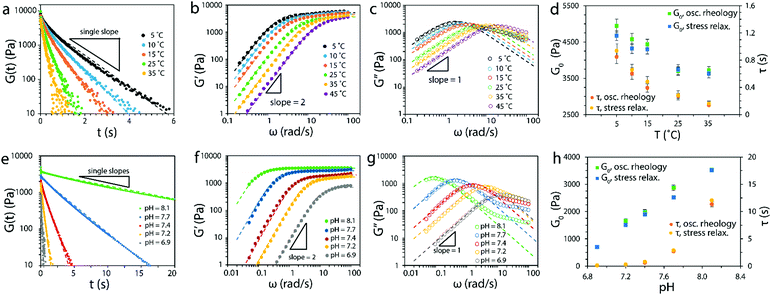 | ||
| Fig. 6 (a) Relaxation shear moduli, (b) storage moduli and (c) loss moduli of the 4-arm PEG reversible networks at pH = 7.2 and various temperatures. Non-linear fittings to eqn (15), (16a) and (16b) are shown as dashed lines. (d) Comparison of G0 and τ values obtained from oscillatory rheology and stress relaxation at pH = 7.2 and various temperatures. (e) Relaxation shear moduli, (f) storage moduli and (g) loss moduli of the 4-arm PEG reversible networks at T = 25 °C and various pH values. Non-linear fittings to eqn (15), (16a) and (16b) are shown as dashed lines. (g) Comparison of G0 and τ values obtained from oscillatory rheology and stress relaxation at T = 25 °C and various pH values. The molecular weight of the macromers used was 5000 g mol−1 and the total concentration was 15 mM. | ||
In principle it is possible to have additional relaxation mechanisms in a polymer network such as entanglements or Rouse-type modes of relaxation.69,71 As shown by Sakai and colleagues,1,2,10 entanglements can be avoided by using small 4-arm macromers near the overlap concentration. As for Rouse chain relaxation, the longest relaxation timescale is given by τ1 ∼ τsegN2, where N is the number of Kuhn monomers in the chain and τseg is the relaxation time of a single Kuhn monomer.69,71 Since the macromers used in this work have low molecular weight (5000 g mol−1), the Rouse relaxation times (∼10−6–10−4 s) are at least three orders of magnitude below the reversible crosslink relaxation times,72 and won’t be observed in these experiments.
The storage moduli G′(ω) and loss moduli G′′(ω) measured at various temperatures as functions of frequency ω are plotted in Fig. 6b and c. The curves obtained at various temperatures were fitted to the Maxwell model eqn (15), (16a) and (16b) and plotted as dashed lines. The fitting was adequate and showed the expected scaling as a function of ω, that is, G′ ∼ ω2 and G′′ ∼ ω up to the crossover frequency. Deviations on the G′′(ω) curve were seen at high frequencies, observation that will be discussed in the next paragraph. In addition, the instantaneous shear modulus G0 and relaxation timeτof the network obtained from two different tests (stress relaxation and oscillatory rheology) at the same temperature were consistent with each other (Fig. 6d).
Similarly, the measurements of the 4-arm PEG reversible network at 25 °C and various pH values indicated the network followed the Maxwell model (Fig. 6e–g) up to the crossover frequency (deviations in G′′(ω) were also present). The measured values of instantaneous shear modulus G0 and relaxation time τ from the two tests at the same pH were also consistent with each other (Fig. 6h). The results shown in Fig. 6a–h validated the prediction of our theory that ideal reversible polymer networks at various temperatures and pH values have Maxwell-like mechanical responses (the deviations seen at high frequencies will be discussed below). In addition, the results showed that the instantaneous shear moduli G0 and relaxation timeτ of the network can be tuned by varying the temperature and pH of the network.
The proposed ideal reversible polymer network theory assumes the association and dissociation of crosslinks takes place at experimental timescales. Therefore the model proposed is applicable when the experimental timescale texp ∼ 1/ω is greater or equal than the dissociation timescale τ. When the network is tested in a regime in which texp ≪ τ, the reversible crosslinks cannot dissociate so the network will resemble a covalently-crosslinked network, characterized by no stress relaxation and G′ and G′′ independent of ω. The effect of these two different regimes in rheology experiments is that the networks will exhibit Maxwell behavior up to frequencies near the crossover frequency ωc = 1/τ, and will transition to the covalent-like regime for frequencies above. The deviations from a Maxwell behavior seen in Fig. 6c and g at high frequencies arose from such transition, as the G′′ curve will plateau to match the scaling at the covalent-like regime. No transition was observed in the G′ curves as the plateau scaling is already realized.
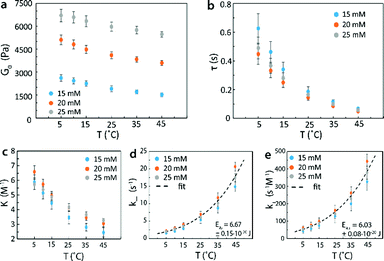
In order to validate that the proposed methods can control mechanical properties of reversible networks and measure kinetic parameters of reversible crosslinks, we systematically varied the concentration and molecular weight of the 4-arm PEG, the temperature and pH of the network. We then measured G0 and τ for the resultant networks via stress relaxation and small amplitude oscillatory shear rheology tests. In Fig. 7a, we plotted the instantaneous shear moduli G0 of 4-arm PEG reversible networks with macromer molecular weight of 5k at an estimated pH of 7.2 as functions of macromer concentration and temperature. It is evident that both varying macromer concentration and temperature could be used to tune G0. In Fig. 7b, we further plotted the relaxation time values of the same set of reversible networks. While τ could be tuned by changing temperature, it could not be significantly tuned by macromer concentration at the same temperature since the properties of reversible crosslinks are not affected by changing macromer concentration alone. These results validated that the mechanical properties of reversible networks can be controlled according to the methods proposed in this work.
In addition, G0 was proportional to the concentration of elastically-active chains υe (per eqn (10)). With the known υe and the functional group concentration NA, eqn (6) and (17) were solved to determine the equilibrium constants K at every temperature [Fig. 7c]. The measured relaxation time τ further gave the dissociation rates at every temperature, since k− = 1/τ (Fig. 7d). Then, the association rates of reversible crosslink at various temperatures were calculated as k+ = Kk− (Fig. 7e). It is noted that the measured K, k− and k+ for 4-arm PEG reversible networks did not depend on macromer concentration, as predicted by the theory. By fitting the k+ and k− curves to eqn (2a) and (2b), we obtained the activation energies for forward and reverse reactions of the reversible crosslink, respectively. For this network, the values were EA+ = 6.03 ± 0.08 × 10−20 J and EA− = 6.67 ± 0.15 × 10−20 J. These values indicate that the forward reaction was more energetically favorable (with lower activation energy) at pH = 7.2, which led to the formation of a crosslinked network. The kinetic parameters of the reversible crosslink measured by our proposed method were in the same range as published activation energy values (note that the reported numbers are for different boronic acid and diol species).73,74
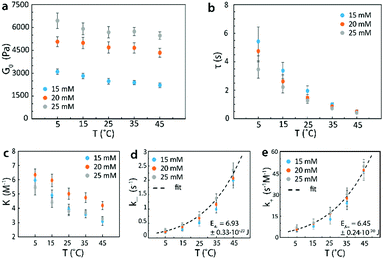
In Fig. 8, we repeated the process with identical 4-arm PEG reversible networks at a higher pH of 7.7. It can be seen that the trends of G0 and τ vs. temperature measured at this higher pH value (Fig. 8a and b) were the same as those measured at pH = 7.2 (Fig. 7a and b). However, at the same temperature, values for G0 and τ at pH = 7.7 were higher than the corresponding values pH = 7.2, as increasing pH leads to lower dissociation rates and higher equilibrium constants for the phenylboronic acid–diol reversible reaction.44–47 These results were consistent with our theory's predictions, and validated that changing pH can also be used to tune G0 and τ of reversible networks. In addition, from the mechanical properties of reversible network, we could again determine the activation energies. These values were EA+ = 6.45 ± 0.24 × 10−20 J for the forward reaction and EA− = 6.93 ± 0.33 × 10−20 J for the reverse one. These values were also in the same range as the published values and higher than the values measured at pH 7.2.
Conclusions
This work introduced ideal reversible polymer networks, defined as networks crosslinked by reversible junctions that would revert to ideal covalent polymer networks if all reversible junctions were replaced by covalent bonds. Through a combination of theory and experiments, we showed that the viscoelasticity of ideal reversible polymer network follows the Maxwell model, characterized by instantaneous shear modulus G0 and relaxation time τ. The value of G0 for ideal covalent polymer networks can be tuned by varying concentration and molecular weight of the macromers and pH and temperature of the aqueous solution of the network. The relaxation time τ is controlled by pH and temperature of the aqueous solution of the network, but not concentration or molecular weight of the macromers. These results not only lay the theoretical foundation for ideal reversible polymer network but also provide simple yet general methods to quantitatively control viscoelasticity of polymer networks and to measure kinetic properties of reversible crosslinks based on their viscoelasticity. We expect the current work will facilitate the design of polymer networks to achieve extraordinary properties via reversible crosslinks and the understanding of reversible polymer networks in various synthetic and biological polymers.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The work was supported by NSF (CMMI-1661627), ONR (N00014-17-1-2920) and MIT Institute for Soldier Nanotechnologies. We thank the assistance from Prof. Gareth McKinley and Dr Alexander Barbati for access and training in the use of the rheometer.Notes and references
- T. Matsunaga, T. Sakai, Y. Akagi, U.-I. Chung and M. Shibayama, SANS and SLS Studies on Tetra-Arm PEG Gels in As-Prepared and Swollen States, Macromolecules, 2009, 42(16), 6245–6252 CrossRef.
- T. Matsunaga, T. Sakai, Y. Akagi, U.-I. Chung and M. Shibayama, Structure Characterization of Tetra-PEG Gel by Small-Angle Neutron Scattering, Macromolecules, 2009, 42(4), 1344–1351 CrossRef.
- S. C. Grindy, R. Learsch, D. Mozhdehi, J. Cheng, D. G. Barrett, Z. B. Guan, P. B. Messersmith and N. Holten-Andersen, Control of hierarchical polymer mechanics with bioinspired metal-coordination dynamics, Nat. Mater., 2015, 14(12), 1210–1216 CrossRef PubMed.
- K. Kawamoto, S. C. Grindy, J. Liu, N. Holten-Andersen and J. A. Johnson, Dual Role for 1,2,4,5-Tetrazines in Polymer Networks: Combining Diels-Alder Reactions and Metal Coordination To Generate Functional SupramolecularGels, ACS Macro Lett., 2015, 4(4), 458–461 CrossRef.
- D. M. Loveless, S. L. Jeon and S. L. Craig, Rational Control of Viscoelastic Properties in Multicomponent Associative Polymer Networks, Macromolecules, 2005, 38(24), 10171–10177 CrossRef.
- W. C. Yount, D. M. Loveless and S. L. Craig, Small-molecule dynamics and mechanisms underlying the macroscopic mechanical properties of coordinatively cross-linked polymer networks, J. Am. Chem. Soc., 2005, 127(41), 14488–14496 CrossRef PubMed.
- M. Rikkou-Kalourkoti, C. S. Patrickios and T. Georgiou, 6.08 – Model Networks and Functional Conetworks, in Polymer Science: A Comprehensive Reference, ed. K. Matyjaszewski and M. Moller, Elsevier, 2012, vol. 6, pp. 293–308 Search PubMed.
- G. Hild, Model networks based on ‘endlinking’ processes: synthesis, structure and properties, Prog. Polym. Sci., 1998, 23(6), 1019–1149 CrossRef.
- Y. Akagi, T. Katashima, Y. Katsumoto, K. Fujii, T. Matsunaga, U.-I. Chung, M. Shibayama and T. Sakai, Examination of the Theories of Rubber Elasticity Using an Ideal Polymer Network, Macromolecules, 2011, 44(14), 5817–5821 CrossRef.
- T. Matsunaga, H. Asai, Y. Akagi, T. Sakai, U.-I. Chung and M. Shibayama, SANS Studies on Tetra-PEG Gel under Uniaxial Deformation, Macromolecules, 2011, 44(5), 1203–1210 CrossRef.
- M. Zhong, R. Wang, K. Kawamoto, B. D. Olsen and J. A. Johnson, Quantifying the impact of molecular defects on polymer network elasticity, Science, 2016, 353(6305), 1264–1268 CrossRef PubMed.
- T. Hiroi, M. Ohl, T. Sakai and M. Shibayama, Multiscale Dynamics of Inhomogeneity-Free Polymer Gels, Macromolecules, 2014, 47(2), 763–770 CrossRef.
- K. Hashimoto, K. Fujii, K. Nishi, T. Sakai and M. Shibayama, Nearly Ideal Polymer Network Ion Gel Prepared in pH-Buffering Ionic Liquid, Macromolecules, 2016, 49(1), 344–352 CrossRef.
- T. Sakai, Y. Akagi, S. Kondo and U. Chung, Experimental verification of fracture mechanism for polymer gels with controlled network structure, Soft Matter, 2014, 10(35), 6658–6665 RSC.
- M. J. Webber, E. A. Appel, E. W. Meijer and R. Langer, Supramolecular biomaterials, Nat. Mater., 2016, 15(1), 13–26 CrossRef PubMed.
- C. J. Kloxin and C. N. Bowman, Covalent adaptable networks: smart, reconfigurable and responsive network systems, Chem. Soc. Rev., 2013, 42(17), 7161–7173 RSC.
- H. Wang and S. C. Heilshorn, Adaptable hydrogel networks with reversible linkages for tissue engineering, Adv. Mater., 2015, 27(25), 3717–3736 CrossRef PubMed.
- L. Voorhaar and R. Hoogenboom, Supramolecular polymer networks: hydrogels and bulk materials, Chem. Soc. Rev., 2016, 45(14), 4013–4031 RSC.
- E. B. Stukalin, L. H. Cai, N. A. Kumar, L. Leibler and M. Rubinstein, Self-Healing of Unentangled Polymer Networks with Reversible Bonds, Macromolecules, 2013, 46(18), 7525–7541 CrossRef PubMed.
- F. Herbst, D. Dohler, P. Michael and W. H. Binder, Self-healing polymers via supramolecular forces, Macromol. Rapid Commun., 2013, 34(3), 203–220 CrossRef PubMed.
- O. Chaudhuri, L. Gu, D. Klumpers, M. Darnell, S. A. Bencherif, J. C. Weaver, N. Huebsch, H. P. Lee, E. Lippens, G. N. Duda and D. J. Mooney, Hydrogels with tunable stress relaxation regulate stem cell fate and activity, Nat. Mater., 2016, 15(3), 326–334 CrossRef PubMed.
- X. Zhao, N. Huebsch, D. J. Mooney and Z. Suo, Stress-relaxation behavior in gels with ionic and covalent crosslinks, J. Appl. Phys., 2010, 107(6), 63509 CrossRef PubMed.
- N. Holten-Andersen, M. J. Harrington, H. Birkedal, B. P. Lee, P. B. Messersmith, K. Y. C. Lee and J. H. Waite, pH-induced metal-ligand cross-links inspired by mussel yield self-healing polymer networks with near-covalent elastic moduli, Proc. Natl. Acad. Sci. U. S. A., 2011, 108(7), 2651–2655 CrossRef PubMed.
- X. Zhao, Multi-scale multi-mechanism design of tough hydrogels: building dissipation into stretchy networks, Soft Matter, 2014, 10(5), 672–687 RSC.
- S. S. Nabavi, P. Fratzl and M. A. Hartmann, Energy dissipation and recovery in a simple model with reversible cross-links, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2015, 91(3), 032603 CrossRef PubMed.
- J. Blass, M. Albrecht, G. Wenz, Y. N. Zang and R. Bennewitz, Single-molecule force spectroscopy of fast reversible bonds, Phys. Chem. Chem. Phys., 2017, 19(7), 5239–5245 RSC.
- H. Gao, W. Shi and L. B. Freund, Mechanics of receptor-mediated endocytosis, Proc. Natl. Acad. Sci. U. S. A., 2005, 102(27), 9469–9474 CrossRef PubMed.
- G. Bell, Models for the specific adhesion of cells to cells, Science, 1978, 200(4342), 618–627 Search PubMed.
- F. Tanaka and S. F. Edwards, Viscoelastic properties of physically crosslinked networks. Transient network theory, Macromolecules, 1992, 25(5), 1516–1523 CrossRef.
- F. Tanaka and S. F. Edwards, Viscoelastic properties of physically crosslinked networks. Part 2: Dynamic Mechanical Moduli, J. Non-Newtonian Fluid Mech., 1992, 43(2–3), 273–288 CrossRef.
- K. E. Feldman, M. J. Kade, E. W. Meijer, C. J. Hawker and E. J. Kramer, Model Transient Networks from Strongly Hydrogen-Bonded Polymers, Macromolecules, 2009, 42(22), 9072–9081 CrossRef.
- D. Xu and S. L. Craig, Scaling Laws in Supramolecular Polymer Networks, Macromolecules, 2011, 44(13), 5465–5472 CrossRef PubMed.
- V. Yesilyurt, M. J. Webber, E. A. Appel, C. Godwin, R. Langer and D. G. Anderson, Injectable Self-Healing Glucose-Responsive Hydrogels with pH-Regulated Mechanical Properties, Adv. Mater., 2016, 28(1), 86–91 CrossRef PubMed.
- V. Yesilyurt, A. M. Ayoob, E. A. Appel, J. T. Borenstein, R. Langer and D. G. Anderson, Mixed Reversible Covalent Crosslink Kinetics Enable Precise, Hierarchical Mechanical Tuning of Hydrogel Networks, Adv. Mater., 2017, 1605947 CrossRef PubMed.
- D. E. Apostolides, T. Sakai and C. S. Patrickios, Dynamic Covalent Star Poly(ethylene glycol) Model Hydrogels: A New Platform for Mechanically Robust, Multifunctional Materials, Macromolecules, 2017, 50(5), 2155–2164 CrossRef.
- N. Holten-Andersen, B. P. Lee, P. B. Messersmith, J. H. Waite and K. Y. C. Lee, Mussel-Inspired Self-Healing Hydrogels, Biophys. J., 2010, 98(3), 604a CrossRef.
- D. G. Barrett, D. E. Fullenkamp, L. H. He, N. Holten-Andersen, K. Y. C. Lee and P. B. Messersmith, pH-Based Regulation of Hydrogel Mechanical Properties Through Mussel-Inspired Chemistry and Processing, Adv. Funct. Mater., 2013, 23(9), 1111–1119 CrossRef PubMed.
- W. C. Yount, D. M. Loveless and S. L. Craig, Strong Means Slow: Dynamic Contributions to the Bulk Mechanical Properties of Supramolecular Networks, Angew. Chem., 2005, 117(18), 2806–2808 CrossRef.
- M. Rubinstein and A. N. Semenov, Dynamics of Entangled Solutions of Associating Polymers, Macromolecules, 2001, 34(4), 1058–1068 CrossRef.
- D. Amin, A. E. Likhtman and Z. Wang, Dynamics in Supramolecular Polymer Networks Formed by Associating Telechelic Chains, Macromolecules, 2016, 49(19), 7510–7524 CrossRef.
- B. J. Gold, C. H. Hövelmann, N. Lühmann, N. K. Székely, W. Pyckhout-Hintzen, A. Wischnewski and D. Richter, Importance of Compact Random Walks for the Rheology of Transient Networks, ACS Macro Lett., 2017, 6(2), 73–77 CrossRef.
- R. Merkel, P. Nassoy, A. Leung, K. Ritchie and E. Evans, Energy landscapes of receptor-ligand bonds explored with dynamic force spectroscopy, Nature, 1999, 397(6714), 50–53 CrossRef PubMed.
- E. Evans, Probing the relation between force – lifetime – and chemistry in single molecular bonds, Annu. Rev. Biophys. Biomol. Struct., 2001, 30, 105–128 CrossRef PubMed.
- G. Springsteen and B. Wang, A detailed examination of boronic acid–diol complexation, Tetrahedron, 2002, 58(26), 5291–5300 CrossRef.
- J. Yan, G. Springsteen, S. Deeter and B. Wang, The relationship among pKa, pH, and binding constants in the interactions between boronic acids and diols—it is not as simple as it appears, Tetrahedron, 2004, 60(49), 11205–11209 CrossRef.
- Y. Furikado, T. Nagahata, T. Okamoto, T. Sugaya, S. Iwatsuki, M. Inamo, H. D. Takagi, A. Odani and K. Ishihara, Universal reaction mechanism of boronic acids with diols in aqueous solution: kinetics and the basic concept of a conditional formation constant, Chemistry, 2014, 20(41), 13194–13202 CrossRef PubMed.
- J. W. Tomsho and S. J. Benkovic, Elucidation of the mechanism of the reaction between phenylboronic acid and a model diol, Alizarin Red S, J. Org. Chem., 2012, 77(5), 2098–2106 CrossRef PubMed.
- J. Y. Sun, X. H. Zhao, W. R. K. Illeperuma, O. Chaudhuri, K. H. Oh, D. J. Mooney, J. J. Vlassak and Z. G. Suo, Highly stretchable and tough hydrogels, Nature, 2012, 489(7414), 133–136 CrossRef PubMed.
- H. Yuk, T. Zhang, G. A. Parada, X. Liu and X. Zhao, Skin-inspired hydrogel-elastomer hybrids with robust interfaces and functional microstructures, Nat. Commun., 2016, 7, 12028 CrossRef PubMed.
- H. Yuk, T. Zhang, S. Lin, G. A. Parada and X. Zhao, Tough bonding of hydrogels to diverse non-porous surfaces, Nat. Mater., 2016, 15(2), 190–196 CrossRef PubMed.
- T. Zhang, H. Yuk, S. Lin, G. Parada and X. Zhao, Tough and Tunable Adhesion of Hydrogels: Experiments and Models, Acta Mech. Sin., 2017, 543–554 CrossRef.
- S. Lin, H. Yuk, T. Zhang, G. A. Parada, H. Koo, C. Yu and X. Zhao, Stretchable Hydrogel Electronics and Devices, Adv. Mater., 2016, 28(22), 4497–4505 CrossRef PubMed.
- X. Liu, H. Yuk, S. Lin, G. A. Parada, T. C. Tang, E. Tham, C. de la Fuente-Nunez, T. K. Lu and X. Zhao, 3D Printing of Living Responsive Materials and Devices, Adv. Mater., 2018, 30(4), 1704821 CrossRef PubMed.
- G. A. Parada, H. Yuk, X. Liu, A. J. Hsieh and X. Zhao, Impermeable Robust Hydrogels via Hybrid Lamination, Adv. Healthcare Mater., 2017, 6(19), 1700520 CrossRef PubMed.
- H. Yuk, S. Lin, C. Ma, M. Takaffoli, N. X. Fang and X. Zhao, Hydraulic hydrogel actuators and robots optically and sonically camouflaged in water, Nat. Commun., 2017, 8, 14230 CrossRef PubMed.
- Q. C. Li, D. G. Barret, P. B. Messersmith and N. Holten-Andersen, Controlling Hydrogel Mechanics via Bio-Inspired Polymer-Nanoparticle Bond Dynamics, ACS Nano, 2016, 10(1), 1317–1324 CrossRef PubMed.
- D. Mozhdehi, J. A. Neal, S. C. Grindy, Y. Cordeau, S. Ayala, N. Holten-Andersen and Z. B. Guan, Tuning Dynamic Mechanical Response in Metallopolymer Networks through Simultaneous Control of Structural and Temporal Properties of the Networks, Macromolecules, 2016, 49(17), 6310–6321 CrossRef.
- R. Wang, M. K. Sing, R. K. Avery, B. S. Souza, M. Kim and B. D. Olsen, Classical Challenges in the Physical Chemistry of Polymer Networks and the Design of New Materials, Acc. Chem. Res., 2016, 49(12), 2786–2795 CrossRef PubMed.
- S. Tang and B. D. Olsen, Relaxation Processes in Supramolecular Metallogels Based on Histidine–Nickel Coordination Bonds, Macromolecules, 2016, 49(23), 9163–9175 CrossRef.
- R. Wang, T.-S. Lin, J. A. Johnson and B. D. Olsen, Kinetic Monte Carlo Simulation for Quantification of the Gel Point of Polymer Networks, ACS Macro Lett., 2017, 6(12), 1414–1419 CrossRef.
- T.-S. Lin, R. Wang, J. A. Johnson and B. D. Olsen, Topological Structure of Networks Formed from Symmetric Four-Arm Precursors, Macromolecules, 2018, 51(3), 1224–1231 CrossRef.
- Y. Liang, L. Li, R. A. Scott and K. L. Kiick, Polymeric Biomaterials: Diverse Functions Enabled by Advances in Macromolecular Chemistry, Macromolecules, 2017, 50(2), 483–502 CrossRef PubMed.
- O. Chaudhuri, Viscoelastic hydrogels for 3D cell culture, Biomater. Sci., 2017, 5(8), 1480–1490 RSC.
- G. R. Gossweiler, G. B. Hewage, G. Soriano, Q. Wang, G. W. Welshofer, X. Zhao and S. L. Craig, Mechanochemical Activation of Covalent Bonds in Polymers with Full and Repeatable Macroscopic Shape Recovery, ACS Macro Lett., 2014, 3(3), 216–219 CrossRef.
- Q. Wang, G. R. Gossweiler, S. L. Craig and X. Zhao, Mechanics of mechanochemically responsive elastomers, J. Mech. Phys. Solids, 2015, 82, 320–344 CrossRef.
- C. W. Macosko and D. R. Miller, A New Derivation of Average Molecular Weights of Nonlinear Polymers, Macromolecules, 1976, 9(2), 199–206 CrossRef PubMed.
- N. R. Langley and K. E. Polmanteer, Relation of elastic modulus to crosslink and entanglement concentrations in rubber networks, J. Polym. Sci., Polym. Phys. Ed., 1974, 12(6), 1023–1034 CrossRef.
- M. S. Green and A. V. Tobolsky, A New Approach to the Theory of Relaxing Polymeric Media, J. Chem. Phys., 1946, 14(2), 80–92 CrossRef.
- M. Rubinstein and R. Colby, Polymer Physics, Oxford University Press, 2003 Search PubMed.
- Y. Guan and Y. Zhang, Boronic acid-containing hydrogels: synthesis and their applications, Chem. Soc. Rev., 2013, 42(20), 8106–8121 RSC.
- P. C. Hiemenz and T. P. Lodge, Polymer Chemistry, Taylor and Francis Group, Boca Raton, FL, 2nd edn, 2007 Search PubMed.
- M. Miyara, I. Takashima, K. Sasaki, R. Kita, N. Shinyashiki and S. Yagihara, Dynamics of uncrystallized water in partially crystallized poly(ethylene glycol)–water mixtures studied by dielectric spectroscopy, Polym. J., 2017, 49(6), 511–518 CrossRef.
- H. Monajemi, M. H. Cheah, V. S. Lee, S. M. Zain and W. A. T. W. Abdullah, On the kinetics and reaction mechanisms of boronic acid in interaction with diols for non-enzymatic glucose monitoring applications: a hybrid DFT study, RSC Adv., 2014, 4(21), 10505 RSC.
- S. W. Sinton, Complexation chemistry of sodium borate with poly(vinyl alcohol) and small diols: a boron-11 NMR study, Macromolecules, 1987, 20(10), 2430–2441 CrossRef.
| This journal is © The Royal Society of Chemistry 2018 |