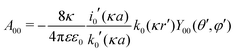DOI:
10.1039/C8SM00399H
(Paper)
Soft Matter, 2018,
14, 4053-4063
Ionic structure around polarizable metal nanoparticles in aqueous electrolytes
Received
27th February 2018
, Accepted 4th April 2018
First published on 10th April 2018
Abstract
Metal nanoparticles are receiving increased scientific attention owing to their unique physical and chemical properties that make them suitable for a wide range of applications in diverse fields, such as electrochemistry, biochemistry, and nanomedicine. Their high metallic polarizability is a crucial determinant that defines their electrostatic character in various electrolyte solutions. Here, we introduce a continuum-based model of a metal nanoparticle with explicit polarizability in the presence of different kinds of electrolytes. We employ several, variously sophisticated, theoretical approaches, corroborated by Monte Carlo simulations in order to elucidate the basic electrostatics principles of the model. We investigate how different kinds of asymmetries between the ions result in non-trivial phenomena, such as charge separation and a build-up of a so-called zero surface-charge double layer.
1 Introduction
The field of electrostatic interactions in classical soft-matter and biological systems has a long and rich history, recognized by many intellectual challenges and ideas.1–3 Maybe one of the most remarkable concepts is the approximation of implicit solvent, a continuum-level approach where a system composed of charged species and solvent molecules is simply treated as a gas of the charged species only, now with their interactions attenuated by the relative dielectric permittivity ε of the solvent.4 Remarkably, this so-called primitive model or dielectric approximation works very well for simple ions in aqueous solutions down to only several layers of water molecules between the ions.5,6 This is also one of the reasons for the efficiency of the Poisson–Boltzmann equation to describe monovalent ions in the water environment. Nonetheless, an implementation of this approximation can become technically involved if dielectric discontinuities are present in the system. This is unfortunately also one of the reasons why dielectric discontinuities are commonly neglected in (too) many studies. Neglecting them is not always justified, because in the presence of charges, a dielectric discontinuity leads to a polarization surface charge density at the boundary, which further influences the local electrostatic potential and interactions with surrounding charges.
In the case of a planar dielectric discontinuity, the electrostatic potential can simply be expressed as the electrostatic potential arising from a fictive “image charge” residing on the other side of the discontinuity. Therefore, in this context, the dielectric discontinuity effects are sometimes referred to as image charges. The dielectric effects in double-layer problems of planar geometry have been elaborated by Torrie, Valleau, and Patey,7 and by Bratko, Jonsson, and Wennerström8 using computer simulations, and by Kjellander and Marčelja9 and Outhwaite, Bhuiyan, and Levine10 utilizing various theoretical frameworks. The image-charge concepts have been adapted to spherical symmetry by Linse.1,11,12 He showed that approximating the exact mathematical expressions for the spherical geometry leads to a simplified picture in which the polarization is described by image charges as in planar cases. The image charges in the spherical geometry are of paramount importance, since a vast majority of the soft-matter electrostatics research in the recent decades has focused on colloidal and biological systems, where various macromolecular structures (e.g., colloids, proteins, polysaccharides, micelles) in water can be modeled as spherical entities with a lower dielectric interior ε′ (due to their predominantly hydrocarbon architectures) than the surrounding water environment (ε′ ≪ ε).1,13–24
The other side of the spectrum, containing spherical bodies of a much higher dielectric interior than water (ε′ ≫ ε), such as for example small metal particles in aqueous environments, has been much less explored. However, the interest in this field has boosted with recent advances in metal nanoparticle chemistry and physics, which have emerged as a broad new discipline in a subdomain of colloids and surfaces.25,26 One of the most prominent discoveries was that gold nanoparticles (of a size 1–10 nm) are active catalysts for oxidation reactions.27 This has triggered a tremendous research activity in nanocatalysis, which presently remains one of the fastest growing areas of nanoscience.28–30 Furthermore, applications involving metal nanoparticles can for instance be found in electrochemistry for nanoelectrodes,31 photovoltaic cells32 electro-osmosis,33 or in biochemistry and nanomedicine for drug delivery, therapeutics, diagnostics, and bioimaging.34–38 At the same time, experimental findings pointed out cytotoxic features of some metal nanoparticles.39,40 Several studies suggested that metal nanoparticles interact with cell membranes in a complex way,41–44 governed by electrochemical potentials and ion distributions around the membrane and a nanoparticle. These achievements emphasize the importance of a deeper theoretical understanding of the interface between a nanoparticle and the solvent, which acts as a determining factor for many properties of the nanoparticle and its complexes in aqueous environments.45
On a simplified level of theoretical description, a basic elucidation involves an implicit-solvent treatment of the electrostatic double-layer problem, adopted from the well-established framework of colloidal science. Now of course, the high dielectric interior inverses the role of the image charges as compared to the case of low-dielectric colloidal particles, which thus become attractive and can trigger completely new physics. The attraction between the metal nanoparticle surface and ions can lead to their accumulation and adsorption and thus to a build-up of an electric double layer surrounding the particle, which crucially impacts the colloidal stability46–50 and interactions with other molecules. This phenomenon is also of great importance in the catalysis by metal nanoparticles in liquid phase.30,51 The reaction rates of surface-catalyzed bimolecular reactions depend on the concentration at the nanoparticle surface of both reactants,52,53 which typically have asymmetric properties (charge, specific adsorption,30etc.).
In this work, we employ theoretical approaches established in the colloidal electrostatics framework, and apply them to less investigated systems of neutral polarizable nanoparticles in different electrolytes. We corroborate the theoretical outcomes by Monte Carlo (MC) simulations, which enable us to assess their regimes of applicability. We show how different kinds of asymmetries between ions result in non-trivial phenomena, such as charge separation and a build-up of net electrostatic potential and effective surface charge.
2 Model and methods
We consider a metal nanoparticle as a neutral sphere with a radius a and a relative permittivity ε′ that is much larger than the permittivity of the surrounding electrolyte solution ε. The electrolyte comprises a mixture of cations with valency q+ and anions with valency q− with bulk concentrations n(+)0 and n(−)0, respectively, by which the electroneutrality condition, q+n(+)0 + q−n(−)0 = 0, has to be fulfilled. We express all distances by the Bjerrum length at ambient temperature, defined as λB = e02/(4πεε0kBT) (in water at room temperature, the value is λB = 0.72 nm), where kB is the Boltzmann constant and T the absolute temperature. The ions are treated as spherical charges with the radius r0 = 0.2λB, which specifies the closest approach to other ions as well as to the nanoparticle surface (see Fig. 1).
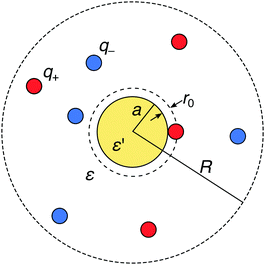 |
| | Fig. 1 Schematic description of a neutral polarizable nanoparticle of radius a (yellow circle) immersed in an electrolyte solution of cations and anions (red and blue circles). The ions have a radius r0, which specifies the closest-approach distance to other ions and to the nanoparticle. The solvent is treated as a background continuum with the relative permittivity ε that is much smaller than the permittivity ε′ of the nanoparticle. In the MC simulations, the whole system is enclosed in a spherical simulation box of radius R with a reflecting boundary condition. | |
The presence of the dielectric inhomogeneity across the boundary of the sphere influences the electrostatic potential, which can be thus described by the Green's function connecting two points r and r′ outside the sphere as
| | | u(r,r′) = u0(r,r′) + uim(r,r′) | (1) |
Here,
u0 is the direct standard Coulomb kernel in the absence of the dielectric inhomogeneities,
| | 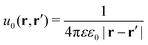 | (2) |
and
uim is the “image correction” term (sometimes referred to also as the “reaction field”) due to the dielectric jump, just as in the case of a planar discontinuity. It turns out that for spherical dielectrics in the limit
ε′ ≫
ε there is an elegant analytical solution for the electrostatic potential, which is obtained with the help of “image charges”.
11,54 Namely, the electrostatic potential of a point charge
q at distance
r′ from the center of the sphere is the same as if there were two additional “image” charges instead of the sphere: one in the center of the sphere with the charge
q(
a/
r′) and the other one with the charge −
q(
a/
r′) dislocated by
a2/
r′ from the center on the line towards the real charge,
| | 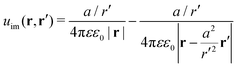 | (3) |
with this exact Green's function at hand, we now turn to investigate the behavior of ions in the proximity of neutral metal nanoparticles in terms of analytical theories as well as MC simulations.
2.1 Theoretical approaches
The most common theoretical framework for treatment of electrostatics problems is the Poisson–Boltzmann (PB) equation, based on mean-field premises.2,3 As such, it cannot describe any image-charge effects on its own. Therefore, for our setting, the PB equation yields a trivial result of non-perturbed ionic distributions around the nanoparticle. In order to account for the polarizability effects, we follow the original ideas of Onsager and Samaras:55 we first calculate the self-energy (i.e., the potential of mean force) of an ion near the dielectric boundary and then combine it with the PB equation.
2.1.1 Onsager–Samaras self-energy.
The simplest theoretical treatment to calculate the self-energy of the above introduced model would be to ignore interactions between ions and considering only the image-charge attraction of an ion with the nanoparticle as dictated by eqn (3). The self-energy of the ion in this approach is given simply by the interaction potential of the ion with its own images, that is (1/2)e02uim(r,r). But due to the screening action of the “ionic atmosphere” caused by surrounding ions, the image force is considerable only within distances of the order of the Debye length from the surface, defined in terms of the screening coefficient κ (i.e., the inverse Debye length) as| | 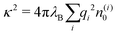 | (4) |
where the sum runs over all ion species. In order to heal the impairments stemming from the surrounding ions, Onsager and Samaras55 proposed a “screening coefficient” to the image charge in the form of exp(−2κz), where z is the distance of the charge from the dielectric plane. The factor of 2 in the exponent arises because the total “action–reaction” screening distance from the ion to the surface and back to the ion is 2z. Besides, the distance 2z corresponds also to the distance between the ion and its virtual image charge in the planar geometry. Note that Onsager and Samaras originally proposed the correction for the planar geometry as a first approximation in order to simplify the laborious calculations by Wagner56 who used a spatially varying screening length. Their primary aim was to compute the excess surface tension of electrolyte solutions by integrating the Gibbs adsorption equation.55
In our first two approaches, we adopt the screening coefficient of Onsager and Samaras to derive an approximate image self-energy of a monovalent ion near a metal sphere. Yet, in the spherical geometry, we have at least two possibilities of adapting the screening distance 2z. In the first approach, we assume twice the distance between the ion and the sphere surface, 2(r − a), which gives the self-energy
| | | wOS0(r) = (1/2)e02uim(r,r)e−2κ(r−a) | (5) |
In the combination with the spherical non-screened image interaction
uim given by
eqn (3), this yields a simple analytical expression (rescaled by the thermal energy
β−1 =
kBT), which we will refer to as “Onsager–Samaras” (OS) image-charge interaction
| | 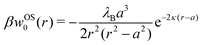 | (6) |
This interaction can be also seen as the adsorption potential of a monovalent ion to the metal nanoparticle.
In our second approach, we consider the screening distance as the separation between the ion and its images. In this case, each of the two induced image charges is screened by its own screening coefficient, which is exp(−κr) for the first and exp[−κ(r − a2/r)] for the second image term in eqn (3). The resulting Onsager–Samaras* (OS*) expression of this approach (which we denote with an asterisk) is then
| | 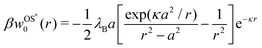 | (7) |
Note that both expressions, OS and OS*, have not been self-consistently derived but obtained by an ad hoc “stitching” together the effects of dielectric discontinuity and ionic screening, and are therefore not exact. Consequently, it is also not a priori clear, which of the two approaches yields more accurate results.
2.1.2 Debye–Hückel self-energy.
In our third approach, we base the image self-energy on the exact Green's function uDH(r,r′) of the Debye–Hückel (DH) equation in the presence of a metal sphere,50,57viz.| | 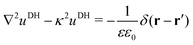 | (8) |
The Green's function simultaneously accounts for dielectric and screening discontinuities at the surface of the metal sphere. The derivation details are provided in Appendix. The final result for the “DH image self-energy” of a monovalent ion reads| | 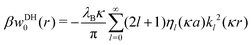 | (9) |
with| | 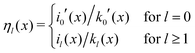 | (10) |
Here, the primes denote derivatives of the spherical modified Bessel functions of the first and second kind, which are defined as| | 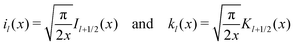 | (11) |
where Il+1/2(x) and Kl+1/2(x) are the conventional modified Bessel functions of the first and second kind, respectively.
In the limit of infinitely large radius a → ∞ (i.e., planar metal wall), eqn (6), (7), and (9) simplify to
| | 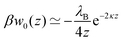 | (12) |
where
z is the distance of the ion from the wall. Exactly the same expression but with the opposite sign applies in the case of an ion near a planar wall with much lower dielectric interior than the electrolyte solution (
ε′ ≪
ε).
58
2.1.3 Boltzmann distribution.
In cases when cations and anions have symmetric properties, no electrostatic potential is generated, and their distribution around the nanoparticle is solely governed by the image self-energy. In a thermodynamic equilibrium, we therefore expect the ion densities to follow the Boltzmann distribution. Using the OS [eqn (6)] and OS* [eqn (7)] self-energies, this leads respectively to| | n(i)(r) = n(i)0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp[−βqi2wOS0(r)] (B–OS) exp[−βqi2wOS0(r)] (B–OS) | (13) |
and| | 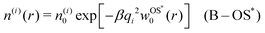 | (14) |
which we will term as “Boltzmann–Onsager–Samaras” approximations (B–OS and B–OS*, respectively). Similarly, using the DH form (9), gives us| | n(i)(r) = n(i)0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp[−βqi2wDH0(r)] (B–DH) exp[−βqi2wDH0(r)] (B–DH) | (15) |
which we term the “Boltzmann–Debye–Hückel” (B–DH) approximation. Here, qi is the valency and n(i)0 the bulk concentration of species i.
2.1.4 Modified Poisson–Boltzmann.
If cations and anions redistribute dissimilarly around the nanoparticle, the resulting charge separation can lead to a net electrostatic potential, and thus eqn (13)–(15) become inaccurate. As already mentioned, the standard PB equation, which relates electrostatic potential and charge distributions, lacks the image self-energy term. A simple heuristic “remedy” to account for the image effects is to insert by hand the self-energy correction into the Boltzmann factor, thus leading to a modified Poisson–Boltzmann equation59,60 in the form| | 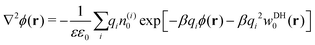 | (16) |
Here, the summation runs over all ion species i. The self-energy term is in principle given either by eqn (6), (7), or (9). In our analyses, however, we will limit ourselves only to the DH-based form, eqn (9). Once the potential ϕ(r) is known, the ion densities can be evaluated as| | n(i)(r) = n(i)0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp[−βqiϕ(r) − βqi2wDH0(r)] (PB–DH) exp[−βqiϕ(r) − βqi2wDH0(r)] (PB–DH) | (17) |
which we term as the “Poisson–Boltzmann–Debye–Hückel” (PB–DH) approach in this paper. In the case of a symmetry between cations and anions, the electrostatic potential vanishes, ϕ = 0, and eqn (17) reduces to eqn (15).
Note again, that the obtained expressions, eqn (13)–(17), cannot be considered as mean-field results, because they do not follow from the PB equation. Even though many studies61–65 generalized the seminal work of Onsager and Samaras, it nevertheless remains widely misinterpreted what is the actual theoretical framework of their approach. In fact, these results extend beyond the mean-field level and can be deduced from the thermodynamic fluctuations of the instantaneous electric fields around the PB solution.66 Alternatively, the PB–DH equation can be derived from a self-consistent variational analysis67–70 by setting by hand the screening coefficient κ(r) to be location independent.
2.2 Monte Carlo simulations
In order to provide “exact” solutions to the introduced model, we perform MC simulations in the canonical NVT ensemble using the standard Metropolis algorithm.71 The system with mobile ions is enclosed in a spherical simulation box with an outer radius R, containing N+ cations and N− anions with valencies q+ and q−, respectively, such that their amounts fulfill the electroneutrality condition N+q+ + N−q− = 0, see Fig. 1. A reflecting boundary condition is applied to the external box boundary. As opposed to periodic boundary conditions, this treatment significantly simplifies the implementation and increases the performance of the simulations (as no Ewald summation is needed), whereas it distorts ionic distributions near the outer boundary. In all simulations, the radius of the spherical box is set to R = 17λB, which is significantly larger than the largest Debye length of κ−1 ≈ 9λB in the study. This guarantees that the outer boundary does not impact the ionic behavior near the nanoparticle.
3 Results and discussions
3.1 Symmetric case
We start our theoretical analysis by first considering symmetric electrolytes (q+ = −q−). In Fig. 2 we plot ion profiles for 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 (top) and 2
1 (top) and 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 (bottom) cases at three different bulk concentrations (from left to right: 2.2, 22, and 220 mM) at a nanoparticle of size a = λB as predicted by all three theoretical approaches eqn (13)–(15) and MC simulations. Since in this case the cations and anions have symmetric properties, their density distributions are equivalent. As seen from the plots, ions are considerably attracted to the metal nanoparticle surface due to attractive image charge interactions. The density peaks right at the surface vicinity (at r = a + r0) and is therefore highly sensitive to the minimum approach distance of an ion to the surface, or to be more precise, to the dielectric boundary, in our model determined by the ion radius r0. From the OS eqn (6), it can be easily appraised that the attractive adsorption energy at the surface (i.e., at r = a + r0), scales as w0 ∼ −1/r0, thus making it very sensitive to the choice of r0. Nevertheless, we will keep the value fixed at r0 = 0.2λB for all further results in this study.
2 (bottom) cases at three different bulk concentrations (from left to right: 2.2, 22, and 220 mM) at a nanoparticle of size a = λB as predicted by all three theoretical approaches eqn (13)–(15) and MC simulations. Since in this case the cations and anions have symmetric properties, their density distributions are equivalent. As seen from the plots, ions are considerably attracted to the metal nanoparticle surface due to attractive image charge interactions. The density peaks right at the surface vicinity (at r = a + r0) and is therefore highly sensitive to the minimum approach distance of an ion to the surface, or to be more precise, to the dielectric boundary, in our model determined by the ion radius r0. From the OS eqn (6), it can be easily appraised that the attractive adsorption energy at the surface (i.e., at r = a + r0), scales as w0 ∼ −1/r0, thus making it very sensitive to the choice of r0. Nevertheless, we will keep the value fixed at r0 = 0.2λB for all further results in this study.
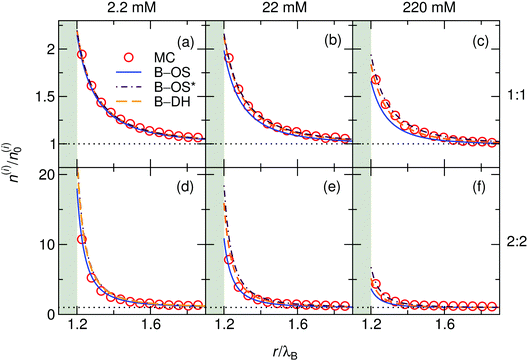 |
| | Fig. 2 Ionic densities for symmetric 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 (top panels) and 2 1 (top panels) and 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 (bottom panels) electrolytes of concentrations 2.2 mM (left), 22 mM (middle), and 220 mM (right) at the metal nanoparticle with the radius a = λB. The shaded areas denote an inaccessible region to ions, r < a + r0, where r0 = 0.2λB is the radius of the ions. 2 (bottom panels) electrolytes of concentrations 2.2 mM (left), 22 mM (middle), and 220 mM (right) at the metal nanoparticle with the radius a = λB. The shaded areas denote an inaccessible region to ions, r < a + r0, where r0 = 0.2λB is the radius of the ions. | |
For very low ion concentrations (2.2 mM), the screening length is considerably large (κ−1 = 9λB for the monovalent and 4λB for the divalent case), such that the interaction near the surface is predominantly governed by the unscreened part of the image charge interaction. Moreover, in the limit of vanishing salt concentration, all three theories become equivalent and exact. In the cases shown in the figure, all the theories agree very well even for salt concentrations up to 220 mM.
The size of the nanoparticle is another important parameter that determines the strength of the image attraction. To demonstrate this effect, we plot in Fig. 3 the density profiles for a monovalent 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 electrolyte at 220 mM for different radii a of the nanoparticle. With an increasing size, the densities at the surface get higher. Larger metal nanoparticles have namely higher polarizability, thus attracting the ions more efficiently. From the plot it can also be observed that all three theories are becoming equivalent as the particle size increases. Fig. 3d shows a normalized ion density at the nanoparticle surface (i.e., at r = a + r0) as a function of its radius a. In the limiting case of vanishing particle (a → 0), clearly, the polarizability vanishes and the density becomes bulk-like. The density increases with the radius and saturates at the limit of a planar wall (indicated by arrows), where the interaction is given by eqn (12). In the limit of vanishing ionic strength (blue solid line), both theories become exact, since in that case the ion–ion interactions become rare and negligible. For higher concentrations (220 mM), the particle of size of a ∼ 2λB already nearly reaches the planar-wall limit. Here, it can also be noted that the theories (except B–OS* in the case of small particles) tend to slightly underestimate the densities near the surface compared with MC simulations. This can be attributed to several effects. One of them might be the absence of screening in the ion-free layer of the width r0 around the surface, which has been for instance discussed by Levin and Mena.72
1 electrolyte at 220 mM for different radii a of the nanoparticle. With an increasing size, the densities at the surface get higher. Larger metal nanoparticles have namely higher polarizability, thus attracting the ions more efficiently. From the plot it can also be observed that all three theories are becoming equivalent as the particle size increases. Fig. 3d shows a normalized ion density at the nanoparticle surface (i.e., at r = a + r0) as a function of its radius a. In the limiting case of vanishing particle (a → 0), clearly, the polarizability vanishes and the density becomes bulk-like. The density increases with the radius and saturates at the limit of a planar wall (indicated by arrows), where the interaction is given by eqn (12). In the limit of vanishing ionic strength (blue solid line), both theories become exact, since in that case the ion–ion interactions become rare and negligible. For higher concentrations (220 mM), the particle of size of a ∼ 2λB already nearly reaches the planar-wall limit. Here, it can also be noted that the theories (except B–OS* in the case of small particles) tend to slightly underestimate the densities near the surface compared with MC simulations. This can be attributed to several effects. One of them might be the absence of screening in the ion-free layer of the width r0 around the surface, which has been for instance discussed by Levin and Mena.72
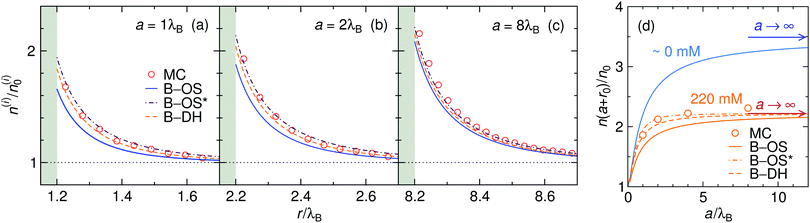 |
| | Fig. 3 The influence of the nanoparticle size. (a–c) Ion densities at nanoparticles of different radii a in a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 electrolyte with the bulk concentration of 220 mM. The shaded areas indicate the excluded region. (d) Ion density at the nanoparticle surface, r = a + r0, as a function of its radius a for vanishing salt concentration, ∼0 mM, and for 220 mM. In the case of vanishing concentration the theories become exact (blue solid line). The arrows indicate the theoretical predictions at a flat interface (all three theories become equivalent). The ion size is set to r0 = 0.2λB. 1 electrolyte with the bulk concentration of 220 mM. The shaded areas indicate the excluded region. (d) Ion density at the nanoparticle surface, r = a + r0, as a function of its radius a for vanishing salt concentration, ∼0 mM, and for 220 mM. In the case of vanishing concentration the theories become exact (blue solid line). The arrows indicate the theoretical predictions at a flat interface (all three theories become equivalent). The ion size is set to r0 = 0.2λB. | |
Coming to the question of which of the three theoretical approaches is the most accurate: it is of course expected that B–DH should predict more accurate results than either B–OS or B–OS*, because it properly takes into account the spherical geometry of the problem on the DH level. As can be seen from Fig. 2 and 3, the results of both approximate theories are very close to the results of B–DH. Interestingly, B–OS seems to consistently yield a bit lower densities than B–DH, meaning that it underestimates the overall attraction of the ion to the metal sphere. On the contrary, B–OS* predicts consistently slightly larger results than B–DH. It seems that for small spheres, the B–OS* performs slightly better than B–OS. However, this cannot be claimed for larger spheres, as shown in Fig. 3c, where both B–OS and B–OS* are approximately equally off, yet in opposite directions. However, the advantage of the approximate OS and OS* expressions is their much simpler mathematical form than B–DH.
3.2 Asymmetric case: specific adsorption
Continuum theoretical descriptions based on the dielectric approximation generally treat ions as equivalent point charges and neglect the nonelectrostatic interactions between ions and the particle surface, which occur in realistic systems.73 The origin of these ion-specific interactions is still the subject of vivid debate, but in recent years, it has become well established that they are mainly influenced by three parameters: ion–surface, ion–water, as well as water–surface interactions, namely hydrophilicity and hydrophobicity.74–77 Different ions are expected to bind to nanoparticle surfaces with different affinities, which typically follow the Hofmeister series.77–79 Binding of ions to the nanoparticle significantly influences their surface charge and the surface potential, which are crucial for the stability of colloidal suspensions based on electrostatic repulsion.48,49,79
On the continuum-level description, the specific effects can be phenomenologically incorporated via various approximate approaches. In the simplest approximation, the specifically adsorbed ions in the Stern layer close to the surface can be, for instance, treated as a fixed pre-determined surface charge, which is a concept adopted in many theoretical approaches. The main shortcoming of this approximation is that it neglects the dependence of the adsorbed amount of ions on the bulk concentration. Furthermore, it also neglects the influence of surface polarizability and ion correlations. Another approach, which we will adopt here, is to assume an additional attractive potential Us(r) between the ions and the nanoparticle. For simplicity, we use a square-well potential of depth ΔU = −2kBT and the range of rs = 0.3λB from the effective nanoparticle surface, as presented in Fig. 4. In order to introduce an asymmetry in our system, we apply this potential only to cations, while we assume no specific interactions for anions. We plug the potential Us(r) into the Boltzmann factor of eqn (15) and (17). This break of the symmetry, assumed in the previous section, has far-reaching consequences as we will see in the following.
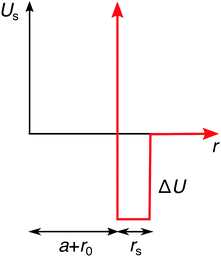 |
| | Fig. 4 Additional specific adsorption potential for cations. | |
The ion distributions, shown in Fig. 5, now exhibit a distinct accumulation of cations due to the specific adsorption potential. Notably, the simple Boltzmann-based approach B–DH [eqn (15)] already captures the densities sufficiently well at low concentrations, since the generated electrostatic potential has negligible influence on ions. But as we increase the concentration, the relative cation density n(+)(r)/n(+)0 near the surface starts to decrease and anion density slightly to increase. Namely, the potential generated by the adsorbed cations is hindering further accumulation of cations. This behavior is well captured by PB–DH [eqn (17)], whereas the simple B–DH starts breaking down. A crucial difference between PB–DH and B–DH shows up when zooming in to the far-field region [panel (d)] that extends beyond the specific adsorption potential. There, the ion distributions are considerably influenced by the generated potential. As can be noted, the anion density is higher than the cationic, since anions have to compensate the accumulated positive charge at the surface. An interesting comparison can be made when considering only a PB equation with the specific adsorption but without the image-charge self-energy,
| | 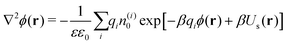 | (18) |
The resulting densities are shown in
Fig. 5d by dash-dotted lines and are in the vicinity of the surface expectedly flatter and lower than the other results due to the missing image-charge attraction. Nevertheless, the PB provides reasonable agreement for the ion densities for distances beyond the specific potential.
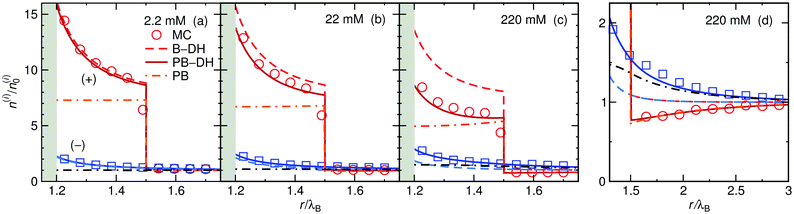 |
| | Fig. 5 Ion density profiles at a nanoparticle of radius a = λB with the specific adsorption of ΔU = −2kBT for cations in (a) 2.2 mM, (b) 22 mM, and (c) 220 mM of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 electrolyte. The red-shaded curves correspond to cation (+) densities and the blue-shaded to anion (−) densities. (d) Far-field region of the case in (c). 1 electrolyte. The red-shaded curves correspond to cation (+) densities and the blue-shaded to anion (−) densities. (d) Far-field region of the case in (c). | |
By integrating the density profiles, we obtain the cumulative charge Z(r) contained within a sphere of radius r around the nanoparticle,
| | 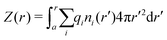 | (19) |
which can be then used to evaluate the electrostatic potential (
e.g., in MC simulations) as
| | 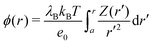 | (20) |
The electrostatic potential generated due to the specific adsorption is shown in
Fig. 6a for 22 and 220 mM of a 1
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
:
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
1 electrolyte. The results of PB–DH compare excellent to the MC results. On the other hand, PB that neglects the polarization [
eqn (18)] yields a bit smaller potentials. It is interesting to examine, how the surface potential, defined as the electrostatic potential at the nanoparticle surface,
ϕ0 =
ϕ(
a), evolves with the ionic strength. As shown in
Fig. 6b,
ϕ0 first linearly rises with concentration, but the rise is becoming gradually weaker for higher concentrations. This slow-down can be attributed to higher repulsion due to accumulated ions and to more effective screening (larger
κ) at higher concentrations. The potential stemming from the B–DH approximation
(15) can be estimated
via the cumulative charge integration,
eqn (20), as is also done for MC data. Since the B–DH approach neglects the potential, which is especially important for far-field behavior, its predictions are severely off compared with other approaches. The B–DH is therefore in this case only a useful predictor for local ion densities, but it fails for far-field.
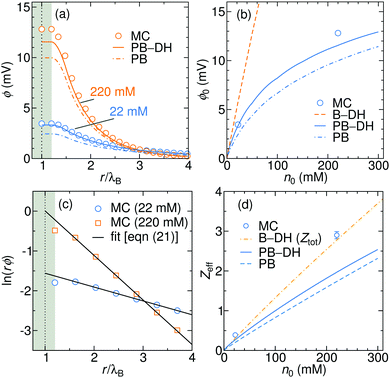 |
| | Fig. 6 (a) Generated electrostatic potential at the nanoparticle stemming from the specific adsorption potential as predicted by the PB and PB–DH theories and MC simulations for 22 and 220 mM of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 salt. (b) The corresponding surface potential, ϕ0 = ϕ(a), as a function salt concentration. (c) Linear fits of eqn (21) to the MC data points for 22 and 220 mM electrolyte concentrations. (d) The effective charge of the metal nanoparticle obtained from the fits of eqn (21) as a function of salt concentration. For the case of B–DH, the total cumulative charge is shown instead. 1 salt. (b) The corresponding surface potential, ϕ0 = ϕ(a), as a function salt concentration. (c) Linear fits of eqn (21) to the MC data points for 22 and 220 mM electrolyte concentrations. (d) The effective charge of the metal nanoparticle obtained from the fits of eqn (21) as a function of salt concentration. For the case of B–DH, the total cumulative charge is shown instead. | |
As is well established in colloid science, we expect the generated potential ϕ(r) to follow a well-known DH law in the far-field,
| | 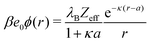 | (21) |
where
Zeff is the effective charge (normalized by the unit charge
e0) of the nanoparticle. Indeed, by fitting
eqn (21) with
Zeff and
κ as fitting parameters to the electrostatic potentials at large distances (shown in
Fig. 6c for MC data), we obtain very good agreement. The effective charge hence arises as a result of charge separation around an otherwise neutral particle.
Fig. 6d further demonstrates that the effective charge rises almost linearly with the salt concentration. Both PB-based approaches PB–DH and PB predict very good results (comparable to MC) at low salinities, but tend to underestimate (PB slightly more) the values at higher concentrations. On the other hand, estimating
Zeff from the B–DH approach is not possible, since the accumulated charge is effectively not screened by the electrolyte and the evaluated potential in this theory does not follow the DH form of
eqn (21). Instead, B–DH predicts a saturation of the cumulative charge
Z(
r) at a non-zero value, whereas it is realistically expected to vanish at
r → ∞, as is the case for the other two theories and MC simulations. Even though this is due to a deficiency of the B–DH approach, the value reflects the charge accumulation right at the surface, where B–DH performs reasonably well. Therefore, it is meaningful to compare the total cumulative charge
Ztot =
Z(
r → ∞) from B–DH to
Zeff from other approaches. Indeed, in
Fig. 6d we see that
Ztot values are comparable to
Zeff.
3.3 Asymmetric case: valency
From specific adsorption we now turn our attention to a different kind of asymmetry, the asymmetry that stems from different ion valencies in an electrolyte. According to eqn (13)–(15), the self-image attraction of an ion to a metal sphere exhibits a square dependence on its charge, ∼q2. Consequently, in cases of asymmetric electrolytes, such as 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 or 3
1 or 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, this valency dependence engenders strong differences in adsorption between both ion species. As opposed to specific adsorption, where the particle polarizability is only an accompanying effect to asymmetric adsorption and related phenomena, it is the main agent for similar phenomena in the case of asymmetric ion valencies.
1, this valency dependence engenders strong differences in adsorption between both ion species. As opposed to specific adsorption, where the particle polarizability is only an accompanying effect to asymmetric adsorption and related phenomena, it is the main agent for similar phenomena in the case of asymmetric ion valencies.
As before, we first look into the ion distributions, which are shown in Fig. 7 for asymmetric 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and 3
1 and 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 electrolytes, and compare the theoretical approaches B–DH and PB–DH with MC simulations. As in the case of the ion-specific adsorption, the theories yield better results at low salt concentrations. At higher concentrations, they perform worse due to delicate ion–ion interactions, in particular for higher asymmetry (i.e., 3
1 electrolytes, and compare the theoretical approaches B–DH and PB–DH with MC simulations. As in the case of the ion-specific adsorption, the theories yield better results at low salt concentrations. At higher concentrations, they perform worse due to delicate ion–ion interactions, in particular for higher asymmetry (i.e., 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1). This theoretical break-down is not unexpected, since multivalent ions are known for significant correlation effects, not accounted for on a mean-field level, a feature that is well established in the double layer literature.80–86 As such, Fig. 7 demonstrates a dramatic influence of the valency on the local densities of ions. The relative ionic density at the surface, n(a + r0)/n0, scales namely as ∼exp(const. × q2), which for low ionic strengths leads “only” to around 2-fold enrichment of monovalent ions in our system (Fig. 2), 16-fold (∼24) of divalent, and an enormous 512-fold (∼29) enrichment of trivalent ions compared to bulk. This implies high ability of metal particles to take-up multivalent ions from a solution. Cases of highly asymmetric electrolytes are very relevant also in catalytic science, where one of well-studied benchmark “model reactions” involves the reduction of trivalent hexacyanoferrate(III) ions by monovalent borohydride ions catalyzed by metal nanoparticles.30,87 The local density of the reactant at the surface is one of the governing factors that determines the reaction rate.52
1). This theoretical break-down is not unexpected, since multivalent ions are known for significant correlation effects, not accounted for on a mean-field level, a feature that is well established in the double layer literature.80–86 As such, Fig. 7 demonstrates a dramatic influence of the valency on the local densities of ions. The relative ionic density at the surface, n(a + r0)/n0, scales namely as ∼exp(const. × q2), which for low ionic strengths leads “only” to around 2-fold enrichment of monovalent ions in our system (Fig. 2), 16-fold (∼24) of divalent, and an enormous 512-fold (∼29) enrichment of trivalent ions compared to bulk. This implies high ability of metal particles to take-up multivalent ions from a solution. Cases of highly asymmetric electrolytes are very relevant also in catalytic science, where one of well-studied benchmark “model reactions” involves the reduction of trivalent hexacyanoferrate(III) ions by monovalent borohydride ions catalyzed by metal nanoparticles.30,87 The local density of the reactant at the surface is one of the governing factors that determines the reaction rate.52
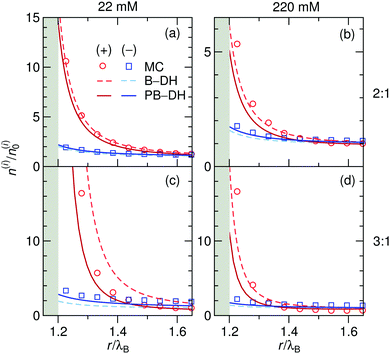 |
| | Fig. 7 Normalized ion density profiles for 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and 3 1 and 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 electrolytes of concentrations 22 mM (left) and 220 mM (right) near a metal nanoparticle of radius a = λB. Cations are considered as the multivalent and anions as the monovalent components. Theoretical approaches B–DH [eqn (9)] and PB–DH [eqn (16)] are compared with MC simulation results. 1 electrolytes of concentrations 22 mM (left) and 220 mM (right) near a metal nanoparticle of radius a = λB. Cations are considered as the multivalent and anions as the monovalent components. Theoretical approaches B–DH [eqn (9)] and PB–DH [eqn (16)] are compared with MC simulation results. | |
In Fig. 8a and b we plot the electrostatic potentials generated by asymmetric electrolytes. While PB–DH gives satisfactory agreement at 22 mM of 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 salt, it becomes poorer at 220 mM, where the deviation reaches a factor of 2. The situation significantly worsens for 3
1 salt, it becomes poorer at 220 mM, where the deviation reaches a factor of 2. The situation significantly worsens for 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 case. The surface potential ϕ0 as a function of concentration is plotted in panel (c). The theoretical prediction, which is now only qualitative, predicts non-monotonic behavior. The surface potential first rapidly rises with concentration due to increased adsorption of ions. At larger concentrations, the rise of the adsorption slows down with increasing concentration due to electrostatic repulsion of already adsorbed ions. Additionally, increasing the salt concentration increases also the screening of the electrolyte, which eventually leads to a drop in the surface potential at high concentrations. Whereas PB–DH yields satisfactory agreement for the 2
1 case. The surface potential ϕ0 as a function of concentration is plotted in panel (c). The theoretical prediction, which is now only qualitative, predicts non-monotonic behavior. The surface potential first rapidly rises with concentration due to increased adsorption of ions. At larger concentrations, the rise of the adsorption slows down with increasing concentration due to electrostatic repulsion of already adsorbed ions. Additionally, increasing the salt concentration increases also the screening of the electrolyte, which eventually leads to a drop in the surface potential at high concentrations. Whereas PB–DH yields satisfactory agreement for the 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 case (deviating by a factor of 2 from MC at large concentrations), it fails considerably for the 3
1 case (deviating by a factor of 2 from MC at large concentrations), it fails considerably for the 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 case. As predicted by the MC simulations, a 3
1 case. As predicted by the MC simulations, a 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 electrolyte creates approximately 20 mV of surface potential in the range of 20–220 mM. This is comparable to the specific-adsorption model discussed in the previous section.
1 electrolyte creates approximately 20 mV of surface potential in the range of 20–220 mM. This is comparable to the specific-adsorption model discussed in the previous section.
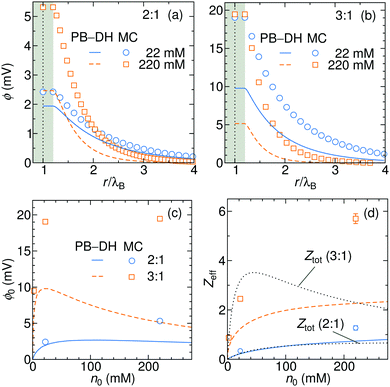 |
| | Fig. 8 Electrostatic potentials for 22 and 220 mM of (a) 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and (b) 3 1 and (b) 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 electrolytes. (c) Surface electrostatic potential as a function of concentrations of 2 1 electrolytes. (c) Surface electrostatic potential as a function of concentrations of 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and 3 1 and 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 electrolytes as obtained from the PB–DH theory (lines) and MC simulations (symbols). (d) Effective charge Zeff of the nanoparticle evaluated from fitting eqn (21) to the potential curves [same legend as in (c)]. In addition, the total accumulative charge Ztot from the B–DH theory is plotted by dotted curves. 1 electrolytes as obtained from the PB–DH theory (lines) and MC simulations (symbols). (d) Effective charge Zeff of the nanoparticle evaluated from fitting eqn (21) to the potential curves [same legend as in (c)]. In addition, the total accumulative charge Ztot from the B–DH theory is plotted by dotted curves. | |
We now fit the DH theory [eqn (21)] to the long-distance potential, which gives us the effective charge Zeff, shown in (d). Contrary to the specific-adsorption model in the previous section, the effective charge in this case is notably a non-linear function of concentration. It first shows a rapid increase with the concentration that turns into a more gradual trend at higher concentrations. Consistently with the results for ϕ0 in (c), the PB–DH theory underestimates the effective charge. Similarly as in the previous section, the total cumulative charge Ztot from the B–DH approach is very similar to Zeff from MC and PB–DH, with an exception for high concentrations of the 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 electrolyte.
1 electrolyte.
The last plot is revealing an immense influence of the valency asymmetry on the effective charge. According to the MC result, a neutral nanoparticle of a radius λB gains an effective charge of around 1 e0 at 220 mM of 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 electrolyte, and an impressive 6 e0 in a 3
1 electrolyte, and an impressive 6 e0 in a 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 electrolyte of the same concentration. Here we note that the expected effective charge scales with an increasing nanoparticle size faster than its surface, since, as we have seen in Fig. 3, larger particles adsorb ions more effectively due to their higher polarizability. In the limit of large nanoparticle sizes, we then expect Zeff ∼ a2. That means that in the case of a polydisperse solution with various particle sizes, larger ones gain significantly larger charges than smaller ones.
1 electrolyte of the same concentration. Here we note that the expected effective charge scales with an increasing nanoparticle size faster than its surface, since, as we have seen in Fig. 3, larger particles adsorb ions more effectively due to their higher polarizability. In the limit of large nanoparticle sizes, we then expect Zeff ∼ a2. That means that in the case of a polydisperse solution with various particle sizes, larger ones gain significantly larger charges than smaller ones.
The presented model points to a practical relevance in the physical chemistry, namely the build-up of an electric double layer even in the absence of surface charge, solely because of the difference in cation and anion concentrations in the surface vicinity. The so-called “zero surface-charge double layer”, a concept introduced by theoretical models a few decades ago,88,89 helped to interpret several experimental facts, such as electrokinetic effects of uncharged colloids.33,90,91 A charged nanoparticle surface enhances its chemical reactivity and consequently has a strong impact on its growth.92 In reality, metal nanoparticles can also possess an intrinsic charge. Partially because nanoparticles can be contaminated with various compounds from electrolytes and oxidized material.92,93 On the other hand, some syntheses techniques of gold nanoparticles (e.g., pulsed laser ablation) lead to partial oxidation (3.3–6.6%94) of surface atoms, forming a pH-dependent equilibrium of Au–OH/AuO− terminal groups, which thus contribute to the overall negative charge of gold nanoparticles.
4 Conclusions
In this study, we revisited a continuum electrostatics problem of image-charge interactions and applied it to a model of a metal nanoparticle, featuring a high dielectric interior and hence high polarizability. We compared the predictions of various theoretical approaches, differing in their mathematical complexity and applicability regimes, with Monte Carlo simulations.
Focusing first on the case of symmetric electrolyte, we found very good agreement between the theoretical approaches and MC simulations. Here, the polarizability effects lead to sizable ion accumulation near the nanoparticle surface, which further depends on the ionic strength as well as on the nanoparticle size. In addition, we investigated how an asymmetry in the adsorption affinities for cations and anions influences their distributions. We separately considered two different kinds of asymmetries, in one case stemming from an additional specific adsorption potential to one ionic species, and in the other case stemming from an asymmetric electrolyte (i.e., 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and 3
1 and 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1). The asymmetries, which give rise to asymmetric distributions of ionic profiles, engender a net electrostatic potential and an effective charge of the nanoparticle. Here, even the most simple approaches that neglect the generated potentials can nevertheless very satisfactorily predict local ion densities (i.e., in the surface vicinity). Of course, at larger distances, where ions tend to neutralize the accumulated charge, it is necessary to invoke a Poisson–Boltzmann description with implemented image-charge corrections. For very high charge asymmetries, such as in a 3
1). The asymmetries, which give rise to asymmetric distributions of ionic profiles, engender a net electrostatic potential and an effective charge of the nanoparticle. Here, even the most simple approaches that neglect the generated potentials can nevertheless very satisfactorily predict local ion densities (i.e., in the surface vicinity). Of course, at larger distances, where ions tend to neutralize the accumulated charge, it is necessary to invoke a Poisson–Boltzmann description with implemented image-charge corrections. For very high charge asymmetries, such as in a 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 electrolyte, the theories face difficulties when compared with the “exact” solutions of MC simulations. The difficulties may be associated with correlation effects between multivalent ions, which are not captured within our theoretical framework. Still, the theories are able to capture the qualitative behavior considerably well and thus help to elucidate basic principles of electrostatics of metal nanoparticles in electrolyte solutions.
1 electrolyte, the theories face difficulties when compared with the “exact” solutions of MC simulations. The difficulties may be associated with correlation effects between multivalent ions, which are not captured within our theoretical framework. Still, the theories are able to capture the qualitative behavior considerably well and thus help to elucidate basic principles of electrostatics of metal nanoparticles in electrolyte solutions.
Finally, we need to be aware of various conceptual challenges that occur in such systems containing metal-like particles in aqueous solutions. Due to high ionic adsorption affinities, the surface details become very important. This is in stark contrast to low-dielectric macromolecules, where ions are typically repelled from the surfaces, and therefore their molecular structure becomes less relevant. One of such details is for instance the exact geometry of the nanoparticles, which typically possess a well-defined atomic arrangement (e.g., resembling the face-centered cubic structure95) and seems to be critical for the nanoparticle's activity.96 A deeper understanding of fine details of metal nanoparticles calls for approaches beyond the idealized continuum model. In this context, in particular atomistic models that take the granularity of the nanoparticle surface and solvent into account are nowadays becoming the focus of sophisticated simulation approaches.45,97,98
Conflicts of interest
There are no conflicts of interest to declare.
Appendix: Green's function near a metal sphere
We decompose the Debye–Hückel Green's function uDH(r,r′) into the direct and indirect part [similarly as the Coulomb Green's function given by eqn (1)],| | | uDH(r,r′) = uDH0(r,r′) + uDHim(r,r′) | (22) |
We now express it in spherical coordinates with the center of the sphere located in the origin of the coordinate system, that is, r(r,θ,φ) and r′(r′,θ′,φ′). A multipole expansion of the direct part yields a form,99| | 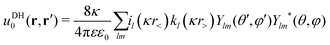 | (23) |
Here, r< and r> correspond respectively to the smaller and the larger radial value among r and  . The functions Ylm are spherical harmonics, the asterisk denotes the complex conjugate value, and the spherical modified Bessel functions are defined by eqn (11). The summation in eqn (23) runs over integer values l = 0, 1, 2… and m = −l,…,+l.
. The functions Ylm are spherical harmonics, the asterisk denotes the complex conjugate value, and the spherical modified Bessel functions are defined by eqn (11). The summation in eqn (23) runs over integer values l = 0, 1, 2… and m = −l,…,+l.
A general Ansatz for the second term in eqn (22) is50,57
| | 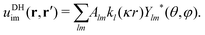 | (24) |
In order to determine coefficients
Alm, we apply two boundary conditions. The first condition requires that the potential on the surface of the metal sphere with a radius
a is constant, that is, independent of the solid angle
Ω| | 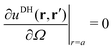 | (25) |
which leads to
| | 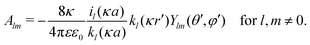 | (26) |
Note that for
l =
m = 0,
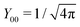
, and consequently ∂
Y00/∂
Ω = 0, thus trivially satisfying
eqn (25). For that reason,
A00 has to be determined by an additional boundary condition. Since the sphere is electrically isolated, it is overall charge neutral. We apply the Gaussian law,
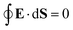
, where we integrate the electric field
E = −
e0∇
uDH over the sphere surface. This provides the second boundary condition
| | 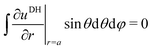 | (27) |
where we integrate over the entire solid angle. Using the identity
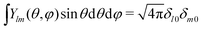
, which eliminates all the terms but
l =
m = 0 when performing the integration in
eqn (27), provides the remaining coefficient
| | 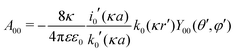 | (28) |
The self-energy of a monovalent ion then follows as
wDH0 = (1/2)
e0uDH(
r,
r), which is
eqn (9) in the main text.
Acknowledgements
The authors thank Won Kyu Kim, Victor G. Ruiz López, Matthias Ballauff, and Rudolf Podgornik for useful discussions. This project has received funding from the European Research Council (ERC) under the European Union's Horizon 2020 research and innovation programme (grant agreement no. 646659-NANOREACTOR). The simulations were performed with resources provided by the North-German Supercomputing Alliance (HLRN).
References
- P. Linse, J. Chem. Phys., 2008, 128, 214505 CrossRef PubMed.
-
C. Holm, P. Kékicheff and R. Podgornik, Electrostatic Effects in Soft Matter and Biophysics: Proceedings of the NATO Advanced Research Workshop on Electrostatic Effects in Soft Matter and Biophysics Les Houches, France 1–13 October 2000, Springer Science & Business Media, 2012, vol. 46 Search PubMed.
-
D. S. Dean, J. Dobnikar, A. Naji and R. Podgornik, Electrostatics of Soft and Disordered Matter, CRC Press, 2014 Search PubMed.
-
C. Böttcher, O. Van Belle, P. Bordewijk and A. Rip, Theory of Electric Polarization, 1973 Search PubMed.
- S. Gavryushov and P. Linse, J. Phys. Chem. B, 2006, 110, 10878–10887 CrossRef CAS PubMed.
- B. Hess, C. Holm and N. van der Vegt, Phys. Rev. Lett., 2006, 96, 147801 CrossRef PubMed.
- G. M. Torrie, J. P. Valleau and G. N. Patey, J. Chem. Phys., 1982, 76, 4615–4622 CrossRef CAS.
- D. Bratko, B. Jönsson and H. Wennerström, Chem. Phys. Lett., 1986, 128, 449–454 CrossRef CAS.
- R. Kjellander and S. Marčelja, Chem. Phys. Lett., 1984, 112, 49–53 CrossRef CAS.
- C. W. Outhwaite, L. B. Bhuiyan and S. Levine, J. Chem. Soc., Faraday Trans., 1980, 76, 1388–1408 RSC.
- P. Linse, J. Phys. Chem., 1986, 90, 6821–6828 CrossRef CAS.
- P. Linse and L. Lue, J. Chem. Phys., 2014, 140, 044903 CrossRef PubMed.
- R. Messina, J. Chem. Phys., 2002, 117, 11062–11074 CrossRef CAS.
- J. Zwanikken and R. van Roij, Phys. Rev. Lett., 2007, 99, 178301 CrossRef PubMed.
- J. Reščič and P. Linse, J. Chem. Phys., 2008, 129, 114505 CrossRef PubMed.
- G. I. Guerrero-García, E. González-Tovar, M. Chávez-Páez and M. Lozada-Cassou, J. Chem. Phys., 2010, 132, 054903 CrossRef PubMed.
- A. P. dos Santos, A. Bakhshandeh and Y. Levin, J. Chem. Phys., 2011, 135, 044124 CrossRef PubMed.
- A. Bakhshandeh, A. P. dos Santos and Y. Levin, Phys. Rev. Lett., 2011, 107, 107801 CrossRef PubMed.
- V. Pryamitsyn and V. Ganesan, J. Chem. Phys., 2015, 143, 164904 CrossRef PubMed.
- Z. Gan, X. Xing and Z. Xu, J. Chem. Phys., 2012, 137, 034708 CrossRef PubMed.
- A. P. dos Santos, M. Girotto and Y. Levin, J. Phys. Chem. B, 2016, 120, 10387–10393 CrossRef CAS PubMed.
- R. Wang and Z.-G. Wang, J. Chem. Phys., 2016, 144, 134902 CrossRef PubMed.
- G. I. Guerrero García and M. Olvera de la Cruz, J. Phys. Chem. B, 2014, 118, 8854–8862 CrossRef PubMed.
- V. B. Tergolina and A. P. dos Santos, J. Chem. Phys., 2017, 147, 114103 CrossRef PubMed.
- M.-C. Daniel and D. Astruc, Chem. Rev., 2004, 104, 293–346 CrossRef CAS PubMed.
- R. Sardar, A. M. Funston, P. Mulvaney and R. W. Murray, Langmuir, 2009, 25, 13840–13851 CrossRef CAS PubMed.
- M. Haruta, Catal. Today, 1997, 36, 153–166 CrossRef CAS.
- C. Burda, X. Chen, R. Narayanan and M. A. El-Sayed, Chem. Rev., 2005, 105, 1025–1102 CrossRef CAS PubMed.
- R. Ferrando, J. Jellinek and R. L. Johnston, Chem. Rev., 2008, 108, 845–910 CrossRef CAS PubMed.
- P. Herves, M. Perez-Lorenzo, L. M. Liz-Marzan, J. Dzubiella, Y. Lu and M. Ballauff, Chem. Soc. Rev., 2012, 41, 5577–5587 RSC.
- C. M. Welch and R. G. Compton, Anal. Bioanal. Chem., 2006, 384, 601–619 CrossRef CAS PubMed.
- W. J. Beek, M. M. Wienk and R. A. Janssen, Adv. Mater., 2004, 16, 1009–1013 CrossRef CAS.
- M. Z. Bazant and T. M. Squires, Phys. Rev. Lett., 2004, 92, 066101 CrossRef PubMed.
- T.-H. Chung, S.-H. Wu, M. Yao, C.-W. Lu, Y.-S. Lin, Y. Hung, C.-Y. Mou, Y.-C. Chen and D.-M. Huang, Biomaterials, 2007, 28, 2959–2966 CrossRef CAS PubMed.
- P. AshaRani, G. Low Kah Mun, M. P. Hande and S. Valiyaveettil, ACS Nano, 2008, 3, 279–290 CrossRef PubMed.
- C.-A. J. Lin, T.-Y. Yang, C.-H. Lee, S. H. Huang, R. A. Sperling, M. Zanella, J. K. Li, J.-L. Shen, H.-H. Wang and H.-I. Yeh,
et al.
, ACS Nano, 2009, 3, 395–401 CrossRef CAS PubMed.
- C. J. Ackerson, P. D. Jadzinsky, J. Z. Sexton, D. A. Bushnell and R. D. Kornberg, Bioconjugate Chem., 2010, 21, 214–218 CrossRef CAS PubMed.
- M.-C. Bowman, T. E. Ballard, C. J. Ackerson, D. L. Feldheim, D. M. Margolis and C. Melander, J. Am. Chem. Soc., 2008, 130, 6896–6897 CrossRef CAS PubMed.
- A. Verma, O. Uzun, Y. Hu, Y. Hu, H.-S. Han, N. Watson, S. Chen, D. J. Irvine and F. Stellacci, Nat. Mater., 2008, 7, 588 CrossRef CAS PubMed.
- P. R. Leroueil, S. A. Berry, K. Duthie, G. Han, V. M. Rotello, D. Q. McNerny, J. R. Baker, B. G. Orr and M. M. Banaszak Holl, Nano Lett., 2008, 8, 420–424 CrossRef CAS PubMed.
- Y. Roiter, M. Ornatska, A. R. Rammohan, J. Balakrishnan, D. R. Heine and S. Minko, Nano Lett., 2008, 8, 941–944 CrossRef CAS PubMed.
- R. Chen, T. A. Ratnikova, M. B. Stone, S. Lin, M. Lard, G. Huang, J. S. Hudson and P. C. Ke, Small, 2010, 6, 612–617 CrossRef CAS PubMed.
- A. Verma and F. Stellacci, Small, 2010, 6, 12–21 CrossRef CAS PubMed.
- J. Lin, H. Zhang, Z. Chen and Y. Zheng, ACS Nano, 2010, 4, 5421–5429 CrossRef CAS PubMed.
- E. Heikkilä, A. A. Gurtovenko, H. Martinez-Seara, H. Häkkinen, I. Vattulainen and J. Akola, J. Phys. Chem. C, 2012, 116, 9805–9815 Search PubMed.
- F. Mafuné, J.-y. Kohno, Y. Takeda, T. Kondow and H. Sawabe, J. Phys. Chem. B, 2000, 104, 8333–8337 CrossRef.
- A. Roucoux, J. Schulz and H. Patin, Chem. Rev., 2002, 102, 3757–3778 CrossRef CAS PubMed.
- T. Kim, K. Lee, M.-S. Gong and S.-W. Joo, Langmuir, 2005, 21, 9524–9528 CrossRef CAS PubMed.
- G. S. Perera, G. Yang, C. B. Nettles, F. Perez, T. K. Hollis and D. Zhang, J. Phys. Chem. C, 2016, 120, 23604–23612 CAS.
-
L. Javidpour, A. Lošdorfer Božič, R. Podgornik and A. Naji, 2018, preprint.
- D. Astruc, F. Lu and J. R. Aranzaes, Angew. Chem., Int. Ed., 2005, 44, 7852–7872 CrossRef CAS PubMed.
- R. Roa, W. K. Kim, M. Kanduč, J. Dzubiella and S. Angioletti-Uberti, ACS Catal., 2017, 7, 5604–5611 CrossRef CAS PubMed.
- S. Roy, A. Rao, G. Devatha and P. P. Pillai, ACS Catal., 2017, 7, 7141–7145 CrossRef CAS.
- H. L. Friedman, Mol. Phys., 1975, 29, 1533–1543 CrossRef CAS.
- L. Onsager and N. Samaras, J. Chem. Phys., 1934, 2, 528–536 CrossRef CAS.
- C. Wagner, Z. Phys., 1924, 25, 474 CAS.
- R. A. Curtis and L. Lue, J. Chem. Phys., 2005, 123, 174702 CrossRef CAS PubMed.
- M. Kanduč, A. Naji, J. Forsman and R. Podgornik, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2011, 84, 011502 CrossRef PubMed.
- B. Corry, S. Kuyucak and S.-H. Chung, Biophys. J., 2003, 84, 3594–3606 CrossRef CAS PubMed.
- A. Onuki, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2006, 73, 021506 CrossRef PubMed.
- H. Diamant and D. Andelman, J. Chem. Phys., 1996, 100, 13732–13742 CrossRef CAS.
- D. Dean and R. Horgan, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2004, 69, 061603 CrossRef CAS PubMed.
- Y. Levin, A. P. dos Santos and A. Diehl, Phys. Rev. Lett., 2009, 103, 257802 CrossRef PubMed.
- N. Schwierz, D. Horinek and R. R. Netz, Langmuir, 2010, 26, 7370–7379 CrossRef CAS PubMed.
- T. Markovich, D. Andelman and R. Podgornik, J. Chem. Phys., 2015, 142, 044702 CrossRef PubMed.
- R. Podgornik and B. Žekš, J. Chem. Soc., Faraday Trans., 1988, 84, 611–631 RSC.
- Z.-G. Wang, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2010, 81, 021501 CrossRef PubMed.
- R. Wang and Z.-G. Wang, J. Chem. Phys., 2015, 142, 104705 CrossRef PubMed.
- R. Wang and Z.-G. Wang, J. Chem. Phys., 2016, 144, 134902 CrossRef PubMed.
- R. R. Netz and H. Orland, EPL, 1999, 45, 726 CrossRef CAS.
- N. Metropolis, A. W. Rosenbluth, M. N. Rosenbluth, A. H. Teller and E. Teller, J. Chem. Phys., 1953, 21, 1087–1092 CrossRef CAS.
- Y. Levin and J. E. Flores-Mena, EPL, 2001, 56, 187–192 CrossRef CAS.
- K. D. Collins, Biophys. Chem., 2012, 167, 43–59 CrossRef PubMed.
- M. Manciu and E. Ruckenstein, Adv. Colloid Interface Sci., 2003, 105, 63–101 CrossRef CAS PubMed.
- D. F. Parsons, M. Boström, P. L. Nostro and B. W. Ninham, Phys. Chem. Chem. Phys., 2011, 13, 12352–12367 RSC.
- A. P. dos Santos and Y. Levin, Faraday Discuss., 2013, 160, 75–87 RSC.
- N. Schwierz, D. Horinek, U. Sivan and R. R. Netz, Curr. Opin. Colloid Interface Sci., 2016, 23, 10–18 CrossRef CAS.
- C. Pfeiffer, C. Rehbock, D. Hühn, C. Carrillo-Carrion, D. J. de Aberasturi, V. Merk, S. Barcikowski and W. J. Parak, J. R. Soc., Interface, 2014, 11, 20130931 CrossRef PubMed.
- V. Merk, C. Rehbock, F. Becker, U. Hagemann, H. Nienhaus and S. Barcikowski, Langmuir, 2014, 30, 4213–4222 CrossRef CAS PubMed.
- G. M. Torrie and J. P. Valleau, J. Phys. Chem., 1982, 86, 3251–3257 CrossRef CAS.
- A. Y. Grosberg, T. Nguyen and B. Shklovskii, Rev. Mod. Phys., 2002, 74, 329 CrossRef CAS.
- Y. Levin, Rep. Prog. Phys., 2002, 65, 1577 CrossRef CAS.
- H. Boroudjerdi, Y.-W. Kim, A. Naji, R. R. Netz, X. Schlagberger and A. Serr, Phys. Rep., 2005, 416, 129–199 CrossRef CAS.
- A. Naji, M. Kanduč, J. Forsman and R. Podgornik, J. Chem. Phys., 2013, 139, 150901 CrossRef PubMed.
- L. Bhuiyan and C. Outhwaite, J. Phys.: Condens. Matter, 2017, 20, 33801 CrossRef.
- M. Kanduč, M. Moazzami-Gudarzi, V. Valmacco, R. Podgornik and G. Trefalt, Phys. Chem. Chem. Phys., 2017, 19, 10069–10080 RSC.
- S. Carregal-Romero, J. Pérez-Juste, P. Hervés, L. M. Liz-Marzán and P. Mulvaney, Langmuir, 2009, 26, 1271–1277 CrossRef PubMed.
- S. S. Dukhin and A. E. Yaroshchuk, Kolloidn. Zh., 1982, 44, 884–895 CAS.
- B. V. Derjaguin, S. S. Dukhin and A. E. Yaroshchuk, J. Colloid Interface Sci., 1987, 115, 234–239 CrossRef.
- A. Dukhin, S. Dukhin and P. Goetz, Langmuir, 2005, 21, 9990–9997 CrossRef CAS PubMed.
- M. Z. Bazant and T. M. Squires, Curr. Opin. Colloid Interface Sci., 2010, 15, 203–213 CrossRef CAS.
- J.-P. Sylvestre, S. Poulin, A. V. Kabashin, E. Sacher, M. Meunier and J. H. Luong, J. Phys. Chem. B, 2004, 108, 16864–16869 CrossRef CAS.
- M. Mucalo and C. Bullen, J. Mater. Sci., 2001, 20, 1853–1856 CAS.
- H. Muto, K. Yamada, K. Miyajima and F. Mafuné, J. Phys. Chem. C, 2007, 111, 17221–17226 CAS.
- V. Petkov, Y. Peng, G. Williams, B. Huang, D. Tomalia and Y. Ren, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 72, 195402 CrossRef.
- M. A. Mahmoud, R. Narayanan and M. A. El-Sayed, Acc. Chem. Res., 2013, 46, 1795–1805 CrossRef CAS PubMed.
- X. Chen, A. Munjiza, K. Zhang and D. Wen, J. Phys. Chem. C, 2014, 118, 1285–1293 CAS.
- X. Li and H. Ågren, J. Phys. Chem. C, 2015, 119, 19430–19437 CAS.
- A. H. Boschitsch, M. O. Fenley and W. K. Olson, J. Comput. Phys., 1999, 151, 212–241 CrossRef CAS.
|
| This journal is © The Royal Society of Chemistry 2018 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article ac,
Joachim
Dzubiella
ac,
Joachim
Dzubiella
 ad and
Matej
Kanduč
ad and
Matej
Kanduč
 *a
*a
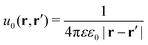
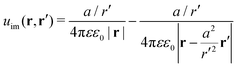
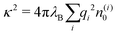
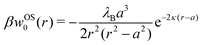
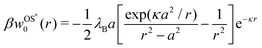
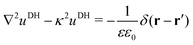
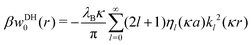
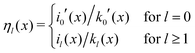
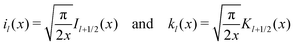
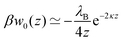
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp[−βqi2wOS0(r)] (B–OS)
exp[−βqi2wOS0(r)] (B–OS)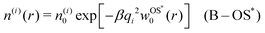
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp[−βqi2wDH0(r)] (B–DH)
exp[−βqi2wDH0(r)] (B–DH)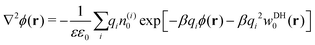
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp[−βqiϕ(r) − βqi2wDH0(r)] (PB–DH)
exp[−βqiϕ(r) − βqi2wDH0(r)] (PB–DH)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 (top) and 2
1 (top) and 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 (bottom) cases at three different bulk concentrations (from left to right: 2.2, 22, and 220 mM) at a nanoparticle of size a = λB as predicted by all three theoretical approaches eqn (13)–(15) and MC simulations. Since in this case the cations and anions have symmetric properties, their density distributions are equivalent. As seen from the plots, ions are considerably attracted to the metal nanoparticle surface due to attractive image charge interactions. The density peaks right at the surface vicinity (at r = a + r0) and is therefore highly sensitive to the minimum approach distance of an ion to the surface, or to be more precise, to the dielectric boundary, in our model determined by the ion radius r0. From the OS eqn (6), it can be easily appraised that the attractive adsorption energy at the surface (i.e., at r = a + r0), scales as w0 ∼ −1/r0, thus making it very sensitive to the choice of r0. Nevertheless, we will keep the value fixed at r0 = 0.2λB for all further results in this study.
2 (bottom) cases at three different bulk concentrations (from left to right: 2.2, 22, and 220 mM) at a nanoparticle of size a = λB as predicted by all three theoretical approaches eqn (13)–(15) and MC simulations. Since in this case the cations and anions have symmetric properties, their density distributions are equivalent. As seen from the plots, ions are considerably attracted to the metal nanoparticle surface due to attractive image charge interactions. The density peaks right at the surface vicinity (at r = a + r0) and is therefore highly sensitive to the minimum approach distance of an ion to the surface, or to be more precise, to the dielectric boundary, in our model determined by the ion radius r0. From the OS eqn (6), it can be easily appraised that the attractive adsorption energy at the surface (i.e., at r = a + r0), scales as w0 ∼ −1/r0, thus making it very sensitive to the choice of r0. Nevertheless, we will keep the value fixed at r0 = 0.2λB for all further results in this study.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 electrolyte at 220 mM for different radii a of the nanoparticle. With an increasing size, the densities at the surface get higher. Larger metal nanoparticles have namely higher polarizability, thus attracting the ions more efficiently. From the plot it can also be observed that all three theories are becoming equivalent as the particle size increases. Fig. 3d shows a normalized ion density at the nanoparticle surface (i.e., at r = a + r0) as a function of its radius a. In the limiting case of vanishing particle (a → 0), clearly, the polarizability vanishes and the density becomes bulk-like. The density increases with the radius and saturates at the limit of a planar wall (indicated by arrows), where the interaction is given by eqn (12). In the limit of vanishing ionic strength (blue solid line), both theories become exact, since in that case the ion–ion interactions become rare and negligible. For higher concentrations (220 mM), the particle of size of a ∼ 2λB already nearly reaches the planar-wall limit. Here, it can also be noted that the theories (except B–OS* in the case of small particles) tend to slightly underestimate the densities near the surface compared with MC simulations. This can be attributed to several effects. One of them might be the absence of screening in the ion-free layer of the width r0 around the surface, which has been for instance discussed by Levin and Mena.72
1 electrolyte at 220 mM for different radii a of the nanoparticle. With an increasing size, the densities at the surface get higher. Larger metal nanoparticles have namely higher polarizability, thus attracting the ions more efficiently. From the plot it can also be observed that all three theories are becoming equivalent as the particle size increases. Fig. 3d shows a normalized ion density at the nanoparticle surface (i.e., at r = a + r0) as a function of its radius a. In the limiting case of vanishing particle (a → 0), clearly, the polarizability vanishes and the density becomes bulk-like. The density increases with the radius and saturates at the limit of a planar wall (indicated by arrows), where the interaction is given by eqn (12). In the limit of vanishing ionic strength (blue solid line), both theories become exact, since in that case the ion–ion interactions become rare and negligible. For higher concentrations (220 mM), the particle of size of a ∼ 2λB already nearly reaches the planar-wall limit. Here, it can also be noted that the theories (except B–OS* in the case of small particles) tend to slightly underestimate the densities near the surface compared with MC simulations. This can be attributed to several effects. One of them might be the absence of screening in the ion-free layer of the width r0 around the surface, which has been for instance discussed by Levin and Mena.72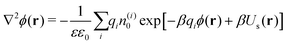
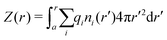
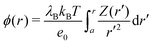
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 electrolyte. The results of PB–DH compare excellent to the MC results. On the other hand, PB that neglects the polarization [eqn (18)] yields a bit smaller potentials. It is interesting to examine, how the surface potential, defined as the electrostatic potential at the nanoparticle surface, ϕ0 = ϕ(a), evolves with the ionic strength. As shown in Fig. 6b, ϕ0 first linearly rises with concentration, but the rise is becoming gradually weaker for higher concentrations. This slow-down can be attributed to higher repulsion due to accumulated ions and to more effective screening (larger κ) at higher concentrations. The potential stemming from the B–DH approximation (15) can be estimated via the cumulative charge integration, eqn (20), as is also done for MC data. Since the B–DH approach neglects the potential, which is especially important for far-field behavior, its predictions are severely off compared with other approaches. The B–DH is therefore in this case only a useful predictor for local ion densities, but it fails for far-field.
1 electrolyte. The results of PB–DH compare excellent to the MC results. On the other hand, PB that neglects the polarization [eqn (18)] yields a bit smaller potentials. It is interesting to examine, how the surface potential, defined as the electrostatic potential at the nanoparticle surface, ϕ0 = ϕ(a), evolves with the ionic strength. As shown in Fig. 6b, ϕ0 first linearly rises with concentration, but the rise is becoming gradually weaker for higher concentrations. This slow-down can be attributed to higher repulsion due to accumulated ions and to more effective screening (larger κ) at higher concentrations. The potential stemming from the B–DH approximation (15) can be estimated via the cumulative charge integration, eqn (20), as is also done for MC data. Since the B–DH approach neglects the potential, which is especially important for far-field behavior, its predictions are severely off compared with other approaches. The B–DH is therefore in this case only a useful predictor for local ion densities, but it fails for far-field.

![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 salt. (b) The corresponding surface potential, ϕ0 = ϕ(a), as a function salt concentration. (c) Linear fits of eqn (21) to the MC data points for 22 and 220 mM electrolyte concentrations. (d) The effective charge of the metal nanoparticle obtained from the fits of eqn (21) as a function of salt concentration. For the case of B–DH, the total cumulative charge is shown instead.
1 salt. (b) The corresponding surface potential, ϕ0 = ϕ(a), as a function salt concentration. (c) Linear fits of eqn (21) to the MC data points for 22 and 220 mM electrolyte concentrations. (d) The effective charge of the metal nanoparticle obtained from the fits of eqn (21) as a function of salt concentration. For the case of B–DH, the total cumulative charge is shown instead.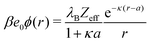
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 or 3
1 or 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, this valency dependence engenders strong differences in adsorption between both ion species. As opposed to specific adsorption, where the particle polarizability is only an accompanying effect to asymmetric adsorption and related phenomena, it is the main agent for similar phenomena in the case of asymmetric ion valencies.
1, this valency dependence engenders strong differences in adsorption between both ion species. As opposed to specific adsorption, where the particle polarizability is only an accompanying effect to asymmetric adsorption and related phenomena, it is the main agent for similar phenomena in the case of asymmetric ion valencies.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and 3
1 and 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 electrolytes, and compare the theoretical approaches B–DH and PB–DH with MC simulations. As in the case of the ion-specific adsorption, the theories yield better results at low salt concentrations. At higher concentrations, they perform worse due to delicate ion–ion interactions, in particular for higher asymmetry (i.e., 3
1 electrolytes, and compare the theoretical approaches B–DH and PB–DH with MC simulations. As in the case of the ion-specific adsorption, the theories yield better results at low salt concentrations. At higher concentrations, they perform worse due to delicate ion–ion interactions, in particular for higher asymmetry (i.e., 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1). This theoretical break-down is not unexpected, since multivalent ions are known for significant correlation effects, not accounted for on a mean-field level, a feature that is well established in the double layer literature.80–86 As such, Fig. 7 demonstrates a dramatic influence of the valency on the local densities of ions. The relative ionic density at the surface, n(a + r0)/n0, scales namely as ∼exp(const. × q2), which for low ionic strengths leads “only” to around 2-fold enrichment of monovalent ions in our system (Fig. 2), 16-fold (∼24) of divalent, and an enormous 512-fold (∼29) enrichment of trivalent ions compared to bulk. This implies high ability of metal particles to take-up multivalent ions from a solution. Cases of highly asymmetric electrolytes are very relevant also in catalytic science, where one of well-studied benchmark “model reactions” involves the reduction of trivalent hexacyanoferrate(III) ions by monovalent borohydride ions catalyzed by metal nanoparticles.30,87 The local density of the reactant at the surface is one of the governing factors that determines the reaction rate.52
1). This theoretical break-down is not unexpected, since multivalent ions are known for significant correlation effects, not accounted for on a mean-field level, a feature that is well established in the double layer literature.80–86 As such, Fig. 7 demonstrates a dramatic influence of the valency on the local densities of ions. The relative ionic density at the surface, n(a + r0)/n0, scales namely as ∼exp(const. × q2), which for low ionic strengths leads “only” to around 2-fold enrichment of monovalent ions in our system (Fig. 2), 16-fold (∼24) of divalent, and an enormous 512-fold (∼29) enrichment of trivalent ions compared to bulk. This implies high ability of metal particles to take-up multivalent ions from a solution. Cases of highly asymmetric electrolytes are very relevant also in catalytic science, where one of well-studied benchmark “model reactions” involves the reduction of trivalent hexacyanoferrate(III) ions by monovalent borohydride ions catalyzed by metal nanoparticles.30,87 The local density of the reactant at the surface is one of the governing factors that determines the reaction rate.52
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and 3
1 and 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 electrolytes of concentrations 22 mM (left) and 220 mM (right) near a metal nanoparticle of radius a = λB. Cations are considered as the multivalent and anions as the monovalent components. Theoretical approaches B–DH [eqn (9)] and PB–DH [eqn (16)] are compared with MC simulation results.
1 electrolytes of concentrations 22 mM (left) and 220 mM (right) near a metal nanoparticle of radius a = λB. Cations are considered as the multivalent and anions as the monovalent components. Theoretical approaches B–DH [eqn (9)] and PB–DH [eqn (16)] are compared with MC simulation results.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 salt, it becomes poorer at 220 mM, where the deviation reaches a factor of 2. The situation significantly worsens for 3
1 salt, it becomes poorer at 220 mM, where the deviation reaches a factor of 2. The situation significantly worsens for 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 case. The surface potential ϕ0 as a function of concentration is plotted in panel (c). The theoretical prediction, which is now only qualitative, predicts non-monotonic behavior. The surface potential first rapidly rises with concentration due to increased adsorption of ions. At larger concentrations, the rise of the adsorption slows down with increasing concentration due to electrostatic repulsion of already adsorbed ions. Additionally, increasing the salt concentration increases also the screening of the electrolyte, which eventually leads to a drop in the surface potential at high concentrations. Whereas PB–DH yields satisfactory agreement for the 2
1 case. The surface potential ϕ0 as a function of concentration is plotted in panel (c). The theoretical prediction, which is now only qualitative, predicts non-monotonic behavior. The surface potential first rapidly rises with concentration due to increased adsorption of ions. At larger concentrations, the rise of the adsorption slows down with increasing concentration due to electrostatic repulsion of already adsorbed ions. Additionally, increasing the salt concentration increases also the screening of the electrolyte, which eventually leads to a drop in the surface potential at high concentrations. Whereas PB–DH yields satisfactory agreement for the 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 case (deviating by a factor of 2 from MC at large concentrations), it fails considerably for the 3
1 case (deviating by a factor of 2 from MC at large concentrations), it fails considerably for the 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 case. As predicted by the MC simulations, a 3
1 case. As predicted by the MC simulations, a 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 electrolyte creates approximately 20 mV of surface potential in the range of 20–220 mM. This is comparable to the specific-adsorption model discussed in the previous section.
1 electrolyte creates approximately 20 mV of surface potential in the range of 20–220 mM. This is comparable to the specific-adsorption model discussed in the previous section.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and (b) 3
1 and (b) 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 electrolytes. (c) Surface electrostatic potential as a function of concentrations of 2
1 electrolytes. (c) Surface electrostatic potential as a function of concentrations of 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and 3
1 and 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 electrolytes as obtained from the PB–DH theory (lines) and MC simulations (symbols). (d) Effective charge Zeff of the nanoparticle evaluated from fitting eqn (21) to the potential curves [same legend as in (c)]. In addition, the total accumulative charge Ztot from the B–DH theory is plotted by dotted curves.
1 electrolytes as obtained from the PB–DH theory (lines) and MC simulations (symbols). (d) Effective charge Zeff of the nanoparticle evaluated from fitting eqn (21) to the potential curves [same legend as in (c)]. In addition, the total accumulative charge Ztot from the B–DH theory is plotted by dotted curves.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 electrolyte.
1 electrolyte.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 electrolyte, and an impressive 6 e0 in a 3
1 electrolyte, and an impressive 6 e0 in a 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 electrolyte of the same concentration. Here we note that the expected effective charge scales with an increasing nanoparticle size faster than its surface, since, as we have seen in Fig. 3, larger particles adsorb ions more effectively due to their higher polarizability. In the limit of large nanoparticle sizes, we then expect Zeff ∼ a2. That means that in the case of a polydisperse solution with various particle sizes, larger ones gain significantly larger charges than smaller ones.
1 electrolyte of the same concentration. Here we note that the expected effective charge scales with an increasing nanoparticle size faster than its surface, since, as we have seen in Fig. 3, larger particles adsorb ions more effectively due to their higher polarizability. In the limit of large nanoparticle sizes, we then expect Zeff ∼ a2. That means that in the case of a polydisperse solution with various particle sizes, larger ones gain significantly larger charges than smaller ones.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and 3
1 and 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1). The asymmetries, which give rise to asymmetric distributions of ionic profiles, engender a net electrostatic potential and an effective charge of the nanoparticle. Here, even the most simple approaches that neglect the generated potentials can nevertheless very satisfactorily predict local ion densities (i.e., in the surface vicinity). Of course, at larger distances, where ions tend to neutralize the accumulated charge, it is necessary to invoke a Poisson–Boltzmann description with implemented image-charge corrections. For very high charge asymmetries, such as in a 3
1). The asymmetries, which give rise to asymmetric distributions of ionic profiles, engender a net electrostatic potential and an effective charge of the nanoparticle. Here, even the most simple approaches that neglect the generated potentials can nevertheless very satisfactorily predict local ion densities (i.e., in the surface vicinity). Of course, at larger distances, where ions tend to neutralize the accumulated charge, it is necessary to invoke a Poisson–Boltzmann description with implemented image-charge corrections. For very high charge asymmetries, such as in a 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 electrolyte, the theories face difficulties when compared with the “exact” solutions of MC simulations. The difficulties may be associated with correlation effects between multivalent ions, which are not captured within our theoretical framework. Still, the theories are able to capture the qualitative behavior considerably well and thus help to elucidate basic principles of electrostatics of metal nanoparticles in electrolyte solutions.
1 electrolyte, the theories face difficulties when compared with the “exact” solutions of MC simulations. The difficulties may be associated with correlation effects between multivalent ions, which are not captured within our theoretical framework. Still, the theories are able to capture the qualitative behavior considerably well and thus help to elucidate basic principles of electrostatics of metal nanoparticles in electrolyte solutions.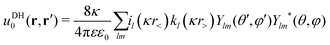
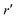 . The functions Ylm are spherical harmonics, the asterisk denotes the complex conjugate value, and the spherical modified Bessel functions are defined by eqn (11). The summation in eqn (23) runs over integer values l = 0, 1, 2… and m = −l,…,+l.
. The functions Ylm are spherical harmonics, the asterisk denotes the complex conjugate value, and the spherical modified Bessel functions are defined by eqn (11). The summation in eqn (23) runs over integer values l = 0, 1, 2… and m = −l,…,+l.
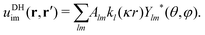
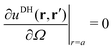
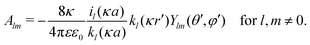
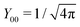 , and consequently ∂Y00/∂Ω = 0, thus trivially satisfying eqn (25). For that reason, A00 has to be determined by an additional boundary condition. Since the sphere is electrically isolated, it is overall charge neutral. We apply the Gaussian law,
, and consequently ∂Y00/∂Ω = 0, thus trivially satisfying eqn (25). For that reason, A00 has to be determined by an additional boundary condition. Since the sphere is electrically isolated, it is overall charge neutral. We apply the Gaussian law, 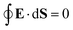 , where we integrate the electric field E = −e0∇uDH over the sphere surface. This provides the second boundary condition
, where we integrate the electric field E = −e0∇uDH over the sphere surface. This provides the second boundary condition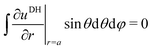
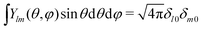 , which eliminates all the terms but l = m = 0 when performing the integration in eqn (27), provides the remaining coefficient
, which eliminates all the terms but l = m = 0 when performing the integration in eqn (27), provides the remaining coefficient