 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Macromolecular diffusion in crowded media beyond the hard-sphere model†
Pablo M.
Blanco
 *ab,
Josep Lluís
Garcés
c,
Sergio
Madurga
*ab and
Francesc
Mas
ab
*ab,
Josep Lluís
Garcés
c,
Sergio
Madurga
*ab and
Francesc
Mas
ab
aDepartment of Material Science and Physical Chemistry, Barcelona University, 08028 Barcelona, Spain. E-mail: fmas@ub.edu; pmblanco@ub.edu; s.madurga@ub.edu
bInstitute of Theoretical and Computational Chemistry (IQTC), Barcelona University, 08028 Barcelona, Spain
cDepartment of Chemistry, University of Lleida (UdL), 25003 Lleida, Spain. E-mail: jlgarces@quimica.udl.cat
First published on 20th March 2018
Abstract
The effect of macromolecular crowding on diffusion beyond the hard-core sphere model is studied. A new coarse-grained model is presented, the Chain Entanglement Softened Potential (CESP) model, which takes into account the macromolecular flexibility and chain entanglement. The CESP model uses a shoulder-shaped interaction potential that is implemented in the Brownian Dynamics (BD) computations. The interaction potential contains only one parameter associated with the chain entanglement energetic cost (Ur). The hydrodynamic interactions are included in the BD computations via Tokuyama mean-field equations. The model is used to analyze the diffusion of a streptavidin protein among different sized dextran obstacles. For this system, Ur is obtained by fitting the streptavidin experimental long-time diffusion coefficient Dlongversus the macromolecular concentration for D50 (indicating their molecular weight in kg mol−1) dextran obstacles. The obtained Dlong values show better quantitative agreement with experiments than those obtained with hard-core spheres. Moreover, once parametrized, the CESP model is also able to quantitatively predict Dlong and the anomalous exponent (α) for streptavidin diffusion among D10, D400 and D700 dextran obstacles. Dlong, the short-time diffusion coefficient (Dshort) and α are obtained from the BD simulations by using a new empirical expression, able to describe the full temporal evolution of the diffusion coefficient.
1 Introduction
Biological media are known to contain a high concentration of a wide variety of macromolecular species such as proteins, polysaccharides or nucleic acids. For instance, the weight fraction of protein is around 5% in lymph, 9% in blood plasma and 35% in hemolysate.1,2 In the cellular cytosol, three-dimensional analysis of electron micrographs revealed a 20% volume fraction of fibrous supramolecular structures (i.e. F-actin, microtubules and intermediate filaments).3 These conditions, known as “macromolecular crowding” involve non-specific interactions among macromolecular species due to the excluded volume, van der Waals, electrostatic and hydrodynamic interactions. Macromolecular crowding substantially alters the diffusion processes, conformational properties and reactivity of the macromolecular species.4–8Several efforts are underway to properly understand the effect of crowding in macromolecular diffusion.9 Recently, in vivo and in vitro experimental studies have been carried out to study macromolecular diffusion in crowded media. In in vivo experiments, fluorescent tracer proteins are introduced into the cell by means of transfection, microinjection or recombinant expression.10 Although this strategy allows the direct study of the macromolecular crowding, the intrinsic differences between the different intracellular microenvironments make the interpretation of the results difficult. In vitro experiments attempt to overcome this problem by reducing the complexity and heterogeneity of the media. The crowded environment is recreated using highly concentrated polymer solutions (usually dextran or ficoll).11–13 The motion of a fluorescent protein is then studied using spectroscopic techniques,14 mainly Fluorescence Correlation Spectroscopy (FCS)11 and Fluorescence Recovery After Photobleaching (FRAP).12,13
In order to interpret the experimental results, an increasing number of computational studies have been performed15 that provide a highly controlled environment. The comparison of the computational results with the experimentally observed results facilitates the quantification of the factors governing macromolecular diffusion in crowded media. Different computational approaches have been applied ranging from on-lattice Monte Carlo simulations16,17 and off-lattice Brownian Dynamics (BD)18–25 to Molecular Dynamics simulations.23,26,27 In implicit solvent simulations like BD, the Hydrodynamic Interactions (HIs) of the macromolecules have been found to be crucial to properly describe their motion in crowded media.28
Macromolecular diffusion is known to become sub-diffusive in crowded media. The time-dependent diffusion coefficient (D) of the macromolecule is defined as D ≡ 〈r2〉/(2dt), where d is the topological dimension of the system and 〈r2〉 is the mean square displacement of the particles. In crowded media, D undergoes a transition from an initial value at short times (Dshort) to an asymptotic final value at long times (Dlong). During the transition between both regimes, macromolecular motion shows a non-linear dependence on time (usually called anomalous diffusion):16,29
| 〈r2〉 = (2d)Γαtα | (1) |
In order to study macromolecular diffusion in the long-time regime, it is necessary to reach μs time scales. However, the large number of atoms present in a highly concentrated macromolecular solution causes atomistic-detailed computations to be limited to smaller time scales. As a consequence, in order to reach larger time scales, coarse grained approaches become necessary. Several approximations have been developed to take into account the HIs. The more accurate descriptions are those that involve the calculation of the diffusion tensor,30 mainly based on the Rotne–Prager–Yamakawa approach.31–33 However, the calculation of the diffusion tensor at every time step is computationally very expensive. An alternative method is based on the mean field equations proposed by Tokuyama,34–36 which introduce an effective diffusion coefficient accounting for the HIs. This effective diffusion coefficient is computed as a function of the volume fraction and the dilute solution diffusion coefficient. However, the Tokuyama method is limited since it was deduced for systems of equal sized hard-core spheres. In previous studies that use Tokuyama equations, macromolecules are considered as hard spheres and implicit solvent via Brownian Dynamics (BD) is used.18,20–23
In general, macromolecules have a flexible structure. As a result, when two macromolecules approach each other, their branches can become entangled and non-specific attractive and/or repulsive interactions between their chains are expected. This fact can play an important role in macromolecular diffusion in crowded media. Therefore, models going beyond the hard-core spheres, in which the conformational dynamic behaviour of macromolecules is lost, are necessary.37 Softened interaction potentials have been previously proposed in the study of colloidal systems such as polymeric micelles38,39 and star-polymers.40–44 These systems consist of a dense core surrounded by a rather sparse corona. For pluronic polymeric micelles, studies based on implicit solvent and coarse grained computations have shown that both attractive and repulsive forces are present. However, the resulting potential of mean force between two particles is found to be purely repulsive.39 Similar behaviour is found in the effective interparticle potentials used in star-polymer models. Star polymers can be modelled as surfaces coated with grafted polymers interacting by excluded volume effects. The particles are large enough to employ the Derjaguin approximation.45–47 The proposed potential is the result of the soft repulsion between the polymeric branches and a hard-core repulsion between the rigid cores.
In this paper, diffusion of the streptavidin protein among dextran molecules will be analysed. Dextran has a branched, highly hydrated, polymeric structure. Dextran molecules are significantly smaller than micelles and star-polymers, so that some approximations previously used in these systems, such as the Derjaguin approximation, are no longer valid. On the other hand, their very sparse structure and chemical composition, including polar alcoholic groups, can compensate in part the steric repulsions and favour macromolecular entanglement, so that a singular treatment becomes necessary.
In Section 2, a new coarse-grained approach is proposed: the Chain Entanglement Softened Potential model (CESP). The CESP model is based on an inter-particle interaction potential depicted in Fig. 1. It includes both hard-core and soft interaction regions at proper characteristic lengths. In the soft region, where the potential is shoulder-shaped, particle overlapping is possible, so that macromolecular branches are allowed to become entangled. A single parameter controls the entanglement energy. This potential is introduced in the BD scheme in which the HIs are implemented using the mean-field Tokuyama equations. Dlong and α are obtained from the simulated temporal evolution of D by using a new empirical expression. The new equation, unlike the mostly used power law (eqn (1)), is able to describe the evolution of D for the three temporal regimes.
 | ||
| Fig. 1 Outline of the Chain Entanglement Softened Potential (CESP) model and the potential energy V(r) vs. interparticle distance r (eqn (2)). Three interaction regions can be observed: no interaction (C), soft interaction where entanglement is allowed (B), and hard-core interaction (A). The chosen parameters are dc = 4.58 nm and de = 10.48 nm, for Ur ranging from −500 to 2000 J mol−1. | ||
In Section 3, the CESP model is used to study streptavidin diffusion in crowded media among dextrans of different sizes and concentrations. Firstly, the shoulder shaped potential is parametrized by fitting the computed Dlong to the experimental values11 for D50 (indicating its molecular weight in kg mol−1) dextran obstacles. The BD simulations performed with the CESP model show a quantitative agreement between the calculated and experimental long time diffusion coefficient (Dlong). This agreement is much better than the one obtained when the hard sphere model is used.24 Once parametrized, we show that the CESP model is able to quantitatively predict Dlong and the anomalous exponent (α) for the rest of the dextran sizes (D10, D400 and D700) in a wide range of macromolecular concentrations. Analysis of the radial distribution functions shows a significant increase in the population of entangled macromolecules with macromolecular concentration. This result highlights the importance of including the conformational dynamics of the macromolecules in the diffusion processes in crowded media.
2 Methodology
2.1 Chain Entanglement Softened Potential (CESP) model
In BD simulations of protein diffusion in crowded media, it is usual to reduce the resolution of the macromolecules to effective hard spheres.18,20–23 This approximation significantly reduces the computational cost allowing larger time scales to be reached. However, the loss of the macromolecular structural properties could become unrealistic in many cases.37 As the volume fraction increases, the macromolecules are expected to start to become entangled, a fact that cannot be properly described within the hard-core sphere model.24In the present work, macromolecular entanglement is introduced via a coarse-grained model, the Chain Entanglement Softened Potential model (CESP). The model relies on an empiric interparticle interaction potential that resembles the continuous shouldered well potential used in computational models of coarse-grained fluids.48,49 In these studies, density anomalies have been reported when a softened inter-particle potential is applied. The obtained radial distribution functions showed that an inner coordination shell is formed when the fluid density increases. Moreover, the population of the inner coordination shell was found to be proportional to the fluid density. Here, a redefinition of this idea is proposed. The coarse grained particles are no longer fluid molecules but macromolecules in solution. As the density of macromolecules in solution increases, they start to become entangled. Similar potentials have been used in the description of protein–surface interactions.50
The interaction potential corresponding to the CESP model is shown in Fig. 1. Two clear interaction regions can be observed that define two characteristic distances: the entanglement distance (de) and the core distance (dc). If the macromolecules are at a distance r larger than de, they are considered to be separated, and they interact weakly (Fig. 1C). However, when the macromolecules are at dc ≤ r ≤ de, they are considered to become entangled (Fig. 1B). In the latter situation, steric repulsions start to arise between the macromolecular chains. Such repulsions can be compensated in part by the presence of van der Waals and hydrogen bonding attraction forces. As a result, a shoulder is developed in the proposed potential (Fig. 1). If the macromolecules get closer (r < dc), the steric repulsion between the macromolecular skeletons dramatically increases and the hard-core region emerges (Fig. 1A). The resulting picture resembles models previously proposed for polymer micelles and star-polymers, composed of a dense core and a sparse corona. Unlike these systems, dextran molecules are polysaccharides with a complex branched structure where no structurally differentiated parts can be identified.51,52 Therefore (de) and (dc) should be regarded as the characteristic lengths of the different interaction regimes rather than chemically defined parts of the macromolecules. The proposed potential V(r) acting between two particles at a distance r reads
 | (2) |
The proposed interaction potential will be used to analyze the diffusion of streptavidin among different sized dextrans acting as inert obstacles,11 tracked down using FCS. Both the tracer protein and the dextran obstacles are considered to be able to become entangled. The differences between protein/dextran and dextran/dextran (protein/protein interactions are not relevant due to the large excess of dextran) are then included in an effective way by the specific values of dc and de for the protein and dextran, while the Ur value should be understood as an average interaction parameter. In order to estimate de and dc, the interaction regions in a macromolecule are considered to be concentric spheres with two characteristic radii: the entanglement radius (Re) and the hard-core radius (Rc), so that for two interacting particles i and j, de,ij = Re,i + Re,j and dc,ij = Rc,i + Rc,j.
In this work, Re is associated with the hydrodynamic radius of the macromolecule in dilute solution. For dextran molecules, it has been computed by fitting experimental hydrodynamic radii vs. molecular weight obtained by quasi-elastic light scattering to an empiric power law function.24,53 The dilute solution diffusion coefficient (D0) for dextrans is calculated by incorporating the resulting Re values into the Stokes–Einstein equation. On the other hand, the HYDROPRO software (Version 10)54 has been used to compute D0 corresponding to streptavidin. HYDROPRO considers each atom in the protein surface as a hydrodynamic frictional sphere. Protein atomic coordinates corresponding to three different crystallographic structures55–57 were used in the calculations. D0 was taken as the average of the values resulting from the three structures. Re of streptavidin is then obtained via the Stokes–Einstein equation.
Here, we propose to estimate Rc as the maximum approach distance between macromolecules, and it has been estimated using the specific volume ν, considering them as compact spheres24
 | (3) |
M w, D0, Re and Rc for streptavidin and different sized dextrans are reported in Table 1. Interestingly, the ratio Re/Rc increases with dextran size, which could be caused by an increase in dextran branching with molecular weight. Note also that D10 and streptavidin have similar D0 and Re values. However, D10 has a higher ratio Re/Rc than streptavidin, in accordance with the very different chemical structures of both macromolecules, much more compact in the last case.
| M w [kDa] | R e [nm] | R c [nm] | R e/Rc | D 0 [nm2 ns−1] | |
|---|---|---|---|---|---|
| Streptavidin | 52.8 | 3.04 | 2.45 | 1.24 | 0.085 |
| D10 | 11.6 | 2.77 | 1.43 | 1.94 | 0.089 |
| D50 | 48.6 | 5.24 | 2.29 | 2.29 | 0.047 |
| D400 | 409.8 | 13.52 | 4.67 | 2.90 | 0.018 |
| D700 | 667.8 | 16.81 | 5.51 | 3.14 | 0.015 |
2.2 Brownian Dynamics algorithm
Brownian Dynamics (BD) simulations make use of the Langevin equation in the over-damped limit,60,61 so that the particles are considered to be under the effect of a stochastic force that accounts for the collisions with the solvent. The stochastic force is mathematically represented by Gaussian random noise,19,24,25,62 and the equation of motion for the N particles reads | (4) |
Since the solvent is simulated implicitly, the HIs must be included in eqn (4). HIs are solvent mediated correlations of the particle motions and they have been found to play an important role in macromolecular diffusion in crowded media.24,28,63 HIs can be included in eqn (4) by calculating D following the Rotne–Prager–Yamakawa (RPY) method at each time step,30 which is computationally very demanding.
Tokuyama equations34–36 offer an alternative to the RPY method based on a mean field approximation. In this approach, an effective diffusion coefficient that accounts for the particle mobility reduction due to the HIs is analytically calculated. The expression for the diffusion coefficient is deduced starting from first principles, i.e., the Fokker–Planck equation for the single-particle distribution function coupled with the Navier–Stokes equations. This equation is analytically solved at short times considering a stationary configuration of equal-sized Brownian particles. In doing so, an approximation of the effective diffusion coefficient at short times (Dshort) is obtained. For a particle diffusing in a system with a volume fraction ϕ, Dshort reads
 | (5) |
 | (6) |
 and
and  .
.
In this approach, D in eqn (4) is replaced by the effective Dshort, which is a function of ϕ and D0. However, the choice of ϕ presents two main difficulties. On the one hand, for a number of obstacles NO, one could naively calculate ϕ as
 | (7) |
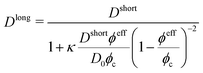 | (8) |
 | (9) |
 , where c is the dextran concentration, ν represents the specific value, and Re/Rc is the characteristic radii ratio. k and m are fitted parameters whose values are k = 3.7 ± 0.1 and m = 1.43 ± 0.08. The best-fitted ϕeff as a function of z for D10 (squares), D50 (circles), D400 (upward-pointing triangles) and D700 (downward-pointing triangles) is shown in Fig. 2. The dashed line represents the best-fitted curve eqn (9). This procedure is actually expected to provide an approximation to ϕeff, whose suitability can only be justified a posteriori, if the BD simulations coupled to the CESP model properly reproduce the experimental Dlong values. This is the case, as will be shown in the next section.
, where c is the dextran concentration, ν represents the specific value, and Re/Rc is the characteristic radii ratio. k and m are fitted parameters whose values are k = 3.7 ± 0.1 and m = 1.43 ± 0.08. The best-fitted ϕeff as a function of z for D10 (squares), D50 (circles), D400 (upward-pointing triangles) and D700 (downward-pointing triangles) is shown in Fig. 2. The dashed line represents the best-fitted curve eqn (9). This procedure is actually expected to provide an approximation to ϕeff, whose suitability can only be justified a posteriori, if the BD simulations coupled to the CESP model properly reproduce the experimental Dlong values. This is the case, as will be shown in the next section.
 | ||
| Fig. 2 Effective volume fraction (ϕeff) as a function of z = kνcRe/Rc estimated using eqn (5)–(8) for D10 (squares), D50 (circles), D400 (upward-pointing triangles) and D700 (downward-pointing triangles) dextran molecules. The dashed line represents the fitted eqn (9). The residuals of the fitting procedure are also depicted and show a very good fitting. | ||
BD simulations are performed in a cubic box under periodic boundary conditions in all directions. The time step is set to 0.1 ns and the simulation time ranges from 10 to 150 μs depending on the time necessary to reach the stationary value of the diffusion coefficient at long times (Dlong). The system temperature is 298.15 K. D is computed viaeqn (5) and (6) using the ϕeff predicted by eqn (9) for each type of particle (dextran and protein). All the studied systems have 100 obstacle dextran particles and only one to five tracer protein particles to ensure that the volume occupied by the tracer is less than 1% of the volume occupied by the obstacles. The length of the simulation box is properly tuned to match the experimental dextran concentration and ranges from 17.56 nm (for the smaller dextran) to 164.32 nm (for the larger dextran). 〈r2〉 is computed after a thermalisation time of 0.5 μs in order to avoid possible initial unrealistic motion due to the random starting configuration. For each studied system, 〈r2〉 is obtained by averaging from 1000 (higher macromolecular concentration) to 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 (lower macromolecular concentration) BD realizations in order to ensure appropriate statistics.
000 (lower macromolecular concentration) BD realizations in order to ensure appropriate statistics.
In Fig. 3, two BD simulation boxes are depicted to illustrate the CESP model. Tracer streptavidin protein molecules (purple) diffuse among D50 dextran obstacles (blue). Each macromolecule is represented as two concentric spheres with radii of Rc and Re, which characterize the soft (transparent) and the hard-core (opaque) interaction regions, respectively. The macromolecular concentrations of the solutions are 25 g L−1 (Fig. 3a) and 100 g L−1 (Fig. 3b). In the less concentrated solution, it can be observed that the soft interaction is enough to avoid macromolecule overlapping. In the more concentrated solutions, steric compression allows the macromolecules to overcome the initial steric repulsion and become entangled.
2.3 Determination of Dlong, Dshort and α from BD simulations: a new empirical equation for the time evolution of D
As mentioned before, the diffusion coefficient D of a particle is known to have a transition between two steady states: Dshort and Dlong. log(D) vs. log(t) profiles computed from BD simulations can be very well fitted to the functionlog(D) = B![[thin space (1/6-em)]](https://www.rsc.org/images/entities/i_char_2009.gif) tanh(β(log(t) − γ)) + A tanh(β(log(t) − γ)) + A | (10) |
In Fig. 4, the time evolution of the simulated diffusion coefficient of streptavidin in a D50 crowded solution, at a macromolecular concentration of 350 g L−1, is shown (blue line). As expected, the diffusion coefficient undergoes a transition from Dshort to Dlong as macromolecular crowding slows down the motion of the tracer particle. It can be observed that eqn (10), depicted in red, fits very well to the computed values over all the temporal regimes, allowing rigorous and easy determination of Dshort, Dlong and α.
 | ||
| Fig. 4 Time evolution of the diffusion coefficient (D) in logarithmic scale. The blue line results from averaging 3000 BD simulations of 100 μs long in a cubic simulation box with a side of 28.466 nm. The simulation box contains 5 tracer particles (streptavidin) diffusing among 100 obstacle particles (D50 dextran). The macromolecular concentration is 350 g L−1. Macromolecular crowding slows down the tracer diffusion coefficient from Dshort to Dlong. The red line is the result of fitting eqn (10) to the simulated results, which allows Dshort, Dlong and α to be easily determined. The resulting fitting is very good, as shown by the residuals. | ||
3 Results and discussion
3.1 Model parametrization
The proposed shoulder-shaped potential used in the CESP model includes only one parameter to be fitted, i.e., the entanglement energetic cost Ur (eqn (2)). In order to properly set Ur, BD simulations have been performed with Ur values ranging from 200 to 2000 J mol−1. In these simulations, Dlong of streptavidin (normalised to D0) has been computed at seven macromolecular concentrations of D50 dextran: 50, 100, 200, 210, 260, 300 and 360 g L−1. Dlong is obtained by fitting the computed log(D) vs. log(t) profile to eqn (10).The obtained values are shown in Fig. 5 in green colour gradation. As can be observed, Dlong decreases with Ur because of the increase in the impenetrability of the particles and the consequent reduction in the available space for the particle to diffuse. Experimental Dlong values reported in ref. 11 are also depicted in the same figure (red markers). For Ur = 500 J mol−1, very good quantitative agreement between simulations and experiments is obtained. In all the BD computations performed in the rest of this work, Ur has been set to this value, which indicates that, for dextran, the repulsion forces arising from chain entanglement slightly dominate over the attractive ones. Dlong values obtained using the hard sphere model, reported in ref. 24, are also depicted in Fig. 5 (black markers). In this previous computational work, dextran macromolecules were modeled considering the dextran molecules as hard-core spheres with an effective radius, which was chosen as an intermediate value lying between the hydrodynamic radius53 and the compact radius. This approach accounted for the possibility of macromolecular overlapping in an average way, but represented a static description of the conformational state, being unable to properly mimic macromolecular entanglement. As is clearly observed in Fig. 5, Dlong values obtained using the CESP model are much closer to the experimental ones than those coming from the hard-core sphere model.24 For the rest of the dextran sizes (D10, D400 and D700), direct comparison of Dlong predicted by the hard-sphere model24 and the CESP model can be found in the ESI.† Again, it is found that the CESP model shows a significant improvement in the prediction of the obtained experimental Dlong over that using the hard-core sphere model. Therefore, the inclusion of coupling of the dynamic and conformational properties seems to be necessary to accurately describe diffusion in crowded media.
 | ||
| Fig. 5 Calculated Dlong/D0 as a function of the concentration corresponding to D50 dextran for Ur values: 200 J mol−1 (green triangles), 500 J mol−1 (empty green inverted triangles), 1000 J mol−1 (green inverted triangles) and 2000 J mol−1 (green diamonds). Black square markers represent the values obtained using the hard sphere model (taken from ref. 24) while red circle markers denote the experimental Dlong value (taken from ref. 11). For Ur = 500 J mol−1, good agreement between the CESP model and the experimental values is observed. Lines are only to guide the eye. | ||
3.2 Model prediction for Dlong and the anomalous exponent α
In the previous section, we have found that for Ur = 500 J mol−1, the CESP model is able to describe Dlong of streptavidin for D50 dextran obstacles. Let us now see that this model can also predict, without any further parametrization, Dlong and α of streptavidin for different dextran sizes (D10, D400 and D700) and concentrations (from 25 to 350 g L−1). Dlong and α are again obtained from the BD simulations by fitting eqn (10) to the computed D time evolution. The curve log(D) versus log(t) has been plotted in Fig. 6, together with the best fitted eqn (10), for four dextran sizes and concentrations: (Fig. 6a) D10 at 300 g L−1, (Fig. 6b) D50 at 200 g L−1, (Fig. 6c) D400 at 100 g L−1 and (Fig. 6d) D700 at 50 g L−1. As can be observed, for all the systems presented, eqn (10) fits very well to the computational results. | ||
| Fig. 6 Time evolution of the diffusion coefficient D versus time in the logarithmic scale obtained from BD computations (red line). The best-fitted eqn (10) is plotted as a black dashed line. Four cases are depicted: (a) D10 at 300 g L−1, (b) D50 at 200 g L−1, (c) D400 at 100 g L−1 and (d) D700 at 50 g L−1. For all the systems presented, eqn (10) fits very well to the computed values, allowing easy determination of Dlong, Dshort and α from the temporal evolution of D. | ||
The computed Dlongversus macromolecular concentration plots are depicted in Fig. 7 for four dextran sizes: D10, D50, D400 and D700. The results are shown together with the experimental values reported in ref. 11 for the same systems. Dashed lines are only to guide the eye and they follow the simulation results. In general, the computed results are in very good quantitative agreement with the experimental values. However, the values corresponding to D10 exhibit some systematic error, which could be explained taking into account that the potential energy barrier Ur has been set, regardless of the dextran size, to the best fit Dlong for D50. This suggests that Ur should be smaller for D10 than for D50, D400 and D700. Since Ur accounts for the energy cost of the macromolecular entanglement, this fact could suggest a lower energy cost for D10 entanglement than the one for D50, D400 and D700. In agreement with the experiments reported in ref. 11, BD simulations predict a decrease in Dlong with macromolecular concentration, as a result of volume exclusion and hydrodynamic interactions. Alternative potentials based on a self-consistent field method appropriate for weak excluded interactions45 have been implemented in BD simulations of star-polymer micelles.42 As in dextran molecules, the computational results exhibit similar Dlong decay with the particle density. However, at the quantitative level, the calculated values are much larger than the experimental ones. The discrepancies could be explained by the fact that HIs were not included in the computations of ref. 42. In the present work, HIs are included in the BD scheme, and it has been found that they are crucial for the quantitative reproduction of the experimental Dlong values.24,28
 | ||
| Fig. 7 log(Dlong/D0) for streptavidin versus macromolecular concentration. The filled markers represent BD simulations and the empty ones correspond to experimental values11 for four dextran sizes: D10 (green squares), D50 (red circles), D400 (upward pointing blue triangles) and D700 (downward pointing purple triangles). Dashed lines are only to guide the eye and they follow the simulation results. | ||
The anomalous exponent α provides information about the transition between the short and the long-time regimes. α values close to unity indicate a smooth transition. As α deviates from unity, the transition becomes more pronounced. The simulated α versus macromolecular concentration plots are depicted in Fig. 8 together with the experimental values obtained using FCS.11 As can be observed, the CESP model qualitatively captures the experimentally observed behaviour. α decays with macromolecular concentration as a result of an increase in particle collisions. Moreover, α also decreases with dextran size, which could be a consequence of the increase of ϕeff, so that the volume fraction of the system seems to play a crucial role in α and therefore in the transition between the Dshort and Dlong steady states. However, quantitative discrepancies are observed, which could be explained not only by the limitations of the model, but by the way in which α has been calculated. The experimental α values have been obtained by fitting the auto-correlation function of the tracer protein fluorescence using the power law described in eqn (1) while here, α has been determined as the slope in the inflection point of the curve log(D) versus log(t) using eqn (10).
 | ||
| Fig. 8 Anomalous exponent α versus macromolecular concentration. Filled markers represent BD simulations and empty markers correspond to the experimental values11 for four dextran sizes: D10 (green squares), D50 (red circles), D400 (upward pointing blue triangles) and D700 (downward pointing purple triangles). Dashed lines are only to guide the eye and they follow the simulation results. | ||
3.3 Radial distribution functions
The simulated radial distribution functions (rdfs) for the cases analyzed in the previous section (D10 (a), D50 (b), D400 (c) and D700 (d)) are shown in Fig. 9 for macromolecular concentrations ranging from 25 g L−1 to 350 g L−1. The rdfs have been computed from the BD computations by calculating the center-to-center distance of every dextran obstacle to the rest of the dextran particles. Averages have been taken over 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 configurations every 2 ns of simulation. As can be observed, the CESP model predicts an increase in the number of entangled macromolecules with macromolecular concentration, as revealed by the gradual increase in the rdf at r = dc. This fact is observed for all the studied dextran sizes. Two sharp peaks at distances slightly lower than dc and de define two coordination shells of entangled macromolecules, corresponding to highly entangled macromolecules (close to dc) and weakly entangled macromolecules (close to de), respectively. It is also interesting to note the presence of two secondary peaks for D400 and D700 at macromolecular concentrations of 250, 300 and 350 g L−1, corresponding to additional coordination shells and suggesting other possible degrees of entanglement for the biggest dextran molecules. Note that the two main peaks in the entanglement region are developed even in the absence of explicit attractive terms in the proposed potential. Entanglement is thus the way the system can minimize the excluded volume effects, even paying a small energetic cost. It is reasonable to conclude that the presence of attractive forces would enhance this effect, although it is not necessary to produce it.
000 configurations every 2 ns of simulation. As can be observed, the CESP model predicts an increase in the number of entangled macromolecules with macromolecular concentration, as revealed by the gradual increase in the rdf at r = dc. This fact is observed for all the studied dextran sizes. Two sharp peaks at distances slightly lower than dc and de define two coordination shells of entangled macromolecules, corresponding to highly entangled macromolecules (close to dc) and weakly entangled macromolecules (close to de), respectively. It is also interesting to note the presence of two secondary peaks for D400 and D700 at macromolecular concentrations of 250, 300 and 350 g L−1, corresponding to additional coordination shells and suggesting other possible degrees of entanglement for the biggest dextran molecules. Note that the two main peaks in the entanglement region are developed even in the absence of explicit attractive terms in the proposed potential. Entanglement is thus the way the system can minimize the excluded volume effects, even paying a small energetic cost. It is reasonable to conclude that the presence of attractive forces would enhance this effect, although it is not necessary to produce it.
The first rdf peak has been integrated in order to determine the number of entangled particles (NE) close to the core of the reference particle. NE is shown in Fig. 10 for the four analyzed dextran sizes. It can be observed that NE increases exponentially with macromolecular concentration, so that entanglement is promoted by steric compression. This effect is enhanced by the increase in dextran size, as a consequence of the increase in ϕeff, so that bigger dextran obstacles are able to effectively occupy higher volumes than the smaller ones for the same macromolecular concentration.
4 Conclusions
A new coarse grained approach to macromolecular diffusion in crowded media that goes beyond the hard sphere model is presented: the Chain Entanglement Softened Potential (CESP) model. Two interaction regions between macromolecules are considered: a soft interaction region caused by chain entanglement, a combination of repulsive and attractive effects, and a hard-core interaction region caused by the dramatic increase in steric repulsions between macromolecular skeletons when they approach below a certain distance. The resulting picture is quantified by means of a shoulder-shaped potential that allows macromolecular conformational flexibility and chain entanglement to be taken into account. The model can be parametrized by a unique parameter (Ur) that is associated with the entanglement energetic cost. For streptavidin protein diffusion in D50 crowded solution, Ur has been quantified by fitting the long time diffusion coefficient (Dlong) resulting from BD simulations to the experimental values obtained using Fluorescence Correlation Spectroscopy (FCS).11In order to determine Dlong and the anomalous exponent α from BD simulations, a new empiric expression for the temporal evolution of the diffusion coefficient, valid for all the temporal regimes, has been proposed. The new function goes beyond the standard power law and depends on the four relevant dynamic properties: Dshort, Dlong, α and the inflection time γ. This function fits very well to the BD computations for all the obstacle concentrations and sizes under study, and it could be useful in forthcoming computational studies focused on anomalous diffusion.
The computed Dlong using the CESP model clearly improves on the results obtained in previous studies based on hard-core spheres.24 Without any further parametrization of V(r), the CESP model is able to provide quantitative predictions of Dlong and α of streptavidin in media crowded by D10, D400 and D700 at several dextran concentrations (25 to 350 g L−1). Radial distribution functions exhibit a significant increase in the population of entangled macromolecules with the macromolecular concentration and dextran size. Our results indicate that an adequate description of macromolecular entanglement is essential to understand macromolecular diffusion in crowded media.
Conflicts of interest
The authors declare no conflicts of interest. The founding sponsors had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.Appendix
The new empirical equation proposed here for the time evolution of D (eqn (10)) contains four parameters that are related to the relevant dynamic properties of the system, i.e., Dshort, Dlong, α and the inflection time γ. At short times (log(t) → −∞), eqn (10) must fulfill log(D) → log(Dshort), while at long times (log(t) → +∞), we have log(D) → log(Dlong). Taking limits in eqn (10) | (11) |
 | (12) |
 and
and  . By construction, γ corresponds to the inflection point of the time evolution curve. Some elementary algebra shows that
. By construction, γ corresponds to the inflection point of the time evolution curve. Some elementary algebra shows that | (13) |
Finally, β can be related to the anomalous diffusion exponent α, used when the transition regime is analyzed in terms of the standard power law (eqn (1))
| D = Γαtα−1⇔ log(D) = (α − 1)log(t) + log(Γα) | (14) |
By taking the first derivative in eqn (10) and comparing to eqn (14), one obtains
 | (15) |
Acknowledgements
We acknowledge the financial support from the Spanish Ministry of Science and Innovation (project CTM2016-78798-C2-1-P) and Generalitat de Catalunya (Grants 2014SGR1017, 2014SGR1132 and XrQTC). Sergio Madurga and Francesc Mas acknowledge the funding of the EU project 8SEWP-HORIZON 2020 (692146). Pablo M. Blanco also acknowledges the financial support from the grant (FI-2017) of Generalitat de Catalunya. The authors also want to thank Prof. Giancarlo Franzese (University of Barcelona) for his suggestion to use a shouldered interaction potential to model macromolecular flexibility.References
- A. P. Minton, Biopolymers, 1981, 20, 2093–2120 CrossRef CAS.
- S. B. Zimmerman and S. O. Trach, J. Mol. Biol., 1991, 222, 599–620 CrossRef CAS PubMed.
- A. Minton, Biophys. J., 1992, 63, 1090–1100 CrossRef CAS PubMed.
- R. J. Ellis, Trends Biochem. Sci., 2001, 26, 597–604 CrossRef CAS PubMed.
- H.-X. Zhou, G. Rivas and A. P. Minton, Annu. Rev. Biophys., 2008, 37, 375–397 CrossRef CAS PubMed.
- C. Balcells, I. Pastor, E. Vilaseca, S. Madurga, M. Cascante and F. Mas, J. Phys. Chem. B, 2014, 118, 4062–4068 CrossRef CAS PubMed.
- I. Pastor, L. Pitulice, C. Balcells, E. Vilaseca, S. Madurga, A. Isvoran, M. Cascante and F. Mas, Biophys. Chem., 2014, 185, 8–13 CrossRef CAS PubMed.
- C. Balcells, I. Pastor, L. Pitulice, M. Via, S. Madurga, E. Vilaseca, A. Isvoran, M. Cascante and F. Mas, New Frontiers in Chemistry, 2015, 24, 3–16 Search PubMed.
- G. Rivas and A. P. Minton, Trends Biochem. Sci., 2016, 41, 970–981 CrossRef CAS PubMed.
- M. C. Konopka, I. A. Shkel, S. Cayley, M. T. Record and J. C. Weisshaar, J. Bacteriol., 2006, 188, 6115–6123 CrossRef CAS PubMed.
- D. S. Banks and C. Fradin, Biophys. J., 2005, 89, 2960–2971 CrossRef CAS PubMed.
- I. Pastor, E. Vilaseca, S. Madurga, M. Cascante and F. Mas, J. Phys. Chem. B, 2010, 114, 4028–4034 CrossRef CAS PubMed.
- I. Pastor, E. Vilaseca, S. Madurga, M. Cascante and F. Mas, J. Phys. Chem. B, 2010, 114, 12182 CrossRef CAS.
- J. A. Dix and A. Verkman, Annu. Rev. Biophys., 2008, 37, 247–263 CrossRef CAS PubMed.
- M. Feig, I. Yu, P.-h. Wang, G. Nawrocki and Y. Sugita, J. Phys. Chem. B, 2017, 1–17 Search PubMed.
- E. Vilaseca, A. Isvoran, S. Madurga, I. Pastor, J. L. Garcés and F. Mas, Phys. Chem. Chem. Phys., 2011, 13, 7396–7407 RSC.
- E. Vilaseca, I. Pastor, A. Isvoran, S. Madurga, J. L. Garcés and F. Mas, Theor. Chem. Acc., 2011, 128, 795–805 CrossRef CAS.
- J. Sun and H. Weinstein, J. Chem. Phys., 2007, 127, 155105 CrossRef PubMed.
- P. Mereghetti and R. C. Wade, J. Phys. Chem. B, 2012, 116, 8523–8533 CrossRef CAS PubMed.
- S. Hasnain, C. L. McClendon, M. T. Hsu, M. P. Jacobson and P. Bandyopadhyay, PLoS One, 2014, 9, 1–12 Search PubMed.
- S. Kondrat, O. Zimmermann, W. Wiechert and E. V. Lieres, Phys. Biol., 2015, 12, 046003 CrossRef PubMed.
- T. Sentjabrskaja, E. Zaccarelli, C. De Michele, F. Sciortino, P. Tartaglia, T. Voigtmann, S. U. Egelhaaf and M. Laurati, Nat. Commun., 2016, 7, 11133 CrossRef CAS PubMed.
- I. Yu, T. Mori, T. Ando, R. Harada, J. Jung, Y. Sugita and M. Feig, eLife, 2016, 5, 1–22 Search PubMed.
- P. M. Blanco, M. Via, J. L. Garcés, S. Madurga and F. Mas, Entropy, 2017, 19, 105 CrossRef.
- S. Smith and R. Grima, J. Chem. Phys., 2017, 146, 024105 CrossRef PubMed.
- S. Bucciarelli, J. S. Myung, B. Farago, S. Das, G. A. Vliegenthart, O. Holderer, R. G. Winkler, P. Schurtenberger, G. Gompper and A. Stradner, Sci. Adv., 2016, 2, e1601432 Search PubMed.
- P. H. Wang, I. Yu, M. Feig and Y. Sugita, Chem. Phys. Lett., 2017, 671, 63–70 CrossRef CAS.
- T. Ando, E. Chow and J. Skolnick, J. Chem. Phys., 2013, 139, 121922 CrossRef PubMed.
- M. Saxton, Biophys. J., 1994, 66, 394–401 CrossRef CAS PubMed.
- D. L. Ermak and J. A. McCammon, J. Chem. Phys., 1978, 69, 1352–1360 CrossRef CAS.
- J. Rotne and S. Prager, J. Chem. Phys., 1969, 50, 4831–4837 CrossRef CAS.
- H. Yamakawa, J. Chem. Phys., 1970, 53, 436–443 CrossRef CAS.
- J. Brady, Annu. Rev. Fluid Mech., 1988, 20, 111–157 CrossRef.
- M. Tokuyama and I. Oppenheim, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1994, 50, 6–9 CrossRef.
- M. Tokuyama, Phys. A, 2006, 364, 23–62 CrossRef.
- M. Tokuyama, T. Moriki and Y. Kimura, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2011, 83, 1–8 CrossRef PubMed.
- A. Irbäck and S. Mohanty, Eur. Phys. J.-Spec. Top., 2017, 226, 627–638 CrossRef.
- D. Bedrov, C. Ayyagari and G. D. Smith, J. Chem. Theory Comput., 2006, 2, 598–606 CrossRef CAS PubMed.
- D. Bedrov, G. D. Smith and J. Yoon, Langmuir, 2007, 23, 12032–12041 CrossRef CAS PubMed.
- C. N. Likos, H. Löwen, A. Poppe, L. Willner, J. Roovers, B. Cubitt and D. Richter, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1998, 58, 6299–6307 CrossRef CAS.
- C. N. Likos, H. Löwen, M. Watzlawek, B. Abbas, O. Jucknischke, J. Allgaier and D. Richter, Phys. Rev. Lett., 1998, 80, 4450–4453 CrossRef CAS.
- B. Loppinet, G. Fytas, D. Vlassopoulos, C. N. Likos, G. Meier and J. L. Guo, Macromol. Chem. Phys., 2005, 206, 163–172 CrossRef CAS.
- L. Liu, W. K. den Otter and W. J. Briels, Soft Matter, 2014, 10, 7874–7886 RSC.
- E. Locatelli, B. Capone and C. N. Likos, J. Chem. Phys., 2016, 145, 174901 CrossRef PubMed.
- S. T. Milner, T. A. Witten and M. E. Cates, Macromolecules, 1988, 21, 2610–2619 CrossRef CAS.
- J. Mewis, W. J. Frith, T. A. Strivens and W. B. Russel, AIChE J., 1989, 35, 415–422 CrossRef CAS.
- U. Genz, B. D'Aguanno, J. Mewis and R. Klein, Langmuir, 1994, 10, 2206–2212 CrossRef CAS.
- P. Vilaseca and G. Franzese, J. Chem. Phys., 2010, 133, 1–11 CrossRef PubMed.
- F. Leoni and G. Franzese, J. Chem. Phys., 2014, 141, 174501 CrossRef PubMed.
- P. Vilaseca, K. A. Dawson and G. Franzese, Soft Matter, 2012, 6978–6985 Search PubMed.
- J. W. Sloan, B. H. Alexander, R. L. Lohmar, I. A. Wolff and C. E. Rist, J. Am. Chem. Soc., 1954, 76, 4429–4434 CrossRef CAS.
- J. Sabatie, L. Choplin, M. Moan, J. L. Doublier, F. Paul and P. Monsan, Carbohydr. Polym., 1988, 9, 87–101 CrossRef CAS.
- J. Armstrong, R. Wenby, H. Meiselman and T. Fisher, Biophys. J., 2004, 87, 4259–4270 CrossRef CAS PubMed.
- A. Ortega, D. Amorós and J. G. De La Torre, Biophys. J., 2011, 101, 892–898 CrossRef CAS PubMed.
- M. Fairhead, D. Krndija, E. D. Lowe and M. Howarth, J. Mol. Biol., 2014, 426, 199–214 CrossRef CAS PubMed.
- T. Terai, M. Kohno, G. Boncompain, S. Sugiyama, N. Saito, R. Fujikake, T. Ueno, T. Komatsu, K. Hanaoka, T. Okabe, Y. Urano, F. Perez and T. Nagano, J. Am. Chem. Soc., 2015, 137, 10464–10467 CrossRef CAS PubMed.
- L. Baugh, I. Le Trong, P. S. Stayton, R. E. Stenkamp and T. P. Lybrand, Biochemistry, 2016, 55, 5201–5203 CrossRef CAS PubMed.
- D. W. Schaefer, Polymer, 1984, 25, 387–394 CrossRef CAS.
- A. Pähler, W. A. Hendrickson, M. A. G. Kolks, C. E. Argaña and C. R. Cantor, J. Biol. Chem., 1987, 262, 13933–13937 Search PubMed.
- H. Mori, Prog. Theor. Phys., 1965, 33, 423–455 CrossRef.
- D. T. Gillespie, Am. J. Phys., 1996, 64, 1246–1257 CrossRef.
- J. K. Dhont, An Introduction to Dynamics of Colloids, Elsevier, Amsterdam, The Netherlands, 1996, ch. 2 Search PubMed.
- R. J. Phillips, J. F. Brady and G. Bossis, Phys. Fluids, 1988, 31, 3462–3472 CrossRef CAS.
- J. L. Garcés, F. Mas, J. Cecília, E. Companys, J. Galceran, J. Salvador, J. Puy and J. Galceran, Phys. Chem. Chem. Phys., 2002, 4, 3764–3773 RSC.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c8sm00201k |
| This journal is © The Royal Society of Chemistry 2018 |



