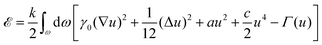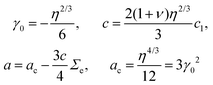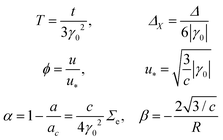Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Defect formation dynamics in curved elastic surface crystals†
Norbert
Stoop
and
Jörn
Dunkel
 *
*
Department of Mathematics, Massachusetts Institute of Technology, 77 Massachusetts Avenue, Cambridge, MA 02139-4307, USA. E-mail: dunkel@mit.edu
First published on 22nd February 2018
Abstract
Topological defects shape the material and transport properties of physical systems. Examples range from vortex lines in quantum superfluids, defect-mediated buckling of graphene, and grain boundaries in ferromagnets and colloidal crystals, to domain structures formed in the early universe. The Kibble–Zurek (KZ) mechanism describes the topological defect formation in continuous non-equilibrium phase transitions with a constant finite quench rate. Universal KZ scaling laws have been verified experimentally and numerically for second-order transitions in planar Euclidean geometries, but their validity for non-thermal transitions in curved and topologically nontrivial systems still poses open questions. Here, we use recent experimentally confirmed theory to investigate topological defect formation in curved elastic surface crystals formed by stress-quenching a bilayer material. For both spherical and toroidal crystals, we find that the defect densities follow KZ-type power laws. Moreover, the nucleation sequences agree with recent experimental observations for spherical colloidal crystals. Our results suggest that curved elastic bilayers provide an experimentally accessible macroscopic system to study universal properties of non-thermal phase transitions in non-planar geometries.
1 Introduction
Topological defects influence the elastic, magnetic, electronic and optical properties in many natural and man-made systems. Examples range from liquid crystals1–4 to grain boundaries in ferromagnets and colloidal crystals,5,6 and charge transport in graphene7,8 and superconductors.9–12 Topological defects can be created by varying a control parameter, such as temperature or a magnetic field, rapidly across a phase transition. Understanding the complex nonequilibrium dynamics induced by these nonadiabatic quenches remains an important theoretical challenge. Early progress in the characterization of topological defects was made by Kibble13 in 1976, while studying domain formation during the rapid cooling of the early universe.14 About a decade later, Zurek9 showed how the defect density is related to the quench rate in general second-order phase transitions; this important breakthrough also advanced significantly the understanding of topological defect formation in quantum superfluids and superconductors.15 Since then, the Kibble–Zurek (KZ) power-law scaling predictions were confirmed experimentally and utilized in a variety of systems, including liquid crystals,3,16 colloidal monolayers,17 ion crystals,18 Bose–Einstein condensates,19 superfluids10,12,20 and cold atomic clouds.21 KZ-scalings were also suggested to govern the defect formation in Rayleigh–Bénard convection,22–24 although, in contrast to theory,25 experimentally measured exponents appeared to depend on non-universal system properties. Moreover, since previous theory and experiments focused primarily on phase transitions in planar Euclidean spaces, much less is known about the existence of KZ-type scaling laws in more complex geometries and topologies.Topological defects in curved two-dimensional (2D) crystal structures arise in many biological and physical processes,27,28 from plant growth29–31 and assembly of bacterial cell walls,32,33 viral capsids34,35 and microtubules36 to the targeted design of carbon nanotube sensors37 and microlense fabrication.38 On closed manifolds, Euler's theorem39 links the net charge of the topological defects to the genus g of the underlying surface, imposing for example the 12 pentagons on a soccer ball. Depending on the details of the crystallization process (quench rate, geometric constraints, etc.), non-planar 2D crystals typically contain additional excess defects with zero total charge.40–42 Recent studies provided important experimental and theoretical insights into the defect statistics and formation dynamics in 2D colloidal crystals assembled on curved liquid–liquid interfaces.26,43–45 Another promising class of experimental systems are curved elastic bilayer systems,46 consisting of a soft substrate and a stiff surface film (Fig. 1A), which can develop hexagonal wrinkling patterns under lateral compression induced by surface swelling47 or substrate depressurization.48,49 Such elastic surface crystals allow the realization of nontrivial shapes of genus g > 0, such as toroids, which are difficult to achieve in liquids. Moreover, because the transition from the unwrinkled to the hexagonal phase is tunable by a global control parameter,49 these soft matter systems also provide an ideal testbed to study generalizations of the KZ scaling laws to curved geometries.
 | ||
| Fig. 1 Growth dynamics of elastic surface crystals in curved geometries. (A) Schematic of the simulated elastic bilayer material consisting of a thin film (thickness h) adhering to a soft substrate (radius R). Upon increasing the compressive film stress, the normal displacement u of the film develops a hexagonal pattern with wavelength λ. (B) Surface crystallization dynamics on a sphere (radius R/h = 80; Movie 1, ESI†) for a slow quench μ = 5 × 10−8. (C) Planar reconstruction of the crystallization process for the sphere in panel B. The growth of the elastic surface crystal from two initial nucleation sites (dark blue) proceeds along a predominantly regular hexagonal lattice structure, in close analogy with recent experimental observations for colloidal crystals on spherical liquid–liquid interfaces.26 (D) Crystallization dynamics on a torus (radii R/h = 120 and r/h = 24; Movie 2, ESI†) for a slow quench (μ = 5 × 10−8). (E) The planar reconstruction for the torus in panel D reveals that toroidal surface crystals also grow sequentially along a regular hexagonal lattice structure, centered around wave-like geodesics of minimal absolute curvature. | ||
The classical KZ argument for thermally induced second-order transitions builds on the fact that the correlation length ξ and relaxation time τ diverge as ξ ∝ ϑ−ν and τ ∝ ϑ−zν (critical slowing down), respectively, when the temperature ϑ is varied to drive the system continuously from the high-symmetry (e.g. isotropic) phase to the lower-symmetry crystal phase. The critical exponents ν and z encode the universality class of the transition. For a linear quench ϑ = μt with rate μ, the system will not be able to relax to equilibrium during the time interval |t| ≲ tf = τ, yielding the freeze-out condition tf ∝ (μtf)−zν or, equivalently, tf ∝ μ−zν/(1+zν). The associated correlation length ξf = ξ(tf) ∝ μ−ν/(1+zν) implies the KZ scaling prediction for the defect density at freeze-out, ρf ∝ ξf−d ∝ μdν/(1+zν), where d is the space dimension. The analysis below shows that this argument also holds for the stress-induced pattern formation transitions observed on the 2D surfaces of curved elastic bilayer materials. Even though our system is (weakly) first-order, its dynamics arrests under sufficiently fast quenches before the coexistence region is entered, so that the classical KZ scalings can be expected to hold (see Discussion below).22,24 Furthermore, our computations identify a dynamical analogy with recent experimental observations26 on colloidal crystal formation in curved liquid–liquid interfaces. Altogether, these results suggest that pattern formation in elastic bilayers provides an experimentally promising system to study the dynamics of phase transitions in non trivial geometries. From a practical perspective, the subsequent analysis offers guidance for how to combine quench dynamics and surface geometry to control both the frequency and localization of topological defects.
2 Theory
To investigate topological defect formation in curved geometries, we analyze an experimentally validated continuum model49 for the surface wrinkling in elastic bilayer materials consisting of a soft core and a stiffer outer shell (Fig. 1A). This generalized Swift–Hohenberg (GSH) theory can reproduce quantitatively the experimentally measured equilibrium phase diagrams,49 but its dynamical implications have not yet been fully explored.2.1 GSH theory for elastic surface crystals
The GSH equations follow from the nonlinear Koiter shell theory50 by expanding the elastic energy of film and substrate in the dominant normal displacement field u.49 Measuring length in units of the film thickness h, the surface energy functional of the GSH theory reads49where k = Ef/(1 − ν2) for a film with Young's modulus Ef and Poisson ratio ν, and dω is the surface element of the undeformed substrate. The nonlinear term Γ(u) = [(1 − ν)bαβ∇αu∇βu + νbαα(∇u)2]u represents stretching forces to leading order in the curvature tensor bαβ, with surface gradient ∇ and Laplace–Beltrami operator Δ (throughout, Greek indices run over the set {1,2} and Einstein's summation convention is used). Taking the variation of
![[scr E, script letter E]](https://www.rsc.org/images/entities/char_e140.gif) with respect to u and assuming overdamped dynamics, the surface wrinkling process is described by the GSH equation41,49
with respect to u and assuming overdamped dynamics, the surface wrinkling process is described by the GSH equation41,49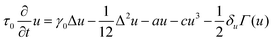 | (1) |
![[scr E, script letter E]](https://www.rsc.org/images/entities/char_e140.gif) . τ0 is the inverse relaxation speed;49 with no loss of generality, we set τ0 = 1 in the following. Explicit expressions49 for the coefficients and δuΓ(u) are summarized in the Appendix Wrinkling theory.
. τ0 is the inverse relaxation speed;49 with no loss of generality, we set τ0 = 1 in the following. Explicit expressions49 for the coefficients and δuΓ(u) are summarized in the Appendix Wrinkling theory.
Linear stability analysis of eqn (1) implies that wrinkling patterns form via a discontinuous transition (see Fig. 4 in ref. 49), when the control parameter a falls below the critical value ac = 3γ02, corresponding to an increase of the film stress σ beyond the critical buckling stress σc. In the following, we use the previously established definition of the excess film stress (or overstress) Σe = (σ/σc) − 1 as control parameter.51 Here, σc is the critical film stress necessary to buckle the film from the homogeneous solution u = 0. σ is the applied film stress, defined as the equi-biaxial equilibrium film stress in the (possibly unstable) unwrinkled solution with u = 0. Therefore, σ and Σe, respectively, are well defined control parameters, but are not measures of the actual stress field in the deformed film. The bifurcation parameter a is related to Σe by49
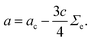 | (2) |
2.2 Stress-quenching of elastic surface crystals
To obtain scaling predictions for the topological defect formation in elastic surface crystals, we first solve eqn (1) numerically for linear stress quenches| Σe(t) = μt | (3) |
To break the symmetry of the initially unwrinkled surface u = 0, a small stationary random field ε with |ε| ≪ 1 is added to the rhs of eqn (1) in simulations (Appendix Wrinkling theory). This ε-inhomogeneity effectively models initial imperfections in the film displacement, thus mimicking realistic experimental conditions.46 We simulate eqn (1) for the linear quench (3) and a given realization of ε using the algorithm described in ref. 49. Numerical results presented below are averages over n different realizations of ε, with n specified on the corresponding graphs.
3 Results
To illustrate the effects of locally varying curvature and surface topology, we compare simulations for spherical and toroidal surfaces.3.1 Surface crystal growth under slow quenching
For slow quasi-adiabatic quenches (μ → 0), we find that the crystallization process is initiated at isolated nucleation sites after a critical time tc and then spreads to cover the entire film (Fig. 1B and D). This behavior is observed for both spheres and tori (Movies 1 and 2, ESI†). Details of the spreading dynamics and local crystal orientation become evident by reconstructing the corresponding planar crystal patterns as suggested by Meng et al.26 (Appendix Pattern analysis). Starting from a random crystal site and one of its neighbors, we determine the relative positions of all other sites connected to this initial pair, resulting in the planar crystal representations of Fig. 1C and E. Neighboring sites on the curved crystal are indicated by gray lines if they appear separated in the planar embedding. The time evolution in these graphs shows how initially separated crystal patches merge to form a single connected crystal covering the entire surface. The radial cuts appearing in Fig. 1C reflect the non-isometric character of the planar representation of spherical crystals, whereas the toroidal crystals unfold nearly isometrically (Fig. 1E). Moreover, crystals on the torus nucleate first near the outer rim (Fig. 1D), suggesting an influence of Gaussian curvature in the pattern-forming process in agreement with previous findings.52 As discussed below, qualitatively similar crystallization sequences were observed in a recent experiment26 that studied the deposition of charged colloids onto a spherical oil–water interface. It is important to stress that the observed crystal nucleation is a consequence of the nonlinear terms in eqn (1). Essential symmetry-breaking of the unwrinkled phase u = 0 however already occurs at earlier times and smaller amplitudes, where these nonlinearities are negligible. Therefore, even though we observe a crystallization reminiscent of a nucleate-and-grow dynamics, the order parameter field has at this point already globally acquired a symmetry-broken phase of small amplitude (Fig. 1B, 2nd snapshot, Movie 4, ESI†). This behavior is similar to the spinodal-assisted nucleation of hexagonal defects.53,54 To connect with the ideas of Kibble13 and Zurek,9 we next use the GSH elasticity model to analyze the relation between topological defect formation and quench rate μ, which is difficult to explore in curved colloidal systems due to experimental limitations on the particle deposition rates.3.2 KZ-type scaling in spherical surface crystals
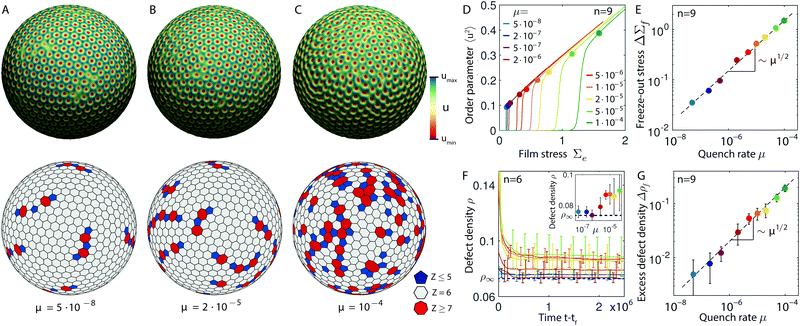
We start our numerical scaling analysis by considering the case of globally constant curvature as realized in spheres (Fig. 2; Movie 1, ESI†). In our simulations of eqn (1), the quench rate is varied over the range μ ∈ [5 × 10−8, 10−4], consistent with the assumption of an overdamped dynamics. Fixing the sphere radius R/h = 80, we characterize the transition from the unwrinkled to the wrinkled phase in terms of the average squared displacement 〈u2〉, where the brackets indicate an instantaneous surface average. In the adiabatic limit μ ↘ 0, this order parameter vanishes in the unwrinkled phase, 〈u2〉 = 0 for Σe < 0, and jumps to a finite value 〈u2〉 > 0 when the excess film stress Σe crosses zero from below. By contrast, for non-adiabatic quenches, we find that the system remains longer in the unwrinkled phase, before eventually breaking symmetry at some finite positive value Σe > 0 (Fig. 2D). Such delayed symmetry-breaking is characteristic of the classical KZ mechanism, reflecting the critical slowing down in the relaxation dynamics near a second-order phase transition. To quantify the scaling behavior in our system, we define the net freeze-out film stress ΔΣf = Σe,f − Σ0, with Σe,f being the value at which the pattern amplitude is fully developed (Appendix Freeze-out). The constant shift Σ0 ≈ 0.1 is required to account for the material imperfections modeled by the ε-inhomogeneity, and is well-studied in the context of delayed bifurcations.55,56 Our simulations confirm power-law scaling ΔΣf ∝ μ1/2 (Fig. 2E), implying that the freeze-out time diverges as tf ∝ μ−1/2.The perhaps most interesting observable is the topological defect density ρf at freeze-out tf. Defects are crystal sites with coordination number Z ≠ 6 and non-zero topological charge s = 6 − Z. To identify the μ-dependence of ρf in the GSH theory, we determined the coordination number for each lattice site from the Voronoi cells of the displacement field u (Appendix Pattern analysis). The resulting Voronoi graphs show that the freeze-out density ρf increases with the quench rate μ (Fig. 2A–C). After a quench is completed, defect pairs are expected to annihilate by grain boundary movements. We tested this hypothesis in simulations by stopping the quench at the freeze-out value, Σ(t) = Σe,f for t > tf, so that the spherical surface crystals could relax to a stress equilibrium. For all considered quench rates, we find that the defect density approaches constant asymptotic values, which converge to the equilibrium value ρ∞ as μ ↘ 0 (Fig. 2F). Note that, although the net topological charge is always +12 in agreement with Euler's theorem for hexagonal sphere tilings,39 charge-neutral pairs of penta- and heptagonal defects can reduce the elastic energy,41,44,57–59 resulting in a non-zero defect density ρ∞ even at equilibrium. Defining the relative excess defect density at freeze-out tf by Δρf = ρf − ρ∞, our numerical data is consistent with a KZ-type power law Δρf ∝ μ1/2 (Fig. 2G).
3.3 KZ-type scaling for toroidal surface crystals
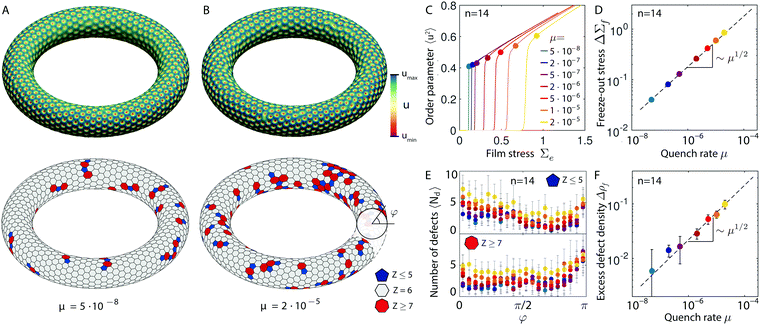
Local curvature variations can influence the equilibrium defect localization in curved elastic crystals.41 Moreover, during crystal growth, local curvature profoundly affects growth rates, orientation, and defect density at impinging domains.52,60 In essence, locally varying curvature thus makes the crystallization process inhomogeneous. It is then a priori not clear if and under what conditions the KZ-scalings found for spherical systems also hold for geometries with non-constant curvature. To test to what degree the defect scaling laws are affected by curvature variations and surface genus, we performed additional parameter scans for tori. For elastic bilayer wrinkling, the locally varying curvature on a torus determines the strength of the symmetry-breaking term δuΓ(u) in eqn (1), implying that in our system purely crystalline toroidal surface patterns exist only for sufficiently small aspect ratios r/R.41 We therefore focus on thin tori with r/R = 0.2 (Fig. 3A, B and Movie 2, ESI†). Adopting the same small random ε-inhomogeneities as for the sphere simulations (and, hence, the same shift value Σ0), we observe that the freeze-out stress ΔΣf ∝ μ1/2 and the freeze-out time tf ∝ μ−1/2 scale exactly as in the case of constant curvature (Fig. 3C and D). Furthermore, one again finds that faster quenches lead to a higher density of defects at freeze-out (Fig. 3A, B, F and Movie 3, ESI†). Although Euler's theorem39 imposes a vanishing total defect charge S = 0 on a torus, excess defects of opposite charge tend to aggregate at the inner (Z = 7) and outer (Z = 5) equators to lower the elastic energy of the toroidal crystal,40,41,61,62 resulting in a non-zero equilibrium defect density ρ∞. As in the sphere case, we find that the relative excess defect density Δρf = ρf − ρ∞ of the toroidal surface crystals follows a square root law Δρf ∝ μ1/2 (Fig. 3F), suggesting that local curvature variations and surface genus do not significantly affect the scaling laws on tori. In the next part, we will rationalize these observations by considering the structure of the amplitude equations63 for the underlying GSH theory.4 Discussion
As outlined in the introduction, the original KZ scaling relations for continuous second-order transitions can be obtained by analyzing how correlation length and relaxation time diverge as a function of the control parameter as one approaches the critical point from the high-symmetry phase. By contrast, the wrinkling transition considered here is subcritical, with a discontinuity in the order parameter at the critical stress Σe = 0. The transition thus carries the signature of a (weakly) first-order transition. We note, however, that the quench starts in the unwrinkled phase u = 0. Increasing Σe < 0 with stationary small perturbations |ε| ≪ 1, the system remains in the unwrinkled phase despite the sub-critically stable hexagonal solution. Within the general Ginzburg–Landau mean-field framework, in this phase the correlation length diverges as the system approaches the critical point, and the critical exponent is ν = 1/2.64 In the subcritical region, this argument is not valid due to the coexistence of solutions. The width δΣe of the subcritical zone is, however, small. For a spherical substrate, we previously found δΣe ≈ (h/R)2/(20 × 0.0192) ≈ 0.02.49 As pointed out in the context of Rayleigh–Bénard convection,22,24 for sufficiently fast quenches, we expect the system dynamics to freeze with a selected correlation length before the coexistence phase is entered. Considering that in our simulations, the slowest quench froze at |ΔΣf| ≈ 0.04 > δΣe (Fig. 1E), we are well within this regime. The critical exponent zν = 1 for the divergence of the relaxation time follows by considering the characteristic time scale of the linearized decay and growth of fluctuations.24,644.1 Amplitude equations
Alternatively, we can determine the quench-dependent freeze-out time directly by inspecting the dynamics of the amplitude equations governing the GSH model. To this end, we assume approximate hexagonal solutions of the form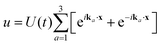 , where k1 = kc(1,0),
, where k1 = kc(1,0), 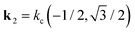 ,
, 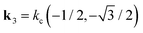 and
and 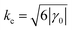 . Inserting this ansatz into the GSH eqn (1), one finds to leading order in U and curvature (Appendix Amplitude equations)
. Inserting this ansatz into the GSH eqn (1), one finds to leading order in U and curvature (Appendix Amplitude equations)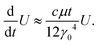 | (4) |
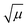 and defining a rescaled time t′ = μ1/2t, we can remove the quench rate dependence at leading order, to obtain
and defining a rescaled time t′ = μ1/2t, we can remove the quench rate dependence at leading order, to obtain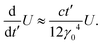 | (5) |
4.2 Nucleation dynamics in curved surface crystals
Crystal growth in planar Euclidean geometry is well understood. By contrast, the complex interplay between kinetics, substrate curvature and defect formation is still being investigated.26,27 The current interest in these topics is in parts driven by recent technological advances in the fabrication of graphene65 and carbon nanotubes37 and by the development of modern confocal imaging techniques that make it possible to track micron-sized colloids and cells at high spatio-temporal resolution. For instance, the formation of hexagonal crystal structures similar to those described above can be observed during the early developmental stages in the fruit fly Drosophila melanogaster, when nuclei migrate to accumulate underneath the surface of the ellipsoidal shell that encapsulates the embryo.66 Similarly, ciliated somatic cells form a spherical crystal on the surface of the colonial alga Volvox carteri,67 with the cells' arrangement determining the phototactic properties of the organism.Important insights into the kinetics of crystal growth on curved substrates were obtained recently in a joint experimental and theoretical study26 on the assembly of charged colloids on spherical liquid–liquid interfaces. The crystal formation dynamics observed in these experiments shares striking similarities with the nucleation sequences of the hexagonal wrinkling patterns shown in Fig. 1C. In both cases, one first observes the formation of several smaller highly regular crystal patches, while the defects form during the later stages when two or more of these patches merge. These kinetic parallels suggest a certain universality in the crystal formation processes on curved surfaces in the slow-quench regime. Extrapolating these similarities to higher quench rates, one may hope that the scaling results identified here translate to other physical and biological systems that develop crystalline structures on their curved surfaces.
5 Conclusions
The above analysis suggest that KZ-type scalings can occur in an experimentally accessible, macroscopic elastic bilayer system. Specifically, we have identified the power law scaling relation between topological defects densities and linear quench rates using a recently validated generalized Swift–Hohenberg theory of elastic bilayer wrinkling.49 Our analysis supports earlier studies which showed that KZ scalings can arise in the context of (weakly) first-order transitions, provided the quench rates are fast enough.22,24 The numerical results above predict universal scalings in spherical and toroidal geometries. Further work will be needed however to test whether these results extend to other geometries with strongly varying curvature, where symmetry-breaking is expected to become inhomogeneous. With regard to applications, the KZ scaling relations for elastic surface crystals offer concrete guidance for controlling the number of topological defects by tuning the quench rate, extending previous work40,41 that showed how substrate geometry can be used for defect localization. The nucleation sequences leading to crystalline hexagonal surface patterns in the thin-film model are qualitatively similar to those reported recently for colloidal crystals on spherical liquid–liquid interfaces.26 This suggests that elastic surface crystals, which have been realized by substrate depressurization46 or surface swelling,47 can offer a flexible testbed for exploring generic aspects of crystal growth kinetics and topological defect formation in complex geometries.Conflicts of interest
There are no conflicts to declare.Appendix
Wrinkling theory
Wrinkling of a thin stiff film that is adhered to a softer curved substrate can effectively be described by a Swift–Hohenberg-type equation for the normal displacement field u.49 Measuring all length in terms of the film thickness h, the associated elastic energy on an arbitrary substrate geometry ω is given by, see eqn (34) and (40a) in the ESI† of ref. 49,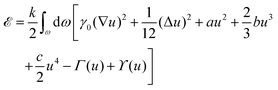 | (6) |
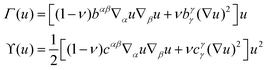 | (7) |
![[scr K, script letter K]](https://www.rsc.org/images/entities/char_e148.gif) − (bγγ/2)2]/2, with
− (bγγ/2)2]/2, with ![[scr K, script letter K]](https://www.rsc.org/images/entities/char_e148.gif) the Gaussian curvature, is of third order in the curvature tensor and thus negligible in comparison to the first-order curvature nonlinearity Γ(u). Moreover, numerical analysis for experimentally relevant parameters49 shows that ϒ(u) is typically smaller than the other energy contributions and, hence, does not significantly affect surface pattern formation. We can therefore neglect the terms bu3 and ϒ(u) in the remainder.
the Gaussian curvature, is of third order in the curvature tensor and thus negligible in comparison to the first-order curvature nonlinearity Γ(u). Moreover, numerical analysis for experimentally relevant parameters49 shows that ϒ(u) is typically smaller than the other energy contributions and, hence, does not significantly affect surface pattern formation. We can therefore neglect the terms bu3 and ϒ(u) in the remainder.
Taking the variation of the remaining energy with respect to the normal displacement field u, and assuming overdamped dynamics, we obtain the generalized Swift–Hohenberg equation (GSHE) given in eqn (1) with49
| δuΓ(u) = (ν − 1)[bαβ∇αu∇βu + 2u∇β(bαβ∇αu)] + ν[bγγ(∇u)2 − 2∇·(bγγu∇u)] | (8) |
To first order in the substrate curvature, the various parameters in the energy and in the GSHE relate to mechanical and geometrical system properties as follows:49
In our simulations, we fix the Poisson ratio ν = 1/2 and η = 0.33, corresponding to a substrate that is approximately one order of magnitude softer than the adhering film, which is in the range of earlier experiments.48 To solve eqn (1) under constant quenches Σe = μt, we use a custom subdivision surface-based finite element code with C1-continuous basis functions.68,69 The simulations use triangular meshes consisting of up to ∼2.7 × 104 mesh nodes and ∼5.5 × 104 elements. To break the symmetry of the initially unwrinkled film u = 0, we add a small stationary random field ε to the rhs of eqn (1). The values of ε at each mesh-node are drawn independently from a uniform distribution over the interval [−0.5 × 10−6, 0.5 × 10−6] and kept fixed throughout a simulation run. To integrate the GSHE in time, we use a standard forward Euler time stepping integrator, noting that the dynamics is overdamped and thus numerically stable and accurate for small time steps Δt. For a given quench μt, the numerical integration is started at time tinit = −103μΔt < 0, so that each simulation spends a comparable number of integration steps in the unwrinkled regime Σe < 0.
Amplitude equations
As outlined in ref. 49, the GSHE on spherical substrates with radius R can be approximated by a standard Swift–Hohenberg (SH) equation by replacing the Γ(u)-term with a quadratic nonlinearity that produces the same average force for a pattern consisting of plane waves ∼eik·x with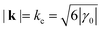 . Keeping only the first-order curvature terms, the resulting standard SH equation can be written in the rescaled standard form49
. Keeping only the first-order curvature terms, the resulting standard SH equation can be written in the rescaled standard form49| ∂Tϕ = αϕ − (1 + ΔX)2ϕ + βϕ2 − ϕ3 | (9) |
For non-spherical substrates, the coefficient β becomes a function of the position on the surface ω and thus generally considerably more complex than in the spherical case. However, since an appropriate β-term can be constructed for a given surface geometry, and the value of β is not important for the subsequent arguments, it suffices to assume in the following that the GSHE can be cast into the form (9).
We note that in the above normal form, patterns with non-zero amplitude and wave length λ = 2π emerge when the bifurcation parameter α > 0: linearizing eqn (9) with the plane-wave ansatz u(x,t) = A![[thin space (1/6-em)]](https://www.rsc.org/images/entities/i_char_2009.gif) exp(ωt + ikx), we obtain the first-order growth rates
exp(ωt + ikx), we obtain the first-order growth rates
| ω = α − 1 + 2k2 − k4 | (10) |
Performing a standard perturbation analysis for the SH equation as outlined in ref. 70, we study the behavior close to bifurcation for α = Bβ2 with |β| ≪ 1 and B = O(1). To this end, we consider a solution to eqn (9) of the form ϕ = βϕ1 + β3ϕ3 +⋯ with ansatz
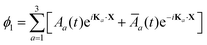 | (11) |
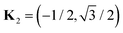 , and
, and 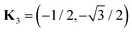 . Substituting this ansatz into eqn (10) and using that K1 + K2 + K3 = 0, one finds at order O(β3) three amplitude equations of the form70
. Substituting this ansatz into eqn (10) and using that K1 + K2 + K3 = 0, one finds at order O(β3) three amplitude equations of the form70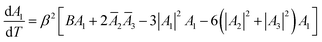 | (12) |
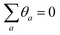 as an attractive fix point, meaning that phases synchronize.70 Without loss of generality, one can assume individually θa = 0,70 corresponding to a real amplitude ansatz.
as an attractive fix point, meaning that phases synchronize.70 Without loss of generality, one can assume individually θa = 0,70 corresponding to a real amplitude ansatz.
Hexagons are characterized by equal amplitudes Ra ≡ ![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) , leading to a single amplitude equation
, leading to a single amplitude equation
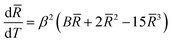 | (13) |
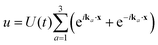 with ka = kcKa as given in Discussion and U(t) = u*β
with ka = kcKa as given in Discussion and U(t) = u*β![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) (t). Hence, combining eqn (10) and (13), we obtain
(t). Hence, combining eqn (10) and (13), we obtain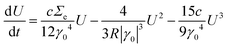 | (14) |
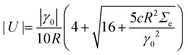 | (15) |
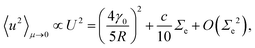 | (16) |
For toroidal geometries (Fig. 3C and 4A), we find a similar behavior for substrates with non-constant curvature, confirming that curvature variations do not greatly affect the surface-averaged amplitude for the considered toroidal geometries. Specifically, we estimate for toroidal geometries from Fig. 3C
| 〈u2〉μ→0 = A + BΣe + O(Σe2) | (17) |
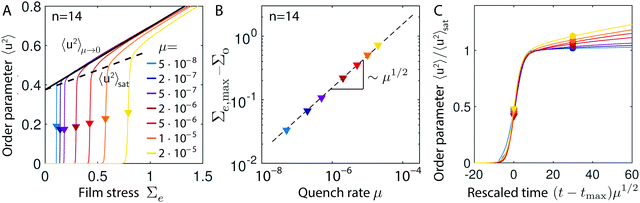 | ||
| Fig. 4 Determination of freeze-out time and stress for toroidal surface crystal. (A) Delayed bifurcation of the order parameter 〈u2〉, identical to Fig. 3C. Markers denote the location Σe,max of largest slope. The solid line is the linear approximation 〈u2〉μ→0 = 0.38 + 0.32Σe, whereas the dashed line, 〈u2〉sat = 0.37 + 0.2Σe demarcates the region where the order parameter begins to saturate. (B) The maximum slope stresses follow the KZ scaling, Σe,max − Σ0 ∝ μ1/2. (C) Close to Σe,max and the corresponding time tmax, the dynamics of the normalized order parameter 〈u2〉/〈u2〉μ→0,sat is universal under the rescaling t → tμ1/2. Circle symbols indicate the freeze-out times tf = tmax + Δτμ−1/2 (Δτ = 30). | ||
Freeze-out
We summarize how the freeze-out time tf and the corresponding stress Σe,f are obtained for toroidal geometries. The procedure for spherical substrates is analogous.We first determine the stress Σmax and corresponding time tmax = Σmax/μ where 〈u2〉 has largest slope. We find that Σmax − Σ0 ∝ μ1/2, confirming the KZ-type scaling (Fig. 4A and B). Since amplitudes are however not yet fully developed at tmax, we add a time delay to allow amplitudes of hexagonal patterns to fully develop. Under a constant-rate quench Σe = μt, the amplitude eqn (14) become quench-rate independent under the rescaling t′ = tμ1/2 at leading order in U. Choosing the delay Δτμ−1/2 thus allows each quench the same (rescaled) time to fully develop the hexagonal amplitudes. We chose the value of Δτ = 30, which is long enough to allow fully developed hexagonal patterns, while also being small enough that defect annihilation is still negligible, thus not affecting the KZ scaling of the defect density. Accordingly, the freeze-out film stress is defined as Σe,f = μtf = Σmax + μ1/2Δτ.
To confirm the scalings of the order parameter in the transition region near tmax, we first shift the measured quench curves of Fig. 4A by tmax and rescale time by μ1/2. For better comparison, we then normalize the order parameter 〈u2〉 as follows: from Fig. 4A, we observe that for all quench rates, the order parameter curves begin to saturate at values of 〈u2〉sat that are linear in Σe (dashed line in Fig. 4A). Estimating the linear trend, we find 〈u2〉sat = 0.37 + 0.2Σe. We thus normalize 〈u〉 by 〈u2〉sat evaluated at Σe,max. Under these rescalings, the curves 〈u2〉/〈u2〉μ→0,sat for various quenches μ collapse onto a single curve in the transition region close to t = tmax (Fig. 4C). We emphasize that it is impossible to simultaneously collapse order parameter curves after the freeze-out, because for t ≫ tmax the order parameter asymptotes to the adiabatic value, which scales linearly in the quench rate and time, 〈u2〉μ→0 ≃ A + BΣe = A + Bμt, explaining the different slopes observed for t ≫ tmax in Fig. 4C.
Pattern analysis
To reconstruct the curved crystal structure and detect topological defects, we first threshold the amplitude field u obtained from simulations to find the center of each crystalline lattice site. Each site is then connected to its nearest neighbors via a Delaunay triangulation, and the hexagonal crystal structure as well as defects are obtained from the dual Voronoi graph. To find the flat crystal representation of Fig. 1C and E, we first construct the Voronoi cells of the crystal. We then randomly select a regular crystal site s0 and its six neighbors as center of the planar lattice. Based on their positions relative to s0, the neighbors can be assigned to one of the six surrounding unit lattice positions. We then repeat this construction sequentially for each neighbor by aligning their closest neighbors with the existing planar lattice structure, following the procedure used in ref. 26. To obtain the time evolution, we first construct the final planar crystal from the fully crystallized configuration at freeze-out time tf. For all earlier times t < tf, we use a Hungarian matching algorithm71 to track identical Voronoi sites and identify them in the fully crystallized planar configuration.References
- I. Chuang, R. Durrer, N. Turok and B. Yurke, Science, 1991, 251, 1336 CAS.
- P.-G. De Gennes and J. Prost, The Physics of Liquid Crystals, Clarendon Press, Oxford, 1995 Search PubMed.
- M. Nikkhou, M. Skarabot, S. Copar, M. Ravnik, S. Zumer and I. Musevic, Nat. Phys., 2015, 11, 183–187 CrossRef CAS.
- X. Wang, D. S. Miller, E. Bukusoglu, J. J. de Pablo and N. L. Abbott, Nat. Mater., 2016, 15, 106–112 CrossRef CAS PubMed.
- P. Weiss, C. R. Acad. Sci., 1906, 143, 1136 CAS.
- T. D. Edwards, Y. Yang, D. J. Beltran-Villegas and M. A. Bevan, Sci. Rep., 2014, 4, 6132 CrossRef CAS PubMed.
- A. Cortijo and M. A. H. Vozmediano, EPL, 2007, 77, 47002 CrossRef.
- O. V. Yazyev and L. Helm, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 75, 125408 CrossRef.
- W. H. Zurek, Nature, 1985, 317, 505–508 CrossRef CAS.
- P. C. Hendry, N. S. Lawson, R. A. M. Lee, P. V. E. McClintock and C. D. H. Williams, Nature, 1994, 368, 315–317 CrossRef CAS.
- M. J. W. Dodgson and M. A. Moore, Phys. Rev. B: Condens. Matter Mater. Phys., 1997, 55, 3816–3831 CrossRef CAS.
- R. Monaco, J. Mygind, R. J. Rivers and V. P. Koshelets, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80, 180501 CrossRef.
- T. W. B. Kibble, J. Phys. A: Math. Gen., 1976, 9, 1387 CrossRef.
- M. Hindmarsh, J. Phys. A: Math. Theor., 2016, 49, 411001 CrossRef.
- W. H. Zurek, Phys. Rep., 1996, 276, 177–221 CrossRef CAS.
- N. Fowler and I. Dierking, ChemPhysChem, 2017, 18, 812–816 CrossRef CAS PubMed.
- S. Deutschländer, P. Dillmann, G. Maret and P. Keim, Proc. Natl. Acad. Sci. U. S. A., 2015, 112, 6925–6930 CrossRef PubMed.
- S. Ulm, J. Roßnagel, G. Jacob, C. Degünther, S. T. Dawkins, U. G. Poschinger, R. Nigmatullin, A. Retzker, M. B. Plenio and F. Schmidt-Kaler, et al. , Nat. Commun., 2013, 4, 2290 CAS.
- M. Anquez, B. A. Robbins, H. M. Bharath, M. Boguslawski, T. M. Hoang and M. S. Chapman, Phys. Rev. Lett., 2016, 116, 155301 CrossRef CAS PubMed.
- V. M. H. Ruutu, V. B. Eltsov, A. J. Gill, T. W. B. Kibble, M. Krusius, Y. G. Makhlin, B. Placais, G. E. Volovik and W. Xu, Nature, 1996, 382, 334–336 CrossRef CAS.
- G. Labeyrie and R. Kaiser, Phys. Rev. Lett., 2016, 117, 275701 CrossRef CAS PubMed.
- S. Casado, W. González-Viñas, H. Mancini and S. Boccaletti, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2001, 63, 057301 CrossRef CAS PubMed.
- M. A. Miranda, D. Laroze and W. González-Viñas, J. Phys.: Condens. Matter, 2013, 25, 404208 CrossRef CAS PubMed.
- S. Casado, W. González-Viñas, S. Boccaletti, P. L. Ramazza and H. Mancini, Eur. Phys. J.-Spec. Top., 2007, 146, 87–98 CrossRef.
- T. Galla and E. Moro, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2003, 67, 035101 CrossRef PubMed.
- G. Meng, J. Paulose, D. R. Nelson and V. N. Manoharan, Science, 2014, 343, 634–637 CrossRef CAS PubMed.
- D. A. Beller and D. R. Nelson, Phys. Rev. E, 2016, 94, 033004 CrossRef PubMed.
- R. E. Guerra, C. P. Kelleher, A. D. Hollingsworth and P. M. Chaikin, Nature, 2018, 554, 346–350 CrossRef CAS PubMed.
- M. Pennybacker and A. C. Newell, Phys. Rev. Lett., 2013, 110, 248104 CrossRef PubMed.
- J. F. Sadoc, J. Charvolin and N. Rivier, J. Phys. A: Math. Theor., 2013, 46, 295202 CrossRef.
- M. F. Pennybacker, P. D. Shipman and A. C. Newell, J. Phys. D: Appl. Phys., 2015, 306, 48–81 Search PubMed.
- A. Amir, F. Babaeipour, D. B. McIntosh, D. R. Nelson and S. Jun, Proc. Natl. Acad. Sci. U. S. A., 2014, 111, 5778–5783 CrossRef CAS PubMed.
- A. Amir, J. Paulose and D. R. Nelson, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2013, 87, 042314 CrossRef PubMed.
- B. Berger, P. W. Shor, L. Tucker-Kellogg and J. King, Proc. Natl. Acad. Sci. U. S. A., 1994, 91, 7732–7736 CrossRef CAS.
- J. Lidmar, L. Mirny and D. R. Nelson, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2003, 68, 051910 CrossRef PubMed.
- D. Chrétien, F. Metoz, F. Verde, E. Karsenti and R. H. Wade, J. Cell Biol., 1992, 117, 1031 CrossRef.
- J. A. Robinson, E. S. Snow, S. C. Badescu, T. L. Reinecke and F. K. Perkins, Nano Lett., 2006, 6, 1747–1751 CrossRef CAS PubMed.
- E. P. Chan and A. J. Crosby, Adv. Mater., 2006, 18, 3238–3242 CrossRef CAS.
- L. Euler, Novi Comment. Acad. Sci. Imp. Petropol., 1758, 4, 109–140 Search PubMed.
- L. Giomi and M. J. Bowick, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2008, 78, 010601 CrossRef PubMed.
- J. Francisc López, N. Stoop, R. Lagrange, J. Dunkel and P. M. Reis, Phys. Rev. Lett., 2016, 116, 104301 CrossRef PubMed.
- R. Backofen, A. Voigt and T. Witkowski, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2010, 81, 025701 CrossRef PubMed.
- V. Vitelli, J. B. Lucks and D. R. Nelson, Proc. Natl. Acad. Sci. U. S. A., 2006, 103, 12323–12328 CrossRef CAS PubMed.
- W. T. M. Irvine, V. Vitelli and P. M. Chaikin, Nature, 2010, 468, 947–951 CrossRef CAS PubMed.
- H. Kusumaatmaja and D. J. Wales, Phys. Rev. Lett., 2013, 110, 165502 CrossRef PubMed.
- M. Brojan, D. Terwagne, R. Lagrange and P. M. Reis, Proc. Natl. Acad. Sci. U. S. A., 2015, 112, 14–19 CrossRef CAS PubMed.
- D. Breid and A. J. Crosby, Soft Matter, 2013, 9, 3624–3630 RSC.
- D. Terwagne, M. Brojan and P. M. Reis, Adv. Mater., 2014, 26, 6608–6611 CrossRef CAS PubMed.
- N. Stoop, R. Lagrange, D. Terwagne, P. M. Reis and J. Dunkel, Nat. Mater., 2015, 14, 337–342 CrossRef CAS PubMed.
- P. G. Ciarlet, Mathematical elasticity, vol. III: Theory of shells, North Holland, Amsterdam, 2000 Search PubMed.
- S. Cai, D. Breid, A. J. Crosby, Z. Suo and J. W. Hutchinson, J. Mech. Phys. Solids, 2011, 59, 1094–1114 CrossRef.
- L. R. Gómez, N. A. Garca, V. Vitelli, J. Lorenzana and D. A. Vega, Nat. Commun., 2015, 6, 6856 CrossRef PubMed.
- A. D. Pezzutti, L. R. Gómez, M. A. Villar and D. A. Vega, Europhys. Lett., 2009, 87, 66003 CrossRef.
- D. A. Vega and L. R. Gómez, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2009, 79, 051607 CrossRef PubMed.
- T. Erneux and P. Mandel, SIAM J. Appl. Math., 1986, 46, 1–15 CrossRef.
- P. Mandel and T. Erneux, J. Stat. Phys., 1987, 48, 1059–1070 CrossRef.
- M. J. Bowick, A. Cacciuto, D. R. Nelson and A. Travesset, Phys. Rev. Lett., 2002, 89, 185502 CrossRef CAS PubMed.
- M. J. Bowick, D. R. Nelson and A. Travesset, Phys. Rev. B: Condens. Matter Mater. Phys., 2000, 62, 8738 CrossRef CAS.
- A. R. Bausch, M. J. Bowick, A. Cacciuto, A. D. Dinsmore, M. F. Hsu, D. R. Nelson, M. G. Nikolaides, A. Travesset and D. A. Weitz, Science, 2003, 299, 1716–1718 CrossRef CAS PubMed.
- N. A. Garca, A. D. Pezzutti, R. A. Register, D. A. Vega and L. R. Gómez, Soft Matter, 2015, 11, 898–907 RSC.
- M. J. Bowick, D. R. Nelson and A. Travesset, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2004, 69, 041102 CrossRef PubMed.
- L. Giomi and M. J. Bowick, Eur. Phys. J. E: Soft Matter Biol. Phys., 2008, 27, 275–296 CrossRef CAS.
- A. Doelman, B. Sandstede, A. Scheel and G. Schneider, Eur. J. Appl. Math., 2003, 14, 85–110 CrossRef CAS.
- P. Hohenberg and A. Krekhov, Phys. Rep., 2015, 572, 1–42 CrossRef.
- A. Chuvilin, U. Kaiser, E. Bichoutskaia, N. A. Besley and A. N. Khlobystov, Nat. Chem., 2010, 2, 450–453 CrossRef CAS PubMed.
- R. Tomer, K. Khairy, F. Amat and P. J. Keller, Nat. Methods, 2012, 9, 755–763 CrossRef CAS PubMed.
- K. Drescher, R. E. Goldstein and I. Tuval, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 11171–11176 CrossRef CAS PubMed.
- F. Cirak, M. Ortiz and P. Schröder, Int. J. Numer. Meth. Eng., 2000, 47, 2039–2072 CrossRef.
- R. Vetter, N. Stoop, T. Jenni, F. K. Wittel and H. J. Herrmann, Int. J. Numer. Meth. Eng., 2013, 95, 791–810 CrossRef.
- A. A. Golovin and A. A. Nepomnyashchy, Self-assembly, pattern formation and growth phenomena in nano-systems, Springer, Dordrecht, 2006 Search PubMed.
- J. Munkres, J. Soc. Ind. Appl. Math., 1957, 5, 32–38 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c7sm02233f |
| This journal is © The Royal Society of Chemistry 2018 |