Self-organization in dipolar cube fluids constrained by competing anisotropies

Abstract

For magnetite spherical nanoparticles, the orientation of the dipole moment in the crystal does not affect the morphology of either zero field or field induced structures. For non-spherical particles however, an interplay between particle shape and direction of the magnetic moment can give rise to unusual behaviors, in particular when the moment is not aligned along a particle symmetry axis. Here we disclose for the first time the unique magnetic properties of hematite cubic particles and show the exact orientation of the cubes' dipole moment. Using a combination of experiments and computer simulations, we show that dipolar hematite cubes self-organize into dipolar chains with morphologies remarkably different from those of spheres, and demonstrate that the emergence of these structures is driven by competing anisotropic interactions caused by the particles' shape anisotropy and their fixed dipole moment. Furthermore, we have analytically identified a specific interplay between energy, and entropy at the microscopic level and found that an unorthodox entropic contribution mediates the organization of particles into the kinked nature of the dipolar chains.

---

Understanding the fundamental interactions between colloidal particles is a crucial aspect for the development of novel functional materials via self-assembly or in external field.^1–3 For magnetic colloids, this is especially important as their magnetic properties can be directly linked to the geometric properties of their assemblies.^4,5 Here we use hematite micron-sized colloids with a cubic shape to show how specific directional dipolar interactions compete with the intrinsic particle shape anisotropy to form unconventional dipolar structures. Hematite colloids represent a unique model system to study this phenomenon: they can be synthesized in different shapes^6,7 and they maintain a permanent dipole moment even at large particle size. The peculiar magnetic properties of hematite arise from parasitic ferromagnetism due to canting of the magnetic spins, in an otherwise antiferromagnetic arrangement, and possible defect moments of its lattice. The spontaneous magnetization of hematite (M_s,hem ≈ 2.2 × 10³ A m⁻¹) is much smaller than that of other magnetic materials such as magnetite (M_s,mag ≈ 4.8 × 10⁵ A m⁻¹). However, its domain size (a material specific volume that sets a size limit above which particles become paramagnetic^8,9) is on the order of 15 μm, much larger than the typical domain size (≤100 nm) of other common iron oxides like magnetite.¹⁰ The consequence of this distinctive magnetism is that micron-sized hematite colloids display a fixed and permanent magnetic dipole moment that is strong enough to allow for the formation of dipolar chains, even in the absence of an external magnetic field.

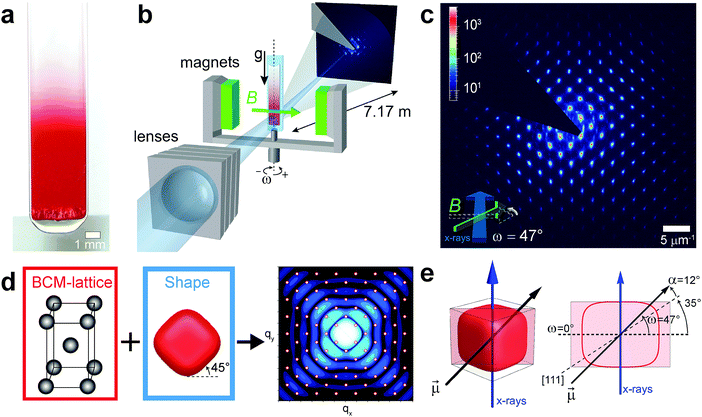
Here, we focus on the magnetic properties of hematite superballs (see Fig. 1), particles whose cubic shape can be described by: (x/a)^m + (y/a)^m + (z/a)^m = 1, where L = 2a is the particle's edge length and m is a parameter that characterizes the roundness of the corners; the higher m the more cubic is the superball. From the magnetism of bulk hematite, we expect the dipole moment of hematite cubes to lay on the plane perpendicular to the c-axis^11–13 (see Fig. 1c). To determine its exact orientation, we have studied the structure of bulk cubic crystals formed under a homogenous magnetic field. Hematite cubes with edge length L = 533 nm coated with a 59 nm thick shell of amorphous silica and with shape parameter m = 3.1 were dispersed in ethanol and allowed to sediment in an applied magnetic field of 25 mT. After 24 hours we observed the formation of a thick crystalline sediment showing Bragg reflections as shown in Fig. 2(a). The crystal structure was investigated in situ using small angle X-ray scattering with microradian resolution (μrad-SAXS) (Fig. 2(b)).¹⁴ The total measured scattering pattern I(q⃑) ∝ P(q⃑)S(q⃑) shown in Fig. 2(c), is a product of the structure factor S(q⃑) of the crystal lattice (a body centered monoclinic (BCM) crystal¹⁵) and the form factor P(q⃑) originating from the cubic shape of the particles.¹⁶ We analyzed 2D μrad-SAXS patterns obtained at different rotation angles ω, where ω = 0° corresponds to the magnetic field perpendicular to the X-ray beam, and found that at ω = 47° the peaks are most strongly enhanced by the form factor and are observed up to the 5th order in the horizontal and vertical directions and the 10th order in all diagonal directions (see Movie 1, ESI†). Given the contribution from the form factor (Fig. 2(d) in blue) we deduce that the cubes are organized with their faces perpendicular to the X-ray beam and tilted 45° with respect to the horizontal plane as shown in the model of Fig. 2(d). Fig. 2(d) also shows the calculated contributions of the crystal lattice (in red) and particle form factor (in blue) to the final scattering pattern, which is consistent with the experimental pattern of panel (c) in the same figure. Assuming that the particle orientation in the crystal is determined by the applied magnetic field, we find that the dipole moment in the hematite cubes is situated at an angle α = 12° into the cube's face with respect to its 111-direction as illustrated in Fig. 2(e). This angle is 7° smaller than the angle one finds assuming a dipole moment located in the plane perpendicular to the c-axis. Implications of this angle discrepancy on the cubes self-assembly behavior are discussed later in the text.

Fig. 1 Colloidal model system. Transmission (a) and scanning (b) electron microscope images of bare (a) and silica coated (b) hematite cubes. (c) Schematic illustration of the c-axis and c-plane (perpendicular to the c-axis) for a superball with shape parameter m = 4.

Fig. 2 Small angle X-ray scattering measurements. (a) Photograph of a glass capillary filled with suspension of silica coated hematite cubes in ethanol after 24 hours of sedimentation. The crystals formation is indicated by the strong Bragg reflections of green light that provide a stark contrast against the red hematite suspension. (b) Schematic representation of the Small Angle X-ray Scattering measurement setup with microradian resolution (μrad-SAXS) composed of compound refractive lenses and the specialized magnetic field setup. (c) Experimental 2D μrad-SAXS pattern obtained at ω = 47°. (d) Calculated contributions of the Body Centered Monoclinic (BCM) lattice (in red) and of the particle form factor (in blue), and the combined SAXS pattern (red peaks: BCM lattice; blue pattern: form factor). (e) Schematic illustration of the spacial orientation of the magnetic dipole moment (black arrow) for a superball with m = 4. The dipole moment is situated at an angle α = 12° into the cube face with respect to the 111-direction (dashed line). The angle of 47° indicates the alignment of the cube's dipole moment with the applied magnetic field and 35° is the angle that the [1 1 1] diagonal forms with the base of the cube.

Having found the orientation of the magnetic dipole, we now examine the interaction behavior of colloidal cubes with and without an applied magnetic field (their estimated total interaction potential is described in Section S2, ESI†). Cubes with edge length L ≈ 1135 nm coated with a 100 nm thick layer of silica and shape parameter m = 4 are confined inside flat glass capillaries where they form a quasi-2D system due to their short gravitational height in water. The capillaries are mounted at the center of a magnetic set-up consisting of three sets of orthogonally oriented Helmholtz coils arranged around the focal point of an inverted microscope. Each pair of coils is controlled by an independent power supply, which allows us to tune magnitude and orientation of the applied magnetic field. A constant background field is applied to cancel the Earth's magnetic field and generate an effective zero-field environment throughout the experiments (see Section S3, ESI†).

Typical optical microscopy images taken in zero-field are shown in Fig. 3(a and d). The formation of colloidal rings and chains is consistent with the expected dipolar structures observed in dispersions of magnetic nanoparticles.¹⁷ However, the cubic shape of the particles has a clear effect on both shape and dynamics of the ring-like structures which are observed to fluctuate between circular and rectangular loops, as visible in Movie 2 (ESI†). The effect of the particles shape becomes particularly evident when an external field is applied (Fig. 3(b, c and e–g)). The external field causes the closed-loops structures to open up into linear chains which quickly buckle as the magnitude of the field increases. To precisely understand this behavior we performed computer simulations on computational analogs of the experimental system. The simulations explored systems with a magnetic coupling parameter of λ* = 10, at surface densities of ρ_s* = (0.01, 0.05), where the field strength was quantified in terms of the Langevin parameter α_L* = (0, 6, 41). The rational was to match the relative, rather than absolute, energy scales of the simulations to those present in experiment. A detailed explanation of this procedure is provided in the Experimental section.

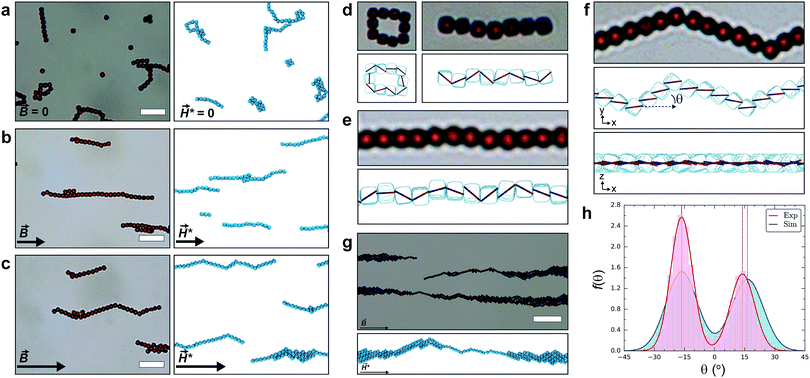Fig. 3 Hematite cube assemblies. (a–g) Experimental observations of silica-coated hematite cubes in water (left), and computer simulations of cubes (right) with the empirical dipole orientation (see Fig. 2(e)). (a) Typical dipolar zero field structures are observed when the Earth's field is cancelled. (b) For weak fields (∼Earth's field), straight chains form and align parallel to the field direction. (c) At high fields (∼three times Earth's field) the chains rearrange to form kinked structures whose average alignment is parallel to the field direction. Visualizing dipoles in the simulated structures elucidates their specific configurations. (d) Flux-closure rings and zig-zag chains are observed at zero field. (e) Weak fields are sufficient to orient the total dipole moment of structures, but insufficient for the alignment of individual cube dipoles. (f) High fields facilitate the complete alignment of cube dipoles, this causes a characteristic rotation of the cubes within assembled structures and the emergence of kinks. This is a vivid illustration of the active competition between shape, dipole and field-induced interactions. (g) Over long time-scales (or at high particle concentration) chains assemble into bundles, and at high field still retain visibly kinked features. (h) Angular distributions of chain alignment at high field from experiment (red) and simulation (blue). Scale bars: 10 μm for (a–c), 20 μm for (g). Simulation parameters: temperature, T* = 1 for (a–h); surface density, ρ_s* = 0.05 for (a–c and g) and ρ_s* = 0.01 for (h); Langevin parameters, α_L* = 0 for (a and d), α_L* = 6 for (b and e) and α_L* = 41 for (c and f–h); snapshots recorded at propagation time, t* = 5 × 10⁴Δt* for (a–f) and t* = 2 × 10⁶Δt* for (g).

In the zero-field regime, when comparing the experimental and simulation images in Fig. 3(a and d), a remarkable similarity between the structure of the formed clusters can be observed: equivalent rectangular rings, chains, and other compact structures materialize (see Movie 3, ESI†). Moreover, branching points are a notable feature in both images, where a single cube can support connections to more than two ‘chain-like’ neighbors. By visualizing the dipoles in single-cluster snapshots (Fig. 3(d)), we see that dipoles within the ring structure form a flux-close circle, while a zig-zag configuration is found in linear chains (Fig. 3(d)). When a weak external magnetic field (or the Earth's field) is applied, we again see a strong correspondence between the experimental and simulated behavior. In Fig. 3(e), we find the field is sufficiently strong to align the total dipole moment of the cluster, whereas the individual dipoles still have a relative amount of freedom and are not perfectly aligned. Increasing the magnetic field-strength induces further alignment of the dipoles with the external field, causing chains to evolve into kinked structures with a well-defined angle (Fig. 3(c and f)). The overall chain direction is in line with the field, but the segments next to a kink are aligned with a specific angle θ as shown in Fig. 3(f). These structures are reversible and when the external field is removed, particles rearrange back into zero-field structures.

To quantify the chain orientations within the field we calculated θ between two neighboring particles in a chain (see Section 4, ESI†). Connectivity networks were used to analyze cluster configurations to facilitate this calculation (see Methods). Fig. 3(h) compares the probability density function, f(θ), of the experimental (red) and simulated (blue) structures at the highest field strengths, with θ = 0° being the direction of the field. The distribution histograms were binned according to the Freedman–Diaconis rule. A clear bimodal distribution is observed for both f(θ) with very good agreement between the peak positions. The difference in peak intensity between experiment and simulation is attributed to the low field of view in the microscope. By fitting the distributions to a bimodal normal distribution (see eqn (S6), ESI†), we find that θ possesses mean values of approximately (−16.4°, +13.9°) in experiment and ±16.3° in simulation, evidently in very good agreement. Consequently, the dipole moment alignment combined with the cubic particle shape has induced a specific kink angle of ϕ_kink = π − 2θ = 149.7°/147.3°, from experiment/simulation respectively.

If the particle concentration increases, the chains start to interact with each other and assemble into bundles¹⁷ (Fig. 3(g)) where it is still possible to recognize the kinked arrangement of the chains. We can also see from Fig. 3(c) how crystal seeds begin to form, where crystalline regions are connected via kinked chains suggesting that kinks provided nucleation sites for further growth.

To verify the empirical dipolar tilt angle α = 12°, we exploit our ability, in simulation, to re-orient the dipole within the cube (Section S5, ESI†). In Fig. S8 (ESI†), we provide snapshots from simulations, with two further orientations of the dipole: a [111] orientation and an orientation with α = −12° from [111] towards the particle edge. For these orientations and others considered in previous investigations,^18–21 the assembled structures do not exhibit the same pronounced kinking behavior, as shown also by a bond angle analysis (Section S4, ESI†), confirming that the tilt towards the cube face has a crucial influence on the particle assembly. In addition, we compared the strong field kinking found at the empirical α = 12° with a tilt α = 19° in the same direction (Section S5, ESI†). This angle was calculated based on the assumption that the dipole moment of bulk hematite lies in the plane perpendicular to the c-axis^11–13 (Fig. S1(a), ESI†). For α = 19°, kinks in the chains are still observed, but are less prevalent than for α = 12°. The difference in the assembly behavior found between cubes with a dipole moment tilt of α = 12° and α = 19° suggests that the kinking behavior is governed by specific tilt angles. This observation further corroborates the accuracy of the experimental angle α = 12° based on the kink angle comparison in Fig. 3(h).

From simulations, we quantified the relationship between chain length and kink formation and mapped the various populations of a small sub-set of chain lengths n ≤ 15 (for reliable statistics) in terms of their corresponding number of kinks, n_k, shown in Fig. 4(a). Kinked clusters were identified from connectivity networks according to the criterion discussed in Section S4 (ESI†). We find that the tendency for multi-kinked chains is extremely low and grows only marginally with increasing n, thus the majority of kinked chains form only a single kink. Nevertheless, the maximum number of kinks observed for each value of n scales in a visibly sub-linear fashion, implying that the maximum kink number is a monotonic, slowly increasing, function of n. This monotonic increase can be attributed to a combination of the growing configurational phase space available to kinks with increasing n, as well as the relative reduction in the cost of subsequent kink formation, i.e. the energetic cost of the first kink is higher than that of the second, as we shall see next.

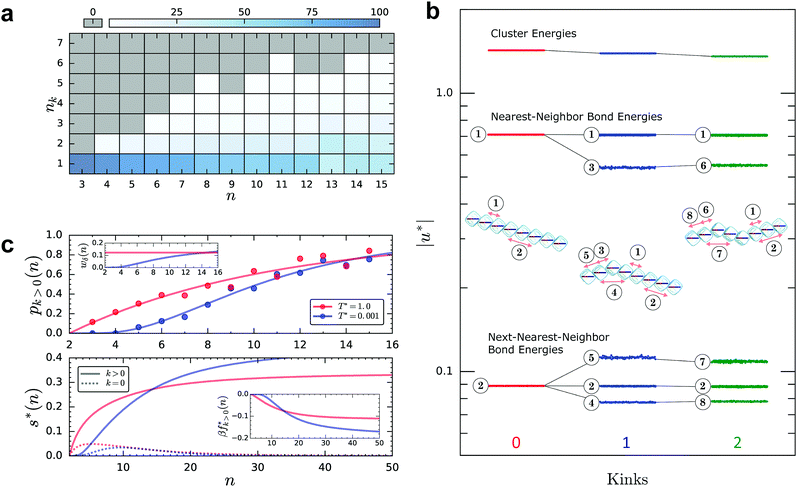Fig. 4 Unconventional dipolar energy-entropy interplay. (a) Number of kinks n_kversus chain length n. Each state point of the n − n_k plane is normalized by the total number of chains of the given length. The percentage of configurations at each state point is encoded according to the overhead color-bar. State points colored grey correspond to a chain percentage of identically zero. (b) Dipolar bond energy diagram of kinked/unkinked chain configurations (n = 8), plotted using a logarithmic energy scaling. The cluster energies are displayed alongside the individual nearest-neighbor and next-nearest-neighbor bond energies. The data points for the straight chain (red), single-kinked chain (blue) and double-kinked chain (green) depict the fluctuations of the respective energy quantity during the final propagation period of the simulations. The various bond-types are labelled numerically (1–8) and the cluster snapshots are annotated with a single instance of each. The splitting of the energy levels is illustrated with black lines. (c) Each quantity, for high (red) and low (blue) temperature, is as plotted as function of n, with n < 16 in the upper panel and n < 50 in the lower panel. Any data appearing as circular symbols is derived from simulation, whereas all lines are derived from the analytical model (Section S6, ESI†). Upper panel: The probability of a chain having at least one kink p_k>0(n). Upper panel inset: The variation of w_δ. Lower panel: The intensive cluster entropy s*(n) for straight (k = 0, dashed-line) and kinked (k > 0, solid-line) cluster types. Lower panel inset: The intensive excess free energy βf_k>0*(n).

To understand the origin of the kink formation, we ran a second set of simulations on single clusters to probe their low temperature configurations. Fig. 4(b) shows a diagram of the dipolar energy levels for a chain with n = 8 and n_k = 0, 1, 2. To enable a logarithmic scaling of the energy, all cluster and bond energies are plotted as the modulus of the intensive variable i.e. the energy per particle, |u*|. It follows that larger values of |u*| indicate a more energetically favorable configuration. The upper portion of the diagram reflects the energy of the entire cluster (n = 8). As the number of kinks increases the energy decreases, proving that linear, and not kinked chains constitute the structural ground state. We have classified the bonds in each cluster according to their energy, each bond-type is labelled numerically (1–8). Each cluster snapshot is annotated with one instance of the corresponding bond types. The central set of energy levels correspond to all nearest-neighbor (n = 2) interactions in the cluster. The splitting of the dipolar bond energies shows that the formation of kinks, at the level of nearest-neighbors, destabilizes the chain through a partial lifting of the bond degeneracy. This destabilization is caused by the unfavorable orientation of the cube that connects the two sides of the chain (bond 3). The energies of all next-nearest-neighbor (n = 2) interactions appear at the bottom of the diagram. Here, a splitting of the bond energy levels and a reduction in degeneracy again occurs. For the next-nearest-neighbor interaction preceding the kink, (bond 5), the bond energy decreases, while for a next-nearest-neighbor across the kink (bond 4), the bond energy increases due to the closer proximity and collinear arrangement of the other dipole. Thus, at the level of next-nearest-neighbors we find an overall favorable contribution, stabilizing kinked configurations. The addition of a secondary kink unfavourably perturbs the values of the existing levels (bonds 6–8). In each of the clusters bonds 1 and 2 reside in portions of the clusters that are truly linear and are sufficiently far from the site of the kink to remain essentially unperturbed. Whereas bond 5 for example, although visually similar to bond 2, is a next-nearest-neighbor bond that incorporates the kink. There is an orientational offset between the particles due to the presence of the kink. This is what differentiates bond 2 from bond 5, and of course means they have different energies.

Having estimated the energetics of kink formation, we turn to an assessment of the entropy contribution using both the bulk and single-cluster simulations that were conducted at high and low temperature respectively. An analytical model for kink formation was devised (Sections S6.1 and S6.2, ESI†) to provide further insight. The upper panel of Fig. 4(c) shows the probability of a chain having at least one kink as a function of chain length, p_k>0(n), calculated from simulation (symbols) and theory (lines), for both low (blue) and high temperature (red). The effect of temperature on the variation of p_k<0(n) is clear: at low temperature, T* = 0.001, we have sigmoidal behavior where the probability of kinking at small cluster sizes is extremely low and increases rapidly with n until it reaches a plateau. In contrast, at high temperature T* = 1.0, there is a distinctly non-zero probability for small cluster sizes. Our analytical model states that p_k>0(n) = 1 − (1 + w_δ)⁽²⁻ⁿ⁾, where w_δ = e^−β*δU* is the Boltzmann factor of the energy cost associated with a single kink, δU*. When comparing this expression to simulation, β*δU* was treated as a fitting function allowing for an implicit scaling of the varying energy contributions from one temperature regime to the other. Based on insight from simulation, the energetic penalty of kink formation at low temperature was assumed to be n dependent and we fit a function of the following form β*δU* = ae^b/n. However, at high temperature the energetic penalty is treated as n independent and we use β*δU* = a. The lines shown in the upper panel of Fig. 4(c) are the results of this fitting procedure, with the following numerical values – a = 2.102 and a = 1.487, b = 4.974 – for high and low temperature respectively. The variation of w_δ at each temperature is plotted in the inset, highlighting the distinct difference in the n dependence at each temperature, and directly correlating with the appearance of kinks. We can gain a relative estimate for the value of δU at T* = 1.0, namely β*δU* = −ln w_δ = 2.1, which when corrected to account for the simulation scaling would correspond to a kink energy penalty on the order of δU = 10kT in experiment.

This analysis has provided further evidence that kinking is energetically unfavorable, highlighting explicitly that the role of entropy must be significant. Using our analytical model we estimated the intensive cluster entropy s*(n) = S*(n)/n. Expressions for the entropic contribution of straight chain configurations (k = 0) and the excess contribution associated with kinked configurations (k > 0) were derived (Section S6.3, ESI†). The lower panel of Fig. 4(c) shows the entropic contribution of the straight (dashed lines) and kinked (solid lines) chain configurations at low (blue) and high temperature (red), where the appropriate form of w_δ was used accordingly. The curves are plotted up to n = 50 to provide an idea of the asymptotic behavior. What is immediately evident, is the large contribution of the kinked chain configuration to the total entropy at both temperatures. More importantly, the initial rate at which the entropy increases with n depends strongly on temperature; s*(n) grows faster at high temperature. A consequence of this fact is propagated in the inset of this panel, where we find estimates of the intensive kink-induced free energy excess β*f_k>0*(n) = β*F_k>0*(n)/n (Section S6.4, ESI†). We see analogous behavior in the rate of decrease of the free energy, whereby for small cluster sizes this is faster at ambient temperatures. Hence, we conclude that at low temperature the formation of kinks is driven by the entropy gain associated with increasing n, while at high temperature thermal fluctuations equalize the energetic cost of a kink, consequently the appearance of kinking for small n is driven by the entropy gain associated with the increased thermodynamic weight of the kink. Clearly, the entropic contribution to the free energy drives the emergence of the kinked structures at both temperatures, attributing kink formation to be predominately, an entropically driven process.

To conclude, we have shown that the shape and dipole orientation of micron-sized hematite cubes influence the assembled structure in a complex manner. μrad-SAXS measurement of bulk crystals demonstrated that the magnetic dipole moment within the hematite cube is oriented at an angle of 12° into the cube face with respect to the cube's 111-direction. We investigate the cube assemblies in zero and applied magnetic fields experimentally and with computer simulations. In zero-field environment we find flux-close rings and zig-zag oriented chains. Applying a weak external magnetic field transforms the structures into straight chains where the cube shape is dominant, while at high field strengths the dipole moment is fully aligned and kinked structures are formed as a consequence of the dipole moment orientation within the cubes. The competing anisotropic interactions between the cube shape and dipole moment orientation are crucial for the formation of these specific dipolar structures. Knowing the properties of the hematite cubes will certainly boost their applications not only because it provides a handhold for new simulation studies to predict novel structures, but also in terms of the variety of applications that hematite cubes find, for instance, in catalysis and active matter. Furthermore the general combination of particle shape and specific directional dipolar interactions can be further employed to design specific building blocks to assemble novel materials with unique programmable structures.

Experimental section

Preparation of silica-coated hematite cubes

Hematite cubes were prepared from condensed ferric hydroxide gel employing a procedure based on ref. 22. Details on the preparation procedure of hematite colloids and silica coating procedure can be found in a previous work by some of the authors.²³ See Section S1 (ESI†) for additional properties of hematite cubes.

Small angle X-ray scattering with microradian resolution

μrad-SAXS measurements were performed at beam-line BM26B DUBBLE^24–26 at the ESRF in Grenoble using a setup employing compound refractive lenses (CRL)^14,27 as described in ref. 15 and 16. In short, the 13 keV X-ray beam was focused on a CCD X-ray detector (9 × 9 μm (Photonic Science)), protected by a wedge shaped beam stop, 7.17 m behind the sample. Samples were prepared of dispersions of silica coated hematite cubes in ethanol (5 wt%) in flame sealed capillaries (0.2 × 4 × 100 mm W3520 Vitrocom). A homogeneous horizontal magnetic field of 25 mT was provided by a magnetic field setup consisting of six permanent magnets with a spacing of 9.1 cm. A completely dispersed sample was placed in the field for a period of 24 hours until a fluid–solid boundary was observed. Next, measurements were performed at this boundary and full structural information was obtained by rotating the sample around its vertical axis over a range of ω = ±70°, with ω = 0° the starting orientation. Dark-current and background corrections were performed on the patterns before analysis. The structure was found to consist of an aligned Body Centered Monoclinic crystal, for analysis details see ref. 15.

Microscopy

Electron microscopy. Particle size and shape were studied by transmission (TEM, Philips TECNAI12) and scanning (SEM, MERLIN (Carl Zeiss) field emission) electron microscopy. TEM samples were prepared by drying drops of diluted particle dispersions on polymer coated copper grids. SEM samples were prepared in the same way and sputter-coated with a few nanometers of platinum prior to imaging.

Optical microscopy. Magnetic cube dispersions were imaged with a Nikon TE-2000U inverted optical microscope, equipped with a 100× Nikon oil objective and a Lumenera INFINITYX camera. Aqueous dispersions (pH ≈ 9) were placed in flat borosilicate glass capillaries (VitroCom 0.1 mm × 2 mm × 4 cm), sealed to a microscopy slide with epoxy glue.

Computer Simulation

Particle model. The full details of the model used in this work can be found in ref. 20. The superball geometry (m = 4) of the cubic particles is represented using forty-six spherical sub-units arranged to form the particle surface. The total interaction potential between two particles is the sum of repulsive contributions (Weeks–Chandler–Anderson potentials) from each spherical sub-unit, approximating the effect of the cubes' silica coating. In this manner, the cubic particles can be treated as nearly hard particles of the prescribed size, h = L + 2t. The peculiar domain-size scaling behavior of hematite already discussed is highly conducive to the use of the dipolar approximation. As such, a single dipole was placed at the centre-of-mass of each cube and oriented as desired, where the interaction between cubes was characterized by the potential in eqn (S2) (ESI†).

Bulk quasi-2D systems. Langevin molecular dynamics was used to study the cube self-assembly in quasi-2D confinement (rotations in 3D, translations in 2D) under the influence of an external magnetic field. The simulation methodology employed here follows that discussed in ref. 20 and the required extension to bulk systems considered in ref. 21. The only additional dimensionless quantities required here are the external magnetic field, (H*)² = H²(4πμ₀h³/ε) and reduced surface density, ρ_s* = ρ_sh². 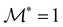The base units, mass, energy and length are, , ε* = 100, and h* = 1 respectively. The magnetic coupling parameter is defined as 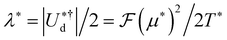. The two-particle ground state energy of the chosen dipolar orientation is denoted 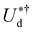, where 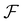is the associated numerical pre-factor. The Langevin parameter, α_L* = μ*H*/T* relates the applied magnetic field to the thermal energy. The simulation protocol consisted of the random distribution, in both position and orientation, of N = 256 cubes over a square plane at ρ_s*, in the centre of a cubic simulation box. The equations of motion were propagated for a total of 2 × 10⁶Δt*, with a time-step of Δt* = 1.5 × 10⁻³. The concept of pre-equilibration in this context is moot, as the experimental systems themselves are not at equilibrium; the self-assembly mechanisms do not result in perfectly equilibrated clusters. A dipole layer correction was introduced, in combination with the dipolar P³M algorithm, to compute the magnetic contributions in quasi-2D periodicity.^28,29 The evolution of aggregation processes was observed and recorded: observables (energy etc.) every 1 × 10⁻²Δt* and particle configurations every 1 × 10³Δt*. An experimental value of λ was calculated, assuming T = 25 °C, as 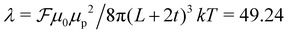, where 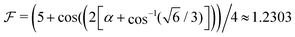for the experimental dipole orientation of α = 12°. Similarly, for α_L = μ₀μ_pH/kT = μ_pB/kT with field values B = (0, 0.045, 0.13, 0.3) mT, we calculated α_L = (0, 32.94, 88.43, 204.06). To achieve conditions in simulation representative of those in experiment, we selected a simulation value of λ* = 10.0; a more practical choice from a computational perspective, but still significantly inside the strong aggregation regime for dipolar particles. Hence, the α_L were scaled as α_L* = λ*α_L/λ ≈ (0, 6, 18, 41) to determine the correct relative magnetic fields. The values of the particle magnetic moment and the magnetic field strength were calculated for each set of parameters according to, 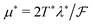and H* = α*T*/μ*. These dipole and field values were systematically investigated at particle surface densities of ρ_s = (0.01, 0.02, 0.05) and at a reduced temperature, T* = 1.

Single-cluster quasi-2D systems

Single cluster simulations were performed to gain a better understanding of the energetics of the observed kinking phenomena. Specifically, to elucidate the low-temperature behavior of hematite cube clusters (n ≤ 15) in the strong-field regime (α_L* = 41). The simulation methodology closely follows that described in the previous section with the following modifications. Clusters are treated as isolated and therefore in a non-periodic system, thus the dipolar interaction is calculated simply by direct summation. To explore the low-temperature states we fix m* = 1, as a way to systematically vary temperature. This facilitated the use of a heuristic technique called simulated annealing to help navigate the complex free energy surfaces that arise as temperature reduces. The implementation of the technique is equivalent to that documented in ref. 20, all of the necessary details can be found therein. A typical run consisted of N replicas of an n-particle cluster propagated, with time-step Δt* = 1 × 10⁻³, to a temperature T* = 0.001. At which point the topologies of each replica were analyzed and the prevalence of kinking assessed. All simulations, bulk and single-cluster, were performed using ESPResSo 3.3.0.³⁰

Connectivity network analysis

To extract quantitative information from both experiment (tracked according to Section S3.2, ESI†) and simulation, we calculated connectivity networks from system configurations as they evolved. The algorithm as applied to magnetic cubes is discussed in ref. 21, the same procedure is applied here. Only a single bonding criterion was used, namely distance, where bonds required an inter-particle separation of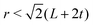 . Constructing connectivity networks identified and followed the evolution of clusters in the system, allowing properties of the kinking phenomenon to be derived.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors would like to thank P. Linse and W. K. Kegel for many helpful discussions. B. Erné is acknowledged for assistance with the alternating gradient magnetometer measurements. Mark Dekker is acknowledged for performing Curie balance measurements. We thank the Netherlands Organization for Scientific Research (NWO) for the provided beam-time and for financial support through a Veni grant (L. R.). J. G. D. and S. S. K. are grateful to the financial support of the Austrian Science Fund (FWF): START-Projekt Y 627-N27. S. S. K. also acknowledges the support of the Program of Russian Federation Ministry of Science and Education, project 3.1438.2017/4.6 and ETN-COLLDENSE (H2020-MSCA-ITN-2014, Grant No. 642774). S. S. acknowledges funding provided by NSF CAREER award DMR-1653465. W. T. M. I. Acknowledges primary support from the University of Chicago Materials Research Science and Engineering Center, which is funded by National Science Foundation under award number DMR-1420709. Additional support was provided by the Packard Foundation. The Chicago MRSEC (US NSF grant DMR-1420709) is also gratefully acknowledged for access to its shared experimental facilities. Mena Youssef is thanked for taking SEM images. The Zeiss Merlin FESEM was acquired through the support of the NSF under award number DMR-0923251. The computational results presented here have been achieved using the Vienna Scientific Cluster (VSC). J. M. M. acknowledges funding provided by the Alexander von Humboldt Foundation. We are also grateful to the DUBBLE personnel of the European Synchrotron Radiation Facility in Grenoble for assistance with the small angle X-ray scattering experiments.

References

1. C. W. Shields, S. Zhu, Y. Yang, B. Bharti, J. Liu, B. B. Yellen, O. D. Velev and G. P. López, Soft Matter, 2013, 9, 9219–9229.
2. K. Han, C. W. Shields, N. M. Diwakar, B. Bharti, G. P. López and O. D. Velev, Sci. Adv., 2017, 3, e1701108.
3. B. Bharti and O. D. Velev, Langmuir, 2015, 31, 7897–7908.
4. G. Singh, H. Chan, A. Baskin, E. Gelman, N. Repnin, P. Král and R. Klajn, Science, 2014, 345, 1149–1153.
5. S. Mehdizadeh Taheri, M. Michaelis, T. Friedrich, B. Förster, M. Drechsler, F. M. Römer, P. Bösecke, T. Narayanan, B. Weber, I. Rehberg, S. Rosenfeldt and S. Förster, Proc. Natl. Acad. Sci. U. S. A., 2015, 112, 14484–14489.
6. E. Matijević and P. Scheiner, J. Colloid Interface Sci., 1978, 63, 509–524.
7. T. Sugimoto, Y. Wang, H. Itoh and A. Muramatsu, Colloids Surf., A, 1998, 134, 265–279.
8. S. Chikazumi and S. H. Charap, Physics of magnetism, Wiley, New York, 1964.
9. P. Hofmann, Solid state physics, Wiley-VCH, Weinheim, 2006.
10. W. Lowrie, Fundamentals of Geophysics, Cambridge University Press, Cambridge, UK, 2nd edn, 2007.
11. M. Ozaki, H. Suzuki, K. Takahashi and E. Matijević, J. Colloid Interface Sci., 1986, 113, 76–80.
12. M. Ozaki, T. Egami, N. Sugiyama and E. Matijević, J. Colloid Interface Sci., 1988, 126, 212–219.
13. G.-S. Park, D. Shindo, Y. Waseda and T. Sugimoto, J. Colloid Interface Sci., 1996, 177, 198–207.
14. A. V. Petukhov, J.-M. Meijer and G. J. Vroege, Curr. Opin. Colloid Interface Sci., 2015, 20, 272–281.
15. J.-M. Meijer, D. V. Byelov, L. Rossi, A. Snigirev, I. Snigireva, A. P. Philipse and A. V. Petukhov, Soft Matter, 2013, 9, 10729–10738.
16. J.-M. Meijer, A. Pal, S. Ouhajji, H. N. W. Lekkerkerker, A. P. Philipse and A. V. Petukhov, Nat. Commun., 2017, 8, 14352.
17. M. Klokkenburg, C. Vonk, E. M. Claesson, J. D. Meeldijk, B. H. Erné and A. P. Philipse, J. Am. Chem. Soc., 2004, 126, 16706–16707.
18. J. G. Donaldson and S. S. Kantorovich, Nanoscale, 2015, 7, 3217–3228.
19. P. Linse, Soft Matter, 2015, 11, 3900–3912.
20. J. G. Donaldson, P. Linse and S. S. Kantorovich, Nanoscale, 2017, 9, 6448–6462.
21. J. G. Donaldson, E. S. Pyanzina and S. S. Kantorovich, ACS Nano, 2017, 11, 8153–8166.
22. T. Sugimoto, M. M. Khan and A. Maramatsu, Colloids Surf., A, 1993, 70, 167–169.
23. L. Rossi, S. Sacanna, W. T. M. Irvine, P. M. Chaikin, D. J. Pine and A. P. Philipse, Soft Matter, 2011, 7, 4139–4142.
24. M. Borsboom, W. Bras, I. Cerjak, D. Detollenaere, D. Glastra van Loon, P. Goedtkindt, M. Konijnenburg, P. Lassing, Y. K. Levine, B. Munneke, M. Oversluizen, R. van Tol and E. Vlieg, J. Synchrotron Radiat., 1998, 5, 518–520.
25. J. H. J. Thijssen, A. V. Petukhov, D. C. 't Hart, A. Imhof, C. H. M. van der Werf, R. E. I. Schropp and A. Van Blaaderen, Adv. Mater., 2006, 18, 1662–1666.
26. A. V. Petukhov, J. H. J. Thijssen, D. C. 't Hart, A. Imhof, A. Van Blaaderen, I. P. Dolbnya, A. Snigirev, A. Moussad and I. Snigireva, J. Appl. Crystallogr., 2006, 39, 137–144.
27. A. Snigirev, V. Kohn, I. Snigireva and B. Lengeler, Nature, 1996, 49–51.
28. J. J. Cerda, V. Ballenegger, O. Lenz and C. Holm, J. Chem. Phys., 2008, 129, 234104.
29. J. de Joannis, A. Arnold and C. Holm, J. Chem. Phys., 2002, 117, 2503–2512.
30. A. Arnold, O. Lenz, S. Kesselheim, R. Weeber, F. Fahrenberger, D. Roehm, P. Košovan and C. Holm, in Meshfree Methods for Partial Differential Equations VI, ed. M. Griebel and M. A. Schweitzer, Lecture Notes in Computational Science and Engineering, Springer Berlin Heidelberg, 2013, vol. 89, pp. 1–23.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c7sm02174g

‡ Current address: Department of Physics, University of Konstanz, D-78457 Konstanz, Germany.

§ Current address: University of California, Merced, Merced, California 95343, USA.

---