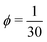Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Form factor for distorted semi-flexible polymer chains
Reinhard
Sigel

Visiting Scientist, Max-Planck-Institut für Eisenforschung GmbH, 40237 Düsseldorf, Germany. E-mail: res314159@aol.de
First published on 12th December 2017
Abstract
The statistical presence of kinks which form defects in semi-flexible polymer chains leads to a polydispersity in the effective persistence length. The form factor of a distorted semi-flexible polymer results as an average over this persistence polydispersity. It turns out that the scattering behavior of an ensemble of distorted semi-flexible polymer chains is quite well approximated by a form factor of an undistorted chain with a Rg-equivalent persistence length. An apparent length polydispersity is observed for short distorted chains. The Rg-equivalent persistence length is significantly smaller than the innate persistence length multiplied by the fraction of regular monomers. The results are compared to related work on DNA from the literature.
1 Introduction
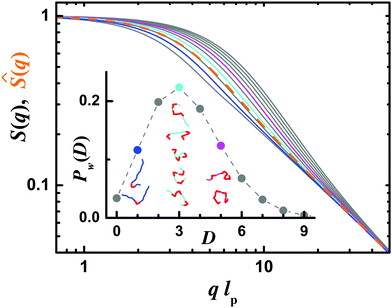
Scattering experiments on dilute polymer solutions provide a wealth of structural information about the dissolved polymer molecules.1 Especially when a wide range of the scattering vector magnitude q is covered, by a combination of either scattering techniques with different wavelengths or by small angle scattering experiments with different sample–detector distances, all relevant length scales of the polymer chains can be accessed. In dilute solution, the variation of scattering intensity with q is described by the form factor (FF) S(q), as illustrated by Fig. 1. In a theta solvent where excluded volume interactions (EVIs) in a polymer chain are screened, the Debye FF (see e.g.ref. 2) outlines the scattering behavior of a flexible polymer chain, while semi-flexible polymer chains4 (SFPCs) can be described by a suitable Pedersen and Schurtenberger (PS) FF2 or the Kholodenko FF.3 The good solvent behavior of a SFPC with active EVIs is captured by another PS FF.2 At small q in the Guinier range, the number of monomers in a chain N, the radius of gyration Rg and information about the length polydispersity of a polymer chain determine the shape of the scattering signal. At intermediate q, a characteristic decay exponent indicates the solvent quality: while chains in a theta solvent without EVIs form Gaussian coils with a characteristic decay q−2 of the scattering intensity, excluded volume chains in a good solvent show a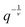 behavior, where ν ≈ 0.588 is Flory's exponent. For SFPCs, a transition to q−1 behavior at higher q follows. At this high resolution a length scale is accessed, where a SFPC looks like a rod. The transition of the power laws in S(q) around ql
behavior, where ν ≈ 0.588 is Flory's exponent. For SFPCs, a transition to q−1 behavior at higher q follows. At this high resolution a length scale is accessed, where a SFPC looks like a rod. The transition of the power laws in S(q) around ql![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) p ≈ 1 indicates the persistence length lp. The pre-factor of the q−1 behavior is connected to the mass per length of the chain. For still larger q, the cross-section of a worm like chain and its radial profile determine S(q). In the limited q range of Fig. 1, a slight down bending away from the q−1 asymptote at high q indicates the onset of cross sectional effects. Scattering experiments have been used to characterize wormlike micelles,5–12 bottle brushes,13–17 and bio molecules.18,19
p ≈ 1 indicates the persistence length lp. The pre-factor of the q−1 behavior is connected to the mass per length of the chain. For still larger q, the cross-section of a worm like chain and its radial profile determine S(q). In the limited q range of Fig. 1, a slight down bending away from the q−1 asymptote at high q indicates the onset of cross sectional effects. Scattering experiments have been used to characterize wormlike micelles,5–12 bottle brushes,13–17 and bio molecules.18,19
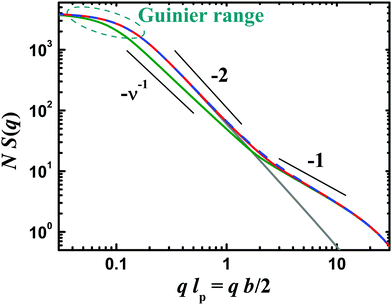 | ||
Fig. 1 Comparison of different form factors S(q) for flexible and semi-flexible polymer chains multiplied by the number of monomers N. The Debye form factor (grey solid line) describes a flexible polymer in a theta solvent, while semi-flexible polymers are represented here by the form factor of Pedersen and Schurtenberger2 with excluded volume interactions, method 3 (olive solid line) and without excluded volume interactions, method 2 (red solid line) as well as the form factor of Kholodenko3 (blue dashed line). The polymers here consist of N = 4000 monomers of length b0, and their Kuhn segment length b is equal to 20b0. For the semi-flexible polymers, b constitutes the persistence length 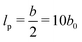 . A locally cylindrical shape with a radius equal to b0/2 is considered for all polymers. . A locally cylindrical shape with a radius equal to b0/2 is considered for all polymers. | ||
Scattering experiments are indirect methods. The extraction of the structural parameters from experimental data requires the fitting of a theoretical FF as a model function. Only if a suitable fitting model is used, one gets reasonable values for the fit parameters. An example is the polydispersity. Besides a polydispersity in length, there might be in addition other types of polydispersity in a sample, e.g. chain branching and imperfect monomer structure, or in random copolymers the distribution of monomer types.1 When the fitting model considers only the length polydispersity, the resulting fit parameter is affected by the other types of polydispersity. Further calculations which combine the extracted fitting parameters can then lead to inconsistent results. Usually, it is considered advisable to combine scattering experiments with complementary microscopy investigations. In microscopy, a small number of molecules adsorbed to a surface is imaged in detail, so it is possible to cross-check if the assumptions of a FF model are fulfilled. Scattering experiments give access to the polymer structure in bulk. They involve a large number of sample molecules, so good statistics is achieved for quantitative results for the structural parameters. The FFs for different architectures of macromolecules are available in the literature.
The motivation for this work stems from the investigation of dendronized polymer molecules20,21 by a combination of light and neutron scattering experiments. The presence of bulky dendritic structures attached to a polymer backbone leads to a stiffening of the polymer molecule. It turned out, however, that data analysis based on the model of a SFPC with a polydispersity of the overall length led to results for which a consistent interpretation has not yet been reached so far. It remains unclear whether the experimental persistence lengths represent molecular properties. On the other hand, microscopy data might hint at the occurrence of right angle kinks in the molecules, besides regularly persistent strands. It should be noted, however, that the apparent kinks might be an artefact in the picture due to the involved projection, or due to the adsorption process of the SFPCs to the substrate.22 So, the often claimed complementarity of the scattering experiments and microscopy might not work in this practical example, unfortunately. In any case, a real occurrence of kinks would not fit the assumed model of SFPCs without distortions. The present work investigates the effect of distortions in SFPCs on scattering experiments.
2 Distorted semi-flexible chain
The persistence defects in distorted SFPCs will be addressed as kinks. These kinks occur statistically and interrupt the directional correlation of the chain. When an ensemble of chains is affected by a random occurrence of kinks, the number of kinks varies among the chains: the random occurrence leads to a distribution in the number of kinks per chain in the ensemble. The inset of Fig. 2 demonstrates this concept. The kinks reduce the effective persistence length of a SFPC. Chains with different numbers of kinks are affected to a different extent. The distribution Pw(D) in the number D of kinks per chain thus leads to a distribution in the effective persistence length of the chains. This distribution forms a new type of polydispersity, which is addressed as persistence polydispersity. The FF for distorted SFPCs results as an average over the persistence polydispersity.A geometrical approach to a SFPC is the freely rotating chain model.23 In this model, a polymer chain consists of N segments of length b0. Two consecutive segments have a fixed angle θ. The rotations of segment (n + 1) around the direction of segment n with fixed θ provides flexibility to the chain. The persistence length lp and the Kuhn segment length b of this model result as:23
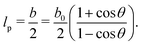 | (1) |
The values in Fig. 1 correspond to θ = 25.2°, while Fig. 2 is based on the Kholodenko FF3 and θ = 10°, leading to lp ≈ 65b0. The notion of a fixed bond length b0 and a discrete number of monomers forms the basis of the discussion below. In particular, b0 enters the discussion as the minimum distance between two kinks. Furthermore, a chain with N segments of length b0 and mass M has the total mass NM and the total length Nb0. The mass per length which determines the q−1 behavior of the scattering intensity at high q results as M/b0. As M is usually a known quantity, the value of b0 of a SFPC can thus be determined in a scattering experiment.
The mathematical treatment is built up on FFs for undistorted SFPCs from the literature. Based on empirical fitting functions for computer simulation data, Pedersen and Schurtenberger (PS) describe 3 methods to calculate the FF for SFPCs without EVIs and two methods to calculate the FF for SFPCs with EVIs.2 A completely different access is offered by Kholodenko, who used an analogy between Dirac's fermions and SFPCs to derive a semi-analytical result for SFPCs without EVIs.3 The good matching in Fig. 1 of the PS FF without EVIs and the FF of Kholodenko despite quite different derivations and calculations is remarkable. For the case of dilute solutions with no overlap of the polymer chains considered here, the scattering contributions of different molecules are uncorrelated and the cross terms average to zero. The self-interferences of scattering contributions from each molecule build up the FF. The absence of cross terms permits the weighted averaging process of FFs with different effective persistence lengths.
Any difference in the scattering of a kink compared to a regular monomer constitutes an incoherent contribution not connected to the chain FF. The concept of coherent and incoherent scattering contributions is common in small angle neutron scattering (SANS) due to the different possible spin orientations of neutrons and sample atoms in the scattering process.1 Coherent and incoherent scattering contributions have also been discussed24 in connection with ellipsometric light scattering.25 In general, the coherent scattering contributions represent the average scattering properties of the molecules, and the incoherent contributions originate from deviations in individual molecules from the average scattering properties. As the kinks occur statistically in the chains, they cause deviations from the average scattering properties in individual molecules, which form the incoherent contribution. This contribution has a radius of gyration comparable to the size of a defect, and so the size of a monomer. It thus stands clearly apart from the chain FF in the coherent contribution, which is connected to a radius of gyration comparable to the size of the whole chain. For simplicity we neglect here any difference in the scattering contrast of kinks and regular monomers and focus on the coherent contribution only. A more detailed discussion of the incoherent contribution where the approach of Endo and Shibayama for flexible chains26 is generalized to SFPCs is postponed to a future extension of the concept of this work to the case of random copolymers, where a contrast difference between monomers of different types can be substantial.
In the first step in Section 2.1, the distribution in the number of kinks in a chain is calculated from a given probability for a monomer to be a kink. For chains with a fixed number of kinks, the length distribution of undistorted strands described in Section 2.2 is used in Section 2.3 in the derivation of the effective persistence length of the chains. After a short discussion of the problems to define the persistence length of chains in a good solvent in Section 2.4, the weighted averaging of FFs to build up the FF for an ensemble of distorted chains is described in Section 2.5. The implementation in Section 2.6 is used for an example plot in Section 2.7. It turns out, that the resulting FF of a distorted SFPC can be quite well approximated by a FF of an undistorted SFPC with a suitable equivalent persistence length, as discussed in Section 2.8. A still better approximation in Section 2.9 is based on a fit of a FF of a distorted SFPC by a FF of an undistorted SFPC with a polydispersity in length. Following an important hint from the peer review process of this publication, the results are compared to related work on DNA in Section 2.10.
2.1 Statistics of distorted polymer chains
The probability for a monomer to be a kink where the chain direction changes abruptly is ϕ. The probability for a regular persistent unit thus becomes (1 − ϕ). The statistical distribution of kinks induces a binomial number distribution for the chains: the probability that a chain consisting of N monomers contains D kink defects reads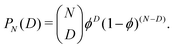 | (2) |
The weighting in a scattering experiment follows the weight distribution of the polymer chains. Since kinks are based on chemical defects in the chain, the molecular weight M + ΔM of a kink monomer might deviate from the molecular weight M of a regular monomer. A mass decrease in a kink is described by the value ΔM < 0. The weight distribution corresponding to (2) reads
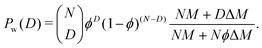 | (3) |
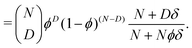 | (4) |
The numerator of the fraction in (3) is the molecular weight of a polymer with D defects, and the denominator is calculated from the normalization condition for the weight distribution; since Nϕ is the average number of defects per chain, the denominator is the average molecular weight of the chains. For a small relative mass deviation δ = ΔM/M ≪ 1, (4) can be approximated (see Appendix) by a binomial distribution
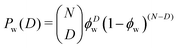 | (5) |
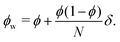 | (6) |
The increase of ϕw relative to ϕ for positive δ reflects the higher weighting of the heavier defective chains in the weight average. ΔM and δ take negative values in cases where the defects have a lower molecular weight than regular monomers; in this case, distorted polymer chains are less weighted in the weight average. With the mean value of defects per chain 〈D〉 = Nϕw and the variance σ2 = Nϕw(1 − ϕw), (6) can be approximated as a Gaussian distribution. The Laplace rule of thumb for the validity of such an approximation reads σ2 > 9. In almost perfect chains with (1 − ϕw) ≈ 1, on average 9 or more defects per chain are needed to justify the Gaussian approximation. In cases where this criterium is not fulfilled, the calculations need to stick to (3) or (5).
2.2 Length distribution of undistorted strands
A distorted chain is subdivided by D defects in [D + 1] regular persistent strands. With the total chain length L, the average length of an undistorted strand is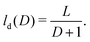 | (7) |
The strand lengths l in this chain with D kinks show an exponential length distribution
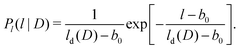 | (8) |
The minimum distance between two kinks is the monomer bond length b0 = L/N, and so Pl(l|D) in (8) is defined for l ≥ b0. The exponential length distribution can be derived based on the conditional probability ϕD that in a chain with D defects a certain monomer is a kink. For a series of monomers in this polymer chain, a conditional length distribution Pn(n|D) of kink-free chain strands results as
| Pn(n|D) = (1 − ϕD)(n−1)ϕD. | (9) |
So, a strand consists of (n − 1) regular persistent units and one kink which ends the otherwise undistorted series. The exponential distributions (8) and (9) have identical mean and are thus equivalent for
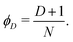 | (10) |
The result is unexpected, since a simple approach would assign the value D/N to the probability that a specific monomer in a chain of length N with D defects is a kink. The occurrence of [D + 1] can be rationalized, when the two chain ends are considered as one additional kink. When N monomers are addressed as a sequence with periodic boundary conditions, and [D + 1] defects 0, 1, 2,…,D are distributed among them, the periodic sequence can be opened at the defect 0. This procedure creates a linear chain with D defects among [D + 1] undistorted strands. In other words: in (9), the undistorted strands are ended by a distortion. The last strand ends at the chain end, and for this reason the chain end has to be counted as an additional kink.
2.3 Effective persistence length of a distorted SFPC
The calculation of the effective persistence length![[l with combining macron]](https://www.rsc.org/images/entities/i_char_006c_0304.gif)
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) p(D) of a chain with D kinks is based on the orientation correlation function27
p(D) of a chain with D kinks is based on the orientation correlation function27Kor(Δl) = 〈![[u with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0075_20d1.gif) (l)· (l)·![[u with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0075_20d1.gif) (l + Δl)〉 (l + Δl)〉 | (11) |
![[u with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0075_20d1.gif) (l) along the chain. Here 〈·〉 denotes an average over chain conformations. For a chain without kinks, Kor(Δl) is an exponential decay
(l) along the chain. Here 〈·〉 denotes an average over chain conformations. For a chain without kinks, Kor(Δl) is an exponential decay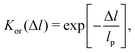 | (12) |
![[R with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0052_20d1.gif) D is expressed as a sum of strand vectors
D is expressed as a sum of strand vectors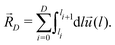 | (13) |
Here, l0 = 0 and lD+1 = L are used for the start and the end point of a chain, respectively. The mean squared end-to-end vector results as
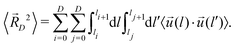 | (14) |
Due to the loss of directional correlation at the kinks, the average scalar product of the unit vectors of two different strands i≠j is zero. With (12), (14) is written as23
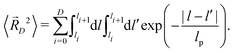 | (15) |
Performing the double integration yields
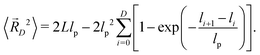 | (16) |
The contour lengths (li+1 − li) are averaged with the exponential distribution (8). With (7), the result reads
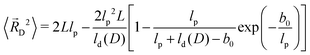 | (17) |
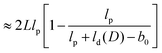 | (18) |
The second form results from the Taylor expansion exp[−b0/lp] ≈ 1 − b0/lp, which is justified for a SFPC with lp ≫ b0. An effective persistence length ![[l with combining macron]](https://www.rsc.org/images/entities/i_char_006c_0304.gif) p(D) of a chain with D kinks is introduced based on the same functional form as (18) for the kink free case D = 0, where (7) yields ld(0) = L:
p(D) of a chain with D kinks is introduced based on the same functional form as (18) for the kink free case D = 0, where (7) yields ld(0) = L:
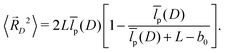 | (19) |
Now, (19) with 〈![[R with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0052_20d1.gif) D2〉 from (18) inserted can be solved for
D2〉 from (18) inserted can be solved for ![[l with combining macron]](https://www.rsc.org/images/entities/i_char_006c_0304.gif) p(D). The result can be written in the intuitive form
p(D). The result can be written in the intuitive form
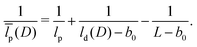 | (20) |
The physics behind this equation becomes clear, when it is multiplied by −Δl and exponential functions of the left and right hand side are taken, similar to (12). With the orientation correlation functions K(0)or(Δl) = exp[−Δl/lp] and K(d)or(Δl) = exp[−Δl/![[l with combining macron]](https://www.rsc.org/images/entities/i_char_006c_0304.gif) p(D)] for the undistorted and the distorted SFPCs, respectively, the result reads
p(D)] for the undistorted and the distorted SFPCs, respectively, the result reads
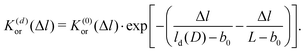 | (21) |
There are two mechanisms in (21) which lead to a decay of K(d)or(Δl): there is a continuous loss of orientation correlation similar to K(0)or(Δl) in the first factor and a probability that the correlation gets completely lost by a kink in the second factor. For the kink-free case D = 0 with ld(0) = L, the second and third terms on the right side of (20) cancel out, and the second factor in (21) becomes unity; the third term in (20) is thus a correction for the finite chain length. The subtraction ld(D) − b0 of one monomer length in (20) and (21) reflects (9), where an undistorted strand consists of (n − 1) stiff monomers and 1 non-stiff kink.
2.4 Persistence length of semi-flexible polymers in a good solvent
The usage of an exponential decay in (12) is strictly valid only for the marginal solvent case with screened EVIs and Gaussian chain statistics. For a good solvent with EVIs, Hsu et al. demonstrated by Monte Carlo simulations in a highly cited work that Kor(Δl) has a power law behavior.28 They discuss the difficulty to define lp from the long range behavior. This result, however, appears not so new. Strobl distinguishes for semi-flexible excluded volume chains an exponential behavior of Kor(Δl) for values Δl smaller than a transition length, and a power law behavior for larger Δl.27 As the power law decay diverges for Δl → 0, it cannot describe the short distance behavior of Kor(Δl), which needs to start as Kor(0) = 1 for an SFPC. With the Taylor expansion exp[−Δl/lp] ≈ 1 − Δl/lp, the initial slope of Kor(Δl) yields lp. So, also for the excluded volume case, an equation similar to (12) is valid for small Δl. More exactly, lp is dependent on the position in the chain, as also Hsu et al. point out and show in their simulations. A closer look at these simulation results reveals that their Kor(Δl) has decayed to a value 0.2 already for the one monomer binding length Δl = b (see Fig. 2 in ref. 28). So, the effect of chain semi-flexibility and the connected exponential decay at small Δl is not really included in their simulations. Slight deviations from the power law behavior at small Δl in the simulation results do in fact hint at chain persistence effects, as also briefly addressed by the authors.The transition of Kor(Δl) to a power law for a good solvent and large Δl can be understood by an intuitive reasoning. As the EVIs are repulsive, they cause an expansion of the polymer coil and a local stretching of the chains. This point of view is the basis of Flory's mean field derivation of ν, where the pressure of an ideal gas of chain segments is compensated by the elastic energy of a stretched coil.29 For a chain in a good solvent with EVIs, it appears thus more appropriate to address chain segments as extended by a local stretching force. The deviation of Kor(Δl) from an exponential at large Δl can be attributed to the local stretching force. As the stretching force at a specific chain location is built up by the EVIs of the chain sections at both sides of this location, it is clear that the chain stretching and the local persistence length decrease towards the chain ends. Based on such a mechanical approach, it might be worth investigating SFPCs in a good solvent by depolarized light scattering, as a local stress is transferred to a birefringence via the polymer's stress-optical coefficient.30,31
The EVIs between the monomers extend the chain, and this effect has a longer range than the chain persistence. The EVIs are basically not affected by chain distortions, and so the large scale behavior of distorted and undistorted SFPCs is very similar. The persistence length thus affects only the Kuhn segment lengths, or the chain orientation correlation at short length scales, where Kor(Δl) is well described by an exponential decay. The calculated ![[l with combining macron]](https://www.rsc.org/images/entities/i_char_006c_0304.gif) p(D) is the appropriate short length scale parameter for distorted SFPCs. In the procedure below, the FF of distorted SFPCs is built up by FFs of undistorted chains with different effective persistence lengths. The power-law behavior of Kor(Δl) at large Δl is already built in the employed FF of a semi-flexible excluded volume chain. The superposition of such FFs of different short scale behaviors yields automatically the appropriate long scale algebraic decay for the orientation correlation of the chains. The model for the distorted SFPCs is as good or as bad as the employed FF for undistorted SFPCs.
p(D) is the appropriate short length scale parameter for distorted SFPCs. In the procedure below, the FF of distorted SFPCs is built up by FFs of undistorted chains with different effective persistence lengths. The power-law behavior of Kor(Δl) at large Δl is already built in the employed FF of a semi-flexible excluded volume chain. The superposition of such FFs of different short scale behaviors yields automatically the appropriate long scale algebraic decay for the orientation correlation of the chains. The model for the distorted SFPCs is as good or as bad as the employed FF for undistorted SFPCs.
2.5 Form factor of distorted SFPCs
Now all ingredients are ready to build up the FF of a distorted SFPC. The starting point is the FF S(q,N,lp,b0) of an undistorted SFPC. Beside its dependence on the magnitude of the scattering vector q, it contains the chain length, the persistence length and the bond length as parameters of the model. Depending on solvent quality, one of the PS FFs2 or the FF of Kholodenko3 can be employed.The distorted SFPC involves the probability of defects ϕ and the relative monomer mass difference of defects δ as additional model parameters. In cases where these parameters are known from independent experiments, e.g. NMR measurements, the FF Ŝ(q) with polydispersity of the persistence length can be written based on the distribution (4) as
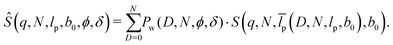 | (22) |
Without previous knowledge of δ and ϕ, it is more suitable to describe the chain distortions by the modified probability (6) with a single additional fitting parameter based on the distribution (5)
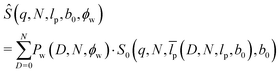 | (23) |
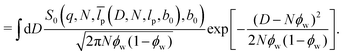 | (24) |
The second form (24) is the Gaussian approximation, valid when the Laplace criterion Nϕw(1 − ϕw) ≥ 9 is fulfilled. Like for a polydispersity in length, there is no closed equation for the FF, and the averaging has to be done numerically. The bond length enters (22)–(24) as the minimum distance between two kinks.
The cross sectional profile of a SFPC is usually considered as a product of a FF Schain(q) of a chain with a negligible cross section and a cross section FF Scs(q):
| S(q) = Schain(q)Scs(q). | (25) |
The latter is an integration
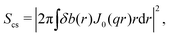 | (26) |
| Scs = |2J1(qRcs)/(qRcs)|2. | (27) |
Here, J0(·) and J1(·) are Bessel functions of the 0th and 1st order, respectively. The product approximation (25) survives the averaging process in (22)–(24). The chain cross thus can either be considered on the level of S(q) before averaging, or equivalently as a multiplication of an average of infinite thin chain FFs Schain(q) with Scs(q). Similarly, the high-q rod-behavior Schain(q) ∼ M/Lq−1 does not depend on ![[l with combining macron]](https://www.rsc.org/images/entities/i_char_006c_0304.gif) p and is thus fulfilled for all FFs. At high q, the averaging process (22)–(24) recovers the q−1 rod behavior with the unchanged prefactor M/L.
p and is thus fulfilled for all FFs. At high q, the averaging process (22)–(24) recovers the q−1 rod behavior with the unchanged prefactor M/L.
2.6 Implementation
A calculation of the FF of SFPCs was realized in C++. The concept of inheritance in object-oriented programming turned out to be quite useful for the formation (22)–(24) of S(q) based on FFs S0(q) of undistorted chains. For a search of errors in the own implementation of the PS FFs, the original Fortran code of ref. 2 was available to the author. The numerical integration in the calculation of the FF of Kholodenko was based on the methods of ref. 32. For the fitting in Section 2.9 based on methods of ref. 32, 61 data points with equidistant spacing on a logarithmic scale in the range 0.002 ≤ qb0 ≤ 2 were calculated for a distorted SFPC with (22). These data points were then fitted by an undistorted SFPC FF with a log-norm length distribution.For the case of SFPCs without EVIs the available FFs offer different advantages, which are illustrated in Fig. 3. The analytical form of the PS FF2 method 2 is very fast in the simulations, while the numerical integration required for the Kholodenko FF takes significantly more time. In particular for the data fitting where numerical parameter derivatives have been used, a high accuracy of this integration is required. On the other hand, for short chains with a length comparable to or smaller than lp, the PS FF in Fig. 3 shows a small bump at intermediate q values which appears to be an artefact. As we scrutinize the calculated FFs of distorted SFPCs for differences to FFs of undistorted SFPCs especially at a short chain length, the smoother Kholodenko FF3 has been used in the simulations. For efficient fitting, the PS FF method 2 was employed as a fitting function in a first step for the case of no EVIs, and the obtained parameter values are inserted as start parameters for the fit with the Kholodenko FF. For the case of SFPCs with EVIs, the corresponding PS FF, method 3 was used directly. The polydispersity in the fit was described as a log-normal length distribution. In all examples below, an innate persistence lp ≈ 65b0 corresponding to an angle θ = 10° in (1) was used.
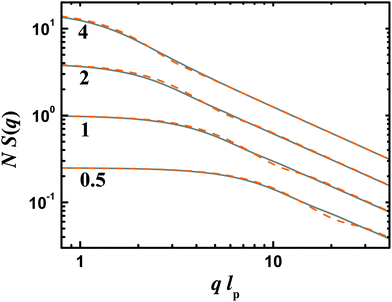 | ||
| Fig. 3 Comparison of the form factors S(q) of Kholodenko3 (grey solid lines) and of Pederson and Schurtenberger,2 method 2 for SFPCs without EVIs (orange dashed lines). The numbers indicate the ratio n = L/lp, and N is chosen as n2. | ||
2.7 Scattering behavior of distorted SFPCs
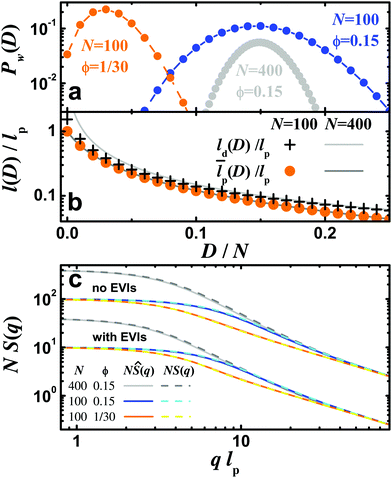
Three examples of FFs for distorted SFPCs for δ = 0 alongside the corresponding distributions Pw(D), the average length ld(D) of undistorted segments, and the effective persistence length![[l with combining macron]](https://www.rsc.org/images/entities/i_char_006c_0304.gif) p(D) are shown in Fig. 4. The discussion starts with the FF for N = 100 and
p(D) are shown in Fig. 4. The discussion starts with the FF for N = 100 and 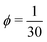 (orange symbols), and hence the values used in Fig. 2. In the range of small D which is accentuated by Pw(D), the change of ld(D) is the most distinct. However, as (20) involves the inverse lengths and ld(D)−1 is significantly smaller than lp−1, the resulting change of
(orange symbols), and hence the values used in Fig. 2. In the range of small D which is accentuated by Pw(D), the change of ld(D) is the most distinct. However, as (20) involves the inverse lengths and ld(D)−1 is significantly smaller than lp−1, the resulting change of ![[l with combining macron]](https://www.rsc.org/images/entities/i_char_006c_0304.gif) p(D)−1 and thus the extent of persistence polydispersity are less pronounced. For longer chains with the same innate persistence lp and similar small values of D, ld(D)−1 is further reduced and its effect on
p(D)−1 and thus the extent of persistence polydispersity are less pronounced. For longer chains with the same innate persistence lp and similar small values of D, ld(D)−1 is further reduced and its effect on ![[l with combining macron]](https://www.rsc.org/images/entities/i_char_006c_0304.gif) p(D)−1 in (20) becomes even smaller. This finding is the first indication that any effect of persistence polydispersity on scattering experiments is most prominent for short SFPCs, i.e. chains with a total length comparable to lp.
p(D)−1 in (20) becomes even smaller. This finding is the first indication that any effect of persistence polydispersity on scattering experiments is most prominent for short SFPCs, i.e. chains with a total length comparable to lp.
The FF of a chain with the same length N = 100 and a higher fraction of distortions ϕ = 0.15 is shown in blue in Fig. 4. The behavior of ld(D) and ![[l with combining macron]](https://www.rsc.org/images/entities/i_char_006c_0304.gif) p(D) is identical to the previous case, but the distribution Pw(D) now emphasizes higher values of D in the averaging process (22)–(24), with smaller values of
p(D) is identical to the previous case, but the distribution Pw(D) now emphasizes higher values of D in the averaging process (22)–(24), with smaller values of ![[l with combining macron]](https://www.rsc.org/images/entities/i_char_006c_0304.gif) p(D). As a result, the radius of gyration decreases compared to the previous case, as can be seen in the Guinier range of the FFs in Fig. 4c: the initial down-bending of the FF is shifted to higher q values. A further effect occurs in the resulting persistence length. Although the q−2 range in the FFs without EVIs and the
p(D). As a result, the radius of gyration decreases compared to the previous case, as can be seen in the Guinier range of the FFs in Fig. 4c: the initial down-bending of the FF is shifted to higher q values. A further effect occurs in the resulting persistence length. Although the q−2 range in the FFs without EVIs and the 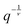 range in the FFs with EVIs are not well built up for the considered short chains, the transition to the q−1 behavior at higher q is well visible in Fig. 4c. The transition at higher q values for ϕ = 0.15 compared to the location of the transition for
range in the FFs with EVIs are not well built up for the considered short chains, the transition to the q−1 behavior at higher q is well visible in Fig. 4c. The transition at higher q values for ϕ = 0.15 compared to the location of the transition for 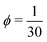 is indicative of a shorter effective persistence length.
is indicative of a shorter effective persistence length.
The third FF in Fig. 4 in grey describes a longer distorted SFPC with N = 400 and the same fraction of distortions ϕ = 0.15 as in the second case. The increased chain length results in a larger radius of gyration, while the resulting persistence lengths are comparable for the two cases. The higher N leads to an increase in the average number of chain defects 〈D〉 = Nϕw and the standard deviation 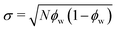 of Pw(D). The relative standard deviation
of Pw(D). The relative standard deviation 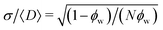 decreases with
decreases with 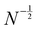 . This decrease shows up in Fig. 4a, where Pw(D) is plotted versus D/N. The decrease of the relative standard deviation of the binomial distribution (5) with increasing N is an inherent property of the statistics of distorted polymer chains in Section 2.1. This constitutes a second reason why the effects of persistence polydispersity are less prominent for longer chain lengths.
. This decrease shows up in Fig. 4a, where Pw(D) is plotted versus D/N. The decrease of the relative standard deviation of the binomial distribution (5) with increasing N is an inherent property of the statistics of distorted polymer chains in Section 2.1. This constitutes a second reason why the effects of persistence polydispersity are less prominent for longer chain lengths.
2.8 The Rg-equivalent persistence length
In the visualization of the averaging process (22)–(24) of FFs S(q,![[l with combining macron]](https://www.rsc.org/images/entities/i_char_006c_0304.gif) p(D)) in Fig. 2, it becomes obvious that the resulting average Ŝ(q) closely matches one of the S(q,
p(D)) in Fig. 2, it becomes obvious that the resulting average Ŝ(q) closely matches one of the S(q,![[l with combining macron]](https://www.rsc.org/images/entities/i_char_006c_0304.gif) p(D)). In order to investigate the effects of the chain distortions in detail, it is worth determining a suitable persistence length
p(D)). In order to investigate the effects of the chain distortions in detail, it is worth determining a suitable persistence length ![[l with combining circumflex]](https://www.rsc.org/images/entities/i_char_006c_0302.gif) p which can be inserted to approximate the FF of distorted SFPCs Ŝ(q) by the FF of an undistorted SFPC S(q,
p which can be inserted to approximate the FF of distorted SFPCs Ŝ(q) by the FF of an undistorted SFPC S(q,![[l with combining circumflex]](https://www.rsc.org/images/entities/i_char_006c_0302.gif) p). We use here a matching of the squared radius of gyration
p). We use here a matching of the squared radius of gyration ![[R with combining circumflex]](https://www.rsc.org/images/entities/i_char_0052_0302.gif) g2 for Ŝ(q) with Rg2 for S(q,
g2 for Ŝ(q) with Rg2 for S(q,![[l with combining circumflex]](https://www.rsc.org/images/entities/i_char_006c_0302.gif) p) for the calculation of
p) for the calculation of ![[l with combining circumflex]](https://www.rsc.org/images/entities/i_char_006c_0302.gif) p. The latter is addressed as the Rg-equivalent persistence length. With the small-q approximation
p. The latter is addressed as the Rg-equivalent persistence length. With the small-q approximation 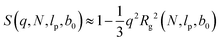 , the average (22) reads
, the average (22) reads 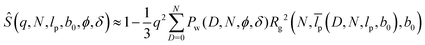 . A comparison with the small-q approximation
. A comparison with the small-q approximation 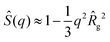 based on
based on ![[R with combining circumflex]](https://www.rsc.org/images/entities/i_char_0052_0302.gif) g yields
g yields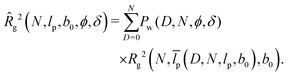 | (28) |
The small q behavior of all PS FFs is traced back to the Debye FF,2 so the latter can be used here. Its squared radius of gyration
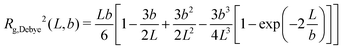 | (29) |
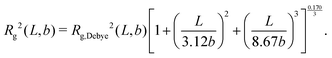 | (30) |
As (29) and (30) increase monotonically with b in the physical range L, b > 0, there is an unambiguous inversion b(Rg2). With this inversion and (28), the Rg-equivalent persistence length results as
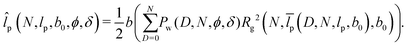 | (31) |
Depending on the solvent quality, the calculation of Rg2 and the inversion b(Rg2) in (31) are based on (29) or (30). For simplicity, ![[l with combining circumflex]](https://www.rsc.org/images/entities/i_char_006c_0302.gif) p is calculated numerically.
p is calculated numerically.
The approximations S(q,![[l with combining circumflex]](https://www.rsc.org/images/entities/i_char_006c_0302.gif) p) by the undistorted FF and the Rg-equivalent persistence length
p) by the undistorted FF and the Rg-equivalent persistence length ![[l with combining circumflex]](https://www.rsc.org/images/entities/i_char_006c_0302.gif) p are included in Fig. 4. They match closely the corresponding FFs Ŝ(q) of distorted SFPCs. The resulting values for
p are included in Fig. 4. They match closely the corresponding FFs Ŝ(q) of distorted SFPCs. The resulting values for ![[l with combining circumflex]](https://www.rsc.org/images/entities/i_char_006c_0302.gif) p/b0 are listed in Table 1. There is a strong decrease of
p/b0 are listed in Table 1. There is a strong decrease of ![[l with combining circumflex]](https://www.rsc.org/images/entities/i_char_006c_0302.gif) p compared to the innate persistence lp ≈ 65b0. The larger values for the case N = 100,
p compared to the innate persistence lp ≈ 65b0. The larger values for the case N = 100, 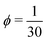 reflect the higher weighting of small D values by Pw(D) in Fig. 4b. The values of
reflect the higher weighting of small D values by Pw(D) in Fig. 4b. The values of ![[l with combining circumflex]](https://www.rsc.org/images/entities/i_char_006c_0302.gif) p/b0 with and without EVIs are almost identical, so the solvent quality has basically no effect. Any effect of chain stretching in a good solvent in the Rg2 calculation in (31) is compensated by an opposite effect for the inversion b(Rg2). Also included in Table 1 are results for δ = −0.5. Even for this large value of the relative mass defect where a kink has only half the mass of a regular monomer, there is basically no change compared to the result of a distorted SFPC without a mass defect.
p/b0 with and without EVIs are almost identical, so the solvent quality has basically no effect. Any effect of chain stretching in a good solvent in the Rg2 calculation in (31) is compensated by an opposite effect for the inversion b(Rg2). Also included in Table 1 are results for δ = −0.5. Even for this large value of the relative mass defect where a kink has only half the mass of a regular monomer, there is basically no change compared to the result of a distorted SFPC without a mass defect.
![[l with combining circumflex]](https://www.rsc.org/images/entities/i_char_006c_0302.gif) p has been determined and a fit with a length polydisperse undistorted SFPC form factor with Ñw = N fixed and the free parameters Ñn and
p has been determined and a fit with a length polydisperse undistorted SFPC form factor with Ñw = N fixed and the free parameters Ñn and ![[l with combining tilde]](https://www.rsc.org/images/entities/i_char_006c_0303.gif) p has been performed for the two cases without and with EVIs, respectively
p has been performed for the two cases without and with EVIs, respectively
| N | ϕ | δ | No EVIs | With EVIs | ||||
|---|---|---|---|---|---|---|---|---|
![[R with combining circumflex]](https://www.rsc.org/images/entities/i_char_0052_0302.gif) g
2
g
2
|
Fit |
![[R with combining circumflex]](https://www.rsc.org/images/entities/i_char_0052_0302.gif) g
2
g
2
|
Fit | |||||
![[l with combining circumflex]](https://www.rsc.org/images/entities/i_char_006c_0302.gif) p/b0
p/b0 |
Ñ n |
![[l with combining tilde]](https://www.rsc.org/images/entities/i_char_006c_0303.gif) p/b0
p/b0 |
![[l with combining circumflex]](https://www.rsc.org/images/entities/i_char_006c_0302.gif) p/b0
p/b0 |
Ñ n |
![[l with combining tilde]](https://www.rsc.org/images/entities/i_char_006c_0303.gif) p/b0
p/b0 |
|||
| 400 | 0.15 | 0 | 5.26 | 396.0 | 5.7 | 5.25 | 389.6 | 5.7 |
| 100 | 0.15 | 0 | 5.36 | 96.9 | 5.8 | 5.34 | 95.9 | 5.8 |
| 100 | 1/30 | 0 | 18.46 | 92.9 | 19.4 | 18.41 | 97.0 | 20.0 |
| 400 | 0.15 | −0.5 | 5.26 | 394.2 | 5.7 | 5.25 | 397.5 | 5.7 |
| 100 | 0.15 | −0.5 | 5.39 | 98.2 | 5.8 | 5.37 | 97.7 | 5.9 |
| 100 | 1/30 | −0.5 | 18.46 | 93.2 | 19.5 | 18.41 | 97.0 | 20.1 |
The strong decrease of ![[l with combining circumflex]](https://www.rsc.org/images/entities/i_char_006c_0302.gif) p compared to the innate persistence lp indicates a synergetic effect of the bonds to achieve a semi-flexibility of the chain. It can be stated, that a chain with a high perfection of 95% of regular monomers and only 5% of defects does not show a Rg-equivalent persistence length of 95% of the innate persistence length, but a much lower value. An interruption of the exponential decay of Kor(Δl) in (12) at a kink has a strong effect on the overall chain persistence. For long chains N ≫ 1, the distribution Pw(D) is peaked at the average number 〈D〉 = Nϕw of distortions in a chain, as the relative standard deviation decreases with
p compared to the innate persistence lp indicates a synergetic effect of the bonds to achieve a semi-flexibility of the chain. It can be stated, that a chain with a high perfection of 95% of regular monomers and only 5% of defects does not show a Rg-equivalent persistence length of 95% of the innate persistence length, but a much lower value. An interruption of the exponential decay of Kor(Δl) in (12) at a kink has a strong effect on the overall chain persistence. For long chains N ≫ 1, the distribution Pw(D) is peaked at the average number 〈D〉 = Nϕw of distortions in a chain, as the relative standard deviation decreases with 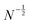 . In this limit,
. In this limit, ![[l with combining circumflex]](https://www.rsc.org/images/entities/i_char_006c_0302.gif) p can be approximated by the effective persistence length
p can be approximated by the effective persistence length ![[l with combining macron]](https://www.rsc.org/images/entities/i_char_006c_0304.gif) p(〈D〉) of a chain with the average number of defects. A combination of (20) and (7) yields a formula for
p(〈D〉) of a chain with the average number of defects. A combination of (20) and (7) yields a formula for ![[l with combining macron]](https://www.rsc.org/images/entities/i_char_006c_0304.gif) p(〈D〉). For large N, it simplifies to
p(〈D〉). For large N, it simplifies to
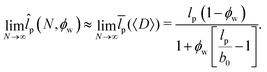 | (32) |
The numerator describes the fraction (1 − ϕw) of the innate persistence length lp, which corresponds to the fraction of regular monomers. The additional decrease due to the denominator accounts for the distortion of the synergy of the semi-flexible monomers by the defects.
An unexpected outcome of the comparison of Ŝ(q) with the approximation S(q,![[l with combining circumflex]](https://www.rsc.org/images/entities/i_char_006c_0302.gif) p) is the very good matching around qlp ≈ 1, and hence the region sensitive to the persistence length. In Fig. 2, FFs of quite different effective persistence lengths
p) is the very good matching around qlp ≈ 1, and hence the region sensitive to the persistence length. In Fig. 2, FFs of quite different effective persistence lengths ![[l with combining macron]](https://www.rsc.org/images/entities/i_char_006c_0304.gif) p(D) contribute to the averaging process to build up Ŝ(q). The expectation was to find some kind of smearing or broadening of the transition of the q−2 behavior for no EVIs or the
p(D) contribute to the averaging process to build up Ŝ(q). The expectation was to find some kind of smearing or broadening of the transition of the q−2 behavior for no EVIs or the 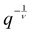 behavior for SFPCs with EVIs to the rod limit q−1 behavior. Such a smearing could be a starting point for an approach to work out the innate persistence length from data of distorted SFPCs. However, basically no smearing is found here after the averaging process. The scattering behavior of undistorted and distorted SFPCs is thus very similar. As a consequence it is not possible to detect chain distortions from scattering experiments.
behavior for SFPCs with EVIs to the rod limit q−1 behavior. Such a smearing could be a starting point for an approach to work out the innate persistence length from data of distorted SFPCs. However, basically no smearing is found here after the averaging process. The scattering behavior of undistorted and distorted SFPCs is thus very similar. As a consequence it is not possible to detect chain distortions from scattering experiments.
In a mathematical treatment by Caravenna et al.,33 it is shown that in the limit of infinite chain length the large scale appearance of semi-flexible statistical hetero-polymers without excluded volume interactions looks like a homo-polymer with a suitable persistence length.33 So for a marginal solvent, the form factor of such a monodisperse heteropolymer starts at small q like in Fig. 1 with a behavior described by 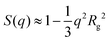 , which bends over to a q−2 decay. The results here go one step further. Also around qlp ≈ 1, which corresponds to a short scale appearance on a monomer level, a suitably chosen average persistence length captures the behavior of an ensemble of semi-flexible polymer chains, where the heterogenity in a chain results from the statistical occurrence of kinks. The result is valid without and with excluded volume interactions.
, which bends over to a q−2 decay. The results here go one step further. Also around qlp ≈ 1, which corresponds to a short scale appearance on a monomer level, a suitably chosen average persistence length captures the behavior of an ensemble of semi-flexible polymer chains, where the heterogenity in a chain results from the statistical occurrence of kinks. The result is valid without and with excluded volume interactions.
The finding that the persistence polydispersity has no effect on the FF can be rationalized with arguments similar to the calculation of ![[R with combining circumflex]](https://www.rsc.org/images/entities/i_char_0052_0302.gif) g by (28) based on an averaging process of Taylor expansions. In Section 2.4, lp−1 was discussed as a short range property of Kor(Δl), so within a first order Taylor expansion to describe Kor(Δl) for small Δl. When Kor(Δl) is averaged over chains with different
g by (28) based on an averaging process of Taylor expansions. In Section 2.4, lp−1 was discussed as a short range property of Kor(Δl), so within a first order Taylor expansion to describe Kor(Δl) for small Δl. When Kor(Δl) is averaged over chains with different ![[l with combining macron]](https://www.rsc.org/images/entities/i_char_006c_0304.gif) p(D), the result has the same functional form as a first order Taylor expansion with a zero order term equal to 1 and a linear term with a slope which defines the resulting inverse persistence length. This form can in turn be considered as the short range behavior of an exponential which is connected to a not smeared transition of Ŝ(q) around qlp ≈1. Deviations are of higher order. The calculation of the statistical weights for the averaging process is not as straightforward as for the small q behavior in the determination of
p(D), the result has the same functional form as a first order Taylor expansion with a zero order term equal to 1 and a linear term with a slope which defines the resulting inverse persistence length. This form can in turn be considered as the short range behavior of an exponential which is connected to a not smeared transition of Ŝ(q) around qlp ≈1. Deviations are of higher order. The calculation of the statistical weights for the averaging process is not as straightforward as for the small q behavior in the determination of ![[R with combining circumflex]](https://www.rsc.org/images/entities/i_char_0052_0302.gif) g2. However, the formal argument applies for any normalized distribution used in the averaging process, especially as
g2. However, the formal argument applies for any normalized distribution used in the averaging process, especially as ![[l with combining macron]](https://www.rsc.org/images/entities/i_char_006c_0304.gif) p(D) > 0, so an average of value 0 for the resulting inverse persistence length can be excluded. This averaging property of the short term behavior of Kor(Δl) is furthermore relevant for the discussion of the orientation correlation function for the good solvent case in Section 2.4. It elucidates why it is possible to assign an average persistence length to SFPC in a good solvent with EVIs, although the local decay of orientation correlation depends on the position within the chain.
p(D) > 0, so an average of value 0 for the resulting inverse persistence length can be excluded. This averaging property of the short term behavior of Kor(Δl) is furthermore relevant for the discussion of the orientation correlation function for the good solvent case in Section 2.4. It elucidates why it is possible to assign an average persistence length to SFPC in a good solvent with EVIs, although the local decay of orientation correlation depends on the position within the chain.
In cases where the fraction ϕw of chain distortions is known from other experiments, scattering data can be used for an estimation of the innate persistence length. For long chains N ≫ 1, an inversion of (32) reads:
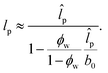 | (33) |
In cases where the denominator in (33) becomes very small or even negative, the finding might be interpreted as that the effect of chain distortions is so strong that it is not possible to estimate lp. A test with the values of Table 1 yields rough estimates for lp, with the closest value lp ≈ 73b0 for the longest chain N = 400. The estimates for lp based on a blowing up of ![[l with combining circumflex]](https://www.rsc.org/images/entities/i_char_006c_0302.gif) p by a small denominator in (33) should generally be used rather carefully. Less critical is an estimation of ϕw based on (33), in cases where lp and
p by a small denominator in (33) should generally be used rather carefully. Less critical is an estimation of ϕw based on (33), in cases where lp and ![[l with combining circumflex]](https://www.rsc.org/images/entities/i_char_006c_0302.gif) p are known.
p are known.
2.9 Distorted SFPCs described as polydisperse undistorted SFPCs
Although the approximations S(q,![[l with combining circumflex]](https://www.rsc.org/images/entities/i_char_006c_0302.gif) p) match the Ŝ(q) of distorted SFPCs quite well, there is a small difference in Fig. 4 at intermediate q values, where the curvature of the down-bending is slightly stronger for the distorted SFPCs compared to the approximations. In scattering experiments on unknown polymers, such a deviation would be interpreted conventionally as the length polydispersity of the chains. A fit of the distorted FFs NŜ(q) of Fig. 4 by polydisperse undistorted FFs in fact leads to a very good matching (not shown, as the differences between Ŝ(q) and the fit cannot be seen anyway). Even in a Holzer plot (qS(q) vs. q) where details in the region of the scattering data sensitive to lp are magnified, the deviation between the distorted SFPC and the fit are tiny and below any realistic experimental resolution. For chains with a polydispersity in length, the mass averaged number of monomers Ñw has to be distinguished from the number averaged chain length Ñn. The apparent length polydispersity results in u = Ñw/Ñn. The fit further includes a persistence length
p) match the Ŝ(q) of distorted SFPCs quite well, there is a small difference in Fig. 4 at intermediate q values, where the curvature of the down-bending is slightly stronger for the distorted SFPCs compared to the approximations. In scattering experiments on unknown polymers, such a deviation would be interpreted conventionally as the length polydispersity of the chains. A fit of the distorted FFs NŜ(q) of Fig. 4 by polydisperse undistorted FFs in fact leads to a very good matching (not shown, as the differences between Ŝ(q) and the fit cannot be seen anyway). Even in a Holzer plot (qS(q) vs. q) where details in the region of the scattering data sensitive to lp are magnified, the deviation between the distorted SFPC and the fit are tiny and below any realistic experimental resolution. For chains with a polydispersity in length, the mass averaged number of monomers Ñw has to be distinguished from the number averaged chain length Ñn. The apparent length polydispersity results in u = Ñw/Ñn. The fit further includes a persistence length ![[l with combining tilde]](https://www.rsc.org/images/entities/i_char_006c_0303.gif) p as a free parameter, while b0 and a chain cross section Rcs can be kept fixed at the values of the distorted SFPC. The limit q → 0, where NŜ(q) = N and the fit function takes the value Ñw requires Ñw = N. The results for the free fit parameters Ñn and
p as a free parameter, while b0 and a chain cross section Rcs can be kept fixed at the values of the distorted SFPC. The limit q → 0, where NŜ(q) = N and the fit function takes the value Ñw requires Ñw = N. The results for the free fit parameters Ñn and ![[l with combining tilde]](https://www.rsc.org/images/entities/i_char_006c_0303.gif) p are listed in Table 1.
p are listed in Table 1.
The results for Ñn are slightly smaller than Ñw = N, so there is a small apparent length polydispersity in the distorted SFPCs. The value of u decreases with increasing N, as expected from the arguments in Section 2.7 ((1) The value of ld(D)−1 for fixed D is smaller for higher N, so lp−1 in (20) dominates more and there is less effect of D on ![[l with combining macron]](https://www.rsc.org/images/entities/i_char_006c_0304.gif) p(D)−1. (2) The relative standard deviation σ/〈D〉 of the distribution of the number of defects in the chains of an ensemble becomes smaller with
p(D)−1. (2) The relative standard deviation σ/〈D〉 of the distribution of the number of defects in the chains of an ensemble becomes smaller with 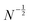 ). The smallness of the apparent length polydispersity can be rationalized as follows: a polymer chain in a dilute solution is a soft and highly fluctuating object. Its FF is an average over all possible conformations, which show already a broad distribution in size. For a distorted SFPC, there is the additional distribution due to the persistence polydispersity. In this case, the total size distribution for all chain conformations and all possible locations of kinks corresponds to a convolution of the conformation distribution and the kink distribution. Obviously, the variance of the conformation distribution of an undistorted chain, which is equal to Rg2, exceeds the additional width contribution due to the kink distribution. So the variance of the convoluted distribution is dominated by the variance of the conformation distribution.
). The smallness of the apparent length polydispersity can be rationalized as follows: a polymer chain in a dilute solution is a soft and highly fluctuating object. Its FF is an average over all possible conformations, which show already a broad distribution in size. For a distorted SFPC, there is the additional distribution due to the persistence polydispersity. In this case, the total size distribution for all chain conformations and all possible locations of kinks corresponds to a convolution of the conformation distribution and the kink distribution. Obviously, the variance of the conformation distribution of an undistorted chain, which is equal to Rg2, exceeds the additional width contribution due to the kink distribution. So the variance of the convoluted distribution is dominated by the variance of the conformation distribution.
The fit result ![[l with combining tilde]](https://www.rsc.org/images/entities/i_char_006c_0303.gif) p for the persistence length is comparable to the Rg-equivalent persistence length
p for the persistence length is comparable to the Rg-equivalent persistence length ![[l with combining circumflex]](https://www.rsc.org/images/entities/i_char_006c_0302.gif) p, with a slightly larger value. The results for δ = 0 and δ = −0.5 are basically the same, so a mass defect of kinks has no substantial effect. It was expected that values δ < 0 would increase the apparent length polydispersity, as chains with more kinks and thus a higher total mass defect would contribute with a smaller Rg value. This argument goes in the same direction as the mechanism in conventional length polydispersity, where shorter chains have a smaller Rg and less weight in scattering due to their smaller mass. Such an effect of δ, however, turned out to be below the resolution of the fitting procedure, even for the higher data quality of simulated data compared to true experimental data.
p, with a slightly larger value. The results for δ = 0 and δ = −0.5 are basically the same, so a mass defect of kinks has no substantial effect. It was expected that values δ < 0 would increase the apparent length polydispersity, as chains with more kinks and thus a higher total mass defect would contribute with a smaller Rg value. This argument goes in the same direction as the mechanism in conventional length polydispersity, where shorter chains have a smaller Rg and less weight in scattering due to their smaller mass. Such an effect of δ, however, turned out to be below the resolution of the fitting procedure, even for the higher data quality of simulated data compared to true experimental data.
2.10 Previous discussion of kinks in DNA molecules
A related literature discussion about kinks in DNA is briefly outlined, and its theoretical descriptions are compared to the approach here. A review by Vologdskii and Kamenetskii34 (VK) summarizes the substantial scientific activities which were induced by a paper in 2004 by Cloutier and Widom,35 who claimed that a spontaneous bending of short DNA segments to circles occurs dramatically more efficiently than the prediction of a worm like chain (WLC) model.4 Examples where the sharp bending of DNA has a biological function were indicated.35,36 The strong bending is assigned to kinks in the DNA,37,38 similar to the kinks considered here. The VK review34 comes to the conclusion that all experimental findings of strong DNA bending can be explained by a splitting of an isolated, single base pair in the DNA double helix,36 which leads to a reduced local persistence. One single kink in a short DNA segment of 70 base pairs is sufficient to account for the formation of circles.34,37While in the classical WLC model the bending energy is quadratic in chain curvature,4 the theoretical description of DNA by Wiggins and coauthors introduces a saturation of the quadratic bending energy at a high chain curvature.37,38 In this way, the conventional WLC behavior at large length scales is combined with the occurrence of local sharp kinks.
There are several similarities and a number of clear differences between the work of Wiggins et al. and the approach described here. In a distinction used by Caravenna et al.,33 the localization of kinks in the description of DNA by Wiggins et al. is ergodic, and hence roughly speaking mobile within the chain. An averaging procedure over the conformations of a single chain is sufficient. The work here classifies as quenched within the Caravenna distinction. The locations of the kinks and their number are fixed and inherent in the chains, and after the averaging over conformations a second averaging step over an ensemble of chains is required. The distribution of the number of kinks in the chains and polydispersity questions become an issue. The mathematical approach of Wiggins et al. is based on quantum mechanical propagators, path integration, Fourier Laplace transformations and the Faltungs theorem, similar to Kholodenko's FF.3 It is far more advanced than the down-to-earth approach discussed here, which is an extension of the freely rotating chain model23 and uses basic geometry and probability theory only. The derivation of Wiggins et al. jumps back and forth between discrete and continuous descriptions of a chain. In this process the notion of a minimum distance between kinks as described here and finite chain length corrections like in (20) and (21) get lost. The access to partition functions in the work of Wiggins et al. allows the description of several experiments, while here the focus is on the FF only. On the other hand, the approach of Wiggins et al. is very specific to chains without EVIs, and hence the marginal solvent case. Here, FFs with and without EVIs are discussed on the same level, and the method can further be applied to distorted macromolecules with a morphology different from a linear chain arrangement of monomers, as long as a FF for non-distorted macromolecules of such a morphology is available. It appears, that EVIs are mostly not considered in the DNA community, apart from rare exceptions.39,40 From a polymer physicists viewpoint, the discarding of EVIs might limit the validity of theoretical descriptions of DNA in solution.
For scattering experiments, Wiggins et al. find no effect of kinks. In this comparison, the parameters of the saturated bending energy are selected in such a way as to obtain the same long range persistence length as in the reference WLC model.38 This finding corresponds to the result of the present work. The apparent length polydispersity as discussed in Section 2.9 has not been addressed by Wiggins et al. For a detection of the saturation of the bending energy, Wiggins et al. discuss experiments which involve a strong bending:38 fluorescence resonance energy transfer (FRET)41 and the formation of circles in short DNA segments (cyclization).
In summary of Section 2.10, the previous work of Wiggins et al.37,38 addresses a similar problem with rather different methods. Their approach and the work here have complementary advantages and disadvantages.
3 Conclusions and outlook
In a nutshell, the question raised in the introduction of how chain distortions in SFPCs show up in scattering experiments is answered as follows: The main effect is a strong reduction of the apparent persistence length, where the Rg-equivalent persistence length![[l with combining circumflex]](https://www.rsc.org/images/entities/i_char_006c_0302.gif) p provides a good description. In addition, there is a small contribution to the length polydispersity of real systems. With increasing chain length, this contribution vanishes. In cases where the kink distortions have a different contrast than regular monomers, there is an additional incoherent contribution which basically does not depend on q (more exactly, a contribution with an Rg comparable to the size of a kink). The innate persistence length of a distorted SFPC cannot be accessed in conventional scattering experiments.
p provides a good description. In addition, there is a small contribution to the length polydispersity of real systems. With increasing chain length, this contribution vanishes. In cases where the kink distortions have a different contrast than regular monomers, there is an additional incoherent contribution which basically does not depend on q (more exactly, a contribution with an Rg comparable to the size of a kink). The innate persistence length of a distorted SFPC cannot be accessed in conventional scattering experiments.
These conclusions have been achieved by a detailed description of the persistence polydispersity caused by statistically distributed kink distortions in the chains. For the dilute systems considered here, inter-chain interferences in scattering experiments average to zero, and the description of intra-chain interferences can be traced back to existing form factors from the literature. Depending on the solvent quality, form factors with and without excluded volume interactions have been considered. The statistical occurrence of kinks leads to a binomial distribution in the number of kinks in a chain. For a chain with a fixed number of kinks, the inverse effective persistence length is derived as the sum of the inverse innate persistence length, the inverse average length of an undistorted chain segment, and a correction term for the finite chain length. The corresponding orientation correlation function is a product of the innate orientation correlation function and the probability of complete correlation loss by a kink. The form factor of an ensemble of distorted chains results as an average based on the distribution in the number of kinks per chain and form factors where the effective persistence lengths are inserted. Three examples of distorted SFPCs calculated with an implementation of this approach are discussed. For a detailed look at the effect of persistence polydispersity, the example form factors of distorted SFPCs are compared to form factors of undistorted SFPCs with the same radius of gyration. Besides the strong decrease of the related Rg-equivalent persistence length compared to the innate persistence length, there is a slight change in curvature at small q, which in a conventional interpretation of experimental data would be assigned to a length polydispersity. A fit of a distorted SFPC form factor by an undistorted SFPC form factor with a length polydispersity provides a very good description. There is basically no smearing in the region qlp ≈ 1.
The procedure developed here can be adapted for the description of semi-flexible random copolymers, as a generalization of the discussion of flexible random copolymers by Endo and Shibayama.26 The occurrence of different monomers introduces different contrast factors with further complications. The variation of scattering contrast might be an interesting tool in scattering experiments on semi-flexible random copolymers. Similar to the distorted SFPCs discussed here, it is expected that there are only minor deviations for semi-flexible random copolymers compared to the scattering behavior of homo-polymers, apart from a strong effect on the Rg-equivalent persistence length. Such a result, however, would be a valuable corner stone for the investigation of semi-flexible random copolymers by scattering experiments, as it could justify data fitting and interpretation by models and methods developed for homo-polymers. Furthermore, the averaging over the persistence polydispersity of SFPCs introduced here might become useful for more advanced scattering experiments. For colloidal particles, experimental light scattering techniques are available to distinguish coherent and incoherent contributions24 and excited and relaxed fluctuations of a soft colloidal shell.42,43 A theoretical description of other advanced light scattering techniques adapted to polymers to be developed in the future with similar abilities might be based on the methods introduced here.
Conflicts of interest
There are no conflicts to declare.Appendix
In order to approximate (4) as a binomial distribution, the last factor of (4) is re-written as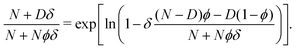 | (34) |
For δ ≪ 1, the approximation ln(1 + x) ≈ x can be used. The difference in the numerator of the right side of (34) leads to a product of two exponentials. The factors (N − D) and D are extracted as external exponents for the exponentials:
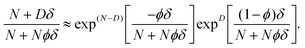 | (35) |
First order Taylor expansions of the exponentials in δ yield
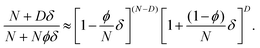 | (36) |
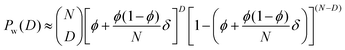 | (37) |
The modified probability ϕw in (6) is extracted from the term of power D in (37). The term of power (N − D) in (37) is equal to (1 − ϕw), and so (37) is really a probability distribution with correct normalization.
Acknowledgements
The author thanks Andreas Erbe and Helgard Sigel for support and Peter Schurtenberger for providing the original FORTRAN source code of the form factors of ref. 2. Open Access funding provided by the Max Planck Society is gratefully acknowledged.References
- J. S. Higgins and H. Benoît, Polymers and Neutron Scattering, Clarendon Press, 1994 Search PubMed.
- J. S. Pedersen and P. Schurtenberger, Macromolecules, 1996, 29, 7602–7612 CrossRef CAS.
- A. L. Kholodenko, Macromolecules, 1993, 26, 4179–4183 CrossRef CAS.
- O. Kratky and G. Porod, Recl. Trav. Chim. Pays-Bas, 1949, 68, 1106–1122 CrossRef CAS.
- G. Jerke, J. S. Pedersen, S. U. Egelhaaf and P. Schurtenberger, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1997, 56, 5772–5788 CrossRef CAS.
- G. Jerke, J. S. Pedersen, S. U. Egelhaaf and P. Schurtenberger, Langmuir, 1998, 14, 6013–6024 CrossRef CAS.
- L. J. Magid, J. Phys. Chem. B, 1998, 102, 4064–4074 CrossRef CAS.
- L. Arleth, M. Bergström and J. S. Pedersen, Langmuir, 2002, 18, 5343–5353 CrossRef CAS.
- S.-H. Tung, Y.-E. Huang and S. R. Raghavan, J. Am. Chem. Soc., 2006, 128, 5751–5756 CrossRef CAS PubMed.
- W.-R. Chen, P. D. Butler and L. J. Magid, Langmuir, 2006, 22, 6539–6548 CrossRef CAS PubMed.
- C. A. Dreiss, Soft Matter, 2007, 3, 956–970 RSC.
- L. M. Walker, Curr. Opin. Colloid Interface Sci., 2009, 14, 451–454 CrossRef CAS.
- S. Lecommandoux, F. Chécot, R. Borsali, M. Schappacher, A. Deffieux, A. Brûlet and J. P. Cotton, Macromolecules, 2002, 35, 8878–8881 CrossRef CAS.
- S. Rathgeber, T. Pakula, A. Wilk, K. Matyjaszewski and K. L. Beers, J. Chem. Phys., 2005, 122, 124904 CrossRef PubMed.
- B. Zhang, F. Gröhn, J. S. Pedersen, K. Fischer and M. Schmidt, Macromolecules, 2006, 39, 8440–8450 CrossRef CAS.
- L. Feuz, P. Strunz, T. Geue, M. Textor and O. Borisov, Eur. Phys. J. E: Soft Matter Biol. Phys., 2007, 23, 237–245 CrossRef CAS PubMed.
- S. L. Pesek, X. Li, B. Hammouda, K. Hong and R. Verduzco, Macromolecules, 2013, 46, 6998–7005 CrossRef CAS.
- H. Chen, S. P. Meisburger, S. A. Pabit, J. L. Sutton, W. W. Webb and L. Pollack, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 799–804 CrossRef CAS PubMed.
- E. Buhler and F. Boué, Macromolecules, 2004, 37, 1600–1610 CrossRef CAS.
- B. Zhang, R. Wepf, K. Fischer, M. Schmidt, S. Besse, P. Lindner, B. T. King, R. Sigel, P. Schurtenberger, Y. Talmon, Y. Ding, M. Kröger, A. Halperin and A. D. Schlüter, Angew. Chem., Int. Ed., 2011, 50, 737–740 CrossRef CAS PubMed.
- R. Pasquino, B. Zhang, R. Sigel, H. Yu, M. Ottiger, O. Bertran, C. Aleman, A. D. Schlüter and D. Vlassopoulos, Macromolecules, 2012, 45, 8813–8823 CrossRef CAS.
- D. Schlüter, private communication.
- M. Doi and S. F. Edwards, The Theory of Polymer Dynamics, Clarendon, Oxford, 1992 Search PubMed.
- R. Sigel and A. Erbe, Appl. Opt., 2008, 47, 2161–2170 CrossRef CAS PubMed; A. Erbe, K. Tauer and R. Sigel, Langmuir, 2009, 25, 2703–2710 CrossRef PubMed.
- A. Erbe, K. Tauer and R. Sigel, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2006, 73, 031406 CrossRef CAS PubMed; A. Erbe and R. Sigel, Eur. Phys. J. E, 2007, 22, 303–309 CrossRef PubMed; A. Erbe, K. Tauer and R. Sigel, Langmuir, 2007, 23, 452–459 CrossRef PubMed.
- H. Endo and M. Shibayama, Polym. J., 2010, 42, 157–160 CrossRef CAS.
- G. Strobl, The Physics of Polymers, Springer, Berlin, 3rd edn, 2007 Search PubMed.
- H.-P. Hsu, W. Paul and K. Binder, Polym. Sci., Ser. C, 2013, 55, 39–59 CrossRef CAS.
- P. de Gennes, Scaling concepts in polymer physics, Cornell University Press, Ithaca, 1979 Search PubMed.
- H. Janeschitz-Kriegl, Polymer Melt Rheology and Flow Birefringence, Springer-Verlag, Berlin, Heidelberg, 1983 Search PubMed.
- R. Sigel, W. Stille, G. Strobl and R. Lehnert, Macromolecules, 1993, 26, 4226–4233 CrossRef CAS.
- W. H. Press, S. A. Teukolsky, W. T. Vetterling and B. P. Flannery, Numerical Recipes: The Art of Scientific Computing, Cambridge University Press, New York, NY, USA, 3rd edn, 2007 Search PubMed.
- F. Caravenna, G. Giacomin and M. Gubinelli, Ann. Inst. Henri Poincare, 2010, 46, 97–118 CrossRef.
- A. Vologodskii and M. D. Frank-Kamenetskii, Nucleic Acids Res., 2013, 41, 6785–6792 CrossRef CAS PubMed.
- T. E. Cloutier and J. Widom, Mol. Cell, 2004, 14, 1097–2765 CrossRef.
- J. Yan and J. F. Marko, Phys. Rev. Lett., 2004, 93, 108108 CrossRef PubMed.
- P. A. Wiggins, R. Phillips and P. C. Nelson, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2005, 71, 021909 CrossRef PubMed.
- P. A. Wiggins and P. C. Nelson, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2006, 73, 031906 CrossRef PubMed.
- K. V. Klenin, A. V. Vologodskii, V. V. Anshelevich, A. M. Dykhne and M. D. Frank-Kamenetskii, J. Biomol. Struct. Dyn., 1988, 5, 1173–1185 CAS.
- A. Y. Grosberg, Phys. Rev. Lett., 2000, 85, 3858–3861 CrossRef CAS PubMed.
- C. Yuan, H. Chen, X. W. Lou and L. A. Archer, Phys. Rev. Lett., 2008, 100, 018102 CrossRef PubMed.
- R. Sigel, Soft Matter, 2017, 13, 1132–1141 RSC.
- D. J. Ross and R. Sigel, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2012, 85, 056710 CrossRef PubMed.
| This journal is © The Royal Society of Chemistry 2018 |