Glycerol carbonate as a fuel additive for a sustainable future†
Milán
Szőri
 a,
Binod Raj
Giri
a,
Binod Raj
Giri
 *b,
Zhandong
Wang
*b,
Zhandong
Wang
 b,
Alaaeldin E.
Dawood
b,
Béla
Viskolcz
b,
Alaaeldin E.
Dawood
b,
Béla
Viskolcz
 a and
Aamir
Farooq
a and
Aamir
Farooq
 *b
*b
aInstitute of Chemistry, Faculty of Materials Science and Engineering, University of Miskolc, Egyetemváros A/4., H-3515 Miskolc, Hungary
bKing Abdullah University of Science and Technology (KAUST), Clean Combustion Research Center, Physical Sciences and Engineering Division, Thuwal 23955-6900, Saudi Arabia. E-mail: Binod.Giri@kaust.edu.sa; Aamir.Farooq@kaust.edu.sa
First published on 6th June 2018
Abstract
Policy-makers and researchers have been considering a shift from conventional fossil fuels to renewable sources due to the growing concerns over global warming and diminishing oil reserves. Biodiesel, a renewable bio-driven fuel, can be derived from vegetable oils and animal fats, and is considered to be bio-degradable, non-toxic and environmentally friendly. The cetane number and calorific power of biodiesel are quite similar to those of conventional diesel. Crude glycerol of about 10–20% by volume appears as a byproduct in biodiesel production. The increasing demand for biodiesel has led to a substantial increase of glycerol supply in the global market and a dramatic fall in the price of glycerol which has warranted alternative uses of glycerol. One potential way to deal with the crude glycerol overflow is to convert it to glycerol carbonate (GC) and use GC as a fuel or fuel additive. Prior studies have indicated that carbonate esters can significantly reduce particulate emissions during engine combustion. In this work, we have explored possible reaction pathways in the initial stage of glycerol carbonate pyrolysis. Ab initio/RRKM-master equation methods are employed to differentiate various reaction pathways and to obtain the pressure- and temperature-dependence of the major channels. We have found that glycerol carbonate decomposes almost exclusively to produce CO2 and 3-hydroxypropanal over 800–2000 K and radical forming channels are unimportant. As 3-hydroxypropanal is one of the main products of GC decomposition, and aldehydes are known to have a very high impact on soot reduction, we conclude that GC has great potential for cleaner combustion as a fuel additive.
1. Introduction
Over the last decade or so, concerns over global warming and diminishing petroleum reserves have continued to rise. Transportation driven by traditional fossil fuels contributes significantly towards CO2 emissions. Such concerns have led to concentrated efforts directed at shifting from conventional fuels to renewable alternatives that can promote cleaner combustion by reducing greenhouse gases and particulate matters. European Union “20/20/20” set mandatory goals for 2020 to reduce the greenhouse gas emissions by 20% compared to 1990, improve energy efficiency by 20% compared to the forecasts for 2020 and make the renewable energy share 20% of the total European energy mix.1 Bio-derived fuels come with fuel-borne oxygen, e.g., 10.8% in rapeseed methyl ester. Fuel-borne oxygen is very effective in reducing the formation and growth of soot nuclei.2 Some studies have even shown that fuel-borne oxygen of 30% or more by weight can make the combustion process smokeless.3–5 The goals of cleaner combustion have encouraged more production of biofuels on a large scale worldwide. Among bio-derived fuels, biodiesel stands out from the health and environmental prospective because (i) these fuels are low in sulfur content, (ii) they emit low levels of hydrocarbons and CO, (iii) they are bio-degradable and non-toxic, and (iv) they have a high cetane number and calorific power similar to that of fossil fuels.6 Biodiesel can be derived from vegetable oils and animal fats via industrial processes of esterification or transesterification. During biodiesel production, crude glycerol of 10–20% by volume is formed as a byproduct. The increasing use of biodiesel has led to a substantial increase of glycerol supply in the global market. This recently led to a dramatic fall in glycerol price, reaching the lowest historic value (3–5 cents a pound of glycerol).6 The low price and huge surplus of glycerol warrants explorations of its alternative uses to make value-added products and to reduce the impacts of disposal. A recent review article by Rodrigues et al.7 highlights the three possible ways to upgrade glycerol into value-added chemical feedstocks.One feasible way to deal with the crude glycerol overflow is its direct use as a fuel or fuel additive. However, the high viscosity (1487 mPa s at 293 K), high melting point (mp = 18.7 °C) and high auto-ignition temperature (370 °C) of glycerol have limited its application as a fuel or additive, and also the presence of mineral salts causes corrosion in engines.6 Instead, conversion of glycerol into value-added chemicals has received much attention.7–10 One promising process is the conversion of glycerol into glycerol carbonate (GC) with a relatively high yield. For example, Ochoa-Gómez et al.11,12 investigated the synthesis of glycerol carbonate from transesterification of glycerol and dimethyl carbonate. They achieved ∼100% conversion and 95% yield in 90 min at a temperature of 95 °C.12 Very recently, Khandey et al.9 reported a transesterification pathway to convert glycerol into glycerol carbonate by using lithium-oil palm ash zeolite (Li-OPAZ) as a catalyst. They were able to achieve a very high yield of ∼98.1% of glycerol carbonate with 100% glycerol conversion in 90 min under the optimal conditions of 343 K, a dimethyl carbonate to glycerol molar ratio of 2, and a catalyst loading of 2% by weight. There are other chemical routes for the synthesis of glycerol carbonate by utilizing CO2, and some of them look very promising for application in the industrial scale.10 Glycerol carbonate is water-soluble, nontoxic, and viscous (85.4 mPa s at 298 K), and has a melting point (mp) of −69 °C), an auto-ignition temperature of 404 °C, and a high oxygen content (59% of oxygen by weight and an O![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) C ratio of 1). Moreover, it is renewable11 and can be a good candidate to sequester CO2 as a chemical feedstock for a sustainable future. Previous studies on carbonate esters13,14 have shown that such oxygenated fuels can significantly reduce unburnt hydrocarbons, CO and particulate matter emissions. However, the effectiveness of oxygenated fuel additives depends on the structure/size of the additive molecule, and a key controlling factor is the oxygen content of the molecule.15,16 The properties of glycerol carbonate, therefore, make it a very promising fuel additive for clean combustion by ensuring the sustainability of future internal combustion engines.
C ratio of 1). Moreover, it is renewable11 and can be a good candidate to sequester CO2 as a chemical feedstock for a sustainable future. Previous studies on carbonate esters13,14 have shown that such oxygenated fuels can significantly reduce unburnt hydrocarbons, CO and particulate matter emissions. However, the effectiveness of oxygenated fuel additives depends on the structure/size of the additive molecule, and a key controlling factor is the oxygen content of the molecule.15,16 The properties of glycerol carbonate, therefore, make it a very promising fuel additive for clean combustion by ensuring the sustainability of future internal combustion engines.
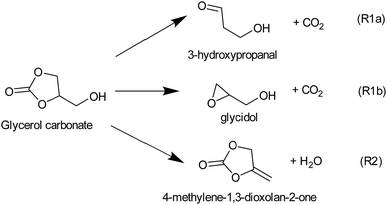
However, efficient utilization of glycerol carbonate (GC) as a biofuel or fuel additive requires detailed understanding of the kinetic behavior of GC to accurately predict combustion behavior and emissions. To the best of our knowledge, there are no data available in the literature describing the combustion/pyrolysis kinetics of GC, even though one can speculate that glycerol carbonate may decompose via C–C and C–O bond scissions as seen in cyclic compounds (e.g., cyclopentane,17 cyclohexane,17,18 methylcyclohexane,19 pyrrolidine,20 tetrahydrofuran21 and 1,4-dioxane22). The resulting radicals may further react to produce a wide spectrum of oxygenated compounds. Besides radical forming pathways, molecular channels eliminating H2, H2O, CO, CO2, and CH2O are also feasible (see Fig. 1S of the ESI for the reaction scheme†). These oxygenated intermediates and/or products of glycerol carbonate decomposition may effectively alter the low-temperature chemistry and may help achieve cleaner burning. This work aims to explore various possible reactions of glycerol carbonate, particularly the initial steps of pyrolysis, and to rationalize the pressure- and temperature-dependence of the rate coefficients using high level ab initio/RRKM-master equation calculations.
2. Computational details
2.1 Ab initio calculations
At first, Gaussian-4 theory (G4)23 was employed to explore the possible reaction pathways of glycerol carbonate (GC, 4-(hydroxymethyl)-1,3-dioxolan-2-one). Intrinsic reaction coordinate (IRC) calculations24,25 with a step size of 0.06 a.u. were carried out by employing the B3LYP functional26,27 using Pople's split-valence 6-31G(2df,p) Gaussian basis set.28 These calculations ensured that the reaction pathways originating from the transition states led to the appropriate minima. Low-energy reaction pathways were identified at the G4 level of theory, and then they were selected for re-optimization with the help of second-order Møller–Plesset (MP2)29 perturbation theory using Dunning's triple-ς basis set (cc-pVTZ)30 applying the “tight” convergence criterion. The optimized structures were further characterized by normal mode analysis to distinguish their identity on the PES. The MP2/cc-pVTZ harmonic vibrational frequencies were scaled31 by a factor of 0.95 and they were used for the calculation of thermodynamic properties and rate coefficients.The reliability of the calculated rate coefficients depends strongly upon the accuracy of the energy barriers. Therefore, the energetics of glycerol carbonate decomposition were refined by performing single-point coupled-cluster calculations with single and double excitations32–34 including the perturbative treatment of triple excitations (CCSD(T)).35 As done in our previous studies,36–38 a two-point extrapolation scheme of Helgaker39 was employed to obtain CCSD(T) energies at the complete basis set limit (CBS) by using cc-pVXZ (X = D,T,Q)30,40 basis sets. This extrapolation scheme allows a high level energetic description of the reaction of glycerol carbonate. Here, the Hartree–Fock limit (E∞HF) was obtained by applying the Feller three-point exponential extrapolation41 according to EHF(X) = E∞HF + b![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−cX) using cc-pVXZ (X = D,T,Q,5,6) basis sets.42,43 This method culminates into three Hartree–Fock energies at the infinite basis set limit (E∞HF) viz. HF/cc-pV(D,T,Q)Z, HF/cc-pV(T,Q,5)Z and HF/cc-pV(Q,5,6)Z. As for the correlation energy, a two-point extrapolation of the form Ecorr (X) = E∞corr + b′X−3 was used, where X was either 2 and 3 or 3 and 4 for cc-pV(D,T)Z and cc-pV(T,Q)Z basis sets, respectively. Finally, CCSD(T) energies at the infinite basis set limit, i.e., CCSD(T)/cc-pV(D,T)Z or CCSD(T)/cc-pV(T,Q)Z, were obtained by adding E∞HF and E∞corr together. The frozen core approximation was applied for all CCSD(T) calculations. To assess the contribution of higher excitations, T1 diagnostics44 were computed. The largest T1 diagnostic value was 0.0223 for one of the transition states (TS1b, see Fig. 3 below) at the CCSD(T)/cc-pVQZ level of theory. This value of T1 may reveal the importance of non-dynamical electron correlation effects.44 For all other species, the T1 diagnostic values suggest that the single reference methods applied here are adequate for an accurate energetic description of the reactions of glycerol carbonate. All electronic structure calculations were performed by using the Gaussian 09 program package.45
exp(−cX) using cc-pVXZ (X = D,T,Q,5,6) basis sets.42,43 This method culminates into three Hartree–Fock energies at the infinite basis set limit (E∞HF) viz. HF/cc-pV(D,T,Q)Z, HF/cc-pV(T,Q,5)Z and HF/cc-pV(Q,5,6)Z. As for the correlation energy, a two-point extrapolation of the form Ecorr (X) = E∞corr + b′X−3 was used, where X was either 2 and 3 or 3 and 4 for cc-pV(D,T)Z and cc-pV(T,Q)Z basis sets, respectively. Finally, CCSD(T) energies at the infinite basis set limit, i.e., CCSD(T)/cc-pV(D,T)Z or CCSD(T)/cc-pV(T,Q)Z, were obtained by adding E∞HF and E∞corr together. The frozen core approximation was applied for all CCSD(T) calculations. To assess the contribution of higher excitations, T1 diagnostics44 were computed. The largest T1 diagnostic value was 0.0223 for one of the transition states (TS1b, see Fig. 3 below) at the CCSD(T)/cc-pVQZ level of theory. This value of T1 may reveal the importance of non-dynamical electron correlation effects.44 For all other species, the T1 diagnostic values suggest that the single reference methods applied here are adequate for an accurate energetic description of the reactions of glycerol carbonate. All electronic structure calculations were performed by using the Gaussian 09 program package.45
2.2 RRKM/master equation calculations
In this work, ChemRate Master Equation (ME) code46 was used to compute the pressure- and temperature-dependent rate coefficients, k(T, p), for the unimolecular decomposition of GC at p = 0.01–100 atm and T = 800–2000 K. The master equation describes the temporal evolution of the energy- and time-dependent population of each species in a chemical system. The internal-energy-dependent master equation (1D-ME) can be written in the following form: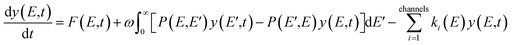 | (1) |
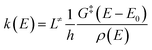 | (2) |
Eqn (1) can be written in a matrix form as given by eqn (3) by replacing continuous functions with vectors. To do so, the energy axis is divided into a large number of small energy “bins” or “energy grains” of the size δE to construct an energy-grained master equation.
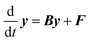 | (3) |
3. Results and discussion
3.1 Potential energy surface and thermodynamic properties
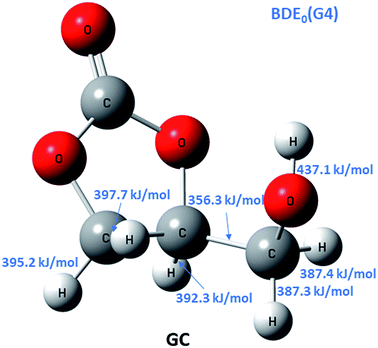
To discriminate among reaction channels, all possible reaction pathways on the potential energy surface (PES) of glycerol carbonate were considered (see the reaction scheme in Fig. 1S in the ESI†). As described earlier, the G4 level of theory was used to map out the PES. It was found that simple bond fission reactions via the C(O)–O bond or O–C and C–C bonds of glycerol carbonate producing open chain di-radicals have a threshold energy of at least 340 kJ mol−1. As can be seen in Fig. 1, the C–H bond dissociation energy of methylene in –CH2OH is the least (BDE0 = 387.3 kJ mol−1) among all C–H bonds of GC. The elimination of the hydroxymethyl (˙CH2OH) radical via C–C bond fission of GC is found to have the lowest threshold energy (BDE0 = 356.3 kJ mol−1). These simple bond fission reactions are unlikely to occur as their threshold energies are very high as compared to the efficient molecular channels, such as CO2 or H2O elimination from GC via a concerted mechanism, as will be discussed later (see Fig. 2 and 3).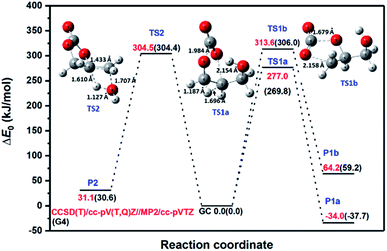 | ||
| Fig. 3 Zero-point corrected CCSD(T)/cc-pV(T,Q)Z//MP2-ccpVTZ energy profile for major channels of glycerol carbonate decomposition. G4 energies are also provided in parentheses for comparison. | ||
Other molecular channels, such as elimination of H2 and CH2O, lie at energetically very high levels (E0 ≥ 400 kJ mol−1), and these proceed via tight transition states. So, these channels are also kinetically irrelevant. Consequently, GC primarily decomposes via the following three major energetically low-lying channels (see Fig. 2).
Both reactions, R1a and R1b, eliminate CO2 to produce 3-hydroxypropanal and glycidol, respectively. However, the two mechanisms are quite different. As can be seen in Fig. 3, reaction R1a occurs via TS1a by overcoming an energy barrier of 269.8 kJ mol−1 and 277.0 kJ mol−1 at the G4 and CCSD(T)/cc-pV(T,Q)Z/MP2/cc-pVTZ levels of theory, respectively. TS1a is formed by stretching of the C–O (rC–O = 1.984 Å) and O–C (rO–C = 2.154 Å) bonds from their respective values (rC–O = 1.354 Å and rO–C = 1.435 Å) in the reactant molecule, and by the simultaneous transfer of an H-atom. This reaction is the exothermic process (Δr,0 KH0 = −37.7 and −34 kJ mol−1 at the G4 and CCSD(T)/cc-pV(T,Q)Z/MP2/cc-pVTZ levels of theory, respectively). In contrast, reaction R1b is endothermic, and unlike R1a, it retains the ring structure in the product after eliminating CO2. Reaction R1b occurs via transition state TS1b which lies ∼36 kJ mol−1 higher in energy than TS1a, and it does not involve an intramolecular H-transfer. However, in both transition states, the C–O bonds being broken are elongated to about 2 Å to eventually release CO2; whereas the O-atom forming the C–O bond (rC–O = 1.19 Å) in the CO2 moiety is found to be close to the final value of rC–O = 1.169 Å. We note here that the geometrical parameters of the transition states obtained at the MP2/cc-pVTZ and B3LYP/6-31G(2df,p) levels of theory show little method dependence. Not surprisingly, the calculated values of the barrier heights are found to be relatively low, which indicates the concerted nature of these reactions. Reaction R2 proceeds via a four-center transition state, TS2, by retaining the ring structure of the parent molecule to produce 4-methylene-1,3-dioxolan-2-one and H2O. This reaction is also concerted in nature and occurs by overcoming an energy barrier of 304.5 kJ mol−1. TS2 is found to be similar in structure to that observed by Kiecherer et al.57 at the MP2(FC)/cc-pVQZ level of theory for H2O elimination in ethanol.
For the major channels (R1a, R1b and R2), the G4 values were further refined at the CCSD(T)/CBS level of theory using the extrapolation methods explained earlier. The results are provided in Fig. 3 and Table 1 for comparison. The G4 method under-predicts the TS energies by ∼7 kJ mol−1 for CO2 elimination, whereas both methods predict the same barrier height for the H2O elimination pathway. Table 1 further compares the standard enthalpy of reaction (Δr,298.15 KH0) obtained at various levels of theory. The different extrapolation schemes, namely Model 1, Model 2 and the Reference Model, predict very similar values for the standard enthalpy of reactions. The deviation given in parentheses is negligibly small with the largest deviation being 1.3 kJ mol−1. Again, the G4 values for the standard enthalpy of reactions were found to be smaller than the values obtained using the Reference Model, HF/cc-pV(Q,5,6)Z + CCSD(T)/cc-pV(T,Q)Z. The energetics obtained with the Reference Model were used for RRKM/master equation calculations, and the highly accurate standard enthalpies of formation for the stable species at 0 K and 298.15 K were estimated using the atomization scheme. The essential highly accurate atomization enthalpies were obtained from Ruscic's Active Thermochemical Tables (ATcT).58
| Δr,298 KH0 kJ mol−1 | G4 | Model 1 | Model 2 | Reference Model | |||
|---|---|---|---|---|---|---|---|
| CCSD(T)/cc-pV(D,T)Z | CCSD(T)/cc-pV(T,Q)Z | CCSD(T)/cc-pV(T,Q)Z | |||||
| HF/cc-pV(D,T,Q)Z | HF/cc-pV(T,Q,5)Z | HF/cc-pV(Q,5,6)Z | |||||
| R1a | −32.5 | (−3.7) | −30.1 | (−1.3) | −28.4 | (0.3) | −28.8 |
| R1b | 63.1 | (−5.0) | 66.9 | (−1.2) | 68.3 | (0.1) | 68.1 |
| R2 | 36.9 | (−0.6) | 38.3 | (0.8) | 37.1 | (−0.4) | 37.5 |
Reaction enthalpies are usually less dependent on the basis set, but the standard enthalpies of formation obtained with the atomization scheme are more sensitive to the basis set used. We assessed this dependency by computing single point energies at the HF and CCSD(T) level of theory using various sizes of basis sets in the extrapolation schemes. We found that the HF/cc-pV(Q,5,6)Z energy values are 4.3 kJ mol−1 lower than the extrapolated values obtained using the cc-pV(T,Q,5)Z basis set. Further comparison with HF/cc-pV6Z energies revealed that HF/cc-pV(Q,5,6)Z values are less by 0.3 kJ mol−1. This clearly suggests that the final HF energies are not prone to any basis set dependency.
Based on the reference level of theory (HF/cc-pV(Q,5,6)Z + CCSD(T)/cc-pV(T,Q)Z//MP2/cc-pVTZ), standard enthalpies of formation were computed using the atomization scheme. Table 2 compiles and compares (wherever possible) the standard enthalpies of formation (ΔfH0) for glycerol carbonate and its decomposition products at 0 and 298.15 K. As can be seen, our computed value of Δf,298.15 KH0 = −702.9 kJ mol−1 for GC agrees very well with the value (−704.1 kJ mol−1) reported by Ezhova et al.59 who used Benson's group contribution method. As for glycidol (P1b), our value of Δf,298.15 KH0 = −246.1 kJ mol−1 matches excellently with that reported in Burcat's database60 (Δf,298.15 KH0 = −239.6 ± 8 kJ mol−1). However, the value reported by Vasiliu61 using the G3MP2 level of theory shows a larger deviation of 12.2 kJ mol−1. The origin of this discrepancy might be the inappropriately chosen conformer of glycidol (missing the intramolecular hydrogen bond between the OH group and O atom of oxirane). Vasiliu61 also reported a value for the standard enthalpy of formation of 3-hydroxypropanal (P1a) (Δf,298.15 KH0 = −327.6 kJ mol−1), but this value appears to be for prop-2-en-1-ol. We confirmed this by checking the reported structure in the ESI of ref. 61. To the best of our knowledge, no other experimental and/or theoretical values for the standard enthalpy of formation of 3-hydroxypropanal (P1a) and 4-methylene-1,3-dioxolan-2-one (P2) are available in the literature for comparison. Tables S1 and S2 (ESI†) further compile the thermodynamic properties of the species (GC, P1a, P1b and P2) in JANAF and NASA formats. Based on the calculated standard enthalpy of formation, the lower heating value (LHV) of glycerol carbonate is found to be 13.5 MJ kg−1, which is comparable to that of dimethyl carbonate (LHV = 15.8 MJ kg−1).14
3.2 Theoretical rate coefficients
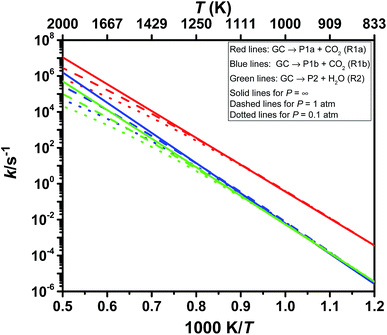
We obtained the pressure- and temperature-dependence of the rate coefficients, k(T, p), for the thermal decomposition of glycerol carbonate by solving the thermal steady-state master equation using ChemRate.46 These calculations used the parameters discussed in the previous section in addition to the vibrational frequencies and rotational constants listed in Table S3 (ESI†). We treat the low torsional mode as a vibration for both the reactant and the transition state. One can safely do so for OH rotors because their corresponding torsional frequencies are high (≥400 cm−1). As for (ring)C–CH2OH hindered rotors in GC and transition states, we assume that there will be systematic cancellation of errors. These torsional modes are shown in bold in Table S3 (ESI†). The calculated values of the rate coefficients, k(T, p), for the three primary channels of GC decomposition are compiled in Table 3 and illustrated in Fig. 4. Our calculated values of the rate coefficients, ktotal(T, p = 1 atm), are close to the high pressure limiting rate coefficients, k∞,total(T). Thus, GC displays negligible pressure dependence which is not surprising in view of its molecular size. For large molecules like GC, it is usual to observe k(T, p) ≈ k∞(T). For such molecular systems, k(E) drops rapidly below the collisional stabilization rate βks[M], i.e., βks[M] ≫ k(E) with bath gas M showing no effect of pressure. Here, β and ks are the collision efficiency and collisional rate, respectively. However, the assumption k(T, p) ≈ k∞(T) may not be valid at high temperatures. For GC decomposition, we observed a pressure fall-off effect at high temperatures, e.g., k∞(T)/k(T, p = 1 atm) ≈5 at 2000 K.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−E/RT) over the temperature range of 800 to 2000 K in units of J, mol, s, and K
exp(−E/RT) over the temperature range of 800 to 2000 K in units of J, mol, s, and K
| S. No. | P (atm) | log(A) | n | E |
|---|---|---|---|---|
| (a) Rate parameters for reaction R1a: GC → P1a + CO 2 | ||||
| 1.1 | 0.01 | 75.73 | −18.05 | 421![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 860 860 |
| 2.2 | 0.1 | 59.46 | −13.15 | 391![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 014 014 |
| 3.3 | 1 | 39.95 | −7.40 | 347![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 411 411 |
| 4.3 | 10 | 23.59 | −2.64 | 308![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 207 207 |
| 5.6 | 100 | 14.75 | −0.075 | 286![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 275 275 |
| 6.7 | ∞ | 14.53 | 0 | 286![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 561 561 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||
| (b) Rate parameters for reaction R1b: GC → P1b + CO 2 | ||||
| 1.1 | 0.01 | 88.82 | −20.55 | 468![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 569 569 |
| 2.2 | 0.1 | 69.32 | −16.05 | 446![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 344 344 |
| 3.3 | 1 | 48.53 | −9.87 | 402![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 664 664 |
| 4.3 | 10 | 28.91 | −4.14 | 356![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 722 722 |
| 5.6 | 100 | 17.30 | −0.77 | 328![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 208 208 |
| 6.7 | ∞ | 14.61 | 0 | 322![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 060 060 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||
| (c) Rate parameters for reaction R2: GC → P2 + H 2 O | ||||
| 1.1 | 0.01 | 76.93 | −18.77 | 439![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 467 467 |
| 2.2 | 0.1 | 61.03 | −13.92 | 411![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 905 905 |
| 3.3 | 1 | 40.23 | −7.77 | 366![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 796 796 |
| 4.3 | 10 | 21.61 | −2.33 | 322![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 693 693 |
| 5.6 | 100 | 10.94 | −0.76 | 296![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 372 372 |
| 6.7 | ∞ | 13.68 | 0 | 305![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 282 282 |
Among the three decomposition channels, reaction R1a is the most favored one contributing more than 85% in the entire temperature range (800–2000 K). This favoritism for the reaction can be attributed to the low value of the threshold energy (ΔE0 = 277.0 kJ mol−1) and also to an entropic gain (Δ298.15 KS≠ = 47.6 J mol−1 K−1). Though R1b has a higher energy barrier than R2 (see Fig. 3), R1b is found to be faster than R2 which again can be explained from entropic insight. R1b is accompanied by an entropic gain (Δ298.15 KS≠ = 60.4 J mol−1 K−1), whereas R2 occurs via a loss in entropy (Δ298.15 KS≠ = −5.3 J mol−1 K−1) due to cyclization in the transition state structure. Transition state TS2 is tight as indicated by its imaginary frequency (ν = 1481.7i). Consequently, R2 contributes less than 4% over 800–2000 K, i.e., CO2 elimination makes the most contribution (≥96%) for GC decomposition over the entire temperature range of this study.
Similar to alkyl or aryl carbonates,62–64 GC also decomposes by utilizing two of its oxygen atoms to sequester just one carbon atom forming CO2. Such oxygenates which dispense fuel-borne oxygen to form CO2 as opposed to CO have lesser propensity for soot reduction. For instance, alkyl or aryl carbonates having β-hydrogens decompose at appreciably low temperature via a low energy barrier of ≤200 kJ mol−1 (ref. 62) to produce olefin, CO2 and alcohol, and their use as fuel additives has been found to be not more effective than alcohols for improving the threshold sooting index (TSI).15 Hence, oxygenated fuel additives such as diethyl carbonate (DEC) do not have a substantial effect in improving the sooting tendency. On the other hand, glycerol carbonate can potentially have higher propensity to reduce soot due to its decomposition to 3-hydroxypropanal and CO2 exclusively. Despite the fact that two oxygen atoms in glycerol carbonate are wasted as CO2, aldehydes, such as 3-hydroxypropanal, are reported to have the greatest impact in improving the TSI.15 The other reason is that the decomposition of alkyl and aryl carbonates is found to be almost three order of magnitude faster than that of GC below 1000 K. Consequently, even in a low temperature oxidative environment (fuel/air mixtures), their unimolecular decomposition to produce alcohol, olefin and CO2 still remains the predominant consumption pathway (see ref. 65 for DEC low temperature oxidation). Therefore, the ignition behavior of such fuels is pretty much governed by their decomposition products. Unlike other carbonates, glycerol carbonate is less reactive and can withstand higher temperatures (t1/2 = 1.8 s at 1000 K). Because of its thermal stability, the reaction pathways for this molecule may drift towards abstraction reactions as opposed to molecular elimination reactions during low temperature oxidation. This expected drift in the reaction mechanism for GC will possibly lead to a wide array of oxygenated intermediates that may have a substantial impact on soot reduction. Therefore, glycerol carbonate appears to be more suitable compared to other oxygenated molecules for use as a fuel additive to reduce soot emissions.
4. Conclusions
Ab initio/RRKM-master equation calculations were performed to compute the pressure- and temperature-dependence of the rate coefficients for glycerol carbonate (GC) decomposition. GC decomposes via a concerted mechanism almost exclusively to yield CO2 and 3-hydroxypropanal. Carbon dioxide is the main decomposition product as in alkyl or aryl carbonates. CO2 pathways contribute ≥96% to the total rate coefficient for GC decomposition. As expected, the unimolecular reaction of GC did not exhibit any pressure effect. Unlike alkyl or aryl carbonates, GC is found to be more thermally stable, which can have a substantial effect on the spectrum of oxygenated intermediates formed during low temperature oxidation. As aldehydes are known to have the greatest impact on soot reduction among oxygenates, and 3-hydroxypropanal is one of the main products of GC decomposition, glycerol carbonate appears to have high potential for use as a soot-reducing fuel additive.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The research reported in this work was funded by King Abdullah University of Science and Technology (KAUST). Milán Szőri acknowledges the support provided by the European Union and the Hungarian State, co-financed by the European Regional Development Fund in the framework of the GINOP-2.3.4-15-2016-00004 project, aimed at promoting cooperation between higher education and industry. Milán Szőri is grateful for the financial support by the János Bolyai Research Scholarship of the Hungarian Academy of Sciences (BO/00113/15/7) and the New National Excellence Program of the Ministry of Human Capacities (ÚNKP-17-4-III-ME/26).References
- F. Fantozzi, A. Frassoldati, P. Bartocci, G. Cinti, F. Quagliarini, G. Bidini and E. M. Ranzi, Appl. Energy, 2016, 184, 68–76 CrossRef.
- P. Eastwood, Critical Topics in Exhaust Gas Aftertreatment, Research Studies Press, Baldock, Hertfordshire, 2001 Search PubMed.
- H. Chen, J. Wang, S. Shuai and W. Chen, Fuel, 2008, 87, 3462–3468 CrossRef.
- N. Miyamoto, H. Ogawa, N. M. Nurun, K. Obata and T. Arima, SAE Technical Paper 980506, 1998, DOI:10.4271/980506.
- H. Teng and J. C. McCandless, SAE Technical Paper 2006-01-0053, 2006, DOI:10.4271/2006-01-0053.
- C. A. G. Quispe, C. J. R. Coronado and J. A. Carvalho Jr, Renewable Sustainable Energy Rev., 2013, 27, 475–493 CrossRef.
- A. Rodrigues, J. C. Bordado and R. G. d. Santos, Energies, 2017, 10, 1817 CrossRef.
- M. Pagliaro, R. Ciriminna, H. Kimura, M. Rossi and C. Della Pina, Angew. Chem., Int. Ed., 2007, 46, 4434–4440 CrossRef PubMed.
- W. A. Khanday, P. U. Okoye and B. H. Hameed, Energy Convers. Manage., 2017, 151, 472–480 CrossRef.
- M. O. Sonnati, S. Amigoni, E. P. Taffin de Givenchy, T. Darmanin, O. Choulet and F. Guittard, Green Chem., 2013, 15, 283–306 RSC.
- J. R. Ochoa-Gómez, O. Gómez-Jiménez-Aberasturi, C. Ramírez-López and M. Belsué, Org. Process Res. Dev., 2012, 16, 389–399 CrossRef.
- J. R. Ochoa-Gómez, O. Gómez-Jiménez-Aberasturi, B. Maestro-Madurga, A. Pesquera-Rodríguez, C. Ramírez-López, L. Lorenzo-Ibarreta, J. Torrecilla-Soria and M. C. Villarán-Velasco, Appl. Catal., A, 2009, 366, 315–324 CrossRef.
- M. Kozak, J. Merkisz, P. Bielaczyc and A. Szczotka, The Influence of Oxygentated Diesel Fuels on a Diesel Vehicle PM/NOx Emission Trade-off, SAE Technical Paper 2009-01-2696, SAE International, 2009, DOI:10.4271/2009-01-2696.
- P. Rounce, A. Tsolakis, P. Leung and A. P. E. York, Energy Fuels, 2010, 24, 4812–4819 CrossRef.
- P. Pepiot-Desjardins, H. Pitsch, R. Malhotra, S. R. Kirby and A. L. Boehman, Combust. Flame, 2008, 154, 191–205 CrossRef.
- Y. Ren, Z. Huang, H. Miao, Y. Di, D. Jiang, K. Zeng, B. Liu and X. Wang, Fuel, 2008, 87, 2691–2697 CrossRef.
- B. Sirjean, P. A. Glaude, M. F. Ruiz-Lopez and R. Fournet, J. Phys. Chem. A, 2006, 110, 12693–12704 CrossRef PubMed.
- J. H. Kiefer, K. S. Gupte, L. B. Harding and S. J. Klippenstein, J. Phys. Chem. A, 2009, 113, 13570–13583 CrossRef PubMed.
- F. Zhang, Z. D. Wang, Z. H. Wang, L. D. Zhang, Y. Y. Li and F. Qi, Energy Fuels, 2013, 27, 1679–1687 CrossRef.
- A. Lucassen, Z. Wang, L. Zhang, F. Zhang, W. Yuan, Y. Wang, F. Qi and K. Kohse-Höinghaus, Proc. Combust. Inst., 2013, 34, 641–648 CrossRef.
- M. Verdicchio, B. Sirjean, L. S. Tran, P.-A. Glaude and F. Battin-Leclerc, Proc. Combust. Inst., 2015, 35, 533–541 CrossRef.
- X. Yang, A. W. Jasper, B. R. Giri, J. H. Kiefer and R. S. Tranter, Phys. Chem. Chem. Phys., 2011, 13, 3686–3700 RSC.
- L. A. Curtiss, P. C. Redfern and K. Raghavachari, J. Chem. Phys., 2007, 126, 084108 CrossRef PubMed.
- H. P. Hratchian and H. B. Schlegel, J. Chem. Phys., 2004, 120, 9918–9924 CrossRef PubMed.
- H. P. Hratchian and H. B. Schlegel, J. Chem. Theory Comput., 2005, 1, 61–69 CrossRef PubMed.
- A. D. Becke, Phys. Rev. A, 1988, 38, 3098–3100 CrossRef.
- P. J. Stephens, F. J. Devlin, C. F. Chabalowski and M. J. Frisch, J. Phys. Chem., 1994, 98, 11623–11627 CrossRef.
- L. A. Curtiss, K. Raghavachari, P. C. Redfern, V. Rassolov and J. A. Pople, J. Chem. Phys., 1998, 109, 7764 CrossRef.
- C. Møller and M. S. Plesset, Phys. Rev., 1934, 46, 618–622 CrossRef.
- R. A. Kendall, T. H. Dunning and R. J. Harrison, J. Chem. Phys., 1992, 96, 6796 CrossRef.
- J. P. Merrick, D. Moran and L. Radom, J. Phys. Chem. A, 2007, 111, 11683–11700 CrossRef PubMed.
- G. D. Purvis and R. J. Bartlett, J. Chem. Phys., 1982, 76, 1910–1918 CrossRef.
- G. E. Scuseria, C. L. Janssen and H. F. Schaefer, J. Chem. Phys., 1988, 89, 7382 CrossRef.
- G. E. Scuseria and H. F. Schaefer, J. Chem. Phys., 1989, 90, 3700 CrossRef.
- J. A. Pople, M. Head-Gordon and K. Raghavachari, J. Chem. Phys., 1987, 87(10), 5968–5975 CrossRef.
- R. Izsak, M. Szori, P. J. Knowles and B. Viskolcz, J. Chem. Theory Comput., 2009, 5, 2313–2321 CrossRef PubMed.
- B. R. Giri, F. Khaled, M. Szőri, B. Viskolcz and A. Farooq, Proc. Combust. Inst., 2017, 36, 143–150 CrossRef.
- M. AlAbbad, B. R. Giri, M. Szőri and A. Farooq, Proc. Combust. Inst., 2017, 36, 187–193 CrossRef.
- T. Helgaker, W. Klopper, H. Koch and J. Noga, J. Chem. Phys., 1997, 106, 9639–9646 CrossRef.
- T. H. Dunning, J. Chem. Phys., 1989, 90, 1007 CrossRef.
- D. Feller, J. Chem. Phys., 1992, 96, 6104–6114 CrossRef.
- T. H. Dunning, J. Chem. Phys., 1989, 90, 1007–1023 CrossRef.
- D. E. Woon and T. H. Dunning, J. Chem. Phys., 1993, 98, 1358–1371 CrossRef.
- T. J. Lee and P. R. Taylor, Int. J. Quantum Chem., 1989, 199–207 Search PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, et al., Gaussian 09 Revision D.01, Gaussian Inc., Wallingford CT, 2009 Search PubMed.
- V. B. Vladimir Mokrushin, W. Tsang, M. R. Zachariah, V. D. Knyazev and W. Sean McGivern, ChemRate, 1.5.8, NIST, Gaithersburg, USA, 2011 Search PubMed.
- R. G. Gilbert and S. C. Smith, Theory of Unimolecular and Recombination Reactions, Blackwell Scientific Publications, 1990 Search PubMed.
- T. Baer and W. L. Hase, Unimolecular Reaction Dynamics: Theory and Experiments, Oxford University Press, 1996 Search PubMed.
- P. J. Robinson and K. A. Holbrook, Unimolecular Reactions, Wiley-Interscience, 1972 Search PubMed.
- T. Beyer and D. F. Swinehart, Commun. ACM, 1973, 16, 379 CrossRef.
- C. Eckart, Phys. Rev., 1930, 35, 1303–1309 CrossRef.
- H. S. Johnston and J. Heicklen, J. Phys. Chem., 1962, 66, 532–533 CrossRef.
- A. M. Zaras, P. Dagaut and Z. Serinyel, J. Phys. Chem. A, 2015, 119, 7138–7144 CrossRef PubMed.
- A. M. Zaras, S. Thion and P. Dagaut, Int. J. Chem. Kinet., 2015, 47, 439–446 CrossRef.
- M. Akbar Ali and A. Violi, J. Org. Chem., 2013, 78, 5898–5908 CrossRef PubMed.
- H. Hippler, J. Troe and H. Wendelken, J. Chem. Phys., 1983, 78, 6709–6717 CrossRef.
- J. Kiecherer, C. Bansch, T. Bentz and M. Olzmann, Proc. Combust. Inst., 2015, 35, 465–472 CrossRef.
- B. Ruscic, R. E. Pinzon, M. L. Morton, G. von Laszevski, S. J. Bittner, S. G. Nijsure, K. A. Amin, M. Minkoff and A. F. Wagner, J. Phys. Chem. A, 2004, 108, 9979–9997 CrossRef.
- N. N. Ezhova, I. G. Korosteleva, N. V. Kolesnichenko, A. E. Kuz'min, S. N. Khadzhiev, M. A. Vasil'eva and Z. D. Voronina, Petrol. Chem., 2012, 52, 91–96 CrossRef.
- E. Goos, A. Burcat and B. Ruscic, Extended Third Millennium Ideal Gas and Condensed Phase Thermochemical Database for Combustion with Updates from Active Thermochemical Tables, 16 July 2016 Search PubMed.
- M. Vasiliu, K. Guynn and D. A. Dixon, J. Phys. Chem. C, 2011, 115, 15686–15702 CrossRef.
- M. AlAbbad, B. R. Giri, M. Szori, B. Viskolcz and A. Farooq, Chem. Phys. Lett., 2017, 684, 390–396 CrossRef.
- H. O'Neal and S. Benson, J. Phys. Chem., 1967, 71, 2903–2921 CrossRef.
- J. Cross, R. Hunter and V. Stimson, Aust. J. Chem., 1976, 29, 1477–1481 CrossRef.
- H. Nakamura, H. J. Curran, A. Polo Córdoba, W. J. Pitz, P. Dagaut, C. Togbé, S. M. Sarathy, M. Mehl, J. R. Agudelo and F. Bustamante, Combust. Flame, 2015, 162, 1395–1405 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c8se00207j |
| This journal is © The Royal Society of Chemistry 2018 |