How to determine optical gaps and voltage losses in organic photovoltaic materials
Abstract
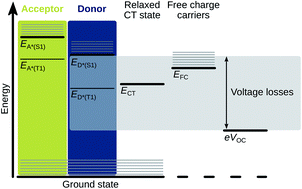
The best performing organic solar cells (OSC) efficiently absorb photons and convert them to free charge carriers, which are subsequently collected at the electrodes. However, the energy lost in this process is much larger than for inorganic and perovskite solar cells, currently limiting the power conversion efficiency of OSCs to values slightly below 14%. To quantify energy losses, the open-circuit voltage of the solar cell is often compared to its optical gap. The latter is, however, not obvious to determine for organic materials which have broad absorption and emission bands, and is often done erroneously. Nevertheless, a deeper understanding of the energy loss mechanisms depends crucially on an accurate determination of the energies of the excited states involved in the photo-conversion process. This perspective therefore aims to summarize how the optical gap can be precisely determined, and how it relates to energy losses in organic photovoltaic materials.
- This article is part of the themed collection: 2018 Sustainable Energy and Fuels HOT Articles


 Please wait while we load your content...
Please wait while we load your content...