Theoretical studies on the reaction kinetics of methyl crotonate with hydroxyl radical†
Received
3rd September 2017
, Accepted 8th November 2017
First published on 23rd November 2017
1 Introduction
Currently, the world is facing a pressing energy crisis and environmental degradation due to the over-use and over-exploitation of fossil fuels.1 Biodiesel fuels, which are renewable, sustainable and environmentally friendly, have long been considered as an attractive substitute for fossil fuels. They can be mixed with petroleum in transportation and heating or can even be directly used as pure fuels.2 Most biodiesel fuels are derived from vegetable oils or animal fats via transesterification processes with the addition of methanol.3,4 The relatively high oxygen content contributes to lower emissions of sulfur oxides (SOX), particulate matter (PM) and greenhouse gases such as CO2.5 However, real biodiesel fuels are usually a mixture of saturated and unsaturated long-chain fatty acid methyl esters (FAMEs), which have complicated and diverse chemical structures. As a result, combustion research progress is significantly limited for the use of biodiesel fuels as practical fuels.6 In view of the complicated structures of long-chain FAMEs, short-chain FAMEs containing similar functional groups have been used as surrogate models to mimic the characteristics of real biodiesel fuels in combustion chemistry. Two representative C4 ester surrogates are methyl butanoate (C5H10O2, MB)7–11 and methyl crotonate (C5H8O2, MC).12–16 As a prototypical unsaturated methyl ester, MC is of great significance in studying the effects of double bonds on combustion chemical reaction kinetics.
Numerous experimental and modeling investigations have been performed on MC combustion. The first detailed kinetic model for MC combustion was reported by Gaïl et al.12 and was later validated and revised utilizing experimental data of ignition delay times and low-pressure premixed flames.17,18 Other important experimental studies, including the jet-stirred reactor experiment by Sarathy et al.13 and the premixed flame experiment by Wang et al.,15 were carried out to explore the combustion chemistry of MC. Additionally, in a theoretical study by Oyeyemi et al.,16 the authors calculated the bond dissociation energies (BDEs) of the MC molecule.
It is generally accepted that the reactions between MC and small radicals such as hydrogen atom or hydroxyl radical (OH) frequently play significant roles in the early stage of combustion.19,20 However, kinetic investigations of these crucial reactions are rather rare, particularly for the reactions between MC and OH. To our knowledge, only one experimental measurement of MC + OH was performed by Teruel et al.21 at a temperature of 298 K and a pressure of one bar utilizing an 80 L Teflon bag located in a wooden box with internal walls covered by aluminum foil. The decay of the organics was monitored by gas chromatography with flame ionization detection (GC-FID), and the rate constants of MC + OH were determined using the relative rate technique with different reference compounds. However, the measured overall rate coefficients of MC + OH reactions are not feasible for direct use at diverse pressure and temperature conditions. Due to the lack of relevant studies, the rate coefficients in the MC + OH reaction mechanism were always estimated by analogy to reactions of MB or other short-chain esters with similar structures.17 Thus, there is a great need to provide accurate rate coefficients for MC + OH reactions and to further explore potentially kinetically significant reaction pathways, such as OH-addition reactions followed by β-scission reactions.
In the present work, the potential energy surfaces (PESs) of MC + OH were investigated using ab initio quantum chemistry methods. The correlative rate constants of the main reaction channels were computed via solution of the time-dependent multiple-well master equation based on Rice–Ramsperger–Kassel–Marcus (RRKM) theory within the temperature range of 500–1800 K and the pressure range of 0.001–100 atm. This work not only provides a large number of necessary rate constants for chemical kinetic modeling of MC combustion, but also serves as a solid starting point for further understanding of the combustion mechanism of real biodiesels. The rate constants were fitted in simple functional forms which are compatible with the prevalent kinetic modeling codes.
2 Theoretical methods
2.1
Ab initio methods
The PES of the MC + OH reaction was constructed using two schemes. The first scheme employed is the compound model chemistry method CBS-QB3.22,23 For this method, the Becke three-parameter functional and the Lee–Yang–Parr correction (B3LYP) with the 6-311G(2d,d,p) basis set were used for geometry optimization and frequency analysis, followed by a series of higher level corrections for the electronic energy.
In the second scheme, the optimized geometries and vibrational frequencies of stationary points were obtained via the quadratic configuration interaction with singles and doubles method with perturbative inclusion of triples (QCISD(T)) calculations24 employing the M062x method25 with the 6-311++G(d,p) basis set.26,27 A scale factor of 0.983 was used for the vibrational frequencies,28 and the zero-point energies (ZPE) were obtained from the M062x/6-311++G(d,p) calculations. Higher level single point energies were obtained from combinations of the QCISD(T) and MP2 calculations.24 As in previous studies29,30 of a similar albeit smaller molecular system, the QCISD(T) energies were calculated with the correlation-consistent, polarized-valence, triple-ζ (cc-pVTZ) and quadruple-ζ (cc-pVQZ) basis sets of Dunning.31 The QCISD(T) energies, extrapolated to the complete basis set (CBS) limit, were approximated by the following expression:32
| | | E[QCISD(T)/CBS] = E[QCISD(T)/CBS]DZ→TZ + {E[MP2/CBS]TZ→QZ − E[MP2/CBS]DZ→TZ} = {E[QCISD(T)/cc-pVTZ] × 1.4629 − E[QCISD(T)/cc-pVDZ] × 0.4629} + {E[MP2/cc-pVQZ] × 1.6938 − E[MP2/cc-pVTZ] × 0.6938} − {E[MP2/cc-pVTZ] × 1.4629 − E[MP2/cc-pVDZ] × 0.4629} | (1) |
In addition, the T1 diagnostics of the transition states and species calculated at the QCISD(T)/cc-pVDZ level are shown in Table S4 in the ESI.† All the T1 values are smaller than 0.03, indicating the appropriateness of the single-reference methods. All these quantum chemistry calculations were performed using the Gaussian 09 program package.33
2.2 Rate coefficient calculations
In this study, the PES of MC + OH was characterized by multiple, interconnected potential energy wells. PAPR code34 has already been proven to be effective in kinetic predictions for this type of reaction system. Therefore, the pressure- and temperature-dependent rate coefficients were computed via solution of the time-dependent master equation based on RRKM theory using PAPR code.34 The calculations cover a temperature range from 500 to 1800 K and a pressure range from 0.001 to 100 atm. For the reaction channels with distinct energy barriers, conventional transition state theory (CTST) was used with rigid-rotor harmonic oscillator (RRHO) assumptions. Furthermore, the low-frequency vibrational modes corresponding to the internal torsions were treated as hindered rotors.35 The tunneling correction was accounted for using the asymmetric Eckart potential.36
In the case of the direct bond dissociation reaction producing CH3CH2COCO and CH3OH (reaction (R8) below), variational transition state theory (VTST) was employed. The minimum energy pathway (MEP) along the C–O reaction coordinate was calculated at the M062x/6-311++G(d,p) level.37 The energies of the MEP were then scaled by the asymptotic dissociation energy of the corresponding reaction obtained from the QCISD(T)/CBS scheme. Similar to previous studies,30,38 the reactions between OH and MC, which contains C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C double bonds in its structure, proceeded via initial formation of a weak van der Waals (vdW) complex through hydrogen bonding at low temperature. The transition state for the barrierless reaction of MC + OH to the vdW complex is fairly loose, and a simplified phase space theory (PST)39 was adopted in the rate constant calculations. In this work, the long-range interaction potential between the reactants and the vdW complex was approximated by a simple isotropic interaction V(R) = −C6/R6, wherein R represents the distance between two fragments and C6 was estimated from the equation C6 = α1α2E1E2/(E1 + E2). In the C6 equation, αi and Ei (i = 1,2) are the polarizability and ionization energy for each fragment,30 respectively; these were obtained from the M062x/6-311++G(d,p) calculations. Notably, in this paper, C6 was estimated to be 5.21 × 105 cm−1 Å6 for MC + OH.
C double bonds in its structure, proceeded via initial formation of a weak van der Waals (vdW) complex through hydrogen bonding at low temperature. The transition state for the barrierless reaction of MC + OH to the vdW complex is fairly loose, and a simplified phase space theory (PST)39 was adopted in the rate constant calculations. In this work, the long-range interaction potential between the reactants and the vdW complex was approximated by a simple isotropic interaction V(R) = −C6/R6, wherein R represents the distance between two fragments and C6 was estimated from the equation C6 = α1α2E1E2/(E1 + E2). In the C6 equation, αi and Ei (i = 1,2) are the polarizability and ionization energy for each fragment,30 respectively; these were obtained from the M062x/6-311++G(d,p) calculations. Notably, in this paper, C6 was estimated to be 5.21 × 105 cm−1 Å6 for MC + OH.
The interaction between the reactants and bath gas N2 was modeled by the Lennard-Jones (L-J) potential. The L-J parameters for MC and N2 were calculated using the method of Chung et al.40,41 with the following empirical formulas:
| | 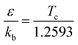 | (2) |
where
kb refers to the Boltzmann constant and
Tc and
Vc are the critical temperature and critical volume, respectively, estimated here using the method of Joback.
42 The L-J parameters obtained for MC were
ε/
kb = 515.19 K,
σ = 5.70 Å. For the bath gas N
2, these parameters were taken as
ε/
kb = 71.40 K,
σ = 3.80 Å from a previous study.
30 Furthermore, the collision energy transfer was represented by a single-exponential down model employing a temperature-dependent form for the average energy transferred,
i.e., 〈Δ
Edown〉 = 200(
T/300)
0.85 cm
−1.
43
3 Results and discussion
The major reaction channels of MC + OH include H-abstraction reactions and OH-addition reactions. The subsequent isomerization and decomposition channels were also identified for the generated primary radicals. For clarity and simplicity, only the energetically and kinetically favorable pathways are presented in the main text, as shown in Fig. 1 and 2. The complete potential energy surfaces are depicted in Fig. S1–S4 in the ESI;† the geometries of all stationary points are also provided. Furthermore, the standard enthalpies of formation (ΔHo298,f) were computed for the major species using the two different schemes on the basis of the ΔHo298,f values of MC, OH and H2O from previous studies.44–46 The computed values for these species are listed in Table 1. In the present work, the uncertainties of the energies were estimated to be 2 and 1 kcal mol−1, respectively, for the QCISD(T)/CBS and CBS-QB3 calculations;47 thus, the uncertainties of the rate constants are a factor of 1.5 for QCISD(T)/CBS and a factor of 2.2 for CBS-QB3. Note that the relative energies in the following discussion were all obtained from the QCISD(T)/CBS scheme because of its higher accuracy.47
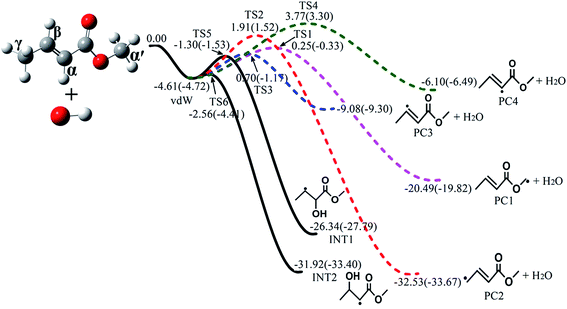 |
| | Fig. 1 Schematic potential energy surfaces for four H-abstraction reactions (colored dashed lines) and two OH-addition reactions (black solid lines) of MC + OH calculated at the QCISD(T)/CBS//M062x/6-311++G(d,p) level (outside brackets) and CBS-QB3 level (in brackets). Only the major pathways are shown. All energies are relative to that of MC + OH, with units of kcal mol−1. | |
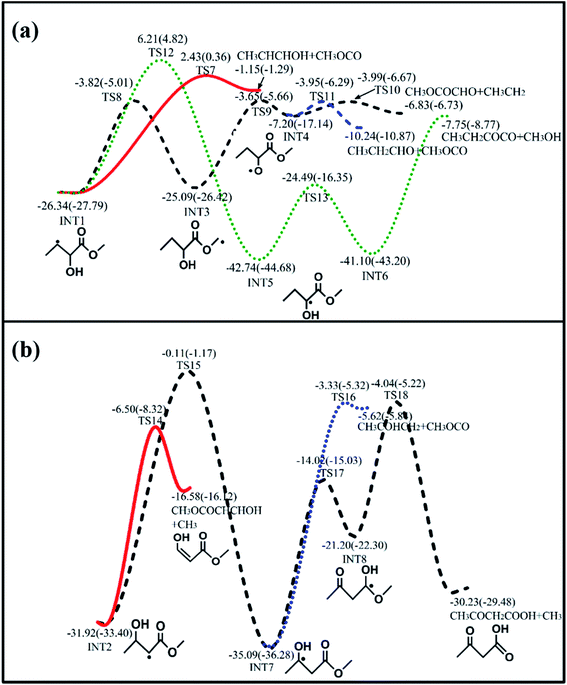 |
| | Fig. 2 Main consumption channels of (a) INT1 and (b) INT2 calculated at the QCISD(T)/CBS//M062x/6-311++G(d,p) level (outside brackets) and CBS-QB3 level (in brackets). All energies are relative to that of MC + OH, with units of kcal mol−1. | |
Table 1 The calculated values of ΔHo298,f (unit: kcal mol−1) for the main species in the QCISD(T)/CBS scheme and the CBS-QB3 scheme
| Species |
QCISD(T)/CBS scheme |
CBS-QB3 scheme |
| INT1 |
−99.79 |
−101.05 |
| INT2 |
−105.78 |
−107.16 |
| PC1 |
−35.03 |
−34.01 |
| PC2 |
−47.17 |
−48.20 |
| PC3 |
−23.32 |
−23.51 |
| PC4 |
−20.30 |
−20.65 |
3.1 Potential energy surfaces
3.1.1 H-abstraction reactions of MC + OH.
As shown in Fig. 1, H-abstraction reactions from MC by OH attack can occur at four sites, i.e., the two vinylic sites (α and β), the allylic site (γ), and the ester methylic site (α′), forming H2O and four C5H7O2 radicals.| | | MC + OH → [MC⋯OH] → CH3CHCHCOOCH2· (PC1) + H2O | (R1) |
| | | → ·CH2CHCHCOOCH3 (PC2) + H2O | (R2) |
| | | → CH3C·CHCOOCH3 (PC3) + H2O | (R3) |
| | | → CH3CHC·COOCH3 (PC4) + H2O | (R4) |
Among the various C–H bonds, the BDE of the bond at the γ site is the lowest; it was found to be 87.7 kcal mol−1via calculations by Oyeyemi et al. using the MR averaged coupled-pair functional (MRACPF2) method.16 This implies that the (R2) reaction which produces an allylic radical will occur much more readily. In addition, according to previous studies of unsaturated esters,14,48 H-abstraction reactions at the allylic site are faster than those at other sites, revealing that the allyl radical should be the most stable fragment during the H-abstraction process; this is consistent with the ab initio results in our calculations. From Fig. 1, it can be seen that the stability of the products follows the sequence of PC2 > PC1 > PC3 > PC4. If the linear Evans–Polanyi principle is followed,48,49i.e., the more stable product is formed via the lower transition state, the order of the transition state energies would be TS2 < TS1 < TS3 < TS4. However, the present calculations show that the energy of TS2 (1.91 kcal mol−1) is even higher than those of TS1 (0.25 kcal mol−1) and TS3 (0.70 kcal mol−1). This can be mainly attributed to the effects of hydrogen bonding in the structures of TS1 and TS3.50
Fig. 3 plots the optimized geometries of TS1 to TS4 at the M062x/6-311++G(d,p) level. Additionally, the optimized geometries of TS5 to TS18 are presented in Fig. S5 in the ESI.† For TS1, the distance between the oxygen atom of the ester carbonyl and the hydrogen atom of OH is about 2.175 Å; at this distance, the hydrogen bond interaction is indeed non-negligible. Due to the seven-member ring structure formed via hydrogen bonding, TS1 is very stable, resulting in a lower energy of TS1 as well as an increased branching ratio of the (R1) reaction. This situation is similar to that of TS3.
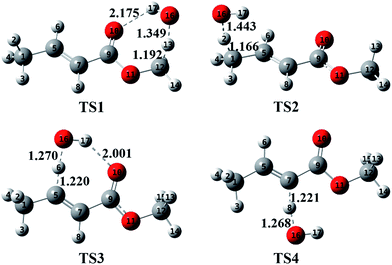 |
| | Fig. 3 Optimized geometries of the transition states (TS1–TS4) calculated at the M062x/6-311++G(d,p) level. The unit of the bond lengths is angstrom. | |
3.1.2 OH-addition reactions of MC + OH.
In addition to H-abstraction reactions, OH-addition is also an important reaction in the MC + OH mechanism. As can be seen from Fig. 1, the OH radical can be added to the α and β carbons of the MC molecule, producing two C5H9O3 radicals, i.e., INT1 and INT2. Note that the transition states of these two OH-addition reactions have relatively low energies of −1.30 and −2.56 kcal mol−1 for TS5 and TS6, respectively. Here, INT2 is more stable than INT1 because of the resonance stabilization arising from the conjugation effect of C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O and the unpaired electron at the adjacent carbon.51
O and the unpaired electron at the adjacent carbon.51
The two intermediate radicals, INT1 and INT2, can further undergo isomerization reactions via H-shifts and β-scissions of C–C or C–H bonds. The energetically favorable reactions are displayed in Fig. 2 ((R5)–(R8) for INT1 and (R9)–(R11) for INT2), with more detailed pathways provided in Fig. S2 and S3 in the ESI.†
| | | MC + OH → [MC⋯OH] → INT1 → CH3CHCHOH + CH3OCO | (R5) |
| | | → INT1 → INT3 → INT4 → CH3OCOCHO + CH3CH2 | (R6) |
| | | → INT1 → INT3 → INT4 → CH3CH2CHO + CH3OCO | (R7) |
| | | → INT1 → INT5 → INT6 → CH3CH2COCO + CH3OH | (R8) |
| | | → INT2 → CH3OCOCHCHOH + CH3 | (R9) |
| | | → INT2 → INT7 → CH3COHCH2 + CH3OCO | (R10) |
| | | → INT2 → INT7 → INT8 → CH3COCH2COOH + CH3 | (R11) |
The four major reaction sequences of INT1 ((R5)–(R8)) are depicted in Fig. 2(a). The first reaction (R5) is β-scission of the C–C bond to produce CH3CHCHOH and CH3OCO, with a barrier height of 28.77 kcal mol−1 (TS7). In the second and third sequences ((R6) and (R7)), INT1 first isomerizes to other adducts (INT3) via intramolecular H-shifts followed by β-scissions of the C–C bonds. These two reaction sequences occur with relatively low barriers compared with other sequences. The fourth reaction sequence (R8) is similar to (R6) and (R7), where fragmented products are formed via β-scissions of C–C bonds after two successive isomerization steps. This reaction sequence features the highest barrier (TS12) in the first isomerization step. It is interesting to note that the reaction of INT6 to generate separate products occurs via barrierless β-scission of the C–O bond accompanied by an intramolecular H-shift. Similar reaction pathways were also observed for dimethyl ether.52 The MEP scanned along the C–O reaction coordinate is shown in Fig. S6 in the ESI.†
For the subsequent consumption of INT2, three major reaction sequences ((R9)–(R11)) are shown in Fig. 2(b). The most energetically favored reaction is direct unimolecular β-C–C scission to produce CH3OCOCHCHOH and CH3(R9); this reaction occurs via a barrier (TS14) that is 25.42 kcal mol−1 above that of INT2. In the other two consumption pathways ((R10) and (R11)), INT2 first undergoes isomerization reactions via intramolecular H-shifts to produce other adducts (INT7), followed by β-scissions of the C–C bonds to yield CH3COHCH2 + CH3OCO (R10) and CH3COCH2COOH + CH3(R11), respectively. The reaction to produce INT7 requires a higher overall barrier of 31.81 kcal mol−1 in comparison to INT2; it is expected that these two sequences are less competitive compared to the (R9) reaction.
3.2 Rate coefficients of MC + OH
In order to further understand the contributions of the different channels, the rate coefficients were computed for the main reactions on the PESs of MC + OH, including H-abstraction, OH-addition, and the subsequent isomerization and β-scission reactions of key adducts. The calculated rate coefficients were fitted in extended Arrhenius expressions, as shown in Table 2, with the temperature range of 500–1800 K and the pressure range of 0.001–100 atm.
Table 2 Extended Arrhenius parameters for the rate coefficients of the dominant channels of MC + OH with N2 as a bath gasa (T = 300 to 1800 K, P = 0.001 to 100 atm)
| Reaction |
P (atm) |
A
1
|
n
1
|
E
1
|
A
2
|
n
2
|
E
2
|
The units of A and E are cm3 per molecule per s and cal mol−1, respectively. Rate coefficients were fitted in the extended Arrhenius expression k(T) = A1Tn1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−E1/RT) + A2Tn2 exp(−E1/RT) + A2Tn2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−E2/RT).
The unit of pressure is atm.
The overall rate coefficient was calculated at 1 atm. exp(−E2/RT).
The unit of pressure is atm.
The overall rate coefficient was calculated at 1 atm.
|
| Total |
1b |
2.50 × 10−11 |
0.03 |
186 |
1.66 × 10−14 |
0.91 |
−1706 |
| MC + OH → PC1 + H2O (k1) |
—c |
2.29 × 10−4 |
−2.02 |
10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 204 204 |
7.31 × 10−13 |
0.10 |
819 |
| MC + OH → PC2 + H2O (k2) |
—c |
1.83 × 10−2 |
−2.39 |
10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 360 360 |
1.27 × 10−9 |
−0.57 |
2858 |
| MC + OH → PC3 + H2O (k3) |
—c |
1.17 × 10−6 |
−1.87 |
9013 |
1.00 × 10−14 |
0.16 |
−33 |
| MC + OH → PC4 + H2O (k4) |
—c |
7.98 × 10−4 |
−2.48 |
12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 377 377 |
1.52 × 10−11 |
−0.55 |
3848 |
| MC + OH → INT1 (k5−1) |
0.001 |
1.26 × 1053 |
−21.67 |
18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 020 020 |
8.18 × 1041 |
−18.34 |
12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 925 925 |
| 0.01 |
4.44 × 1048 |
−19.75 |
18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 503 503 |
9.18 × 1035 |
−17.12 |
7504 |
| 0.1 |
2.98 × 1042 |
−17.42 |
18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 588 588 |
6.21 × 1022 |
−16.80 |
−21![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 106 106 |
| 1 |
2.82 × 1048 |
−18.68 |
25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 983 983 |
1.31 × 1023 |
−11.66 |
9753 |
| 10 |
6.17 × 1042 |
−16.54 |
27![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 642 642 |
3.97 × 1017 |
−9.68 |
9259 |
| 100 |
2.47 × 1031 |
−12.83 |
25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 639 639 |
1.05 × 107 |
−6.23 |
6312 |
| MC + OH → INT2 (k9−1) |
0.001 |
2.38 × 1053 |
−22.03 |
15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 569 569 |
2.68 × 1042 |
−18.53 |
13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 260 260 |
| 0.01 |
8.89 × 1046 |
−19.35 |
16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 402 402 |
8.92 × 1028 |
−19.17 |
−20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 902 902 |
| 0.1 |
6.69 × 1045 |
−18.45 |
19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 501 501 |
7.57 × 1028 |
−14.58 |
5140 |
| 1 |
5.93 × 1036 |
−15.24 |
19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 070 070 |
3.05 × 1015 |
−9.78 |
3532 |
| 10 |
2.19 × 1039 |
−15.48 |
25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 967 967 |
3.90 × 1015 |
−9.09 |
7601 |
| 100 |
6.64 × 1026 |
−11.49 |
23![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 191 191 |
3.03 × 103 |
−5.18 |
4027 |
| MC + OH → CH3CHCHOH + CH3OCO (k5) |
0.001 |
2.88 × 105 |
−5.06 |
18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 465 465 |
7.81 × 10−5 |
−2.47 |
6952 |
| 0.01 |
5.72 × 1020 |
−10.26 |
16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 508 508 |
3.65 × 10 |
−3.65 |
12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 167 167 |
| 0.1 |
8.53 × 1017 |
−8.96 |
18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 874 874 |
3.02 × 109 |
−6.02 |
22![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 911 911 |
| 1 |
7.14 × 1014 |
−7.75 |
21![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 031 031 |
7.48 × 10118 |
−35.52 |
136![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 927 927 |
| 10 |
2.74 × 1027 |
−11.24 |
32![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 058 058 |
2.55 × 10−8 |
−1.27 |
12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 075 075 |
| 100 |
2.48 × 1020 |
−8.95 |
33![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 326 326 |
3.08 × 10−7 |
−1.79 |
13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 378 378 |
| MC + OH → CH3 + CH3OCOCHCHOH (k9) |
0.001 |
5.32 × 1011 |
−7.76 |
7561 |
1.65 × 10−3 |
−2.82 |
6446 |
| 0.01 |
2.44 × 1020 |
−10.21 |
13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 061 061 |
5.51 × 10−2 |
−3.24 |
7916 |
| 0.1 |
2.81 × 1013 |
−7.65 |
14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 194 194 |
8.56 × 1016 |
−8.06 |
29![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 995 995 |
| 1 |
4.90 × 1022 |
−10.15 |
22![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 859 859 |
2.08 × 10−14 |
0.36 |
4016 |
| 10 |
6.93 × 1019 |
−9.03 |
26![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 398 398 |
6.24 × 10−6 |
−2.39 |
8290 |
| 100 |
3.72 × 109 |
−5.91 |
25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 474 474 |
2.88 × 10−18 |
1.38 |
5520 |
In this work, the overall rate coefficients at 300 K and 1 atm based on the CBS-QB3 and QCISD(T)/CBS methods are about 3.14 × 10−11 and 3.58 × 10−12 cm3 per molecule per s, respectively, which can satisfactorily reproduce the value reported by Teruel et al.21 as (4.65 ± 0.65) × 10−11 cm3 per molecule per s. Due to the lack of reference experimental measurements as well as theoretical calculations of MC + OH reactions under combustion conditions, the present calculated overall rate constants were then compared with the correlative original rate coefficients used in the MC combustion model from Gaïl et al.,12 as shown in Fig. 4. It can be seen that the overall rate coefficients of MC + OH at the CBS-QB3 and QCISD(T)/CBS levels demonstrate obvious temperature-dependence. However, there is a large discrepancy between the calculated results and the estimated values from Gaïl's model at 500 to 1800 K and atmospheric pressure. The rate constants in Gaïl's model are mainly estimated from analogous reactions of methyl butanoate; the large discrepancy indicates that simply using rate constants from methyl butanoate introduces large uncertainties. Additionally, the effects of low frequency rotations were investigated by comparing the rate coefficients with or without hindered rotor treatment. It was found that the influence of the internal rotations on the rate coefficients is greatly enhanced as the temperature increases, which is in good agreement with a previous report.48
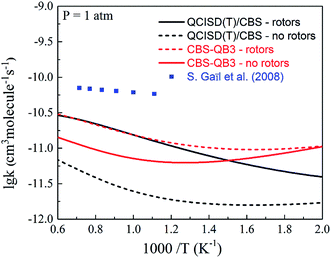 |
| | Fig. 4 The overall rate coefficients for the reactions of MC + OH at 1 atm. The solid lines represent the present calculations, and the dashed lines represent the values from the Gaïl model.12 | |
Fig. 5 compares the rate coefficients of the four H-abstraction reactions ((R1)–(R4)) together with available data from the model of Gaïl.12 Note that Gaïl et al. used completely identical rate coefficients for H-abstraction reactions at different sites. The rate coefficient of (R2) based on the CBS-QB3 scheme is also shown in the plot. From this plot, the (R2) reaction, in which an H-atom is abstracted from the allylic site, is the dominant pathway over the investigated range. However, according to the PES of MC + OH, the competition of (R2) is not favorable when considering the heights of the energy barriers. This phenomenon can be mainly ascribed to the large entropic effect of the transition state (TS2) for this reaction, especially at higher temperatures. In contrast, due to the smaller entropies of TS1 and TS3, the (R1) and (R3) reactions are much less competitive despite their lower barriers.53 At very low temperatures, where the enthalpic effects become more significant, the rate coefficients may follow the order of the barrier heights of the corresponding reactions.54
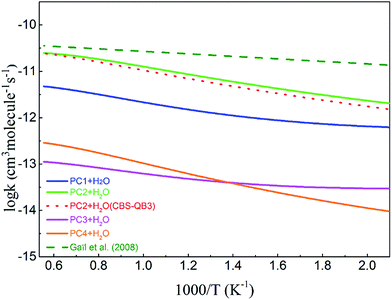 |
| | Fig. 5 The rate coefficients for the H-abstraction reactions of MC + OH. The solid lines represent the present calculations using the QCISD(T)/CBS//M062x/6-311++G(d,p) energy scheme, and the dotted line represents the result for the PC2 + H2O channel using the CBS-QBS energy scheme. The values from the Gaïl model12 are denoted with a dashed line. | |
The 3D plots for the two addition reactions of MC + OH to produce INT1 and INT2 as a function of pressure and temperature are proposed in Fig. 6. At higher temperatures, the pressure effect becomes evident for these two reactions, and the formation of INT1 and INT2 is more favorable with increasing pressure. Moreover, equilibrium is rapidly established between MC + OH and INT1 when the temperature is high, e.g., 1000 K at 1 atm. The PAPR code used in the present work technically adopts a “well merging” treatment for species that are equilibrated with each other.55,56
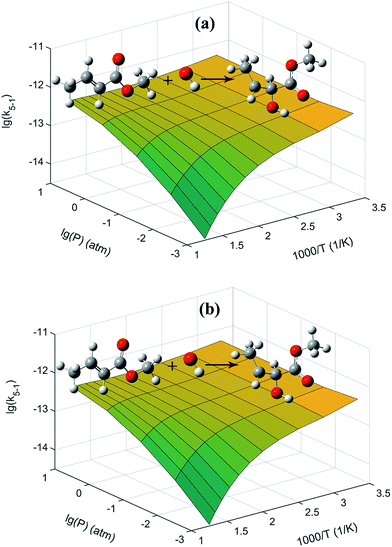 |
| | Fig. 6 Present rate coefficients as a function of pressure and temperature for the reactions of (a) MC + OH → INT1 and (b) MC + OH → INT2, respectively. The unit of the rate coefficients is cm3 per molecule per s. | |
3.3 Branching ratios of the reactions of MC + OH
Branching ratios, which play a crucial role in predicting product distributions, were also calculated in this paper. Fig. 7 illustrates the branching ratios for eight representative channels, including four H-abstraction reactions, two OH-addition reactions and two β-scissions of the initial adducts at 0.001 and 100 atm. The remaining isomerization and β-scission reactions, which have very minor branching ratios (1% or less), are not discussed here.
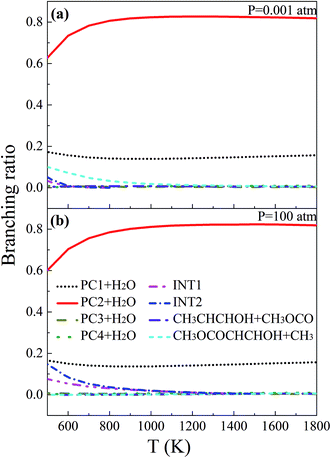 |
| | Fig. 7 Temperature-dependent branching ratios of the main channels of MC + OH at 0.001 and 100 atm, respectively. | |
At 0.001 atm, the H-abstraction reaction (R2) to yield PC2 + H2O is the uppermost channel over the whole temperature range. With increasing temperature, the branching ratio of 63% at 500 K improves slightly to 82% at 900 K and then stabilizes. Another H-abstraction reaction (R1) also makes a significant contribution to the MC + OH reaction, with a branching ratio of about 15%. The (R9) reaction, which produces CH3OCOCHCHOH and CH3, has a branching ratio of 5% to 10% at temperatures below 700 K. In addition, the OH-addition reactions to form INT1 and INT2 make only minor contributions when the temperature is below 600 K.
The situation is quite similar at 100 atm, with the H-abstraction reactions of (R1) and (R2) being the two most favored channels. A comparison of Fig. 7(a) and (b) demonstrates that the rate coefficients of the H-abstraction reactions of MC + OH basically present no significant pressure dependence. As the pressure increases, the contributions of these two MC + OH channels to yield INT1 and INT2 are enhanced over a low broader temperature range of 500–1100 K. However, when the temperature is above 1100 K, these two OH-addition channels make only slight contributions to the MC + OH reaction, which is consistent with the case at 0.001 atm. Furthermore, the contribution of reaction (R9) to produce CH3OCOCHCHOH and CH3 becomes unfavorable at 100 atm, which is different from the case at 0.001 atm. Fig. 7 clearly shows that the H-abstraction reactions greatly dominate the OH-addition reactions under the investigated conditions.
3.4 Validations of the calculated rate coefficients for the kinetic model
In their previous study, Gaïl et al.12 reported a new reaction mechanism for MC combustion on the basis of the jet-stirred reactor (JSR) experiment and the previously described kinetic mechanisms. Notably, the two equivalent, conjugated radicals therein, named MB2D4J (·CH2CHCHCOOCH3) and C5H7O2 (CH2CHCH·COOCH3), which are equivalent to the PC2 radical in our work, were considered as different species with different thermodynamic parameters and standard enthalpies of formation in their kinetic mechanisms. This implies that the overall reaction, including the consumption of fuel and the formation, distribution and mole fractions of the combustion products, would be severely affected.
In order to further validate our calculations, we amended the original Gaïl model using our calculated results to simulate the JSR experiment. To be more specific, we expurgated similar reactions involving the two conjugated radicals (MB2D4J and C5H7O2) and retained only one of them (MB2D4J, named PC2 in our calculations). Additionally, we updated the thermodynamic parameters for PC1 and PC2 and revised the rate constants for H-abstraction by OH attack on the basis of our calculations. The updated rate constants of H-abstraction by OH and the detailed thermodynamic data of MB2D4J and MB2DMJ are listed in Table S5 in the ESI.† The unabridged model, associated with the kinetic and thermochemical files, is also provided in the ESI.† Simulations for the mole fractions of MC and the relevant combustion products of JSR oxidation were performed using the Perfectly Stirred Reactor module in Chemkin-Pro software.57
Fig. 8 shows the fuel conversion of MC combustion with the experimental data from Gaïl et al.12 as well as the simulation results from the Gaïl model12 and the present revised model. Furthermore, comparisons of the JSR experimental data, the simulated results of the Gaïl model and those of the revised model for the major products are presented in Fig. 9–11; also, comparisons of the minor products are presented in Fig. S7 and S8 in the ESI.† It is apparent that the revised model could satisfactorily simulate the experimental data. Furthermore, the results simulated by the revised model show obvious improvement in predicting the fuel consumption under fuel-lean conditions in comparison to the results simulated by the Gaïl model.12 In order to explore the difference between these two models, the detailed reaction pathway network for the consumption of MC at a 50% fuel conversion ratio is shown in Fig. 12 under the oxidation conditions in JSR, with ϕ = 0.375, P = 1 atm and T = 1150 K. Based on the reaction pathway analysis, the H-abstraction reactions by OH attack to form PC1 and PC2 make contributions of 3% and 18% to the consumption of MC, respectively. This phenomenon can be attributed to the fact that the BDEs of the C–H bond at the allylic site are much lower than those at the ester methylic site.16 Furthermore, the reaction pathway analysis shows that the consumption of MC is linked to the H-abstraction reactions, the H-addition reactions and the C–C bond dissociation reaction (MC = BAOJ2D + CH3). Among these reactions, the bond dissociation reaction to yield BAOJ2D radical presents the highest contribution (∼34%) to the MC consumption, followed by the H-abstraction and H-addition reactions by H-atom, with contributions of 22% and 8%, respectively. On the other hand, the H-abstraction reactions via CH3 radical and the H-addition reactions by O-atom further contribute around 6% and 8%, respectively, to the consumption of MC on the basis of the reaction pathway analysis.
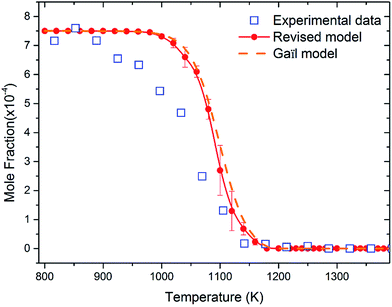 |
| | Fig. 8 Fuel conversion from experimental measurements (open symbols), the modeling simulation by Gaïl et al.12 (dashed line) and the present revised model (symbols with solid lines). The experiment was conducted in a JSR with 750 ppm MC, ϕ = 0.375, P = 1 atm, τ = 0.07 s. | |
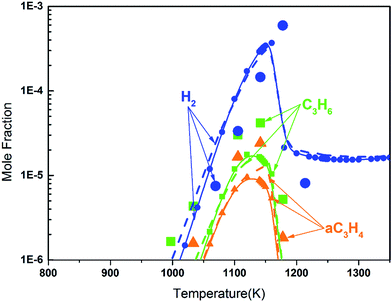 |
| | Fig. 9 Mole fraction profiles of C3H6, H2 and C3H4 for the JSR results from Gaïl et al.12 (symbols), with simulated results of the Gaïl model12 (dashed lines) and of the revised model (symbols with solid lines). The experiment was conducted in a JSR with 750 ppm MC, ϕ = 0.375, P = 1 atm, τ = 0.07 s. | |
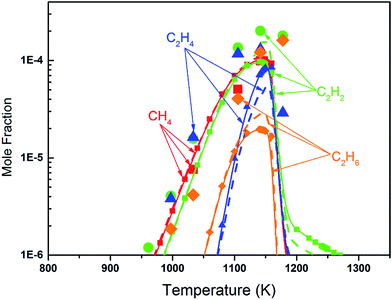 |
| | Fig. 10 Mole fraction profiles of CH4, C2H2, C2H4 and C2H6 for the JSR results from Gaïl et al.12 (symbols), with simulated results of the Gaïl model12 (dashed lines) and of the revised model (symbols with solid lines). The experiment was conducted in a JSR with 750 ppm of MC, ϕ = 0.375, P = 1 atm, τ = 0.07 s. | |
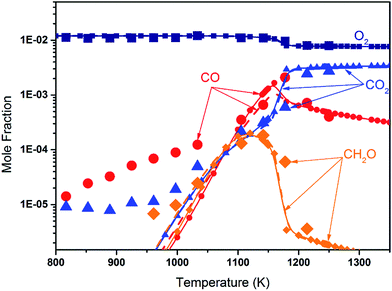 |
| | Fig. 11 Mole fraction profiles of O2, CO, CO2 and CH2O for the JSR results from Gaïl et al.12 (symbols), with simulated results of the Gaïl model12 (dashed lines) and of the revised model (symbols with solid lines). The experiment was conducted in a JSR with 750 ppm MC, ϕ = 0.375, P = 1 atm, τ = 0.07 s. | |
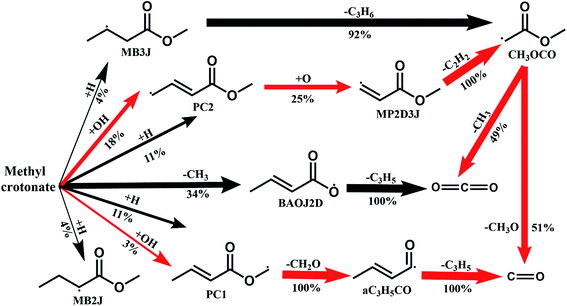 |
| | Fig. 12 The main reaction pathway network of MC under the oxidation conditions in a JSR with ϕ = 0.375, P = 1 atm and T = 1150 K. The thickness of each arrow indicates the reaction flux of the corresponding pathway. The percentage number represents the reaction flux of the pathway divided by the total reaction flux of MC consumption. | |
4 Conclusions
The reaction kinetics of MC + OH has been studied via ab initio quantum chemistry calculations and RRKM/master equation analysis. The H-abstraction reaction at the allylic site (R2) is the most dominant channel over the investigated temperature and pressure region, with a rate constant in good agreement with previously estimated values. It is noteworthy that the H-abstraction reaction at the ester methyl group (R1) is also of great significance, with a branching ratio of about 15%. We deduce that the contribution of (R1) tends to increase at lower temperatures due to its relatively lower chemical barrier. For OH-addition reactions, their branching ratios increase as the pressure increases over a low broader temperature range of 500–1100 K, indicating that these reactions are significant and must be included in the combustion mechanism of MC. The rate coefficients of the major reactions of MC + OH were fitted in modified Arrhenius expressions, facilitating the application of kinetic data in the modeling simulations. Additionally, the calculated rate constants were validated for the revised combustion kinetic model and showed excellent agreement with experimental data. To conclude, the present calculations can not only provide a thorough understanding of the detailed kinetics of the MC + OH reaction, but can also be used as a reliable reference for similar reaction systems.
Conflicts of interest
The authors declare no competing financial interest.
Acknowledgements
This work was supported by the National Key Scientific Instruments and Equipment Development Program of China (2012YQ22011305) and the Natural Science Foundation of China (51676176, 21373193 and 51606122).
References
- K. Kohse-Höinghaus, P. Osswald, T. A. Cool, T. Kasper, N. Hansen, F. Qi, C. K. Westbrook and P. R. Westmoreland, Angew. Chem., Int. Ed., 2010, 49, 3572–3597 CrossRef PubMed.
- E. Buyukkaya, Fuel, 2010, 89, 3099–3105 CrossRef CAS.
- F. Ma and M. A. Hanna, Bioresour. Technol., 1999, 70, 1–15 CrossRef CAS.
- L. Meher, D. Vidyasagar and S. Naik, Renewable Sustainable Energy Rev., 2006, 10, 248–268 CrossRef CAS.
- A. Demirbas, Prog. Energy Combust. Sci., 2007, 33, 1–18 CrossRef CAS.
- C. K. Westbrook, Annu. Rev. Phys. Chem., 2013, 64, 201–219 CrossRef CAS PubMed.
- R. Grana, A. Frassoldati, A. Cuoci, T. Faravelli and E. Ranzi, Energy, 2012, 43, 124–139 CrossRef CAS.
- S. Dooley, H. J. Curran and J. M. Simmie, Combust. Flame, 2008, 153, 2–32 CrossRef CAS.
- S. Gaïl, M. J. Thomson, S. M. Sarathy, S. A. Syed, P. Dagaut, P. Diévart, A. J. Marchese and F. L. Dryer, Proc. Combust. Inst., 2007, 31, 305–311 CrossRef.
- A. Farooq, W. Ren, K. Y. Lam, D. F. Davidson, R. K. Hanson and C. K. Westbrook, Combust. Flame, 2012, 159, 3235–3241 CrossRef CAS.
- K. Kumar and C. J. Sung, Combust. Flame, 2016, 171, 1–14 CrossRef CAS.
- S. Gaïl, S. M. Sarathy, M. J. Thomson, P. Diévart and P. Dagaut, Combust. Flame, 2008, 155, 635–650 CrossRef.
- S. M. Sarathy, S. Gaïl, S. A. Syed, M. J. Thomson and P. Dagaut, Proc. Combust. Inst., 2007, 31, 1015–1022 CrossRef.
- B. Yang, C. K. Westbrook, T. A. Cool, N. Hansen and K. Kohse-Höinghaus, Proc. Combust. Inst., 2013, 34, 443–451 CrossRef CAS.
- Y. L. Wang, Q. Feng, F. N. Egolfopoulos and T. T. Tsotsis, Combust. Flame, 2011, 158, 1507–1519 CrossRef CAS.
- V. B. Oyeyemi, J. A. Keith and E. A. Carter, J. Phys. Chem. A, 2014, 118, 7392–7403 CrossRef CAS PubMed.
- H. K. Ng, S. Gan, J. H. Ng and K. M. Pang, Fuel, 2013, 104, 620–634 CrossRef CAS.
- H. Bennadji, L. Coniglio, F. Billaud, R. Bounaceur, V. Warth, P. A. Glaude and F. Battin-Leclerc, Int. J. Chem. Kinet., 2011, 43, 204–218 CrossRef CAS.
- Q. D. Wang, RSC Adv., 2014, 4, 4564–4585 RSC.
- J. Zádor, C. A. Taatjes and R. X. Fernandes, Prog. Energy Combust. Sci., 2011, 37, 371–421 CrossRef.
- M. A. Teruel, J. Benitez-Villalba, N. Caballero and M. B. Blanco, J. Phys. Chem. A, 2012, 116, 6127–6133 CrossRef CAS PubMed.
- J. A. Montgomery, M. J. Frisch, J. W. Ochterski and G. A. Petersson, J. Chem. Phys., 1999, 110, 2822–2827 CrossRef CAS.
- K. Raghavachari, G. W. Trucks, J. A. Pople and M. Head-Gordon, Chem. Phys. Lett., 1989, 157, 479–483 CrossRef CAS.
- J. A. Pople, M. H. Gordon and K. Raghavachari, J. Chem. Phys., 1987, 87, 5968–5975 CrossRef CAS.
- Y. Zhao and D. G. Truhlar, J. Chem. Theory Comput., 2008, 4, 1849–1868 CrossRef CAS PubMed.
- W. J. Hehre, J. Chem. Phys., 1972, 56, 2257–2261 CrossRef CAS.
- R. Krishnan, J. S. Binkley, R. Seeger and J. A. Pople, J. Chem. Phys., 1980, 72, 650–654 CrossRef CAS.
- I. M. Alecu, J. Zheng, Y. Zhao and D. G. Truhlar, J. Chem. Theory Comput., 2010, 6, 2872–2887 CrossRef CAS PubMed.
- J. Zádor, A. W. Jasper and J. A. Miller, Phys. Chem. Chem. Phys., 2009, 11, 11040–11053 RSC.
- P. Zhang, S. J. Klippenstein and C. K. Law, J. Phys. Chem. A, 2013, 117, 1890–1906 CrossRef CAS PubMed.
- T. H. Dunning, J. Chem. Phys., 1989, 90, 1007–1023 CrossRef CAS.
- J. A. Miller and S. J. Klippenstein, J. Phys. Chem. A, 2003, 107, 7783–7799 CrossRef CAS.
-
M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Gaussian, Inc., Wallingford CT, 2009 Search PubMed.
- Y. Georgievskii, J. A. Miller, M. P. Burke and S. J. Klippenstein, J. Phys. Chem. A, 2013, 117, 12146–12154 CrossRef CAS PubMed.
- J. Li, A. Kazakov and F. L. Dryer, J. Phys. Chem. A, 2004, 108, 7671–7680 CrossRef CAS.
- C. Eckart, Phys. Rev., 1930, 35, 1303–1309 CrossRef CAS.
- Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2007, 120, 215–241 CrossRef.
- J. Daranlot, A. Bergeat, F. Caralp, P. Caubet, M. Costes, W. Forst, J. C. Loison and K. M. Hickson, ChemPhysChem, 2010, 11, 4002–4010 CrossRef CAS PubMed.
- W. Forst, Phys. Chem. Chem. Phys., 1999, 1, 1283–1291 RSC.
- T. H. Chung, L. L. Lee and K. E. Starling, Ind. Eng. Chem. Fundam., 1984, 23, 8–13 CAS.
- T. H. Chung, M. Ajlan, L. L. Lee and K. E. Starling, Ind. Eng. Chem. Res., 1988, 27, 671–679 CrossRef CAS.
- K. G. Joback and R. C. Reid, Chem. Eng. Commun., 2007, 57, 233–243 CrossRef.
- L. D. Zhang, Q. Chen and P. Zhang, Proc. Combust. Inst., 2015, 35, 481–489 CrossRef CAS.
- M. W. Chase, J. Phys. Chem., 1996, 25, 551–603 CAS.
- E. Schjånberg, Z. Phys. Chem., 1936, 175, 289–342 Search PubMed.
-
J. D. Cox, D. D. Wagman and V. A. Medvedev, CODATA Key Values for Thermodynamics, Hemisphere Publishing Corp., NY, USA, 1989 Search PubMed.
- S. J. Klippenstein, V. S. Pande and D. G. Truhlar, J. Am. Chem. Soc., 2014, 136, 528–546 CrossRef CAS PubMed.
- Q. D. Wang and W. Zhang, RSC Adv., 2015, 5, 68314–68325 RSC.
- L. D. Zhang and P. Zhang, Phys. Chem. Chem. Phys., 2015, 17, 200–208 RSC.
- L. L. Ye, L. Zhao, L. D. Zhang and F. Qi, J. Phys. Chem. A, 2011, 116, 55–63 CrossRef PubMed.
- L. Zhao, L. L. Ye, F. Zhang and L. D. Zhang, J. Phys. Chem. A, 2012, 116, 9238–9244 CrossRef CAS PubMed.
- L. L. Xing, X. Y. Zhang, Z. D. Wang, S. Li and L. D. Zhang, Chin. J. Chem. Phys., 2015, 28, 563–572 CrossRef CAS.
- Y. Sumiya, Y. Nagahata, T. Komatsuzaki, T. Taketsugu and S. Maeda, J. Phys. Chem. A, 2015, 119, 11641–11649 CrossRef CAS PubMed.
- E. E. Greenwald, S. W. North, Y. Georgievskii and S. J. Klippenstein, J. Phys. Chem. A, 2005, 109, 6031–6044 CrossRef CAS PubMed.
- J. A. Miller and S. J. Klippenstein, J. Phys. Chem. A, 2011, 105, 7254–7266 CrossRef.
- J. A. Miller and S. J. Klippenstein, Phys. Chem. Chem. Phys., 2013, 15, 4744–4753 RSC.
-
Chemkin-Pro 15092, Reaction Design, San Diego, 2009 Search PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c7se00426e |
| ‡ These authors contributed equally to this work. |
|
| This journal is © The Royal Society of Chemistry 2018 |
Click here to see how this site uses Cookies. View our privacy policy here.  *a
*a
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−10
exp(−10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 204/RT) + 7.31 × 10−13T0.1
204/RT) + 7.31 × 10−13T0.1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−819/RT), k2 (MC + OH → PC2 + H2O) = 1.83 × 10−2T−2.39
exp(−819/RT), k2 (MC + OH → PC2 + H2O) = 1.83 × 10−2T−2.39![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−10
exp(−10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 360/RT) + 1.27 × 10−9T−0.57
360/RT) + 1.27 × 10−9T−0.57![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−2858/RT). The sub-mechanisms of MC + OH and its primary radicals were validated using a previously described combustion model; the updated model well reproduced the previous experimental results. The present rate coefficients provide valuable kinetic data to improve our understanding of the combustion mechanism of MC and can be used as a reliable reference for further investigation of practical fuels.
exp(−2858/RT). The sub-mechanisms of MC + OH and its primary radicals were validated using a previously described combustion model; the updated model well reproduced the previous experimental results. The present rate coefficients provide valuable kinetic data to improve our understanding of the combustion mechanism of MC and can be used as a reliable reference for further investigation of practical fuels.![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C double bonds in its structure, proceeded via initial formation of a weak van der Waals (vdW) complex through hydrogen bonding at low temperature. The transition state for the barrierless reaction of MC + OH to the vdW complex is fairly loose, and a simplified phase space theory (PST)39 was adopted in the rate constant calculations. In this work, the long-range interaction potential between the reactants and the vdW complex was approximated by a simple isotropic interaction V(R) = −C6/R6, wherein R represents the distance between two fragments and C6 was estimated from the equation C6 = α1α2E1E2/(E1 + E2). In the C6 equation, αi and Ei (i = 1,2) are the polarizability and ionization energy for each fragment,30 respectively; these were obtained from the M062x/6-311++G(d,p) calculations. Notably, in this paper, C6 was estimated to be 5.21 × 105 cm−1 Å6 for MC + OH.
C double bonds in its structure, proceeded via initial formation of a weak van der Waals (vdW) complex through hydrogen bonding at low temperature. The transition state for the barrierless reaction of MC + OH to the vdW complex is fairly loose, and a simplified phase space theory (PST)39 was adopted in the rate constant calculations. In this work, the long-range interaction potential between the reactants and the vdW complex was approximated by a simple isotropic interaction V(R) = −C6/R6, wherein R represents the distance between two fragments and C6 was estimated from the equation C6 = α1α2E1E2/(E1 + E2). In the C6 equation, αi and Ei (i = 1,2) are the polarizability and ionization energy for each fragment,30 respectively; these were obtained from the M062x/6-311++G(d,p) calculations. Notably, in this paper, C6 was estimated to be 5.21 × 105 cm−1 Å6 for MC + OH.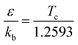
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O and the unpaired electron at the adjacent carbon.51
O and the unpaired electron at the adjacent carbon.51
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−E1/RT) + A2Tn2
exp(−E1/RT) + A2Tn2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−E2/RT).
b The unit of pressure is atm.
c The overall rate coefficient was calculated at 1 atm.
exp(−E2/RT).
b The unit of pressure is atm.
c The overall rate coefficient was calculated at 1 atm.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 204
204![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 360
360![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 377
377![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 020
020![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 925
925![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 503
503![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 588
588![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 106
106![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 983
983![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 642
642![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 639
639![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 569
569![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 260
260![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 402
402![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 902
902![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 501
501![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 070
070![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 967
967![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 191
191![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 465
465![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 508
508![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 167
167![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 874
874![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 911
911![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 031
031![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 927
927![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 058
058![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 075
075![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 326
326![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 378
378![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 061
061![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 194
194![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 995
995![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 859
859![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 398
398![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 474
474











