Embryonic brass: pseudo two electron Cu/Zn clusters

Abstract

The isoelectronic M₇ clusters [Cu₃Zn₄](Cp*)₅ (1) and {[Cu₂Zn₅](Cp*)₅}⁺ (2) are described. While 1 can be isolated only as a minor side product from the reaction of Cu(CH₃CO₂) with equimolar amounts of [Zn₂Cp*₂] with the trigonal cluster [CuZn₂](Cp*)₃ as the major product, 2 is available in acceptable yields from the reaction of [CuZn₂](Cp*)₃ with the Cp*Zn₂-transfer-reagent [Cp*Zn₂(Et₂O)₃][BAr₄^F]. The trigonal bipyramidal Cu/Zn-clusters exhibit exceptional bonding situations: with formally only one skeleton electron pair they can be regarded as highly electron deficient. However, a detailed DFT analysis reveals that the cluster bonding is supported by 3d orbital contributions of the trigonal metal base unit. The data contribute to the development of an advanced tool-box for synthesis of Hume-Rothery intermetallic (e.g. brass) inspired clusters.

---

Introduction

Ligand stabilized metal clusters [M_n](L)_m are fascinating links between molecules and bulk metals. They have attracted persistent interest since Hieber described [Co₄](CO)₁₂ ¹ in 1932 up to the discovery of very high nuclearity transition-metal carbonyl clusters such as Dahl's [Pd₁₄₅](CO)₆₀(PEt₃)₃₀ ² reported in 2000 and finally the thiolate-capped atom-precise gold clusters with the giant [Au₂₄₆](p-MDT)₈₀ ³ as a spectacular and recent example (2016).

A related break-through in main group metal clusters was Schnöckel's work on bottom-up synthesis based on metastable solutions of low valent group-13 species, and [Al₅₀]Cp*₁₂ ⁴ (2004) became an icon of this chemistry (Cp* = C₅(CH₃)₅). The cluster growth reactions are difficult to control and each case is very subtly dependent on the kinetic balance of many interlinked processes, i.e. disproportionation, agglomeration, ligand substitution and/or salt metathesis. Nevertheless, over the years a rich library of small, medium to high nuclearity clusters was successively developed.⁵ In this context we started out to investigate the related organometallic cluster chemistry of Zn and studied the activation of low valent [Zn₂Cp*₂] by oxidative cleavage of one Zn–Cp* bond to induce disproportionation of the initial intermediate [Zn₂Cp*]⁺. From the reaction mixture {[Zn₁₀]Cp*₆(CH₃)}⁺ was isolated as the very first example of a ligated oligonuclear Zn-cluster.⁶

The synthetic scenario becomes even more diverse and challenging for bimetallic clusters [M¹_aM²_b](L)_m, in particular when combining chemically distinctly different metals. A specific tool-box of suitable building blocks and reactions needs to be developed for each metal combination. For example, [Cu₄Zn₄](CN^tBu)₄Cp*₄ is reproducibly available in moderate yields from [Zn₂Cp*₂] and CpCu(CN^tBu) among other side products.⁷ Reaction steps are the reduction of Cu(I) by Zn(I) under formation of [Cp₂Zn], [Cp*CpZn] and [Cp*₂Zn] by involving Zn–Zn bond cleavage as well as Cp transfer from Cu to Zn as a side reaction. The [M¹_aM²_b] cores of such bimetallic clusters often mimic structural cut-outs from of the respective M¹/M² intermetallic solid-state phases.⁸ Thus, the M₈-core of [Cu₄Zn₄](CN^tBu)₄Cp*₄ is linked to an embryonic state of γ-brass, the classic Hume-Rothery intermetallic compound.

A rational design of the synthesis procedure to yield a specific Cu/Zn-cluster also requires knowledge of potentially preferred stability islands of “magic” compositions including the role of the capping ligands. While the electronic structures of classic transition metal carbonyl-clusters are often consistent with the Wade–Mingos rules originally developed for borane clusters, the electronic situation in metal clusters in general is more complicated and needs to be addressed by computational methods in every single case.⁹ For example, the electron deficiency of {[Zn₁₀](Cp*)₆(CH₃)}⁺ results mainly from the fact that Zn can behave flexible in participating to cluster skeletal bonding, sometimes providing one frontier orbital (like Group 11 metals) and sometimes providing three frontier orbitals (like Group 13 elements).^6,10 Following this research guidelines towards a library of oligonuclear Cu/Zn-clusters as embryonic brass species we report here on two astonishing cases. At a first glance they completely disobey the Wade–Mingos rules for deltahedral clusters. The two isoelectronic, trigonal bipyramidal M₇ clusters, namely the neutral [Cu₃Zn₄]Cp*₅ (1) and the cation {[Cu₂Zn₅]Cp*₅}⁺ (2) are teaching us an interesting lesson.

Results and discussion

Synthesis and characterization of [Cu₃Zn₄](Cp*)₅ (1)

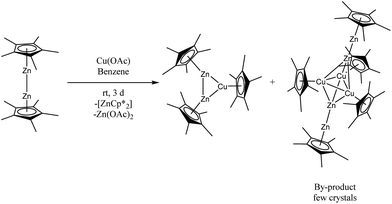
Reaction of Cu(CH₃CO₂) with equimolar amounts of [Zn₂Cp*₂] ^11–13 in benzene at room temperature for three days leads to the formation of a dark red suspension of a mixture of unsoluble Zn(CH₃CO₂)₂, the known cluster [CuZn₂](Cp*)₃ and the novel cluster [Cu₃Zn₄](Cp*)₅ (1) as soluble components (Scheme 1).

Scheme 1 Synthesis of [CuZn₂]Cp*₃ and [Cu₃Zn₄]Cp*₅ (1).

From the filtered and concentrated reaction solution, [CuZn₂](Cp*)₃ deposits as the main product in the form of yellow crystals at 8 °C in 57% isolated yield (based on Cp*). Further workup of the remaining solution gives [Cu₃Zn₄](Cp*)₅ (1) co-crystallizing together with [CuZn₂](Cp*)₃ at −30 °C in THF in form of dark red crystals. The single crystals of 1 could be isolated by manual separation from [CuZn₂](Cp*)₃ with the aid of an optical microscope in a glove box under argon atmosphere. It should be noted, that we were not successful in increasing the yield of 1 by the change of reaction parameters such as time, temperature or stoichiometric ratio of the reactants. A more rational approach by using Cp*Zn₂-transfer reagents similar to the synthesis of 2 (vide infra), is not possible in this case due to the inexistence of the required base unit [Cu₃](Cp*)₃ (no skeleton bonding electrons). The formation mechanism of 1 is yet not clear. However, redox-reactions between Zn(I) and Cu(I) must play a role. While in the formation of the main product [Zn₂Cu](Cp*)₃ from Cu(CH₃CO₂) and [Zn₂Cp*₂] no redox-chemistry but only Cp* transfer reactions are involved, formation of 1 requires the reduction of M(I) to M(0). The accompanying oxidation process is obviously the formation of Zn(CH₃CO₂)₂ from the Zn(I) source.

In situ ¹H NMR spectroscopy of the reaction mixture indicates rather clean formation of [CuZn₂](Cp*)₃ under complete consumption of [Zn₂Cp*₂] (Fig. S4†) with [Cp*₂Zn] and 1 as minor by-products. An unidentified Cp*-containing intermediate can be detected, which almost completely disappears in the course of the reaction. The mechanism involves Cp* transfer from Zn to Cu as well as disproportionation of Zn(I) to Zn(0) and Zn(II). The identity of [CuZn₂](Cp*)₃ has been confirmed by single crystal XRD measurement as well as NMR spectroscopic analysis. The data are in good agreement with the data reported in literature.¹⁴ The separated single crystals of [Cu₃Zn₄](Cp*)₅ (1) are stable under inert gas atmosphere for several months at −30 °C and are fairly soluble in non-polar solvents like n-hexane and benzene, but 1 dissolves very well in toluene, THF or fluorobenzene. However, it readily decomposes in solution at room temperature within a few hours under precipitation of metallic particles. This property limits further characterization of its reactivity.

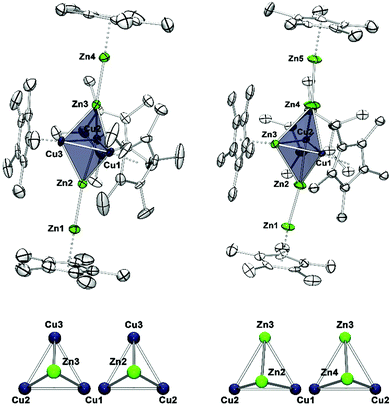
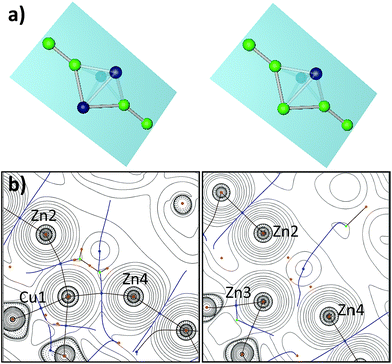
Compound 1 crystallizes in the monoclinic space group Pn with four distinct molecules in the asymmetric unit. Fig. 1 (left) shows only one of the four crystallographically distinct units for clarity. Note that Cu and Zn are not easily distinguishable by standard X-ray techniques, thus the assignment of Cu and Zn in the structure refinement has been supported by spectroscopic data (vide infra). The metal atoms are arranged in a trigonal bipyramidal fashion, with the apical positions occupied by ZnZnCp* units and the remaining equatorial triangle by CuCp* groups. Trigonal Cu₃ units are rather common in molecular clusters. However, in all species known the Cu–Cu contacts are supported by μ₂/μ₃-bridging and chelating ligands and are not bridged by other metal atoms as it is the case for 1.^15–18 The Cu–Cp*_centr. distances of 1 range from 1.827–1.828 Å and are shorter than the respective distances in the terminal Zn1–Cp*_centr. (1.901 Å) and Zn4–Cp*_centr. (1.922 Å) units.

Fig. 1 Molecular structure of [Cu₃Zn₄](Cp*)₅ (1) (left) and {[Cu₂Zn₅](Cp*)₅}⁺ (2) (right). The trigonal bipyramids are highlighted. Orthogonal view on the Cu1, Cu2, Cu3 plane showing the Cu1, Cu2, Cu3, Zn3/2 tetrahedrons of 1 (bottom, left). Orthogonal view on the Cu1, Cu2, Zn3 plane showing the Cu1, Cu2, Zn3, Zn2/4 tetrahedrons of 2 (bottom, right). Displacement ellipsoids are shown at the 50% probability level, the hydrogen atoms and disorders are omitted for clarity. Selected interatomic distances [Å] and angles [°] for 1: Zn1–Zn2 = 2.318(2), Zn3–Zn4 = 2.317(2), Cu1–Cu2 = 2.446(2), Cu2–Cu3 = 2.431(2), Cu1–Cu3 = 2.442(2), Zn1–Cp*_centr. = 1.901, Zn4–Cp*_centr. = 1.922; Cu1–Cp*_centr. = 1.828; Cu2–Cp*_centr. = 1.827; Cu3–Cp*_centr. = 1.827; Cu3–Cu1–Cu2 = 59.65(5), Cu3–Cu2–Cu1 = 60.10(6), Zn2–Zn1–Cp*_centr. = 175.74, Zn3–Zn4–Cp*_centr. = 176.00. Selected interatomic distances [Å] and angles [°] for 2: Zn1–Zn2 = 2.299(6), Zn4–Zn5 = 2.323(6), Cu1–Cu2 = 2.415(3), Cu1–Zn3 = 2.400(4), Zn3–Zn4 = 2.688(7), Cu1–Zn4 = 2.527(6), Cu2–Zn4 = 2.446(6); Cu1–Zn3–Cu2 = 60.47(9), Cu2–Cu1–Zn3 = 59.68(9), Zn3–Cu2–Cu1 = 59.85(10), Zn2–Zn1–Cp*_centr. = 174.62, Zn4–Zn5–Cp*_centr. = 172.05.

However, all values are in good agreement to literature known Zn–Cp*_centr. (1.83–2.19 Å) and Cu–Cp*_centr. (1.82–1.96 Å) distances. The Zn1–Zn2 and Zn4–Zn5 bond lengths are almost identical with 2.318(2) and 2.317(2) Å, respectively. These values are well comparable to the Zn–Zn distance in [Cp*Zn₂(THF)₃]⁺ (2.317(7) Å) (Fig. S12†). All other M–M distances are distinctively longer with a narrow range of 2.431(2) (Cu1–Zn3)–2.458(2) Å (Cu2–Zn3). These data are similar to the Cu–Cu distance in [Cu₄Zn₄](CN^tBu)₄(Cp*)₄ (2.471(4) Å)⁷ and the average Zn–Zn distance in {[Zn₃](Cp*)₃}⁺ (2.430 Å), but elongated compared to the Zn–Cu distances (2.381(1) Å) of [CuZn₂](Cp*)₃.^6,19 As a consequence, the trigonal bipyramid consists of two almost perfect [Cu₃Zn] tetrahedrons sharing one trigonal Cu₃ face. Accordingly, the angles within the Cu1–Cu2–Cu3 triangle are all very close to 60° (59.65(5) for Cu3–Cu1–Cu2 and 60.25(6)° for Cu2–Cu3–Cu1). The Zn2–Zn1–Cp*_centr. and Zn3–Zn4–Cp*_centr. moieties are slightly deviated from linearity with angles of 175,74 and 176.00°, respectively.

Liquid injection field desorption mass spectrometry (LIFDI-MS) confirms the molecular composition of 1 with a well detectable [M]˙⁺ ion peak at m/z [a.u.] = 1128 (Fig. 2) as well as two fragment peaks [M–ZnCp*]˙⁺ and [M–ZnZnCp*]˙⁺ at m/z [a.u.] = 927 and 861, respectively (Fig. S3†). Interestingly, no loss of CuCp* is observed in the fragment ions, confirming the assignment of elements in the X-ray single crystal structure with equatorial CuCp* and apical ZnZnCp* units.

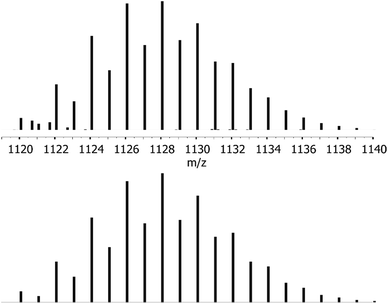Fig. 2 Molecular ion peak of 1 (m/z = 1128) from LIFDI-MS measurements (top) and calculated isotopic pattern for 1 (bottom).

The ¹H NMR spectrum of 1 in C₆D₆ at room temperature shows two Cp* resonances at 2.08 and 2.19 ppm in a 45 : 30 integral ratio, corresponding to the three chemically equivalent CuCp* groups as well as two equivalent apical ZnZnCp* groups. Accordingly, the ¹³C NMR spectrum shows the expected set of signals for two different Cp* moieties (δ = 10.90 (s, CuC₅Me₅), 12.17 (s, ZnZnC₅Me₅), 104.62 (s, CuC₅Me₅), 110.18 (s, ZnZnC₅Me₅) ppm). Note, that the only assignment of metal atoms which is in agreement with this observed D_3h symmetry of the cluster in solution is the allocation of the four Zn atoms to the apical positions and the three Cu atoms to the equatorial triangle (Scheme S1†).

Synthesis and characterization of {[Cu₂Zn₅](Cp*)₅}[BAr₄^F] (2[BAr₄^F])

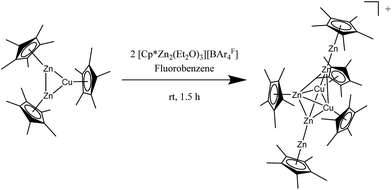
The reaction of [Zn₂Cu](Cp*)₃ with two equivalents of the Cp*Zn₂ transfer-reagent [Zn₂(Cp*)(Et₂O)₃][BAr₄^F]²⁰ in fluorobenzene at room temperature for 1.5 h (Scheme 2) gives a dark red solution with very little amount of metallic precipitate. The product cluster {[Zn₅Cu₂](Cp*)₅}[BAr₄^F]·5C₆H₅F (2[BAr₄^F]·5C₆H₅F) crystallizes from the concentrated an filtered reaction solution at −30 °C in the form of dark red needles.

Scheme 2 Synthesis of [Zn₅Cu₂]Cp*₅[BAr₄^F] (2[BAr₄^F]).

Minor amounts of an unidentified side product are removed by repeated recrystallization of the crude product in fluorobenzene at −30 °C giving 2[BAr₄^F] in 23% analytically pure yield (based on Cu). As described for the formation of 1, the reaction leading to 2 proceeds via a Cp* exchange mechanism. This is in nice accordance with the reactivity studies of [Cp*Zn₂(THF)₃]⁺ showing that this cation can act as both, a Cp* donor as well as a Cp* acceptor forming {[Zn₂](THF)₆}²⁺ or [Zn₂Cp*₂] (Scheme S4†).⁶ Likewise, an in situ NMR experiment of a mixture of [Cp*Zn₂(Et₂O)₃]⁺ and [CuZn₂](Cp*)₃ at room temperature in fluorobenzene points to a rapid Cp* exchange between the metal atoms, indicated by the detection of only one coalescence signal for all Cp* groups. This signal decoalesces into two peaks at temperatures below −20 °C (see Fig. S7†). Due to incomplete separation of the signals at −50 °C, no integral ratio of the two peaks could be determined. As in the case of 1, changing reaction parameters such as temperature, time or stoichiometric ratio of the reactants did not result in any increase of the isolated yield. The complete pathway leading from the reactants to cluster 2 appears rather complex, as evident from the composition of the central trigonal M₃ unit. While the product exhibits a [Cu₂Zn] central unit, the starting cluster consists of a [CuZn₂] triangle. However, despite the obviously involved redox chemistry, no oxidized side products as it is the case in the synthesis of 1 could be detected.

The compound 2[BAr₄^F]·5C₆H₅F crystallizes in the monoclinic space group Cc with two distinct ion pairs in the asymmetric unit. Only one of these two independent units is shown in Fig. 1 (above) for clarity. Similar to compound 1, the metal atoms of cation 2 are arranged in a trigonal bipyramidal fashion, however, with higher deviations from the ideal polyhedral structure. Again, assignment of metal atoms to the atomic positions in the crystal structure has been done with the support of spectroscopic data (vide infra). The equatorial triangle consists of a Cu₂Zn unit capped by ZnZnCp* units on both sides. The apical Zn1–Zn2 (2.299(6) Å) and Zn4–Zn5 (2.323(6) Å) bond lengths are comparable to the respective apical Zn1–Zn2 (2.318(2) Å) and Zn3–Zn4 (2.317(2) Å) distances in 1. The Cu1–Cu2 bond length in 2 (2.415(3) Å) is shorter than the Cu–Cu distances in [Cu₄Zn₄](CN^tBu)₄Cp*₄ (2.471(4) Å) and in 1 (2.431(2)–2.446(2) Å).⁷ The equatorial Cu₂Zn triangle is almost perfectly equilateral (Cu1–Cu2 = 2.415(3), Cu1–Zn3 = 2.400(4), Cu2–Zn3 = 2.396(3) Å). However, the intersection of the apical Zn2–Zn4 axis does not coincide with the centre of gravity of the equatorial Cu₃-plane, but is rather dislocated towards the Cu₂ edge. Thus, the contacts of the apical Zn atoms are not equidistant to the three equatorial metal atoms: the Zn3–Zn2 (2.745(6) Å) and Zn3–Zn4 (2.688(7) Å) distances are considerably longer than the Cu–Zn2 (avg. 2.463 Å) and Cu–Zn4 (avg. 2.487 Å) distances.

The molecular composition of 2[BAr₄^F] as determined by EA (C, H) and AAS (Zn, Cu, B, F) is in good agreement with the sum formula (calculated for H₈₇BC₈₂F₂₄Cu₂Zn₅ [%]: H 4.40, B 0.54, C 49.41, F 22.87, Cu 6.38, Zn 16.40; found: H 4.62, B 0.47, C 51.48, F 20.20, Cu 6.48, Zn 15.98). The deviations in the carbon and fluorine values are attributed to the thermal instability of the compound and the difficulty in handling the pure samples. The ¹H NMR spectrum of 2[BAr₄^F] in CD₂Cl₂ at room temperature shows three resonances at 1.96 (s, 30, ZnZnC₅Me₅), 2.04 (s, 15H, ZnC₅Me₅) and 2.12 (s, 30H, CuC₅Me₅) ppm for the three chemically non-equivalent Cp* groups in a 2 : 1 : 2 ratio, which points to a C_2v symmetry of 2 in solution. In addition, the expected set of signals for the [BAr₄^F]⁻ anion 7.56 (s, 4H) and 7.72 ppm (s, 8H) are detected. Due to the high lability of 2[BAr₄^F] in solution and the moderate solubility of 2[BAr₄^F] at low temperatures meaningful ¹³C NMR spectra could not be obtained. The IR spectrum reveals typical absorption bands for the Cp* moieties at 2905 and 2860 cm⁻¹ and the C–F vibration of the [BAr₄^F]⁻ anion at 1272 cm⁻¹.²⁰ The only reasonable assignment of elements to the metal core of the molecular structure of 2, which is in agreement with the symmetry of the cation in solution (C_2v), is the allocation of four Zn atoms in the axial MMCp* moieties, leaving a [ZnCu₂] triangle in the equatorial plane (Scheme S2†).

Cluster bonding analysis of 1 and 2

The polyhedral structure types of clusters are strongly related to their electronic structure, associating specific cluster shapes with specific numbers of electrons.^21–25 Stable closed-shell organometallic clusters (e.g. protected by hydrocarbon ligands via metal–carbon bonds) most often obey the Wade–Mingos electron-counting rules.^23–25 These rules state that the number of skeletal electron pairs (SEPs) associated with cluster bonding is equal to the number of vertices of the deltahedron in which the cluster is inscribed, plus one. Accordingly, the trigonal bipyramidal skeletons of 1 and 2, should be associated with 5 + 1 = 6 SEPs. Cluster 1 can be formally considered as constituted of five fragments, three CuCp* and two Zn–ZnCp* units. Assuming first that, as generally admitted, the Cu and Zn 3d electrons are not significantly involved in the bonding, CuCp* and Zn–ZnCp* are 0- and 1-electron donor moieties, respectively. One thus ends up with only 1 SEP for 1, as for its isoelectronic relative 2. This makes 1 and 2 highly electron-deficient with respect to the Wade–Mingos rules. It should be however kept in mind that these rules assume that the fragments constituting the cluster participate to cluster bonding with 3 frontier orbitals, one of σ-type and two of π-type.^23–25 This is obviously the case for the Zn–ZnCp* moiety, the external Zn atom having two available non-bonding 4p_π frontier orbitals as well as one 4s/4p hybrid of σ-type (the other sp hybrid is involved in the Zn–Zn single bond). On the other hand, the case of the CuCp* (or [ZnCp*]⁺) fragment is different since it is generally considered as participating to the bonding with only one frontier orbital of σ-type (a 4s/4p hybrid), the occupied low-lying 3d-block being, as said above, discarded. Thus, the Wade–Mingos standard “reference” should be considered with caution when dealing with 1 and 2. To clear out this situation, we have performed density functional (DFT) calculations on these two clusters as well as on several cluster models (BP86/STO-TZ2P level with Grimme D3BJ dispersion corrections, see Computational details in the ESI†). For the sake of simplicity we have first replaced the pentamethylcyclopentadienyl (Cp*) ligands in 1 and 2 by simple cyclopentadienyls (Cp). The optimized structures of the resulting models, namely 1′ and 2′, were found to be energy minima for C_s symmetry, with their symmetry plane containing the Cu₃ and ZnCu₂ triangle, respectively. The optimized metrical data of 1′ and 2′ (Table 1) are consistent with their experimental counterparts in 1 and 2. The [Cu₃Zn₄] metal core of 1′ is very close to D_3h symmetry. Its Kohn–Sham orbital diagram is shown in Fig. 3.

Table 1 Selected averaged experimental (X-ray) and optimized (DFT) distances for 1, 1′, 2 and 2′ (in Å). The corresponding averaged computed Wiberg indices are given in parenthesis for 1′ and 2′. The Zn′ and Zn′′ labels designate the zinc atom bonded to Cp*/Cp and that belonging to the Cu₂Zn triangle in 2/2′, respectively

(avg)	1 (X-ray)	1′ (DFT)	1 (DFT)
Cu–Cu	2.440	2.414 (0.270)	2.426
Cu–Zn	2.443	2.470 (0.091)	2.432
Zn–Zn′	2.318	2.345 (0.600)	2.314

---

(avg)	2 (X-ray)	2′ (DFT)	2 (DFT)
Cu–Cu	2.417	2.385 (0.339)	2.401
Cu–Zn	2.475	2.490 (0.074)	2.437
Cu–Zn′′	2.399	2.399 (0.268)	2.401
Zn–Zn′	2.311	2.338 (0.606)	2.299
Zn–Zn′′	2.717	2.872 (0.025)	2.682

---

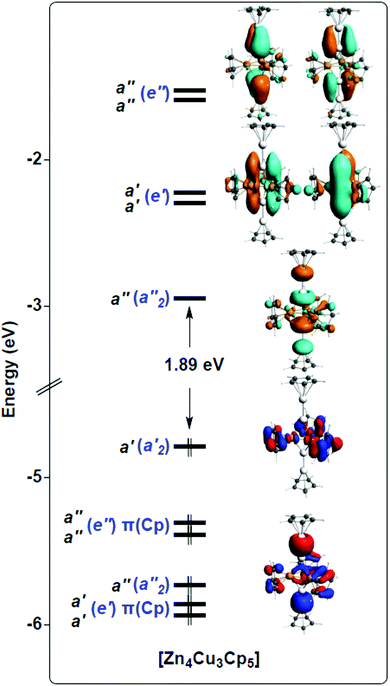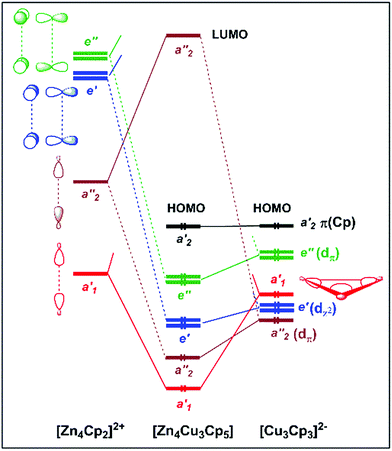
Fig. 3 Kohn–Sham orbital diagram of [Cu₃Zn₄](Cp)₅ (1′). The levels are labelled according to C_s symmetry (in black) and D_3h pseudo-symmetry (in blue). The C_s symmetry plane contains the Cu₃ triangle.

The large HOMO–LUMO gap is consistent with the stability of 1. In order to get a better insight into its bonding, a Morokuma–Ziegler energy decomposition analysis (EDA)^26–28 was carried out, considering the interaction between two fragments: A {[Cu₃](Cp)₃}²⁻ triangular unit and a bi-capping [CpZn₂⋯Zn₂Cp]²⁺ “dimeric” unit. The formal fragment charges were chosen for closed-shell simplicity and also considering that {[Cu₃](Cp)₃}²⁻ is isostructural and isoelectronic to the known [CuZn₂](Cp*)₃ (see above),¹⁴ which can be viewed as an isolobal^29,30 analogue of [H₃]⁺ (σ-aromatic 2-electron/3-center bonding). A similar fragmentation has been suggested for the cluster [{Pd(C₆H₄F)}₃(μ₂-SC₆H₄Cl)₃Ag(H₂O)₂][BF₄]₂ implying that an aromatic [Pd₃]⁺ triangle acts as a donor ligand to a Ag⁺ ion.³¹ The same approach has also been used for treating a related [Pd₄]²⁺ system.³² The EDA results are given in Table 2.

Table 2 Morokuma–Ziegler energy decomposition analysis (EDA) of 1′ and 2′. All values in eV. E_Pauli = Pauli repulsion; E_elstat = electrostatic interaction; E_orb = orbital interaction. TBE = total bonding energy = E_Pauli + E_elstat + E_orb + E_disp

	1′ (Cs)		2′ (Cs)
Fragments	[Cu3Cp3]^2− + [CpZn2⋯Zn2Cp]^2+		[Cu2ZnCp3]^− + [CpZn2⋯Zn2Cp]^2+
E Pauli	14.92		10.37
E elstat	−24.53		−14.15
E orb,decomposition	a′	−6.30	a′	−4.30
	a′′	−4.55	a′′	−3.48
E orb	−10.85		−7.78
E disp	−1.24		−1.16
TBE	−21.70		−12.72

---

Unsurprisingly, with such a formal fragment partitioning in 1′, the electrostatic interaction component dominates the total bonding energy. Representing 44% of the former, the orbital interaction component is, however, not negligible. Its a′ and a′′ components, respectively of σ- and π-type with respect to the Cu₃ plane, are of similar order, the a′ interaction being the strongest. A detailed analysis of the 1′ Kohn–Sham orbital compositions based on its fragment orbitals allowed us to describe the covalent component of the bonding interaction through the simplified qualitative interaction orbital diagram sketched in Fig. 4, considering D_3h pseudo-symmetry.

Fig. 4 Simplified orbital diagram describing the interaction of the [Cu₃Cp₃]²⁻ and [CpZn₂⋯Zn2Cp]²⁺ fragments in 1′ (D_3h pseudo-symmetry assumed). The occupied 3d(Zn) and (most of) the 3d(Cu) combinations, not involved in the interaction, are not represented.

The [CpZn₂⋯Zn₂Cp]²⁺ “dimer” has six accepting frontier orbitals, the in-phase and out-of-phase combinations of the three accepting orbitals on the terminal Zn of each [CpZn₂]⁺ “monomer” (see above). In the D_3h pseudo-symmetry of 1′, the sp(Zn) hybrids give rise to a′₁ and a′′₂ combinations, whereas the 4p_π(Zn) AO's lead to e′ and e′′ combinations (see left side of Fig. 4). On the other hand, the {[Cu₃](Cp)₃}²⁻ unit has no accepting orbitals. Its highest occupied levels are the π(Cp) and 3d(Cu) combinations, among which is buried the strongly bonding a′₁ orbital, principally of 4s/4p composition, which contains the 3-center bonding electron pair of this fragment. This Cu₃ a′₁ orbital interacts strongly with the a′₁ LUMO of the [CpZn₂⋯Zn₂Cp]²⁺ “dimeric” fragment, giving rise to a fully in-phase, strongly bonding, combination which contains the unique SEP that one would consider for cluster bonding if no 3d(Cu) orbitals were involved (see above).

But in fact 3d(Cu) combinations of proper symmetry interact with the other accepting orbitals of the [CpZn₂⋯Zn₂Cp]²⁺ fragment. This can be traced by the occupation of it's a′′₂, e′ and e′′ frontier orbitals, which is 0.54, 2 × 0.10 and 2 × 0.11, respectively. For comparison, the a′₁ occupation is 1.02. The 3d(Cu) counterparts are of 3d_π (a′′₂ and e′′) and 3d_z² (e′) character. Counting the resulting bonding pairs, one ends up with 6 SEPs, all of the proper symmetry (a′₁, a′′₂, e′ and e′′) as in clusters satisfying the classical Wade–Mingos rules. Thus, to some extent, 1 satisfies the Wade–Mingos rules, despite not all, but only specific, 3d_π and 33d_z² combinations are involved. Moreover, the e′ and e′′ interactions are not very strong, because of the relatively poor energy match between 4p(Zn) and 3d(Cu). On the other hand, some second-order participation to the bonding (not represented in Fig. 4) and involving the a₁′ and a′′₂ combinations associated with the Zn–Zn bonding pairs can also be traced. This tends to weaken somewhat the strength of the Zn–Zn bonds at the expenses of Zn–Cu bonding, as exemplified by the computed Zn–Zn Wiberg index in 1′ (0.600), significantly weaker than in CpZnZnCp (0.811).

To summarize the above MO analysis, the bonding within the [Cu₃Zn₂] trigonal bipyramidal skeleton in 1 can be viewed as intermediate between that of a hypothetical electron-deficient 1-SEP cluster and that of a regular Wade–Mingos 6-SEP species. It should be pointed out that, although not preponderant, the role of the 4p_π(Zn) AOs in the framework stability is crucial. This can be shown by replacing in 1′ the [CpZnZn]⁺ capping units by [CpZn]⁺ fragments which, assuming η⁵-Cp coordination, do not possess 4p_π accepting frontier orbitals. Indeed, the optimized geometry of the resulting M₅ cluster [Cu₃Zn₂](Cp)₅ (see ESI†) exhibits (η¹-Cp)Zn units, rather than (η⁵-Cp)Zn, thus leaving the 4p_π(Zn) orbitals available for bonding within the [Zn₂Cu₃] trigonal bipyramidal skeleton. With such a low coordination mode associated with the rather fragile electron-poor character of the [Cu₃Zn₂] skeleton, the hypothetical [Cu₃Zn₂](Cp)₅ cluster appears unlikely to be isolable.

The optimized structure of the model 2′ is also in good agreement with the X-ray structure of 2 (see Table 1). In particular it shows a rather long Zn(apical)–Zn′′(equatorial) bond of 2.872 Å. It is noteworthy that when the dispersion corrections are not included in the calculations, the Zn–Zn′′ distance is elongated to 3.019 Å, a no-bond value. Thus, despite the small E_disp component in the fragment energy decomposition of Table 2, the dispersion forces appear to play a significant role in the overall cluster structure. The weak covalent Zn–Zn′′ bonding is also exemplified by its low Wiberg index (0.025). It can be explained by the fact that the highest 3d-type combinations of the {[Cu₂Zn](Cp)₃}⁻ fragment have little Zn participation (3d(Zn) levels are lower) and therefore interact with the 4p_π(Zn) combinations of the [CpZn₂⋯Zn₂Cp]²⁺ “dimer” primarily through the copper atoms.

The structures of the real methylated compounds 1 and 2 were also optimized and were found to be of C₁ symmetry, slightly distorted away from C_s due to the steric effect of the methyl groups. Their selected metrical data reported in Table 1 are in good agreement with that of the X-ray structures. For these compounds, it was not possible to perform a 2-fragment EDA analysis similar to that carried out for the 1′ and 2′ models. As a matter of fact, it was not possible to converge the [Cp*Zn₂⋯Zn₂Cp*]²⁺ unit in the proper closed-shell configuration. However, a 3-fragment analysis in which this “dimeric” unit is split into two [Cp*Zn₂]⁺ fragments was possible. The corresponding results, together with that obtained in a similar way for 1′ and 2′ are provided in Table S2.† It appears clearly that the 2- and 3-fragment EDA analyses of 1′ and 2′ are fully consistent and indicate negligible interaction between the two capping [Cp*Zn₂]⁺ units. Comparing in Table S2,† the results obtained for 1 and 2 with that of 1′ and 2′ indicate that the bonding analysis carried out for the non-methylated models applies to the real methylated compounds. Among the changes upon ligand methylation (i.e. Cp vs. Cp*), one can note an increase of the absolute value of the E_orb component by ∼1.6/1.8 eV due a destabilization of the [Cu₃] or [Cu₂Zn] 3d(Cu) block. The E_disp component is also doubled upon methylation, due to methyl⋯methyl van der Waals interactions. However, with an absolute value increase of ∼1.3/1.4 eV, its contribution to the total bonding interaction remains relatively small (7–10% of the sum of the stabilizing components).

Going back to the long Zn–Zn′′ bond in 2 (exp: 2.717 Å, calc: 2.872 Å; averaged values), it is interesting to note that, within the series of pseudo-homoleptic [TM(ZnR)_n] compounds (TM = d-block metal) the shortest intramolecular Zn–Zn contact was found to be 2.676(1) Å in [Ru(ZnCp*)₄(ZnMe)₆]³³ being only slightly shorter than the corresponding contacts in 2. Investigations of the bonding in these compounds revealed that the Zn–Zn interactions should not be interpreted as strong Zn–Zn covalent bonds but rather as weak Zn⋯Zn interactions. Therefore, the rather small Wiberg bond index of 0.16 found for the Zn3–Zn2/Zn3–Zn4 contacts in 2 can also be interpreted as rather weak interactions. In this respect a complementary view is obtained from Quantum Theory of Atoms in Molecules (QTAIM, see Computational details in the ESI†) analysis of 1 and 2. Bond critical points and bond paths are found for all M–M interactions, except for the long Zn–Zn′′ contacts in 2 (see Fig. 5 where they are labelled Zn3–Zn2 and Zn3–Zn4 as in the X-ray structures). In accordance to these observations, ring and cage critical points can be found for all M₃ triangles and M₄ pyramides in 1, whereas in 2 ring critical points are only found for the Cu₂Zn triangles. Alternatively, especially cluster 2 can be viewed as a copper triple bonded moiety [Cp*CuCuCp*]²⁻ (with occupied π-like orbitals),³⁴ which is “ligated” by three groups [ZnR]⁺ (R = Cp*, ZnCp*). This picture is in accordance with the results of the QTAIM analysis, which suggests isolated [ZnR]⁺ fragments (see ESI†).

Fig. 5 (a) M₇ cluster unit of 1 (left) and 2 (right) showing the M₅ plane that was used for QTAIM analysis. (b) Contour line map of the Laplacian ∇²ρ(r) of 1 in the plane containing Zn2, Cu1 and Zn4 (left) and of 2 in the plane containing Zn2, Zn3 and Zn4 (right). Solid lines indicate areas of charge concentration while dashed lines show area of charge depletion. The thick solid lines (brown) connecting the atomic nuclei are the bonds paths. The thick solid lines (blue) separating the atomic basins indicate the zero-flux surfaces crossing the molecular plane. Blue dots are (3,−1) bond critical points, orange dots (3,1) ring critical points and green dots (3,3) cage critical points.

Summary and perspectives

In summary, the homoleptic all-hydrocarbon Cp*-protected M₇ Cu/Zn-clusters [Cu₃Zn₄](Cp*)₅ (1) and {[Cu₂Zn₅](Cp*)₅}⁺ (2) have been synthesized and characterized. They expand the unique series {[Cu_aZn_b](Cp*)_c}ⁿ⁺ with varying Cu/Zn ratios a : b and Cp* content. The series starts with the M₃ clusters {[Zn₃](Cp*)₃}⁺ and [CuZn₂](Cp*)₃, it includes the (heteroleptic) M₈ cluster [Cu₄Zn₄](Cp*)₄(CN^tBu)₄. The series so far ends with the M₉ and M₁₀ all-zinc clusters [Zn₉](Cp*)₆ and {[Zn₁₀](Cp*)₆(CH₃)}⁺ (see the Introduction).^2–4 The new M₇ clusters 1 and 2 demonstrate the feasibility to substitute Zn and Cu on a molecular level in small nuclearity clusters while keeping the cluster's polyhedral structural type. As to that the preparation of further isoelectronic structural pairs of {[Cu_aZn_b](L)_c}ⁿ⁺ (a + b = 4–6) and expanded versions of such clusters (i.e. with higher nuclearity a + b > 10), which only differ in the Zn : Cu ratio appears feasible. The trigonal bipyramidal clusters 1 and 2 are at first glance with 1 SEP highly electron deficient with regard to the Wade–Mingos rules, owing to the fact that the basal MCp* units lack 4p frontier orbitals. However, according to EDA analysis of the model 1′ based on the fragments {[Cu₃](Cp)₃}²⁻ and [CpZn₂⋯Zn₂Cp]²⁺ not only 4s/p orbitals of the trigonal M₃ basal unit are involved in skeletal bonding, but even if to a lower extend, also 3d_π and 3d_z² combinations. The latter provide frontier orbitals of proper symmetry and 5 additional SEPs to satisfy the Wade–Mingos rules for trigonal bipyramidal clusters. In spite of the fact that some of these additional SEPs have only moderate bonding character, the metal skeletons of 1 and 2 do not need the help of μ₂/μ₃ ligands for maintaining their unbridged bipyramidal trigonal structures. Dispersion interactions between the Cp* protecting ligands provide additional stabilization to the structures. This is a specific property of Cp* as a ligand,^19,35 among others such as its flexible coordination mode (η¹⋯η⁵), its transferability between Cu and Zn centres, its steric bulk and the stabilization of elimination products such as [Cp*₂Zn] (related to disproportionation reactions). It can be expected that other oligonuclear Cu/Zn clusters on the borderline between electron deficient and regular Wade–Mingos species are likely to be highly reactive and thus should allow further cluster expansion reactions, eventually reaching stability islands of larger clusters predicted by the superatom model. Our ultimate goal along these lines would be the demonstration of high nuclearity atom-precise Hume-Rothery intermetallics inspired superatom clusters solely protected by all-hydrocarbon ligands, such as the recently discovered M₅₅ magic number Al/Cu cluster [Cu₄₃Al₁₂](Cp*)₁₂.³⁵

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was supported by the Deutsche Forschungs-gemeinschaft (grant Fi-502/23-2). H. B. is grateful for a PhD scholarship donated by the German Chemical Industry Fund. We thank Prof. T. Marder and his co-workers at the Julius-Maximilians-Universität Würzburg and Linden CMS GmbH for support in mass spectrometry. The GENCI French national computer resource center is acknowledged (grant x2016-087367). F. G. thanks the Région Bretagne for a PhD studentship grant (ARED NANOCLU 9334).

Notes and references

1. W. Hieber, F. Mühlbauer and E. A. Ehmann, Ber. Dtsch. Chem. Ges. A/B, 1932, 65, 1090–1101.
2. N. T. Tran, D. R. Powell and L. F. Dahl, Angew. Chem., Int. Ed., 2000, 39, 4121–4125.
3. C. Zeng, Y. Chen, K. Kirschbaum, K. J. Lambright and R. Jin, Science, 2016, 354, 1580–1584.
4. J. Vollet, J. R. Hartig and H. Schnöckel, Angew. Chem., Int. Ed., 2004, 43, 3186–3189.
5. H. Schnöckel, Chem. Rev., 2010, 110, 4125–4163.
6. H. Banh, K. Dilchert, C. Schulz, C. Gemel, R. W. Seidel, R. Gautier, S. Kahlal, J.-Y. Saillard and R. A. Fischer, Angew. Chem., Int. Ed., 2016, 55, 3285–3289.
7. K. Freitag, H. Banh, C. Gemel, R. W. Seidel, S. Kahlal, J. Y. Saillard and R. A. Fischer, Chem. Commun., 2014, 50, 8681–8684.
8. K. Mayer, J. Weßing, T. F. Fässler and R. A. Fischer, Angew. Chem., Int. Ed., 2018, 57, 14372–14393.
9. T. Fehlner, J. F. Halet and J. Y. Saillard, Molecular Clusters: A Bridge to Solid-State Chemistry, Cambridge University Press, 2013.
10. K. Freitag, C. Gemel, P. Jerabek, I. M. Oppel, R. W. Seidel, G. Frenking, H. Banh, K. Dilchert and R. A. Fischer, Angew. Chem., Int. Ed., 2015, 54, 4370–4374.
11. I. Resa, E. Carmona, E. Gutierrez-Puebla and A. Monge, Science, 2004, 305, 1136–1138.
12. M. Carrasco, R. Peloso, I. Resa, A. Rodriguez, L. Sanchez, E. Alvarez, C. Maya, R. Andreu, J. J. Calvente, A. Galindo and E. Carmona, Inorg. Chem., 2011, 50, 6361–6371.
13. M. Carrasco, R. Peloso, A. Rodriguez, E. Alvarez, C. Maya and E. Carmona, Chem.–Eur. J., 2010, 16, 9754–9757.
14. K. Freitag, C. Gemel, P. Jerabek, I. M. Oppel, R. W. Seidel, G. Frenking, H. Banh, K. Dilchert and R. A. Fischer, Angew. Chem., Int. Ed., 2015, 54, 4370–4374.
15. M. Zhang, B.-C. Su, C.-L. Li, Y. Shen, C.-K. Lam, X.-L. Feng and H.-Y. Chao, J. Organomet. Chem., 2011, 696, 2654–2659.
16. J. Li, J. M. White, R. J. Mulder, G. E. Reid, P. S. Donnelly and R. A. O'Hair, Inorg. Chem., 2016, 55, 9858–9868.
17. W.-Y. Lo, C.-H. Lam, V. W.-W. Yam, N. Zhu, K.-K. Cheung, S. Fathallah, S. Messaoudi, B. Le Guennic, S. Kahlal and J.-F. Halet, J. Am. Chem. Soc., 2004, 126, 7300–7310.
18. M. I. Bruce, J.-F. Halet, B. Le Guennic, B. W. Skelton, A. N. Sobolev, C. J. Sumby and A. H. White, Coord. Chem. Rev., 2018, 375, 2–12.
19. K. Freitag, H. Banh, C. Gemel, P. Jerabek, R. W. Seidel, G. Frenking and R. A. Fischer, Inorg. Chem., 2015, 54, 352–358.
20. K. Freitag, H. Banh, C. Ganesamoorthy, C. Gemel, R. W. Seidel and R. A. Fischer, Dalton Trans., 2013, 42, 10540–10544.
21. H. A. Jahn and E. Teller, Proc. Roy. Soc. Lond. Math. Phys. Sci., 1937, 161, 220.
22. A. C. Reber and S. N. Khanna, Acc. Chem. Res., 2017, 50, 255–263.
23. D. M. Mingos and D. J. Wales, in Introduction to cluster chemistry, Prentice-Hall, Englewood Cliffs, 1990.
24. D. M. P. Mingos, Nat. Phys. Sci., 1972, 236, 99–102.
25. K. Wade, in Transition Metal Clusters, ed. B. F. G. Johnhson, John Wiley & Sons, Chichester, 1980, pp. 193–264.
26. K. Morokuma, J. Chem. Phys., 1971, 55, 1236–1244.
27. T. Ziegler and A. Rauk, Inorg. Chem., 1979, 18, 1558–1565.
28. F. M. Bickelhaupt and E. J. Baerends, J. Rev. Comput. Chem., Wiley, New York, 2000.
29. M. Elian, M. M. L. Chen, D. M. P. Mingos and R. Hoffmann, Inorg. Chem., 1976, 15, 1148–1155.
30. R. Hoffmann, Angew. Chem., Int. Ed., 1982, 21, 711–724.
31. Y. Wang, A. Monfredini, P. A. Deyris, F. Blanchard, E. Derat, G. Maestri and M. Malacria, Chem. Sci., 2017, 8, 7394–7402.
32. A. Muñoz-Castro, D. M.-L. Carey and R. Arratia-Pérez, J. Chem. Phys., 2010, 132, 164308.
33. T. Cadenbach, T. Bollermann, C. Gemel, M. Tombul, I. Fernandez, H. M. van, G. Frenking and R. A. Fischer, J. Am. Chem. Soc., 2009, 131, 16063–16077.
34. Y. Xie, H. F. Schaefer III and R. B. King, J. Am. Chem. Soc., 2005, 127, 2818–2819.
35. J. Wessing, C. Ganesamoorthy, S. Kahlal, R. Marchal, C. Gemel, O. Cador, A. C. H. Da Silva, J. L. F. Da Silva, J. Y. Saillard and R. A. Fischer, Angew. Chem., Int. Ed., 2018, 57, 14630–14634.

---

Footnotes

† Electronic supplementary information (ESI) available: CCDC 1854851 and 1854852. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/c8sc03902j

‡ Hung Banh and Julius Hornung equally contributed to this work.

---