Open Access Article
Open Access ArticleDirect observation of the intermediate in an ultrafast isomerization†
Tyler M.
Porter‡
 a,
Jiaxi
Wang‡
a,
Yingmin
Li
a,
Bo
Xiang
a,
Catherine
Salsman
a,
Joel S.
Miller
b,
Wei
Xiong
a,
Jiaxi
Wang‡
a,
Yingmin
Li
a,
Bo
Xiang
a,
Catherine
Salsman
a,
Joel S.
Miller
b,
Wei
Xiong
 *a and
Clifford P.
Kubiak
*a and
Clifford P.
Kubiak
 *a
*a
aDepartment of Chemistry and Biochemistry, University of California San Diego, 9500 Gilman Drive, La Jolla, California 92093-0358, USA. E-mail: ckubiak@ucsd.edu; w2xiong@ucsd.edu
bDepartment of Chemistry, University of Utah, 315 South 1400 East, Room 2124, Salt Lake City, Utah 84112-0850, USA
First published on 8th October 2018
Abstract
Using a combination of two-dimensional infrared (2D IR) and variable temperature Fourier transform infrared (FTIR) spectroscopies the rapid structural isomerization of a five-coordinate ruthenium complex is investigated. In methylene chloride, three exchanging isomers were observed: (1) square pyramidal equatorial, (1); (2) trigonal bipyramidal, (0); and (3) square pyramidal apical, (2). Exchange between 1 and 0 was found to be an endergonic process (ΔH = 0.84 (0.08) kcal mol−1, ΔS = 0.6 (0.4) eu) with an isomerization time constant of 4.3 (1.5) picoseconds (ps, 10−12 s). Exchange between 0 and 2 however was found to be exergonic (ΔH = −2.18 (0.06) kcal mol−1, ΔS = −5.3 (0.3) eu) and rate limiting with an isomerization time constant of 6.3 (1.6) ps. The trigonal bipyramidal complex was found to be an intermediate, with an activation barrier of 2.2 (0.2) kcal mol−1 and 2.4 (0.2) kcal mol−1 relative to the equatorial and apical square pyramidal isomers respectively. This study provides direct validation of the mechanism of Berry pseudorotation – the pairwise exchange of ligands in a five-coordinate complex – a process that was first described over fifty years ago. This study also clearly demonstrates that the rate of pseudorotation approaches the frequency of molecular vibrations.
Introduction
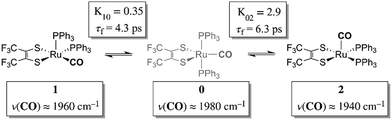
Chemical exchange dynamics is often studied by using Bloch equation analysis of coalescing lineshapes in nuclear magnetic resonance (NMR) spectroscopy. The typical (radio) frequencies used in the NMR experiment determine that dynamical time scales in the range of milliseconds to microseconds can be studied. A similar treatment has been applied to systems exchanging on the IR vibrational time scale.1–3 For reactions occurring on the picosecond time scale, lineshape analysis of FTIR and Raman vibrational spectra can be applied. In practice, there are comparatively few examples of chemical exchange measurable by linear IR or Raman vibrational spectroscopy, because inhomogeneous broadening, solvent environment fluctuation and multiple dynamic processes in addition to chemical exchange can contribute to the overall lineshape. Examples of fast reactions can include intramolecular electron transfers,2,4,5 proton transfers,6 and isomerizations.1,7 Here, we present the study of the rapid structural isomerization of a five-coordinate ruthenium complex on the ultrafast (vibrational) time scale (Fig. 1).The ruthenium complex, Ru(S2C2(CF3)2)(CO)(PPh3)2, was first reported by Miller and Balch in 1971.8 The solvent from which the complex is recrystallized determines whether orange crystals or a mixture of orange and violet crystals are obtained. X-ray crystal structure analysis revealed that both the orange and violet isomers were square pyramidal, differing only in the position of the carbonyl ligand.9 The more stable orange isomer was found to have the CO in the apical position, and is referred to as 2 here, while the violet isomer had the CO in the equatorial plane, and is referred to as 1. The solid state FTIR stretching frequencies for the CO in each of these isomers are separated by ca. 30 cm−1 (orange: ν(COap), 1944 cm−1; violet: ν(COeq), 1973 cm−1),8 while in methylene chloride (DCM) solutions at 20 °C, only one broad absorption (FWHM ≈ 50 cm−1) appears near the average frequency of the violet and orange isomers, (ca. 1958 cm−1).
Complete fittings of the solution 1D IR lineshape consisting of contributions from only these two isomers are less than satisfactory; owing to extra absorbance in the vicinity of 1980 cm−1 from a possible third minor component (vide infra). The solution state 31P NMR in DCM-d2 shows only one resonance at 47.57 ppm indicating that the ruthenium bound triphenylphosphine ligands experience an identical average environment, and the fluxional behavior of the ligands is faster than the NMR timescale (Fig. S1,†kex > 106 s−1).10 Together, these spectroscopic observations suggest dynamic averaging on the ultrafast timescale of molecular vibrational modes.
Ultrafast two-dimensional infrared (2D IR) spectroscopy is a powerful method that can obtain molecular structure and provide details of dynamical processes with sub-picosecond time resolution.11–17 2D IR spectroscopy has been applied to measure chemical exchange between two conformations in solution phase under thermal equilibrium.15,18–24 In 2D IR spectroscopy, three ultrafast mid-IR pulses interact with the sample sequentially: the first two pulses initialize and interrogate vibrational coherences, which generate a transient vibrational tag, and the third pulse probes the evolution of these tagged vibrational modes (Fig. S2†). Because vibrational modes of molecules are sensitive to molecular conformations, local solvent environments, and excess internal energy, scanning the waiting time (t2) between the second and third pulses can track the dynamics of chemical exchange,15,19,20,24 solvent fluctuation25–28 and vibrational energy relaxation.29–32 In the present study, 2D IR is employed to understand chemical exchange.
Results and discussion
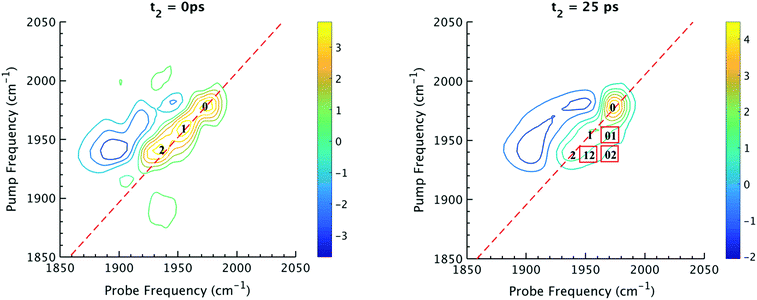
The 2D IR spectra of Ru(S2C2(CF3)2)(CO)(PPh3)2 are shown in Fig. 2. The spectra are essentially 2D frequency correlation maps of vibrational coherences, which are plotted against the initially tagged pump frequency, along the y-axis, and the probe frequency, along the x-axis. On the diagonal (Fig. 2, dashed line), we observe three individual peaks for Ru(S2C2(CF3)2)(CO)(PPh3)2 in DCM solution at t2 = 0 ps, labeled as peak 0 (1980 cm−1), peak 1 (1960 cm−1), and peak 2 (1940 cm−1). The three diagonal peaks indicate three different ν(CO) modes in the system. The 1960 and 1940 cm−1 peaks correspond to the two isomers (1 and 2, respectively) as previously observed in the solid state FTIR spectra. The third ν(CO) band at 1980 cm−1 corresponds to a third isomer of the ruthenium complex 0 that was not isolable in the solid state, and appears only as a small shoulder in solution phase FTIR spectra. The third isomer has been determined to be a metastable trigonal bipyramidal structure of Ru(S2C2(CF3)2)(CO)(PPh3)2 (vide infra).The dynamics between the three isomers are revealed by 2D IR spectra collected at a series of t2 time delays. As t2 increases, the three diagonal peaks decay due to population relaxation of the vibrational modes, while cross peaks increase relative to the diagonal peaks (Fig. S3†). Cross peaks in the 2D IR represent chemical exchanges between the species appearing on the diagonal, at peaks 0, 1, and 2. For instance, a cross peak located at the pump frequency of 1 and the probe frequency of 0, indicates exchange between isomers 1 and 0. Chemical exchange time constants between each isomer are extracted by fitting cross peak intensities at different t2 times and plotting them as a function of t2. (Fig. S4†). The extracted time constants indicate that the transition from 1 to 0 occurs with a 4.3 (1.5) ps time constant, while the transition from 0 to 2 requires 6.3 (1.6) ps. A cross peak for the conversion of 1 to 2 was also observed with a time constant of 8.6 (2.0) ps; however, the dynamics of a direct conversion between 1 and 2 are not expected to compete with the faster interconversions via0 as an intermediate (see kinetic analysis in ESI†). We note that spectral diffusion could be another source of lineshape change that manifests as an off-diagonal component growth.16,17,25–27 For Ru(S2C2(CF3)2)(CO)(PPh3)2 in DCM, spectral diffusion was observed separately with a time constant 83.3 (15.3) ps, which is much longer than the cross peak intensity growth, indicating that the cross peak dynamics reflect chemical exchange.33 It is also important to note that the power of the mid-IR pulses interacting with the system is insufficient to perturb the system from thermal equilibrium, and does not drive the system away from a persistent steady-state population. The IR pulse sequence serves only to tag and probe the vibrational modes at different time delays. This allows the observation of the intramolecular rearrangement of interest under thermal equilibrium.
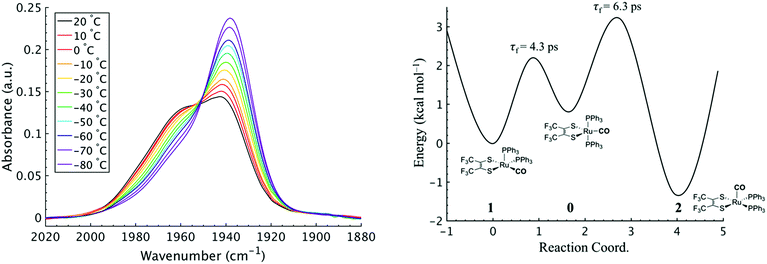
To investigate the thermodynamics of the chemical exchange process observed here, the variable temperature 1D FTIR (VT-FTIR) spectra of the complex was collected using a SPECAC flow-through optical cryostat. The sample was enclosed in a CaF2 crystal windowed sample cell contained in a vacuum jacketed housing and cooled from 20 to −80 (1) °C using a methanol liquid nitrogen slurry. Upon cooling, the broad band centred at ca. 1958 cm−1 shifts to lower frequencies (ca. 1938 cm−1), sharpens and gains intensity while the shoulders near 1960 and 1980 cm−1 significantly lose intensity (Fig. 3). The temperature dependence is completely reversible and suggests that at low temperature, DCM solutions contain predominantly the more favoured COapical isomer, 2. After solvent subtraction, the 1D FTIR line shapes were fit to three Gaussian functions centred about the equilibrium positions for each isomer (Fig. S5 and S6,†ν(CO) ≈ 0: 1980, 1: 1960, 2: 1940 cm−1) and allowed to move ±4 cm−1. Using the determined spectral areas, the population ratios of the isomers at all temperatures were then determined and a Van't Hoff analysis was performed (Fig. S7†). Exchange between 1 and 0 was found to be endergonic in nature with ΔH = 0.84 (0.08) kcal mol−1, ΔS = 0.6 (0.4) eu, and ΔG298 = 0.7 (0.1) kcal mol−1, while exchange between 0 and 2 was found to be exergonic with ΔH = −2.18 (0.06) kcal mol−1, ΔS = −5.3 (0.3) eu, and ΔG298 = −0.6 (0.1) kcal mol−1. The exchange process overall from 1 to 2 (COequitorial to COapical) was found to be thermodynamically favoured in DCM with ΔH = −1.3 (0.1) kcal mol−1, ΔS = −4.8 1 (0.5) eu (Table 1). While the direct exchange between 1 and 2 is possible, given literature precedent, the kinetic analysis and DFT results (vide infra) all exchange is believed to involve the TBP intermediate (0) (Fig. 3).34,35
| K eq | ΔH (kcal mol−1) | ΔS (eu) | τ f (ps) | E a (kcal mol−1) | ||
|---|---|---|---|---|---|---|
| IR | K 10 | 0.35 (0.03) | 0.84 (0.08) | 0.6 (0.4) | 4.3 (1.5) | 2.2 (0.2) |
| K 02 | 2.9 (0.2) | −2.18 (0.06) | −5.3 (0.3) | 6.3 (1.6) | 2.4 (0.1) | |
| K 12 | 1.0 (0.1) | −1.3 (0.1) | −4.8 (0.5) | 8.6 (2.0) | 2.6 (0.1) | |
| UV-vis | K 12 | 1.4 (0.3) | −1.3 (0.1) | −3.4 (0.2) | — | — |
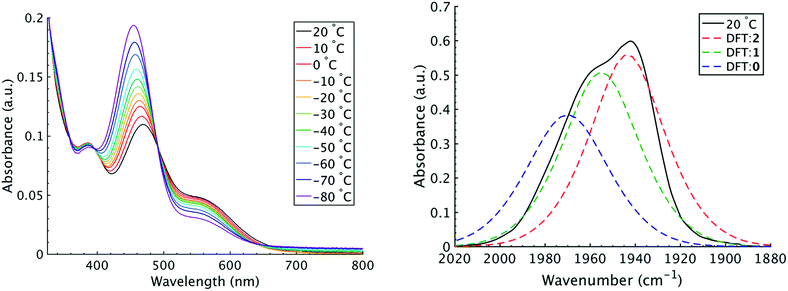
It is important to note that since both the equilibrium constant and the rate constant for exchange will contribute to the overall FTIR lineshape it is useful to determine the equilibrium constants for the isomers independently. This was done by variable temperature UV-visible electronic spectroscopy. Electronic spectra of the solid state isomers in a KBr pellet present a single transition for the orange isomer (2) at 466 nm while the violet isomer (1) presents three transitions at 571 nm, 460 nm, and 396 nm (Fig. S8†). In DCM solutions at 20 °C three transitions are present with band maxima at 386, 466 and 561 nm. Upon cooling to −80 °C, the bands at 386 and 561 nm are seen to decrease in intensity while the band at 470 gains significant intensity and blue shifts to 455 nm (Fig. 4). The bands are assigned to the equatorial (1) and apical (2) isomers respectively and both are related by clear isosbestic points at 396 and 490 nm indicative of absorbing species in equilibrium. After spectral deconvolution (Fig. S8 and S9†), the equilibrium constants were estimated from the spectral areas and a Van't Hoff analysis gave a ΔH = −1.21 (0.06) kcal mol−1 and ΔS = −3.4 (0.2) eu (Fig. S11†). These values are in excellent agreement with those determined from the analysis of 1D FTIR spectra described above.
The most closely related examples of transition metal complexes undergoing dynamic exchange on the IR timescale can be found in both [(η4-diene)Fe(CO)3] complexes and Co2(CO)8.15 In the former [(η4-diene)Fe(CO)3] complexes, the three carbonyl ligands exchange through a very low barrier, turnstyle type, Berry pseudorotation.1,3,36–39 This corresponds to a degenerate self-exchange, quite different from the exchange between populations of two structurally different isomers, sharing an observable intermediate as observed in both Ru(S2C2(CF3)2)(CO)(PPh3)2 (vide supra) and Co2(CO)8.15 An Arrhenius analysis (eqn (1)) provides the barrier heights of the observed exchange process.
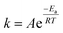 | (1) |
Using the determined rate constants from 2D IR and an estimate of the exponential prefactor (A) to be on the order of 1013 s−1,1,3,24,36,37 the barrier to exchange from 1 to 0 was found to be 2.2 (0.2) kcal mol−1, while the barrier to exchange from 0 to 2 was found to be 2.4 (0.1) kcal mol−1 (Table 1, Fig. 3). These values are sufficiently low to be expected to produce the dynamic exchange coalesced lineshapes, like those observed in the 1D FTIR spectra.3,37 We also note that careful examination of the structures and application of simple principles of least motion would predict that isomerization between 1 and 0 would require less rearrangement than that required to proceed between 0 to 2, consistent with the experimentally determined barriers.
The isomers are believed to exchange from 1 to 0 by movement of a phosphine ligand in 1 from an equatorial to axial position (Fig. 3). Isomerization between 0 and 2 then occurs following twisting the dithiolene ligand in 0 to place the dithiolene ligand in the equatorial plane. Calculated structures and frequency calculations were obtained using density functional theory (DFT) at the BP86 level of theory with basis sets def2-TZVP (Ru, S, P, and O) and def2-SVP (H and C) for the isolated molecules. The reported crystal structure data for 1and 2 were used for the initial geometries,40,41 while the TBP (0) isomer was adapted from the reported crystal structure of 1. After geometry optimization, frequency calculations were performed at the same level of theory to verify optimized geometries as minima. The predicted FTIR spectrum from the DFT frequency calculation was in excellent agreement with that observed experimentally (Fig. 4, ν(CO) DFT: 0 = 1975 cm−1; 1 = 1955 cm−1; 2 = 1940 cm−1) supporting the experimental observation of the TBP isomer. These ideas of isomerization are further supported by consideration of the vibrational normal modes as calculated from the DFT frequency analysis. For all three isomers, several low frequency normal modes have been identified in which nuclear displacements align with the described rearrangement pathways (Movies S1–S4†).
Conclusions
The fact that a relatively large transition metal complex undergoes isomerization at rates comparable to the rotational isomerization reactions of small organic molecules is surprising.4,24,42,43 To our knowledge, this is the first observation of an ultrafast dynamic equilibrium involving two distinct structural isomers and the intermediate connecting them. This work confirms that the ground states of five-coordinate transition metal complexes can have remarkably low kinetic barriers for axial–equatorial exchange. This study also validates the mechanism of Berry pseudorotation39 and clearly demonstrates its dynamical time scale. This work presents new opportunities for potential molecular device applications based on switching between three distinct states of a system exhibiting electronic tri-stability on the ps time scale.Conflicts of interest
The authors declare no competing financial interests.Acknowledgements
The authors would like to thank Dr Starla Glover for insightful conversations about these systems. We are grateful to Dr Anthony Mrse of the UCSD NMR facility for assistance and Robert Konecny of the W. M. Keck Foundation for the computing resources at the W. M. Keck Laboratory for Integrated Biology II. T. M. P. and C. P. K. acknowledge support from NSF CHE–1461632 and CHE-1759460. J. W., Y. L., B. X. and W. X. acknowledge support from AFOSR FA9550-17-0094.Notes and references
- F.-W. Grevels, J. Jacke, W. E. Klotzbücher, C. Krüger, K. Seevogel and Y.-H. Tsay, Angew. Chem., Int. Ed., 1987, 26, 885–887 CrossRef.
- T. Ito, T. Hamaguchi, H. Nagino, T. Yamaguchi, J. Washington and C. P. Kubiak, Science, 1997, 277, 660–663 CrossRef CAS.
- F.-W. Grevels, K. Kerpen, W. E. Klotzbücher, R. E. D. McClung, G. Russell, M. Viotte and K. Schaffner, J. Am. Chem. Soc., 1998, 120, 10423–10433 CrossRef CAS.
- B. Cohen and S. Weiss, J. Chem. Phys., 1980, 72, 6804 CrossRef CAS.
- B. Cohen and S. Weiss, J. Chem. Phys., 1981, 74, 3635 CrossRef.
- B. Cohen and S. Weiss, Spectrochim. Acta, Part A, 1988, 44, 529–531 CrossRef.
- V. J. Johnston, F. W. B. Einstein and R. K. Pomeroy, Organometallics, 1988, 7, 1867–1869 CrossRef CAS.
- A. L. Balch and J. Miller, Inorg. Chem., 1971, 10, 1410–1415 CrossRef CAS.
- I. Bernal, A. Clearfield, E. F. Epstein, J. S. Ricci, A. Balch and J. S. Miller, Chem. Commun., 1973, 39–40 RSC.
- P. R. Hoffman and K. G. Caulton, J. Am. Chem. Soc., 1975, 97, 4221–4228 CrossRef CAS.
- J. Zheng, K. Kwak and M. D. Fayer, Acc. Chem. Res., 2007, 40, 75–83 CrossRef CAS.
- P. Hamm, M. Lim and R. M. Hochstrasser, J. Phys. Chem. B, 1998, 102, 6123–6138 CrossRef CAS.
- M. C. Asplund, M. T. Zanni and R. M. Hochstrasser, Proc. Natl. Acad. Sci. U. S. A., 2000, 97, 8219–8224 CrossRef CAS.
- M. Khalil, N. Demirdöven and A. Tokmakoff, J. Phys. Chem. A, 2003, 107, 5258–5279 CrossRef CAS.
- J. M. Anna, M. R. Ross and K. J. Kubarych, J. Phys. Chem. A, 2009, 113, 6544–6547 CrossRef CAS.
- I. A. Nilsen, D. G. Osborne, A. M. White, J. M. Anna and K. J. Kubarych, J. Chem. Phys., 2014, 141, 134313 CrossRef.
- P. A. Eckert and K. J. Kubarych, J. Phys. Chem. A, 2017, 121, 608–615 CrossRef CAS.
- K. Kwak, J. Zheng, H. Cang and M. D. Fayer, J. Phys. Chem. B, 2006, 110, 19998–20013 CrossRef CAS PubMed.
- Y. S. Kim and R. M. Hochstrasser, Proc. Natl. Acad. Sci. U. S. A., 2005, 102, 11185–11190 CrossRef CAS.
- J. Zheng, K. Kwak, J. Asbury, X. Chen, I. R. Piletic and M. D. Fayer, Science, 2005, 309, 1338 CrossRef CAS.
- J. F. Cahoon, K. R. Sawyer, J. P. Schlegel and C. B. Harris, Science, 2008, 319, 1820 CrossRef CAS.
- S. T. Roberts, K. Ramasesha and A. Tokmakoff, Acc. Chem. Res., 2009, 42, 1239–1249 CrossRef CAS.
- J. M. Anna and K. J. Kubarych, J. Chem. Phys., 2010, 133, 174506 CrossRef.
- K.-K. Lee, K.-H. Park, C. Joo, H.-J. Kwon, H. Han, J.-H. Ha, S. Park and M. Cho, Chem. Phys., 2012, 396, 23–29 CrossRef CAS.
- S. T. Roberts, J. J. Loparo and A. Tokmakoff, J. Chem. Phys., 2006, 125, 084502 CrossRef.
- D. E. Rosenfeld, Z. Gengeliczki, B. J. Smith, T. D. P. Stack and M. D. Fayer, Science, 2011, 334, 634 CrossRef CAS.
- D. E. Rosenfeld, J. Nishida, C. Yan, S. K. K. Kumar, A. Tamimi and M. D. Fayer, J. Phys. Chem. C, 2013, 117, 1409–1420 CrossRef CAS.
- L. M. Kiefer and K. J. Kubarych, J. Phys. Chem. A, 2015, 119, 959–965 CrossRef CAS.
- I. V. Rubtsov, Acc. Chem. Res., 2009, 42, 1385–1394 CrossRef CAS PubMed.
- J. T. King, J. M. Anna and K. J. Kubarych, Phys. Chem. Chem. Phys., 2011, 13, 5579–5583 RSC.
- J. T. King, M. R. Ross and K. J. Kubarych, J. Phys. Chem. B, 2012, 116, 3754–3759 CrossRef CAS.
- M. Fedoseeva, M. Delor, S. C. Parker, I. V. Sazanovich, M. Towrie, A. W. Parker and J. A. Weinstein, Phys. Chem. Chem. Phys., 2015, 17, 1688–1696 RSC.
- D. C. Urbanek, D. Y. Vorobyev, A. L. Serrano, F. Gai and R. M. Hochstrasser, J. Phys. Chem. Lett., 2010, 1, 3311–3315 CrossRef CAS.
- E. L. Mutterties and R. A. Schunn, Q. Rev., Chem. Soc., 1966, 20, 245–299 RSC.
- E. P. A. Couzijn, J. C. Slootweg, A. W. Ehlers and K. Lammertsma, J. Am. Chem. Soc., 2010, 132, 18127–18140 CrossRef CAS.
- A. N. Giordano and B. J. Lear, J. Phys. Chem. A, 2013, 117, 12313–12319 CrossRef CAS.
- A. N. Giordano and B. J. Lear, J. Phys. Chem. A, 2015, 119, 3545–3555 CrossRef CAS.
- A. D. Hill, M. C. Zoerb, S. C. Nguyen, J. P. Lomont, M. A. Bowring and C. B. Harris, J. Phys. Chem. B, 2013, 117, 15346–15355 CrossRef CAS.
- R. S. Berry, J. Chem. Phys., 1960, 32, 933–938 CrossRef CAS.
- I. Bernal, A. Clearfield and J. S. Ricci, J. Cryst. Mol. Struct., 1974, 4, 43–54 CrossRef CAS.
- A. Clearfield, E. F. Epstein and I. Bernal, J. Coord. Chem., 1977, 6, 227–240 CrossRef CAS.
- B. Cohen and S. Weiss, J. Phys. Chem., 1983, 87, 3606–3610 CrossRef CAS.
- J. Zheng, K. Kwak, J. Xie and M. D. Fayer, Science, 2006, 313, 1951 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c8sc03258k |
| ‡ These authors contributed equally. |
| This journal is © The Royal Society of Chemistry 2019 |