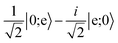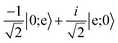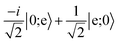Open Access Article
Open Access ArticleDipolar exchange quantum logic gate with polar molecules
Kang-Kuen
Ni
 *abc,
Till
Rosenband
*abc,
Till
Rosenband
 b and
David D.
Grimes
b and
David D.
Grimes
 abc
abc
aDepartment of Chemistry and Chemical Biology, Harvard University, Cambridge, Massachusetts 02138, USA. E-mail: ni@chemistry.harvard.edu
bDepartment of Physics, Harvard University, Cambridge, Massachusetts 02138, USA
cHarvard-MIT Center for Ultracold Atoms, Cambridge, Massachusetts 02138, USA
First published on 13th July 2018
Abstract
We propose a two-qubit gate based on dipolar exchange interactions between individually addressable ultracold polar molecules in an array of optical dipole traps. Our proposal treats the full Hamiltonian of the 1Σ+ molecule NaCs, utilizing a pair of nuclear spin states as storage qubits. A third rotationally excited state with rotation-hyperfine coupling enables switchable electric dipolar exchange interactions between two molecules to generate an iSWAP gate. All three states are insensitive to external magnetic and electric fields. Impacts on gate fidelity due to coupling to other molecular states, imperfect ground-state cooling, blackbody radiation and vacuum spontaneous emission are small, leading to potential fidelity above 99.99% in a coherent quantum system that can be scaled by purely optical means.
1 Introduction
Important progress has been made towards a laboratory quantum computer with state-of-the-art demonstrations reaching a combination of 5 qubits and 98.3% CNOT gate fidelity.1,2 The criteria for quantum computation3 have been identified as (1) a scalable system of qubits (2) initialization (3) coherence (4) universal set of qubit gates (5) measurement. Items 2 through 5 have been demonstrated at sufficient fidelities,4–8 showing that computation with many qubits9–11 may be possible. But the route toward scalability remains challenging. Here, we focus on the problem of producing a high-fidelity two-qubit gate using optically trapped dipolar molecules, with the hope that this physical system allows for easier scalability. Recent demonstrations of flexible optical tweezer arrays12,13 show a method by which many qubits could be rearranged to implement quantum algorithms.Optically trapped, electrically dipolar neutral molecules have long been recognized as potential qubits14–18 where the dipole–dipole interaction between two molecules mediates a two-qubit gate. However, most proposals rely on static or oscillating dressing electric fields to polarize the molecules, where the molecular Stark energy is much larger than the dipolar interaction. This imposes stringent constraints on field stability.
Here we describe concretely how the natural dipolar interaction between two molecules can produce an iSWAP gate, without the need for additional polarizing fields, thereby removing an important source of implementation complexity and qubit decoherence. This iSWAP gate, together with single qubit rotations, forms a universal set of qubit gates.19,20 We exploit the rich molecular internal structure and use NaCs as an example to find molecular qubits that are expected to have long coherence (item 3). The gate relies on two-qubit interactions that are switched on by driving one qubit state to a third state via a microwave transition. We find parameters that allow gates with high fidelity (F > 1 − 10−4) in 10 ms at a magnetic field of 1 Gauss when light shifts due to the optical trap are neglected. For an optical trap depth of 600 kHz, the same fidelity and duration can be reached for a 35 Gauss magnetic field. The gate duration could be reduced by applying shaped pulses rather than the square pulses considered here.
2 Exchange and the iSWAP gate
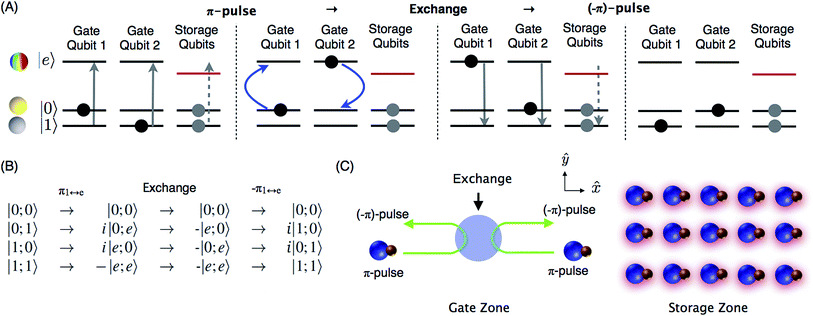
It is a well known phenomenon that if two identical systems interact weakly, where one system has an energy excitation and the other does not, the excitation eventually transfers. This effect can form the basis for a two-qubit gate17,20–24 and has been discussed in the context of molecule-based quantum simulations of spin models.25,26 The transfer of excitation via the dipole–dipole interaction has been demonstrated for ultracold KRb molecules27,28 and atoms with large magnetic dipoles29 in optical lattices.We rely on the natural dipole–dipole interaction between molecules to enable evolution of the type |0;e〉 ↔ |e;0〉 where |0〉 is a sub-level of the rotational ground state, and |e〉 is a sub-level of the first rotational excited state (see Fig. 1A and B). In the two-particle state, the first position refers to the first molecule, and the second position refers to the second molecule. This exchange interaction leaves the states |0;0〉 and |e;e〉 unchanged, and the overall unitary evolution in the basis |0;0〉, |0;e〉, |e;0〉, |e;e〉 is28
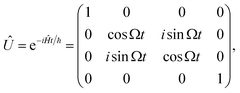 | (1) |
![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) , which is also the magnetic field direction. For the 35 Gauss example, which includes the effects of a 600 kHz deep optical trap, we use an interaction duration of t = 2 ms with r = 2.5 μm along
, which is also the magnetic field direction. For the 35 Gauss example, which includes the effects of a 600 kHz deep optical trap, we use an interaction duration of t = 2 ms with r = 2.5 μm along ![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) and the magnetic field direction is ẑ. While the resolution of optical tweezers with beam waist below 1 μm supports smaller separation and gates as fast as t = 50 μs, two effects place additional constraints. (1) Off-resonant population leakage degrades the gate fidelity for short durations (Section 6) and (2) smaller molecule separation (r) makes the gate more sensitive to motional excitation (Section 7).
and the magnetic field direction is ẑ. While the resolution of optical tweezers with beam waist below 1 μm supports smaller separation and gates as fast as t = 50 μs, two effects place additional constraints. (1) Off-resonant population leakage degrades the gate fidelity for short durations (Section 6) and (2) smaller molecule separation (r) makes the gate more sensitive to motional excitation (Section 7).
Quantum computing requires two qubit states |0〉 and |1〉 that are coherent and couple minimally to the environment and other qubits. In this proposal, we utilize two hyperfine sublevels of the rotational ground state of a molecule as states |0〉 and |1〉. Long-lasting coherence of such states has recently been demonstrated in a gas of ultracold NaK molecules.30 While the hyperfine levels offer coherence, they do not produce strong dipole–dipole interactions between nearby molecules. To enable this interaction and produce an iSWAP gate, the |1〉 state in two molecules is temporarily transferred to the rotationally excited state |e〉 via a microwave π-pulse. Then, after energy exchange, the |e〉 population is transferred back to |1〉. The propagator in eqn (1) still applies, but now in the computational basis |0;0〉, |0;1〉, |1;0〉, |1;1〉 as shown in Fig. 1(B).
The above sequence requires an excited state |e〉 that couples to two different hyperfine levels (|0〉 and |1〉) of the ground state via electric fields. We rely on the hyperfine interaction term of the internal molecular Hamiltonian that couples molecular rotation to nuclear spin via the nuclear electric quadrupole moment31,32 to produce eigenstates that contain superpositions of different nuclear spin states. This interaction requires a nuclear spin greater than 1/2. Even though external electric fields do not change the nuclear spin directly, they can change the nuclear spins by driving transitions between states with different superpositions.33,34 In this manuscript, we use 23Na133Cs as an example because it has a large permanent electric dipole moment (4.6 Debye), and full quantum control of individually trapped molecules is being developed.35,36 A similar gate scheme that makes use of internal molecular couplings could also be applied to other ultracold polar molecules, including other bialkalis where a single internal quantum state can already be prepared34,37–40 and molecules of 2Σ electronic structure with spin-rotational coupling.41–44
3 Qubit array
For a quantum computer, a large number of molecular qubits could be held in an array of optical tweezers for storage (see Fig. 1C). Two arbitrary qubits can be selected for gate operations by means of a configurable tweezer array12,13 and moved so they are separated from the other qubits and initially far from each other. Off-resonant light is applied to the array of stored qubits to shift their |e〉 energy level so that the π-pulses have no effect. Individual addressability of qubits requires a spatial light pattern with high contrast ratio between stored and gate qubits, which can be generated by similar optics as the array of optical tweezers. The light causes only very small differential shifts for the storage states |0〉 and |1〉. A spatially uniform microwave π-pulse of well-defined polarization then transfers |1〉 to |e〉 for the two gate qubits. Then the qubits are moved near each other and back apart to allow for the interaction. This movement naturally produces a temporally shaped interaction with gradually rising and falling strength to reduce off-resonant population leakage. The final π-pulse transfers the |e〉 population to |1〉. An enhanced gate sequence can include a central spin-echo pulse to mitigate slowly drifting energies (Section 6). More advanced dynamical-decoupling sequences can be applied to further reduce decoherence and the sensitivity to qubit motion (Section 7).4 Gate calculation
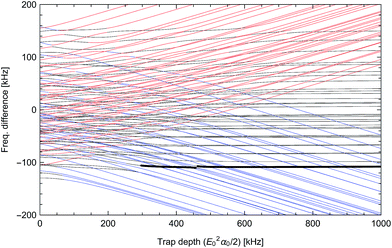
Because the molecule is in a 1Σ+ state, the electronic spin and orbital angular momentum are zero, and do not enter the calculation. We identify quantum states in the uncoupled basis by the quantum numbers N, mN, m1, and m2, where N is the angular momentum associated with molecular rotation and mN, m1, m2 are projections of this angular momentum and the two nuclear spins onto the magnetic field axis. While the uncoupled basis is convenient for calculations, the basis states generally do not coincide with eigenstates of the molecular Hamiltonian. Nevertheless, we label Hamiltonian eigenstates as |N, mN, m1, m2〉, where we use the quantum numbers of the uncoupled basis state with maximum overlap. Although this labeling scheme could in principle assign the same quantum numbers to two different eigenstates, we have verified that this does not occur for the specific states discussed here. When two-molecule states are described, they are written as |a;b〉 where a and b are the states of molecules 1 and 2 respectively.We solve for the eigenstates associated with the molecular hyperfine Hamiltonian for NaCs32 at various magnetic fields and optical trap depths. The energy levels are shown as a function of magnetic field in Fig. 2 and trap depth in Fig. 4. The dipole–dipole interaction and electric-field-driven π-pulses both depend on the electric dipole moments of the molecules. The Hamiltonian associated with an externally applied electric field to molecule j is
ĤE = −![[d with combining circumflex]](https://www.rsc.org/images/entities/b_char_0064_0302.gif) j·E j·E | (2) |
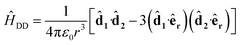 | (3) |
![[d with combining circumflex]](https://www.rsc.org/images/entities/b_char_0064_0302.gif) j is the dipole moment operator of molecule j. Here, êr is the unit vector along the separation direction for the two molecules and the dot products are evaluated as sums over the three spatial directions. The dipole moment operators are determined by the rotational part of the energy eigenstates and for a basis state N, mN, this axis has an orientation whose quantum wave function is the spherical harmonic YmN. From the eigenstates of the molecular Hamiltonian we calculate the matrices associated with the dipole operators
j is the dipole moment operator of molecule j. Here, êr is the unit vector along the separation direction for the two molecules and the dot products are evaluated as sums over the three spatial directions. The dipole moment operators are determined by the rotational part of the energy eigenstates and for a basis state N, mN, this axis has an orientation whose quantum wave function is the spherical harmonic YmN. From the eigenstates of the molecular Hamiltonian we calculate the matrices associated with the dipole operators ![[d with combining circumflex]](https://www.rsc.org/images/entities/i_char_0064_0302.gif) x,
x, ![[d with combining circumflex]](https://www.rsc.org/images/entities/i_char_0064_0302.gif) y,
y, ![[d with combining circumflex]](https://www.rsc.org/images/entities/i_char_0064_0302.gif) z for the laboratory coordinate system.28 These matrix elements are diagonal in the quantum numbers m1 and m2 of the uncoupled basis and can be reduced to Wigner-3j symbols.31
z for the laboratory coordinate system.28 These matrix elements are diagonal in the quantum numbers m1 and m2 of the uncoupled basis and can be reduced to Wigner-3j symbols.31
For each step (π-pulse and exchange), we calculate unitary evolution according to the time-independent Hamiltonians in eqn (2) and (3). The resonant couplings drive the desired gate behavior, while off-resonant couplings to other states cause population leakage and Stark shifts. For a low magnetic field without light, the most important Hamiltonian terms are listed in Tables 1 and 2. The unitary transformation is applied to many test states in the computational basis to determine the minimum gate fidelity.45 The approximate population leakage can also be calculated more simply via perturbation theory (Appendix A).
| From (i) | To (j) | H ij /ℏ [s−1] | H jj /ℏ [s−1] |
|---|---|---|---|
| |e〉 | |1〉 | 521.9 | 0 |
| |1〉 | |e〉 | 521.9 | 6.3 |
| |0〉 | |0〉 | — | 117851.0 |
| |1〉 | |1,1,1/2,7/2〉 | 1135.6 | −285144.0 |
| |1〉 | |1,1,3/2,5/2〉 | 2.3 | −82709.5 |
| |e〉 | |0,0,3/2,5/2〉 | 470.8 | 122454.0 |
| |0〉 | |1,1,3/2, 7/2〉 | 1249.8 | −86537.2 |
| From (i) | To (j) | H ij /ℏ [s−1] | H jj /ℏ [s−1] |
|---|---|---|---|
| |e;0〉 | |0;e〉 | −390.7 | 0 |
| |e;0〉 | |0;1,1,3/2,5/2〉 | −195.6 | −82715.8 |
| |e;0〉 | |0,0,3/2,5/2;1,1,3/2,7/2〉 | 107.6 | −81940.9 |
| |e;0〉 | |0;1,1,1/2,7/2〉 | 180.0 | −285151.0 |
| |e;0〉 | |1;1,1,3/2,7/2〉 | 119.3 | −204395.0 |
5 Gate speed and fidelity
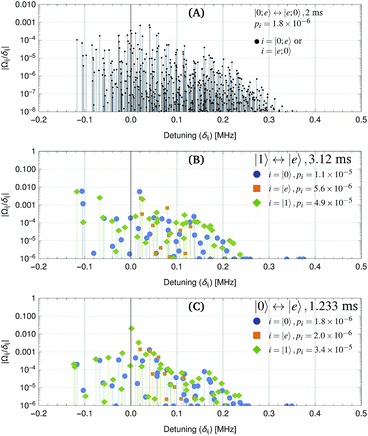
In addition to the desired evolution in eqn (1), the iSWAP gate sequence causes off-resonant coupling to other molecular states. This causes a trade-off between gate speed and fidelity. Although two NaCs molecules could be brought to a separation below 1 μm, with an exchange duration of 50 μs, such an interaction would limit the gate fidelity to 99.6%. At low magnetic field with NaCs, we find that the interactions couple off-resonantly to other states with δ > 10 kHz detuning both for the π-pulses and the exchange. For the square pulses considered here, time-energy uncertainty causes off-resonant population transfer out of the computational basis states and a gate error of order (τδ)−2. Off-resonant coupling to other states also causes dynamic Stark shifts which result in small reproducible phase and frequency shifts. We expect that these can be corrected for without loss of fidelity.We have calculated the unitary time evolution for all states that could couple via microwave pulses (ĤE) and dipole–dipole interactions (ĤDD) to the states in Fig. 1B. For low magnetic field (1 Gauss), details of the Hamiltonian terms are given is Tables 1 and 2, where we have chosen the states |0〉 = |0,0,3/2,7/2〉, |1〉 = |0,0,1/2,7/2〉 and |e〉 = |1,0,3/2,7/2〉.
We find that a gate with 10 ms duration has a fidelity of F = 1 − 3.6 × 10−5. The exchange part of the example gate holds the two molecules at a distance of 2.9 μm for a duration τx = 4.02 ms. The π-pulses of duration 3.01 ms utilize a σ+ polarized microwave electric field at a frequency of 3.48 GHz and amplitude 0.03 V m−1. The π-pulse and exchange fidelities due to population leakage are shown separately in Fig. 3. Population leakage out of the computational basis must be corrected for to support long gate sequences.46 Off-resonant coupling can likely be reduced by use of shaped pulses rather than square ones, to reach the same fidelity in a shorter duration.47 At a higher magnetic field of 35 Gauss with 600 kHz trap depth, the best states (F = 1 − 6 × 10−5 at 9.4 ms) are |1〉 = |0,0,3/2,5/2〉 and |e〉 = |1,−1,3/2,7/2〉, with |0〉 as above.
6 Intensity fluctuations and light shifts
If the molecule is optically trapped, light shifts significantly perturb the energy eigenstates and transition frequencies. To reach the wavefunction spread described in Section 7, we assume a 600 kHz trap depth (12.9 kW cm−2 intensity) with elliptical polarization.48 We also assume a trapping laser wavelength of 1030 nm. The resulting energy levels are shown in Fig. 4 for a magnetic field of 35 Gauss. The higher magnetic field was chosen, because the Zeeman splitting reduces off-resonant couplings during the |1〉 ↔ |e〉 π-pulses that are induced by the light shift Hamiltonian. Fig. 5 shows the magnitude of off-resonant coupling terms to other molecular states. For interactions that turn on and off sharply, the loss of fidelity due to off-resonant population leakage is given by a sum of terms involving off-resonant coupling strengths and detunings (see Appendix A). Overall, we find that the exchange interaction has reduced leakage compared to the 1 Gauss case, even for a faster interaction. The |1〉 ↔ |e〉 π-pulses cause slightly higher leakage, which may be reduced by shaped or DRAG pulse techniques.47For an optical trap with elliptical polarization, the quadratic sensitivity to intensity is calculated to be Δf = (ΔI/I)2 × 12.6 kHz, leading to gate errors of 5 × 10−6 for relative intensity fluctuations of ΔI/I = 2 × 10−3. A more significant effect is polarization drift. For quartz waveplates with a temperature sensitivity of retardance of 10−4 K−1, one may expect polarization ellipticity fluctuations of 10−5 and light shift fluctuations of 4 × 10−6 (2.5 Hz). Because these fluctuations are slow thermal effects, spin echo pulses can reduce their impact. If the quadratic light shift changes slowly, e.g. due to recoil heating, the effect is also mitigated. One possible implementation is shown in Table 3 where a |0〉 ↔ |e〉 π-pulse is inserted in the middle of the gate sequence. This leads to first-order insensitivity of the gate error with respect to constant light shift errors. The result is equivalent to an iSWAP gate between the qubits, followed by inversion of the individual qubits. Note that this spin-echo example was chosen for simplicity, and other dynamical decoupling techniques to compensate slow drifts could also be applied. The |0〉 ↔ |e〉 π-pulses, which are used for the spin-echo have little off-resonant coupling, even for a 1 ms duration (see Fig. 5).
The differential light shift between two hyperfine ground states for NaK was measured30 as 5 × 10−5 Hz (W/cm−2)−1. With the assumption that the states |0〉 and |1〉 in NaCs have similar differential shifts, a beam with 10 kW cm−2 intensity and 1064 nm wavelength can Stark shift the |e〉 states of the stored qubits by 200 kHz while shifting their |0〉 and |1〉 states by only 0.6 Hz differentially. In this case, the polarization is adjusted for maximum differential Stark shift of |e〉 with respect to |0〉 and a spatially patterned beam can be generated in the same way as the tweezer array. If the Stark shifting beam has a relative intensity stability of 2 × 10−3, the loss of fidelity is 1 − F ≈ 7 × 10−10 for a single stored qubit. The large ratio between |0〉 − |e〉 and |0〉 − |1〉 sensitivities makes it possible to individually address certain molecules by light-shifting the |e〉 state of the other molecules.
7 Effects of molecule motion
In the ideal gate, both molecules are in the motional ground state of their optical tweezer, and the exchange interaction strength is always the same. However, ground-state cooling is imperfect and the molecules gain kinetic energy due to photon recoil. Given the imaginary polarizability of NaCs Im[α] ≈ 10−4 (atomic units),49 the total scattering rate for a 600 kHz deep trap is approximately 0.8 Hz with a heating rate of 0.44 quanta per second axially and 0.023 quanta per second for each radial direction. Therefore, it is desirable for the gate fidelity to exceed the ground-state occupation fidelity. Here we examine the effect of motional excitations where the spatial coupling constant of eqn (3) is modified. For the proposed situation where the molecular dipoles lie along![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) , this coupling scales as (1 − 3
, this coupling scales as (1 − 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos2
cos2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ)/r3 where θ is the angle between the separation axis and
θ)/r3 where θ is the angle between the separation axis and ![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) , and r is the separation distance (2.5 μm here). For θ ≈ 0, a series expansion in terms of spatial coordinates yields a change in the interaction Rabi rate Ω per motional quantum of
, and r is the separation distance (2.5 μm here). For θ ≈ 0, a series expansion in terms of spatial coordinates yields a change in the interaction Rabi rate Ω per motional quantum of| Δ〈m|Ω|m〉/Δnj,k ≈ fkΩ0(sk/r)2 | (4) |
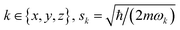 are the zero-point wave function spreads, fx = 12, fy,z = −6, and the approximation includes terms up to second order in position. The above trap depth corresponds to motional frequencies of ωx,y = 2π·12.4 kHz and ωz = 2π·2.8 kHz for NaCs, where a Gaussian beam radius of 1 μm is assumed. Because the loss of fidelity is proportional to the square of the Rabi rate deviation from the mean, 1 − F can calculated from the variance of the Rabi rate, which can be expressed in terms of mean motional quantum numbers
are the zero-point wave function spreads, fx = 12, fy,z = −6, and the approximation includes terms up to second order in position. The above trap depth corresponds to motional frequencies of ωx,y = 2π·12.4 kHz and ωz = 2π·2.8 kHz for NaCs, where a Gaussian beam radius of 1 μm is assumed. Because the loss of fidelity is proportional to the square of the Rabi rate deviation from the mean, 1 − F can calculated from the variance of the Rabi rate, which can be expressed in terms of mean motional quantum numbers ![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) j,k for a thermal distribution of motional states:
j,k for a thermal distribution of motional states: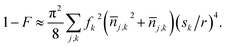 | (5) |
If the molecules are near the motional ground state with excitations dominated by imperfect cooling of Na,50 the mean excitation numbers of each molecule along x, y, and z are 0.019, 0.024, and 0.024 respectively. Then motional effects cause a fidelity loss of 9 × 10−6 for the above trap strength. The effect of motion on the two-qubit gate can be reduced by implementing a BB1 sequence.51,52 Because the sign of fz is opposite fx, it is possible to choose a separation direction that makes the interaction Rabi rate first-order insensitive to nj,z. This occurs for ![[r with combining circumflex]](https://www.rsc.org/images/entities/i_char_0072_0302.gif) =
= ![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif)
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ + ẑ
θ + ẑ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin
sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ with θ = (1/4)cos−1(3/35), and the interaction strength is reduced by 20%. An optical lattice in the weakly confining direction would also reduce the effects of axial motion. Note that the term
θ with θ = (1/4)cos−1(3/35), and the interaction strength is reduced by 20%. An optical lattice in the weakly confining direction would also reduce the effects of axial motion. Note that the term ![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) j,k2sk4 in eqn (5), which limits fidelity for
j,k2sk4 in eqn (5), which limits fidelity for ![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) j,k > 1, is independent of trap intensity when
j,k > 1, is independent of trap intensity when ![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) j,k is dominated by recoil heating.
j,k is dominated by recoil heating.
The motional state also affects the average light shift, because the tweezer intensity drops away from the trap center. For a Gaussian beam trap with thermally excited molecules whose mean quantum numbers are ![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) k, we find the relative intensity variance
k, we find the relative intensity variance 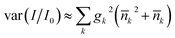 where gk = −4(sk/w)2 for the radial directions, gz = −2(szλ/(πw2))2 and w is the beam radius. The associated standard deviation in relative intensity is 2 × 10−3 for the residual motion after ground-state cooling described above. This corresponds to the intensity stability assumed in Section 6.
where gk = −4(sk/w)2 for the radial directions, gz = −2(szλ/(πw2))2 and w is the beam radius. The associated standard deviation in relative intensity is 2 × 10−3 for the residual motion after ground-state cooling described above. This corresponds to the intensity stability assumed in Section 6.
8 Other effects
Effects from blackbody radiation and spontaneous emission are small for the system we have outlined above. The dominant effect at room temperature is due to blackbody radiation and for NaCs the vibrational transition absorption rate is 1.7 × 10−3 s−1 while the rotational transition rate is negligible.53 The spontaneous emission rate from the N = 1 rotationally excited state is of order 10−8 s−1.The rate of decoherence due to scattering of optical tweezer photons has not been calculated. However, where long coherence between hyperfine ground states of NaK was observed, the decoherence was attributed to spatial intensity variation in the optical trap rather than scattering.30 A calculation of scattering rates should distinguish between internal-state-preserving (Rayleigh) and internal-state-changing (Raman) scattering, as the rate of Raman scattering can be several orders of magnitude lower than Rayleigh scattering.54,55
Magnetic field fluctuations cause dephasing of quantum states if their energies have an unequal slope with respect to field changes. For both the 1 Gauss and 35 Gauss examples, we find that the relative sensitivities of the |0〉, |1〉, and |e〉 states are below 1 kHz Gauss−1. While this field sensitivity is small, the associated loss of fidelity grows with a factor N2 if maximally entangled states such as 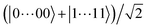 with N qubits are stored in the qubit array. The same scaling applies to light that differentially shifts the phase of |0〉 and |1〉 (see Section 6). Such common-mode dephasing errors can be reduced by use of dynamical decoupling or decoherence-free subspaces.56
with N qubits are stored in the qubit array. The same scaling applies to light that differentially shifts the phase of |0〉 and |1〉 (see Section 6). Such common-mode dephasing errors can be reduced by use of dynamical decoupling or decoherence-free subspaces.56
9 Single qubit rotations
Single qubit X and Y rotations are less complex than two-qubit gates and can be accomplished by individually addressing only one molecule and using a simplified sequence without dipole–dipole exchange. It may be advantageous to first perform a π-pulse from |0〉 to |e〉, then a rotation between |1〉 and |e〉 and finally a π-pulse from |e〉 to |0〉 as shown in Table 4. The |0〉 ↔ |e〉 π-pulses can have less off-resonant coupling than the previously discussed |1〉 ↔ |e〉 pulses (see Fig. 5), and high fidelity can be achieved for a shorter gate duration than in the two-qubit case. Rotation about the Z axis can be accomplished by a |0〉 ↔ |e〉 π-pulse with one oscillator phase, followed by a second |0〉↔ |e〉 π-pulse with a different oscillator phase.| π0↔e | Rot. | −π0↔e | ||||
|---|---|---|---|---|---|---|
| |1〉 | → | |1〉 | → | α|1〉 − β|e〉 | → | α|1〉 + β|0〉 |
| |0〉 | → | −|e〉 | → | γ|1〉 − δ|e〉 | → | γ|1〉 + δ|0〉 |
10 Conclusion
We have described a room-temperature scheme for quantum computing based on iSWAP gates performed by dipolar molecules, individually trapped in optical tweezers. Calculations indicate a potential gate fidelity above 0.9999 with low decoherence, although the rate of Raman scattering of optical tweezer photons remains to be determined. A modest magnetic field is used, and electric fields or field gradients are not needed. Scaling to many qubits would require an equal number of optical dipole traps in a movable pattern. For this gate to be realized, individual neutral ground-state molecules must still be produced, and improved state-measurement is needed. We expect that long gate sequences will require the mitigation of population leakage and recoil heating, e.g. by periodically teleporting the state of used molecules onto new ones.46 While this proposal utilizes two hyperfine ground levels of NaCs, thirty other ground levels exist, which might allow each molecule to contain several qubits.Although the proposed iSWAP gate is slower than quantum gates in other systems, decoherence effects can be small due to the fact that the qubit states are isolated from the environment by the symmetry of 1Σ+ states. The longer gate duration also reduces the noise bandwidth of actively stabilized parameters. For the foreseeable future, experimental quantum computing will aim to increase the number of available qubits and gate fidelity, and molecules have the potential to advance both goals.
A. Off-resonant coupling
We wish to calculate the population leakage during gate interactions. In this case, there are two “main” states (here |a〉 and |b〉) and leakage states |j〉 to which the main states connect with large detuning and/or weak coupling. For simplicity, we assume that the Hamiltonian associated with the interaction turns on and off instantaneously to produce time-independent coupling. In a real implementation, it will be important to ramp the interactions up and down smoothly to minimize off-resonant coupling.One approach for calculating leakage is to generate the full Hamiltonian matrix and diagonalize it to compute the unitary time evolution. While straightforward, this is computationally expensive when there are many leakage states. Complementary to the full calculation of unitary time evolution, we use first-order perturbation theory below to calculate the population leakage as a simple sum. A comparison of the techniques can be seen in Fig. 3. Note that this does not account for coherent population buildup, which may develop if several interactions are combined without phase randomization.
During interactions between degenerate primary states |a〉 and |b〉 with coupled leakage states |j〉, the Hamiltonian can be written in terms of “desired” coupling Ĥ0 and “leakage” couplings Ĥ′ as
| Ĥ = Ĥ0 + Ĥ′ | (6) |
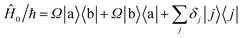 | (7) |
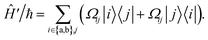 | (8) |
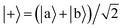 | (9) |
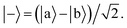 | (10) |
According to first-order perturbation theory, the perturbed eigenstates (assuming that different |j〉 states don't couple to one another) are
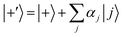 | (11) |
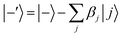 | (12) |
 | (13) |
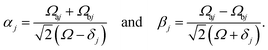 These states approximately diagonalize the time-evolution operator and can be used to estimate the transitions from the initial state |a〉 into states |j〉 due to unitary time evolution Û(t) = e−iĤt/ℏ:
These states approximately diagonalize the time-evolution operator and can be used to estimate the transitions from the initial state |a〉 into states |j〉 due to unitary time evolution Û(t) = e−iĤt/ℏ: | (14) |
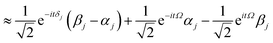 | (15) |
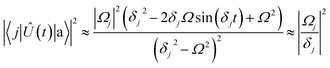 | (16) |
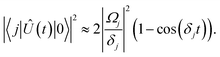 | (17) |
A careful choice of π-time reduces this leakage term, equivalent to minimizing leakage via alignment of power-spectrum zeros.
To evaluate the fidelity of each interaction step, we calculate the total population leakage probability from each nominally-populated state |i〉 as
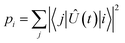 | (18) |
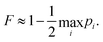 | (19) |
Conflicts of interest
There are no conflicts to declare.References
- N. M. Linke, D. Maslov, M. Roetteler, S. Debnath, C. Figgatt, K. A. Landsman, K. Wright and C. Monroe, Proc. Natl. Acad. Sci. U. S. A., 2017, 114, 3305–3310 CrossRef PubMed.
- P. H. Leung, K. A. Landsman, C. Figgatt, N. M. Linke, C. Monroe and K. R. Brown, Phys. Rev. Lett., 2018, 120, 020501 CrossRef PubMed.
- D. P. DiVincenzo, Fortschr. Phys., 2000, 48, 771–783 CrossRef.
- K. R. Brown, A. C. Wilson, Y. Colombe, C. Ospelkaus, A. M. Meier, E. Knill, D. Leibfried and D. J. Wineland, Phys. Rev. A: At., Mol., Opt. Phys., 2011, 84, 030303 CrossRef.
- C. J. Ballance, T. P. Harty, N. M. Linke, M. A. Sepiol and D. M. Lucas, Phys. Rev. Lett., 2016, 117, 060504 CrossRef PubMed.
- J. P. Gaebler, T. R. Tan, Y. Lin, Y. Wan, R. Bowler, A. C. Keith, S. Glancy, K. Coakley, E. Knill, D. Leibfried and D. J. Wineland, Phys. Rev. Lett., 2016, 117, 060505 CrossRef PubMed.
- S. Sheldon, L. S. Bishop, E. Magesan, S. Filipp, J. M. Chow and J. M. Gambetta, Phys. Rev. A, 2016, 93, 012301 CrossRef.
- R. Barends, J. Kelly, A. Megrant, A. Veitia, D. Sank, E. Jeffrey, T. C. White, J. Mutus, A. G. Fowler, B. Campbell, Y. Chen, Z. Chen, B. Chiaro, A. Dunsworth, C. Neill, P. O'Malley, P. Roushan, A. Vainsencher, J. Wenner, A. N. Korotkov, A. N. Cleland and J. M. Martinis, Nature, 2014, 508, 500 CrossRef PubMed.
- A. R. Calderbank and P. W. Shor, Phys. Rev. A: At., Mol., Opt. Phys., 1996, 54, 1098–1105 CrossRef.
- A. Steane, Proc. R. Soc. London, Ser. A, 1996, 452, 2551–2577 CrossRef.
- J. Preskill, Proc. R. Soc. London, Ser. A, 1998, 454, 385–410 CrossRef.
- D. Barredo, S. de Léséleuc, V. Lienhard, T. Lahaye and A. Browaeys, Science, 2016, 354, 1021–1023 CrossRef PubMed.
- M. Endres, H. Bernien, A. Keesling, H. Levine, E. R. Anschuetz, A. Krajenbrink, C. Senko, V. Vuletic, M. Greiner and M. D. Lukin, Science, 2016, 354, 1024–1027 CrossRef PubMed.
- D. DeMille, Phys. Rev. Lett., 2002, 88, 067901 CrossRef PubMed.
- S. F. Yelin, K. Kirby and R. Côté, Phys. Rev. A: At., Mol., Opt. Phys., 2006, 74, 050301 CrossRef.
- J. Zhu, S. Kais, Q. Wei, D. Herschbach and B. Friedrich, J. Chem. Phys., 2013, 138, 024104 CrossRef PubMed.
- F. Herrera, Y. Cao, S. Kais and K. B. Whaley, New J. Phys., 2014, 16, 075001 CrossRef.
- M. Karra, K. Sharma, B. Friedrich, S. Kais and D. Herschbach, J. Chem. Phys., 2016, 144, 094301 CrossRef PubMed.
- D. P. DiVincenzo, Phys. Rev. A: At., Mol., Opt. Phys., 1995, 51, 1015–1022 CrossRef.
- N. Schuch and J. Siewert, Phys. Rev. A: At., Mol., Opt. Phys., 2003, 67, 032301 CrossRef.
- D. Loss and D. P. DiVincenzo, Phys. Rev. A: At., Mol., Opt. Phys., 1998, 57, 120–126 CrossRef.
- D. Mozyrsky, V. Privman and M. L. Glasser, Phys. Rev. Lett., 2001, 86, 5112–5115 CrossRef PubMed.
- A. Blais, R.-S. Huang, A. Wallraff, S. M. Girvin and R. J. Schoelkopf, Phys. Rev. A: At., Mol., Opt. Phys., 2004, 69, 062320 CrossRef.
- A. Andre, D. DeMille, J. M. Doyle, M. D. Lukin, S. E. Maxwell, P. Rabl, R. J. Schoelkopf and P. Zoller, Nat. Phys., 2006, 2, 636–642 Search PubMed.
- R. Barnett, D. Petrov, M. Lukin and E. Demler, Phys. Rev. Lett., 2006, 96, 190401 CrossRef PubMed.
- A. V. Gorshkov, S. R. Manmana, G. Chen, J. Ye, E. Demler, M. D. Lukin and A. M. Rey, Phys. Rev. Lett., 2011, 107, 115301 CrossRef PubMed.
- B. Yan, S. A. Moses, B. Gadway, J. P. Covey, K. R. A. Hazzard, A. M. Rey, D. S. Jin and J. Ye, Nature, 2013, 501, 521–525 CrossRef PubMed.
- M. L. Wall, K. R. A. Hazzard and A. M. Rey, Quantum magnetism with ultracold molecules, in From atomic to mesoscale: The Role of Quantum Coherence in Systems of Various Complexities, ed. S. Malinovskaya and I. Novikova, World Scientific, 2015 Search PubMed.
- A. de Paz, A. Sharma, A. Chotia, E. Maréchal, J. H. Huckans, P. Pedri, L. Santos, O. Gorceix, L. Vernac and B. Laburthe-Tolra, Phys. Rev. Lett., 2013, 111, 185305 CrossRef PubMed.
- J. W. Park, Z. Z. Yan, H. Loh, S. A. Will and M. W. Zwierlein, Science, 2017, 357, 372–375 CrossRef PubMed.
- R. Zare, Angular momentum: understanding spatial aspects in chemistry and physics, Wiley, 1988 Search PubMed.
- J. Aldegunde and J. M. Hutson, Phys. Rev. A, 2017, 96, 042506 CrossRef.
- J. Aldegunde, H. Ran and J. Hutson, Phys. Rev. A: At., Mol., Opt. Phys., 2009, 80, 043410 CrossRef.
- S. Ospelkaus, K.-K. Ni, G. Quéméner, B. Neyenhuis, D. Wang, M. H. G. de Miranda, J. L. Bohn, J. Ye and D. S. Jin, Phys. Rev. Lett., 2010, 104, 030402 CrossRef PubMed.
- L. R. Liu, J. T. Zhang, Y. Yu, N. R. Hutzler, Y. Liu, T. Rosenband and K.-K. Ni, ArXiv: 1701.03121, 2017.
- L. R. Liu, J. D. Hood, Y. Yu, J. T. Zhang, N. R. Hutzler, T. Rosenband and K.-K. Ni, Science, 2018, 360, 900–903 CrossRef PubMed.
- T. Takekoshi, L. Reichsöllner, A. Schindewolf, J. M. Hutson, C. R. Le Sueur, O. Dulieu, F. Ferlaino, R. Grimm and H.-C. Nägerl, Phys. Rev. Lett., 2014, 113, 205301 CrossRef PubMed.
- S. A. Will, J. W. Park, Z. Z. Yan, H. Loh and M. W. Zwierlein, Phys. Rev. Lett., 2016, 116, 225306 CrossRef PubMed.
- P. D. Gregory, J. A. Blackmore, J. Aldegunde, J. M. Hutson and S. L. Cornish, Phys. Rev. A, 2017, 96, 021402 CrossRef.
- M. Guo, X. Ye, J. He, G. Quéméner and D. Wang, Phys. Rev. A, 2018, 97, 020501 CrossRef.
- J. F. Barry, D. J. McCarron, E. B. Norrgard, M. H. Steinecker and D. DeMille, Nature, 2014, 512, 286–289 CrossRef PubMed.
- S. Truppe, H. J. Williams, M. Hambach, L. Caldwell, N. J. Fitch, E. A. Hinds, B. E. Sauer and M. R. Tarbutt, Nat. Phys., 2017, 13, 1173 Search PubMed.
- L. Anderegg, B. L. Augenbraun, E. Chae, B. Hemmerling, N. R. Hutzler, A. Ravi, A. Collopy, J. Ye, W. Ketterle and J. M. Doyle, Phys. Rev. Lett., 2017, 119, 103201 CrossRef PubMed.
- L. Anderegg, B. L. Augenbraun, Y. Bao, S. Burchesky, L. W. Cheuk, W. Ketterle and J. M. Doyle, ArXiv: 1803.04571, 2018.
- M. Nielsen and I. Chuang, Quantum Computation and Quantum Information, Cambridge University Press, 2000 Search PubMed.
- A. G. Fowler, Phys. Rev. A: At., Mol., Opt. Phys., 2013, 88, 042308 CrossRef.
- F. Motzoi, J. M. Gambetta, P. Rebentrost and F. K. Wilhelm, Phys. Rev. Lett., 2009, 103, 110501 CrossRef PubMed.
- T. Rosenband, D. D. Grimes and K.-K. Ni, Optics Express, ArXiv: 1804.01030, 2018, in press Search PubMed.
- R. Vexiau, D. Borsalino, M. Lepers, A. Orban, M. Aymar, O. Dulieu and N. Bouloufa-Maafa, Int. Rev. Phys. Chem., 2017, 36, 709–750 Search PubMed.
- Y. Yu, N. R. Hutzler, J. T. Zhang, L. R. Liu, J. D. Hood, T. Rosenband and K.-K. Ni, Phys. Rev. A, 2018, 97, 063423 CrossRef.
- S. Wimperis, J. Magn. Reson., Ser. A, 1994, 109, 221–231 CrossRef.
- J. A. Jones, Proc. R. Soc. London, Ser. A, 2003, 361, 1429–1440 Search PubMed.
- N. Vanhaecke and O. Dulieu, Mol. Phys., 2007, 105, 1723–1731 CrossRef.
- R. A. Cline, J. D. Miller, M. R. Matthews and D. J. Heinzen, Opt. Lett., 1994, 19, 207–209 CrossRef PubMed.
- H. Uys, M. J. Biercuk, A. P. VanDevender, C. Ospelkaus, D. Meiser, R. Ozeri and J. J. Bollinger, Phys. Rev. Lett., 2010, 105, 200401 CrossRef PubMed.
- P. Zanardi and M. Rasetti, Phys. Rev. Lett., 1997, 79, 3306–3309 CrossRef.
| This journal is © The Royal Society of Chemistry 2018 |



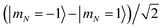
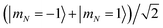
![[small epsilon, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e107.gif)