Open Access Article
Open Access Article“Found in Translation”: predicting outcomes of complex organic chemistry reactions using neural sequence-to-sequence models†
Philippe
Schwaller‡
 *,
Théophile
Gaudin‡
,
Dávid
Lányi
,
Costas
Bekas
and
Teodoro
Laino
*,
Théophile
Gaudin‡
,
Dávid
Lányi
,
Costas
Bekas
and
Teodoro
Laino
IBM Research, Zurich, Switzerland. E-mail: {phs,tga,dla,bek,teo}@zurich.ibm.com
First published on 22nd June 2018
Abstract
There is an intuitive analogy of an organic chemist's understanding of a compound and a language speaker's understanding of a word. Based on this analogy, it is possible to introduce the basic concepts and analyze potential impacts of linguistic analysis to the world of organic chemistry. In this work, we cast the reaction prediction task as a translation problem by introducing a template-free sequence-to-sequence model, trained end-to-end and fully data-driven. We propose a tokenization, which is arbitrarily extensible with reaction information. Using an attention-based model borrowed from human language translation, we improve the state-of-the-art solutions in reaction prediction on the top-1 accuracy by achieving 80.3% without relying on auxiliary knowledge, such as reaction templates or explicit atomic features. Also, a top-1 accuracy of 65.4% is reached on a larger and noisier dataset.
1 Introduction
After nearly 200 years of documented research, the synthesis of organic molecules remains one of the most important tasks in organic chemistry. The construction of a target molecule from a set of existing reactants and reagents via chemical reactions is attracting much attention because of its economical implications.Multiple efforts have been made in the past 50 years to rationalize the large number of chemical compounds and reactions identified, which form the large knowledge bases for solving synthetic problems. In 1969, Corey and Wipke1 demonstrated that both synthesis and retrosynthesis could be performed by a machine. Their pioneering contribution involved the use of handcrafted rules made by experts, which are commonly known as reaction templates. The templates encode the local changes to the atoms' connectivity under certain conditions accounting for various subtleties of retrosynthesis. A similar algorithm emerged in the late 1970s2 which also requires a set of expert rules. Unfortunately, rules writing is a tedious task, both time and labor-intensive, and may not cover the entire domain for complex organic chemistry problems. In such cases, profound chemical expertise is still required, and the solutions are usually developed by trained organic chemists. However, it can be extremely challenging even for them to synthesize a relatively complex molecule, which may take several reaction steps to construct. In fact, navigating the chemical space of drug-related compounds by relying only on intuition may turn a synthesis into a nearly impossible task, especially if the problem is slightly outside the expert's knowledge.
Other approaches extract reaction templates directly from data.3–6 In this specific context, candidate products are generated from the templates and then are ranked according to their likelihood. Satoh and Funatsu3,4 used various hard-coded criterion to perform the ranking whereas more recent approaches5,6 used a deep neural network. However, these types of approaches are fundamentally dependent on the rule-based system component and thus inherit some of its major limitations. In particular, these approaches do not produce sufficiently accurate predictions outside of the training domain.
Nevertheless, the class of algorithms1–6 that is based on rules manually encoded by human experts or automatically derived from a reaction database is not the only way to approach the problem of organic synthesis. A second approach for predicting chemical reactions exploits the advancements in computational chemistry to evaluate the energy barriers of a reaction, based on first-principle calculations.7–9 Although it is possible to reach very accurate levels of predictions for small systems (chemical reactions involving few hundred atoms), it is still a very computationally daunting task which limits, among other things, the sampling of the solvent degrees of freedom, possibly resulting in unrealistic entropy contributions. Therefore, while computational chemistry may intrinsically solve the problem of reaction prediction, its prohibitive cost does prevent the systematic treatment of all those degrees of freedom that may drive the chemical reaction along a specific route. For such reasons, its current field of applicability in industry is mainly limited to problems that may have a purely academic interest.
One way to view the reaction prediction task is to cast it as a translation problem, where the objective is to map a text sequence that represents the reactants to a text sequence representing the product. Molecules can equivalently be expressed as text sequences in line notation format, such as the simplified molecular-input line-entry system (SMILES).10 Intuitively, there is an analogy between a chemist's understanding of a compound and a language speaker's understanding of a word. No matter how imaginative such an analogy is, it was only very recently that a formal verification was proved.11 Cadeddu et al.11 showed that organic molecules contain fragments whose rank distribution is essentially identical to that of sentence fragments. Moreover, it has already been shown that a text representation of molecules has been effective in chemoinformatics.12–16 This has strengthened our belief that the methods of computational linguistics can have an immense impact on the analysis of organic molecules and reactions.
In this work, we build on the idea of relating organic chemistry to a language and explore the application of state-of-the-art neural machine translation methods, which are sequence-to-sequence (seq2seq) models. We intend to solve the forward-reaction prediction problem, where the starting materials are known and the interest is in generating the products. This approach was first pioneered by Nam and Kim.17 Here, we propose a model with higher capacity and a different attention mechanism, which better captures the relation between reactants and products. For the tokenization, we combine an atom-wise tokenization for the reactants similar to the work of Nam and Kim17 with a one-hot reagent tokenization suggested by Schneider et al.18 Given that training data for reaction condition were available, the tokenization would be arbitrarily extensible with tokens describing those conditions. In this work, we only use a set of the most common reagents.19 The overall network architecture is simple, and the model is trained end-to-end, fully data-driven and without additional external information. With this approach, we improved the top-1 accuracy by 0.7% compared to current template-free solutions, achieving a value of 80.3% using their own training and test data sets.20 The model presented set also a first score of 65.4% on a noisy single product reactions dataset extracted from US patents.
2 Related work
2.1 Template-based reaction prediction
Template-based reaction prediction methods have been widely researched in the past couple of years.5,6,21 Wei et al.21 used a graph-convolution neural network proposed by Duvenaud et al.22 to infer fingerprints of the reactants and reagents. They trained a network on the fingerprints to predict which reaction templates to apply to the reactants. Segler and Waller5 built a knowledge graph using reaction templates and discovered novel reactions by searching for missing nodes in the graph. Coley et al.6 generated for a given set of reactants all possible product candidates from a set of reaction templates extracted from US patents23 and predicted the outcome of the reaction by ranking the candidates with a neural network. One major advancement by Segler and Waller5 and Coley et al.6 was to consider alternative products as negative examples. Recently, Segler and Waller24 introduced a neural-symbolic approach. They extracted reaction rules from the commercially available Reaxys database. Then, they trained a neural network on molecular fingerprints to prioritize templates. The reaction products were generated using the top-ranked templates. In any case, template-based methods have the limitation that they cannot predict anything outside the space covered by the previously extracted templates.2.2 Template-free reaction prediction
While template-free approaches existed for decades,25–28 a first rule-free approach was introduced by Kayala et al.29 Using fingerprints and hand-crafted features, they predicted a series of mechanistic steps to obtain one reaction outcome. Owing to the sparsity of data on such mechanistic reaction steps, the dataset was self-generated with a template-based expert system. Recently, Jin et al.20 used a novel approach based on Weisfeiler–Lehman Networks (WLN). They trained two independent networks on a set of 400![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 reactions extracted from US patents. The first WLN scored the reactivity between atom pairs and predicted the reaction center. All possible bond configuration changes were enumerated to generate product candidates. The candidates that were not removed by hard-coded valence and connectivity rules are then ranked by a Weisfeiler–Lehman Difference Network (WLDN). Their method achieved a top-1 accuracy of 79.6% on a test set of 40
000 reactions extracted from US patents. The first WLN scored the reactivity between atom pairs and predicted the reaction center. All possible bond configuration changes were enumerated to generate product candidates. The candidates that were not removed by hard-coded valence and connectivity rules are then ranked by a Weisfeiler–Lehman Difference Network (WLDN). Their method achieved a top-1 accuracy of 79.6% on a test set of 40![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 reactions. Jin et al.20 claimed to outperform template-based approaches by a margin of 10% after augmenting the model with the unknown products of the initial prediction to have a product coverage of 100% on the test set. The dataset with the exact training, validation and test split have been released.§ The complexity of the reaction prediction problem was significantly reduced by removing the stereochemical information.
000 reactions. Jin et al.20 claimed to outperform template-based approaches by a margin of 10% after augmenting the model with the unknown products of the initial prediction to have a product coverage of 100% on the test set. The dataset with the exact training, validation and test split have been released.§ The complexity of the reaction prediction problem was significantly reduced by removing the stereochemical information.
2.3 Seq2seq models in organic reaction prediction and retrosynthesis
The closest work to ours is that of Nam and Kim,17 who also used a template-free seq2seq model to predict reaction outcomes. Whereas their network was trained end-to-end on patent data and self-generated reaction examples, they limited their predictions to textbook reactions. Their model was based on the Tensorflow translate model (v0.10.0),30 from which they took the default values for most of the hyperparameters. Compared to Nam and Kim,17 our model uses Luong's attention mechanism,31 through which a mapping between input and output tokens is obtained.Retrosynthesis is the opposite of reaction prediction. Given a product molecule, the goal is to find possible reactants. In contrast to major product prediction, in retrosynthesis more than one target string might be correct, e.g. a product could be the result of two different reactant pairs. Having no distinct target, the training of a seq2seq model can be more difficult. The first attempt of using a seq2seq model in retrosynthesis was achieved by Liu et al.32 They used a set of 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 reactions extracted and curated by Schneider et al.19 The reactions from that set include stereochemical information and are classified into ten different reactions classes. Overall, none of the previous works was able to demonstrate the full potential of seq2seq models.
000 reactions extracted and curated by Schneider et al.19 The reactions from that set include stereochemical information and are classified into ten different reactions classes. Overall, none of the previous works was able to demonstrate the full potential of seq2seq models.
3 Dataset
All the openly available chemical reaction datasets were derived in some form from the patent text-mining work of Daniel M. Lowe.23 Lowe's dataset has recently been updated and contains data extracted from US patents grants and applications dating from 1976 to September 2016.33 What makes the dataset particularly interesting is that the quality and noise may be similar to the data a chemical company might own. The portion of granted patents is made of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 808
808![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 938 reactions, which are described using SMILES.10
938 reactions, which are described using SMILES.10
Looking at the original patent data, it is surprising that a complex chemical synthesis process consisting of multiple steps, performed over hours or days, can be summarized in a simple string. Such reaction strings are composed of three groups of molecules: the reactants, the reagents, and the products, which are separated by a ‘>’ sign. The process actions and reaction conditions, for example, have been neglected so far.
To date, there is no standard way of filtering duplicates, incomplete or erroneous reactions in Lowe's dataset. We kept the filtering to a minimum to show that our network is able to handle noisy data. We removed 720![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 768 duplicates by comparing reaction strings without atom mapping and an additional 780 reactions, because the SMILES string could not be canonicalized with RDKit,34 as the explicit number of valence electrons for one of the atoms was greater than permitted. We took only single product reactions, corresponding to 92% of the dataset, to have distinct prediction targets. Although this is a current limitation in the training procedure of our model, it could be easily overcome in the future, for example by defining a specific order for the product molecules. Finally, the dataset was randomly split into training, validation and test sets (18
768 duplicates by comparing reaction strings without atom mapping and an additional 780 reactions, because the SMILES string could not be canonicalized with RDKit,34 as the explicit number of valence electrons for one of the atoms was greater than permitted. We took only single product reactions, corresponding to 92% of the dataset, to have distinct prediction targets. Although this is a current limitation in the training procedure of our model, it could be easily overcome in the future, for example by defining a specific order for the product molecules. Finally, the dataset was randomly split into training, validation and test sets (18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1).¶ Reactions with the same reactants, but different reagents and products were kept in the same set.
1).¶ Reactions with the same reactants, but different reagents and products were kept in the same set.
To compare our model and results with the current state of the art, we used the USPTO set recently published by Jin et al.20 It was extracted from Lowe's grants dataset33 and contains 479![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 035 atom-mapped reactions without stereochemical information. We restricted ourselves to single product reactions, corresponding to 97% of the reactions in Jin's USPTO set. An overview of the datasets taken as ground truths for this work is shown in Table 1.
035 atom-mapped reactions without stereochemical information. We restricted ourselves to single product reactions, corresponding to 97% of the reactions in Jin's USPTO set. An overview of the datasets taken as ground truths for this work is shown in Table 1.
In general, we observe that if reactions that do not work well with the model are removed under the assumption that they are erroneous, the model's accuracy will improve suggesting the presence of a specific tradeoff between coverage and accuracy. This calls for open datasets. The only fair way to compare models is to use datasets to which identical filtering was applied or where the reactions that the model is unable to predict are counted as false predictions.
3.1 Data preprocessing
To prepare the reactions, we first used the atom mappings to separate reagents from reactants. Input molecules with atoms appearing in the product were classified as reactants and the others without atoms in the product as reagents. Then, we removed the hydrogen atoms and the atom mappings from the reaction string, and canonicalized the molecules. Afterwards, we tokenized reactants and products atom-wise using the following regular expression:| token_regex = "(\[[^\]]+]|Br?|Cl?|N|O|S|P|F|I|b|c|n|o|s|p|\(|\)|\.|=|#|−|\+|\\\\\/|:|∼|@|\?|>|\*|\$|\%[0–9]{2}|[0–9])". |
As reagent atoms are never mapped into product atoms, we employed a reagent-wise tokenization using a set of the 76 most common reagents, according to the analysis in ref. 19. Reagents belonging to this set were added as distinct tokens after the first ‘>’ sign, ordered by occurrence. Other reagents, which were not in the set, were neglected and removed completely from the reaction string. The separate tokenization would allow us to extend the reaction information and add tokens for reaction conditions without changing the model architecture. The final source sequences were made up of tokenized “reactants > common reagents” and the target sequence of a tokenized “product”. The tokens were separated by space characters. The preprocessing steps together with examples are summarized in Table 2. The same preprocessing steps were applied to all datasets.
| Step | Example (entry 23![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 738, Jin's USPTO test set20): reactants > reagents > products 738, Jin's USPTO test set20): reactants > reagents > products |
|
|---|---|---|
| (1) | Original string | [Cl:1][c:2]1[cH:3][c:4]([CH3:8])[n:5][n:6]1[CH3:7].[OH:14][N+:15]([O−:16])=[O:17].[S:9](=[O:10])(=[O:11])([OH:12])[OH:13]≫[Cl:1][c:2]1[c:3]([N+:15](=[O:14])[O−:16])[c:4]([CH3:8])[n:5][n:6]1[CH3:7] |
| (2) | Reactants and reagent separation | [Cl:1][c:2]1[cH:3][c:4]([CH3:8])[n:5][n:6]1[CH3:7].[OH:14][N+:15]([O−:16])=[O:17]>[S:9](=[O:10])(=[O:11])([OH:12])[OH:13]>[Cl:1][c:2]1[c:3]([N+:15](=[O:14])[O−:16])[c:4]([CH3:8])[n:5][n:6]1[CH3:7] |
| (3) | Atom-mapping removal and canonicalization | Cc1cc(Cl)n(C)n1.O=[N+]([O−])O>O=S(=O)(O)O>Cc1nn(C)c(Cl)c1[N+](=O)[O−] |
| (4) | Tokenization | C![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) c c![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) c c![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) c c![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ( (![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) C C![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) l l![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ) )![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) n n![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ( (![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) C C![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ) )![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) n n![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) . .![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) O O![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) = =![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) [ [![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) N+ N+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ] ]![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ( (![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) [ [![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) O− O−![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ] ]![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ) )![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) O> O>![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) A1 A1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) > >![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) C C![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) c c![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) n n![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) n n![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ( (![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) C C![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ) )![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) c c![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ( (![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) C C![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) l l![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ) )![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) c c![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) [ [![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) N+ N+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ] ]![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ( (![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) = =![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) O O![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ) )![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) [ [![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) O−] O−] |
| Source | C![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) c c![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) c c![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) c c![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ( (![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) C C![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) l l![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ) )![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) n n![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ( (![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) C C![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ) )![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) n n![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) . .![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) O O![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) = =![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) [ [![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) N+ N+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ] ]![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ( (![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) [ [![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) O− O−![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ] ]![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ) )![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) O> O>![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) A1 A1 |
|
| Target | C![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) c c![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) n n![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) n n![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ( (![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) C C![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ) )![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) c c![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ( (![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) C C![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) l l![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ) )![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) c c![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) [ [![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) N+ N+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ] ]![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ( (![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) = =![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) O O![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ) )![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) [ [![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) O− O−![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ] ] |
4 Model
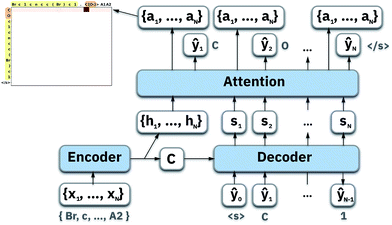
To map the sequence of the reactants/reagents to the sequence of the products, we adapted an existing implementation35 with minor modifications. Our model architecture, illustrated in Fig. 1, consists of two distinct recurrent neural networks (RNN) working together: (1) an encoder that processes the input sequence and emits its context vector C, and (2) a decoder that uses this representation to output a probability over a prediction. For these two RNNs, we rely on specific variants of long short-term memory (LSTM)36 because they are able to handle long-range relations in sequences. An LSTM consists of units that process the input data sequentially. Each unit at each time step t processes an element of the input xt and the network's previous hidden state ht−1. The output and the hidden state transition is defined by| it = σ(Wixt + Uiht−1 + bi) | (1) |
| ft = σ(Wfxt + Ufht−1 + bf) | (2) |
| ot = σ(Woxt + Uoht−1 + bo) | (3) |
| ct = ft ⊗ ct−1 + it ⊗ tanh(Wcxt + Ucht−1 + bc) | (4) |
| ht = ot ⊗ tanh(ct−1), | (5) |
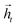 and
and 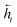 for each time step. The hidden states of a BLSTM are defined as
for each time step. The hidden states of a BLSTM are defined as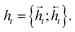 | (6) |
Thus we can formalize our encoder as
| C = f(Wext,ht−1), | (7) |
![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) n are the hidden states at time t; xt is an element of an input sequence x = {x0, …, xT}, which is a one-hot encoding of our vocabulary; and We are the learned embedding weights. Generally, C is simply the last of the encoder's hidden states:
n are the hidden states at time t; xt is an element of an input sequence x = {x0, …, xT}, which is a one-hot encoding of our vocabulary; and We are the learned embedding weights. Generally, C is simply the last of the encoder's hidden states:| C = hT | (8) |
The second part of the model – the decoder – predicts the probability of observing a product ŷ = {ŷ1, …, ŷM}:
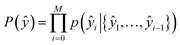 | (9) |
| p(ŷi|{ŷ1, …, ŷi−1},ci) = g(ŷi−1,si,ci), | (10) |
4.1 Luong's attention mechanism
To compute the context vector, we first have to compute the attention weights α: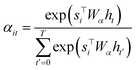 | (11) |
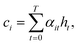 | (12) |
The attention vector is then defined by
| ai = tanh(Wa{ci;si}). | (13) |
Both Wα and Wa are learned weights. Then a can be used to compute the probability for a particular token:
| p(yi|{y1, …, yi−1},ci) = softmax(Wpai), | (14) |
4.2 Training details
During training, all parameters of the network were trained jointly using a stochastic gradient descent. The loss function was a cross-entropy function, expressed as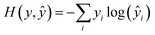 | (15) |
5 Architecture & hyperparameter search
Finding the best-performing set of hyperparameters for a deep neural network is not trivial. As mentioned in Section 4, our model has numerous parameters that can influence both its training and its architecture. Depending on those parameters, the performance of the model can vary notably. In order to select the best parameters efficiently, we build a framework around scikit-optimize.40 After the evaluation of 10 random sets, a gradient-boosted tree model41 was used as surrogate model together with expected improvement as acquisition function42 to guide the hyperparameter search on a space defined in Table 3. The sets of hyperparameters were evaluated according to their accuracy on the validation set. In total, we trained 100 models for 30 epochs. The set of best hyperparameters found with this method is highlighted in bold. This model has been further trained to 80 epochs to improve its final accuracy.| Parameter | Possible values |
|---|---|
| Number of units | 128, 256, 512 or 1024 |
| Number of layers | 2, 4 or 6 |
| Type of encoder | LSTM, BLSTM |
| Output dropout | 0–0.9 (0.7676) |
| State dropout | 0–0.9 (0.5374) |
| Learning rate | 0.1–5 (0.355) |
| Decay factor | 0.85–0.99 (0.854) |
| Type of attention | “Luong” or “Badhanau” |
6 Experiments
6.1 Reaction prediction
We evaluated our model on two data sets and compared the performance with other state-of-the-art results. After the hyperparameter optimization, we continued to train our best model on the 395![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 496 reactions in Jin's USPTO train set and tested the fully trained model on Jin's USPTO test set. Additionally, we trained a second model with the same hyperparameters on 902
496 reactions in Jin's USPTO train set and tested the fully trained model on Jin's USPTO test set. Additionally, we trained a second model with the same hyperparameters on 902![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 581 randomly chosen single-product reactions from the more complex and noisy Lowe dataset and tested it on a set of 50
581 randomly chosen single-product reactions from the more complex and noisy Lowe dataset and tested it on a set of 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 258 reactions. As molecules are discrete data, changing a single character, such as in source code or arithmetic expressions, can lead to completely different meanings or even invalidate the entire string. Therefore we use full-sequence accuracy, the strictest criteria possible, as our evaluation metric by which a test prediction is considered correct only if all tokens are identical to the ground truth.
258 reactions. As molecules are discrete data, changing a single character, such as in source code or arithmetic expressions, can lead to completely different meanings or even invalidate the entire string. Therefore we use full-sequence accuracy, the strictest criteria possible, as our evaluation metric by which a test prediction is considered correct only if all tokens are identical to the ground truth.
The network had to solve three major challenges. First, it had to memorize the SMILES grammar to predict synthetically correct sequences. Second, because we trained it on canonicalized molecules, the network had to learn the canonical representation. Third, the network had to map the reactants plus reagents space to the product space.
Although the training was performed without a beam search, we used a beam width of 10 without length penalty for the inference. Therefore the 10 most probable sequences were kept at every time step. This allowed us to know what probability the network assigned to each of the sequences. We used the top-1 probabilities to analyze the prediction confidence of the network.
The final step was to canonicalize the network output. This simple and deterministic reordering of the tokens improved the accuracy by 1.5%. Thus, molecules that were correctly predicted, but whose tokens were not enumerated in the canonical order, were still counted as correct. The prediction accuracies of our model on different datasets are reported in Table 4. For single product reactions, we achieved an accuracy of 83.2% on Jin's USPTO test dataset and 65.4% on Lowe's test set.
An additional validation can be found in the ESI,† were we used the model trained on Lowe's dataset to predict reactions from pistachio,45 a commercial database of chemical reactions extracted from the patent literature. Because the Lowe's dataset used to train the model contained reactions until September 2016, we only predicted the reactions from 2017 and hence, we had a time split.
6.2 Comparison with the state of the art
To the best of our knowledge, no previous work has attempted to predict reactions on the complete US patent dataset of Lowe.33Table 5 shows a comparison with the Weisfeiler–Lehman difference networks (WLDN) from Jin et al.20 on their USPTO test set. To make a fair comparison, we count all the multiple product reactions in the test set as false predictions for our model because we trained only on the single product reactions. By achieving 80.3% top-1 accuracy, we perform quantitatively nearly identical. As our model does not rank candidates, but was trained on accurately predicting the top-1 outcome, it is not surprising that the WLDN beats our model in the top-3 and top-5 accuracy. The decoding of the 38![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 648 USPTO test set reactions takes on average 25 ms per reaction, inferred with a beam search. Our model can therefore compete with the state of the art.
648 USPTO test set reactions takes on average 25 ms per reaction, inferred with a beam search. Our model can therefore compete with the state of the art.
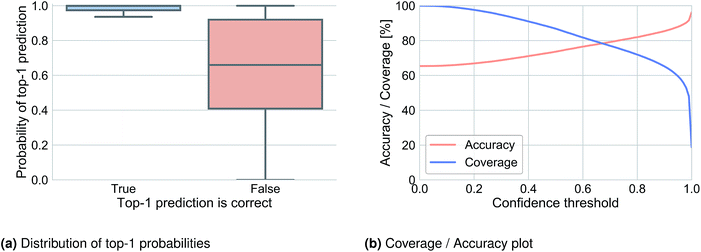
6.3 Prediction confidence
We analyzed the top-1 beam search probability to obtain information about prediction confidence and to observe how this probability was related to accuracy. Fig. 2a illustrates the distribution of the top-1 probability for Lowe's test set in cases where the top-1 prediction is correct (left) and where it is wrong (right). A clear difference can be observed and used to define a threshold under which we determine that the network does not know what to predict. Fig. 2b shows the top-1 accuracy and coverage depending on the confidence threshold. For example, for a confidence threshold of 0.83 the model would predict the outcome of 70.2% of the reactions with an accuracy of 83.0% and for the remaining 29.8% of the reaction it would not know the outcome.6.4 Attention
Attention is the key to take into account complex long-range dependencies between multiple tokens. Specific functional groups, solvents or catalysts have an impact on the outcome of a reaction, even if they are far from the reaction center in the molecular graph and therefore also in the SMILES string. Fig. 3 shows how the network learned to focus first on the C[O−] molecule, to map the [O−] in the input correctly to the O in the target, and to ignore the Br, which is replaced in the target. A few more reaction predictions together with the attention weights, confidence and token probabilities are found in the ESI.†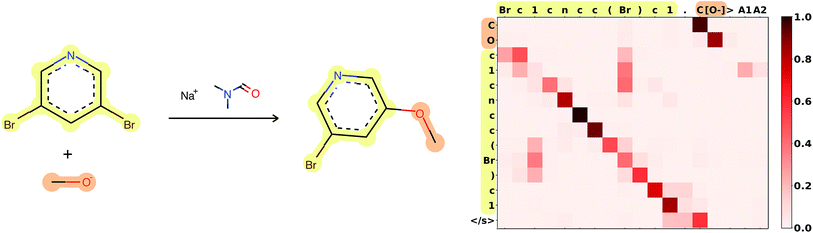 | ||
| Fig. 3 Attention weights of reaction 120 from Jin's USPTO test set. The atom mapping between reactants and product is highlighted. SMILES: Brc1cncc(Br)c1.C[O−]>CN(C)C=O.[Na+]>COc1cncc(Br)c1. Reaction plotted with RDKit.34 | ||
6.5 Limitations
Our model is not without limitations. An obvious disadvantage compared to template-based methods is that the strings are not guaranteed to be a valid SMILES. Incorporating a context-free grammar layer, as was done in ref. 12, could bring minor improvements. Fortunately, only 1.3% of the top-1 predictions are grammatically erroneous for our model.Another limitation of the training procedure are multiple product reactions. In contrast to words in a sentence, the exact order in which the molecules in the target string are enumerated does not matter. A viable option would be to include in the training set all possible permutations of the product molecules.
Our hyperparameter space during optimization was restricted to a maximum of 1024 units for the encoder. Using more units could have led to improvements. On Jin's USPTO dataset, the training plateaued because an accuracy of 99.9% was reached and the network had memorized almost the entire training set. Even on Lowe's noisier dataset, a training accuracy of 94.5% was observed. A hyperparameter optimization could be performed on Lowe's dataset to improve the prediction accuracy.
7 Conclusion
Predicting reaction outcomes is a routine task of many organic chemists trained to recognize structural and reactivity patterns reported in a wide number of publications. Not only did we show that a seq2seq model with correctly tuned hyperparameters can learn the language of organic chemistry, our approach also improved the current state-of-the-art in patent reaction outcome prediction by achieving 80.3% on Jin's USPTO dataset and 65.4% on single product reactions of Lowe's dataset. Similar to the work of Nam and Kim,17 our approach is fully data driven and free of chemical knowledge/rules and compared to their work,17 we take full advantage of the attention mechanism. Also worth mentioning is the overall simplicity of our model that jointly trains the encoder, decoder and attention layers end-to-end. Our hope is that, with this type of model, chemists can codify and perhaps one day fully automate the art of organic synthesis.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We thank Nadine Schneider, Greg Landrum and Roger Sayle for the helpful discussions on RDKit and the datasets. We also would like to acknowledge Marwin Segler and Hiroko Satoh for useful feedback on our approach.Notes and references
- E. J. Corey and W. T. Wipke, Science, 1969, 166, 178–192 CrossRef PubMed.
- T. D. Salatin and W. L. Jorgensen, J. Org. Chem., 1980, 45(11), 2043–2051 CrossRef.
- H. Satoh and K. Funatsu, J. Chem. Inf. Comput. Sci., 1995, 35, 34–44 CrossRef.
- H. Satoh and K. Funatsu, J. Chem. Inf. Comput. Sci., 1996, 36, 173–184 CrossRef.
- M. H. S. Segler and M. P. Waller, Chem.–Eur. J., 2017, 23, 6118–6128 CrossRef PubMed.
- C. W. Coley, R. Barzilay, T. S. Jaakkola, W. H. Green and K. F. Jensen, ACS Cent. Sci., 2017, 3, 434–443 CrossRef PubMed.
- W. R. J. Dolbier, K. Henryk, K. Houk and S. Chimin, Acc. Chem. Res., 1996, 29, 471–477 CrossRef.
- D. Mondal, S. Y. Li, L. Bellucci, T. Laino, A. Tafi, S. Guccione and S. D. Lepore, J. Org. Chem., 2013, 78, 2118–2127 CrossRef PubMed.
- O. Engkvist, P.-O. Norrby, N. Selmi, Y.-h. Lam, Z. Peng, E. C. Sherer, W. Amberg, T. Erhard and L. A. Smyth, Drug Discovery Today, 2018, 23(6), 1203–1218 CrossRef PubMed.
- D. Weininger, J. Chem. Inf. Comput. Sci., 1988, 281413, 31–36 CrossRef.
- A. Cadeddu, E. K. Wylie, J. Jurczak, M. Wampler-Doty and B. A. Grzybowski, Angew. Chem., Int. Ed., 2014, 53, 8108–8112 CrossRef PubMed.
- R. Gómez-Bombarelli, J. N. Wei, D. Duvenaud, J. M. Hernández-Lobato, B. Sánchez-Lengeling, D. Sheberla, J. Aguilera-Iparraguirre, T. D. Hirzel, R. P. Adams and A. Aspuru-Guzik, ACS Cent. Sci., 2018, 4, 268–276 CrossRef PubMed.
- S. Jastrzębski, D. Leśniak and W. M. Czarnecki, Learning to SMILE(S), 2016, http://arxiv.org/abs/1602.06289.
- M. J. Kusner, B. Paige and J. M. Hernández-Lobato, ICML, 2017 Search PubMed.
- E. J. Bjerrum, SMILES Enumeration as Data Augmentation for Neural Network Modeling of Molecules, 2017, http://arxiv.org/abs/1703.07076 Search PubMed.
- M. H. S. Segler, T. Kogej, C. Tyrchan and M. P. Waller, ACS Cent. Sci., 2018, 4, 120–131 CrossRef PubMed.
- J. Nam and J. Kim, Linking the Neural Machine Translation and the Prediction of Organic Chemistry Reactions, 2016, https://arxiv.org/pdf/1612.09529.pdf Search PubMed.
- N. Schneider, D. M. Lowe, R. A. Sayle and G. A. Landrum, J. Chem. Inf. Model., 2015, 55, 39–53 CrossRef PubMed.
- N. Schneider, N. Stiefl and G. A. Landrum, J. Chem. Inf. Model., 2016, 56, 2336–2346 CrossRef PubMed.
- W. Jin, C. Coley, R. Barzilay and T. Jaakkola, NIPS, 2017, pp. 2607–2616 Search PubMed.
- J. N. Wei, D. Duvenaud and A. Aspuru-Guzik, ACS Cent. Sci., 2016, 2, 725–723 CrossRef PubMed.
- D. K. Duvenaud, D. Maclaurin, J. Iparraguirre, R. Bombarell, T. Hirzel, A. Aspuru-Guzik and R. P. Adams, NIPS, 2015 Search PubMed.
- D. M. Lowe, Ph.D. thesis, University of Cambridge, 2012.
- M. H. S. Segler and M. P. Waller, Chem.–Eur. J., 2017, 23, 5966–5971 CrossRef PubMed.
- J. Bauer, E. Fontain, D. Forstmeyer and I. Ugi, Tetrahedron Comput. Methodol., 1988, 1, 129–132 CrossRef.
- P. Röse and J. Gasteiger, Anal. Chim. Acta, 1990, 235, 163–168 CrossRef.
- W. L. Jorgensen, E. R. Laird, A. J. Gushurst, J. M. Fleischer, S. A. Gothe, H. E. Helson, G. D. Paderes and S. Sinclair, Pure Appl. Chem., 1990, 62, 1921–1932 Search PubMed.
- W. A. Warr, Mol. Inf., 2014, 33, 469–476 CrossRef PubMed.
- M. A. Kayala and P. Baldi, J. Chem. Inf. Model., 2012, 52, 2526–2540 CrossRef PubMed.
- M. Abadi, P. Barham, J. Chen, Z. Chen, A. Davis, J. Dean, M. Devin, S. Ghemawat, G. Irving, M. Isard, M. Kudlur, J. Levenberg, R. Monga, S. Moore, D. G. Murray, B. Steiner, P. Tucker, V. Vasudevan, P. Warden, M. Wicke, Y. Yu, X. Zheng and G. Brain, OSDI, 2016 Search PubMed.
- M.-T. Luong, H. Pham and C. D. Manning, EMNLP, 2015 Search PubMed.
- B. Liu, B. Ramsundar, P. Kawthekar, J. Shi, J. Gomes, Q. Luu Nguyen, S. Ho, J. Sloane, P. Wender and V. Pande, ACS Cent. Sci., 2017, 3, 1103–1113 CrossRef PubMed.
- D. M. Lowe, Chemical reactions from US pat. (1976-Sep2016), 2017, https://figshare.com/articles/Chemical_reactions_from_US_patents_1976-Sep2016_/5104873.
- G. Landrum, B. Kelley, P. Tosco, S. Riniker, Gedeck, N. Schneider, R. Vianello, A. Dalke, S. Alexander, S. Turk, M. Swain, B. Cole, J. P, Strets123, JLVarjo, A. Pahl, P. Fuller, G. Doliath, M. Wójcikowski, D. Cosgrove, G. Sforna, M. Nowotka, J. H. Jensen, J. Domański, D. Hall, N. O'Boyle, W.-G. Bolick, Nhfechner and S. Roughley, Rdkit/Rdkit: 2017_09_1 (Q3 2017) Release, 2017, https://zenodo.org/record/1004356#.Wd3LDY6l2EI Search PubMed.
- R. Zhao, T. Luong and E. Brevdo, Neural Machine Translation (seq2seq) Tutorial, 2017, https://github.com/tensorflow/nmt Search PubMed.
- S. Hochreiter and J. Schmidhuber, Neural Comput., 1997, 9, 1735–1780 CrossRef PubMed.
- A. Graves and J. Schmidhuber, Neural Network., 2005, 18, 602–610 CrossRef PubMed.
- D. Bahdanau, K. Cho and Y. Bengio, ICLR, 2015 Search PubMed.
- R. J. Williams and D. Zipser, Neural Comput., 1989, 1, 270–280 CrossRef.
- T. Head, N. Campos, M. Cherti, A. Fabisch, T. Fan, M. Kumar, G. Louppe, K. Malone, M. Pak, I. Shcherbatyi, T. Smith and Z. Vinícius, Scikit-Optimize, 2017, http://scikit-optimize.github.io/ Search PubMed.
- J. H. Friedman, Ann. Stat., 2001, 29(5), 1189–1232 CrossRef.
- J. Mockus, J. Global Optim., 1994, 4, 347–365 CrossRef.
- K. Papineni, S. Roukos, T. Ward and W.-J. Zhu, ACL, 2001 Search PubMed.
- C.-Y. Lin, ACL, 2004 Search PubMed.
- N. Schneider, D. M. Lowe, R. A. Sayle, M. A. Tarselli and G. A. Landrum, J. Med. Chem., 2016, 59, 4385–4402 CrossRef PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available: Time-split test set and example predictions, together with attention weights, confidence and token probabilities. See DOI: 10.1039/c8sc02339e |
| ‡ P. S. and T. G. contributed equally to this work. |
| § https://github.com/wengong-jin/nips17-rexgen. |
| ¶ https://ibm.box.com/v/ReactionSeq2SeqDataset. |
| This journal is © The Royal Society of Chemistry 2018 |