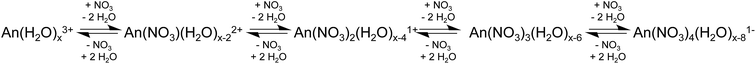Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
The coordination chemistry of CmIII, AmIII, and AcIII in nitrate solutions: an actinide L3-edge EXAFS study†‡
Maryline G.
Ferrier
a,
Benjamin W.
Stein
a,
Sharon E.
Bone
a,
Samantha K.
Cary
a,
Alexander S.
Ditter
ab,
Stosh A.
Kozimor
 *a,
Juan S.
Lezama Pacheco
c,
Veronika
Mocko
a and
Gerald T.
Seidler
b
*a,
Juan S.
Lezama Pacheco
c,
Veronika
Mocko
a and
Gerald T.
Seidler
b
aLos Alamos National Laboratory,, Los Alamos, New Mexico 87545, USA. E-mail: stosh@lanl.gov
bDepartment of Physics, University of Washington, Seattle, Washington 98195-1560, USA
cStanford University, Stanford, California 94305, USA
First published on 1st August 2018
Abstract
Understanding actinide(III) (AnIII = CmIII, AmIII, AcIII) solution-phase speciation is critical for controlling many actinide processing schemes, ranging from medical applications to reprocessing of spent nuclear fuel. Unfortunately, in comparison to most elements in the periodic table, AnIII speciation is often poorly defined in complexing aqueous solutions and in organic media. This neglect – in large part – is a direct result of the radioactive properties of these elements, which make them difficult to handle and acquire. Herein, we surmounted some of the handling challenges associated with these exotic 5f-elements and characterized CmIII, AmIII, and AcIII using AnIII L3-edge X-ray absorption spectroscopy (XAS) as a function of increasing nitric acid (HNO3) concentration. Our results revealed that actinide aquo ions, An(H2O)x3+ (x = 9.6 ± 0.7, 8.9 ± 0.8, and 10.0 ± 0.9 for CmIII, AmIII, and AcIII), were the dominant species in dilute HNO3 (0.05 M). In concentrated HNO3 (16 M), shell-by-shell fitting of the extended X-ray fine structure (EXAFS) data showed the nitrate complexation increased, such that the average stoichiometries of Cm(NO3)4.1±0.7(H2O)5.7±1.3(1.1±0.2)−, Am(NO3)3.4±0.7(H2O)5.4±0.5(0.4±0.1)−, and Ac(NO3)2.3±1.7(H2O)8.3±5.2(0.7±0.5)+ were observed. Data obtained at the intermediate HNO3 concentration (4 M) were modeled as a linear combination of the 0.05 and 16 M spectra. For all three metals, the intermediate models showed larger contributions from the 0.05 M HNO3 spectra than from the 16 M HNO3 spectra. Additionally, these efforts enabled the Cm–NO3 and Ac–NO3 distances to be measured for the first time. Moreover, the AnIII L3-edge EXAFS results, contribute to the growing body of knowledge associated with CmIII, AmIII, and AcIII coordination chemistry, in particular toward advancing understanding of AnIII solution phase speciation.
Introduction
The actinide(III) (AnIII) cations of CmIII, AmIII, and AcIII occupy central roles in numerous nuclear technologies important to society. These range from the medical applications in the targeted alpha therapeutic treatment of disease (AcIII)1–3 to being critical components in advanced nuclear fuel cycles (AmIII and CmIII).4–9 Solving technical problems in these areas require detailed understanding of fundamental +3 f-element chemistry. Unfortunately, aside from a limited number of experimental and computational studies,10–21 the chemistry of CmIII, AmIII, and AcIII is underdeveloped in comparison to the d-block, main group, and many other 4f- and 5f-elements. This discrepancy – in large part – is related to the rarity of these elements combined with handling difficulties that accompany the radioactive Cm, Am, and Ac isotopes.This manuscript documents our latest effort to address needs for advancing fundamental CmIII, AmIII, and AcIII chemistry. We focused on characterizing the coordination chemistry of these elements in an aqueous environment that contained actinide complexation agents, namely within nitric acid (HNO3) solutions. These results are of particular relevance, given the importance of HNO3 matrices in AnIII separation processing. For CmIII and AmIII, HNO3 solutions find widespread application in almost every advanced nuclear fuel processing flow chart.4,22–24 Additionally, HNO3 is widely used in the production of 225Ac for medical purposes (targeted alpha therapy), both in terms of purifying 225Ac from 232Th targets irradiated with high energy protons25–27 and when isolating 225Ac from 229Th generators.28–30 Towards these ends, we contribute an AnIII L3-edge X-ray absorption spectroscopy (XAS) study focused on characterizing CmIII, AmIII, and AcIII solution-phase coordination chemistry as a function of increasing HNO3 concentration. Our data provided the first AnIII–NO3 bond distance measurements for CmIII and AcIII of any kind (i.e. solid or solution) and represented the first AmIII–NO3 measurement made in HNO3 solutions. We observed that at low HNO3 concentrations (0.05 M), CmIII, AmIII, and AcIII existed as aquo ions. The propensity of NO3− to complex the AnIII cations increased with increasing HNO3 concentration, such that in HNO3 (16 M) solutions there were 2 to 4 bound NO3− ligands. The results have been presented in the context of the limited number of HNO3 speciation studies reported previously.
Results and discussion
Sample preparation
Samples were generated by first preparing chemically pure CmIII, AmIII and AcIII stock solutions, as previously described.12,20,31 Next, aliquots that contained CmIII (0.5 mg in 0.5 mL, 4.0 mM), AmIII (0.5 mg in 0.5 mL, 4.1 mM), and AcIII (28 μg in 0.3 mL, 0.4 mM) were heated to soft dryness. The resulting residues were dissolved in the desired concentration of nitric acid (HNO3; 0.05, 4, or 16 M). This process was repeated for a total of three times to ensure that the final HNO3 concentrations were as close to 0.05, 4 and 16 M as possible. Samples were then loaded into XAS holders equipped with three layers of containment to guard against release of radiological material during shipment and data acquisition. Next, the holders were shipped to the Stanford Synchrotron Radiation Lightsource (SSRL) for XAS analysis at the AnIII L3-edge on beam line 11-2.AnIII L3-edge X-ray absorption near edge spectroscopy (XANES)
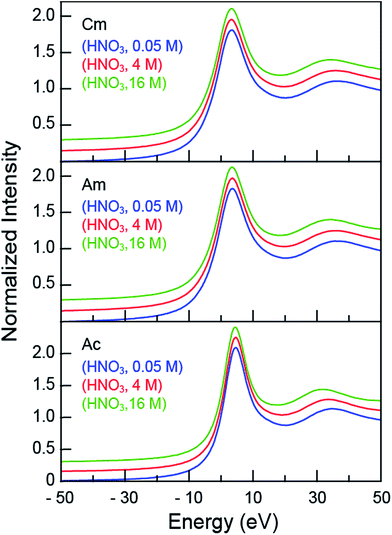
The room temperature CmIII, AmIII and AcIII L3-edge XANES spectra obtained from aqueous solutions that contained increasing amounts of nitric acid (HNO3; 0.05, 4, 16 M) were background subtracted and normalized (Fig. 1). Each spectrum contained a pronounced absorption peak superimposed on an ionization threshold. From the perspective of the free ion, the edge-feature could be crudely described as originating from electric-dipole allowed transitions from the actinide 2p-orbitals to unoccupied states that contained actinide 6d-character, i.e. for AcIII 2p6⋯5f0 6d0 → 2p5⋯5f0 6d1.32,33 The inflection points and peak maxima were determined graphically where the second derivatives (inflection point) and first derivatives (peak maxima) of the data equaled zero (Table 1). These values were impacted marginally by changes in HNO3 concentration: the inflection points for CmIII were centered around 18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 976 eV, for AmIII near 18
976 eV, for AmIII near 18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 514 eV, and for AcIII close to 15
514 eV, and for AcIII close to 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 875 eV. Based on our previous experience in reproducing actinide L3-edge features,12,21,34–41 uncertainties in edge and peak positions were estimated to be on the order of 0.2 eV. Hence, for a given element (CmIII, AmIII, or AcIII), the 0.05, 4, and 16 M absorption edges and peak positions were nearly equivalent.
875 eV. Based on our previous experience in reproducing actinide L3-edge features,12,21,34–41 uncertainties in edge and peak positions were estimated to be on the order of 0.2 eV. Hence, for a given element (CmIII, AmIII, or AcIII), the 0.05, 4, and 16 M absorption edges and peak positions were nearly equivalent.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 013.3 eV) while the AcIII spectra were calibrated to the first inflection point of a RbCl pellet (15
013.3 eV) while the AcIII spectra were calibrated to the first inflection point of a RbCl pellet (15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 203.8 eV)
203.8 eV)
| Inflection point (eV) | Peak position (eV) | 2nd peak position (eV) | |
|---|---|---|---|
a The Cm aquo complex in 1 M HClO4 was calibrated with Nb foil (18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 986 eV). 986 eV).
|
|||
| Cm aquo (1 M HClO4),47a | 18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 973.0 973.0 |
— | — |
| Cm (HNO3, 0.05 M) | 18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 976.4 976.4 |
18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 980.3 980.3 |
19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 013.5 013.5 |
| Cm (HNO3, 4 M) | 18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 976.3 976.3 |
18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 980.2 980.2 |
19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 012.9 012.9 |
| Cm (HNO3, 16 M) | 18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 976.3 976.3 |
18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 980.2 980.2 |
19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 011.4 011.4 |
| Am (0.11 M HO3SCF3),21 | 18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 514.3 514.3 |
18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 517.9 517.9 |
|
| Am (HNO3, 0.05 M) | 18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 514.0 514.0 |
18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 517.5 517.5 |
18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 550.6 550.6 |
| Am (HNO3, 4 M) | 18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 513.8 513.8 |
18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 517.4 517.4 |
18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 549.9 549.9 |
| Am (HNO3, 16 M) | 18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 513.8 513.8 |
18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 517.4 517.4 |
18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 547.1 547.1 |
| Ac (0.11 M HO3SCF3),12 | 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 874.3 874.3 |
15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 876.9 876.9 |
|
| Ac (HNO3, 0.05 M) | 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 874.7 874.7 |
15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 877.6 877.6 |
15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 908.1 908.1 |
| Ac (HNO3, 4 M) | 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 874.6 874.6 |
15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 877.5 877.5 |
15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 906.7 906.7 |
| Ac (HNO3, 16 M) | 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 874.6 874.6 |
15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 877.5 877.5 |
15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 905.0 905.0 |
Although the absorption peak position showed essentially no dependence on the HNO3 concentration, changing the HNO3 concentration from 0.05 M to 16 M had a marked impact on the energy of the post-edge feature approximately 30 to 40 eV above the inflection point (Fig. 1). This peak marks the first extended X-ray absorption fine structure (EXAFS) oscillation. Increasing the HNO3 concentration systematically lowered the energy for the oscillation maximum (Table 1). For CmIII, moving from 0.05 M to 4 M HNO3 caused a 0.6 eV oscillation maximum decrease. Similarly, moving from 4 M to 16 M HNO3 caused a −2.1 eV energy shift. Similar trends were observed for AmIII and AcIII, albeit the 3.5 (AmIII) and 3.1 (AcIII) energy shifts were larger. Dependence of the post-edge line-shape on the HNO3 concentration foreshadowed structural changes that accompanied coordination of AnIII cations by NO3− ligands, which were revealed when the EXAFS spectra were rigorously analyzed.
AnIII L3-edge extended X-ray absorption fine structure (EXAFS) spectroscopy
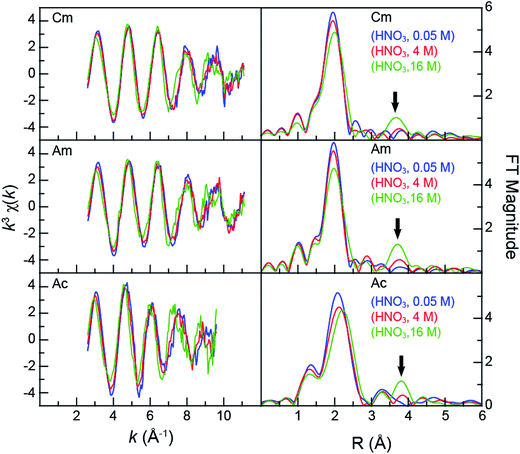
Speciation metrics (i.e. coordination numbers and bond distances) for solution-phase samples were extracted from the k3χ(k) solution-phase measurements (Fig. 2). For CmIII and AmIII – present in relatively high concentrations (0.5 mg in 0.5 mL per sample) – high quality data were obtained from 2.7 to 11 Å−1 (in k-space). This energy range provided shell-by-shell resolution in the CmIII and AmIII measurements to be approximately 0.19 Å (resolution = π/2Δk; in R-space). The CmIII and AmIII L3-edge k3χ(k) spectra were quite similar and changed uniformly with increasing HNO3 concentration (Fig. 2). The first three oscillations were nearly superimposable despite the changes in HNO3 concentration. Upon reaching the fourth and fifth oscillations, some dependence on the HNO3 concentration became apparent. For example, moving from 0.05 M to 4 M HNO3 caused a subtle shoulder to emerge in the fifth oscillation (ca. 9 Å−1). Changing to concentrated HNO3 (16 M) increased the magnitude of this shoulder and caused a second shoulder to emerge on the low energy side of the fourth oscillation (ca. 7.5 Å−1). These line shape changes suggested that some of the scattering pathways were moving out of phase.In general, the AcIII spectra were similar to those of CmIII and AmIII. For example, increased HNO3 concentrations had little impact on the first three oscillations and showed evidence of out-of-phase scattering pathways for the fourth and fifth oscillations. The AcIII L3-edge data differed in two notable ways. First, the signal-to-noise ratio was smaller, on account of the smaller quantity of AcIII (28 μg). This restricted the energy range over which high quality data were available; from 2.7 to 9.5 in k-space (resolution = 0.23 Å in R-space). Second, the EXAFS oscillation frequency increased in comparison to those of CmIII and AmIII. This frequency increase was somewhat expected. For example, the frequency in k-space (left, Fig. 2) is inversely related to the interatomic distance. Higher frequencies result from longer bonds. As shown in Fig. 2, the large AcIII ionic radius42 should provide longer bond distances (higher oscillation frequencies) than those for CmIII and AmIII, as long as the analytes have similar chemical compositions. Given the observed change in frequency upon moving from CmIII and AmIII to AcIII and the similar interference pattern, these data suggested – superficially – that the AcIII speciation was similar to that of AmIII and CmIII.
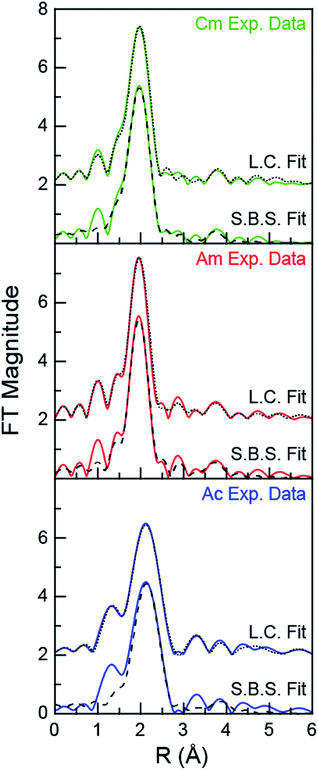
Closer examination of the CmIII, AmIII, and AcIII L3-edge EXAFS spectra supported the proposition that chemical speciation was similar for these three compounds, revealing only subtle differences in CmIII, AmIII, and AcIII coordination environments. The experimental data were analyzed using well-established shell-by-shell curve fitting techniques.43 Interpretations of the data were guided by identifying scattering pathways using FEFF8 (ref. 44 and 45) and DFT geometry optimized AnIII structures that contained a combination of water molecules and bidentate nitrate ligands, An(H2O)9−2x(NO3)x3−x (An = CmIII, AmIII, AcIII; x = 0, 1, 2, 3). The coordination numbers (CN), bond lengths (R), Debye–Waller factors (σ2), and energy shifts (E0) were allowed to converge to reasonable values. The amplitude reduction factor was set to 0.9. The fitting results have been summarized and compared with other relevant EXAFS studies in Table 2.12,21,46,47 For the sake of discussion, we begin by reporting on spectra collected in dilute HNO3 (0.05 M), then move to concentrated HNO3 (16 M), and conclude at the intermediate HNO3 concentration (4 M).
| ΔE0 (eV) | R M–O (Å) | CNbound oxygen | σ bound oxygen 2 | R M⋯N (Å) | CNnitrogen | R M⋯O terminal oxygen | σ terminal oxygen 2 | |
|---|---|---|---|---|---|---|---|---|
| a Additionally, σN2 was fixed to σO2 and CNterminal oxygen set to CNnitrogen. Data found in the literature and marked with an asterisk (*) had S02 values set to 1. | ||||||||
| Cm aquo (0.25 M HCl),46,* | −13.0 | 2.450 ± 0.002 | 10.2 ± 0.3 | 0.009 (fixed) | — | — | — | — |
| Cm aquo (1 M HClO4),47,* fit 1 | −2.0 ± 0.9 | 2.469 ± 0.007 | 7.0 ± 0.4 | 0.0071(8) | — | — | — | — |
| Cm aquo (1 M HClO4),47,* fit 2 | −0.7 ± 0.7 | 2.470 ± 0.006 | 6 (fixed) | 0.0053(2) | — | — | — | — |
| 2.63 ± 0.02 | 3 (fixed) | 0.009 (2) | ||||||
| Cm (HNO3, 0.05 M) | −5.5 ± 0.8 | 2.47 ± 0.01 | 9.6 ± 0.7 | 0.009(1) | — | — | — | — |
| Cm (HNO3, 4 M) | 1.5 ± 1.3 | 2.45 ± 0.01 | 7 (fixed) | 0.007(3) | 2.93 ± 0.07 | 1 fixed | 4.25 ± 0.03 | 0.006 (4) |
| 2.54 ± 0.05 | 2 (fixed) | |||||||
| 2.63 ± 0.04 | 2 (fixed) | |||||||
| Cm (HNO3, 16 M) | 3.4 ± 1.1 | 2.49 ± 0.02 | 8.9 ± 2.2 | 0.009(2) | 2.95 ± 0.02 | 4.1 ± 0.7 | 4.25 ± 0.02 | 0.010(3) |
| 2.64 ± 0.03 | 5.7 ± 1.3 | |||||||
| Am (0.25 M HCl),46,* | −8.7 | 2.480 ± 0.002 | 10.3 ± 0.3 | 0.009 (fixed) | — | — | — | — |
| Am (0.11 M HO3SCF3),21 | −4.7 ± 0.9 | 2.48 ± 0.01 | 9.5 ± 0.9 | 0.0088(9) | — | — | — | — |
| Am (HNO3, 0.05 M) | −5.0 ± 1.0 | 2.47 ± 0.01 | 8.9 ± 0.8 | 0.008(1) | — | — | — | — |
| Am (HNO3, 4 M) | 2.1 ± 1.3 | 2.46 ± 0.01 | 6 (fixed) | 0.003(1) | 2.98 ± 0.04 | 1 (fixed) | 4.27 ± 0.04 | 0.003 (2) |
| 2.57 ± 0.03 | 2 (fixed) | |||||||
| 2.67 ± 0.02 | 2 (fixed) | |||||||
| Am (HNO3, 16 M) | 3.3 ± 0.8 | 2.50 ± 0.01 | 7.7 ± 0.8 | 0.005(1) | 2.97 ± 0.01 | 3.4 ± 0.7 | 4.26 ± 0.01 | 0.006(2) |
| 2.67 ± 0.01 | 5.4 ± 0.5 | |||||||
| Ac (0.11 M HO3SCF3),12 | −3.9 ± 1.0 | 2.63 ± 0.01 | 10.9 ± 0.5 | 0.009 (fixed) | — | — | — | — |
| Ac (HNO3, 0.05 M) | −2.9 ± 1.6 | 2.63 ± 0.02 | 10.0 ± 0.9 | 0.009 (fixed) | — | — | — | — |
| Ac (HNO3, 4 M) | 3.9 ± 2.0 | 2.61 ± 0.02 | 6 (fixed) | 0.006(4) | 3.24 ± 0.11 | 1 (fixed) | 4.42 ± 0.05 | 0.003 (5) |
| 2.75 ± 0.04 | 2 (fixed) | |||||||
| Ac (HNO3, 16 M) | 4.4 ± 2.1 | 2.70 ± 0.02 | 12.9 ± 4.0 | 0.012(4) | 3.20 ± 0.12 | 2.3 ± 1.7 | 4.42 ± 0.03 | 0.003(6) |
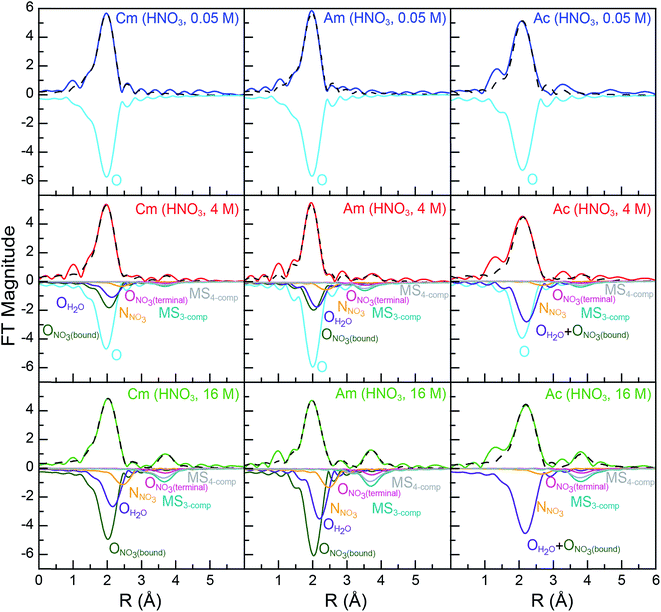
As shown in Fig. 2, all spectra collected from dilute HNO3 (0.05 M) solutions were best described by a single frequency whose amplitude in k-space (left, Fig. 2) dampened with increased energy. Best fits for the data (top, Fig. 3; Table 2) – those with the smallest residuals and lowest reduced chi-squared values – confirmed this superficial interpretation. The histogram of frequencies shown in the Fourier transform spectra (right, Fig. 2; top, Fig. 3) contained a single peak near R = 2 Å. As the frequency resolution ranged from 0.19 to 0.23 Å for CmIII, AmIII, and AcIII, we refrained from attempting to resolve multiple M–OH2O scattering pathways within this first water shell. Furthermore, the data quality was not sufficient for observing H2O molecules at longer distances, i.e. in the second and third hydration shells. Fitting the data with a single H2O shell revealed approximately nine water molecules for CmIII (9.6 ± 0.7) and AmIII (8.9 ± 0.8) with equivalent M–OH2O distances of 2.47(1) Å. These results agreed well with the literature values for CmIII and AmIII aquo ions. The single crystal structure of the CmIII aquo ion showed nine H2O ligands with an average Cm–OH2O distance of 2.51(8) Å.48 Previous EXAFS measurements obtained from the CmIII aquo ion in dilute HCl (0.25 M)46 and dilute HClO4 (1 M)47 showed 10.2 ± 0.3 oxygen atoms at 2.450(2) Å and 7.0 ± 0.4 oxygen atoms at 2.469(7) Å, respectively. Similarly, recent EXAFS studies characterized the AmIII aquo ion as having 9.5 ± 0.9 oxygen atoms at 2.48(1) Å (HO3SCF3; 0.11 M)21 and 10.3 ± 0.3 oxygen atoms at 2.480(2) Å (HCl; 0.25 M).46 A single crystal structure for the AmIII aquo ion has also been reported, showing nine H2O ligands with a 2.52(8) Å average Am–OH2O distance.48
For the larger AcIII cation, a longer Ac–OH2O distance of 2.63(2) Å was observed. In comparison to the CmIII and AmIII aquo ions described above, the larger Ac–OH2O bond distance was statistically relevant. The AcIII coordination number also seemed larger than those from CmIII and AmIII with 10.0 ± 0.9 inner sphere H2O ligands. However, these values were equivalent when the measurement uncertainties were considered. The Ac–OH2O bond distance and H2O coordination numbers were consistent with the only other data obtained on an AcIII aquo ion,12 despite differences in the solution matrices; HNO3 (0.05 M) vs. HO3SCF3 (0.11 M). This previous analysis showed 10.9 ± 0.5 oxygen atoms at 2.63(1) Å. Additional confidence in these Ac–OH2O distances was provided by comparison with previous AcIII L3-edge EXAFS measurements made in HCl (11.7 M) solutions, which gave a 2.59(3) Å Ac–OH2O distance.21 Overall, all of our An–OH2O (An = CmIII, AmIII, AcIII) distances were in agreement with the Shannon ionic radii.42 For example, subtracting the six coordinate ionic radii from the experimental M–OH2O distances gave 1.50, 1.50, and 1.51 Å for CmIII, AmIII, and AcIII, respectively. These values were bracketed by the calculated (1.67 Å) and crystallographically measured (1.38 Å) H2O ionic radii.49 In all of the AnIII aquo spectra (HNO3, 0.05 M for CmIII, AmIII, and AcIII; HO3SCF3, 0.11 M for AmIII and AcIII), there was no evidence of AnIII aquo ion dimerization. No AnIII⋯AnIII scattering pathways were detected nor was there evidence for short AnIII–OH interactions, which would result from hydrolysis. Hence, these data were consistent with previous EXAFS studies on AnIII and LnIII aquo ions,12,50–54 suggesting that CmIII, AmIII, and AcIII aquo ions existed primarily as discrete AnIII(H2O)x3+ species. However, EXAFS spectroscopy is relatively insensitive to dilute impurities, and dimeric species present at less than 10% of the total sample would be difficult to detect.43
Consistent with the AcIII aquo L3-edge EXAFS spectra reported previously in dilute HO3SCF3, the data reported here contained a feature near 3.2 Å in the Fourier transform. To date, we have been unable to identify physically realistic models to explain these high-frequency oscillations. Given the instability of these features in various k ranges (7, 8, 9, 10 Å−1), at this time we believe their origin is not related to the AcIII coordination chemistry and likely results from systematic artifacts related to the data quality. While not conclusive, this proposition was supported by the absence of this mysterious peak in the higher quality CmIII and AmIII spectra, as long as one assumes analogous coordination chemistry exists for all three cations.
Comparison between 0.05 and 16 M HNO3 offered the highest probability to identify differences in AnIII speciation. Our approach to modeling these EXAFS data was consistent with previous models used to explain spectra from LnIII and AnIII cations dissolved in HNO3 (6.8 M,55 13 M) (Scheme 1; bottom, Fig. 3). For CmIII and AmIII, there were two short oxygen scattering pathways. The shorter path was assigned to metal bound oxygen atoms from NO3− ligands (ONO3(bound), olive trace); meanwhile the other was attributed to a shell of oxygen atoms from the H2O ligands (OH2O, purple trace, Fig. 3; Scheme 1). However, because these designations resulted from calculations on static actinide nitrate molecules, we do not have high confidence in the rigidity of these assignments. For example, in solution, NO3− and H2O ligand exchange could likely occur. For AcIII, the data were not sufficient to resolve the two OH2O and ONO3(bound) scattering pathways. Hence, in the AcIII model, the OH2O and ONO3(bound) shells were combined (purple trace, bottom right, Fig. 3).
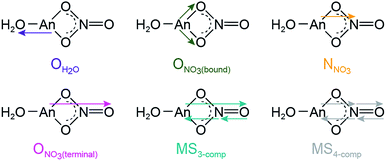 | ||
| Scheme 1 Scattering pathways deployed in fitting An L3-edge EXAFS data from AnIII cations dissolved in 16 M HNO3. | ||
Consistent with AnIII–NO3− binding was the presence of four higher frequency scattering pathways, characteristic of inner-sphere NO3− ligands.55 There was a pathway at intermediate distances associated with the central nitrogen of the NO3− anion, referred to as NNO3 (orange trace, Fig. 3; ca. R = 2.5 Å). This shell was followed by the NO3− terminal oxygen (ONO3(terminal); pink trace, ca. R = 3 Å). Subsequently, between ca. 3 < R < 4.5 Å there were two linear multiple scattering pathways. There was the three component AnIII → ONO3(terminal) → NNO3 → AnIII (MS3-comp; blue-green trace) pathway and the four component AnIII → NNO3 → ONO3(terminal) → NNO3 → AnIII (MS4-comp; grey trace) pathway (Scheme 1). Our attempts to model the data with bent multiple scattering pathways (i.e. AnIII → ONO3(bound) → NNO3 → AnIII) or as dimers and oligomers (with An⋯An scattering paths) were unsuccessful. Best fits for the data contained η2-NO3− (bidentate) ligands and were modeled using the following constraints. The ONO3(terminal) amplitude (coordination number) was fixed to NNO3, which in turn was allowed to converge. In addition, the NNO3 and ONO3(bound) Debye–Waller factors (σ2) were fixed to that associated with OH2O, as all three scattering pathways had similar frequencies and because these three scattering pathways combined to form a single peak in the Fourier transform. This constraint additionally minimized the number of free fitting parameters.
For CmIII, refinement of the model to experimental data showed 8.9 ± 2.2 ONO3(bound) atoms at 2.49(2) Å. There were also 5.7 ± 1.3 OH2O at 2.64(3) Å and 4.1 ± 0.7 NNO3 atoms at 2.95(2) Å. The CmIII–ONO3(terminal) distance was 4.25(2) Å (Table 2, Fig. 3). To determine the number of NO3− ligands, two options existed involving either the NNO3 coordination number or the ONO3(bound) coordination number. Although, similar stoichiometries were obtained for both scenarios, reported here is a chemical formula based on NNO3(bound) to facilitate comparison with the AcIII data below. Overall, these data indicated that the average CmIII species present in concentrated HNO3 (16 M) had a stoichiometry of Cm(NO3)4.1±0.7(H2O)5.7±1.3(1.1±0.2)− with an overall coordination number of 13.9 ± 1.9. Stoichiometric self-consistency associated with the coordination number ratio for NNO3, ONO3(bound), ONO3(terminal) (2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) – as well as the magnitude of the multiple scattering pathways – provided additional confidence in our model.
1) – as well as the magnitude of the multiple scattering pathways – provided additional confidence in our model.
The AmIII data in 16 M HNO3 resembled that from CmIII (Table 2), albeit with slightly smaller uncertainties. For instance, this analysis showed that the average coordination numbers for all of the AmIII species present in concentrated HNO3 had 7.7 ± 0.8 ONO3(bound) atoms at 2.50(1) Å, 5.4 ± 0.5 OH2O atoms at 2.67(1) Å, 3.4 ± 0.7 NNO3 atoms at 2.97(1) Å, and an Am–ONO3(terminal) distance of 4.26(1) Å (Table 2, Fig. 3). Based on the NNO3 and OH2O values, the analysis suggested an average stoichiometry of Am(NO3)3.4±0.7(H2O)5.4±0.5(0.4±0.1)− (mean coordination number of 12.2 ± 1.5). Again, the ONO3(bound), NNO3, and ONO3(terminal) coordination numbers and magnitudes from the multiple scattering pathways were all self-consistent with this average stoichiometry.
Moving to the larger AcIII ion had little effect on the overall coordination number, showing 12.9 ± 4 inner-sphere oxygen atoms. The average Ac(NO3)2.3±1.7(H2O)8.3±5.2(0.7±0.5)+ solution phase stoichiometry was (essentially) equivalent to that from CmIII and AmIII; however, the uncertainties associated with the AcIII L3-edge measurements were larger. The presence of 2.3 ± 1.7 NNO3 atoms at 3.20(12) Å and AcIII–ONO3(terminal) atoms at 4.42(3) Å confirmed the presence of inner-sphere NO3− ligands in HNO3 (16 M; Table 2, Fig. 3). The largest differences between the CmIII, AmIII, and AcIII L3-edge EXAFS data were associated with the AcIII interatomic distances. As expected based on the ∼0.15 Å increase in AcIII six coordinate ionic radii, the AnIII–OH2O and AnIII–ONO3(bound) distances increased by approximately 0.2 Å from CmIII and AmIII to AcIII.
Because EXAFS spectroscopy probes all species in solution, it does not exclude AnIII access to other stoichiometric ratios of NO3− and H2O, Scheme 2. Instead, it provides an average signal from all of the molecules in the sample. In this context, good models of the data were only obtained with η2-NO3− ligands (bidentate), which were consistent with many models previously reported for lanthanide and actinide EXAFS data.50,56–58 One notable exception was identified by Antonio and coworkers. These authors successfully identified monodentate η1-NO3− binding for CeIII in 3 M HNO3, a notably lower concentration than the 16 M HNO3 discussed here.59 Our attempts to introduce η1-NO3− (monodentate) binding increased the AnIII → NNO3 and AnIII → ONO3(terminal) distances into unrealistic regions of the spectra where no intensity was present. Additionally, η1-NO3− diminished the amplitude for linear multiple scattering pathways, giving an appreciable misfit between 3 < R < 4.5 Å in the Fourier transform. We interpret these results as suggesting that in 16 M HNO3 AnIII–η2-NO3 binding was preferred for CmIII, AmIII, and AcIII over monodentate modes, likely due to the chelation effect.60 Consistent with this observation were quantum calculations on M(NO3)x(H2O)y3−x (M = AmIII, EuIII) reported by Xi and coworkers.61 Their calculations predicted that η2-NO3 binding was preferred energetically in aqueous solutions, especially when the first coordination shell was sterically saturated. Xi's calculated 2.45 Å Am–[η2-ONO3(bound)] bond distance is in excellent agreement with our EXAFS results, lending confidence to our η2-NO3 binding model. As pointed out to us privately by Antonio, the larger An–NO3− stability constants62 may be responsible for CmIII, AmIII, and AcIII preference for η2-NO3− binding.59,63
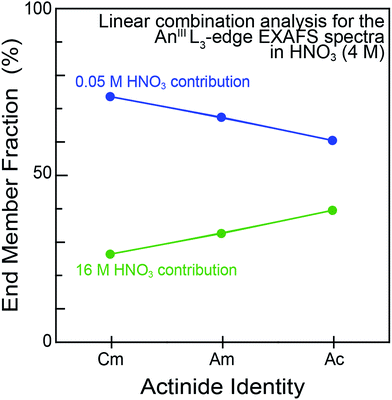
For experiments conducted at the intermediate HNO3 concentration (4 M), an alternative fitting method was pursued. The initial model was generated from a linear combination of the two end members, namely AnIII dissolved in 0.05 and 16 M HNO3. This fit (Fig. 4) suggested that the 4 M HNO3 CmIII speciation could be described as containing 73.6(1.8)% of the CmIII aquo ion and 26.4(1.8)% of the Cm(NO3)4.1±0.7(H2O)5.7±1.3(1.1±0.2)− (Fig. 5). The slightly larger AmIII cation gave a similar ratio; 67.4(1.4)% of the AmIII aquo and 32.6(1.4)% Am(NO3)3.4±0.7(H2O)5.4±0.5(0.4±0.1)−. More substantial differences were observed when moving to the much bigger AcIII ion. The analysis showed 60.5(1.4)% of the AcIII aquo and 39.5(1.4)% of the Ac(NO3)2.3±1.7(H2O)8.3±5.2(0.7±0.5)+. These analyses assisted subsequent modeling efforts that used shell-by-shell methods, similar to those described above to fit the 0.05 and 16 M HNO3 spectra. The fitting routine for the HNO3 (4 M) data differed in that it included all of the scattering pathways used in the 0.05 and 16 M models. To keep the number of fitted parameters less than half of the total number of independent variables,64 the coordination numbers were fixed in accordance with the percentages determined from the linear combination analyses (Fig. 4 and 5). Under these conditions, variables associated with the interatomic distance (R) and Debye–Waller factors (σ2) were allowed to converge to reasonable values, as shown in Table 2. The good agreement of these shell-by-shell fits with the experimental data validated conclusions from the linear combination analyses, suggesting that the H2O and NO3− coordination numbers were between those of the 0.05 and 16 M end-members.
Outlook
The AnIII L3-edge XAS results described herein represent a humble contribution to the growing body of knowledge associated with CmIII, AmIII, and AcIII coordination chemistry, aqueous speciation, and chemical reactivity.10–21,65–69 To most effectively communicate the significance of these results, we find it instructive to present the data within the context of some relevant studies reported for NO3− binding of CmIII, AmIII, and AcIII. For example, in the solid state, there are only two single crystal X-ray structures reported that contain Am–NO3 bonds. In these complexes the Am–ONO3 distances ranged from 2.514 to 2.635(12) Å,70,71 which was in good agreement with our Am–ONO3 results, 2.50(1) and 2.57(3). To date, we have been unaware of any Cm single crystal structures that contain Cm–NO3 bonds and no single crystal data of any kind have been reported for Ac. Solution-phase characterization using EXAFS spectroscopy is equally sparse. There is a report from Den Auwer on the Am(NO3)3(TEMA)2 complex,72 another by Girnt on Am(NO3)x(dmpbipy)x,73 one by Bremer involving Am(NO3)x(C5-BPP)x,74 and finally Ekberg investigated [Am(NO3)(CyMe4-BTBP)2]2+.75 These studies showed an average Am–ONO3 distance of 2.49 ± 0.01 Å. For Cm, numerous measurements have been made on NO3− species. These include (but are not limited to) time resolved laser fluorescence and luminescence measurements made on CmIII in nitrate containing solutions,11,76,77 numerous studies documenting the extraction of CmIII from HNO3 solutions,78–81 as well as thermal decomposition of CmIII(NO3)3.82,83 For Cm we are unaware of EXAFS measurements made in HNO3 solutions and for Ac the Ac–NO3− interaction has not been characterized previously.In the context of what is understood regarding complexation of CmIII, AmIII, and AcIII by NO3− in aqueous media, the EXAFS results reported herein provide hard data that can be used broadly to assist applied and fundamental efforts that require AnIII cations to be dissolved in HNO3(aq). Our data suggested that CmIII, AmIII, and AcIII existed as aquo ions in dilute HNO3 matrices (0.05 M). These results agreed with the small AnIII–NO3 stability constants: ([AnIII–NO3]/[AnIII][NO3−]; log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K, ionic strength = 1 M, 25 °C) 0.34 (CmIII),84 0.25 ± 0.02 (AmIII),85 and 0.1 (AcIII).85 Along these lines, Choppin and coworkers used CmIII fluorescence to evaluate NO3− complexation in aqueous solutions with varied HNO3 concentrations. In this study, moving from 0.1 to 13 M HNO3 decreased the number of bound H2O molecules, presumably accompanied by NO3− complexation. A total of four H2O molecules were reportedly removed in 13 M HNO3, suggesting that a bis-nitrato [M(NO3)2(H2O)5]1+ complex had formed.86 Consistent with Choppin and coworkers' results,86 our EXAFS data showed that nitrate complexation for CmIII, AmIII, and AcIII increased with increasing HNO3 concentration. In 4 M HNO3, we observed approximately one inner sphere NO3−. Moving past Choppin and Coworkers' 13 M HNO3 to concentrated HNO3 (16 M), increased the number of coordinated NO3− ligands, ranging from 4.1 ± 0.7 for CmIII, to 3.4 ± 0.7 for AmIII, and 2.3 ± 1.7 for AcIII. It is interesting that the NO3− coordination numbers seemed to decrease with increasing metal ionic radius. While tempting to correlate these results with the stability constants referenced above and with the Lewis acidity for the AnIII cations, we refrain since the NO3− coordination numbers were equivalent when the uncertainties for the measurements were considered.
K, ionic strength = 1 M, 25 °C) 0.34 (CmIII),84 0.25 ± 0.02 (AmIII),85 and 0.1 (AcIII).85 Along these lines, Choppin and coworkers used CmIII fluorescence to evaluate NO3− complexation in aqueous solutions with varied HNO3 concentrations. In this study, moving from 0.1 to 13 M HNO3 decreased the number of bound H2O molecules, presumably accompanied by NO3− complexation. A total of four H2O molecules were reportedly removed in 13 M HNO3, suggesting that a bis-nitrato [M(NO3)2(H2O)5]1+ complex had formed.86 Consistent with Choppin and coworkers' results,86 our EXAFS data showed that nitrate complexation for CmIII, AmIII, and AcIII increased with increasing HNO3 concentration. In 4 M HNO3, we observed approximately one inner sphere NO3−. Moving past Choppin and Coworkers' 13 M HNO3 to concentrated HNO3 (16 M), increased the number of coordinated NO3− ligands, ranging from 4.1 ± 0.7 for CmIII, to 3.4 ± 0.7 for AmIII, and 2.3 ± 1.7 for AcIII. It is interesting that the NO3− coordination numbers seemed to decrease with increasing metal ionic radius. While tempting to correlate these results with the stability constants referenced above and with the Lewis acidity for the AnIII cations, we refrain since the NO3− coordination numbers were equivalent when the uncertainties for the measurements were considered.
In terms of structural characterization, the AcIII–OH2O and AcIII–ONO3(bound) bond distance measurements represent another impactful component of this manuscript. Prior to these experiments, there were two reported Ac–OH2O bond distances, both measured by solution-phase AcIII L3-edge EXAFS spectroscopy. One was in concentrated HCl (11 M) solutions (2.59 ± 0.03 Å)21 and the other in dilute HO3SCF3 (0.11 M; 2.63 ± 0.01 Å).12 Contributed here are three additional Ac–OH2O measurements; 2.63 ± 0.02 (0.05 M HNO3), 2.61 ± 0.02 (4 M HNO3), and 2.70 ± 0.02 (16 M HNO3). This brings the total number of reported Ac–OH2O bond distances to five, averaging 2.63 ± 0.04 Å (error reported as the standard deviation of the mean, 1 σ). Their consistency provides confidence in the accuracy of these AcIII L3-edge EXAFS measurements. In terms of NO3− complexation, these results are also exciting as they represent the first AcIII–NO3− interaction observed spectroscopically. Although the AcIII–ONO3 distance was not resolved from the inner-sphere AcIII–OH2O interaction, the AcIII–ONO3 bond length can be indirectly inferred based on the measured AcIII–NNO3 distance. For example, the Ac–ONO3(bound) distance can be calculated using the cosine rule; assuming an average N–O distance of 1.31 Å and an average Ac–N–O angle of 113°.57 This analysis gives an AcIII–ONO3 distance of 2.70 ± 0.10 Å.
In terms of fundamental exploratory science, the chemistry of CmIII, AmIII, and AcIII presents uncharted landscapes in comparison to many other elements in the periodic table. Unique safety hazards and limited access to sizable quantities of material represent significant technical challenges faced during experimental studies of these elements. Even interactions with common ligands – such as the An–H2O and An–NO3 bonds – are poorly defined. On top of scientific curiosity is the need to support innovation for AnIII processing. This need includes developing advanced nuclear fuel cycles, medical isotope production, and targeted alpha therapy. It seems likely that our approach for characterizing An–NO3 and An–H2O (An = CmIII, AmIII, AcIII) interactions using AnIII L3-edge EXAFS can be broadly applied to other AnIII–ligands interactions, which are equally relevant for nuclear processing and medical applications. We hope that the results presented herein will provide insight aiding our current efforts – as well as those associated with other researchers embarking on their own fundamental and applied scientific campaigns – to solve complicated technical problems associated with CmIII, AmIII, and AcIII.
Experimental section
General consideration
Caution! The 246/248Cm [t1/2 = 4706(40) years/3.48(6) × 105 years],87243Am [t1/2 = 7364(22) years],87 and 227Ac [t1/2 = 21.772(3) years]87 isotopes present serious health threats due to their (as well as their daughters) direct neutron-, α-, β-, and γ- emissions of their radioactive daughters. Hence, all studies that involved uncontained manipulations were conducted in a radiation laboratory equipped with HEPA filtered hoods, continuous air monitors, negative pressure gloveboxes, and monitored equipment appropriate neutron-, α-, β-, and γ-particle detection. All free-flowing solids were handled within negative pressure gloveboxes equipped with HEPA filters. The 246/248Cm, 243Am, and 227Ac isotopes were supplied by the United States Department of Energy Office of Science Isotope Program in the Office of Nuclear Physics. Chemically pure CmIII, AmIII, and AcIII stock solutions were prepared as previously described.12,20,31 Optima grade nitric acid was obtained commercially (Fisher Scientific). Water was purified to 18.2 MΩ cm−1 resistivity using Thermo-Scientific Barnstead Nanopure or Millipore Nanopure water purification systems. For AcIII, the water was further purified by using a Teflon distilling apparatus.Sample preparation
Three solution-phase XAS samples were prepared for each element. The first was prepared in 0.05 M HNO3, the second in 4 M HNO3 and the third in 16 M (concentrated) HNO3. To prepare the samples, aliquots from purified CmIII (0.5 mg; 2.02 μmol), AmIII (0.5 mg; 2.06 μmol), and AcIII (28 μg; 0.123 μmol) stock solutions were transferred to conical glass vials. The aqueous solution was removed by heating the samples on a hot plate at around 110 °C under a flow of argon gas until soft dryness was achieved. The residue was dissolved in aqueous nitric acid of desired molarity. Each sample was boiled and dissolved three times to ensure that the HNO3 concentration was actually 0.05, 4, or 16 M. The solution volumes for each sample were 0.5 mL (Am), 0.5 mL (Cm), and 0.3 (Ac). The resulting solutions were transferred to an XAS holder.Radiological containment for XAS samples
The XAS holders and handling procedures provided adequate containment (three layers) and administrative/engineering controls that guarded against release of radiological material during shipment and during data acquisition. The holder consisted of a plastic body with a 5 mm well for CmIII and AmIII and a 2 mm well for AcIII equipped with a set of Teflon windows (1 mil) and a Kapton window (1 mil). Solutions were introduced into the holder through an injection hole sealed with a Teflon gasket that was held in place by an aluminum plate. This primary holder was then held within a secondary container, which in turn was held within the tertiary container. The secondary and tertiary containers are best described as a set of nested aluminum holders equipped with Kapton windows (2 mil) and rubber gaskets.XAS data acquisition
The actinide L3-edge XANES and EXAFS measurements were made at the Stanford Synchrotron Radiation Lightsource (SSRL) under dedicated operating conditions (3.0 GeV, 5%, 500 mA) on end station 11-2. This beamline was equipped with a 26-pole and a 2.0 tesla wiggler. Using a liquid nitrogen-cooled double-crystal Si(220) (Φ = 0° for CmIII; Φ = 90° for AmIII and AcIII) monochromator and employing collimating and focusing mirrors, a single energy was selected from the incident white beam. Vertical acceptance was controlled by slits positioned before the monochromator. For CmIII, the monochromator crystals were 35% detuned. Meanwhile, AmIII and AcIII L3-edge measurements were conducted with the monochromator crystals fully-tuned. For these experiments, higher harmonics from the monochromatic light were removed using a 370 mm Rh coated harmonic rejection mirror. The Rh coating was 50 nm with a 20 nm seed coating and the substrate was Zerodur. The harmonic rejection cut-off was set by the mirror angle, controlling which photons experience total external reflection. The samples were attached to the beamline 11-2 XAS rail. The rail was equipped with three ionization chambers through which nitrogen gas was continually flowed. One chamber was positioned before the sample holder to monitor the incident radiation (I0, 10 cm). The second chamber was positioned after the sample holder, such that sample transmission (I1, 30 cm) could be evaluated against I0, while a third chamber (I2, 30 cm) was positioned downstream from I1 so that the XANES of a calibration foil could be measured in situ during the XAS experiments against I1. All actinide L3-edge XAS spectra were measured by monitoring sample fluorescence against the incident radiation (I0). The detector was positioned 90° to the incident radiation (I0). For CmIII and AmIII a Lytle detector, equipped with Soller slits and Sr (3 absorption lengths) filters were used. For AcIII measurements, a solid-state 100-element Ge detector was used. This detector was windowed on the AcIII Lα1-emission line (12.652 keV). High-energy contributions to the fluorescence signal were removed using a bromine filter (6 absorption lengths). Using a Se filter, detector dead time was characterized approximately 400 eV above the Se K-edge by defining the detector response from 0 to ∼70% dead (windowed counts of the emission line versus the total of incoming counts in the solid-state detector).XAS data analysis
Data manipulation and analysis was conducted as previously described.21,43 All calibration spectra were measured in situ. The CmIII and AmIII spectra were calibrated to the energy of the absorption peak maximum of a Zr foil (18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 013.3 eV (ref. 88)). The actinium sample data were dead time corrected and calibrated to the energy of the first inflection point of a rubidium(II) chloride, RbCl, pellet diluted with boron nitride (BN) to a 1 absorption length thickness. The energy for the first inflection point for RbCl was determined in comparison to the Bi L2-edge of a bismuth foil (15
013.3 eV (ref. 88)). The actinium sample data were dead time corrected and calibrated to the energy of the first inflection point of a rubidium(II) chloride, RbCl, pellet diluted with boron nitride (BN) to a 1 absorption length thickness. The energy for the first inflection point for RbCl was determined in comparison to the Bi L2-edge of a bismuth foil (15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 711 eV) to be 15
711 eV) to be 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 203.8 eV.
203.8 eV.
The XAS data were analyzed by fitting a line to the pre-edge region, which removed the background from experimental data in the spectra. Then a third order polynomial fit was chosen for the post-edge region. The difference between pre and post edge lines was set to unity at the first inflection point, normalizing the absorption jump to 1.0. Samples were measured for several hours resulting in the collection of multiple scans. The EXAFS data were analyzed by either shell-by-shell fitting methods using IFEFFIT software88 and FEFF8 calculations44,45 or linear combination analyses (IFEFFIT).88 Atomic coordinates for the FEFF8 calculations were obtained by geometry optimizations generated from DFT calculations (see below). Data were fit over the following ranges; for curium and americium 2.7 < k < 11 Å−1 and 1.1 < R < 4.5 Å (to 3 Å for 0.05 M) and for actinium 2.7 < k < 9.5 Å−1 and 1.25 < R < 4.5 Å.
DFT calculations
All DFT calculations were performed with ORCA version 4.0.1.89 Calculations utilized the PBE functional,90 the SARC-ZORA-TZVP91,92 and def2 (ref. 93) basis sets, and the D3 dispersion corrections.94,95 Coordinates of the DFT optimized structures are given in the ESI.†Conflicts of interest
There are no conflicts to declare.Acknowledgements
We would like to thank Dr Mark R. Antonio for thought provocative discussions that motivated this research and for his guidance in preparing this manuscript. The Am and Cm work was funded under the Heavy Element Chemistry Program by the Division of Chemical Sciences, Geosciences, and Biosciences, Office of Basic Energy Sciences, U.S. Department of Energy and the U.S. Department of Energy. All Ac work in this article was supported by the Laboratory Directed Research and Development program of Los Alamos National Laboratory under project number [20180005DR]. Portions of this work were supported by postdoctoral fellowships from the Glenn T. Seaborg Institute (Ferrier, Stein), the distinguished Darleane Christian Hoffman Fellowship (Cary), and the Agnew National Security Fellowship (Bone). Los Alamos National Laboratory is operated by Los Alamos National Security, LLC, for the National Nuclear Security Administration of U.S. Department of Energy (contract DE-AC52-06NA25396). We gratefully recognize the United States Department of Energy, Office of Science, Isotope Development and Production for Research and Application subprogram within Office of Nuclear Physics for their support in supplying the 246,248Cm, 243Am, and 227Ac isotopes. Use of the Stanford Synchrotron Radiation Lightsource, SLAC National Accelerator Laboratory, was supported by the U.S. Department of Energy, Office of Science, Office of Basic Energy Sciences under Contract No. DE-AC02-76SF00515.References
- Y. S. Kim and M. W. Brechbiel, Tumor Biol., 2012, 33, 573–590 CrossRef PubMed.
- D. A. Mulford, D. A. Scheinberg and J. G. Jurcic, J. Nucl. Med., 2005, 46, 199S–204S Search PubMed.
- B. J. Allen, C. Raja, S. Rizvi, Y. Li, W. Tsui, D. Zhang, E. Song, C. F. Qu, J. Kearsley, P. Graham and J. Thompson, Phys. Med. Biol., 2004, 49, 3703–3712 CrossRef PubMed.
- D. Warin, IOP Conf. Ser.: Mater. Sci. Eng., 2010, 9, 012063 Search PubMed.
- J. C. Braley, D. R. McAlister, E. Philip Horwitz and K. L. Nash, Solvent Extr. Ion Exch., 2013, 31, 107–121 CrossRef.
- I. A. Shkrob, T. W. Marin and M. P. Jensen, Ind. Eng. Chem. Res., 2014, 53, 3641–3653 CrossRef.
- A. V. Gelis and G. J. Lumetta, Ind. Eng. Chem. Res., 2014, 53, 1624–1631 CrossRef.
- B. J. Mincher, N. C. Schmitt, R. D. Tillotson, G. Elias, B. M. White and J. D. Law, Solvent Extr. Ion Exch., 2014, 32, 153–166 CrossRef.
- M. Carrott, A. Geist, X. Hères, S. Lange, R. Malmbeck, M. Miguirditchian, G. Modolo, A. Wilden and R. Taylor, Hydrometallurgy, 2015, 152, 139–148 CrossRef.
- R. M. Diamond, K. Street Jr. and G. T. Seaborg, J. Am. Chem. Soc., 1954, 76, 1461–1469 CrossRef.
- B. Gannaz, R. Chiarizia, M. R. Antonio, C. Hill and G. Cote, Solvent Extr. Ion Exch., 2007, 25, 313–337 CrossRef.
- M. G. Ferrier, B. W. Stein, E. R. Batista, J. M. Berg, E. R. Birnbaum, J. W. Engle, K. D. John, S. A. Kozimor, J. S. Lezama Pacheco and L. N. Redman, ACS Cent. Sci., 2017, 3, 176–185 CrossRef PubMed.
- M. P. Kelley, J. Su, M. Urban, M. Luckey, E. R. Batista, P. Yang and J. C. Shafer, J. Am. Chem. Soc., 2017, 139, 9901–9908 CrossRef PubMed.
- B. J. Mincher, L. R. Martin and N. C. Schmitt, Inorg. Chem., 2008, 47, 6984–6989 CrossRef PubMed.
- S. R. Daly, J. M. Keith, E. R. Batista, K. S. Boland, D. L. Clark, S. A. Kozimor and R. L. Martin, J. Am. Chem. Soc., 2012, 134, 14408–14422 CrossRef PubMed.
- G. L. Law, C. M. Andolina, J. Xu, V. Luu, P. X. Rutkowski, G. Muller, D. K. Shuh, J. K. Gibson and K. N. Raymond, J. Am. Chem. Soc., 2012, 134, 15545–15549 CrossRef PubMed.
- T. F. Wall, S. Jan, M. Autillo, K. L. Nash, L. Guerin, C. Le Naour, P. Moisy and C. Berthon, Inorg. Chem., 2014, 53, 2450–2459 CrossRef PubMed.
- M. P. Jensen, R. Chiarizia, I. A. Shkrob, J. S. Ulicki, B. D. Spindler, D. J. Murphy, M. Hossain, A. Roca-Sabio, C. Platas-Iglesias, A. De Blas and T. Rodríguez-Blas, Inorg. Chem., 2014, 53, 6003–6012 CrossRef PubMed.
- M. J. Polinski, K. A. Pace, J. T. Stritzinger, J. Lin, J. N. Cross, S. K. Cary, S. M. Van Cleve, E. V. Alekseev and T. E. Albrecht-Schmitt, Chem.–Eur. J., 2014, 20, 9892–9896 CrossRef PubMed.
- J. N. Cross, J. A. Macor, J. A. Bertke, M. G. Ferrier, G. S. Girolami, S. A. Kozimor, J. R. Maassen, B. L. Scott, D. K. Shuh, B. W. Stein and S. C. E. Stieber, Angew. Chem., Int. Ed., 2016, 55, 12755–12759 CrossRef PubMed.
- M. G. Ferrier, E. R. Batista, J. M. Berg, E. R. Birnbaum, J. N. Cross, J. W. Engle, H. S. La Pierre, S. A. Kozimor, J. S. Lezama Pacheco, B. W. Stein, S. C. E. Stieber and J. J. Wilson, Nat. Commun., 2016, 1–8 Search PubMed.
- S. Hotoku, T. Asakura, H. Mineo and G. Uchiyama, J. Nucl. Sci. Technol., 2002, 39, 313–316 CrossRef.
- K. Bell, A. Geist, F. McLachlan, G. Modolo, R. Taylor and A. Wilden, Procedia Chem., 2012, 7, 152–159 CrossRef.
- G. J. Lumetta, T. G. Levitskaia, A. Wilden, A. J. Casella, G. B. Hall, L. Lin, S. I. Sinkov, J. D. Law and G. Modolo, Solvent Extr. Ion Exch., 2017, 35, 377–395 CrossRef.
- V. Radchenko, J. W. Engle, J. J. Wilson, J. R. Maassen, F. M. Nortier, W. A. Taylor, E. R. Birnbaum, L. A. Hudston, K. D. John and M. E. Fassbender, J. Chromatogr. A, 2015, 1380, 55–63 CrossRef PubMed.
- R. A. Aliev, S. V. Ermolaev, A. N. Vasiliev, V. S. Ostapenko, E. V. Lapshina, B. L. Zhuikov, N. V. Zakharov, V. V. Pozdeev, V. M. Kokhanyuk, B. F. Myasoedov and S. N. Kalmykov, Solvent Extr. Ion Exch., 2014, 32, 468–477 CrossRef.
- T. Mastren, V. Radchenko, A. Owens, R. Copping, R. Boll, J. R. Griswold, S. Mirzadeh, L. E. Wyant, M. Brugh, J. W. Engle, F. M. Nortier, E. R. Birnbaum, K. D. John and M. E. Fassbender, Sci. Rep., 2017, 7, 2–8 CrossRef PubMed.
- B. Zielinska, C. Apostolidis, F. Bruchertseifer and A. Morgenstern, Solvent Extr. Ion Exch., 2007, 25, 339–349 CrossRef.
- C. Apostolidis, R. Molinet, G. Rasmussen and A. Morgenstern, Anal. Chem., 2005, 77, 6288–6291 CrossRef PubMed.
- R. A. Boll, D. Malkemus and S. Mirzadeh, Appl. Radiat. Isot., 2005, 62, 667–679 CrossRef PubMed.
- S. K. Cary, J. Su, S. S. Galley, T. E. Albrecht-Schmitt, E. R. Batista, M. G. Ferrier, S. A. Kozimor, V. Mocko, B. L. Scott, B. W. Stein, F. D. White and P. Yang, Dalton Trans., 2018 Search PubMed , manuscript submitted.
- B. K. Teo, EXAFS: basic principles and data analysis, Springer-Verlag, New-York, Berlin, 1986 Search PubMed.
- J. Stohr, NEXAFS spectroscopy, Springer-Verlag, Berlin, 1st edn, 1992 Search PubMed.
- S. K. Cary, M. Livshits, J. N. Cross, M. G. Ferrier, V. Mocko, B. W. Stein, S. A. Kozimor, B. L. Scott and J. J. Rack, Inorg. Chem., 2018, 57, 3782–3797 CrossRef PubMed.
- S. A. Pattenaude, K. C. Mullane, E. J. Schelter, M. G. Ferrier, B. W. Stein, S. E. Bone, J. S. Lezama Pacheco, S. A. Kozimor, P. E. Fanwick, M. Zeller and S. C. Bart, Inorg. Chem., 2018, 57, 6530–6539 CrossRef PubMed.
- F. Li, S. H. Carpenter, R. F. Higgins, M. G. Hitt, W. W. Brennessel, M. G. Ferrier, S. K. Cary, J. S. Lezama-Pacheco, J. T. Wright, B. W. Stein, M. P. Shores, M. L. Neidig, S. A. Kozimor and E. M. Matson, Inorg. Chem., 2017, 56, 7065–7080 CrossRef PubMed.
- J. J. Kiernicki, M. G. Ferrier, J. S. Lezama Pacheco, H. S. La Pierre, B. W. Stein, M. Zeller, S. A. Kozimor and S. C. Bart, J. Am. Chem. Soc., 2016, 138, 13941–13951 CrossRef PubMed.
- N. H. Anderson, S. O. Odoh, U. J. Williams, A. J. Lewis, G. L. Wagner, J. L. Pacheco, S. A. Kozimor, L. Gagliardi, E. J. Schelter and S. C. Bart, J. Am. Chem. Soc., 2015, 137, 4690–4700 CrossRef PubMed.
- S. K. Cary, M. G. Ferrier, R. E. Baumbach, M. A. Silver, J. Lezama Pacheco, S. A. Kozimor, H. S. La Pierre, B. W. Stein, A. A. Arico, D. L. Gray and T. E. Albrecht-Schmitt, Inorg. Chem., 2015, 137(14), 4690–4700 Search PubMed.
- M. W. Löble, J. M. Keith, A. B. Altman, S. C. E. Stieber, E. R. Batista, K. S. Boland, S. D. Conradson, D. L. Clark, J. Lezama Pacheco, S. A. Kozimor, R. L. Martin, S. G. Minasian, A. C. Olson, B. L. Scott, D. K. Shuh, T. Tyliszczak, M. P. Wilkerson and R. A. Zehnder, J. Am. Chem. Soc., 2015, 137(14), 4690–4700 CrossRef PubMed.
- M. E. Fieser, M. G. Ferrier, J. Su, E. Batista, S. K. Cary, J. W. Engle, W. J. Evans, J. S. Lezama Pacheco, S. A. Kozimor, A. C. Olson, A. J. Ryan, B. W. Stein, G. L. Wagner, D. H. Woen, T. Vitova and P. Yang, Chem. Sci., 2017, 8, 6076–6091 RSC.
- R. D. Shannon, Acta Crystallogr., Sect. A: Found. Crystallogr., 1976, 32, 751–767 CrossRef.
- S. Calvin, XAFS for everyone, CRC Press Tayor and Francis Group, 2013 Search PubMed.
- A. L. Ankudinov, B. Ravel, J. J. Rehr and S. D. Conradson, Phys. Rev. B, 1998, 58, 7565–7576 CrossRef.
- J. J. Rehr, Rev. Mod. Phys., 2000, 72, 621–654 CrossRef.
- P. G. Allen, J. J. Bucher, D. K. Shuh, N. M. Edelstein and I. Craig, Inorg. Chem., 2000, 39, 595–601 CrossRef PubMed.
- S. Skanthakumar, M. R. Antonio, R. E. Wilson and L. Soderholm, Inorg. Chem., 2007, 46, 3485–3491 CrossRef PubMed.
- P. Lindqvist-Reis, C. Apostolidis, J. Rebizant, A. Morgenstern, R. Klenze, O. Walter, T. Fanghänel and R. G. Haire, Angew. Chem., Int. Ed., 2007, 46, 919–922 CrossRef PubMed.
- C. W. Kammeyer and D. R. Whitman, J. Chem. Phys., 1972, 56, 4419–4421 CrossRef.
- T. Yaita, H. Narita, S. Suzuki, S. Tachimori, H. Motohashi and H. Shiwaku, J. Radioanal. Nucl. Chem., 1999, 239, 371–375 CrossRef.
- R. Spezia, M. Duvail, P. Vitorge and P. D'Angelo, J. Phys.: Conf. Ser., 2009, 190, 0–6 CrossRef.
- P. D'Angelo, A. Zitolo, V. Migliorati, G. Chillemi, M. Duvail, P. Vitorge, S. Abadie and R. Spezia, Inorg. Chem., 2011, 50, 4572–4579 CrossRef PubMed.
- I. Persson, P. D'Angelo, S. De Panfilis, M. Sandström and L. Eriksson, Chem.–Eur. J., 2008, 14, 3056–3066 CrossRef PubMed.
- P. D'Angelo, F. Martelli, R. Spezia, A. Filipponi and M. A. Denecke, Inorg. Chem., 2013, 52, 10318–10324 CrossRef PubMed.
- A. Ikeda, T. Yaita, Y. Okamoto, H. Shiwaku, S. Suzuki, T. Suzuki and Y. Fujii, Anal. Chem., 2007, 79, 8016–8023 CrossRef PubMed.
- L. Rao and G. Tian, Inorg. Chem., 2009, 48, 964–970 CrossRef PubMed.
- P. G. Allen, D. K. Veirs, S. D. Conradson, C. A. Smith and S. F. Marsh, Inorg. Chem., 1996, 35, 2841–2845 CrossRef.
- The Chemistry of the Actinide and Transactinide Elements, ed. L. R. Morss, N. M. Edelstein and J. Fuger, Springer, Dordrecht, The Netherlands, 4th edn, 2010 Search PubMed.
- M. R. Antonio, R. J. Ellis, S. L. Estes and M. K. Bera, Phys. Chem. Chem. Phys., 2017, 19, 21304–21316 RSC.
- G. T. Morgan and H. D. K. Drew, J. Chem. Soc., Trans., 1920, 117, 1456–1465 RSC.
- J. Xi, J.-H. Lan, G.-W. Lu, Y.-L. Zhao, Z.-F. Chai and W.-Q. Shi, Mol. Simul., 2014, 40, 379–386 CrossRef.
- S. Andersson, K. Eberhardt, C. Ekberg, J.-O. Liljenzin, M. Nilsson and G. Skarnemark, Radiochim. Acta, 2006, 94, 469–474 Search PubMed.
- A. Fratiello, V. Kubo-Anderson, S. Azimi, E. Marinez, D. Matejka, R. Perrigan and B. Yao, J. Solution Chem., 1992, 21, 651–666 CrossRef.
- S. Kelly, D. Hesterberg and B. Ravel, in Methods of Soil Analysis. Part 5: Mineralogical Methods, ed. A. L. Ulery and L. R. Drees, Soil Science Society of America, Madison, WI, 2008, pp. 387–464 Search PubMed.
- M. A. Silver and T. E. Albrecht-Schmitt, Coord. Chem. Rev., 2016, 323, 36–51 CrossRef.
- S. K. Cary, M. A. Silver, G. Liu, J. C. Wang, J. A. Bogart, J. T. Stritzinger, A. A. Arico, K. Hanson, E. J. Schelter and T. E. Albrecht-Schmitt, Inorg. Chem., 2015, 54, 11399–11404 CrossRef PubMed.
- J. A. Drader, M. Luckey and J. C. Braley, Solvent Extr. Ion Exch., 2016, 34, 114–125 CrossRef.
- A. W. Knight, R. Chiarizia and L. Soderholm, Solvent Extr. Ion Exch., 2017, 35, 266–279 CrossRef.
- G. K. Liu, V. V. Zhorin, M. R. Antonio, S. T. Li, C. W. Williams and L. Soderholm, J. Chem. Phys., 2000, 112, 1489–1496 CrossRef.
- I. A. Charushnikova, A. M. Fedoseev and V. P. Perminov, Radiochemistry, 2015, 57, 111–121 CrossRef.
- J. F. Corbey, B. M. Rapko, Z. Wang, B. K. McNamara, R. G. Surbella, K. L. Pellegrini and J. M. Schwantes, Inorg. Chem., 2018, 57, 2278–2287 CrossRef PubMed.
- C. Den Auwer, M. C. Charbonnel, M. G. B. Drew, M. Grigoriev, M. J. Hudson, P. B. Iveson, C. Madic, M. Nierlich, M. T. Presson, R. Revel, M. L. Russell and P. Thuéry, Inorg. Chem., 2000, 39, 1487–1495 CrossRef PubMed.
- D. Girnt, P. W. Roesky, A. Geist, C. M. Ruff, P. J. Panak and M. A. Denecke, Inorg. Chem., 2010, 49, 9627–9635 CrossRef PubMed.
- A. Bremer, C. M. Ruff, D. Girnt, U. Müllich, J. Rothe, P. W. Roesky, P. J. Panak, A. Karpov, T. J. J. Müller, M. A. Denecke and A. Geist, Inorg. Chem., 2012, 51, 5199–5207 CrossRef PubMed.
- C. Ekberg, E. Löfström-Engdahl, E. Aneheim, M. R. S. Foreman, A. Geist, D. Lundberg, M. Denecke and I. Persson, Dalton Trans., 2015, 44, 18395–18402 RSC.
- T. S. Grimes, P. R. Zalupski and L. R. Martin, J. Phys. Chem. B, 2014, 118, 12725–12733 CrossRef PubMed.
- A. B. Usov, Radiokhimiya, 1987, 29, 118–121 Search PubMed.
- V. N. Kosyakov, E. A. Yerin and V. M. Vitutnev, J. Radioanal. Chem., 1980, 56, 83–92 CrossRef.
- R. Chiarizia, P. R. Danesi, G. Scibona and L. Magon, J. Inorg. Nucl. Chem., 1973, 35, 3595–3604 CrossRef.
- G. F. Best, E. Hesford and H. A. C. McKay, J. Inorg. Nucl. Chem., 1959, 12, 136–140 CrossRef.
- M. P. Jensen and A. H. Bond, J. Am. Chem. Soc., 2002, 124, 9870–9877 CrossRef PubMed.
- V. I. Vasilyev, E. S. Kalevich, V. M. Radchenko, E. V. Shimbarev, V. P. Egunov, A. N. Izmalkov and V. Y. Vasilyev, J. Radioanal. Nucl. Chem., 1990, 143, 269–274 CrossRef.
- V. I. Vasilyev, E. S. Kalevich, V. Radchenko, V. P. Egunov, A. N. Izmalkov, E. V. Shimbarev and V. Y. Vasilyev, Radiokhimiya, 1990, 32, 6–8 Search PubMed.
- R. M. Smith and A. E. Martell, Critical Stability Constants, Plenum Press, New York, 1989, vol. 4, p. 443 Search PubMed.
- R. M. Smith and A. E. Martell, Critical Stability Constants, Springer Science, New York, 1976, vol. 4 Search PubMed.
- T. Kimura, Y. Kato, H. Takeishi and G. R. Choppin, J. Alloys Compd., 1998, 271–273, 719–722 CrossRef.
- Brookhaven National Laboratory, National Nuclear Data Center, http://www.nndc.bnl.gov/chart/.
- B. Ravel and M. Newville, J. Synchrotron Radiat., 2005, 12, 537–541 CrossRef PubMed.
- F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2018, 8, 4–9 Search PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef PubMed.
- D. A. Pantazis and F. Neese, J. Chem. Theory Comput., 2009, 5, 2229–2238 CrossRef PubMed.
- D. A. Pantazis and F. Neese, J. Chem. Theory Comput., 2011, 7, 677–684 CrossRef.
- F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297 RSC.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456–1465 CrossRef PubMed.
Footnotes |
| † LA-UR-18-22688. |
| ‡ Electronic supplementary information (ESI) available. See DOI: 10.1039/c8sc02270d |
| This journal is © The Royal Society of Chemistry 2018 |