Open Access Article
Open Access ArticleOrigin of stereoselectivity in the amination of alcohols using cooperative asymmetric dual catalysis involving chiral counter-ions†
Soumi
Tribedi
 a,
Christopher M.
Hadad
a,
Christopher M.
Hadad
 b and
Raghavan B.
Sunoj
b and
Raghavan B.
Sunoj
 *a
*a
aDepartment of Chemistry, Indian Institute of Technology Bombay, Powai, Mumbai 400076, India. E-mail: sunoj@chem.iitb.ac.in
bDepartment of Chemistry and Biochemistry, The Ohio State University, Columbus, Ohio 43210, USA
First published on 25th June 2018
Abstract
Asymmetric catalysis using two chiral catalysts in combination using one-pot reaction conditions is in its initial stages of development and understanding. We employ density functional theory (SMD(toluene)/M06/6-31G**,SDD(Ir)) computations to shed light on the action of chiral phosphoric acid and a chiral Cp*Ir(diamine) in stereoinduction in an asymmetric amination reaction of an alcohol. First, the protonation of the Ir–diamine complex by the phosphoric acid forms an ion-pair of the active catalytic dyad. Both chiral catalysts are involved throughout the catalytic cycle, thus constituting an important example of true cooperative catalysis. A borrowing hydrogen mechanism operates, wherein the phosphate abstracts the hydroxyl proton of the alcohol while the electrophilic Ir(III) simultaneously extracts the α-hydrogen to form a [Ir]–H species. The ketone thus derived from the alcohol through dehydrogenation condenses with aniline to form an imine. In the diastereocontrolling transition state, the hydride adds to the activated iminium, held in position in the chiral pocket of the catalytic dyad through a network of noncovalent interactions (C–H⋯π, N–H⋯O and C–H⋯O). The enantioselectivity in this DYKAT process is identified as taking place at an earlier stage of the catalytic cycle prior to the diastereo-determining transition state.
Introduction
The synthesis of optically pure chiral compounds is an area of immense importance, primarily owing to their pharmaceutical potential. Among the plethora of strategies developed over the years, asymmetric chiral counteranion directed catalysis (ACDC) is an interesting protocol.1 In an ACDC protocol, the interaction of chiral counterions in the stereocontrolling charged transition states is considered vital. While the use of chiral counterions in phase-transfer catalysis is reasonably well established,2 related examples in homogeneous catalysis making use of the axially chiral binaphthyl (BINOL) or spirobiindane (SPINOL) family of phosphoric acids is still in its developmental stage.3The mechanism of such Brønsted acid catalysis is expected to become increasingly more intricate when it is used in conjunction with other chiral transition metal catalysts.1b Phosphoric acid and transition metal catalysts when used together under one-pot reaction conditions can present different mechanistic scenarios wherein the former can act as (a) a ligand coordinated to the metal, (b) a Brønsted acid hydrogen bonded to a basic center of the transition metal complex, or (c) a counteranion to the in situ formed positively charged intermediate.4 Deeper mechanistic understanding is required to ascertain the role of chiral Brønsted acids in such forms of catalytic reactions.
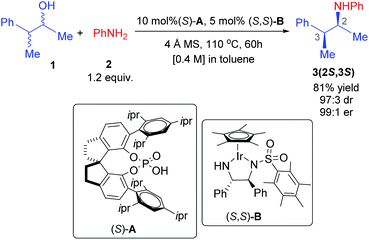
In a recent demonstration of dual catalysis, Zhao and coworkers have employed the borrowing hydrogen method for the asymmetric amination of alcohols. Importantly, both the organocatalyst (phosphoric acid) and the transition metal catalyst (Cp*Ir(diamine)) used as the catalytic dyad are chiral.5 The borrowing hydrogen method is an encouraging strategy to directly engage the readily available and low-cost alcohols in C–C bond formation reactions.6 The method can help oxidize an alcohol to a carbonyl compound, which in turn, can open up a gamut of transformations such as condensation with amines. The resulting imines can then be reduced to respective amines by the transfer of the “borrowed” hydrogen from the catalyst. Chiral amines can also be synthesized through the transfer hydrogenation strategy using small molecules such as alcohols and formic acids or Hantzsch esters as a sacrificial species.7 However, the borrowing hydrogen method offers a major advantage over transfer hydrogenation in that it does not require a sacrificial hydrogen donor; rather, the source of hydrogen is the substrate alcohol itself. While the idea showed early promise,8 the enantioselective variants of such reactions became available only recently by employing catalyst combinations involving compatible organocatalysts and transition metal catalysts.5 Zhao and coworkers reported an elegant asymmetric dual chiral catalytic (ADCC) method for the stereoconvergent amination between four isomers of a chiral alcohol and aryl amine (Scheme 1).9 The action of two chiral catalysts is not a well-understood concept owing to the scarcity of reports focusing on the mechanism and origin of stereoinduction in dual chiral catalytic systems.10
 | ||
| Scheme 1 A representative example of the asymmetric amination of an alcohol using two chiral catalysts.9 | ||
The fascinating feature in this reaction is that although all of the four stereoisomers of the parent alcohol (a pair of enantiomers and a pair of diastereomers) are involved in the reaction as a racemic mixture, only one stereoisomer of the product amine is obtained in excellent enantio- and diastereo-selectivity. The yield of the major diastereomer is more than 80%, suggesting that all of the stereoisomers of the reactant convert to the product. In this article, we wish to present the first molecular insights of stereoinduction in the asymmetric amination of a racemic alcohol using the borrowing hydrogen method under dual chiral catalytic conditions. In particular, we wish to probe whether both catalysts act in a cooperative/synergistic manner or in independent steps in a sequential manner in the catalytic cycle.
Computational details
All free energy values reported in this work are calculated using the M06 density functional11 as implemented in the Gaussian 09 Rev. E.01, suite of programs.12 The effect of a solvent continuum, in toluene, was evaluated using the Cramer–Truhlar SMD continuum solvation model that employs quantum mechanical charge densities of solutes.13 The 6-31G** basis set was employed for all atoms, except iridium,14 for which the SDD basis set consisting of Stuttgart–Dresden effective core potential (ECP) was used.15 The preliminary mechanistic study using model systems of the catalysts (as shown in Fig. S1†) and conformational analysis of important transition states (Tables S6 and S7†) were carried out at the B3LYP-D3 level of theory.16 The lowest energy conformer was then re-optimized with the M06 functional and the same free energy is used for discussion in the manuscript. Furthermore, the free energies of stationary points involved in the formation of the major stereoisomer were recalculated by adding the entropic corrections to the refined single point electronic energies obtained at some of the widely employed level of theories.17 The quasi rigid-rotor harmonic oscillator (RRHO) model was employed for obtaining improved estimates of the entropic contribution due to low frequency vibrational modes.18 Intrinsic reaction coordinate (IRC) calculation was carried out on the transition state geometries to verify that they are connected to the expected minima (toward the reactant and product).19 Topological analyses of electron densities were carried out using AIM2000 software which operates within Bader's Atoms-in-Molecule (AIM) framework20 and NCIPLOT 3.0 which is used to analyze the noncovalent interactions (NCI) qualitatively.21Results and discussion
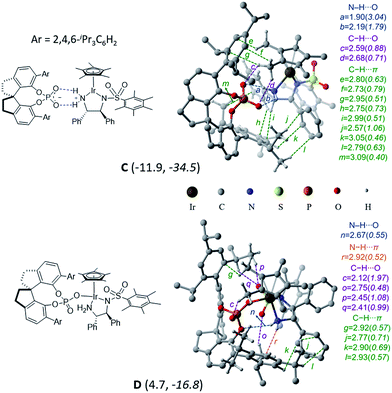
In the title reaction, an iridium 1,2-diamido complex bearing two adjacent chirality centres is the transition metal catalyst (B) and a spirobiindane phosphoric acid serves as the chiral organocatalyst (A) (Scheme 1). A very likely situation when both catalysts interact is a protonation of the –NH group of catalyst B by the Brønsted acid catalyst A. Such a proton transfer can lead to an electrophilic cationic iridium complex and a chiral phosphate as its counteranion.22 The formation of this ion-pair complex C with respect to the infinitely separated reactants is found to be exoergic by −11.9 kcal mol−1 (Fig. 1). Alternatively, the formation of complex D when the chiral phosphate is directly bound to the iridium center as a ligand is endoergic by 4.7 kcal mol−1. The enthalpic advantage towards the formation of the ion-pair C over the neutral complex D is even more pronounced. There are two opposing factors here that render the ion-pair formation more likely: (a) two effective N–H⋯O hydrogen bonding interactions in C between the phosphate and the protonated amino group of the iridium complex (Fig. 1),23 which are absent in D, and (b) the undesirable crowding near the iridium center arising due to the bulky 3,3′ triisopropylaryl groups of the chiral SPINOL phosphate in the case of complex D.Several attempts to optimize any other conformer of D that maintains at least one of the stronger N–H⋯O interactions (a and b) did not succeed. Such geometries converged to the minima, wherein the free oxygen of the covalently bound phosphate participates in a number of C–H⋯O interactions. A comparison of the atoms-in-molecule (AIM) features of C and D revealed a well-woven network of noncovalent interactions such as N–H⋯O (a, b, and n), C–H⋯O (c, d, o, p, and q), and C–H⋯π (e, f, g, h, i, j, k, l, and m) and a unique N–H⋯π (r) interaction between the two catalysts. The ion-pair complex C has a larger number of C–H⋯π contacts, which are lost in D. Due to the loss of the stronger electrostatic N–H⋯O interactions, the free oxygen of the phosphate in D engages in a larger number of C–H⋯O contacts (c, o, p, and q). The overall stabilization of C by 16.6 kcal mol−1 over D can be rationalized by (i) the absence of the stronger interactions in D (a and b) due to conformational constraints and (ii) an enthalpic advantage of the ionic over the covalent interaction between the two catalysts.
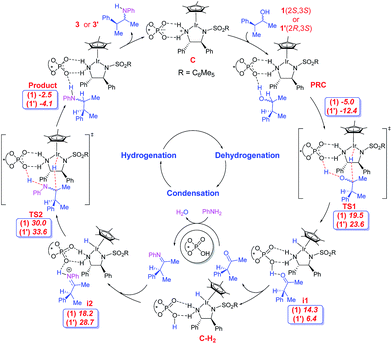
The first important catalytic step is the dehydrogenation of the alcohol to form the corresponding ketone. The dual catalytic combination can act on the substrate alcohol, in two mechanistically distinct modes: inner-sphere or outer-sphere.24 The most preferred dehydrogenation is found to involve a concerted outer-sphere pathway,25 as shown as TS1 in Scheme 2. Interestingly, dehydrogenation in this mode enjoys a cooperative action of both phosphate and Ir(III) catalysts. The phosphate abstracts the proton of the hydroxyl group at one end while the electrophilic Ir(III) center simultaneously extracts the α-hydrogen in the form of a hydride from the other end of the substrate. The whole process can be considered as ‘borrowing’ of a molecule of hydrogen from the substrate in a heterolytic manner, thereby forming a ketone and a hydrogenated catalyst complex, i1. The dehydrogenation of the alcohol directly by the iridium catalyst B, in the absence of the phosphate counterion, is found to be much higher in energy than the cooperative mode involving the ion-pair C.26
Of the four stereoisomers of the substrate alcohol bearing two chirality centres, we focus on a pair of diastereomers (1(2S,3S) and 1′(2R,3S)) to probe the mechanism of the reaction as shown in Scheme 2. Here, the first and second configurational descriptors are respectively for the hydroxyl and the phenyl ring bearing chirality centres in the alcohol. The important issue at this juncture is to examine whether or not the catalyst dyad will dehydrogenate one or both diastereomers. The question is relevant as both catalysts and the substrate are chiral, giving rise to a chiral recognition or a match-mismatch situation. Interestingly, the relative Gibbs free energies (with respect to the separated reactants) of the transition states for concerted dehydrogenation of the two diastereomers of alcohol 1 are found to vary from 19.5 kcal mol−1 for 1(2S,3S) to 23.6 kcal mol−1 in the case of 1′(2R,3S).27
The ketone can now condense with aniline in the presence of the chiral phosphoric acid catalyst to form the respective imine. More details on the condensation steps are provided in Scheme S1 and Fig. S11 in the ESI.† After the loss of chirality at the α-C center due to the formation of the ketone and then the imine, only the configuration of the β-C remains unaltered as (S). Such imine intermediates can be protonated by the chiral phosphoric acid, leading to a second ion-pair species i2 with the chiral phosphate as the counterion (Scheme 2).28 The phosphate-bound iminium can then be intercepted by the [Ir]–H at the imino carbon. In other words, the hydrogen “borrowed” from the substrate by the catalyst dyad in the initial step of the reaction is effectively returned to the developing product in the final step. The hydride transfer to the ion-pair intermediate i2, as shown in Fig. 3, can lead to two diastereomeric products 3(2S,3S) and 3′(2R,3S) depending on the hydride addition to the re or the si prochiral face respectively. While both (E) and (Z)-imines can give both the products, the most favoured hydrogenation TS is found to be when the (E)-imine is involved. The relative energies and geometries of the (Z)-imine are provided in Fig. S15 in the ESI.†
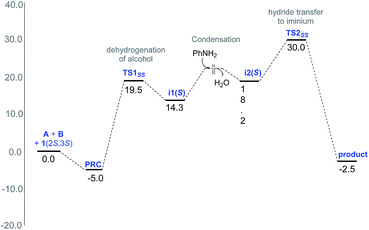
The Gibbs free energy profile for the formation of the preferred stereoisomer 3(2S,3S) is provided in Fig. 2. It can be noticed that the hydride transfer to the iminium viaTS2SS is the rate-determining step with a barrier of 35 kcal mol−1 with respect to the exoergic PRC. Such a barrier can be regarded as a modest over-estimation for a reaction temperature of 110 °C. We have refined the energies of various species involved in the profile using larger basis sets, the details of which are given in Table S9 in the ESI.† The best estimate of the barrier for the rate determining step is found to be about 29.5 kcal mol−1 at the SMD(toluene)/B3LYP-D3/6-31G**,def2-TZVP (Ir)//SMD(toluene)/M06/6-31G**,SDD(Ir) level of theory. This energetic estimate is in line with the reaction conditions and further endorses the action of the two chiral catalysts in the critical hydride transfer step of the reaction. The transition state for the attack of [Ir]–H on the si-face of S-iminium is 3.6 kcal mol−1 higher than that on the re-face. Such a large difference in the energies between the transition states for the re face and si face hydrogenation corresponds to a de of 99.5% in favor of 3(2S,3S), which is in excellent agreement with the experimentally observed de of 94%. The origin of the energy difference can be analyzed at this stage, by probing the molecular features more closely.
Since the chirality at the second carbon chirality centre in the product gets fixed through this hydride transfer transition state, we have carefully analyzed the geometric features to understand more about the counterion-induced chirality transfer. The key interactions are electrostatic and are denoted by using letters a, b, and t in Fig. 3(i) and (ii). In both of these transition states, one of the phosphate oxygen atoms is involved in two relatively stronger N–H⋯O interactions (b and t) with both the electrophilic and nucleophilic partners. The other oxygen atom of the phosphate interacts strongly with one of the hydrogen atoms of the –NH2 group of the iridium catalyst (a). A network of weak non-covalent interactions, such as C–H⋯O (c, d, and v′), C–H⋯π (e, f, g, h, j, l, m, and m′), lpO⋯π (s) and π⋯π (z), between the 3,3′-substituents of the chiral phosphoric acid and the metal catalyst is noticed. The chiral counterion with its bulky aryl arms provides a chiral space for the electrophilic and nucleophilic partners to interact. The topological analysis reveals that the noncovalent interactions offered by the counterion help bring the two reacting partners together and hold them in a suitable geometric position. The mapping of the catalyst–catalyst interactions in both the diastereomeric transition states, as shown in Fig. 3, reveals that the C–H⋯O (c and d) and C–H⋯π (e, f, l, m, and m′) interactions between the chiral phosphate and the metal hydride are better in the case of the hydride transfer to the re face. An effective ‘communication’ between the catalysts, enabled by a series of noncovalent interactions, is noticed in the stereocontrolling transition state, in addition to the expected catalyst–substrate interactions (vide infra). We believe that such camaraderie between the catalysts is vital to their cooperative action in dual chiral catalysis.
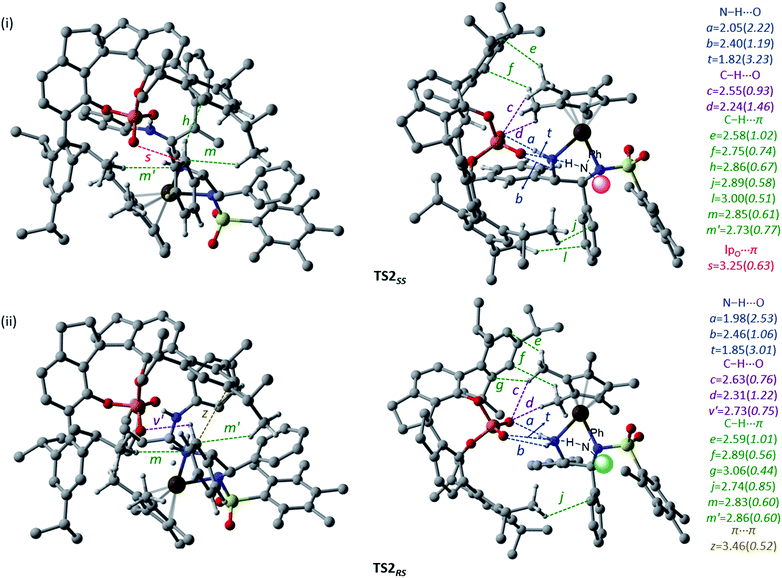 | ||
| Fig. 3 The general representation of the catalyst–catalyst interactions between the chiral phosphate counterion and Ir(III)–H complex (i) in TS2SS and (ii) in TS2RS. Two different orientations of the transition states are shown to improve the clarity of various weak interactions operating between the two chiral catalysts. The noncovalent contacts are in Å and the corresponding electron densities (ρ × 10−2 au) at the bcps are given in parentheses. Hydrogen atoms have been omitted wherever possible, to ensure better clarity. Only the interactions of electrophiles and nucleophiles with the phosphate are shown. Refer to Fig. 1 for atom colour codes. | ||
A comparison of the space-filling models of the transition states for stereoselective hydrogenation is provided in Fig. 4. The chiral phosphate counterion is represented using a grey shade and the Ir-catalyst in red. It can be noticed that both the catalysts together create a chiral pocket into which the substrate iminium fits in. An improved fit of iminium occurs when its re face is exposed for the [Ir]–H addition rather than the si face. In the most favoured transition state TS2SS for the re face addition of [Ir]–H, all the substituents of the iminium such as the N-phenyl and that on the β-chirality centre participate in noncovalent interactions with the catalyst dyad. However, in the higher energy TS2RS, the si face of the iminium should point toward the [Ir]–H. In such an arrangement the β-phenyl substituent on the chirality centre is found to remain away from the catalyst in a perpendicular arrangement. An interesting difference between these diastereomeric transition states in the region where the iminium fits in is also noticed. In the chiral pocket of the catalyst dyad, the upper region is relatively more compact than the lower region, as shown in Fig. 4. In TS2SS, the tetrahedral β-chirality centre occupies the spacious lower region of the catalyst leading to a relatively better fit of the substituents. In such a fit, better N–H⋯O and C–H⋯O interactions (t and w) between the iminium and the chiral phosphate are noticed. In the higher energy TS2RS, the larger tetrahedral carbon would have to fit into the compact upper region of the catalyst dyad. In order to accommodate the tetrahedral center, distortion in the dihedral angle ϕ1(C1–C2–C3–C4), up to −102° is noticed in the higher energy TS2RS as compared to −94° in the most preferred TS2SS.
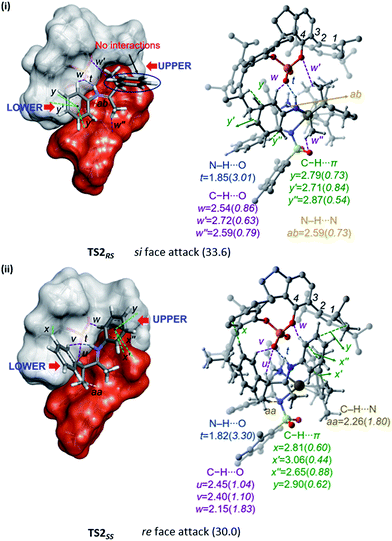 | ||
| Fig. 4 Space-filling models (left) of the diastereomeric transition states (i) TS2RS and (ii) TS2SS for the asymmetric hydride transfer to (S)-iminium. Given on the right side are all the important interatomic distances (Å) of noncovalent interactions and the corresponding electron densities (ρ × 10−2 au) at the bond critical points (bcps). Hydrogen atoms have been omitted wherever required, to ensure better clarity. Relative free energies are given in parentheses in kcal mol−1. Refer to Fig. 1 for atom color codes. | ||
The noncovalent interactions only between the catalysts and substrate are shown in Fig. 4.29 The most important interaction is an N–H⋯O electrostatic interaction (denoted as t) between the iminium and phosphate. In addition, the catalyst dyad exhibits a network of weak contacts such as C–H⋯O (u, v, w, w′, w′′) and C–H⋯π (x, x′, x′′, y, y′, y′′) with the substrate through (i) 3,3′-aryl substituents of the phosphate and (ii) the substituents on the Ir-catalyst. In the hydride transfer transition state, there are only two or three interactions between the substrate and the [Ir]–H whereas six interactions are noted with the chiral phosphate. This led us to infer that the chiral phosphate is mostly, if not entirely, responsible for the stereochemical outcome in this dual catalytic reaction. Since chiral induction by the phosphate is recognized as more impactful than that by the chiral iridium complex, we propose that further modifications to this dual catalytic strategy could focus on the phosphoric acid 3,3′-aryl substituents. It would also be of interest to see the stereochemical outcome with a substrate alcohol bearing one more chirality centre.
The difference in the catalyst–catalyst and catalyst–substrate non-covalent interactions in the two diastereomeric hydride addition TSs from the same (S)-iminium phosphate ion-pair intermediate, i2(S), is found to be an important factor impacting the diastereoselectivity. However, enantiomers of the product amine are formed from different intermediates, i.e., 3(2S,3S) from i2(S) and 3′′(2R,3R) from i2(R). In other words, intermediate i2(S) cannot give the minor enantiomer 3′′, neither can i2(R) form the major enantiomer. It should also be noted that i2(S) and i2(R) are diastereomeric intermediates and have different energies. Therefore, the standard approach for calculating ee, on the basis of the difference in the relative free energies of the hydride addition TSs, does not directly apply in this situation. In most asymmetric reactions, enantioselectivity is achieved through a crucial step where one of the prochiral faces of the substrate reacts faster than the other. In such cases, all elementary steps leading up to the stereodetermining TS are expected to show no particular preference towards the formation of any one enantiomer. In the present example, the diastereoselectivity in the formation of 3(2S,3S) is due to the difference in the free energies of the corresponding hydride transfer TS only. However, the question of enantioselectivity presents a non-trivial scenario. The initial dehydrogenation and ensuing condensation as well as the hydride addition might impact the enantioselectivity, as the R or S configuration at the β-C of the substrate is preserved in these steps. Since the yield of the major product under the optimised reaction conditions is more than 80%, one can infer the involvement of a DYKAT mechanism,30 in which case, at some point during the course of the reaction, the R substrate is expected to convert to the S substrate prior to the final hydride transfer step.
We have considered an epimerization of the β-R stereocentre to β-S at the ketone stage, i.e., in intermediate i1′ (Scheme 3).31 The final product is formed through a condensation of the (S)-ketone with aniline and a hydride addition to the resulting (S)-iminium intermediate. The two key steps in condensation are (a) nucleophilic attack of aniline on the carbonyl carbon viaTSi-k(R) giving intermediate k(R), and (b) H2O elimination to form (R)-iminium l(R) viaTSk-l(R). The epimerisation to the (S)-ketone also involves two steps such as (a) a deprotonation of the β-C–H mediated by the chiral phosphoric acid, and (b) re-protonation through the other prochiral face of the enol j to give the (S)-ketone. The epimerization of the (R) to the (S) ketone via a common enol intermediate is found to be energetically more favoured than its condensation to form (R)-iminium (Fig. 5).
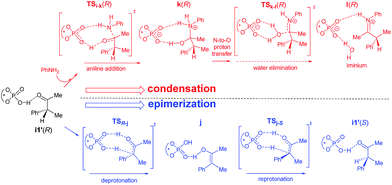 | ||
| Scheme 3 Two plausible pathways for the involvement of the (R)-ketone in the reaction. The solid arrows represent a faster pathway as compared to the dotted arrow. | ||
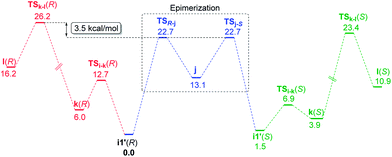 | ||
| Fig. 5 Comparison of the free energy profiles (kcal mol−1) for epimerisation of the (R) to the (S) ketone and the condensation of the (R)-ketone to form the (R)-iminium intermediate. | ||
As the calculation of enantiomeric excess in a DYKAT situation is not quite straightforward, we approached the problem as follows. Two critical mechanistic routes that can impact the configuration of the products are (a) the ease of conversion of i1′(R) to i1′(S) followed by condensation to form (S)-iminium and subsequent hydride addition to give the (2S,3S) product, or (b) a direct condensation of i1′(R) to form the respective iminium and then the hydride transfer to (R)-iminium to form the minor stereoisomer 3′′(2R,3R). In the present example, the configuration of the product is determined in the phosphoric acid catalysed epimerization of the (R)-ketone to the (S)-ketone through TSR-j and TSj-S (Scheme 3). The Gibbs free energy profile, as given in Fig. 5, indicates that the most energy demanding elementary step in the direct condensation path-(b), which leads to the 3R configuration in the product, is the expulsion of water viaTSk-l(R). On the other hand, ketone epimerization viaTSj-S in path-(a) would result in the 3S configuration. It should be noted that the configuration at the C2 centre would depend on the preferred prochiral face involved in the hydride addition. Hence, the energetic origin of enantioselectivity can be considered as the difference in the relative Gibbs free energies of TSs with the highest energy in the epimerization and condensation pathways for the (R)-ketone, as shown in Scheme 3. This difference amounts to (26.2–22.7) 3.5 kcal mol−1, which is equivalent to an ee of 99.4%, in very good agreement with the experimental value of 98%.32
Conclusions
In summary, we have found that the asymmetric amination of alcohols by the borrowing hydrogen mechanism involves a true cooperative action of both the [Ir]-catalyst and phosphoric acid, implying that both the catalysts display interaction with each other as well as with the substrate in the diastereoselectivity determining hydride transfer step. The chiral phosphate contributes to stereoinduction in the form of a counterion through strong (N–H⋯O) electrostatic interaction: (i) one with the substrate and (ii) two with the [Ir]-catalyst, as well as through (iii) a series of weak noncovalent interactions (C–H⋯O and C–H⋯π). The cumulative effect of this bifunctionality (provided by the phosphate oxygen atoms and the 3,3′-aryl substituents) offers to create a stereo-differentiating chiral pocket resulting in hydride transfer to the re-face of the vital iminium intermediate. The computed diastereoselectivity (99.5%) is in excellent agreement with experimental observation (94%). On the other hand, the enantioselectivity in this DYKAT reaction is found to depend on steps other than the hydride transfer. The formation of the minor enantiomer (2R,3R) depends on the percentage of the (3R)-iminium intermediate available for the hydride addition. We find that the (R)-ketone intermediate formed through the initial dehydrogenation has a better propensity to epimerize to the (S)-ketone, which subsequently condenses to (S)-iminium for the final hydride addition. The ee calculated by using the Boltzmann distribution of the most energetically demanding transition states for the direct condensation and the epimerization of the (R)-ketone is in excellent agreement with the experimental values (calculated 99.4%, observed 98%).Conflicts of interest
There are no conflicts to declare.Acknowledgements
We acknowledge the Industrial Research and Consultancy Center (IRCC), SpaceTime supercomputing at IIT Bombay and Ohio Supercomputing Centre (OSC), Ohio, USA for generous computing time.Notes and references
- (a) J. Lacour and D. Moraleda, Chem. Commun., 2009, 7073 RSC; (b) R. J. Phipps, G. L. Hamilton and F. D. Toste, Nat. Chem., 2012, 4, 603 CrossRef PubMed; (c) K. Brak and E. N. Jacobsen, Angew. Chem., Int. Ed., 2013, 52, 534 CrossRef PubMed; (d) M. Mahlau and B. List, Angew. Chem., Int. Ed., 2013, 52, 5183 CrossRef PubMed; (e) G. L. Hamilton, E. J. Kang, M. Mba and F. D. Toste, Science, 2007, 317, 496 CrossRef PubMed; (f) T. J. Seguin and S. E. Wheeler, Angew. Chem., Int. Ed., 2016, 55, 15889 CrossRef PubMed.
- (a) T. Ooi and K. Maruoka, Angew. Chem., Int. Ed., 2007, 46, 4222 CrossRef PubMed; (b) S. Shirakawa and K. Maruoka, Angew. Chem., Int. Ed., 2013, 52, 4312 CrossRef PubMed; (c) C. M. Avila, J. S. Patel, Y. Reddi, M. Saito, H. M. Nelson, H. P. Shunatona, M. S. Sigman, R. B. Sunoj and F. D. Toste, Angew. Chem., Int. Ed., 2017, 56, 5806 CrossRef PubMed; (d) E. Yamamoto, M. J. Hilton, M. Orlandi, V. Saini, F. D. Toste and M. S. Sigman, J. Am. Chem. Soc., 2016, 138, 15877 CrossRef PubMed; (e) H. M. Nelson, B. D. Williams, J. Miró and F. D. Toste, J. Am. Chem. Soc., 2015, 137, 3213 CrossRef PubMed; (f) F. Duarte and R. S. Paton, J. Am. Chem. Soc., 2017, 139, 8886 CrossRef PubMed.
- (a) J. Lacour and D. Linder, Science, 2007, 317, 462 CrossRef PubMed; (b) D. Parmar, E. Sugiono, S. Raja and M. Rueping, Chem. Rev., 2014, 114, 9047 CrossRef PubMed; (c) D.-F. Chen, Z.-Y. Han, X.-L. Zhou and L.-Z. Gong, Acc. Chem. Res., 2014, 47, 2365 CrossRef PubMed.
- (a) R. Maji, P. A. Champagne, K. N. Houk and S. E. Wheeler, ACS Catal., 2017, 7, 7332 CrossRef; (b) K. H. Hopmann, Chem.–Eur. J., 2015, 21, 10020 CrossRef PubMed.
- Y. Zhang, C.-S. Lim, D. S. B. Sim, H.-J. Pan and Y. Zhao, Angew. Chem., Int. Ed., 2014, 53, 1399 CrossRef PubMed.
- For selected reviews on borrowing hydrogen methodology, see, (a) M. H. S. A. Hamid, P. A. Slatford and J. M. J. Williams, Adv. Synth. Catal., 2007, 349, 1555 CrossRef; (b) A. J. A. Watson and J. M. J. Williams, Science, 2010, 329, 635 CrossRef PubMed; (c) G. Guillena, D. J. Ramón and M. Yus, Chem. Rev., 2010, 110, 1611 CrossRef PubMed.
- (a) J. G. de Vries and N. Mršić, Catal. Sci. Technol., 2011, 1, 727 RSC; (b) C. Zheng and S. L. You, Chem. Soc. Rev., 2012, 41, 2498 RSC; (c) J.-H. Xie, S.-F. Zhu and Q.-L. Zhou, Chem. Rev., 2011, 111, 1713 CrossRef PubMed; (d) A. Bartoszewicz, N. Ahlsten and B. Martín-Matute, Chem.–Eur. J., 2013, 19, 7274 CrossRef PubMed; (e) H.-J. Pan, Y. Zhang, C. Shan, Z. Yu, Y. Lan and Y. Zhao, Angew. Chem., Int. Ed., 2016, 55, 9615 CrossRef PubMed; (f) R. Noyori, M. Yamakawa and S. Hashiguchi, J. Org. Chem., 2001, 66, 7931 CrossRef PubMed.
- (a) R. Grigg, T. R. B. Mitchell, S. Sutthivaiyakit and N. Tongpenyai, J. Chem. Soc., Chem. Commun., 1981, 611 RSC; (b) K. Fujita, K. Yamamoto and R. Yamaguchi, Org. Lett., 2002, 4, 2691 CrossRef PubMed; (c) K. Fujita, T. Fujii and R. Yamaguchi, Org. Lett., 2004, 6, 3525 CrossRef PubMed; (d) R. Yamaguchi, S. Kawagoe, C. Asai and K. Fujita, Org. Lett., 2008, 10, 181 CrossRef PubMed; (e) D. Balcells, A. Nova, E. Clot, D. Gnanamgari, R. H. Crabtree and O. Eisenstein, Organometallics, 2008, 27, 2529 CrossRef.
- Z.-Q. Rong, Y. Zhang, R. H. B. Chua, H.-J. Pan and Y. Zhao, J. Am. Chem. Soc., 2015, 137, 4944 CrossRef PubMed.
- (a) B. Bhaskararao and R. B. Sunoj, ACS Catal., 2017, 7, 6675 CrossRef; (b) B. Bhaskararao and R. B. Sunoj, J. Am. Chem. Soc., 2015, 137, 15712 CrossRef PubMed.
- (a) Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2008, 120, 215 Search PubMed; (b) Y. Zhao and D. G. Truhlar, Acc. Chem. Res., 2008, 41, 157 CrossRef PubMed. For suitability of M06 functional for transition metal and organocatalytic systems, see: (c) Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2008, 120, 215 Search PubMed; (d) Y. Zhao and D. G. Truhlar, Acc. Chem. Res., 2008, 41, 157 CrossRef PubMed; (e) Q. Peng, F. Duarte and R. S. Paton, Chem. Soc. Rev., 2016, 45, 6093 RSC.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, T. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski, and D. J. Fox, Gaussian 09, Revision E.01, Gaussian, Inc., Wallingford CT, 2013 Search PubMed.
- A. V. Marenich, C. J. Cramer and D. G. Truhlar, J. Phys. Chem. B, 2009, 113, 6378 CrossRef PubMed.
- (a) W. J. Hehre, R. Ditchfield and J. A. Pople, J. Chem. Phys., 1972, 56, 2257 CrossRef; (b) P. C. Hariharan and J. A. Pople, Theor. Chim. Acta, 1973, 28, 213 CrossRef; (c) C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785 CrossRef; (d) A. D. Becke, J. Chem. Phys., 1993, 98, 5648 CrossRef.
- (a) D. Andrae, U. Haussermann, M. Dolg, H. Stoll and H. Preuss, Theor. Chim. Acta, 1990, 77, 123 CrossRef; (b) P. Fuentealba, H. Stoll, L. von Szentpály, P. Schwerdtfeger and H. Preuss, J. Phys. B: At. Mol. Phys., 1983, 16, L323 CrossRef.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- (a) E. Erbing, A. Sanz-Marco, A. Vázquez-Romero, J. Malmberg, M. J. Johansson, E. Gómez-Bengoa and B. Martín-Matute, ACS Catal., 2018, 8, 920 CrossRef; (b) L. Fang, T. G. Saint-Denis, B. L. H. Taylor, S. Ahlquist, K. Hong, S. Liu, L. Han, K. N. Houk and J.-Q. Yu, J. Am. Chem. Soc., 2017, 139, 10702 CrossRef PubMed; (c) B. Chattopadhyay, J. E. Dannatt, I. L. Andujar-De Sanctis, K. A. Gore, R. E. Maleczka, D. A. Singleton and M. R. Smith, J. Am. Chem. Soc., 2017, 139, 7864 CrossRef PubMed; (d) M. Zhang, L. Hu, Y. Lang, Y. Cao and G. Huang, J. Org. Chem., 2018, 83, 2937 CrossRef PubMed; (e) B. Tutkowski, S. Kerdphon, E. Limé, P. Helquist, P. G. Andersson, O. Wiest and P.-O. Norrby, ACS Catal., 2018, 8, 615 CrossRef; (f) C. M. Le, T. Sperger, R. Fu, X. Hou, Y. H. Lim, F. Schoenebeck and M. Lautens, J. Am. Chem. Soc., 2016, 138, 14441 CrossRef PubMed; (g) C. C. C. Johansson Seechurn, T. Sperger, T. G. Scrase, F. Schoenebeck and T. J. Colacot, J. Am. Chem. Soc., 2017, 139, 5194 CrossRef.
- S. Grimme, Chem.–Eur. J., 2012, 18, 9955 CrossRef PubMed.
- (a) C. Gonzalez and H. B. Schlegel, J. Chem. Phys., 1989, 90, 2154 CrossRef; (b) C. Gonzalez and H. B. Schlegel, J. Phys. Chem., 1990, 94, 5523 CrossRef.
- (a) AIM2000 Version 2.0; Buro fur Innovative Software, SBK-Software, Bielefeld, Germany, 2002 Search PubMed; (b) R. F. W. Bader, Chem. Rev., 1991, 91, 893 CrossRef; (c) C. F. Matta and R. J. Boyd, in Quantum Theory of Atoms in Molecules: Recent Progress in Theory and Application, Wiley-VCH, Weinheim, 2007 CrossRef.
- (a) E. R. Johnson, S. Keinan, P. Mori-Sanchez, J. Contreras-Garcia, A. J. Cohen and W. T. Yang, J. Am. Chem. Soc., 2010, 132, 6498 CrossRef PubMed; (b) J. Contreras-Garcia, E. R. Johnson, S. Keinan, R. Chaudret, J.-P. Piquemal, D. N. Beratan and W. Yang, J. Chem. Theory Comput., 2011, 7, 625 CrossRef PubMed.
- (a) W. Tang, S. Johnston, J. A. Iggo, N. G. Berry, M. Phelan, L. Lian, J. Bacsa and J. Xiao, Angew. Chem., Int. Ed., 2013, 52, 1668 CrossRef PubMed; (b) The NPA charges on the cationic Ir-complex are used to identify the most likely site for counterion binding (Fig. S2†).
- The presence of hydrogen bonding interactions are probed by using the atoms-in-molecule formalism. The value of the electron density at the N–H⋯O bond critical points in the case of the ion-pair complex C is found be as high as 3.04 × 10−2 a.u., indicating a strong ionic hydrogen bonding. See Fig. S10 in the ESI† for the NCI plots.
- The details of the inner-sphere TS are provided in Fig. S8 and Table S4 and that of the outer-sphere alternative in Fig. S6 and Table S3 in the ESI.†.
- More details of extended Internal Reaction Coordinate plot is provided in Fig. S7 in the ESI† that confirmed that the dehydrogenation is a concerted process.
- (a) Additional dehydrogenation possibilities by B is found to be less favored compared to the cooperative mode involving the ion-pair C (Fig. S4 and S5 and Tables S1 and S2†); (b) Alternative possibilities of dehydrogenation by D, concerted (Fig. S9 and Table S5) are described in the ESI.†.
- The Gibbs free energy difference between two diastereomeric forms of 1 is ∼0.5 kcal mol−1. Hence, the average Gibbs free energy is taken as the common reference point for comparison.
- (a) L. Simón and J. M. Goodman, J. Am. Chem. Soc., 2008, 130, 8741 CrossRef PubMed; (b) T. Marcelli, P. Hammar and F. Himo, Adv. Synth. Catal., 2009, 351, 525 CrossRef; (c) L. Simón and J. M. Goodman, J. Org. Chem., 2011, 76, 1775 CrossRef PubMed; (d) T. Marcelli, P. Hammar and F. Himo, Chem.–Eur. J., 2008, 14, 8562 CrossRef PubMed; (e) N. Sorgenfrei, J. Hioe, J. Greindl, K. Rothermel, F. Morana, N. Lokesh and R. M. Gschwind, J. Am. Chem. Soc., 2016, 138, 16345 CrossRef PubMed.
- (a) Details of full mapping of noncovalent interactions are provided in Fig. S19 and S20 and Table S8 in the ESI.†; (b) Importance of noncovalent interactions in asymmetric catalysis has been recently documented. See, ; (c) A. J. Neel, M. J. Hilton, M. S. Sigman and F. D. Toste, Nature, 2017, 543, 637 CrossRef PubMed; (d) J. P. Wagner and P. R. Schreiner, Angew. Chem., Int. Ed., 2015, 54, 12274 CrossRef PubMed; (e) R. B. Sunoj, Acc. Chem. Res., 2016, 49, 1019 CrossRef PubMed.
- (a) V. Bhat, E. R. Welin, X. Guo and B. M. Stoltz, Chem. Rev., 2017, 117, 4528 CrossRef PubMed; (b) B. M. Trost and D. R. Fandrick, Aldrichimica Acta, 2007, 40, 59 Search PubMed.
- Another likely epimerization route i2(R) to i2(S) via the iminium intermediate was found to be not as effective as that with the ketone. See Fig. S17 and S18.†.
- Alternatively, if epimerization of i1′(S) to i1′(R) is considered, the epimerization of (S)-ketone is found to be favoured by 0.7 kcal mol−1 over its condensation to form (S)-iminium. Therefore, (R)-ketone can epimerise faster and form (S)-ketone and further drive the reaction towards the hydride addition to (S)-iminium. As an alternative approach, if the difference of the energy by which epimerization is favoured over condensation is considered for calculating ee, i.e., 3.5 − 0.7 = 2.8 kcal mol−1, the ee works out to be 98.2%, which is close to that of the experimental value of 98%.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c8sc01433g |
| This journal is © The Royal Society of Chemistry 2018 |