Open Access Article
Open Access ArticleRevitalizing the concept of bond order through delocalization measures in real space†
Carlos
Outeiral
 abc,
Mark A.
Vincent
abc,
Mark A.
Vincent
 ab,
Ángel
Martín Pendás
ab,
Ángel
Martín Pendás
 c and
Paul L. A.
Popelier
c and
Paul L. A.
Popelier
 *ab
*ab
aManchester Institute of Biotechnology (MIB), 131 Princess Street, Manchester M1 7DN, UK. E-mail: pla@manchester.ac.uk
bSchool of Chemistry, University of Manchester, Oxford Road, Manchester M13 9PL, UK
cDepartment of Physical and Analytical Chemistry, University of Oviedo, Julián Clavería 8, Oviedo, Spain
First published on 13th June 2018
Abstract
Ab initio quantum chemistry is an independent source of information supplying an ever widening group of experimental chemists. However, bridging the gap between these ab initio data and chemical insight remains a challenge. In particular, there is a need for a bond order index that characterizes novel bonding patterns in a reliable manner, while recovering the familiar effects occurring in well-known bonds. In this article, through a large body of calculations, we show how the delocalization index derived from Quantum Chemical Topology (QCT) serves as such a bond order. This index is defined in a parameter-free, intuitive and consistent manner, and with little qualitative dependency on the level of theory used. The delocalization index is also able to detect the subtler bonding effects that underpin most practical organic and inorganic chemistry. We explore and connect the properties of this index and open the door for its extensive usage in the understanding and discovery of novel chemistry.
Introduction
Central to chemistry is the development of concepts capable of capturing the complexities of the behaviour of matter with as far reaching predictive power as possible. Among these concepts, the Lewis pair1 shines brighter than any other, even a hundred years after its introduction. Indeed, chemical bonds are intimately linked to electron sharing between atoms. This pair idea soon spawned a number of quantitative reifications, as well as answers to how many pairs, or to how evenly these pairs are shared between atoms. Bond order, for instance, is one of these basic quantitative measures that has proven crucial to the taxonomic success of practical organic and inorganic chemistry.As with many pre-quantum mechanics chemical concepts, the Lewis pair does not fit directly into the abstract algebraic structure of the quantum mechanical edifice. Wavefunctions, dwelling in a Hilbert functional space, are entities devoid of atoms and bonds. Hence, reconciling the Lewis picture with the quantum mechanical world has been one of the classical conundrums of theoretical chemistry, leading to several, diverse solutions. Very succinctly, different formal landscapes end up reifying chemical concepts through different plausibility arguments. First, in the formalism of naïve molecular orbital theory, bond order is obtained by simple electron counting after identifying bonding and antibonding occupied orbitals. Secondly, if orbitals are constructed from nucleus-centered localized primitive functions, then the electron population of a molecule can be partitioned into atomic and interatomic (overlap) contributions, the latter being associated to electron sharing and to bond orders.
Difficulties arise in the first formalism in the step of identifying bonding versus antibonding, or whenever a single electron configuration is not a good approximation to the electronic structure. A plethora of more or less arbitrarily founded modifications have been proposed over the years to cope with these situations. Similarly, in second formalism, a branch of Mulliken's population analysis,2 is heavily dependent on the nature of the basis functions. The latter cease to have any physical meaning with a delocalized basis set, such as the plane waves used in many modern periodic calculations. Within this framework, several well-known indices, from Coulson's charge-bond order matrix in Hückel theory to Wiberg's index, have recently been reviewed by Mayer.3,4
To emphasize today's blurry state of affairs, the IUPAC's Gold Book introduces bond order as “The electron population in the region between atoms A and B of a molecular entity at the expense of electron density in the immediate vicinity of the individual atomic centers”.5 This definition leans more towards population analyses than towards counting shared electrons.
The issues surrounding the uniqueness in definitions have contributed to the slow decay of quantitative measures of bond orders, and that of several other fuzzy chemical indicators in the modern literature. Often, these descriptors are left as qualitative devices that are not taken too seriously. In this inexorable ageing process, much predictive power may have fallen by the wayside. Nonetheless, we feel that the situation can be reversed if physically and mathematically well-founded characterizations of these concepts are found and if the chemical community agrees with them. Focusing on bond order, ideal indices should simultaneously gauge electron sharing and electron population partitioning, all of which should appear in the wake of a sensible atomic decomposition.
A formalism meeting these requirements exists, and is based on using measurable quantities (Dirac observables in the language of quantum mechanics). Its conclusions are guaranteed to be independent of modelling particularities (i.e. what orbitals are used, what level of theory, and if the basis functions are localized or delocalized). We apply the probability of finding electrons at a point in space, using the electron density or one-particle density, to define atoms. The electron density leads to the fertile terrain of Quantum Chemical Topology (QCT) as pioneered by the group of Bader.6,7Fig. 1 shows the result of such a real-space and parameter-free partitioning. Similarly, we employ the probability of finding pairs of electrons at two points in space, called the electron pair density or two-particle density,8 in order to introduce electron sharing and bond order, which is referred9 to as the Delocalization Index (DI).
 | ||
| Fig. 1 Quantum atoms appearing in the N8 molecule. The values of the delocalization indices, one for each bond, and calculated at the HF/6-311++G(2d,2p) level of theory, are marked in white. | ||
DIs have been used for some years in the specialized literature,10–16 including recent generalizations such as localization–delocalization matrices17,18 or n-center DIs,19,20 but they have not yet permeated many other chemical disciplines. In this paper we intend to show, through an extensive analysis of nearly 200 diverse chemical compounds, how DIs can actually account for the bond order where its predecessors experienced difficulties providing powerful insight into the nature of electron sharing.
This paper is structured as follows. First we briefly develop the theoretical background behind the delocalization index. Subsequently, we point out the general trends of the delocalization indices, and show how not only to recover bond order but also especially how to understand electron sharing properly. Finally, we apply the results to three examples of uncommon bonding patterns: the molecule N8, an example of planar tetracoordinated carbon, and an iron complex whose structure has been discussed in the literature.
Theory
Quantum chemical topology is a branch of theoretical chemistry that employs the mathematical language of dynamical systems (e.g. critical point, basin, attractor, separatrix) to partition a quantum mechanical density function. When this function is the electron density then one defines atoms within a system. This is what the Quantum Theory of Atoms in Molecules (QTAIM) achieves, as part of the QCT approach. Here, the quantum mechanical density function is the electron density, an important function legitimized by the Hohenberg and Kohn theorems. Thus, one defines an atomic basin Ω, also called quantum atom for our purpose, as a subspace of![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) 3 bounded by a number of interatomic surfaces S, each surface being defined by the zero-flux condition or
3 bounded by a number of interatomic surfaces S, each surface being defined by the zero-flux condition or| ∇ρ(r)·n(r) = 0 ∀ r ∈ S | (1) |
The justification for this partitioning is quantum mechanical in nature, and it may be shown that all molecular properties can be rigorously partitioned as a sum of atomic (or atomic plus interatomic) contributions defined through basins (or basins and pairs of basins). This formalism allows recovering the vivid and chemically appealing picture of atoms within a molecule, without abandoning the theoretical stability of Dirac observables and the well-developed methods of computational quantum chemistry.
Once the quantum atoms {ΩA, ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ΩB, …} constituting a molecular or condensed system have been defined, their electronic properties can be rigorously studied through the formalism of Reduced Density Matrices (RDM). Following McWeeny's convention,21 the spinless RDMs of first and second order are respectively defined as
ΩB, …} constituting a molecular or condensed system have been defined, their electronic properties can be rigorously studied through the formalism of Reduced Density Matrices (RDM). Following McWeeny's convention,21 the spinless RDMs of first and second order are respectively defined as
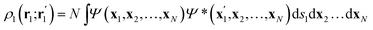 | (2) |
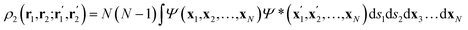 | (3) |
From the 2-RDM it is possible to extract its diagonal part in order to define the second order reduced density (2-RD) or pair density ρ2(r1,r2), which is the probability density of finding a pair of electrons at the volume elements dr1 and dr2. This magnitude has a natural partition in three terms: Coulomb ρ1(r1)ρ1(r2), exchange ρ1(r1;r2)ρ1(r2;r1) and correlation, which is the difference between the 2-RD and the HF 2-RD (the latter lacks correlation). In general, the last two terms are grouped in the exchange–correlation density ρxc(r1,r2), which is formally equal to ρ1(r1)ρ1(r2) − ρ2(r1,r2). Note that ρxc(r1,r2) is sometimes23 defined with the opposite sign.
If the exchange–correlation density is averaged over a pair of basins, one obtains a measure of the number of electron pairs that are being shared between quantum atoms ΩA and ΩB. We then arrive at a definition23 of the delocalization index:
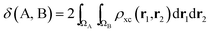 | (4) |
In the same vein, a localization index λ can be defined by integration in the same basin
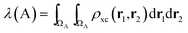 | (5) |
As the quantum atoms are non-overlapping and fill all of ![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) 3 space, it is evident that the integration of the exchange–correlation density over the whole real space yields:
3 space, it is evident that the integration of the exchange–correlation density over the whole real space yields:
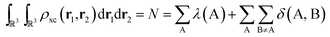 | (6) |
We can ask how to obtain the number of electron pairs Np shared between two quantum atoms, ΩA and ΩB. Depending on whether we prefer to think24 of ordered or unordered pairs, ρ2(r1,r2) will integrate over all space either to Np = N(N − 1) or to Np = N(N − 1)/2 depending on the normalization chosen. We adopt the first option here. A system with two quantum atoms contains (NA + NB) electrons in total. Hence the total number of (ordered) pairs is given by Np = (NA + NB)(NA + NB − 1). Imagine that the electrons contained in ΩA are not shared, i.e. they are localized in ΩA. Imagine also that the same applies to ΩB. Counting the number of pairs formed by the electrons of ΩA and ΩB then yields NANB. Similarly, the number of pairs within ΩA and ΩB (called intra-pairs) will be NA(NA − 1) and NB(NB − 1), respectively. However, when some electrons are shared, i.e. whenever electrons are allowed to delocalize between basins ΩA and ΩB, then the number of pairs is obtained by six-dimensional integration of ρ2(r1,r2), that is, simultaneously over two electrons. If both electrons are averaged over the same region then we obtain the number of intra-basin pairs, NpAA and NpBB. If one electron is averaged in ΩA and the other in ΩB then we obtain the number of inter-basin pairs, NpAB. Obviously, Np = NpAA + NpBB + 2NpAB. Now it is useful to define the discrepancy, denoted dAA, between the number of pairs found if the average number of electrons in A were completely localized in A, i.e. NA(NA − 1), and the number of pairs that one actually sees in A, NpAA. So dAA = NA(NA − 1) − NpAA. Similarly one can define dBB = NB(NB − 1) − NpBB, and dAB = NANB − NpAB. Using the last three equations and the earlier equation, Np = NpAA + NpBB + 2NpAB, a straightforward derivation shows that dAA + dBB + 2dAB = 0, which means that the total difference vanishes over the whole system. Finally, one can show that the discrepancy dAA is directly to λ(A), and dAB to δ(A, B). Indeed, from eqn (5) and ρxc(r1,r2) = ρ1(r1)ρ1(r2) − ρ2(r1,r2) it follows that λ(A) is NANA − NpAA, which is equal to NA(NA − 1) + NA − NpAA = NA + dAA. Secondly and similarly, from eqn (4) and ρxc(r1,r2) = ρ1(r1)ρ1(r2) − ρ2(r1,r2) it follows that δ(A, B) = NANB − NpAB = dAB. All this provides the sought link, because if all the electrons in A are localized then dAA = 0 and λ(A) = NA. Similarly, the delocalization index measures directly the number of inter-basin pairs.
Counting the number of delocalized pairs through delocalization indices provides a mean to partition the electron pairs of an atom into two subsets: (i) those pairs that are unshared, localized in the atom, and (ii) those that are shared or delocalized between that atom and other atoms. These subsets are of paramount importance, since they link the two prevailing images of what bond order is and how it can be properly obtained. Indeed, on the one hand there is the Lewis picture of electron sharing, while on the other hand, there is the picture of electron population partitioning contained in the IUPAC definition and in the standard population analyses going from Mulliken to Wiberg and Mayer.
Being constructed from quantum mechanical observables (i.e. the one- and two-particle densities), the delocalization index possesses a large number of properties, and is related to many modern chemical bonding interpretations. One of these interpretations is the Interacting Quantum Atoms (IQA) formalism,25 which has been extensively used to understand molecular interactions. We show here how the delocalization index is a first-order approximation to the exchange energy Vx in Hartree–Fock theory. Let us write the exchange–correlation energy as
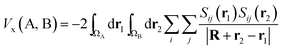 | (7) |
| Sij(r) = ψi(r)ψj(r) | (8) |
Note that the numerator in eqn (7) is the exchange–correlation density in Hartree–Fock theory. The 6D integral in this expression can be simplified by a binomial Taylor expansion of |R + r2 − r1|−1 and subsequent application of the spherical harmonics addition theorem.26 This allows the factorization of the electronic (r1, r2) and the geometric coordinates (R) as follows:
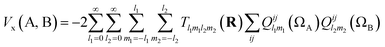 | (9) |
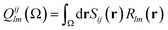 | (10) |
If we truncate the expansion of Vx(A, B) given in eqn (9) after the first term then we obtain
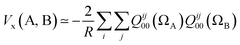 | (11) |
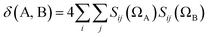 | (12) |
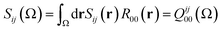 | (13) |
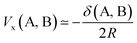 | (14) |
This equation enables one to interpret the delocalization index as the equivalent of a charge–charge interaction albeit then not for the Coulomb energy but for the exchange energy. A generalization of these arguments to general correlated wavefunctions also exists.28
There are other interesting statements to make about the delocalization index: it reduces to the Wiberg–Mayer bond order when the quantum atoms are imagined to collapse over the nuclear positions, such that the region associated with each atom is effectively point-like and the domain overlap integrals Sij(Ω) in eqn (13) can be reduced to the product of the coefficients of the Ω-centered primitives of orbitals ψi and ψj. Also, the delocalization index can be shown to directly measure the fluctuation (covariance) of the electron population of two atoms. The latter result is most remarkable and its consequence should appear in chemical textbooks: bonded atoms display statistically correlated electron counts. When the population of one atom increases, that of the other atom decreases, and vice versa. In fact, this insight may be used to introduce the concept of multi-center bonding in a general way, as a many-atom statistical covariance among electron populations.
Finally, as will be made evident in further sections, the delocalization indices are sensitive to electron correlation. When the orbital model fails (i.e. when more than a Slater determinant is necessary to obtain even a qualitative description of a system), the number of effectively shared electron pairs may become considerably smaller than those obtained from naïve counting techniques. This explains why large formal bond orders, like those proposed in some transition metal diatomics, fail29 to correlate to experimental bond strengths.
We remark that all the information needed to obtain a delocalization index is experimentally observable in principle, and that no further theoretical model is needed to obtain it. Since the exchange–correlation density is the expectation value of a Hermitian quantum mechanical operator (i.e. it is a Dirac observable), all that is needed is an appropriate experimental setup able to measure electron densities and pair densities. Actually, quantum atoms are obtained today routinely through the electron densities provided by high precision X-ray diffraction data. Unfortunately, there is still no reliable way to measure pair densities, although efforts in that direction are being made in the field of quantum crystallography.30
Results and discussion
Methodology
The basic aim of this work is to show that revitalizing bond orders in chemistry is worth the effort. To that end, we have performed electronic structure calculations on almost 200 molecules, both organic and inorganic. Our scope covers the majority of the most typical functional groups in organic chemistry: saturated and unsaturated (including several aromatic) hydrocarbons, halo-alkanes, alcohols, aldehydes, ketones, acids (and derivatives), amines, sulphides, several heterocyclic derivatives (of pyrrole and thiophene, as well as the nitrogenated bases), cyanides and isocyanides, ethers, diazo-compounds and nitro-derivatives, and additionally the most common amino acids. We also included 28 simple inorganic molecules. This study is, to our knowledge, the most complete to date.The calculations were carried out with the GAUSSIAN09 (ref. 31) package using the 6-311++G(2d,2p) basis set, in conjunction with the Hartree–Fock (HF) and CCSD levels of theory. Unless otherwise stated, default values correspond to HF data. Once the wave function was obtained, quantum atoms and QTAIM descriptors, including the delocalization index between each pair of atoms, were calculated using the AIMAll code.32
As a note of caution, AIMAll employs Müller's approximation33 to calculate the two-particle density matrix for correlated wavefunctions. To properly account for this source of error, we performed a calibration through the PROMOLDEN code,34 which makes use of the real two-particle density matrix. This benchmark is described in the next section.
A detailed account of the results may be found in the ESI.†
Müller's approximation
The AIMAll code makes use of Müller's approximation: instead of employing the full 2-RDM, this magnitude is approximated in terms of the 1-RDM in an expression that is reminiscent of 2-RDM HF formula. This estimation has a number of problems, mainly that ρ2(x,x) ≠ 0. This means that two same-spin electrons would be able to occupy the same point of space, which violates the Pauli principle. Although there is theoretical work comparing Müller's approximation with the full 2-RDM,35–39 (and how to approximate higher-order density matrices from lower-order ones) here we perform a short benchmark on 21 small molecules, using CCSD/6-311++G(2d,2p) and the computer program PROMOLDEN, which avoids approximations. The 2-RDMs were calculated with pySCF,40 employing the optimized geometries from GAUSSIAN. The basis set 6-311++G(2d,2p) was obtained from EMSL Basis Set Exchange,41 for PROMOLDEN studies only, while the internally held 6-311++G(2d,2p) was used in the GAUSSIAN calculations. A comparison of the HF, CCSD/Müller and CCSD values is provided in Table 1.| Molecule | Bond | HF | CCSD/Müller | CCSD | Müller's relative error |
|---|---|---|---|---|---|
| H2 | H–H | 1.000 | 0.844 | 0.850 | −0.6% |
| LiH | Li–H | 0.192 | 0.199 | 0.203 | −1.9% |
| O2 | O–O | 2.272 | 1.615 | 1.548 | 4.4% |
| N2 | N–N | 3.042 | 2.310 | 2.073 | 11.4% |
| F2 | F–F | 1.284 | 1.243 | 0.927 | 34.1% |
| Ne2 | Ne–Ne | 0.005 | 0.009 | 0.009 | −7.1% |
| Ar2 | Ar–Ar | 0.002 | 0.015 | 0.016 | −7.6% |
| CO | C–O | 1.573 | 1.452 | 1.446 | 0.4% |
| HCN | H–C | 0.928 | 0.816 | 0.810 | 0.8% |
| C–N | 2.340 | 1.977 | 1.795 | 10.1% | |
| HNC | H–C | 0.668 | 0.648 | 0.645 | 0.5% |
| C–N | 1.766 | 1.586 | 1.536 | 3.2% | |
| CH4 | C–H | 0.982 | 0.846 | 0.803 | 5.4% |
| H2O | O–H | 0.616 | 0.614 | 0.617 | −0.4% |
| NH3 | N–H | 0.894 | 0.792 | 0.772 | 2.6% |
| BH3 | B–H | 0.508 | 0.522 | 0.520 | 0.4% |
| H2O2 | O–H | 1.298 | 0.972 | 0.960 | 1.2% |
| O–O | 0.583 | 0.584 | 0.572 | 2.0% | |
| H2CO | C–O | 1.379 | 1.271 | 1.203 | 5.6% |
| C–H | 0.898 | 0.778 | 0.753 | 3.2% | |
| HCOOH | H–C | 0.860 | 0.752 | 0.728 | 3.2% |
C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O O |
1.137 | 1.125 | 1.080 | 4.1% | |
| C–O | 0.733 | 0.748 | 0.747 | 0.2% | |
| O–H | 0.544 | 0.551 | 0.544 | 1.3% | |
| CH3OH | O–H | 0.618 | 0.610 | 0.602 | 1.3% |
| C–O | 0.824 | 0.785 | 0.753 | 4.2% | |
| C–H | 0.933 | 0.807 | 0.762 | 5.8% | |
| CH3CH2OH | O–H | 0.618 | 0.610 | 0.602 | 1.3% |
| C–O | 0.800 | 0.762 | 0.728 | 4.7% | |
| C–C | 0.954 | 0.828 | 0.777 | 6.6% | |
| HOCH–H | 0.920 | 0.795 | 0.747 | 6.4% | |
| HOCH2CH2–H | 0.963 | 0.826 | 0.779 | 6.0% | |
| HF⋯HF | H–F (donor) | 0.339 | 0.339 | 0.379 | −10.5% |
| H⋯F | 0.037 | 0.037 | 0.047 | −22.2% | |
| H–F (acceptor) | 0.381 | 0.381 | 0.426 | −10.6% | |
| H2O⋯H2O | H–O (donor) | 0.574 | 0.574 | 0.576 | −0.4% |
| H⋯O | 0.061 | 0.061 | 0.016 | 273% | |
| H–O (acceptor) | 0.597 | 0.597 | 0.596 | 0.1% |
As stated in Müller's original paper,33 the complications of his approximation can be compensated by its mean accuracy for large numbers of electrons. It is expected that this approach will become asymptotically better as the system size increases. In this sense, the results shown in Table 1 can be interpreted as an approximate upper bound in the error and justify a qualitative use of the approximation in realistically-sized systems where the full CCSD approach is intractable.
As expected, Müller's approximation works best when the inclusion of correlation has a minor influence on the system. As a result, most of the bonds show relative errors below 5%, which is pleasing given the enormous computational savings of using this approximation. However, when correlation is important, the errors can be large. This is made evident in N2 and HCN, where the inadequate description of the triple bond causes a relative error greater than 10%; this is a consequence of the lack of static correlation. In addition, our analysis of non-bonding interactions, which cannot be described in the absence of dynamic correlation, shows errors in the range 20–70% and always negative. An exception is the hydrogen bonds which, as shown in Table 1, are overestimated by the Müller approximation, and generally by a significant amount.
Another, more important exception is introduced by the molecule of F2. This system is well known to pose difficulties for conventional levels of theory, being unbounded at the HF level42 and needing high levels of theory. This issue has traditionally being related to the lone pair weakening effect,43 and more recently to the concept of the so-called charge shift bond, in which it is the covalent-ionic valence bond resonance that stabilizes the system.44 The important role of dynamic correlation in this system makes the Müller approximation behave particularly badly in this system. Similar arguments can explain the exceptionally large error in the HF dimer.
In any case, these results show that Müller delocalization indices can offer a chemically rich and qualitative vision of bonding. In the first place, results for single bonds show good agreement with the exact case, and there is enough evidence to expect that higher-order bonds will be overestimated by Müller's approximation. In addition, as non-bonding interactions (with the exception of hydrogen bonds) are always underestimated by Müller, it is possible to employ the approximate values as a lower bound.
The computation of exact values for correlated methods is a very expensive task, both in terms of CPU time and memory, which is prohibitive for even small molecules. Our benchmark validates the use of Müller's approximation in a qualitative manner, and provides insight on when this approach might yield significant errors.
The influence of correlation
Following Table 1, we analyze the influence of the level of theory in the delocalization indices. Previous work has compared HF calculations with MP2, CISD and DFT;11,12 here, we add the comparison with CCSD/Müller, and extend the analysis to non-covalent interactions.It is found that the HF results are closer to the Lewis picture, recovering well-known bond orders. For example, HF/6-311++G(2d,2p) yields δ(N, N) = 3.043 for nitrogen or δ(O, O) = 2.272 for oxygen. However, the inclusion of Coulomb correlation tends to decrease the value of the delocalization index, and at the CCSD/Müller level we find that, respectively, δ(N, N) = 2.310 and δ(O, O) = 1.615 for the same molecules. Thus, the inclusion of Coulomb correlation induces a decrease in electron sharing. After all, including Coulomb correlation (i.e. the correlation among opposite spin electrons) means that, on average, electrons repel more strongly than if only same spin correlation is included (i.e. the Fermi correlation, which is present in the Hartree–Fock model).
On the other hand, when turning to weak interactions, the opposite effect is observed. For example, for Ar2 we obtain DIs of 0.002 and 0.015 for HF and CCSD/Müller, respectively, corresponding to an increase of almost one order of magnitude. This is also a Coulomb effect, because the instantaneous fluctuations that give rise to, for example, dispersion forces cannot be accounted by mean field approximations,45 such as Hartree–Fock theory (or DFT functionals with local approximations). We also note that, as explained above, the CCSD/Müller values for non-bonded interactions are a lower bound of the exact CCSD values; the interactions mentioned here are thus stronger in the exact case.
In similar vein, ionic compounds show virtually no change when Coulomb correlation is included. The two model ionic molecules, LiH and NaCl, show δ(Li, H) = 0.193 and δ(Na, Cl) = 0.216 for HF, and δ(Li, H) = 0.199 and δ(Na, Cl) = 0.222 for CCSD/Müller; in both cases relative errors are below 3%. Although the change in DI upon inclusion of electron correlation is small in these systems, it is rather clear that the DI increases, like in the weak-interaction limit.
In any case, delocalization indices obtained at the CCSD/Müller level are highly correlated with the HF values: Pearson's correlation coefficient for the 1666 bonds analyzed is 0.938. In fact, the correlation coefficients are all above 0.9 for each functional group.
In summary, as our calculated wave function approaches the exact wave function, so does our view of the molecule. The deviations from Lewis's scheme are not a theoretical miscarriage, nor a failure to recover the bond order; quite the contrary: they offer a deeper understanding into the physical nature of bonding, be it a realization that electrons cannot be shared in closed pairs, or an increased awareness of the importance of weak interactions. The delocalization index thus provides a tool that extends the classical idea of bond order towards general domains.
The stability of the classical bonding patterns
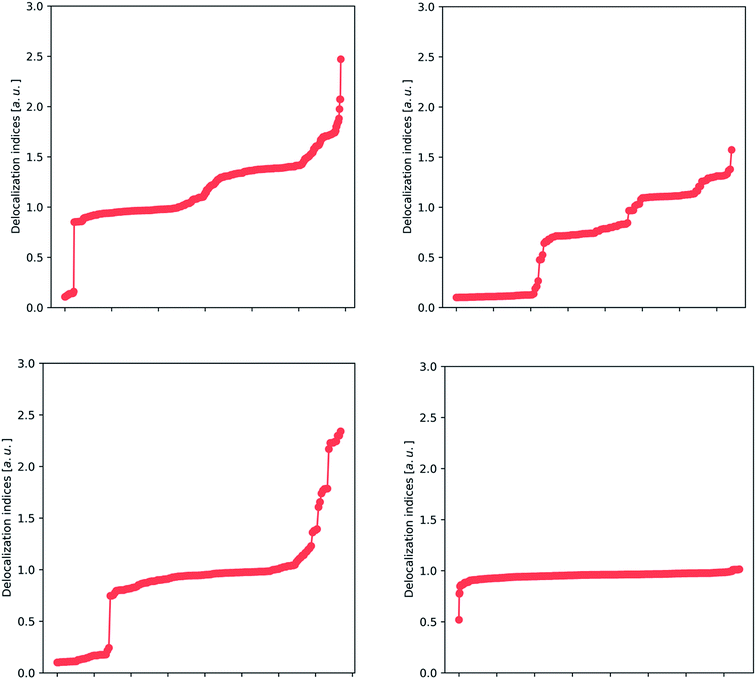
After building a database of almost 200 compounds (accounting for 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 756 entries of delocalization indices, only for Hartree–Fock calculations), we can apply different analysis techniques to scan for chemical insight in the delocalization indices. This analysis focuses on the most abundant atom pairs in the study: carbon–carbon (2364 data points), carbon–oxygen (632 data points), carbon–nitrogen (724 data points) and carbon–hydrogen interactions (5497 data points), and these are displayed in Fig. 2 and 3.
756 entries of delocalization indices, only for Hartree–Fock calculations), we can apply different analysis techniques to scan for chemical insight in the delocalization indices. This analysis focuses on the most abundant atom pairs in the study: carbon–carbon (2364 data points), carbon–oxygen (632 data points), carbon–nitrogen (724 data points) and carbon–hydrogen interactions (5497 data points), and these are displayed in Fig. 2 and 3.
In Fig. 2, we show the spread of the delocalization indices for several classes of bonds. There is a particular trend that stands out: the presence of several plateaus. For example, in the carbon–carbon plot (upper left panel), there is a wide plateau around 1.0 that contains, among others, the C–C bonds of the hydrocarbons, and many other bonds that are recognizable as single. There are two other plateaus: one plateau around 1.4 contains many aromatic bonds (including benzene, thiophene and pyrrole), and a small plateau at 1.8, which contains double bonds. There are also some points in the extreme that correspond to triple bonds, but these are underrepresented in our study (not only because of their scarcity, but also due to the well-known formation of a non-nuclear maximum in triple bonds,46 which tends to hinder the analysis).
The upper right plot of Fig. 2 covers carbon–oxygen interactions, where we again recognize several plateaus. The wide plateau between 0.8 and 0.9 comprises the typical single C–O bond that can be found in alcohols and carboxylic acids, while the other two plateaus in the area 1.2–1.4 correspond to double C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bonds. These two plateaus refer to aldehydes (∼1.2) and ketones (∼1.4) whose C
O bonds. These two plateaus refer to aldehydes (∼1.2) and ketones (∼1.4) whose C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bond has been, respectively, depleted or enriched in electron density. Finally, at the top of the plot lies the triple bond occurring in carbon monoxide, with a value considerably smaller than 3, due to the considerable polarization of this bond. The reason that the delocalization indices for carbon–oxygen bonds are slightly smaller than those for carbon–carbon bonds is again polarization, and will be discussed fully vide infra. In the lower left plot of Fig. 2, we encounter the clear plateau of the single C–N bond, such as in amines, and also the several intermediate points, such as the C–N in amides and resonant heterocycles, and less common double and triple bonds. Finally, the lower right plot shows a unique plateau, around 0.8–1.0, as expected from carbon–hydrogen bonds. The only outlier, at 0.5, corresponds to a through-space bond between two atoms in the amino acid lysine that are not directly bonded according to classical Lewis theory (but show a bond critical point connecting them, at HF level).
O bond has been, respectively, depleted or enriched in electron density. Finally, at the top of the plot lies the triple bond occurring in carbon monoxide, with a value considerably smaller than 3, due to the considerable polarization of this bond. The reason that the delocalization indices for carbon–oxygen bonds are slightly smaller than those for carbon–carbon bonds is again polarization, and will be discussed fully vide infra. In the lower left plot of Fig. 2, we encounter the clear plateau of the single C–N bond, such as in amines, and also the several intermediate points, such as the C–N in amides and resonant heterocycles, and less common double and triple bonds. Finally, the lower right plot shows a unique plateau, around 0.8–1.0, as expected from carbon–hydrogen bonds. The only outlier, at 0.5, corresponds to a through-space bond between two atoms in the amino acid lysine that are not directly bonded according to classical Lewis theory (but show a bond critical point connecting them, at HF level).
These results lead to the conclusion that there are several very stable bonding patterns, which correlate with the classical vision of single, double and triple bonds, as well as aromatic intermediates, while there are also intermediate cases that give rise to a quasi-continuous distribution. In this way, the delocalization index confirms and extends Lewis's vision. Additionally, the sharp discontinuity between non-bonded (separate cluster of DI values appearing at the bottom left of each panel) and bonded interactions revitalizes the picture of the chemical bond.
In Fig. 3 we perform a more sophisticated statistical analysis, through k-means clustering, a common technique to recognize clustering of data points in a scatter plot. This analysis has been performed on the (δ, d) (where d is the internuclear distance) pairs computed from optimized HF wavefunctions. The DI values corresponding to non-bonded pairs, as well as some outliers arising from the presence of non-nuclear critical points (most of the triple bonds) have been removed. In both cases, the clusters can be easily identified with the plateaus described above.
The subtler bonding effects
Since it condenses information about the full electronic structure of a system, the delocalization index is also sensitive to the environment of a given bond and is able to reflect certain classical effects in practical chemistry. We may understand the delocalization index to be under the influence of two responses: one from the atoms constituting the “bond”, and the other from the surroundings.In terms of the first response, the DI is an indicator of covalency: it measures the amount of electron pairs shared between two atoms. Thus, apolar bonds will return larger DI values than polar bonds because then no atom has a greater electronegativity than another atom, and thus the electrons are equally shared. On the other hand, in polar bonds, one of the atoms tends to hoard the electrons, making equal sharing less favourable. A clear example of this effect is that of N2 and HCN where δ(N, N) = 3.043 and δ(C, N) = 2.340, at HF level. This phenomenon can also be read in terms of the partition of electrons into localized and delocalized sets. For instance, on changing from a two-center, two-electron non-polar link to a polar one, the electrons that were originally delocalized between the two centers tend to localize toward the electronegative atom. From eqn (6) it follows that the increase in the number of localized electrons must necessarily be accompanied by a decrease in the number of delocalized electrons. The end results is that polarity decreases the DI, as we observed for LiH and NaCl vide supra.
In terms of the second response, the DI recovers all textbook bonding effects. Here we will focus on two effects that are ubiquitous throughout chemistry: the inductive effect and the resonance effect. We discuss these two effects in turn, starting with the inductive effect.
The inductive effect is the action of a charged group, or one with a significant electronegativity difference compared to the surrounding atoms in a given bonded interaction. An electronegative atom or group positioned near a bond under study will withdraw electron density from the pair of atoms of interest. As the withdrawal of electron density will probably occur through mobile (i.e. participating in delocalization) electrons, we expect that the number of electron pairs delocalized between both atoms will decrease. This effect manifests itself in a homologous series, where the DI between two atoms in a given bond converges to a constant value with an increasing number of carbons separating it from the electronegative group. Because carbon is more electronegative than hydrogen, it polarizes the electron density towards itself. Of course, this effect is highly local, and almost vanishes with more than two intermediate carbon atoms. A straightforward example of the inductive effect is the comparison of the C–C bond in ethanol, δ(C, C) = 0.828, and that in ethanamine, δ(C, C) = 0.960, which has the less electronegative substituent. Thus, the presence of an electronegative element near a bond decreases its number of delocalized electron pairs and thus the DI of this bond.
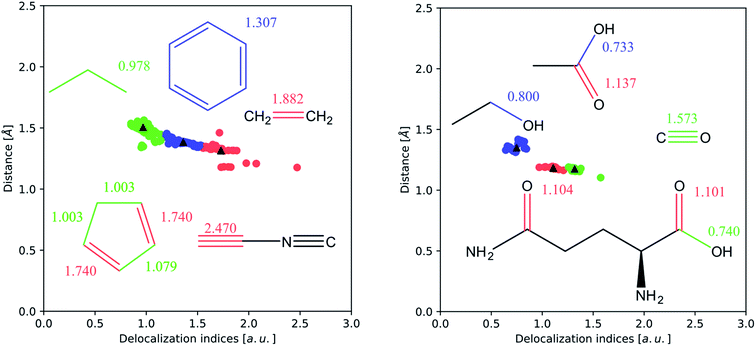
Secondly, the resonance effect appears in the form of electron delocalization. In conjugated systems, the delocalization index takes account of this effect, for example, by reducing the double bond character in double bonds, while enhancing the double bond character in single bonds. In this way, the standard arrow-pushing rules used in the explanation of mesomerism are reproduced. This effect is shown, for example, in Fig. 4: in phenol, δ(C, O) = 0.829, which is higher compared to propanol's value of δ(C, O) = 0.798, while in benzaldehyde δ(C, O) = 1.297, compared to propanal's δ(C, O) = 1.312. Similarly, δ(C, O) = 1.070 for phenoxide, reflecting that the resonant forms with a formal positive charge on the oxygen are less favourable.
Delocalization indices in uncommon bonding patterns
In the previous section we have shown how delocalization indices can contain a significant amount of chemical information. However, our study has been limited to very well-known molecules. Here, we take a step forward and apply the knowledge, acquired in the previous part, to some uncommon bonding patterns. We hope that this will pave the way for a more widespread application of delocalization indices and help towards the understanding of molecular interactions.The N8 molecule
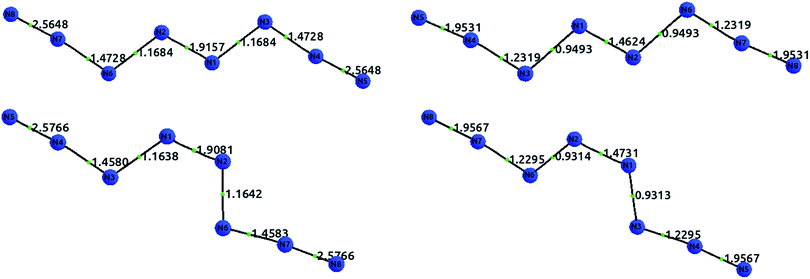
The existence of a molecule of N8 was first analyzed in 2000 by Gordon's group.47 In 2012, this line of research was revitalized after Hirshberg et al. described calculations predicting the remarkable stability of a molecular crystal consisting of N8 molecules.48 Additionally, Wu et al. described the synthesis of an N8 anion stabilized on multi-wall carbon nanotubes.49Here, we briefly compare the bond orders proposed by Hirshberg et al. (which are derived from NBO calculations) with the information provided by the delocalization indices. The suggested Lewis structures are depicted in Fig. 5.
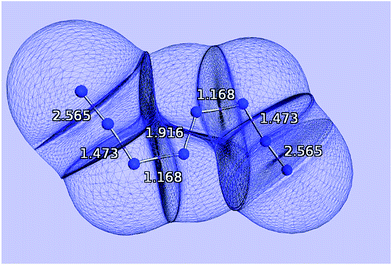
Fig. 6 displays the optimized structures of the EEE and EZE isomers, calculated at the HF (left) and CCSD (right) levels of theory, together with the computed delocalization indices. Most of the DI results seem to agree with the picture proposed by Hirshberg et al. The terminal pairs, N8–N7 and N4–N5, show large DI values, close to 2.00 (in CCSD), which are reminiscent of acetylene suggesting triple bonds. In addition, the central bond N1–N2 has a clear double character, while the N6–N2 and N3–N1 are clearly single.
However, the intermediate bonds N6–N7 and N3–N4 do not comply with the picture of “strong ionic character” proposed by Hirshberg et al. The delocalization index δ(N, N) = 1.17 corresponds to a single bond that is enriched by some conjugation. In fact, although ionicity and covalency are not necessarily opposed concepts,50 the calculation of QTAIM charges disagrees with the presence of charge transfer. Indeed, the largest charges are of the order of 0.14e, and contrary to what was suggested by Hirshberg et al., lie on terminal nitrogen atoms. These findings altogether seem to suggest a pentavalent nitrogen (depicted in the right part of Fig. 5) that is reminiscent of the bonding pattern in N2O.
A molecule with planar tetracoordinate carbon
The tetrahedral coordination of carbon is, since van't Hoff and Le Bel, one of the milestones of modern organic chemistry. However, since more than a decade ago, several compounds with planar tetracoordinate carbon have been studied both theoretically and experimentally. Here, we address one of these compounds, a cyclopropane where both hydrogens, attached to one of the carbon, have been substituted by lithium.51 The optimized structures, together with the delocalization indices, are displayed in Fig. 7. In the first place, carbon–carbon bonds are clearly single: the values of 0.98 and 1.11 lie in the first plateau of the upper left plot of Fig. 2. The increase of the delocalization index for the C3–C1 and C3–C2 bonds, in comparison with the C1–C2, is explained by the enormous negative charge in C3 (−1.42e) induced by the two lithium atoms, who of course release their electronic charge due to their electropositive character. On the other hand, both C–Li bonds are basically ionic, with a DI value that is almost identical to that in LiH. In similar vein, we observe that the CCSD values are slightly larger than the HF results, a feature that is not observed in covalent bonds (but seen in ionic molecules, e.g. LiH and NaCl as discussed vide supra).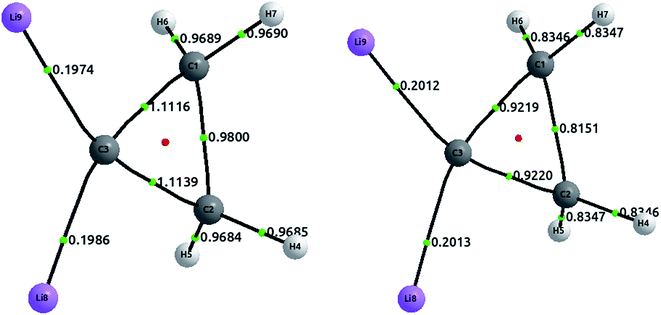 | ||
| Fig. 7 Optimized structures with delocalization indices displayed for the dilithium-substituted cyclopropane. The left structure corresponds to HF values, and the right to CCSD values. | ||
A discussed organometallic complex
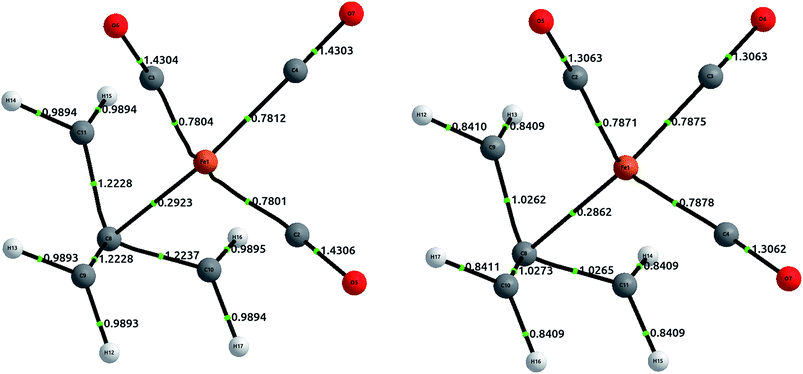
To conclude, we extend our study to the realm of organometallic chemistry. We will analyse the complex (η4-C4H6)Fe(CO)3, which has been used as an example of the absence of QTAIM bond paths in chemically intuitive bonds,52 since the terminal carbons in the trimethylenemethane (TMM) ligand are not directly bonded in the equilibrium geometry (although this paths appear upon deformations such as in ab initio molecular dynamics53).Metallic complexes are notoriously multiconfigurational, and the inability of Müller's approximation to treat static correlation has led us to avoid these compounds during this study. However, (η4-C4H6)Fe(CO)3 is an organometallic complex fulfilling the 18-electron rule, and thus with a notable HOMO–LUMO separation that suggests scarce multiconfigurational character. In fact, a CASSCF(10,10) calculation shows that the single determinant contribution has a coefficient of 0.91 (in comparison with an approximate coefficient of 0.8 for an analogous calculation in methane). This seems to indicate that the correlation is mostly dynamic, and can therefore be modelled appropriately with CCSD.
The geometry was optimized at the B3LYP/6-311++G(2d,2p) level of theory, and single point calculations were performed at the HF and CCSD levels of theory. The delocalization indices, computed with AIMAll, are displayed in Fig. 8. The results show that, while there is a direct bond path between the iron atom and the central carbon in TMM, the bonding interaction is actually stronger with the rest of the carbons. Proof of this assertion is the difference between δ(Fe, Cα) = 0.292 and δ(Fe, Cβ) = 0.469 at the HF level, the latter being about 60% larger. CCSD results only emphasize this difference, with δ(Fe, Cα) = 0.286 and δ(Fe, Cβ) = 0.788.
Altogether, the three Fe–Cβ and the Fe–Cα bond account for a somewhat “total delocalization index” of 1.7, which seems quite close to a η4 double bond, as would be expected from simple electron-counting techniques. Although the value of the DI in coupled cluster theory is significantly larger (around 2.5), this is a result of the increased π delocalization in the TMM.
Conclusions
To the best of our knowledge the current data set is the largest ever surveyed in terms of a delocalization index. We have shown how the delocalization index derived from quantum chemical topology can account for bond order. In particular, we have analyzed a large dataset comprising almost 200 molecules calculated at the HF and CCSD levels of theory, and shown how it recovers many well-known bonding effects. We have also shown, through a reduced benchmark, that the Müller approximation can compute qualitatively trustworthy (within a 5% error) delocalization indices at the CCSD level of theory.Delocalization indices emerge from a rigorous topological formulation of electron sharing in terms of reduced density matrices, and recover the IUPAC formulation of bond order in terms of population analysis. Moreover, it can be shown that their distribution provides a natural clustering of values that is reminiscent of the classical single, double and triple bonds described in practical chemistry textbooks. In particular, the values of this index evaluated at Hartree–Fock level are closest to the formal bond orders appearing in Lewis diagrams.
We have found this index capable of recovering many widely known chemical effects in a natural way. For example, the presence of an electronegative element in the proximity of a bond provokes a reduction in the surrounding delocalization indices as a result of electron withdrawal. Equally, the presence of delocalized electrons favours the equal sharing of electron pairs, thus increasing the delocalization indices. In this way, phenomena such as induction or resonance are suitably reflected in the variation of the delocalization index at every level of theory.
In addition, the delocalization index can be shown to directly measure the fluctuation (covariance) of the electron population shared between two atoms. As Coulomb correlation is added, the delocalization index approaches its real world value, where electrons are not shared in the form of complete pairs, because they repel each other.
All these results have led us to conclude that the delocalization index is a generalization of the bond order that can be suitably applied to any quantum chemical calculation. We hope that this work lays the foundation for a novel tool in the study of chemical bonding.
Conflicts of interest
The authors declare no competing financial interests.Acknowledgements
C. O. thanks Fundación María Cristina Masaveu Peterson, which funded his stay in Manchester. A. M. P. thanks the Spanish MINECO, grant CT2015-65790-P, the FICyT, grant GRUPIN14-049, and the FEDER funds of the European Union. P. L. A. P. and M. V. thank EPSRC for the award of an Established Career Fellowship (EP/K005472). The authors also wish to thank J. L. Casals-Sainz for helpful discussions and support in calculations involving Müller's approximation.References
- G. N. Lewis, The Atom and the Molecule, J. Am. Chem. Soc., 1916, 38, 762–785 CrossRef.
- R. S. Mulliken, Electronic Population Analysis on LCAO-MO Molecular Wave Functions, J. Chem. Phys., 1955, 23, 1833–1840 CrossRef.
- I. Mayer, Bond order and valence indices: A personal account, J. Comput. Chem., 2007, 28(1), 204–221 CrossRef PubMed.
- I. Mayer, Bond orders and energy components: extracting chemical information from molecular wave functions, CRC Press, 2016 Search PubMed.
- A. D. McNaught and A. Wilkinson, IUPAC. Compendium of Chemical Terminology (the “Gold Book”), 2nd edn, 1997 Search PubMed.
- R. F. W. Bader, Atoms in Molecules. A Quantum Theory, Oxford Univ. Press, Oxford, Great Britain, 1990 Search PubMed.
- P. Popelier, F. Aicken and S. O'Brien, Atoms in molecules, Chem. Modell., 2000, 1, 143–198 Search PubMed.
- R. F. W. Bader and M. E. Stephens, Spatial Localization of the Electronic Pair and Number Distributions in Molecules, J. Am. Chem. Soc., 1975, 97, 7391–7399 CrossRef.
- X. Fradera, M. A. Austen and R. F. W. Bader, The Lewis Model and Beyond, J. Phys. Chem. A, 1999, 103, 304–314 CrossRef.
- Y. G. Wang and N. H. Werstiuk, A Practical and Efficient Method to Calculate AIM Localization and Delocalization Indices at Post-HF Levels of Theory, J. Comput. Chem., 2002, 24, 379–385 CrossRef PubMed.
- Y. G. Wang, C. F. Matta and N. H. Werstiuk, Comparison of localization and delocalization indices obtained with Hartree–Fock and conventional correlated methods: Effect of Coulomb correlation, J. Comput. Chem., 2004, 24(2), 1720–1729 Search PubMed.
- J. Poater, M. Sola, M. Duran and X. Fradera, The calculation of electron localization and delocalization indices at the Hartree–Fock, density functional and post-Hartree–Fock levels of theory, Theor. Chem. Acc., 2002, 107(6), 362–371 CrossRef.
- M. García-Revilla, P. L. A. Popelier, E. Francisco and A. Martín Pendás, Nature of chemical interactions from the profiles of electron delocalization indices, J. Chem. Theory Comput., 2011, 7(6), 1704–1711 CrossRef PubMed.
- A. Gallo-Bueno, E. Francisco and A. Martín Pendás, Decay rate of real space delocalization measures: a comparison between analytical and test systems, Phys. Chem. Chem. Phys., 2016, 18(17), 11772–11780 RSC.
- X. Fradera, J. Poater, S. Simon, M. Duran and M. Solà, Electron-pairing analysis from localization and delocalization indices in the framework of the atoms-in-molecules theory, Theor. Chem. Acc., 2002, 108(4), 214–224 CrossRef.
- C. F. Matta and J. Hernández-Trujillo, Bonding in polycyclic aromatic hydrocarbons in terms of the electron density and of electron delocalization, J. Phys. Chem. A, 2003, 107(38), 7496–7504 CrossRef.
- C. F. Matta, Molecules as networks: A localization–delocalization matrices approach, Comput. Theor. Chem., 2018, 1124, 1–14 CrossRef.
- C. F. Matta, Modeling biophysical and biological properties from the characteristics of the molecular electron density, electron localization and delocalization matrices, and the electrostatic potential, J. Comput. Chem., 2014, 35(16), 1165–1198 CrossRef PubMed.
- F. Feixas, M. Solà, J. M. Barroso, J. M. Ugalde and E. Matito, New Approximation to the Third-Order Density. Application to the Calculation of Correlated Multicenter Indices, J. Chem. Theory Comput., 2014, 10(8), 3055–3065 CrossRef PubMed.
- M. Rodriguez-Mayorga, E. Ramos-Cordoba, F. Feixas and E. Matito, Electron correlation effects in third-order densities, Phys. Chem. Chem. Phys., 2017, 19(6), 4522–4529 RSC.
- R. McWeeny, Methods of Molecular Quantum Mechanics, Academic Press, San Diego, USA, 2nd edn, 1992 Search PubMed.
- P. Maxwell, A. Martín Pendás and P. L. A. Popelier, Extension of the interacting quantum atoms (IQA) approach to B3LYP level density functional theory, Phys. Chem. Chem. Phys., 2016, 18, 20986–21000 RSC.
- A. Martín Pendás, M. A. Blanco and E. Francisco, Chemical Fragments in Real Space: Definitions, Properties, and Energetic Decompositions, J. Comput. Chem., 2007, 28, 161–184 CrossRef PubMed.
- P.-O. Löwdin, Quantum theory of many-particle systems. I. Physical interpretations by means of density matrices, natural spin-orbitals, and convergence problems in the method of configurational interaction, Phys. Rev., 1955, 97(6), 1474 CrossRef.
- M. A. Blanco, A. Martín Pendás and E. Francisco, Interacting quantum atoms: a correlated energy decomposition scheme based on the quantum theory of atoms in molecules, J. Chem. Theory Comput., 2005, 1, 1096–1109 CrossRef PubMed.
- D. A. Varshalovich, A. N. Moskalev and V. K. Khersonskii, Theory of Angular Momentum, World Scientific, 1988 Search PubMed.
- J. G. Angyan, M. Loos and I. Mayer, Covalent Bond Orders and Atomic Valence Indices in the Topological Theory of Atoms in Molecules, J. Phys. Chem., 1994, 98, 5244–5248 CrossRef.
- E. Francisco, D. Menendez Crespo, A. Costales and A. Martín Pendás, A Multipolar Approach to the Interatomic Covalent Interaction Energy, J. Comput. Chem., 2017, 38, 816–829 CrossRef PubMed.
- L. Gagliardi and B. O. Roos, Quantum chemical calculations show that the uranium molecule U2 has a quintuple bond, Nature, 2005, 433, 848–851 CrossRef PubMed.
- A. Genoni, L. Bucinsky, N. Claiser, J. Contreras-Garcia, B. Dittrich, P. M. Dominiak, E. Espinosa, C. Gatti, P. Giannozzi and J.-M. Gillet, Quantum Crystallography: Current Developments and Future Perspectives, Chem.–Eur. J., 2018 DOI:10.1002/chem.201705952.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, N. J. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, Ö. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Gaussian, Inc., Wallingford CT, 2009 Search PubMed.
- T. A. Keith, AIMAll 2015 (Version 15.09.12), TK Gristmill Software, Overland Park KS, USA, http://aim.tkgristmill.com Search PubMed.
- A. Müller, Explicit approximate relation between reduced two- and one-particle density matrices, Phys. Lett. A, 1984, 105(9), 446–452 CrossRef.
- A. Martín Pendás and E. Francisco, PROMOLDEN: A QTAIM. IQA Code, unpublished, 2012.
- M. García-Revilla, E. Francisco, A. Costales and A. Martín Pendás, Performance of the density matrix functional theory in the quantum theory of atoms in molecules, J. Phys. Chem. A, 2011, 116(4), 1237–1250 CrossRef PubMed.
- E. Matito, M. Sola, P. Salvador and M. Duran, Electron sharing indexes at the correlated level. Application to aromaticity calculations, Faraday Discuss., 2007, 135(0), 325–345 RSC.
- I. Ruiz, E. Matito, F. J. Holguín-Gallego, E. Francisco, Á. Martín Pendás and T. Rocha-Rinza, Fermi and Coulomb correlation effects upon the interacting quantum atoms energy partition, Theor. Chem. Acc., 2016, 135(9), 209 CrossRef.
- M. Rodriguez-Mayorga, E. Ramos-Cordoba, M. Via-Nadal, M. Piris and E. Matito, Comprehensive benchmarking of density matrix functional approximations, Phys. Chem. Chem. Phys., 2017, 19(35), 24029–24041 RSC.
- F. Feixas, J. Vandenbussche, P. Bultinck, E. Matito and M. Sola, Electron delocalization and aromaticity in low-lying excited states of archetypal organic compounds, Phys. Chem. Chem. Phys., 2011, 13(46), 20690–20703 RSC.
- Q. Sun, T. C. Berkelbach, N. S. Blunt, G. H. Booth, S. Guo, Z. Li, J. Liu, J. D. McClain, E. R. Sayfutyarova and S. Sharma, PySCF: the Python-based simulations of chemistry framework, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2018, 8(1), e1340 CrossRef.
- K. L. Schuchardt, B. T. Didier, T. Elsethagen, L. Sun, V. Gurumoorthi, J. Chase, J. Li and T. L. Windus, Basis Set Exchange:
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) A Community Database for Computational Sciences, J. Chem. Inf. Model., 2007, 47(3), 1045–1052 CrossRef PubMed.
A Community Database for Computational Sciences, J. Chem. Inf. Model., 2007, 47(3), 1045–1052 CrossRef PubMed. - A. C. Wahl, Analytic Self-Consistent Field Wavefunctions and Computed Properties for Homonuclear Diatomic Molecules, J. Chem. Phys., 1964, 41(9), 2600–2611 CrossRef.
- S. Shaik, D. Danovich, W. Wu and P. C. Hiberty, The Valence Bond Perspective of the Chemical Bond, Chem. Bond, 2014, 159–198 Search PubMed.
- S. Shaik, D. Danovich, W. Wu and P. C. Hiberty, Charge-shift bonding and its manifestations in chemistry, Nat. Chem., 2009, 1(6), 443 CrossRef PubMed.
- S. Grimme, Density functional theory with London dispersion corrections, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2011, 1(2), 211–228 CrossRef.
- A. Martín Pendás, M. A. Blanco, A. Costales, P. M. Sanchez and V. Luana, Non-nuclear maxima of the electron density, Phys. Rev. Lett., 1999, 83(10), 1930–1933 CrossRef.
- G. Chung, M. W. Schmidt and M. S. Gordon, An ab initio study of potential energy surfaces for N8 isomers, J. Phys. Chem. A, 2000, 104(23), 5647–5650 CrossRef.
- B. Hirshberg, R. B. Gerber and A. I. Krylov, Calculations predict a stable molecular crystal of N8, Nat. Chem., 2014, 6(1), 52 CrossRef PubMed.
- Z. Wu, E. M. Benchafia, Z. Iqbal and X. Wang, N8− Polynitrogen Stabilized on Multi-Wall Carbon Nanotubes for Oxygen-Reduction Reactions at Ambient Conditions, Angew. Chem., 2014, 126(46), 12763–12767 CrossRef.
- J. L. McDonagh, A. F. Silva, M. A. Vincent and P. L. Popelier, Quantifying Electron Correlation of the Chemical Bond, J. Phys. Chem. Lett., 2017, 8(9), 1937–1942 CrossRef PubMed.
- G. Merino, M. A. Méndez-Rojas, A. Vela and T. Heine, Recent advances in planar tetracoordinate carbon chemistry, J. Comput. Chem., 2007, 28(1), 362–372 CrossRef PubMed.
- L. J. Farrugia, C. Evans and M. Tegel, Chemical bonds without “chemical bonding”? A combined experimental and theoretical charge density study on an iron trimethylenemethane complex, J. Phys. Chem. A, 2006, 110(25), 7952–7961 CrossRef PubMed.
- F. Cortés-Guzmán, T. Rocha-Rinza, J. M. Guevara-Vela, G. Cuevas and R. M. Gómez, Dynamic Molecular Graphs: “Hopping” Structures, Chem.–Eur. J., 2014, 20(19), 5665–5672 CrossRef PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c8sc01338a |
| This journal is © The Royal Society of Chemistry 2018 |