Open Access Article
Open Access ArticlePolariton chemistry: controlling molecular dynamics with optical cavities
Raphael F. Ribeiro ,
Luis A. Martínez-Martínez
,
Luis A. Martínez-Martínez ,
Matthew Du,
Jorge Campos-Gonzalez-Angulo
,
Matthew Du,
Jorge Campos-Gonzalez-Angulo and
Joel Yuen-Zhou*
and
Joel Yuen-Zhou*
Department of Chemistry and Biochemistry, University of California San Diego, La Jolla, California 92093, USA. E-mail: joelyuen@ucsd.edu
First published on 12th June 2018
Abstract
Molecular polaritons are the optical excitations which emerge when molecular transitions interact strongly with confined electromagnetic fields. Increasing interest in the hybrid molecular-photonic materials that host these excitations stems from recent observations of their novel and tunable chemistry. Some of the remarkable functionalities exhibited by polaritons include the ability to induce long-range excitation energy transfer, enhance charge conductivity, and inhibit or accelerate chemical reactions. In this review, we explain the effective theories of molecular polaritons which form a basis for the interpretation and guidance of experiments at the strong coupling limit. The theoretical discussion is illustrated with the analysis of innovative applications of strongly coupled molecular-photonic systems to chemical phenomena of fundamental importance to future technologies.
1 Introduction
Light plays a fundamental role in chemistry. It is an essential ingredient in many biological and synthetic chemical reactions and a basic tool for the investigation of molecular properties.1,2 However, in most cases where photons participate in a chemical event, the interaction of light and matter is weak enough that it may be treated as a small perturbation. In this weak coupling regime, radiation provides only a gateway for a molecular system to change its quantum state. This paradigm is the basis of spectroscopy and photochemical dynamics, but fails entirely when the interaction of a single photon with many molecules is intense enough to overcome their dissipative processes. In this case, just as strongly interacting atoms form molecules, hybrid states (molecular polaritons) with mixed molecular and photonic character result from the strong coupling of the electromagnetic (EM) field with molecules.3–5 In this regime, both photons and molecular excited-states lose their individuality, just as atoms do when they form molecules.The generic setup of a device with polaritonic excitations consists of a nanostructure that confines EM fields to the microscale and a condensed-phase molecular ensemble with one or more bright (optical) transitions nearly resonant with the EM modes of the nanomaterial. Typically, this corresponds to an optical microcavity6,7 or to a metal layer supporting (surface) plasmons.8,9 Their main differences are that surface plasmons are more lossy, and their EM field is generally confined to much lower volumes than microcavity photons.6 The former property is a disadvantage for the achievement of strong coupling with surface plasmons, but their low mode volumes imply their electric field is generally stronger in comparison to microcavity electric fields. Hereafter, we will consider the EM confinement medium to be an optical microcavity unless otherwise mentioned, but all of the discussed chemical phenomena are insensitive to the choice of EM environment. The molecular transitions can be well approximated to have no wave vector dependence (since optical wavelengths are much larger than molecular length scales) with linewidth dominated by the coupling to intra- and intermolecular degrees of freedom. Conversely, the microcavity spectra shows a well-defined wave vector dependence (Fig. 1) and homogeneous broadening due to the weak interaction with the external EM fields.6 The strong coupling regime is achieved when the rate of energy exchange between microcavity photons and the molecular system is larger than the rate of cavity-photon leakage and molecular dephasing. In this case, the elementary optical excitations (quasiparticles) of the heterostructure consist of superpositions of delocalized (coherent) molecular states and photonic degrees of freedom, with energies and lifetimes which can significantly differ from those of the bare excitations. The capacity to tune the energies and photon/molecular content of polariton states is a main attraction of the strong coupling regime (Section 2). Nevertheless, the hybrid cavity also contains a large number of incoherent (also called dark) molecular states. These belong to a dense nearly-degenerate manifold of states which interact weakly with the cavity photons, and thus are much more sensitive to disorder than polaritons. In particular, while polaritons have microscopic coherence lengths, dark states may be more or less localized depending on the imperfections10,11 and geometry12 of the hybrid system. Despite their weak contribution to the optical response, the dark states are fundamentally important for a description of the novel chemical dynamics emergent at the strong coupling regime.
While theoretical studies of hybrid states of light and matter date back to the 1950s,3,4 and observations of atomic and solid-state cavity-polaritons first happened in the 1980s13,14 and 1990s,15,16 respectively, it is only recently that experimental17–38 and theoretical39–58 activity have flourished in the field of strongly coupled chemistry. This attention can be attributed in part to the experimental observations of polariton effects on chemical dynamics, which thus offer novel pathways for the control of molecular processes.5
In this review we provide a theoretical perspective on the recent advances in molecular polaritons arising from electronic (organic exciton-polaritons) or vibrational (vibrational polaritons) degrees of freedom. Our discussions are primarily based on quantum-mechanical effective models, which are general enough to be applied in regimes where a classical description is inaccurate.59 Furthermore, the models discussed here describe only the relevant low-energy degrees of freedom probed by experiments. This allows a consistent and predictive description of the behavior of strongly coupled ensembles including a macroscopic number of molecules. First-principles approaches are explored in ref. 50, 51 and 60. Finally, it is not our intent to provide a complete review of the fast-growing molecular polariton literature. We have decided to present the basic theory and illustrate it with examples, that we believe, show general principles which might be useful for future investigations of polariton chemistry. For reviews on other aspects of molecular polaritons not emphasized here, see ref. 5, 8, 9 and 61–66.
This review is organized as follows. In Section 2 we present the general concepts that form the basis for molecular polaritonics. Section 3 provides an overview of the theory of organic exciton-polaritons. This is illustrated with applications to polariton-mediated chemical reactivity (Section 3.3), energy transfer (Section 3.4) and singlet fission (Section 3.5). In Section 4 we discuss the theory and phenomenology of vibrational polaritons. We focus on the effects of vibrational anharmonicity on their nonlinear response, and revisit exciting experimental results probing the thermodynamics and kinetics under vibrational strong coupling in Sections 4.2 and 4.3, respectively. The ultrastrong regime of light-matter interaction is briefly introduced in Section 5. This review is concluded in Section 6.
2 Polariton basics
We introduce the basic notions of polariton behavior in this section by examining the simplest models displaying strong coupling between light and matter. The bare microcavity modes are reviewed in Section 2.1, and the spectrum resulting from the strong coupling of two-level systems with a single cavity mode is discussed in Section 2.2. The intuition given by the results discussed in this section will guide all later developments.2.1 Optical microcavity spectra
The optical cavities employed for molecular strong coupling studies generally consist of two highly reflective (at the frequencies of interest) parallel metallic or dielectric mirrors separated by a distance L on the order of µm.6 The length of the cavity is typically chosen to be resonant with a molecular transition. The EM modes of these devices are classified by the in-plane wave vector q, the integer band number m (where qZ = mπ/L) associated with the transverse confinement direction, and the electric field polarization [transverse magnetic (TM) or transverse electric (TE)]6,67 (see Fig. 1a). The TE polarization is perpendicular to the incidence plane, while the TM belongs to it. The former vanishes at the mirrors, in contrast to the latter. However, in lossless planar microcavities, the TM and TE modes are degenerate, and when |q| → 0 their spatial distributions become identical. The microcavity is typically engineered to have a single band (Fig. 1b) containing a resonance with the material (though there exist exceptions28,68). The remaining bands are highly off-resonant, and thus, may be neglected in a low-energy theory of polaritons. It is also sometimes useful to perform a long-wavelength approximation which disregards the spatial variation of the electric field, and includes explicitly only a single microcavity mode which interacts with a macroscopic collection of optically-active molecular transitions. This is appropriate whenever the density of accessible molecular states is much larger than the photonic [total internal reflection of incident radiation with ϕ > ϕc (Fig. 1a) establishes a natural cut-off frequency for the cavity modes which can be accessed by excitation with external radiation; alternatively, a cutoff can be imposed on cavity photons which are highly detuned from the molecular transition41,69]. Such condition is fulfilled in most observations of molecular polaritons in condensed-phase media.2.2 Jaynes–Cummings and Tavis–Cummings models
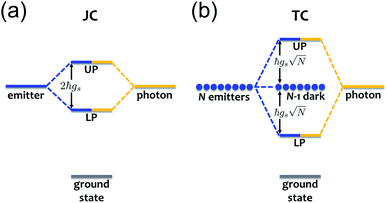
When we introduce a bright two-level system to a single-mode microcavity we obtain the Jaynes–Cummings (JC) model.70 In particular, it consists of a lossless cavity mode of frequency ωc interacting with a two-level system of transition energy ℏωs. Thus, the effective Hamiltonian of the JC model is given by| HJC = ℏωca†a + ℏωsσ+σ− − ℏgs(a†σ− + aσ+), | (1) |
 is the strength of the radiation–matter interaction, where ε is the dielectric constant of the intracavity medium, Vc is the effective mode volume of the (cavity) photon,71E is the photon electric field amplitude at the emitter position, and µ is the transition dipole moment of the latter. Notably, this Hamiltonian implicitly assumes that the coupling between light and matter is strong relative to the damping of each degree of freedom, yet weak compared to both ωc and ωs. Thus, only states with equal total number of excitations
is the strength of the radiation–matter interaction, where ε is the dielectric constant of the intracavity medium, Vc is the effective mode volume of the (cavity) photon,71E is the photon electric field amplitude at the emitter position, and µ is the transition dipole moment of the latter. Notably, this Hamiltonian implicitly assumes that the coupling between light and matter is strong relative to the damping of each degree of freedom, yet weak compared to both ωc and ωs. Thus, only states with equal total number of excitations| Nexc = a†a + σ+σ− | (2) |
| |LP〉 = sin(θJC)|g, 1〉 + cos(θJC)|e, 0〉, |
| |UP〉 = cos(θJC)|g, 1〉 − sin(θJC)|e, 0〉, | (3) |
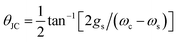 is the polariton mixing-angle, which determines the probability amplitude for a photon or emitter to be observed when the state of the system is either |LP〉 or |UP〉. The state |LP〉 is called lower polariton, while |UP〉 is the upper polariton. Their energy difference is
is the polariton mixing-angle, which determines the probability amplitude for a photon or emitter to be observed when the state of the system is either |LP〉 or |UP〉. The state |LP〉 is called lower polariton, while |UP〉 is the upper polariton. Their energy difference is 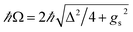 , where Δ = ωc − ωs is the detuning between the photon and emitter frequencies. At resonance (ωc = ωs), the LP and UP become a maximally entangled superposition of emitter and cavity photon, with vacuum Rabi splitting ℏΩR = 2ℏgs [the terminology refers to the process by which introduction of an emitter to the cavity vacuum (initial-state |e, 0〉) leads to coherent (Rabi) oscillations with frequency ΩR/2 in the probability to detect a photon or a material excited-state inside the cavity72,73]. For positive detunings, the UP (LP) has a higher photon (material) character, while the opposite is true when ωc < ωs. The JC model shows other interesting features, such as photon blockade.74 However, because it contains no more than a single structureless [i.e., the internal (vibronic, vibro-rotational, etc.) structure of molecular excitations is not considered] emitter, the JC model is only of pedagogical significance for chemistry, although conditions in which a single-molecule is strongly coupled to a microcavity have recently been achieved in few studies.31,75,76 In fact, for reasons we will discuss next, most experiments which probe the strong coupling regime employ a molecular ensemble including a macroscopic number of emitters.
, where Δ = ωc − ωs is the detuning between the photon and emitter frequencies. At resonance (ωc = ωs), the LP and UP become a maximally entangled superposition of emitter and cavity photon, with vacuum Rabi splitting ℏΩR = 2ℏgs [the terminology refers to the process by which introduction of an emitter to the cavity vacuum (initial-state |e, 0〉) leads to coherent (Rabi) oscillations with frequency ΩR/2 in the probability to detect a photon or a material excited-state inside the cavity72,73]. For positive detunings, the UP (LP) has a higher photon (material) character, while the opposite is true when ωc < ωs. The JC model shows other interesting features, such as photon blockade.74 However, because it contains no more than a single structureless [i.e., the internal (vibronic, vibro-rotational, etc.) structure of molecular excitations is not considered] emitter, the JC model is only of pedagogical significance for chemistry, although conditions in which a single-molecule is strongly coupled to a microcavity have recently been achieved in few studies.31,75,76 In fact, for reasons we will discuss next, most experiments which probe the strong coupling regime employ a molecular ensemble including a macroscopic number of emitters.
The generalization of the JC model for the case where N identical two-level emitters interact strongly with a lossless cavity mode is denoted the Tavis–Cummings (TC)77,78 or Dicke model.79 It is described with the Hamiltonian
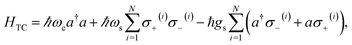 | (4) |
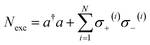 remains a constant of motion. Thus, similar to HJC, the TC model only allows hybrid states in which all components share the same Nexc. Specifically, there exists N + 1 basis states with Nexc = 1: a single state with all emitters in the ground-state and a cavity photon, |g, 1〉 ≡|0, 0, 0…, 0;1〉, and N states where a single emitter is excited and the cavity EM field is in its ground-state, |e(i), 0〉 ≡|0, 0, …, e(i),…, 0, 0, ;0〉,i ∈ {1,…, N}. The stationary states with Nexc = 1 (Fig. 2b) not only include the polaritons, but also a degenerate manifold of dark states |Dµ〉, µ ∈ {1,…, N − 1}, for which an orthogonal basis may be given by delocalized non-totally-symmetric (under any permutation of the emitters) excited-states orthogonal to the permutationally-invariant bright state.80,81 This can be easily seen by rewriting HTC in terms of bright and dark state operators,
remains a constant of motion. Thus, similar to HJC, the TC model only allows hybrid states in which all components share the same Nexc. Specifically, there exists N + 1 basis states with Nexc = 1: a single state with all emitters in the ground-state and a cavity photon, |g, 1〉 ≡|0, 0, 0…, 0;1〉, and N states where a single emitter is excited and the cavity EM field is in its ground-state, |e(i), 0〉 ≡|0, 0, …, e(i),…, 0, 0, ;0〉,i ∈ {1,…, N}. The stationary states with Nexc = 1 (Fig. 2b) not only include the polaritons, but also a degenerate manifold of dark states |Dµ〉, µ ∈ {1,…, N − 1}, for which an orthogonal basis may be given by delocalized non-totally-symmetric (under any permutation of the emitters) excited-states orthogonal to the permutationally-invariant bright state.80,81 This can be easily seen by rewriting HTC in terms of bright and dark state operators, 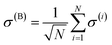 and σ(Dµ), respectively, where σ denotes operators acting on the total Hilbert space of the two-level system ensemble, and the normalization is chosen so that the commutation relations of the σ matrices are preserved. In this basis, HTC is given by
and σ(Dµ), respectively, where σ denotes operators acting on the total Hilbert space of the two-level system ensemble, and the normalization is chosen so that the commutation relations of the σ matrices are preserved. In this basis, HTC is given by
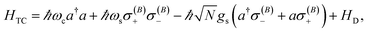 | (5) |
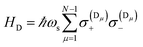 is the dark Hamiltonian. From eqn (5) and its similarity with eqn (1), it is clear that the hybrid eigenstates of HTC with Nexc = 1 are given by
is the dark Hamiltonian. From eqn (5) and its similarity with eqn (1), it is clear that the hybrid eigenstates of HTC with Nexc = 1 are given by| |LP〉 = sin(θTC)|g, 1〉 + cos(θTC)|B, 0〉, |
| |UP〉 = cos(θTC)|g, 1〉 − sin(θTC)|B, 0〉, | (6) |
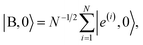 | (7) |
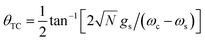 . Notably, these states are simple generalizations of the JC polaritons provided in eqn (3). However, the vacuum Rabi splitting given by eqn (5) is significantly enhanced compared to that of JC, as a result of the collective light-matter coupling
. Notably, these states are simple generalizations of the JC polaritons provided in eqn (3). However, the vacuum Rabi splitting given by eqn (5) is significantly enhanced compared to that of JC, as a result of the collective light-matter coupling 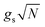 which couples a cavity photon to a delocalized bright emitter. In fact, at resonance, the (collective) vacuum Rabi splitting in the TC model is given by
which couples a cavity photon to a delocalized bright emitter. In fact, at resonance, the (collective) vacuum Rabi splitting in the TC model is given by 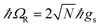 . Since
. Since 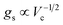 , it follows that ℏΩR scales with the square root of the density of emitters in the optical mode volume. Thus, it is much easier to reach strong coupling between light and matter with a large concentration of optically active material.
, it follows that ℏΩR scales with the square root of the density of emitters in the optical mode volume. Thus, it is much easier to reach strong coupling between light and matter with a large concentration of optically active material.
Introduction of emitter disorder and cavity losses to the JC and TC models does not change the essential conclusions of the above discussion as long as ℏΩR remains larger than the broadening due to the photonic and emitter damping. For instance, while inhomogeneous broadening breaks the degeneracy of the dark manifold and leads to photonic transfer (intensity borrowing) from the LP and UP to these states, the fraction of transferred photon is proportional to |η/ℏΩR|2, where η is the energetic width of the inhomogeneous disorder. In the strong coupling regime ℏΩR ≫ η, so the photonic contribution to the TC dark states is very small and may be neglected in most cases (although it can be significant for a complete description of absorption10 and photoluminescence47,82). It follows from the same argument that molecular inhomogeneous broadening is suppressed in polariton spectra. Specifically, perturbation theory gives energy fluctuations for polaritons which are smaller than those of the bare molecular system by a factor of η/ℏΩR. This suppression has been observed in atomic and inorganic semiconductor quantum well cavity-polaritons where the emitters are approximately structureless (see, e.g., ref. 83).
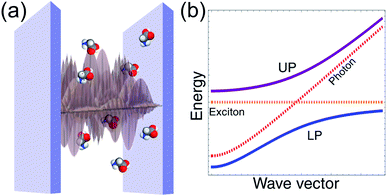
We emphasize the above discussion disregards any dependence of the hybrid cavity Hamiltonian on real-space position or wave vector. In reality, the emitters are spatially distributed within the cavity volume and interact differently with the cavity mode continuum (Fig. 1) according to their positions (in the case of molecular systems there is also a dependence on the orientation of the transition dipole moment). Thus, the LP and UP define bands with dispersion given by ωLP(q) and ωUP(q), respectively (Fig. 3). The effects of disorder are more complex in this case, since they may lead to strong polariton localization and scattering.11,84–86 Nevertheless, if the emitter density of states (DOS) is much larger than that of the cavity EM field, then the dark molecular modes still constitute the majority of the states of the hybrid microcavity. This observation is crucial for the investigation of relaxation dynamics in molecular polaritons, and we devote more attention to it in Section 3.2.
The aspects of the strong coupling regime discussed in this section are essential for a description of molecular polaritons. Nonetheless, the TC model is still too primitive for most chemistry purposes since the two-level systems mimicking electronic states carry no internal (for example, vibronic) structure which is fundamental for the description of molecular dynamics.
3 Organic exciton-polaritons
Organic semiconductors are suitable materials for strong coupling due to their large transition dipole moments and sufficiently narrow linewidths.87 In fact, the observations of molecular cavity-polaritons originated first from the coupling of an optical microcavity with the organic excitons of a Zn-porphyrin dye,17 and later with J-aggregate films.88 Recent years have seen many remarkable developments including demonstrations of reversible optical switching,24 suppression of photochemical reactivity,26 room-temperature polariton lasing22 and Bose–Einstein condensation,89 enhanced charge conductivity,90 and long-range excitation energy transfer.30,91,92 We introduce the effective Hamiltonian of organic polaritons in Section 3.1, review their relaxation dynamics in Section 3.2, and discuss some of their applications in light of the presented theoretical framework in Sections 3.3, 3.4, and 3.5.3.1 Effective descriptions
The main novelty introduced by organic (Frenkel) exciton-polaritons87,102 is the significant local vibronic coupling of the molecular excited-states with inter- and intramolecular vibrational modes. This gives rise to inhomogeneously broadened linewidths, vibronic progressions, and Stokes shifts in the optical spectra of organic systems.87,102 It also gives rise to photochemical reactivity. Thus, it is unsurprising that vibronic coupling—absent from the JC and TC models—is a source of novel organic exciton-polariton behavior. The simplest way exciton-phonon coupling affects polariton behavior is by introducing an efficient channel for nonradiative polariton decay (Table 1). This happens because observed organic microcavity Rabi splittings are of the order of a few hundred meVs (Table 1). In this energy interval, it is common for the molecular environment to have significant phonon DOS, which therefore plays an important role in assisting polariton relaxation. Agranovich et al. first recognized, in a seminal work,11 the effects of inhomogeneities on the organic polariton spectrum, and similarly, the role of resonant phonon emission and absorption on polariton relaxation dynamics. In particular, in ref. 11, the authors employed a macroscopic electrodynamics model to show that, when the main source of disorder is inhomogeneous broadening of the molecular system (typically the case for organic microcavities), only the LP and UP states within a specific region of wave vector space (near the photon-exciton resonance) achieve large coherence lengths (typically a few µm).11,25 The remaining states with significant molecular character may be considered for practical purposes to form an incoherent reservoir [containing both the dark states described in Section 2.2 (Fig. 2) and also polaritons localized due to inhomogeneities] which is weakly coupled to the cavity. Given that the reservoir states are much more numerous than molecular polaritons, they form energy traps fundamentally important in relaxation dynamics, as we discuss in Sections. 3.2, 3.4, and 3.5. Here we note that while the treatment in ref. 11 is phenomenological, its fundamental conclusions were later confirmed by various numerical simulations and experimental data.84,85,99,103–105 We discuss the relaxation dynamics of organic microcavities according to this picture in more detail in Section 3.2.| Process | Initial state(s) | Final state(s) | Timescale | Ref. |
|---|---|---|---|---|
| a In typical organic dyes, vibrational relaxation following electronic excitation occurs on the order of 10–1000 fs.97,98 | ||||
| Rabi oscillations | — | — | 15–50 fs (80–300 meV) | 93 |
| Cavity leakage | Cavity photon | — | 35–100 fs | 94–96 |
| UP | Dark states | ∼ 50 fs | 11 | |
| Vibrational relaxation | Dark states | LP | ∼ 10 fs | 99 |
| UP | — | ∼ 100 fs | 95 | |
| Photoluminescence | LP | — | ∼ 1 fs | 100 |
| Bare exciton | — | ∼ 1–10 ps | 27, 94, 100 and 101 | |
An alternative approach to the investigation of organic cavity-polaritons was introduced by Ćwik et al.,39 who investigated their properties with a generalization of the Holstein Hamiltonian106 appropriate for the study of strongly coupled systems. In this Holstein–Tavis–Cummings (HTC) model, the TC emitters (eqn (5)) are assigned one or more independent vibrational degrees of freedom; these are linearly coupled to each organic exciton in accordance with the displaced oscillator model of vibronic coupling106
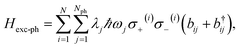 | (8) |
| HHTC = HTC + Hph + Hexc-ph, | (9) |
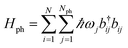 generates the free dynamics of Nph phonon modes per exciton. The single-photon/single-exciton eigenstates of eqn (9) (with Nph = 1) were systematically investigated by Herrera and Spano in ref. 42, 47, 65 and 107 (see also ref. 52 and 108). These authors reported qualitatively distinct stationary states for HHTC depending on the ratio of Rabi splitting and phonon frequency ΩR/ωv. An important limit (with consequences discussed in Sections 3.3 and 3.5) occurs when the light-matter interaction is much stronger than the local vibronic coupling, i.e., ΩR/λvωv ≫ 1. In this case, the phenomenon of polaron decoupling is manifested.42,109 This refers to a significant suppression of the vibronic coupling in the polariton states of a molecular ensemble strongly coupled to a microcavity (as discussed in Section 2.2). It occurs as a consequence of the delocalized character of the polariton states (inherited from the photonic coherence volume and forced by the strong light-matter interaction); when the Rabi splitting is a few times larger than the considered vibronic couplings, the polaritons become (to a large extent) immune to the local (vibronic) perturbations acting on the excitonic states. This intuitive effect was studied long ago, as it is also the reason that delocalized excitations of organic J-aggregates have narrower lineshapes and weaker Stokes shift than the corresponding monomers.110 Further discussion of the different regimes of the HTC model is given in ref. 52 and 65. It was also applied to the study of polariton effects on electron transfer42 (Section 3.3), Raman spectrum,111 and organic polariton photoluminescence.107 Notably, when vibrational relaxation and cavity leakage happen at comparable rates to the Rabi frequency,65 the behavior of the HTC eigenstates is essentially similar to that given by the theory first introduced by Agranovich et al.11 In this case, a simpler kinetic approach11,65 where vibronic coupling acts as a weak perturbation inducing incoherent scattering (see next sections.) is well-suited to the description of organic polariton relaxation dynamics and photoluminescence. In particular, simulations of both phenomena are consistent with the LP being the main source of photoluminescence in microcavity experiments (though it was recently shown that, with surface plasmons as the EM component, van Hove singularities arise and enable ultrafast photoluminescence from the UP53). Given the timescales presented in Table 1, the incoherent treatment of polariton-phonon dynamics is well-justified in many cases. Our further considerations will be based on it unless otherwise mentioned.
generates the free dynamics of Nph phonon modes per exciton. The single-photon/single-exciton eigenstates of eqn (9) (with Nph = 1) were systematically investigated by Herrera and Spano in ref. 42, 47, 65 and 107 (see also ref. 52 and 108). These authors reported qualitatively distinct stationary states for HHTC depending on the ratio of Rabi splitting and phonon frequency ΩR/ωv. An important limit (with consequences discussed in Sections 3.3 and 3.5) occurs when the light-matter interaction is much stronger than the local vibronic coupling, i.e., ΩR/λvωv ≫ 1. In this case, the phenomenon of polaron decoupling is manifested.42,109 This refers to a significant suppression of the vibronic coupling in the polariton states of a molecular ensemble strongly coupled to a microcavity (as discussed in Section 2.2). It occurs as a consequence of the delocalized character of the polariton states (inherited from the photonic coherence volume and forced by the strong light-matter interaction); when the Rabi splitting is a few times larger than the considered vibronic couplings, the polaritons become (to a large extent) immune to the local (vibronic) perturbations acting on the excitonic states. This intuitive effect was studied long ago, as it is also the reason that delocalized excitations of organic J-aggregates have narrower lineshapes and weaker Stokes shift than the corresponding monomers.110 Further discussion of the different regimes of the HTC model is given in ref. 52 and 65. It was also applied to the study of polariton effects on electron transfer42 (Section 3.3), Raman spectrum,111 and organic polariton photoluminescence.107 Notably, when vibrational relaxation and cavity leakage happen at comparable rates to the Rabi frequency,65 the behavior of the HTC eigenstates is essentially similar to that given by the theory first introduced by Agranovich et al.11 In this case, a simpler kinetic approach11,65 where vibronic coupling acts as a weak perturbation inducing incoherent scattering (see next sections.) is well-suited to the description of organic polariton relaxation dynamics and photoluminescence. In particular, simulations of both phenomena are consistent with the LP being the main source of photoluminescence in microcavity experiments (though it was recently shown that, with surface plasmons as the EM component, van Hove singularities arise and enable ultrafast photoluminescence from the UP53). Given the timescales presented in Table 1, the incoherent treatment of polariton-phonon dynamics is well-justified in many cases. Our further considerations will be based on it unless otherwise mentioned.
3.2 Relaxation dynamics
Given the lossy character of the microcavities and plasmonic layers routinely employed in strong coupling experiments,6 any practical use of organic polariton devices must account for the dissipative processes which may affect their performance. Typically, the damping of both bare cavity-photons and organic excitons can be reasonably approximated with a Markovian Master equation treatment.112,113 Said approach assumes these degrees of freedom interact weakly with a macroscopic bath characterized by a system-dependent spectral density.112 A choice needs to be made of whether each molecule has an independent bath, or a single set of environment modes interacts with all excitons. Both situations were explored in the work of del Pino et al.41 (see also ref. 114). Our discussion will assume the independent-baths scenario, which is the more realistic description for the study of disordered organic aggregates.The main dissipation channel for molecular polaritons involves the coupling of their photonic part to the external EM field modes via transmission through the cavity mirrors.6,115 This happens because most experiments employ optical resonators with low quality factor Q (=ωc/κ, where κ is the cavity leakage rate and also the full-width at half-maximum of the cavity mode of interest), thus leading to cavity-photon escape rates which are faster than exciton decay (Table 1).
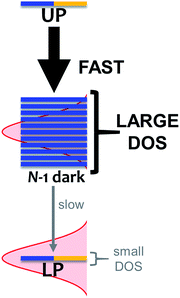
As mentioned, organic exciton-polaritons may also decay nonradiatively due to vibronic coupling (Table 1). Such relaxation occurs between polariton and dark states and is well described with Fermi's golden rule (FGR).116 According to this framework, a quantum transition with higher density of final states exhibits a faster rate compared to that with lower DOS if both processes are mediated by the same perturbations. The prominence of this DOS dependence in organic polariton relaxation dynamics was first characterized in ref. 11, which showed that via local phonon emission (eqn (8)), the UP decays to the dark manifold much faster than the latter decays to the LP (Fig. 4). Agranovich et al.11 considered a single Raman-active phonon mode117 with frequency nearly matching the Rabi splitting in eqn (8) and inhomogeneously broadened spectral distribution of incoherent excitons for the dark band. The resulting vibrational-relaxation time to these “dark” states (with one phonon) from the UP (with zero phonons and formed from exciton-resonant cavity mode) was determined to be ∼50 fs (Table 1). This timescale is in good agreement with the low UP photoluminescence observed experimentally, given that the typical resolution of these measurements is on the order of 100 fs.30 In contrast, a timescale of ∼10 ps (Table 1) for the transition from the dark states to the LP band was obtained in ref. 99. Qualitatively, the difference between the rates of these relaxation processes is a direct manifestation of the final DOS in each case (Fig. 4). Indeed, even when considering light-matter coupling to the entire cavity mode continuum (Section 2.1), the vast majority (70–99%)11,99,118 of states with significant exciton character are dark/incoherent. Therefore, such states form a reservoir which acts as an energy sink. To further corroborate the association of vibrational relaxation with photoluminescence, Michetti and LaRocca simulated organic microcavity emission with a kinetic model based on rates obtained with FGR.95,119 Experimental results were accurately reproduced, specifically the ratio of photoluminescence intensity of both polariton bands, as well as their temperature dependence.95,119
3.3 Polariton-mediated photochemical reactivity
The first report of drastic effects of polaritons on photochemistry was given by Hutchison et al.26 In particular, a reduced rate was observed for spiropyran–merocyanine photoisomerization under conditions where the product of the transformation is resonant with the optical cavity. Later, Galego et al.43 showed a mechanism for the suppression of polariton-mediated photochemical reactions where the reactants are the strongly coupled species. In this case, the reaction rate decreases because the effective LP potential energy surface (PES) has a contribution from the (largely) non-reactive electronic ground-state PES (the reaction was assumed to proceed through the LP).43 Yet another example of polariton-mediated chemical reactivity was presented by Herrera and Spano.42 In this work, the regime of polaron decoupling (Section 3.1) was assumed to show that nonadiabatic intramolecular electron transfer (ET) rates can be enhanced or suppressed when the electron-donor is strongly coupled with an optical cavity. A lower (higher) ET rate was shown to arise when the bare excited-donor and acceptor equilibrium geometries are displaced along the same (opposite) direction(s) relative to the electronic ground-state. In this case, the strong light-matter interaction induces an increase (reduction) of the difference between the electronically excited donor and acceptor equilibrium geometries, which effectively inhibits (accelerates) the reaction. Given that the energetics of the electronically excited-states determines the ET driving force, the manipulation of the polariton energies (Section 2.2) provides yet another knob for the control of ET processes.3.4 Polariton-assisted remote long-range energy transfer
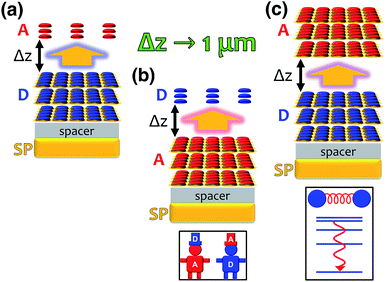
Excitation energy transfer (EET) converts the excitation of a donor (D) molecular species into that of a resonant acceptor (A) species.102 In most cases, this process is mediated by nonradiative dipole–dipole interactions and referred to as Förster resonance energy transfer (FRET).120 However, it is limited to molecular separations of ∼1–10 nm.121 Recently, it has been shown experimentally that efficient long-range EET (50–200 nm) can be achieved in organic microcavities under the strong coupling regime.30,91,92 A variant of this process was first studied by Basko et al.,122 who investigated the effects of acceptor strong coupling on the decay of donor excited-states (weakly-coupled to the cavity) without emphasis on the dependence of energy transfer on donor–acceptor distance.In a recent work,55 we provided a comprehensive theory of this phenomenon, which was denominated polariton-assisted remote energy transfer (PARET, Fig. 5). The setup included separated donor and acceptor molecular slabs placed above a plasmonic layer. The distance-dependence of energy transfer rates was examined for exclusive donor or acceptor strong coupling, and also for the case where both chemical species are strongly coupled to the plasmonic layer. The effective Hamiltonian we employed is a simple generalization of the previously discussed models; it is given by
| H = HD + HA + HP + HDA + HDP + HAP, | (10) |
Each strong coupling scenario (whether only one or both molecular slabs are strongly coupled) is associated to a distinct partitioning of H into a zeroth-order Hamiltonian H0 and a (weak) perturbation V. Given the partitioning appropriate for each situation, the EET rates are obtained with FGR. For instance, when the donor is the only strongly coupled species (Fig. 5a), H0 = HA + HD + HP + HDP and V = HDA + HAP. In this “Förster-like”120 regime (where electrostatic interactions mediate EET), we predicted transfer from donor polaritons to bare acceptors even at micron donor–acceptor separations.55 Such PARET is attributable to the PRET contribution, which evanescently decays from the metal surface across distances as long as microns depending on the wave vector of the resonant SP. In contrast, the EET rate from the purely excitonic (donor) dark states to acceptors approaches that obtained in bare FRET for a sufficiently thick donor slab, as intuitively expected for a dense set of purely excitonic states. Conversely, strong coupling to only acceptors actually leads to a donor-to-polariton rate that is significantly smaller than the bare FRET. In analogy to our discussion of relaxation dynamics in Section 3.2, this arises because the polariton band onto which the transfer is expected to happen has a much lower DOS than the dark state manifold. Furthermore, as in donor-exclusive strong coupling, the donor-to-dark-acceptors EET rate converges to the bare FRET rate (for a sufficiently thick acceptor slab). However, for intense enough acceptor–SP coupling, the donors and acceptors actually reverse roles (“carnival effect”, Fig. 5b).55
In contrast, in a different “Davydov/Redfield-like”124,125 regime where strong coupling is realized with both donors and acceptors (Fig. 5c), long-range EET is mediated by vibrational relaxation.55 This induces transitions among polaritons—delocalized across donors and acceptors—and dark states with common excitonic character. By the same DOS arguments just discussed, EET to polaritons is much slower than that to the dark state manifolds. Nevertheless, the former is calculated to outcompete fluorescence, and the latter occurs as fast as molecular vibrational relaxation.55 Consequently, PARET from a mainly-donor to a mostly-acceptor state is theoretically attainable for chromophoric-slab separations of at least hundreds of nm. In fact, the computed rates for this case are in qualitative agreement with experimental data, even when the nature of the EM modes differ from one study to the other.91
It is worth mentioning that other schemes have been theoretically proposed to enhance excitation energy transport by exploiting strong light-matter coupling126,127 (in conjunction with novel methods of topological protection128,129).
3.5 Polariton-assisted singlet fission
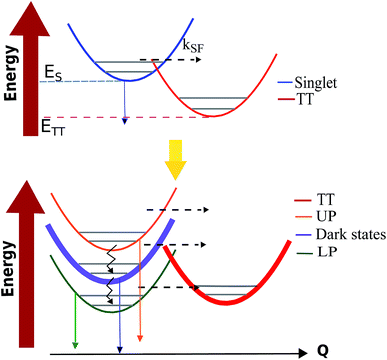
Singlet fission (SF) is a spin-allowed process where a (one-body) singlet exciton is converted into a (two-body) triplet–triplet (TT) state with vanishing total spin (Fig. 6).130,131 This phenomenon is of fundamental importance to the energy sciences, as it has been proven to enhance the efficiency of organic solar cells132,133 by increasing the number of excitons produced per photon absorbed by an organic photovoltaic device, i.e., the external quantum yield (EQY). Given the demonstrated ability of molecular polaritons to influence chemical dynamics, it is natural to enquire what possibilities exist for the control of singlet fission in organic microcavities.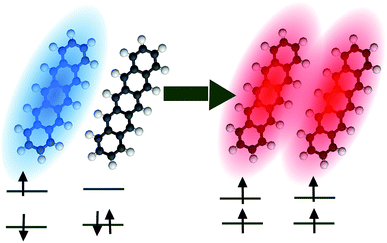 | ||
| Fig. 6 Pictorial representation of singlet fission in pentacene. Blue (red) denotes a singlet (triplet) exciton. | ||
In ref. 56, we proposed a model for the investigation of polariton-assisted SF of acene chains in a microcavity which, for comparison purposes, also considered the competition of SF with other singlet quenching mechanisms. In order to quantitatively establish the effects of singlet strong coupling on TT yield, Martínez-Martínez et al. employed the Pauli master equation formalism.102,112 The results highlight again (Sections 3.2 and 3.4) the essential (Fig. 4) influence of strong coupling on the DOS of donor and acceptor manifolds: the polariton manifold has a small DOS in comparison to the dark and TT. As a consequence, polariton decay to either dark or TT states is significantly faster than the reverse process. Another important finding is that to achieve polariton-based enhancement in the TT yield of an arbitrary SF material, the ideal candidate must have ΔGSF = ETT − ES ≪ 0 (see Fig. 7). In this way, for sufficiently large Rabi splitting, the LP can be tuned close to resonance with a high-frequency bath mode (known as the inner-sphere in Marcus theory literature134) of the TT states. This reduces the energy barrier between the donor (LP) and acceptor states with respect to the bare material. Moreover, detailed balance implies thermal suppression of vibrational relaxation upward from LP to dark states at large Rabi splittings, and the most favorable decay channel directs LP population to the TT manifold. In summary, ref. 56 indicates that under experimentally accessible conditions polariton-assisted SF can outcompete SF quenching mechanisms, and turn materials with poor EQY into highly-efficient sensitizers.
4 Vibrational polaritons
Vibrational polaritons occur when dipole-active molecular vibrations interact strongly with the EM field of a microcavity (Fig. 8). Studies of these novel excitations are stimulated by the possibilities they may offer for the selective control of chemical bonds. In particular, there exists interest in employing vibrational strong coupling (VSC) to, e.g., catalyze or inhibit chemical reactions,29 suppress or enhance intramolecular vibrational relaxation, and control the nonlinear optical response of molecular systems in the infrared (IR).36,135 Furthermore, vibrational polaritons might also provide desired novel sources of coherent mid-IR light.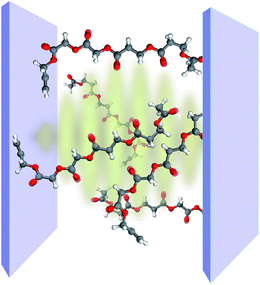 | ||
| Fig. 8 Representation of strong coupling between a planar optical cavity and the carbonyl bonds of polyvinyl acetate chains. | ||
Solid-state phonon-polaritons have been investigated since the 1960s,136,137 and some early studies of liquid-phase molecular vibrational polaritons date back to the 1980s.138 However, it is only recently that cavity or (surface-plasmon) vibrational polaritons have been observed and systematically studied in condensed-phases.28,29,34,139–149 This is important because many important chemical reactions happen in the solution. Notably, under illumination with weak fields, the response of vibrational microcavities is similar to that of organic exciton-polaritons.150 However, fundamentally novel behavior of vibrational polaritons can be observed when higher excitations151,152 of the hybrid system are optically36,57,135,146 or thermally29,153 accessed. In this section we provide an overview of the properties of vibrational polaritons with emphasis on their features which are qualitatively distinct from those of exciton-polaritons. We review the basic theory of VSC in Section 4.1, and discuss recently reported experimental and theoretical results on the nonlinear interactions of vibrational polaritons in Section 4.2. We conclude our discussion of IR strong coupling in Section 4.3 with some comments on recent tantalizing experimental observations of non-trivial VSC effects on chemical reactivity and IR emission which have been reported by the Ebbesen group.29,153
4.1 Basic features of vibrational strong coupling
In contrast to the electronic, the dynamics of a bare vibrational degree of freedom can be well-approximated at low energies by a weakly anharmonic oscillator.154 This implies, e.g., that the v = 1 → v = 2 vibrational transition frequency ω12 is only weakly detuned from ω01, and the effective transition dipole moment µ12 can be expressed as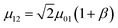 where β is typically a small number. However, these anharmonic properties can only be manifested in experiments that probe the nonlinear151,155 optical response of vibrational polaritons (Section 4.2). Still, there are important differences between the linear optical response of vibrational- and organic exciton-polaritons. For instance, while strong coupling of organic aggregates is facilitated by their large transition dipole moments (the exciton transition dipole moment varies between 5 and 15D in the case of J-aggregates156), the intensity of vibrational transitions is often much weaker in comparison (in general µ01 < 1.5 D). Thus, the Rabi splittings of vibrational polaritons [5–20 meV (ref. 29, 34, 139–141, 144, 145 and 149)] are generally weaker than those of organic microcavities (Table 1). However, vibrational linewidths are often much smaller compared to those of organic excitons. In addition, resonant IR microcavities have lower photon leakage rates [0.1–5 ps (ref. 29, 34, 139–141, 144, 145 and 149)] than the organic (Table 1), for the wavelength of vibrational transitions generally belongs to the mid-IR (λ = 3–30 µm). Thus, there exist many opportunities for strong coupling of cavity EM fields with molecular vibrational degrees of freedom.
where β is typically a small number. However, these anharmonic properties can only be manifested in experiments that probe the nonlinear151,155 optical response of vibrational polaritons (Section 4.2). Still, there are important differences between the linear optical response of vibrational- and organic exciton-polaritons. For instance, while strong coupling of organic aggregates is facilitated by their large transition dipole moments (the exciton transition dipole moment varies between 5 and 15D in the case of J-aggregates156), the intensity of vibrational transitions is often much weaker in comparison (in general µ01 < 1.5 D). Thus, the Rabi splittings of vibrational polaritons [5–20 meV (ref. 29, 34, 139–141, 144, 145 and 149)] are generally weaker than those of organic microcavities (Table 1). However, vibrational linewidths are often much smaller compared to those of organic excitons. In addition, resonant IR microcavities have lower photon leakage rates [0.1–5 ps (ref. 29, 34, 139–141, 144, 145 and 149)] than the organic (Table 1), for the wavelength of vibrational transitions generally belongs to the mid-IR (λ = 3–30 µm). Thus, there exist many opportunities for strong coupling of cavity EM fields with molecular vibrational degrees of freedom.
Typically, molecular vibrations with large optical absorptivity are dominated by polar functional groups such as carbonyl (C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O), amide (H2N–C
O), amide (H2N–C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O) and cyanide (C
O) and cyanide (C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) N). In fact, most of the observed vibrational polaritons arose from the strong coupling of IR cavities with the C
N). In fact, most of the observed vibrational polaritons arose from the strong coupling of IR cavities with the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O or C
O or C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) N bonds of organic polymers,139,141,143 neat organic liquids,140 polypeptides,145 transition metal complexes,28,144 and liquid crystals.157 Yet, given the dependence of the collective Rabi splitting on the molecular density, there is no requirement that the strongly coupled bonds need to be significantly polarizable; in fact, vibrational polaritons have been also been reported for alkene (C
N bonds of organic polymers,139,141,143 neat organic liquids,140 polypeptides,145 transition metal complexes,28,144 and liquid crystals.157 Yet, given the dependence of the collective Rabi splitting on the molecular density, there is no requirement that the strongly coupled bonds need to be significantly polarizable; in fact, vibrational polaritons have been also been reported for alkene (C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C),140 and silane (C–Si)29 bonds. The harmonic Hamiltonian describing VSC of a lossless single-mode IR cavity with an ensemble of N independent identical molecular vibrational degrees of freedom is given by
C),140 and silane (C–Si)29 bonds. The harmonic Hamiltonian describing VSC of a lossless single-mode IR cavity with an ensemble of N independent identical molecular vibrational degrees of freedom is given by
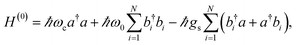 | (11) |
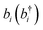 denotes the bosonic annihilation (creation) operator for the vibration localized at molecule i, and the other constants are defined in Section 2. A more realistic description of the system would include the dissipative dynamics of both cavity and matter degrees of freedom. However, here simplifications arise relative to the description of organic exciton-polaritons: vibrational spectra show no Stokes shift, and their absorption bands are in some cases dominated by homogeneous broadening. Thus, it is in general easier to model the effects of cavity and vibrational damping on the polariton linewidths. In particular, the vibrational environment (represented by both intra- and intermolecular degrees of freedom) may be accurately modeled as a thermal distribution of harmonic oscillators (bath) which interact weakly with the system.112 It is again reasonable to assume that the bath of each vibrational degree of freedom is independent (Section 3.2). Under these conditions and the usual assumptions of dissipative Markovian dynamics,102,113 it can be shown that the IR cavity optical response is determined by the normal mode frequencies and dissipation rates of the classical problem of two coupled damped oscillators representing the cavity photon and the bright superposition of molecular excited-states (see, e.g., ref. 57).
denotes the bosonic annihilation (creation) operator for the vibration localized at molecule i, and the other constants are defined in Section 2. A more realistic description of the system would include the dissipative dynamics of both cavity and matter degrees of freedom. However, here simplifications arise relative to the description of organic exciton-polaritons: vibrational spectra show no Stokes shift, and their absorption bands are in some cases dominated by homogeneous broadening. Thus, it is in general easier to model the effects of cavity and vibrational damping on the polariton linewidths. In particular, the vibrational environment (represented by both intra- and intermolecular degrees of freedom) may be accurately modeled as a thermal distribution of harmonic oscillators (bath) which interact weakly with the system.112 It is again reasonable to assume that the bath of each vibrational degree of freedom is independent (Section 3.2). Under these conditions and the usual assumptions of dissipative Markovian dynamics,102,113 it can be shown that the IR cavity optical response is determined by the normal mode frequencies and dissipation rates of the classical problem of two coupled damped oscillators representing the cavity photon and the bright superposition of molecular excited-states (see, e.g., ref. 57).
4.2 Transient vibrational polaritons
The first pump-probe (pp) spectra of vibrational polaritons were obtained by Dunkelberger et al.146 These experiments employed liquid-phase solutions of W(CO)6 in hexane. The T1µ triply-degenerate carbonyl mode was chosen to couple to the cavity as its effective transition dipole moment is relatively large (≈1 D), and its linewidth is sufficiently small (≈3 cm−1). Further insight on the nonlinear behavior of strongly coupled W(CO)6 was reported recently by Xiang et al.,135 who also provided the first 2D spectra of vibrational polaritons. These experiments provide direct information on both the relaxation dynamics and the nonlinear optical properties of vibrational polaritons induced by molecular anharmonicity. For instance, both the pp and 2D spectra showed excited-state absorption resonances which indicate asymmetric polariton–dark state nonlinear interactions [note that while LP, UP and dark states are exact eigenstates of eqn (11), by writing localized nonlinear couplings [eqn (12)] in terms of polariton and dark state operators it can be seen that some of the higher excited-states of the system will have contributions from both polaritons and dark states],135,146even when linear optical measurements showed equally intense LP and UP response. In particular, the IR cavity differential probe transmission (pp transmission minus linear probe transmission) displayed a consistently large (small) negative feature at the linear LP (UP) frequency, and positive shifted (relative to the linear spectrum) transmission resonances for the LP and UP (Fig. 9). As we discuss below, these nonlinear properties of vibrational polaritons are expected to be generic. Therefore, the information gathered by these experiments is likely going to be essential for the development of protocols for laser-controlled VSC chemistry, and for the design of infrared-operated nonlinear optical devices.36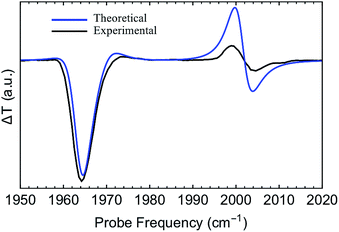 | ||
Fig. 9 Experimental and theoretical pump-probe (differential) transmission spectra of strongly coupled W(CO)6 in an optical microcavity.57 These results correspond to the case where the cavity photon and the molecular vibration (asymmetric C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O stretch) are resonant. O stretch) are resonant. | ||
In ref. 57, the aforementioned experiments were interpreted with a microscopic model of vibrational polaritons which includes the effect of vibrational anharmonicity on the polariton optical response. Both mechanical and electrical nonlinearities were added to the model described by eqn (11). Mechanical (or bond) anharmonicity represents the tendency that bonds break at high energies, while electrical anharmonicity occurs due to nonlinearity of the effective vibrational transition dipole moment with respect to small displacements of the nuclei from equilibrium (e.g., due to non-Condon effects158–160). In practice, the main consequence of mechanical and electrical nonlinearities is to redshift overtone transitions from the fundamental and give band absorption intensities which violate the harmonic oscillator scaling, respectively. Thus, the effective Hamiltonian of anharmonic vibrational polaritons interacting with a single cavity mode can be written as57
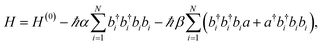 | (12) |
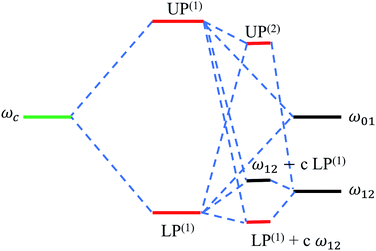 | ||
| Fig. 10 Energy level hybridization diagram including the photonic (ωc) and vibrational transitions (ω01,ω12) involved in the formation of linear [LP(1), UP(1)] and (effective) transient vibrational polaritons [UP(2), and the combination of LP(1) and the 1 → 2 vibrational transition].135 Note the significant interaction between the linear LP mode and the 1 → 2 excitations (represented by the coefficient c) arising from the incoherent population of vibrational modes induced by a pump after sufficiently long probe-delay times. | ||
4.3 Applications: chemical kinetics and thermal emission
We conclude our discussion of vibrational polaritons by mentioning two recent observations of the effects of VSC on chemical reactions and thermal emission. First, Thomas et al.29 provided evidence that an organic silane deprotection reaction proceeds via a different mechanism under conditions where the C–Si bond is strongly coupled to an optical microcavity, even in the absence of external photon pumping of the polariton system. Specifically, the reaction rate was measured as a function of temperature under normal and VSC conditions, and the resulting kinetic curves provided transition-state theory estimates for the entropy and enthalpy of activation. The entropy of activation was reported to be positive under VSC, but negative otherwise. In addition, the kinetics was significantly dependent on the Rabi splitting, and the observed rate in an off-resonant cavity was shown to be indistinguishable from that measured outside the cavity. Similarly puzzling results were shown recently by Chervy et al.,153 who reported non-thermalized thermal emission of cavity vibrational polaritons of an organic polymer at 373 K. It was also observed that while the bare polymer and cavity emission spectra matched the theoretical thermal emission, the strongly coupled system showed emission peaks at frequencies displaced from the expected (based on the linear optical spectra).These experiments show additional examples of the rich dynamics featured by vibrational polaritons. In particular, both the barrier crossing and the anomalous thermal emission phenomena reported in hybrid infrared microcavities likely arise from anharmonic molecular excited-state dynamics activated by thermal fluctuations. However, further work is needed to understand the sources of the observed behaviors. We expect that their microscopic interpretation will likely shed light on novel ways to control chemical bonds with VSC.
5 Ultrastrong coupling
All of our previous considerations assumed that the (collective) Rabi splitting was stronger than the dissipative couplings of the bare molecule (or cavity), but also much weaker than the transition energy of interest. The ultrastrong coupling (USC) regime is characterized by the violation of the latter assumption.161,162 In particular, the onset of USC is conventionally defined to arise for vacuum Rabi splittings that satisfy ΩR/ωc, ΩR/ωs > 10%.161,163 When this condition is fulfilled, significant deviations from the approximate light-matter coupling assumed in eqn (1) and (4) become relevant.An important feature of USC is that states with different excitation number (number of photons + molecular excited-states) are allowed to hybridize, while our previous discussions assumed that the interaction of radiation with bright-molecular states preserves the total excitation number of the system. An essential consequence is that while the ground-state of a strongly coupled system (|0〉) is indistinguishable from the decoupled where all degrees of freedom are at their ground-state, the lowest-energy state of an ultrastrongly coupled system is a superposition of states consisting of correlated photons and delocalized bright molecular excitations.161,162 Notably, molecular USC was first achieved less than ten years ago.24 While this field has seen considerable progress including recent reports of organic exciton24,164–167 and vibrational USC,168 its effects on chemical transformations are only beginning to be understood. We discuss a specific case below.
In a recent work,54 we studied the effects of USC in the electronic ground-state energy landscape of a molecular ensemble. In particular, we considered a simplified model of a molecular slab interacting with a plasmonic field in the USC regime. The Born–Oppenheimer Hamiltonian of the system is given by
| HBO = Tnuc + Hel(R), | (13) |
| Hel(R) = Hg(R) + Hpl + He(R) + Hpl-e(R), | (14) |
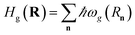 is the Born–Oppenheimer electronic ground-state energy of the ensemble at an arbitrary nuclear configuration {Rn} (Rn is the nuclear coordinate of the molecule located at site n within the molecular slab),
is the Born–Oppenheimer electronic ground-state energy of the ensemble at an arbitrary nuclear configuration {Rn} (Rn is the nuclear coordinate of the molecule located at site n within the molecular slab), 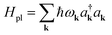 is the Hamiltonian of bare plasmon modes with dispersion E(k) = ℏωk (where k is the plasmon in-plane wave vector) and creation (annihilation) operators
is the Hamiltonian of bare plasmon modes with dispersion E(k) = ℏωk (where k is the plasmon in-plane wave vector) and creation (annihilation) operators 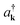 (ak). The exciton Hamiltonian for an ensemble nuclear configuration {Rn} is given by
(ak). The exciton Hamiltonian for an ensemble nuclear configuration {Rn} is given by 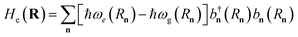 , where
, where 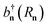 [bn(Rn)] is the creation (annihilation) operator of the nth-site. The exciton–plasmon interaction is given by
[bn(Rn)] is the creation (annihilation) operator of the nth-site. The exciton–plasmon interaction is given by
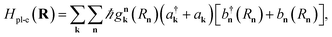 | (15) |
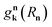 is the interaction between the plasmon with wave vector k and the nth exciton. It depends on the position and geometry of the molecule since the plasmonic electric fields vary in space and the molecular transition dipole moment is a function of Rn. Notice the explicit inclusion in Hpl-e of terms that do not preserve the total number of excitations (see also Fig. 11). We also note that the maximal value of the collective couplings obtained with this model does not surpass 20% of the exciton frequency; this justifies the neglect of the EM field diamagnetic terms in eqn (14).169
is the interaction between the plasmon with wave vector k and the nth exciton. It depends on the position and geometry of the molecule since the plasmonic electric fields vary in space and the molecular transition dipole moment is a function of Rn. Notice the explicit inclusion in Hpl-e of terms that do not preserve the total number of excitations (see also Fig. 11). We also note that the maximal value of the collective couplings obtained with this model does not surpass 20% of the exciton frequency; this justifies the neglect of the EM field diamagnetic terms in eqn (14).169
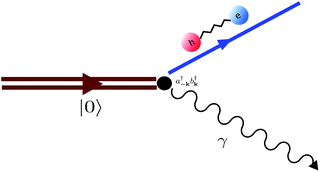 | ||
Fig. 11 Diagram representing spontaneous production of correlated exciton–photon pairs from the bare system ground-state |0〉. This process is significant in the ultrastrong coupling regime where light-matter couplings of the form 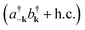 become relevant (see eqn (15)). become relevant (see eqn (15)). | ||
The molecules that constitute the referred ensemble can undergo isomerization. This is described by the electronic ground and excited adiabatic PESs, ℏωg(Rn) and ℏωe(Rn), respectively. The former has a double-well structure and an avoided-crossing with the latter. Ref. 54 analyzed various cross-sections of the dressed (collective) ground-state PES arising under USC. This included the cut where all molecular coordinates were frozen at the reactant configuration except for a single molecule. Such reaction coordinate represents an effective single-molecule PES. However, it was observed that the corresponding reaction barrier is almost unaffected by the collective light-matter coupling. Rather, the maximal energetic modifications to the ground-state induced by USC were identified as Lamb shifts which are small in comparison to the thermal energy. However, these results do not discourage further application of USC to chemical systems. The conditions studied in ref. 54 were such that the light-matter interaction was near the edge of the USC regime, where the total exciton (photon) population in the dressed ground-state is small, and a perturbative treatment of their effects is valid. In this case, the USC ground-state deviation from the bare system is nearly inconsequential. We believe that future theoretical and experimental studies of USC in the non-perturbative regime will present novel possibilities for the manipulation of ground-state chemical dynamics in optical microcavities.
6 Epilogue
We hope to have convinced the reader that: (i) the phenomena emergent from the (ultra)strong coupling regime presents novel opportunities for the control of chemical transformations induced by electronic and vibrational dynamics, and (ii) there remains much experimental and theoretical work to be done to unravel all of the intricacies and possibilities of polariton-mediated chemistry. Future experimental work will certainly entertain creative ways to steer chemical events using optical cavities in various regimes of external pumping and thermodynamic conditions, as well as new opportunities to harness many-body quantum effects towards the control of physicochemical properties of molecules. From the theoretical perspective, we expect novel applications and further development of effective condensed matter theories that describe the diverse phenomenology afforded by molecular polaritons. As we have shown here, these theories are particularly powerful in predicting nontrivial thermodynamic-limit behavior which can be directly employed to guide experiments.42,43,56–58,170,171 Lastly, there is a push towards the development of ab initio quantum chemistry and quantum and semiclassical dynamics methodologies to simulate molecular polaritonic systems with atomistic detail.45,60,172–174 Future studies of molecular polariton theory are expected to integrate quantum optics with the standard toolbox of chemical dynamics including e.g., surface-hopping methods,175 quantum master equations, and path-integral approaches.176,177 Still, the complex interplay between electronic, nuclear, and photonic degrees of freedom in complex dissipative environments presents a whole new set of challenges for computational methods, which will require novel solutions.Conflicts of interest
There are no conflicts to declare.Acknowledgements
RFR, MD, JCGA, and JYZ acknowledge support from the NSF CAREER Award CHE-164732. LAMM and JCGA are grateful for the support of the UC-Mexus CONACyT scholarship for doctoral studies. All authors were partially supported by generous UCSD startup funds. We acknowledge illuminating discussions we had throughout our collaborations with Wei Xiong, Stephane Kena-Cohen, Vinod Menon, Jeff Owrutsky, Adam Dunkelberger, Blake Simpkins, and Bo Xiang.Notes and references
- N. J. Turro, Modern Molecular Photochemistry, University science books, 1991 Search PubMed.
- V. Balzani, P. Ceroni and A. Juris, Photochemistry and Photophysics: Concepts, Research, Applications, John Wiley & Sons, 2014 Search PubMed.
- J. J. Hopfield, Phys. Rev., 1958, 112, 1555–1567 CrossRef.
- V. M. Agranovich, Soviet Physics - JETP, 1959, 10, 307–313 Search PubMed.
- T. W. Ebbesen, Acc. Chem. Res., 2016, 49, 2403–2412 CrossRef PubMed.
- A. V. Kavokin, J. J. Baumberg, G. Malpuech and F. P. Laussy, Microcavities, Oxford University Press, 2017, vol. 21 Search PubMed.
- D. G. Baranov, M. Wersäll, J. Cuadra, T. J. Antosiewicz and T. Shegai, ACS Photonics, 2018, 5, 24–42 CrossRef.
- P. Törmä and W. L. Barnes, Rep. Prog. Phys., 2015, 78, 013901 CrossRef PubMed.
- P. Vasa and C. Lienau, ACS Photonics, 2018, 5, 2–23 CrossRef.
- R. Houdré, R. P. Stanley and M. Ilegems, Phys. Rev. A, 1996, 53, 2711–2715 CrossRef.
- V. M. Agranovich, M. Litinskaia and D. G. Lidzey, Phys. Rev. B, 2003, 67, 085311 CrossRef.
- C. Gonzalez-Ballestero, J. Feist, E. Gonzalo Badía, E. Moreno and F. J. Garcia-Vidal, Phys. Rev. Lett., 2016, 117, 156402 CrossRef PubMed.
- D. Meschede, H. Walther and G. Müller, Phys. Rev. Lett., 1985, 54, 551–554 CrossRef PubMed.
- M. G. Raizen, R. J. Thompson, R. J. Brecha, H. J. Kimble and H. J. Carmichael, Phys. Rev. Lett., 1989, 63, 240–243 CrossRef PubMed.
- C. Weisbuch, M. Nishioka, A. Ishikawa and Y. Arakawa, Phys. Rev. Lett., 1992, 69, 3314–3317 CrossRef PubMed.
- R. Houdré, R. P. Stanley, U. Oesterle, M. Ilegems and C. Weisbuch, J. Phys. IV, 1993, 03, C5-51–C5-58 CrossRef.
- D. G. Lidzey, D. D. C. Bradley, M. S. Skolnick, T. Virgili, S. Walker and D. M. Whittaker, Nature, 1998, 395, 53 CrossRef.
- P. Schouwink, H. V. Berlepsch, L. Dähne and R. F. Mahrt, Chem. Phys. Lett., 2001, 344, 352–356 CrossRef.
- R. J. Holmes and S. R. Forrest, Phys. Rev. Lett., 2004, 93, 186404 CrossRef PubMed.
- J. Dintinger, S. Klein, F. Bustos, W. L. Barnes and T. W. Ebbesen, Phys. Rev. B, 2005, 71, 035424 CrossRef.
- S. Kéna-Cohen, M. Davanço and S. R. Forrest, Phys. Rev. Lett., 2008, 101, 116401 CrossRef PubMed.
- S. Kéna-Cohen and S. R. Forrest, Nat. Photonics, 2010, 4, 371–375 CrossRef.
- T. Virgili, D. Coles, A. M. Adawi, C. Clark, P. Michetti, S. K. Rajendran, D. Brida, D. Polli, G. Cerullo and D. G. Lidzey, Phys. Rev. B, 2011, 83, 245309 CrossRef.
- T. Schwartz, J. A. Hutchison, C. Genet and T. W. Ebbesen, Phys. Rev. Lett., 2011, 106, 196405 CrossRef PubMed.
- S. Aberra Guebrou, C. Symonds, E. Homeyer, J. C. Plenet, Y. N. Gartstein, V. M. Agranovich and J. Bellessa, Phys. Rev. Lett., 2012, 108, 066401 CrossRef PubMed.
- J. A. Hutchison, T. Schwartz, C. Genet, E. Devaux and T. W. Ebbesen, Angew. Chem., Int. Ed., 2012, 51, 1592–1596 CrossRef PubMed.
- T. Schwartz, J. A. Hutchison, J. Léonard, C. Genet, S. Haacke and T. W. Ebbesen, ChemPhysChem, 2013, 14, 125–131 CrossRef PubMed.
- B. S. Simpkins, K. P. Fears, W. J. Dressick, B. T. Spann, A. D. Dunkelberger and J. C. Owrutsky, ACS Photonics, 2015, 2, 1460–1467 CrossRef.
- A. Thomas, J. George, A. Shalabney, M. Dryzhakov, S. J. Varma, J. Moran, T. Chervy, X. Zhong, E. Devaux, C. Genet, J. A. Hutchison and T. W. Ebbesen, Angew. Chem., Int. Ed., 2016, 55, 11462–11466 CrossRef PubMed.
- X. Zhong, T. Chervy, L. Zhang, A. Thomas, J. George, C. Genet, J. A. Hutchison and T. W. Ebbesen, Angew. Chem., Int. Ed., 2017, 56, 9034–9038 CrossRef PubMed.
- R. Chikkaraddy, B. de Nijs, F. Benz, S. J. Barrow, O. A. Scherman, E. Rosta, A. Demetriadou, P. Fox, O. Hess and J. J. Baumberg, Nature, 2016, 535, 127–130 CrossRef PubMed.
- D. Melnikau, A. A. Govyadinov, A. Sánchez-Iglesias, M. Grzelczak, L. M. Liz-Marzán and Y. P. Rakovich, Nano Lett., 2017, 17, 1808–1813 CrossRef PubMed.
- S. Baieva, O. Hakamaa, G. Groenhof, T. T. Heikkilä and J. J. Toppari, ACS Photonics, 2017, 4, 28–37 CrossRef.
- V. F. Crum, S. R. Casey and J. R. Sparks, Phys. Chem. Chem. Phys., 2018, 20, 850–857 RSC.
- G. G. Rozenman, K. Akulov, A. Golombek and T. Schwartz, ACS Photonics, 2018, 5, 105–110 CrossRef.
- A. D. Dunkelberger, R. B. Davidson II, W. Ahn, B. S. Simpkins and J. C. Owrutsky, J. Phys. Chem. A, 2018, 122(4), 965–971 CrossRef PubMed.
- C.-Y. Cheng, R. Dhanker, C. L. Gray, S. Mukhopadhyay, E. R. Kennehan, J. B. Asbury, A. Sokolov and N. C. Giebink, Phys. Rev. Lett., 2018, 120, 017402 CrossRef PubMed.
- B. Munkhbat, M. Wersäll, D. G. Baranov, T. J. Antosiewicz and T. Shegai, 2018, arXiv:1802.06616 [cond-mat, physics:physics].
- J. A. Ćwik, S. Reja, P. B. Littlewood and J. Keeling, Europhys. Lett., 2014, 105, 47009 CrossRef.
- J. Galego, F. J. Garcia-Vidal and J. Feist, Phys. Rev. X, 2015, 5, 041022 Search PubMed.
- J. del Pino, J. Feist and F. J. Garcia-Vidal, New J. Phys., 2015, 17, 053040 CrossRef.
- F. Herrera and F. C. Spano, Phys. Rev. Lett., 2016, 116, 238301 CrossRef PubMed.
- J. Galego, F. J. Garcia-Vidal and J. Feist, Nat. Commun., 2016, 7, 13841 CrossRef PubMed.
- M. Kowalewski, K. Bennett and S. Mukamel, J. Chem. Phys., 2016, 144, 054309 CrossRef PubMed.
- K. Bennett, M. Kowalewski and S. Mukamel, Faraday Discuss., 2016, 194, 259–282 RSC.
- N. Wu, J. Feist and F. J. Garcia-Vidal, Phys. Rev. B, 2016, 94, 195409 CrossRef.
- F. Herrera and F. C. Spano, Phys. Rev. Lett., 2017, 118, 223601 CrossRef PubMed.
- Z. Zhang and S. Mukamel, Chem. Phys. Lett., 2017, 683, 653–657 CrossRef.
- J. Feist, J. Galego and F. J. Garcia-Vidal, ACS Photonics, 2017, 5(1), 205–216 CrossRef.
- T. Dimitrov, J. Flick, M. Ruggenthaler and A. Rubio, New J. Phys., 2017, 19, 113036 CrossRef.
- J. Flick, H. Appel, M. Ruggenthaler and A. Rubio, J. Chem. Theory Comput., 2017, 13, 1616–1625 CrossRef PubMed.
- M. A. Zeb, P. G. Kirton and J. Keeling, ACS Photonics, 2018, 5, 249–257 CrossRef.
- J. Yuen-Zhou, S. K. Saikin and V. Menon, 2017, arXiv:1711.11213 [cond-mat].
- L. A. Martínez-Martínez, R. F. Ribeiro, J. Campos-González-Angulo and J. Yuen-Zhou, ACS Photonics, 2018, 5, 167–176 CrossRef.
- M. Du, L. A. Martínez-Martínez, R. F. Ribeiro, Z. Hu, V. M. Menon and J. Yuen-Zhou, Chem. Sci., 2017 10.1039/c8sc00171e.
- L. A. Martínez-Martínez, M. Du, R. F. Ribeiro, S. Kéna-Cohen and J. Yuen-Zhou, J. Phys. Chem. Lett., 2018, 9, 1951–1957 CrossRef PubMed.
- R. F. Ribeiro, A. D. Dunkelberger, B. Xiang, W. Xiong, B. S. Simpkins, J. C. Owrutsky and J. Yuen-Zhou, J. Phys. Chem. Lett., 2017 DOI:10.1021/acs.jpclett.8b01176.
- J. P. Bergfield and J. R. Hendrickson, Sci. Rep., 2018, 8, 2314 CrossRef PubMed.
- I. Carusotto and C. Ciuti, Rev. Mod. Phys., 2013, 85, 299–366 CrossRef.
- M. Ruggenthaler, J. Flick, C. Pellegrini, H. Appel, I. V. Tokatly and A. Rubio, Phys. Rev. A, 2014, 90, 012508 CrossRef.
- R. J. Holmes and S. R. Forrest, Org. Electron., 2007, 8, 77–93 CrossRef.
- V. M. Agranovich, Y. N. Gartstein and M. Litinskaya, Chem. Rev., 2011, 111, 5179–5214 CrossRef PubMed.
- S. Kéna-Cohen and S. R. Forrest, Exciton Polaritons in Microcavities, Springer, Berlin, Heidelberg, 2012, pp. 349–375 Search PubMed.
- M. Sukharev and A. Nitzan, J. Phys.: Condens. Matter, 2017, 29, 443003 CrossRef PubMed.
- F. Herrera and F. C. Spano, ACS Photonics, 2018, 5, 65–79 CrossRef.
- D. S. Dovzhenko, S. V. Ryabchuk, Y. P. Rakovich and I. R. Nabiev, Nanoscale, 2018, 10, 3589–3605 RSC.
- D. A. Steck, Quantum and Atom Optics, revision 0.12.0, 16 May 2017, edn, 2007 Search PubMed.
- D. M. Coles and D. G. Lidzey, Appl. Phys. Lett., 2014, 104, 191108 CrossRef.
- K. S. Daskalakis, S. A. Maier and S. Kéna-Cohen, Quantum Plasmonics, Springer International Publishing, Cham, 2017, pp. 151–163 Search PubMed.
- E. T. Jaynes and F. W. Cummings, Proc. IEEE, 1963, 51, 89–109 Search PubMed.
- K. Ujihara, A. Nakamura and O. Manba, Jpn. J. Appl. Phys., 1991, 30, 3388 CrossRef.
- I. I. Rabi, Phys. Rev., 1937, 51, 652–654 CrossRef.
- G. S. Agarwal, Phys. Rev. Lett., 1984, 53, 1732–1734 CrossRef.
- K. M. Birnbaum, A. Boca, R. Miller, A. D. Boozer, T. E. Northup and H. J. Kimble, Nature, 2005, 436, 87–90 CrossRef PubMed.
- F. Benz, M. K. Schmidt, A. Dreismann, R. Chikkaraddy, Y. Zhang, A. Demetriadou, C. Carnegie, H. Ohadi, B. de Nijs, R. Esteban, J. Aizpurua and J. J. Baumberg, Science, 2016, 354, 726–729 CrossRef PubMed.
- D. Wang, H. Kelkar, D. Martin-Cano, T. Utikal, S. Götzinger and V. Sandoghdar, Phys. Rev. X, 2017, 7, 021014 Search PubMed.
- M. Tavis and F. W. Cummings, Phys. Rev., 1968, 170, 379–384 CrossRef.
- M. Tavis and F. W. Cummings, Phys. Rev., 1969, 188, 692–695 CrossRef.
- R. H. Dicke, Phys. Rev., 1954, 93, 99–110 CrossRef.
- P. A. Vetter, L. Wang, D.-W. Wang and M. O. Scully, Phys. Scr., 2016, 91, 023007 CrossRef.
- G. S. Agarwal, J. Mod. Opt., 1998, 45, 449–470 CrossRef.
- L. Mazza, L. Fontanesi and G. C. La Rocca, Phys. Rev. B, 2009, 80, 235314 CrossRef.
- J.-M. Manceau, G. Biasiol, N. L. Tran, I. Carusotto and R. Colombelli, Phys. Rev. B, 2017, 96, 235301 CrossRef.
- M. Litinskaya and P. Reineker, Phys. Rev. B, 2006, 74, 165320 CrossRef.
- V. M. Agranovich and Y. N. Gartstein, Phys. Rev. B, 2007, 75, 075302 CrossRef.
- M. Litinskaya, Phys. Lett. A, 2008, 372, 3898–3903 CrossRef.
- V. M. Agranovich, Excitations in Organic Solids, OUP Oxford, 2009, vol. 142 Search PubMed.
- D. G. Lidzey, D. D. C. Bradley, T. Virgili, A. Armitage, M. S. Skolnick and S. Walker, Phys. Rev. Lett., 1999, 82, 3316–3319 CrossRef.
- J. D. Plumhof, T. Stöferle, L. Mai, U. Scherf and R. F. Mahrt, Nat. Mater., 2014, 13, 247–252 CrossRef PubMed.
- E. Orgiu, J. George, J. A. Hutchison, E. Devaux, J. F. Dayen, B. Doudin, F. Stellacci, C. Genet, J. Schachenmayer, C. Genes, G. Pupillo, P. Samorì and T. W. Ebbesen, Nat. Mater., 2015, 14, 1123–1129 CrossRef PubMed.
- D. M. Coles, N. Somaschi, P. Michetti, C. Clark, P. G. Lagoudakis, P. G. Savvidis and D. G. Lidzey, Nat. Mater., 2014, 13, 712 CrossRef PubMed.
- K. Georgiou, P. Michetti, L. Gai, M. Cavazzini, Z. Shen and D. G. Lidzey, ACS Photonics, 2018, 5, 258–266 CrossRef.
- P. A. Hobson, W. L. Barnes, D. G. Lidzey, G. A. Gehring, D. M. Whittaker, M. S. Skolnick and S. Walker, Appl. Phys. Lett., 2002, 81, 3519–3521 CrossRef.
- J.-H. Song, Y. He, A. V. Nurmikko, J. Tischler and V. Bulovic, Phys. Rev. B, 2004, 69, 235330 CrossRef.
- P. Michetti and G. C. La Rocca, Phys. Rev. B, 2008, 77, 195301 CrossRef.
- D. M. Coles, P. Michetti, C. Clark, W. C. Tsoi, A. M. Adawi, J.-S. Kim and D. G. Lidzey, Adv. Funct. Mater., 2011, 21, 3691–3696 CrossRef.
- A. J. Taylor, D. J. Erskine and C. L. Tang, Chem. Phys. Lett., 1984, 103, 430–435 CrossRef.
- D. Reiser and A. Laubereau, Opt. Commun., 1982, 42, 329–334 CrossRef.
- M. Litinskaya, P. Reineker and V. M. Agranovich, J. Lumin., 2004, 110, 364–372 CrossRef.
- S. Wang, T. Chervy, J. George, J. A. Hutchison, C. Genet and T. W. Ebbesen, J. Phys. Chem. Lett., 2014, 5, 1433–1439 CrossRef PubMed.
- K. Miyano, H. Ishikawa and A. Tomioka, Mater. Sci. Eng., B, 1997, 48, 122–125 CrossRef.
- V. May and O. Kühn, Charge and Energy Transfer Dynamics in Molecular Systems, 2nd, Revised and Enlarged Edition, ed. V. May and O. Kühn, Wiley-VCH, February 2004, p. 490. ISBN 3-527-40396-5 Search PubMed.
- P. Michetti and G. C. La Rocca, Phys. Rev. B, 2005, 71, 115320 CrossRef.
- P. Michetti and G. C. La Rocca, Phys. E, 2008, 40, 1926–1929 CrossRef.
- L. Fontanesi, L. Mazza and G. C. La Rocca, Phys. Rev. B, 2009, 80, 235313 CrossRef.
- T. Holstein, Ann. Phys., 1959, 8, 325–342 Search PubMed.
- F. Herrera and F. C. Spano, Phys. Rev. A, 2017, 95, 053867 CrossRef.
- J. A. Ćwik, P. Kirton, S. De Liberato and J. Keeling, Phys. Rev. A, 2016, 93, 033840 CrossRef.
- F. C. Spano, J. Chem. Phys., 2015, 142, 184707 CrossRef PubMed.
- E. W. Knapp, Chem. Phys., 1984, 85, 73–82 CrossRef.
- A. Strashko and J. Keeling, Phys. Rev. A, 2016, 94, 023843 CrossRef.
- A. Nitzan, Relaxation, Transfer and Reactions in Condensed Molecular Systems, Chemical Dynamics in Condensed Phases, Oxford University Press, 2006 Search PubMed.
- C. W. Gardiner and H. Haken, Quantum Noise, Springer, Berlin, 1991, vol. 26 Search PubMed.
- L. A. Martínez-Martínez and J. Yuen-Zhou, New J. Phys., 2018, 20, 018002 CrossRef.
- V. Savona, L. C. Andreani, P. Schwendimann and A. Quattropani, Solid State Commun., 1995, 93, 733–739 CrossRef.
- P. a. M. Dirac, Proc. R. Soc. London, Ser. A, 1927, 114, 243–265 CrossRef.
- A. I. Tartakovskii, M. Emam-Ismail, D. G. Lidzey, M. S. Skolnick, D. D. C. Bradley, S. Walker and V. M. Agranovich, Phys. Rev. B, 2001, 63, 121302 CrossRef.
- V. Agranovich, M. Litinskaia and D. Lidzey, Phys. Status Solidi B, 2002, 234, 130–138 CrossRef.
- P. Michetti and G. C. La Rocca, Phys. Rev. B, 2009, 79, 035325 CrossRef.
- T. Förster, Ann. Phys., 1948, 437, 55–75 CrossRef.
- I. L. Medintz and N. Hildebrandt, FRET-Förster Resonance Energy Transfer: From Theory to Applications, John Wiley & Sons, 2013 Search PubMed.
- D. M. Basko, F. Bassani, G. C. La Rocca and V. M. Agranovich, Phys. Rev. B, 2000, 62, 15962–15977 CrossRef.
- G. L. Liu, Y.-T. Long, Y. Choi, T. Kang and L. P. Lee, Nat. Methods, 2007, 4, 1015–1017 CrossRef PubMed.
- A. Davydov, Zh. Eksp. Teor. Fiz., 1948, 18, 210–218 Search PubMed.
- A. G. Redfield, Advances in Magnetic and Optical Resonance, Academic Press, 1965, vol. 1, pp. 1–32 Search PubMed.
- J. Feist and F. J. Garcia-Vidal, Phys. Rev. Lett., 2015, 114, 196402 CrossRef PubMed.
- J. Schachenmayer, C. Genes, E. Tignone and G. Pupillo, Phys. Rev. Lett., 2015, 114, 196403 CrossRef PubMed.
- J. Yuen-Zhou, S. K. Saikin, N. Y. Yao and A. Aspuru-Guzik, Nat. Mater., 2014, 13, 1026–1032 CrossRef PubMed.
- J. Yuen-Zhou, S. K. Saikin, T. Zhu, M. C. Onbasli, C. A. Ross, V. Bulovic and M. A. Baldo, Nat. Commun., 2016, 7, 11783 CrossRef PubMed.
- M. B. Smith and J. Michl, Chem. Rev., 2010, 110, 6891–6936 CrossRef PubMed.
- M. B. Smith and J. Michl, Annu. Rev. Phys. Chem., 2013, 64, 361–386 CrossRef PubMed.
- D. N. Congreve, J. Lee, N. J. Thompson, E. Hontz, S. R. Yost, P. D. Reusswig, M. E. Bahlke, S. Reineke, T. V. Voorhis and M. A. Baldo, Science, 2013, 340, 334–337 CrossRef PubMed.
- S. R. Yost, J. Lee, M. W. B. Wilson, T. Wu, D. P. McMahon, R. R. Parkhurst, N. J. Thompson, D. N. Congreve, A. Rao, K. Johnson, M. Y. Sfeir, M. G. Bawendi, T. M. Swager, R. H. Friend, M. A. Baldo and T. V. Voorhis, Nat. Chem., 2014, 6, 492 CrossRef PubMed.
- J. Jortner, J. Chem. Phys., 1976, 64, 4860–4867 CrossRef.
- B. Xiang, R. F. Ribeiro, A. D. Dunkelberger, J. Wang, Y. Li, B. S. Simpkins, J. C. Owrutsky, J. Yuen-Zhou and W. Xiong, Proc. Natl. Acad. Sci. U. S. A., 2018, 201722063 Search PubMed.
- C. H. Henry and J. J. Hopfield, Phys. Rev. Lett., 1965, 15, 964–966 CrossRef.
- D. L. Mills and E. Burstein, Rep. Prog. Phys., 1974, 37, 817 CrossRef.
- V. N. Denisov, B. N. Mavrin and V. B. Podobedov, Phys. Rep., 1987, 151, 1–92 CrossRef.
- A. Shalabney, J. George, J. Hutchison, G. Pupillo, C. Genet and T. W. Ebbesen, Nat. Commun., 2015, 6, 5981 CrossRef PubMed.
- J. George, A. Shalabney, J. A. Hutchison, C. Genet and T. W. Ebbesen, J. Phys. Chem. Lett., 2015, 6, 1027–1031 CrossRef PubMed.
- J. P. Long and B. S. Simpkins, ACS Photonics, 2015, 2, 130–136 CrossRef.
- M. Muallem, A. Palatnik, G. D. Nessim and Y. R. Tischler, Ann. Phys., 2016, 528, 313–320 CrossRef.
- M. Muallem, A. Palatnik, G. D. Nessim and Y. R. Tischler, J. Phys. Chem. Lett., 2016, 7, 2002–2008 CrossRef PubMed.
- S. R. Casey and J. R. Sparks, J. Phys. Chem. C, 2016, 120, 28138–28143 CrossRef.
- R. M. A. Vergauwe, J. George, T. Chervy, J. A. Hutchison, A. Shalabney, V. Y. Torbeev and T. W. Ebbesen, J. Phys. Chem. Lett., 2016, 7, 4159–4164 CrossRef PubMed.
- A. D. Dunkelberger, B. T. Spann, K. P. Fears, B. S. Simpkins and J. C. Owrutsky, Nat. Commun., 2016, 7, 13504 CrossRef PubMed.
- W. Ahn, I. Vurgaftman, A. D. Dunkelberger, J. C. Owrutsky and B. S. Simpkins, ACS Photonics, 2018, 5, 158–166 CrossRef.
- O. Kapon, R. Yitzhari, A. Palatnik and Y. R. Tischler, J. Phys. Chem. C, 2017, 121, 18845–18853 CrossRef.
- H. Memmi, O. Benson, S. Sadofev and S. Kalusniak, Phys. Rev. Lett., 2017, 118, 126802 CrossRef PubMed.
- U. Fano, Phys. Rev., 1956, 103, 1202–1218 CrossRef.
- S. Mukamel, Principles of Nonlinear Optical Spectroscopy, Oxford University Press on Demand, 1999 Search PubMed.
- P. Hamm and M. Zanni, Concepts and Methods of 2D Infrared Spectroscopy, Cambridge University Press, 2011 Search PubMed.
- T. Chervy, A. Thomas, E. Akiki, R. M. A. Vergauwe, A. Shalabney, J. George, E. Devaux, J. A. Hutchison, C. Genet and T. W. Ebbesen, ACS Photonics, 2018, 5, 217–224 CrossRef.
- G. Herzberg and J. Spinks, Molecular Spectra and Molecular Structure: Infrared and Raman Spectra of Polyatomic Molecules, Van Nostrand, 1939 Search PubMed.
- J. Yuen-Zhou, J. Krich, A. Aspuru-Guzik, I. Kassal and A. Johnson, Ultrafast Spectroscopy: Quantum Information and Wavepackets, Institute of Physics Publishing, 2014 Search PubMed.
- S. Valleau, S. K. Saikin, M.-H. Yung and A. A. Guzik, J. Chem. Phys., 2012, 137, 034109 CrossRef PubMed.
- M. Hertzog, P. Rudquist, J. A. Hutchison, J. George, T. W. Ebbesen and K. Börjesson, Chem.–Eur. J., 2017, 23, 18166–18170 CrossRef PubMed.
- G. Herzberg, Infrared and Raman Spectra of Polyatomic Molecules, Van Nostrand, 1968 Search PubMed.
- M. Khalil, N. Demirdöven and A. Tokmakoff, J. Phys. Chem. A, 2003, 107, 5258–5279 CrossRef.
- K. Ishii, S. Takeuchi and T. Tahara, J. Chem. Phys., 2009, 131, 044512 CrossRef PubMed.
- C. Ciuti, G. Bastard and I. Carusotto, Phys. Rev. B, 2005, 72, 115303 CrossRef.
- C. Ciuti and I. Carusotto, Phys. Rev. A, 2006, 74, 033811 CrossRef.
- A. Moroz, Ann. Phys., 2014, 340, 252–266 Search PubMed.
- S. Kéna-Cohen, S. A. Maier and D. D. C. Bradley, Adv. Opt. Mater., 2013, 1, 827–833 CrossRef.
- S. Balci, Opt. Lett., 2013, 38, 4498–4501 CrossRef PubMed.
- S. Gambino, M. Mazzeo, A. Genco, O. Di Stefano, S. Savasta, S. Patanè, D. Ballarini, F. Mangione, G. Lerario, D. Sanvitto and G. Gigli, ACS Photonics, 2014, 1, 1042–1048 CrossRef.
- J. George, S. Wang, T. Chervy, A. Canaguier-Durand, G. Schaeffer, J.-M. Lehn, J. A. Hutchison, C. Genet and T. W. Ebbesen, Faraday Discuss., 2015, 178, 281–294 RSC.
- J. George, T. Chervy, A. Shalabney, E. Devaux, H. Hiura, C. Genet and T. W. Ebbesen, Phys. Rev. Lett., 2016, 117, 153601 CrossRef PubMed.
- S. De Liberato, Phys. Rev. Lett., 2014, 112, 016401 CrossRef PubMed.
- D. Hagenmüller, J. Schachenmayer, S. Schütz, C. Genes and G. Pupillo, Phys. Rev. Lett., 2017, 119, 223601 CrossRef PubMed.
- M. A. Sentef, M. Ruggenthaler and A. Rubio, 2018, arXiv:1802.09437 [cond-mat, physics:quant-ph].
- J. Flick, M. Ruggenthaler, H. Appel and A. Rubio, Proc. Natl. Acad. Sci. U. S. A., 2017, 114, 3026–3034 CrossRef PubMed.
- H. L. Luk, J. Feist, J. J. Toppari and G. Groenhof, J. Chem. Theory Comput., 2017, 13, 4324–4335 CrossRef PubMed.
- O. Vendrell, Chem. Phys., 2018, 509, 55–65 CrossRef.
- J. E. Subotnik, A. Jain, B. Landry, A. Petit, W. Ouyang and N. Bellonzi, Annu. Rev. Phys. Chem., 2016, 67, 387–417 CrossRef PubMed.
- N. Makri, J. Math. Phys., 1995, 36, 2430–2457 CrossRef.
- Y. Tanimura, J. Phys. Soc. Jpn., 2006, 75, 082001 CrossRef.
| This journal is © The Royal Society of Chemistry 2018 |

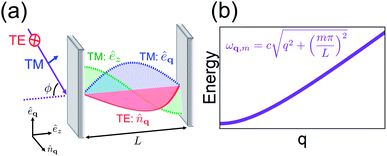
![[n with combining circumflex]](https://www.rsc.org/images/entities/i_char_006e_0302.gif)