Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Counting charges on membrane-bound peptides†
Alicia C.
McGeachy‡
 a,
Emily R.
Caudill‡
a,
Emily R.
Caudill‡
 b,
Dongyue
Liang‡
b,
Qiang
Cui
b,
Dongyue
Liang‡
b,
Qiang
Cui
 bd,
Joel A.
Pedersen
bd,
Joel A.
Pedersen
 bcef and
Franz M.
Geiger
bcef and
Franz M.
Geiger
 *a
*a
aDepartment of Chemistry, Northwestern University, 2145 Sheridan Road, Evanston, IL 60660, USA. E-mail: geigerf@chem.northwestern.edu
bDepartment of Chemistry, University of Wisconsin-Madison, 1101 University Avenue, Madison, WI 53706, USA
cEnvironmental Chemistry and Technology Program, University of Wisconsin-Madison, 660 North Park Street, Madison, WI 53706, USA
dDepartment of Chemistry, Boston University, 590 Commonwealth Ave., Boston, MA 02215, USA
eDepartment of Soil Science, University of Wisconsin-Madison, 1525 Observatory Drive, Madison, WI 53706, USA
fDepartment of Civil & Environmental Engineering, University of Wisconsin-Madison, 1415 Engineering Drive, Madison, WI 53706, USA
First published on 3rd April 2018
Abstract
Quantifying the number of charges on peptides bound to interfaces requires reliable estimates of (i) surface coverage and (ii) surface charge, both of which are notoriously difficult parameters to obtain, especially at solid/water interfaces. Here, we report the thermodynamics and electrostatics governing the interactions of L-lysine and L-arginine octamers (Lys8 and Arg8) with supported lipid bilayers prepared from a 9![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 mixture of 1,2-dimyristoyl-sn-glycero-3-phosphocholine (DMPC) and 1,2-dimyristoyl-sn-glycero-3-phospho-(1′-rac-glycerol) (sodium salt) (DMPG) from second harmonic generation (SHG) spectroscopy, quartz crystal microbalance with dissipation monitoring (QCM-D) and nanoplasmonic sensing (NPS) mass measurements, and atomistic simulations. The combined SHG/QCM-D/NPS approach provides interfacial charge density estimates from mean field theory for the attached peptides that are smaller by a factor of approximately two (0.12 ± 0.03 C m−2 for Lys8 and 0.10 ± 0.02 C m−2 for Arg8) relative to poly-L-lysine and poly-L-arginine. These results, along with atomistic simulations, indicate that the surface charge density of the supported lipid bilayer is neutralized by the attached cationic peptides. Moreover, the number of charges associated with each attached peptide is commensurate with those found in solution; that is, Lys8 and Arg8 are fully ionized when attached to the bilayer. Computer simulations indicate Lys8 is more likely than Arg8 to “stand-up” on the surface, interacting with lipid headgroups through one or two sidechains while Arg8 is more likely to assume a “buried” conformation, interacting with the bilayer through up to six sidechains. Analysis of electrostatic potential and charge distribution from atomistic simulations suggests that the Gouy–Chapman model, which is widely used for mapping surface potential to surface charge, is semi-quantitatively valid; despite considerable orientational preference of interfacial water, the apparent dielectric constant for the interfacial solvent is about 30, due to the thermal fluctuation of the lipid–water interface.
1 mixture of 1,2-dimyristoyl-sn-glycero-3-phosphocholine (DMPC) and 1,2-dimyristoyl-sn-glycero-3-phospho-(1′-rac-glycerol) (sodium salt) (DMPG) from second harmonic generation (SHG) spectroscopy, quartz crystal microbalance with dissipation monitoring (QCM-D) and nanoplasmonic sensing (NPS) mass measurements, and atomistic simulations. The combined SHG/QCM-D/NPS approach provides interfacial charge density estimates from mean field theory for the attached peptides that are smaller by a factor of approximately two (0.12 ± 0.03 C m−2 for Lys8 and 0.10 ± 0.02 C m−2 for Arg8) relative to poly-L-lysine and poly-L-arginine. These results, along with atomistic simulations, indicate that the surface charge density of the supported lipid bilayer is neutralized by the attached cationic peptides. Moreover, the number of charges associated with each attached peptide is commensurate with those found in solution; that is, Lys8 and Arg8 are fully ionized when attached to the bilayer. Computer simulations indicate Lys8 is more likely than Arg8 to “stand-up” on the surface, interacting with lipid headgroups through one or two sidechains while Arg8 is more likely to assume a “buried” conformation, interacting with the bilayer through up to six sidechains. Analysis of electrostatic potential and charge distribution from atomistic simulations suggests that the Gouy–Chapman model, which is widely used for mapping surface potential to surface charge, is semi-quantitatively valid; despite considerable orientational preference of interfacial water, the apparent dielectric constant for the interfacial solvent is about 30, due to the thermal fluctuation of the lipid–water interface.
I. Introduction
Peptides and their interactions with biological and engineered membranes are of importance in the development of antimicrobial surfaces and therapeutics,1–6 non-viral vectors,7–12 layer-by-layer thin films,13–15 and for understanding the progression of many neurodegenerative diseases.16,17 Cell penetrating peptides containing cationic amino acids such as arginine and lysine can be used to cross cell membranes18 and deliver compounds to the cell interior by exploiting the surface charge of biological membranes.9 Small peptides also provide an opportunity to probe how short segments of polycations may interact with surfaces, with direct relevance to understanding how engineered nanomaterials, often manufactured with polycationic wrappings, interact with their environment.19,20 Despite the importance of charge density in these cases, a need remains to quantify polypeptide/membrane interactions from a perspective of the number of charges present at interfaces and the extent to which these charges are subject to contact ion pairing or pKa shifts.21–23 Indeed, the ability to “count” the number of charges on peptides attached to solid or soft matter surfaces, especially in a label-free fashion, would represent a significant step towards understanding, controlling, and predicting peptide–surface interactions. However, doing so requires reliable estimates of (i) surface coverage and (ii) surface charge, both of which are notoriously difficult parameters to obtain at solid/water interfaces, especially if one wishes to avoid complications commonly associated with the use of external labels.Recent mechanistic studies pairing molecular dynamic simulations and fluorescence assays have shown that arginine nonamers bind to lipid bilayers with a higher degree of cooperativity than do lysine nonamers,21 possibly explaining the cell-penetrating effectiveness of peptides containing arginine groups.18 Other studies of peptide interactions with lipid bilayers and cellular surfaces have reported on concomitant structural2,24–26 and electrostatic potential changes.8,21,27 The recent work by Cremer and co-workers employed a pH-sensitive fluorescence assay to provide qualitative and semi-quantitative information about the binding of lysine and arginine nonamers to supported lipid bilayers formed from zwitterionic (phosphatidylcholine, PC) and negatively charged (phosphatidylglycerol, PG) lipids on the basis of changes in local proton concentration upon nonamer adsorption.21 However, the surface charge density of the bilayer and those of the attached oligomers was not provided. To this end, the mass of the attached peptides and the interfacial charge density are necessary, albeit elusive, parameters which we focus on here.
Our present work combines estimates of interfacial mass with nonlinear spectroscopic studies of interfacial electrostatics and atomistic simulations of octamers of lysine (Lys8) and arginine (Arg8) interacting with supported lipid bilayers used as idealized model systems mimicking some aspects of biological membranes (see Scheme 1). These peptides are amenable to investigations by atomistic computer simulations, which we employ to obtain further mechanistic information on the peptide–bilayer interactions.
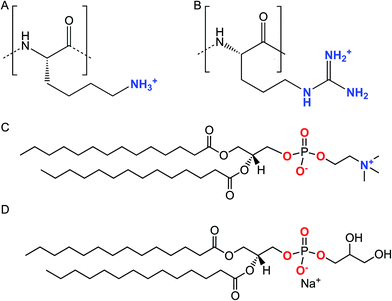 | ||
| Scheme 1 Chemical structures of the lysine (A) and arginine (B) repeat units in Lys8 and Arg8. Chemical structures of DMPC (C) and DMPG (D). | ||
We assess attached mass using acoustic and optical sensing techniques which are commonly employed to monitor the adsorption of biomacromolecules to surfaces,28–33 including cell surface models.11,34–36 Quartz crystal microbalance with dissipation monitoring (QCM-D) is used to obtain the acoustic mass of the attached oligomers (including the mass of dynamically coupled water).29 Simultaneous optical sensing by localized surface plasmon resonance spectroscopy (LSPR) yields estimates of the optical (solvent-free) mass of adsorbed species. Using this combined acoustic and optical sensing approach, we report on the water contents of oligomer films adsorbed to the supported lipid bilayer surface. The interfacial charge density and potentials and free adsorption energies are estimated by second harmonic generation spectroscopy (SHG), specifically using the Eisenthal χ(3) method.37,38 This coherent nonlinear optical technique has been used previously to estimate interfacial charge densities and potentials, as well as free energies of adsorption and ion pairing/pKa shifts for peptides,8 polycations,39 and anionic and cationic engineered nanoparticles40,41 and nanosheets42,43 interacting with model biological surfaces. Analysis of electrostatic potential and charge distribution from atomistic simulations helps evaluate mean-field models (e.g., Gouy–Chapman)44 commonly used to map surface potential through the Eisenthal χ(3) method to an apparent surface charge density, when the interface is rough at the molecular scale.
II. Experimental methods
A. Oligopeptide and lipid vesicle preparation
Lys8 and Arg8 were synthesized by and purchased from GenScript (Piscataway, NJ, purity ≥ 98%). Powders of Lys8 and Arg8 were stored in sealed plastic vials at −20 °C prior to use and were used without further purification. Powders (∼50 mg) were dissolved in 50–100 μL of ultrapure water (>18 MΩ cm; GenPure Pro or Millipore, Thermo Scientific) containing 0.001 M NaCl and vortexed, producing solutions with concentrations on the order of hundreds of mM. Lower concentrations were achieved through serial dilution. These stock solutions were then covered with Parafilm and stored in glass vials or microcentrifuge tubes at 4 °C. Immediately before use, the appropriate volume of oligomer solution was diluted to the desired concentration in 0.1 M NaCl buffered to pH 7.4 with 0.01 M Tris.Small unilamellar vesicles were prepared at 9![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 molar ratios from 1,2-dimyristoyl-sn-glycero-3-phosphocholine (DMPC, Avanti Polar Lipids) and 1,2-dimyristoyl-sn-glycero-3-phospho-(1′-rac-glycerol) (sodium salt) (DMPG, Avanti Polar Lipids) as previously described.45,46 Here, we made the following modifications to our previously published method: lipid films were reconstituted with 0.001 M NaCl buffered to pH 7.4 with 0.01 M Tris, vortexed, sonicated for 30 min, and subjected to three freeze–thaw cycles by freezing in liquid N2 and thawing in a bath sonicator. Lipids were mechanically extruded as previously described.45,46 Immediately before use, extruded lipids were diluted to 0.5 mg mL−1 for SHG experiments or 0.125 mg mL−1 for QCM-D/NPS experiments in solutions composed of 0.1 M or in 0.15 M NaCl containing 0.005 M CaCl2, and buffered to pH 7.4 with 0.01 M Tris. Briefly, SLBs were formed via the vesicle fusion method. Specific experimental details are provided in the ESI.† For reference, all experiments described in the remainder of the article employed solutions buffered to pH 7.4 with 0.01 M Tris in the presence of 0.1 M NaCl.
1 molar ratios from 1,2-dimyristoyl-sn-glycero-3-phosphocholine (DMPC, Avanti Polar Lipids) and 1,2-dimyristoyl-sn-glycero-3-phospho-(1′-rac-glycerol) (sodium salt) (DMPG, Avanti Polar Lipids) as previously described.45,46 Here, we made the following modifications to our previously published method: lipid films were reconstituted with 0.001 M NaCl buffered to pH 7.4 with 0.01 M Tris, vortexed, sonicated for 30 min, and subjected to three freeze–thaw cycles by freezing in liquid N2 and thawing in a bath sonicator. Lipids were mechanically extruded as previously described.45,46 Immediately before use, extruded lipids were diluted to 0.5 mg mL−1 for SHG experiments or 0.125 mg mL−1 for QCM-D/NPS experiments in solutions composed of 0.1 M or in 0.15 M NaCl containing 0.005 M CaCl2, and buffered to pH 7.4 with 0.01 M Tris. Briefly, SLBs were formed via the vesicle fusion method. Specific experimental details are provided in the ESI.† For reference, all experiments described in the remainder of the article employed solutions buffered to pH 7.4 with 0.01 M Tris in the presence of 0.1 M NaCl.
B. Determination of Lys8 and Arg8 surface mass densities
Our combined QCM-D and NPS setup allows us to simultaneously determine acoustic and optical surface mass densities of the lipid bilayers and the attached peptides. QCM-D measures changes in the resonance frequency (Δfν) and energy dissipation (ΔDν) of the fundamental frequency and odd harmonics (ν = 3–11) of a (coated) AT-cut piezoelectric quartz crystal caused by interaction with an analyte.47 The acoustic mass sensed by QCM-D includes the mass of the analyte and that of any dynamically coupled solvent. The model used to estimate acoustic mass from the QCM-D frequency and dissipation response depends on the nature of the adlayer and the dissipation response.48 For rigidly coupled adlayers (taken as those with ΔDν/(Δfν/ν) ≪ 0.4 × 10−6 Hz−1),48 the acoustic surface mass density (ΔΓQCM-D) can be estimated here for the supported lipid bilayers from the Sauerbrey relation:48,49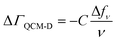 | (1) |
Nanoplasmonic sensing relies on the sensitivity to changes in local refractive index of the localized surface plasmon resonance produced by illumination of noble metal nanoparticles.51 In the combined QCM-D/NPS setup employed, an array of nanoplasmonic gold discs embedded in the QCM-D sensor coating are illuminated in reflection mode and changes in the wavelength of maximum extinction (Δλmax) are monitored. The de Feijter equation52 is used here to estimate optical surface mass density (ΔΓLSPR) from Δλmax:53
 | (2) |
The combined QCM-D/NPS setup was used to investigate the association of Lys8 and Arg8 with supported lipid bilayers formed via vesicle fusion from 9![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 DMPC/DMPG vesicles as described in the ESI.† For the Lys8 and Arg8 adlayers on supported lipid bilayers, ΔDν/(Δfν/ν) values did not satisfy the Sauerbrey relation (ΔDν/(Δfν/ν) ≪ 0.4 × 10−6 Hz−1). We therefore calculated acoustic masses of Lys8 and Arg8 adlayers on supported lipid bilayers using the Kelvin–Voigt viscoelastic model50 as implemented in QTools software (Version 3.0, Biolin Scientific). The bulk liquid phase was treated as a Newtonian fluid with a density of 1000 kg m−3 and dynamic viscosity of 0.001 kg m−1 s−1. Details on the analysis of the NPS data are presented in the ESI.†
1 DMPC/DMPG vesicles as described in the ESI.† For the Lys8 and Arg8 adlayers on supported lipid bilayers, ΔDν/(Δfν/ν) values did not satisfy the Sauerbrey relation (ΔDν/(Δfν/ν) ≪ 0.4 × 10−6 Hz−1). We therefore calculated acoustic masses of Lys8 and Arg8 adlayers on supported lipid bilayers using the Kelvin–Voigt viscoelastic model50 as implemented in QTools software (Version 3.0, Biolin Scientific). The bulk liquid phase was treated as a Newtonian fluid with a density of 1000 kg m−3 and dynamic viscosity of 0.001 kg m−1 s−1. Details on the analysis of the NPS data are presented in the ESI.†
C. SHG laser system and SHG χ(3) theory
Our SHG system, experimental setup, and analysis of the χ(3) datasets have been previously described.39,45 Briefly, incident light (800 nm, 0.5 W, 120 fs pulse duration, 80 MHz reparation rate, s-in/all-out polarization combination) is focused onto the fused silica/bilayer/water interface near the angle of total internal reflection. A brief overview regarding SHG from charged interfaces is provided in the accompanying ESI† and more detailed work is published elsewhere.38,54–57SHG χ(3) measurements lend insight into binding thermodynamics and electrostatics.8,38,39,58 The second harmonic process is a second-order nonlinear optical process and as such, is not generally allowed in centrosymmetric systems under the electric dipole approximation. SHG signal intensity is directly proportional to the electric field generated at the second harmonic as shown in eqn (3),
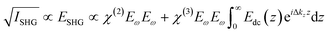 | (3) |
The SHG intensity from an initially negatively charged surface decreases upon cation adsorption, as the surface potential is rendered less negative, according to:
| ESHG ∝ A + BΦ0 | (4) |
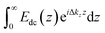 . The SHG adsorption isotherms were generated and analyzed largely as described previously,39,72 but employed the Hill model as discussed in the ESI.†
. The SHG adsorption isotherms were generated and analyzed largely as described previously,39,72 but employed the Hill model as discussed in the ESI.†
D. Molecular dynamics (MD) simulations
To provide additional structural information on the peptide/bilayer interaction sites and the conformations assumed by the peptides upon attachment, atomistic molecular dynamics simulations were conducted using the CHARMM36 (ref. 73–75) force field to investigate Lys8 and Arg8 interacting with either a DMPC or a 9![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 DMPC/DMPG lipid bilayer; note that the NBFIX76 modification to the Lennard-Jones interactions associated with ions was applied to ensure proper description of ion adsorption to anionic lipids. Additionally, the simulations provided guidance to the analysis of interfacial charge density based on surface potential. The lipid bilayers were prepared with the CHARMM-GUI77 input generator. Each system had a starting dimension of 10 × 10 × 10 nm3, consisting of 288 DMPC, 32 DMPG and 36 peptide octamers. This initial peptide
1 DMPC/DMPG lipid bilayer; note that the NBFIX76 modification to the Lennard-Jones interactions associated with ions was applied to ensure proper description of ion adsorption to anionic lipids. Additionally, the simulations provided guidance to the analysis of interfacial charge density based on surface potential. The lipid bilayers were prepared with the CHARMM-GUI77 input generator. Each system had a starting dimension of 10 × 10 × 10 nm3, consisting of 288 DMPC, 32 DMPG and 36 peptide octamers. This initial peptide![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) lipid ratio was chosen based on our previous study of poly-allylamine hydrochloride (PAH) binding to the same lipid bilayer systems. Moreover, having multiple peptides adsorbed onto the lipid bilayer facilitated the exploration of the conformation that the peptides adopt upon adsorption. After neutralization, 0.15 M KCl was added to each system, and the system was solvated with TIP3P water. The NAMD78 and OpenMM79,80 packages were used for production runs on CPU and GPU, respectively; input files generated by CHARMM-GUI were used to ensure consistency among simulations using different hardware and software. For the NAMD simulations, the particle mesh Ewald (PME)81 method was applied with a grid size of 108, 108 and 90 for X, Y, and Z dimensions, respectively. For the peptides, each production run was executed over 500 ns. To evaluate the interfacial electrostatics, additional simulations (50 ns for production) were run for the 9
lipid ratio was chosen based on our previous study of poly-allylamine hydrochloride (PAH) binding to the same lipid bilayer systems. Moreover, having multiple peptides adsorbed onto the lipid bilayer facilitated the exploration of the conformation that the peptides adopt upon adsorption. After neutralization, 0.15 M KCl was added to each system, and the system was solvated with TIP3P water. The NAMD78 and OpenMM79,80 packages were used for production runs on CPU and GPU, respectively; input files generated by CHARMM-GUI were used to ensure consistency among simulations using different hardware and software. For the NAMD simulations, the particle mesh Ewald (PME)81 method was applied with a grid size of 108, 108 and 90 for X, Y, and Z dimensions, respectively. For the peptides, each production run was executed over 500 ns. To evaluate the interfacial electrostatics, additional simulations (50 ns for production) were run for the 9![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 DMPC/DMPG system in which the z-dimension of the box was expanded to 18 nm so as to ensure a proper bulk region in the simulation box. Peptides that dissociated from the surface during the small-box simulations were removed in the large-box simulations (the new systems contain 16/5 Arg8/Lys8, leading to a surface binding density consistent with experimental measurements, see below), and the number of ions was adjusted accordingly based on the salt concentration of 0.15 M NaCl; weak harmonic positional restraints (with a force constant of 10 kJ nm−2) were applied to the amine nitrogen of the Lys sidechains that were bound to the lipid phosphate by the end of the production run for the small-box simulations to prevent any further peptide dissociation in the large-box simulations. The temperature for production run was set to 303.15 K, and NPT ensemble is applied with the x, y dimensions kept constant for all the systems studied here. For the numerical details for the analysis of interfacial electrostatic potential and charge density, see the ESI.†
1 DMPC/DMPG system in which the z-dimension of the box was expanded to 18 nm so as to ensure a proper bulk region in the simulation box. Peptides that dissociated from the surface during the small-box simulations were removed in the large-box simulations (the new systems contain 16/5 Arg8/Lys8, leading to a surface binding density consistent with experimental measurements, see below), and the number of ions was adjusted accordingly based on the salt concentration of 0.15 M NaCl; weak harmonic positional restraints (with a force constant of 10 kJ nm−2) were applied to the amine nitrogen of the Lys sidechains that were bound to the lipid phosphate by the end of the production run for the small-box simulations to prevent any further peptide dissociation in the large-box simulations. The temperature for production run was set to 303.15 K, and NPT ensemble is applied with the x, y dimensions kept constant for all the systems studied here. For the numerical details for the analysis of interfacial electrostatic potential and charge density, see the ESI.†
III. Results and discussion
A. Peptide mass adsorbed to bilayers formed from 9![[thin space (1/6-em)]](https://www.rsc.org/images/entities/h3_char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/h3_char_2009.gif) 1 DMPC/DMPG
1 DMPC/DMPG
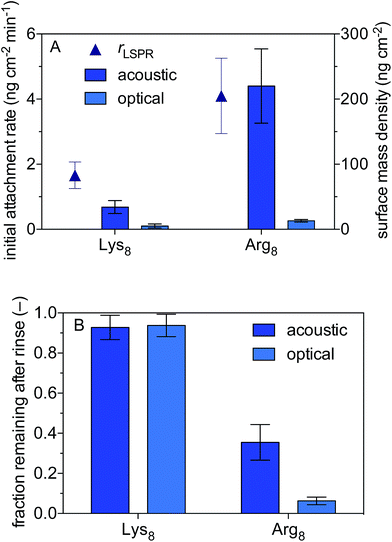
We use a combined QCM-D and NPS setup to examine the initial rates of Lys8 and Arg8 attachment to supported lipid bilayers formed from 9![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 DMPC/DPMG, the surface mass densities of octapeptides adsorbed onto the supported lipid bilayers, and the extent of reversibility (Fig. 1). Representative QCM-D and LSPR traces are presented in Fig. S2 and S3,† respectively. The initial rate of octapeptide attachment to 9
1 DMPC/DPMG, the surface mass densities of octapeptides adsorbed onto the supported lipid bilayers, and the extent of reversibility (Fig. 1). Representative QCM-D and LSPR traces are presented in Fig. S2 and S3,† respectively. The initial rate of octapeptide attachment to 9![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 DMPC/DMPC bilayers was larger for Arg8 than for Lys8 by a factor of 2.5 ± 0.9 (Fig. 1A) indicating that Arg8 had a higher affinity for the bilayer than did Lys8. Likewise, the maximum acoustic and optical surface mass densities attained by Arg8 were larger than those of Lys8 (Fig. 1A, Table 1). The maximum optical surface mass densities of Lys8 and Arg8 correspond to 3 ± 0.3 × 1012 and 5.7 ± 0.63 × 1012 molecules per cm2. If we assume that the peptides laid down individually on the bilayer, approximately 12 ± 1.3% and 27 ± 3.0% of the bilayer surface would be occupied by Lys8 and Arg8, respectively. Calculation details are provided in the ESI.†
1 DMPC/DMPC bilayers was larger for Arg8 than for Lys8 by a factor of 2.5 ± 0.9 (Fig. 1A) indicating that Arg8 had a higher affinity for the bilayer than did Lys8. Likewise, the maximum acoustic and optical surface mass densities attained by Arg8 were larger than those of Lys8 (Fig. 1A, Table 1). The maximum optical surface mass densities of Lys8 and Arg8 correspond to 3 ± 0.3 × 1012 and 5.7 ± 0.63 × 1012 molecules per cm2. If we assume that the peptides laid down individually on the bilayer, approximately 12 ± 1.3% and 27 ± 3.0% of the bilayer surface would be occupied by Lys8 and Arg8, respectively. Calculation details are provided in the ESI.†
| Binding constant, Kads [×106 M−1] | Adsorption free energy, ΔGads [kJ mol−1] | Surface charge density, σ [C m−2] | Hill coefficient, n | Acoustica and optical mass density [ng cm−2] | % ionization | |
|---|---|---|---|---|---|---|
| a Maximum adsorbed acoustic mass at from viscoelastic modeling of 7th, 9th, 11th harmonics prior to rinsing with peptide-free buffer. | ||||||
| Arg8 | 1.6 ± 0.4 | −45 ± 1 | 0.10 ± 0.02 | 0.54 ± 0.09 | 210 ± 56 | ∼100 |
| 13 ± 2 | ||||||
| Lys8 | 1.0 ± 0.3 | −44 ± 1 | 0.12 ± 0.03 | 0.52 ± 0.09 | 34 ± 10 | ∼100 |
| 5 ± 3 | ||||||
LSPR measurements indicate that dynamically coupled water contributes considerably to the overall acoustic mass estimated by QCM-D for both peptides. In fact, a comparison of the acoustic and optical surface mass densities for Lys8 and Arg8 reveals that 83 ± 11% and 93 ± 3% of the acoustic masses is attributable to dynamically coupled water, respectively (Table S1†). Studies that employ both acoustic and optical sensing techniques find similarly high water contents for amino acids or amino acid-rich polymers adsorbed to surfaces.82,83 The large number of coupled water molecules associated with the highly charged Arg8 is likely a consequence of solvation effects which help to stabilize Arg–Arg pairs at the interface.84
After 10 min of rinsing with peptide-free buffer, we find that the attachment of both peptides is partially reversible over experimental time scales (Fig. 1) with Arg8 attachment being more reversible than that of Lys8. The Arg8 adlayer remaining after rinsing was more dissipative (ΔD7/(−Δf7/7) = 2.0 ± 0.5 × 10−6 Hz−1) and had a higher water content (99 ± 0.8%) than that of Lys8 (ΔD7/(−Δf7/7) = 0.02 ± 0.3 × 10−6 Hz−1; water content 82 ± 12%).
B. Interfacial free binding energy and cooperativity
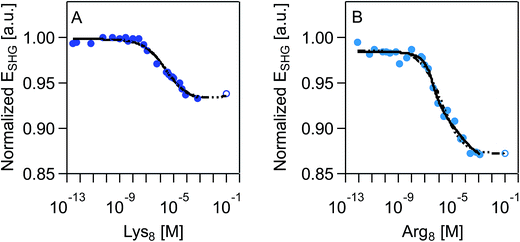
SHG adsorption isotherms for Lys8 and Arg8 were recorded by exposing supported lipid bilayers formed from 9![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 DMPC/DMPG to increasingly higher concentrations of the respective octamers. An expected outcome of these surface potential-sensitive SHG experiments is that the observed SHG signal intensity decreases as the concentration, and thus the surface coverage, of the cationic Lys8 and Arg8 increases. Fig. 2 shows that this response is indeed observed. Moreover, we observe a nearly 10% larger decrease in the SHG E-field in the case of Arg8 than Lys8, suggesting that the adsorption of Lys8 results in a smaller change in interfacial potential than Arg8. This observation is in line with previous experimental21 and theoretical85 studies of these systems, which indicate that the interfacial potential (i.e., surface charge) does indeed decrease (becoming more positive) upon exposure to lysine and arginine oligomers.
1 DMPC/DMPG to increasingly higher concentrations of the respective octamers. An expected outcome of these surface potential-sensitive SHG experiments is that the observed SHG signal intensity decreases as the concentration, and thus the surface coverage, of the cationic Lys8 and Arg8 increases. Fig. 2 shows that this response is indeed observed. Moreover, we observe a nearly 10% larger decrease in the SHG E-field in the case of Arg8 than Lys8, suggesting that the adsorption of Lys8 results in a smaller change in interfacial potential than Arg8. This observation is in line with previous experimental21 and theoretical85 studies of these systems, which indicate that the interfacial potential (i.e., surface charge) does indeed decrease (becoming more positive) upon exposure to lysine and arginine oligomers.
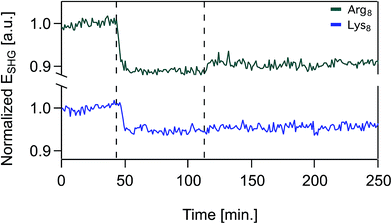
Over the timescales of our experiments, Lys8 and Arg8 interaction with the bilayer is partially reversible, as determined by SHG reversibility studies (Fig. 3 and S1A†) and confirmed by QCM-D mass estimates during (Fig. 1) and after exposure (ESI†). Yet, we cannot rule out that at t = ∞, the binding events are fully reversible. We therefore analyzed our adsorption isotherms, described next, with the caveat that full reversibility is not observed over the timescales of our experiments.
We fit our SHG adsorption isotherms using the combined Gouy–Chapman and Hill models we have used previously for polycations39 to obtain estimates (Table 1) of apparent equilibrium constants, charge densities, and Hill coefficients. The latter parameter describes the degree of cooperativity (or the lack thereof). While our isotherms approach surface saturation, due to the limited amounts of peptide available to us, complete saturation is not reached. Fitting these datasets results in large errors in the apparent equilibrium constants and charge densities likely because of difficulty achieving sufficiently high concentrations (>0.01 M) in our SHG experiments. However, prior literature indicates that saturation coverage is reached in the mM peptide concentration regime.21,86 We therefore analyzed the SHG adsorption isotherms by including one extrapolated SHG signal intensity point estimate for a peptide concentration of 0.1 M. This approach yielded similar point estimates relative to the ones obtained from fitting the isotherms while excluding the SHG signal intensity estimated for 0.1 mM peptide concentration (ESI†).
In contrast to the study by Cremer and co-workers,21 who reported significant differences in the cooperativity of adsorption of Lys9 (n = 0.22) and Arg9 (n = 0.73) to lipid bilayers formed from 9![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 molar ratios of 1-palmitoyl-2-oleoyl-sn-glycero-3-phosphocholine (POPC) and 1-palmitoyl-2-oleoyl-sn-glycero-3-phospho-(1′-rac-glycerol) (sodium salt) (POPG) (and 0.5 mol% ortho-rhodamine B which impacted at least Arg9 adsorption to POPC bilayers), we find comparable Hill coefficients of ∼0.5 (Table 1) for Lys8 and Arg8. This result suggests that the adsorption process is not cooperative for either octapeptide. The large Hill coefficient reported by Cremer and co-workers for Arg9 may be attributable to differences in bilayer fluidity between POPC/POPG and the addition of ortho-rhodamine B studied in their work in contrast to the label-free DMPC/DMPG system used here. The authors speculated that the inability of the lysine peptide to penetrate the lipid headgroup region could contribute to the apparent anti-cooperativity of lysine.21 However, we note that lower n values may also be explained by molecular heterogeneity where the experimentally derived binding curve is actually composed of an ensemble of individual binding curves.87 Indeed, such heterogeneity could arise from a number of factors including those introduced by differences in bilayer phase (liquid versus gel crystalline phases) and propensity and favorability of the octamers to bind to PC and/or PG lipid headgroups.
1 molar ratios of 1-palmitoyl-2-oleoyl-sn-glycero-3-phosphocholine (POPC) and 1-palmitoyl-2-oleoyl-sn-glycero-3-phospho-(1′-rac-glycerol) (sodium salt) (POPG) (and 0.5 mol% ortho-rhodamine B which impacted at least Arg9 adsorption to POPC bilayers), we find comparable Hill coefficients of ∼0.5 (Table 1) for Lys8 and Arg8. This result suggests that the adsorption process is not cooperative for either octapeptide. The large Hill coefficient reported by Cremer and co-workers for Arg9 may be attributable to differences in bilayer fluidity between POPC/POPG and the addition of ortho-rhodamine B studied in their work in contrast to the label-free DMPC/DMPG system used here. The authors speculated that the inability of the lysine peptide to penetrate the lipid headgroup region could contribute to the apparent anti-cooperativity of lysine.21 However, we note that lower n values may also be explained by molecular heterogeneity where the experimentally derived binding curve is actually composed of an ensemble of individual binding curves.87 Indeed, such heterogeneity could arise from a number of factors including those introduced by differences in bilayer phase (liquid versus gel crystalline phases) and propensity and favorability of the octamers to bind to PC and/or PG lipid headgroups.
Previous studies by McLaughlin and co-workers have reported that the incremental increase in the free energy of adsorption upon elongating Lys oligomers by one Lys residue is ∼5.9 kJ per mol per residue (similar results were noted for arginine).86,88 We therefore expect free binding energies of −5.9 kJ mol−1 × 8 = −47.2 kJ mol−1 for our octamers. Our experiments show the binding energy estimate from the isotherms is ∼−44 ± 1 kJ mol−1 and −45 ± 1 kJ mol−1 for Lys8 and Arg8, respectively. As the comparison to McLaughin's data shows, the octamers attached without much noticeable cooperativity or anti-cooperativity (2 kJ mol−1 destabilization for the octamers vs. the purely additive expectation value) in terms of the free energy of adsorption. We therefore interpret the Hill coefficients from our fits (0.5) to indicate not anti-cooperativity but instead structural heterogeneity at the interface (as observed in atomistic molecular dynamics simulations, see below), a common alternate reason for Hill coefficients smaller than unity.87,89
C. Interfacial charge densities and number of charges per attached peptide
Fitting SHG adsorption isotherms yields charge density estimates for Lys8 and Arg8 of 0.12 ± 0.03 C m−2 and 0.10 ± 0.02 C m−2, respectively. A sensitivity analysis shows that the approach is robust, as varying the value of the SHG intensity estimated for the 0.1 M peptide concentrations by 10% results in comparable charge densities, ranging from 0.02–0.16 C m−2 and 0.02–0.2 C m−2 for Lys8 and Arg8, respectively (Fig. S1†). Based on our previous estimates for the charge density of supported lipid bilayers formed from 9![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 DMPC/DMPG on fused silica (−0.1 C m−2),39,41 Lys8 and Arg8 attachment to the bilayers appears to result in charge neutralization.
1 DMPC/DMPG on fused silica (−0.1 C m−2),39,41 Lys8 and Arg8 attachment to the bilayers appears to result in charge neutralization.
Using the calculated charge densities from our SHG adsorption isotherms and the mass estimates derived from QCM-D and LPSR measurements, we provide next the lower and upper limits for the fraction of ionizable groups that remain charged upon adsorption to the membrane. Optical mass estimates correspond to surface coverages of about 1016 peptides (both Lys8 and Arg8) per m2, or 0.04 ± 0.02 C m−2 and 0.08 ± 0.01 C m−2 for Lys8 and Arg8, respectively, assuming they are fully (eight-fold) charged.
Our estimates of charge densities from the LSPR data, assuming the attached peptides are fully ionized, and the SHG experiments vary by a factor of about 3 for Lys8. In the absence of more reliable point estimates for the interfacial charge densities obtained from fitting eqn (S1) to the SHG adsorption isotherms, we cannot comment further on this difference. Taken together though, the charge density estimates from LSPR and SHG suggest that attached Lys8 and Arg8 are fully ionized under our experimental condition, consistent with their high bulk solution pKa value.90
D. Bound conformations of peptides and interfacial electrostatics from atomistic simulations
To complement and provide additional insights for the experimental results, we performed MD simulations to explore Lys8 and Arg8 adsorption to lipid bilayers formed from DMPC and 9![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
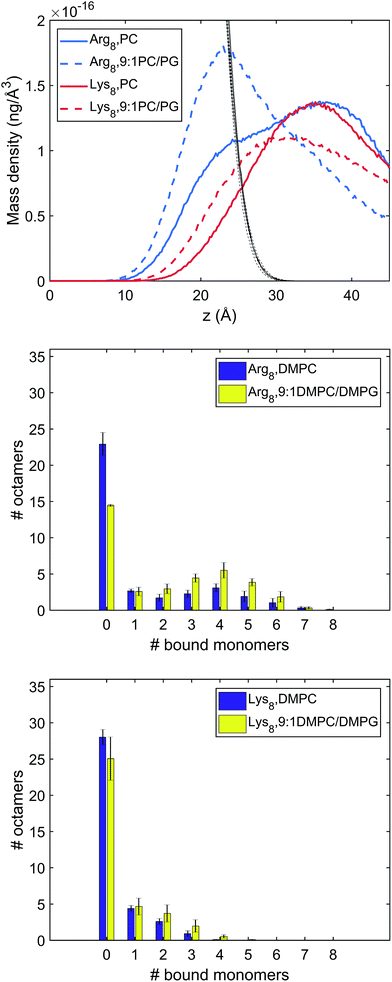
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 DMPC/DMPG. With 36 octamers included in each system, the adsorption conformations of the octamers were extensively sampled. To investigate the conformations and number of bound octamers, we calculated the mass density and binding site distribution for the systems studied (Fig. 4). In our binding site analysis, a monomer is regarded as bound to the membrane surface if the representative atom of the charged group (CZ for arginine, NZ for lysine) is within the first peak of the corresponding radial distribution function (RDF) with respect to the lipid phosphorous atom; the corresponding distances are 5.5 and 4.5 Å for the arginine and lysine monomers, respectively.
1 DMPC/DMPG. With 36 octamers included in each system, the adsorption conformations of the octamers were extensively sampled. To investigate the conformations and number of bound octamers, we calculated the mass density and binding site distribution for the systems studied (Fig. 4). In our binding site analysis, a monomer is regarded as bound to the membrane surface if the representative atom of the charged group (CZ for arginine, NZ for lysine) is within the first peak of the corresponding radial distribution function (RDF) with respect to the lipid phosphorous atom; the corresponding distances are 5.5 and 4.5 Å for the arginine and lysine monomers, respectively.
The mass and binding site distributions (see Fig. 4) indicate that Arg8 and Lys8 bind to the lipid membrane with distinct affinities and conformations. The average number of bound octamers for Arg8 and Lys8 are 13.3 ± 1.6 and 8.4 ± 1.1 for the DMPC bilayer, respectively, while they are 22.6 ± 0.1 and 11.9 ± 3.0 for the 9![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 DMPC/DMPG bilayer, respectively. While each Lys8 peptide is most likely to bind with the bilayer through one or two sidechains with the bilayer, which is qualitatively similar to observations from previous atomistic MD simulations,85 Arg8 is most likely to attach to the bilayer via 3–5 binding sidechains (Fig. 5). Examination of these snapshots also reveals stacking of Arg sidechains91 from either the same peptide or neighboring peptides, and association of Arg8 mediated by the C-terminal carboxylate group, as discussed in recent studies.92,93 These observations indicate that while Lys8 is inclined to “stand-up” on the surface, Arg8 is likely to assume a “buried” conformation, as also evident from the mass density distribution. We note that the simulated bilayers differ from the supported lipid bilayers which are experimentally studied herein. Specifically, in our experimentally evaluated systems, the peptides are expected to approach the lipid bilayer from only one face (the other face is in contact with the solid support); in the simulations, peptides were allowed to interact with both surfaces of the lipid bilayer as a way to efficiently sample multiple peptide–membrane binding conformations.
1 DMPC/DMPG bilayer, respectively. While each Lys8 peptide is most likely to bind with the bilayer through one or two sidechains with the bilayer, which is qualitatively similar to observations from previous atomistic MD simulations,85 Arg8 is most likely to attach to the bilayer via 3–5 binding sidechains (Fig. 5). Examination of these snapshots also reveals stacking of Arg sidechains91 from either the same peptide or neighboring peptides, and association of Arg8 mediated by the C-terminal carboxylate group, as discussed in recent studies.92,93 These observations indicate that while Lys8 is inclined to “stand-up” on the surface, Arg8 is likely to assume a “buried” conformation, as also evident from the mass density distribution. We note that the simulated bilayers differ from the supported lipid bilayers which are experimentally studied herein. Specifically, in our experimentally evaluated systems, the peptides are expected to approach the lipid bilayer from only one face (the other face is in contact with the solid support); in the simulations, peptides were allowed to interact with both surfaces of the lipid bilayer as a way to efficiently sample multiple peptide–membrane binding conformations.
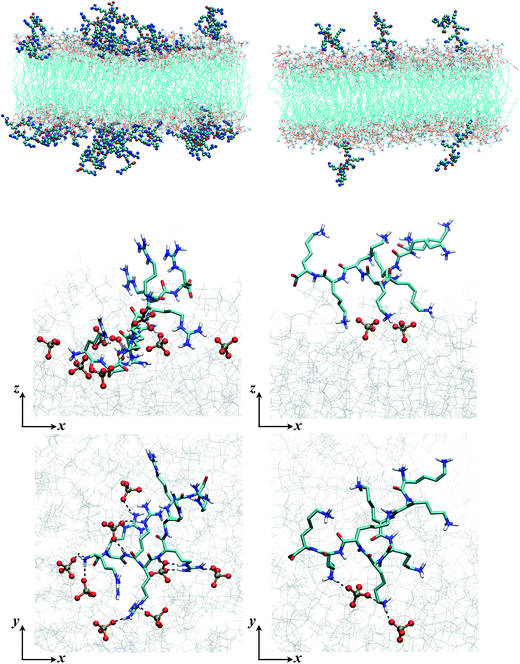 | ||
Fig. 5 Snapshots from MD simulations (Arg8/Lys8 interacting with a 9![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 DMPC/DMPG bilayer) illustrate the different binding modes of the peptides. The left column is for Arg8, and right column for Lys8. The top two rows are sideviews (showing multiple peptides and a single peptide, respectively), which illustrate that due to the different numbers of sidechains interacting with the lipids, Lys8 peptides tend to point into the solution, while Arg8 peptides lay closer to the membrane; these trends are also illustrated by the mass density distributions (Fig. 4, top panel). The bottom row contains the top view of close-ups of the binding interactions; while Arg8 are engaged with multiple phosphate groups (those within 3 Å from Arg8 are shown in CPK), only a few lipid phosphate groups interact with the Lys sidechains. 1 DMPC/DMPG bilayer) illustrate the different binding modes of the peptides. The left column is for Arg8, and right column for Lys8. The top two rows are sideviews (showing multiple peptides and a single peptide, respectively), which illustrate that due to the different numbers of sidechains interacting with the lipids, Lys8 peptides tend to point into the solution, while Arg8 peptides lay closer to the membrane; these trends are also illustrated by the mass density distributions (Fig. 4, top panel). The bottom row contains the top view of close-ups of the binding interactions; while Arg8 are engaged with multiple phosphate groups (those within 3 Å from Arg8 are shown in CPK), only a few lipid phosphate groups interact with the Lys sidechains. | ||
An explicit binding free energy simulation of Arg8/Lys8 to the lipid bilayers was not pursued here. Considering the diverse binding modes of the peptides observed in the unbiased atomistic simulations, it is not straightforward to identify a simple collective variable (e.g., the center-of-mass separation of the peptide and bilayer) that defines the bound state of the peptide while ensuring an extensive sampling of distinct peptide conformations. Nevertheless, the mass density and binding site distributions presented in Fig. 4 suggest that Arg8 tends to interact more strongly with lipid bilayers than Lys8, especially in the presence of anionic lipids which is in agreement with the conclusions drawn from other studies.88 This is also consistent with previous studies that highlighted the differences between Arg and Lys in terms of their interactions with lipid bilayers and impact on lipid structure and organization.94–97 As discussed in previous studies,84,94,98,99 the guanidinium group in the Arg sidechain is able to engage in multiple hydrogen bonding interactions with the phosphate and glycerol groups in lipids, while the amine group in Lys forms localized hydrogen-bonding interactions with phosphate; as a result, Arg is able to insert deeper into the bilayer than Lys, and poly-Arg forms multiple interactions with the lipids. For both peptides, the cationic sidechains preferentially interact with the anionic DMPG lipids compared to the zwitterionic DMPC lipids (see Fig. S6†). The similar apparent binding free energies for Arg8 and Lys8 obtained in our SHG studies likely reflects the notion that the probe depth in our SHG studies is on the order of several nanometers under the specific salt concentration, thus the amount of “bound” peptides may have included those in the interfacial region that are only weakly associated with the bilayer. Yet, we caution that the distance dependence in the SHG signal generation process from charged interfaces, which is subject to phase matching, is only now beginning to be understood.38,54,55,57,69
Despite a considerable number of peptides adsorbed on the lipid bilayer, the net charge distribution at the interface is rather small (the integrated charge density is less than 0.01 C m−2), due to the strong charge compensation by the salt ions and also oriented water molecules (see Fig. S4†). This observation is qualitatively consistent with the SHG estimated charge density, although a direct comparison is difficult since the adsorption densities in the simulation and experiment likely differ.
The microscopic simulations also provide an opportunity to evaluate the relationship between electrostatics (e.g., surface potential) and charge distribution in the interfacial region. In particular, we are interested in the quantitative accuracy of the Gouy–Chapman model,44 which is widely used to map the measured interfacial electrostatic potential to an apparent surface charge density. In the Gouy–Chapman model, the solvent is treated as a dielectric continuum with the bulk dielectric constant and considers the electrostatic interaction between only the surface charge and salt ions. Such approximations are unlikely to be valid for the lipid–water interface, where water molecules are known be strongly oriented and thus contribute significantly to interfacial electrostatics.100,101
Since systems with adsorbed peptides exhibit significant heterogeneity in the mass and charge distributions in the x, y dimensions (e.g., see Fig. 5 top row), it is not straightforward to define an interface and conduct electrostatic analysis. Thus, we focus our electrostatic potential analysis on the 9![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 DMPC/DMPG system without any peptides. Due to preferential orientation of water at the interface, the integrated charge density from the lipid center to a given distance along the membrane normal (z) has considerable contributions from water (Fig. 6 top panel). As a result, the average electrostatic potential at the interface, ϕ(z), exhibits a strong compensation between interfacial water molecules and membrane/ions (Fig. 6 middle panel). Fitting the electrostatic potential (ϕ) and integrated surface charge density (σ) for a series of z values to the Grahame equation (see discussion in ESI†) leads to an apparent dielectric constant of 27 for the solvent at the bulk water/lipid bilayer interface. This value is considerably less than the bulk dielectric constant for water (∼78 at 300 K), which is expected due to the preferential orientation for interfacial water molecules at the bilayer surface. Nevertheless, the apparent dielectric constant we find here is also substantially larger than the value (∼6) used to compute differential charge capacitance for charged solid surfaces.101 This can be explained by the considerable thermal fluctuation of the lipid/water interface, which leads to a rather broad distribution of water orientation compared to the solid/water interface.102,103 Therefore, considering the uncertainty in the surface potential measured from SHG due to the assumption of a sharp interface, the current analysis suggests that the use of Gouy–Chapman model to map the surface potential to an apparent surface charge density is justified at a semi-quantitative level.
1 DMPC/DMPG system without any peptides. Due to preferential orientation of water at the interface, the integrated charge density from the lipid center to a given distance along the membrane normal (z) has considerable contributions from water (Fig. 6 top panel). As a result, the average electrostatic potential at the interface, ϕ(z), exhibits a strong compensation between interfacial water molecules and membrane/ions (Fig. 6 middle panel). Fitting the electrostatic potential (ϕ) and integrated surface charge density (σ) for a series of z values to the Grahame equation (see discussion in ESI†) leads to an apparent dielectric constant of 27 for the solvent at the bulk water/lipid bilayer interface. This value is considerably less than the bulk dielectric constant for water (∼78 at 300 K), which is expected due to the preferential orientation for interfacial water molecules at the bilayer surface. Nevertheless, the apparent dielectric constant we find here is also substantially larger than the value (∼6) used to compute differential charge capacitance for charged solid surfaces.101 This can be explained by the considerable thermal fluctuation of the lipid/water interface, which leads to a rather broad distribution of water orientation compared to the solid/water interface.102,103 Therefore, considering the uncertainty in the surface potential measured from SHG due to the assumption of a sharp interface, the current analysis suggests that the use of Gouy–Chapman model to map the surface potential to an apparent surface charge density is justified at a semi-quantitative level.
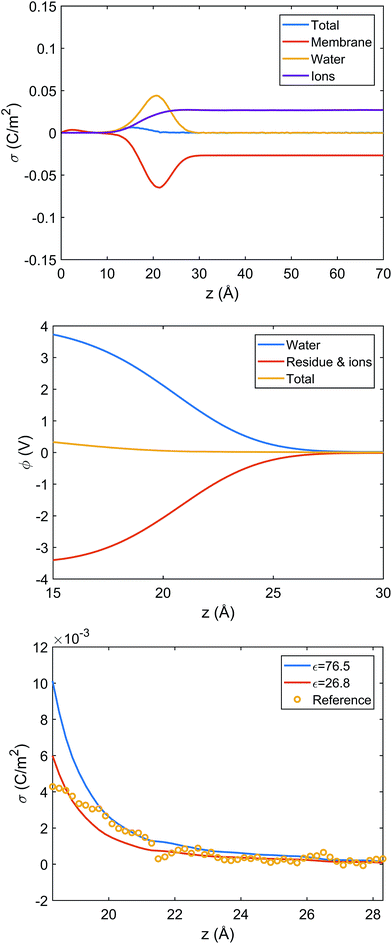 | ||
Fig. 6 Analysis of charge distribution and electrostatic potential near the lipid/water interface for a 9![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 DMPC/DMPG bilayer; corresponding analyses for the bilayer with bound Arg8 and Lys8 peptides are discussed in the ESI.† Top: Integrated charge density from the center of the bilayer (z = 0), 1 DMPC/DMPG bilayer; corresponding analyses for the bilayer with bound Arg8 and Lys8 peptides are discussed in the ESI.† Top: Integrated charge density from the center of the bilayer (z = 0), 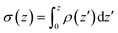 , where ρ(z′) is the charge density binned along z (the direction of the membrane normal) averaged over snapshots from MD simulations; note the significant contribution from interfacial water due to orientational preference. Middle: Electrostatic potential computed based on the charge density from MD simulations (eqn (13) in ESI†) illustrates a strong compensation between interfacial water and other components (lipids and salt ions). Bottom: Surface charge density computed with Grahame's equation and the electrostatic potential from MD simulations using different values of dielectric constant for the interfacial solvent. The open circles indicate integrated charge density from MD simulations (i.e., the top panel). Since the precise location of the interface is not straightforward to determine, calculations based on the Grahame's equation are done for a series of z values near the location of the phosphate groups (z ∼ 20 Å). See ESI† for additional discussions. , where ρ(z′) is the charge density binned along z (the direction of the membrane normal) averaged over snapshots from MD simulations; note the significant contribution from interfacial water due to orientational preference. Middle: Electrostatic potential computed based on the charge density from MD simulations (eqn (13) in ESI†) illustrates a strong compensation between interfacial water and other components (lipids and salt ions). Bottom: Surface charge density computed with Grahame's equation and the electrostatic potential from MD simulations using different values of dielectric constant for the interfacial solvent. The open circles indicate integrated charge density from MD simulations (i.e., the top panel). Since the precise location of the interface is not straightforward to determine, calculations based on the Grahame's equation are done for a series of z values near the location of the phosphate groups (z ∼ 20 Å). See ESI† for additional discussions. | ||
IV. Conclusions
In conclusion, we have presented experiments and molecular dynamics simulations aimed at providing molecular insights into the thermodynamics and electrostatics that govern the interactions of octamers of L-lysine and L-arginine (Lys8 and Arg8) with supported lipid bilayers formed from 9![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 DMPC/DMPG. Comparison of acoustic and optical surface mass density estimates for Arg8 and for Lys8 indicate the presence of considerable amounts of dynamically coupled water. These interfacial water molecules, and how they respond to varying conditions of charge density due to peptide adsorption, can be probed using surface-specific vibrational spectroscopies, such as vibrational sum frequency generation (SFG),104,105 which is underway in one of our laboratories but with a specific emphasis on properly accounting for the interfacial potential-dependent χ(3) contribution and the resulting absorptive–dispersive mixing with the χ(2) contributions.58 SHG adsorption measurements sensitive to surface potential indicate that Lys8 and Arg8 attach without exhibiting noticeable cooperativity, as indicated by Hill coefficients of 0.5 ± 0.1 for both peptides. Yet, the binding free energies (−44 ± 1 kJ mol−1 and −45 ± 1 kJ mol−1 for Lys8 and Arg8, respectively) are purely additive when compared to those reported for arginine and lysine monomers. As such, the Hill coefficients found here are likely to report on interfacial heterogeneity, and not anti-cooperativity. Further, mass estimates from QCM-D and LSPR, and MD simulations suggest that Arg8 binds to a larger extent than Lys8. We find comparable equilibrium constants for both octapeptides by SHG (n. b. we did not determine Kads by QCM-D or LSPR, due to the approximately 2 ng cm−2 sensitivity limit of QCM-D, which would prevent detection of sub-monolayer surface coverages needed to determine Kads in this case). Yet, we caution that the Kads point estimates were derived from the Langmuir-based adsorption model (Hill), whose assumptions (single site, monolayer limit, full reversibility) may not necessarily be applicable for our experimental conditions. In the molecular simulations, we found that Lys8 is more likely to “stand-up” on the bilayer surface, where it interacts through one to two sites, while Arg8 is more likely to assume a “buried” conformation, interacting with the bilayer through up to five sites. However, these simulations do not lead to a straightforward inference of the apparent “binding free energy” of Arg8vs. Lys8, which is a balance between interaction energy, number of dominant binding modes, and configurational entropy of the bound oligomer. These are the subjects of ongoing investigations by our groups.
1 DMPC/DMPG. Comparison of acoustic and optical surface mass density estimates for Arg8 and for Lys8 indicate the presence of considerable amounts of dynamically coupled water. These interfacial water molecules, and how they respond to varying conditions of charge density due to peptide adsorption, can be probed using surface-specific vibrational spectroscopies, such as vibrational sum frequency generation (SFG),104,105 which is underway in one of our laboratories but with a specific emphasis on properly accounting for the interfacial potential-dependent χ(3) contribution and the resulting absorptive–dispersive mixing with the χ(2) contributions.58 SHG adsorption measurements sensitive to surface potential indicate that Lys8 and Arg8 attach without exhibiting noticeable cooperativity, as indicated by Hill coefficients of 0.5 ± 0.1 for both peptides. Yet, the binding free energies (−44 ± 1 kJ mol−1 and −45 ± 1 kJ mol−1 for Lys8 and Arg8, respectively) are purely additive when compared to those reported for arginine and lysine monomers. As such, the Hill coefficients found here are likely to report on interfacial heterogeneity, and not anti-cooperativity. Further, mass estimates from QCM-D and LSPR, and MD simulations suggest that Arg8 binds to a larger extent than Lys8. We find comparable equilibrium constants for both octapeptides by SHG (n. b. we did not determine Kads by QCM-D or LSPR, due to the approximately 2 ng cm−2 sensitivity limit of QCM-D, which would prevent detection of sub-monolayer surface coverages needed to determine Kads in this case). Yet, we caution that the Kads point estimates were derived from the Langmuir-based adsorption model (Hill), whose assumptions (single site, monolayer limit, full reversibility) may not necessarily be applicable for our experimental conditions. In the molecular simulations, we found that Lys8 is more likely to “stand-up” on the bilayer surface, where it interacts through one to two sites, while Arg8 is more likely to assume a “buried” conformation, interacting with the bilayer through up to five sites. However, these simulations do not lead to a straightforward inference of the apparent “binding free energy” of Arg8vs. Lys8, which is a balance between interaction energy, number of dominant binding modes, and configurational entropy of the bound oligomer. These are the subjects of ongoing investigations by our groups.
The binding free energies for the peptides are about 10 kJ mol−1 smaller than those we recently reported for the polymeric counterparts poly-L-lysine (PLL) and poly-L-arginine (PLR).37 However, when we compute the free energy binding estimates for the octamers and polymers using charge, as opposed to molecular concentration, we find that this difference in binding free energy is considerably smaller (ESI Table S2†).
Upon accounting for the charge density of the bare bilayer, the attached peptides show an interfacial charge density that is approximately two times smaller (0.12 ± 0.03 C m−2 for Lys8 and 0.10 ± 0.02 C m−2 for Arg8) when compared to PLL and PLR. These results, and atomistic simulations, indicate that the surface charge density of the supported lipid bilayer is neutralized by the attached cationic peptides. Further, analysis of interfacial electrostatics and charge density based on the atomistic simulations supports that the Gouy–Chapman model used in the analysis of SHG data is appropriate at a semi-quantitative level, especially considering the subtleties associated with the χ(3) approach. From our surface mass density estimates, we find that the number of charges associated with each attached peptide is commensurate with those found in buffer solution, i.e. Lys8 and Arg8 are fully ionized when attached to the bilayer, in contrast to the large range of ionization of the attached polycationic counterparts we reported earlier.37 Overall, the electrostatic, thermodynamic, and structural information reported here provides the opportunity to further understand, control, and predict the charge–charge interactions that govern peptide/membrane interactions at biological and engineered interfaces.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work is supported by the National Science Foundation under the Center for Sustainable Nanotechnology, Grant CHE-1503408. ACM gratefully acknowledges support from the U.S. National Science Foundation Graduate Research Fellowship Program. FMG gratefully acknowledges support from a Friedrich Wilhelm Bessel Prize from the Alexander von Humboldt Foundation. JAP gratefully acknowledges support from the William Rothermel-Bascom Professorship. We thank Alexander Goodman for his contributions to data collection and analysis.References
- L. C. Salay, D. F. S. Petri, C. R. Nakaie and S. Schreier, Adsorption of the Antimicrobial Peptide Tritrpticin onto Solid and Liquid Surfaces: Ion-specific Effects, Biophys. Chem., 2015, 207, 128–134 CrossRef CAS PubMed.
- M. J. Wilhelm, M. S. Gh and H. L. Dai, Chemically Induced Changes to Membrane Permeability in Living Cells Probed with Nonlinear Light Scattering, Biochemistry, 2015, 54, 4427–4430 CrossRef CAS PubMed.
- Y. Gong, D. Andina, S. Nahar, J. C. Leroux and M. A. Gauthier, Releasable and Traceless PEGylation of Arginine-rich Antimicrobial Peptides, Chem. Sci., 2017, 8, 4082–4086 RSC.
- L. Nystrom, R. Nordstrom, J. Bramhill, B. R. Saunders, R. Alvarez-Asencio, M. W. Rutland and M. Malmsten, Factors Affecting Peptide Interactions with Surface-Bound Microgels, Biomacromolecules, 2016, 17, 669–678 CrossRef PubMed.
- R. M. Epand and R. F. Epand, Lipid Domains in Bacterial Membranes and the Action of Antimicrobial Agents, Biochim. Biophys. Acta, Biomembr., 2009, 1788, 289–294 CrossRef CAS PubMed.
- A. C. Da-Silva, S. S. Soares and G. N. M. Ferreira, Acoustic Detection of Cell Adhesion to a Coated Quartz Crystal Microbalance – Implications for Studying the Biocompatibility of Polymers, Biotechnol. J., 2013, 8, 690–698 CrossRef CAS PubMed.
- R. Szabo, F. Hudecz and F. Reig, Interfacial Interactions Between Poly-L-lysine-based Branched Polypeptides and Phospholipid Model Membranes, J. Colloid Interface Sci., 2003, 267, 18–24 CrossRef CAS PubMed.
- Y. Rao, S. J. J. Kwok, J. Lombardi, N. J. Turro and K. B. Eisenthal, Label-free Probe of HIV-1 TAT Peptide Binding to Mimetic Membranes, Proc. Natl. Acad. Sci. U. S. A., 2014, 111, 12684–12688 CrossRef CAS PubMed.
- D. D. Yi, G. M. Li, G. Li and W. Liang, Interaction of Arginine Oligomer with Model Membrane, Biochem. Biophys. Res. Commun., 2007, 359, 1024–1029 CrossRef CAS PubMed.
- S. Liu, J. X. Yang, H. Q. Ren, J. O'Keeffe-Ahern, D. Z. Zhou, H. Zhou, J. T. Chen and T. Y. Guo, Multifunctional Oligomer Incorporation: A Potent Strategy to Enhance the Transfection Activity of Poly(L-lysine), Biomater. Sci., 2016, 4, 522–532 RSC.
- H. A. Rydberg, A. Kunze, N. Carlsson, N. Altgarde, S. Svedhem and B. Norden, Peptide–Membrane Interactions of Arginine-tryptophan Peptides Probed using Quartz Crystal Microbalance with Dissipation Monitoring, Eur. Biophys. J., 2014, 43, 241–253 CrossRef CAS PubMed.
- F. Wei, H. C. Li and S. J. Ye, Specific Ion Interaction Dominates over Hydrophobic Matching Effects in Peptide–Lipid Bilayer Interactions: The Case of Short Peptide, J. Phys. Chem. C, 2013, 117, 26190–26196 CAS.
- I. C. Lee, Y. C. Liu, H. A. Tsai, C. N. Shen and Y. C. Chang, Promoting the Selection and Maintenance of Fetal Liver Stem/Progenitor Cell Colonies by Layer-by-Layer Polypeptide Tethered Supported Lipid Bilayer, ACS Appl. Mater. Interfaces, 2014, 6, 20654–20663 CAS.
- D. Butergerds, C. Cramer and M. Schoenoff, pH-Dependent Growth Laws and Viscoelastic Parameters of Poly-L-Lysine/Hyaluronic Acid Multilayers, Adv. Mater. Interfaces, 2017, 4, 9 Search PubMed.
- L. Szyk-Warszynska, K. Kilan and R. P. Socha, Characterization of casein and poly-L-arginine multilayer films, J. Colloid Interface Sci., 2014, 423, 76–84 CrossRef CAS PubMed.
- X. W. Dong, Y. X. Sun, G. H. Wei, R. Nussinov and B. Y. Ma, Binding of Protofibrillar A Beta Trimers to Lipid Bilayer Surface Enhances A beta Structural Stability and Causes Membrane Thinning, Phys. Chem. Chem. Phys., 2017, 19, 27556–27569 RSC.
- M. Hoernke, S. Tassler, B. Koksch and G. Brezesinski, Membrane Binding of Peptide Models for Early stages of Amyloid Formation: Lipid Packing Counts More than Charge, Chem. Phys. Lipids, 2016, 198, 28–38 CrossRef CAS PubMed.
- D. J. Mitchell, D. T. Kim, L. Steinman, C. G. Fathman and J. B. Rothbard, Polyarginine Enters Cells More Efficiently than Other Polycationic Homopolymers, J. Pept. Res., 2000, 56, 318–325 CrossRef CAS PubMed.
- Q. Cui, R. Hernandez, S. E. Mason, T. Fraunheim, J. A. Pedersen and F. M. Geiger, Sustainable Nanotechnology: Opportunities and Challenges for Theoretical/Computational Studies, J. Phys. Chem. B, 2016, 120, 7297–7306 CrossRef CAS PubMed.
- C. J. Murphy, A. M. Vartania, F. M. Geiger, R. J. Hamers, J. A. Pedersen, Q. Cui, C. L. Haynes, E. E. Carlson, R. Hernandez, R. D. Klaper, G. Orr and Z. Rosenzweig, Biological Responses to Engineered Nanomaterials: Needs for the Next Decade, ACS Cent. Sci., 2015, 1, 117–123 CrossRef CAS PubMed.
- A. D. Robison, S. Sun, M. F. Poyton, G. A. Johnson, J. P. Pellois, P. Jungwirth, M. Vazdar and P. S. Cremer, Polyarginine Interacts More Strongly and Cooperatively than Polylysine with Phospholipid Bilayers, J. Phys. Chem. B, 2016, 120, 9287–9296 CrossRef CAS PubMed.
- L. E. Prevette, N. C. Benish, A. R. Schoenecker and K. J. Braden, Cell-penetrating Compounds Preferentially Bind Glycosaminoglycans over Plasma Membrane Lipids in a Charge Density- and Stereochemistry-dependent Manner, Biophys. Chem., 2015, 207, 40–50 CrossRef CAS PubMed.
- A. Colomer, A. Pinazo, M. T. Garcia, M. Mitjans, M. P. Vinardell, M. R. Infante, V. Martinez and L. Perez, pH-Sensitive Surfactants from Lysine: Assessment of Their Cytotoxicity and Environmental Behavior, Langmuir, 2012, 28, 5900–5912 CrossRef CAS PubMed.
- P. Novotna and M. Urbanova, Vibrational Circular Dichroism Study of Polypeptide Model-membrane Systems, Anal. Biochem., 2012, 427, 211–218 CrossRef CAS PubMed.
- M. Reuter, C. Schwieger, A. Meister, G. Karlsson and A. Blume, Poly-L-lysines and Poly-L-arginines Induce Leakage of Negatively Charged Phospholipid Vesicles and Translocate through the Lipid Bilayer upon Electrostatic Binding to the Membrane, Biophys. Chem., 2009, 144, 27–37 CrossRef CAS PubMed.
- F. Wei, S. J. Ye, H. C. Li and Y. Luo, Phosphate Ions Promoting Association between Peptide and Modeling Cell Membrane Revealed by Sum Frequency Generation Vibrational Spectroscopy, J. Phys. Chem. C, 2013, 117, 11095–11103 CAS.
- E. E. Kooijman, D. P. Tieleman, C. Testerink, T. Munnik, D. T. S. Rijkers, K. N. J. Burger and B. de Kruijff, An Electrostatic/Hydrogen Bond Switch as the basis for the Specific Interaction of Phosphatidic Acid with Proteins, J. Biol. Chem., 2007, 282, 11356–11364 CrossRef CAS PubMed.
- A. R. Ferhan, J. A. Jackman and N. J. Cho, Integration of Quartz Crystal Microbalance-Dissipation and Reflection-Mode Localized Surface Plasmon Resonance Sensors for Biomacromolecular Interaction Analysis, Anal. Chem., 2016, 88, 12524–12531 CrossRef CAS PubMed.
- J. A. Jackman, A. R. Ferhan and N. J. Cho, Nanoplasmonic Sensors for Biointerfacial Science, Chem. Soc. Rev., 2017, 46, 3615–3660 RSC.
- S. Fukusho, H. Furusawa and Y. Okahata, In vitro Selection and Evaluation of RNA Aptamers that Recognize Arginine-rich-motif Model Peptide on a Quartz-crystal Microbalance, Chem. Commun., 2002, 88–89 RSC.
- J. N. Anker, W. P. Hall, M. P. Lambert, P. T. Velasco, M. Mrksich, W. L. Klein and R. P. Van Duyne, Detection and Identification of Bioanalytes with High Resolution LSPR Spectroscopy and MALDI Mass Spectrometry, J. Phys. Chem. C, 2009, 113, 5891–5894 CAS.
- R. M. Onorato, A. P. Yoon, J. T. Lin and G. A. Somorjai, Adsorption of Amino Acids and Dipeptides to the Hydrophobic Polystyrene Interface Studied by SFG and QCM: The Special Case of Phenylalanine, J. Phys. Chem. C, 2012, 116, 9947–9954 CAS.
- R. L. York, G. J. Holinga and G. A. Somorjai, Investigation of the Influence of Chain Length on the Interfacial Ordering of L-Lysine and L-Proline and Their Homopeptides at Hydrophobic and Hydrophilic Interfaces Studied by Sum Frequency Generation and Quartz Crystal Microbalance, Langmuir, 2009, 25, 9369–9374 CrossRef CAS PubMed.
- H. M. Hiep, T. Endo, M. Saito, M. Chikae, D. K. Kim, S. Yamamura, Y. Takamura and E. Tamiya, Label-free Detection of Melittin Binding to a Membrane using Electrochemical-localized Surface Plasmon Resonance, Anal. Chem., 2008, 80, 1859–1864 CrossRef CAS PubMed.
- C. Steinem, A. Janshoff and H. J. Galla, Evidence for Multilayer Formation of Melittin on Solid-supported Phospholipid Membranes by Shear-wave Resonator Measurements, Chem. Phys. Lipids, 1998, 95, 95–104 CrossRef CAS.
- S. Svedhem, D. Dahlborg, J. Ekeroth, J. Kelly, F. Hook and J. Gold, In situ Peptide-modified Supported Lipid Bilayers for Controlled Cell Attachment, Langmuir, 2003, 19, 6730–6736 CrossRef CAS.
- E. H. Chen, S. A. Saslow, S. T. Nguyen and F. M. Geiger, Zinc Ion–Hydroxyl Interactions at Undecanol-Functionalized Fused Silica/Water Interfaces Quantified Using the Eisenthal chi(3) Technique, J. Phys. Chem. C, 2012, 116, 19886–19892 CAS.
- P. E. Ohno, S. A. Saslow, H.-f. Wang, F. M. Geiger and K. B. Eisenthal, Phase-referenced Nonlinear Spectroscopy of the alpha-Quartz/Water Interface, Nat. Commun., 2016, 7, 13587 CrossRef CAS PubMed.
- J. M. Troiano, A. C. McGeachy, L. L. Olenick, D. Fang, D. Liang, J. Hong, T. R. Kuech, E. R. Caudill, J. A. Pedersen, Q. Cui and F. M. Geiger, Quantifying the Electrostatics of Polycation–Lipid Bilayer Interactions, J. Am. Chem. Soc., 2017, 139, 5808–5816 CrossRef CAS PubMed.
- J. M. Troiano, T. R. Kuech, A. M. Vartanian, M. D. Torelli, A. Sen, L. M. Jacob, R. J. Hamers, C. J. Murphy, J. A. Pedersen and F. M. Geiger, On Electronic and Charge Interference in Second Harmonic Generation Responses from Gold Metal Nanoparticles at Supported Lipid Bilayers, J. Phys. Chem. C, 2016, 120, 20659–20667 CAS.
- J. M. Troiano, L. L. Olenick, T. R. Kuech, E. S. Melby, D. Hu, S. E. Lohse, A. C. Mensch, M. Dogangun, A. M. Vartanian, M. D. Torelli, E. Ehimiaghe, S. R. Walter, L. Fu, C. R. Anderton, Z. Zhu, H. Wang, G. Orr, C. J. Murphy, R. J. Hamers, J. A. Pedersen and F. M. Geiger, Direct Probes of 4 nm Diameter Gold Nanoparticles Interacting with Supported Lipid Bilayers, J. Phys. Chem. C, 2015, 119, 534–546 CAS.
- M. Dogangun, M. Hang, J. Machesky, A. C. McGeachy, N. Dalchand, R. J. Hamers and F. M. Geiger, Evidence for Considerable Metal Cation Concentrations from Lithium Intercalation Compounds in the Nano–Bio Interface Gap, J. Phys. Chem. C, 2017, 121, 27473–27482 CAS.
- M. Dogangun, M. N. Hang, J. M. Troiano, A. C. McGeachy, E. S. Melby, J. A. Pedersen, R. J. Hamers and F. M. Geiger, Alteration of Membrane Compositional Asymmetry by LiCoO2 Nanosheets, ACS Nano, 2015, 9, 8755–8765 CrossRef CAS PubMed.
- J.-L. Barrat and J.-P. Hansen, Basic Concepts for Simple and Complex Liquids, Cambridge University Press, Cambridge, UK, 2003 Search PubMed.
- A. C. McGeachy, L. L. Olenick, J. M. Troiano, R. S. Lankone, E. S. Melby, T. R. Kuech, E. Ehimiaghe, D. H. Fairbrother, J. A. Pedersen and F. M. Geiger, Resonantly Enhanced Nonlinear Optical Probes of Oxidized Multiwalled Carbon Nanotubes at Supported Lipid Bilayers, J. Phys. Chem. B, 2017, 121, 1321–1329 CrossRef CAS PubMed.
- L. L. Olenick, H. M. Chase, L. Fu, Y. Zhang, A. C. McGeachy, M. Dogangun, S. R. Walter, H.-f. Wang and F. M. Geiger, Single-component Supported Lipid Bilayers Probed Using Broadband Nonlinear Optics, Phys. Chem. Chem. Phys., 2018, 20, 3063–3072 RSC.
- R. Michael, H. Fredrik, K. Anatol, B. Peter and K. Bengt, Quartz Crystal Microbalance Setup for Frequency and Q-factor Measurements in Gaseous and Liquid Environments, Rev. Sci. Instrum., 1995, 66, 3924–3930 CrossRef.
- I. Reviakine, D. Johannsmann and R. P. Richter, Hearing What You Cannot See and Visualizing What You Hear: Interpreting Quartz Crystal Microbalance Data from Solvated Interfaces, Anal. Chem., 2011, 83, 8838–8848 CrossRef CAS PubMed.
- G. Sauerbrey, Verwendung von Schwingquarzen zur Wägung dünner Schichten und zur Mikrowägung, Z. Phys., 1959, 155, 206–222 CrossRef CAS.
- M. V. Voinova, M. Rodahl, M. Jonson and B. Kasemo, Viscoelastic Acoustic Response of Layered Polymer Films at Fluid–Solid Interfaces: Continuum Mechanics Approach, Phys. Scr., 1999, 59, 391 CrossRef CAS.
- A. J. Haes, S. Zou, J. Zhao, G. C. Schatz and R. P. Van Duyne, Localized Surface Plasmon Resonance Spectroscopy near Molecular Resonances, J. Am. Chem. Soc., 2006, 128, 10905–10914 CrossRef CAS PubMed.
- J. A. De Feijter, J. Benjamins and F. A. Veer, Ellipsometry as a Tool to Study the Adsorption Behavior of Synthetic and Biopolymers at the Air–Water Interface, Biopolymers, 1978, 17, 1759–1772 CrossRef CAS.
- M. P. Jonsson, P. Jönsson and F. Höök, Simultaneous Nanoplasmonic and Quartz Crystal Microbalance Sensing: Analysis of Biomolecular Conformational Changes and Quantification of the Bound Molecular Mass, Anal. Chem., 2008, 80, 7988–7995 CrossRef CAS PubMed.
- G. Gonella, C. Lutgebaucks, A. G. F. de Beer and S. Roke, Second Harmonic and Sum-Frequency Generation from Aqueous Interfaces is Modulated by Interference, J. Phys. Chem. C, 2016, 120, 9165–9173 CAS.
- K. B. Eisenthal, Liquid Interfaces Probed by Second-harmonic and Sum-frequency Spectroscopy, Chem. Rev., 1996, 96, 1343–1360 CrossRef CAS PubMed.
- F. M. Geiger, Second Harmonic Generation, Sum Frequency Generation, and chi(3): Dissecting Environmental Interfaces with a Nonlinear Optical Swiss Army Knife, Annu. Rev. Phys. Chem., 2009, 60, 61–83 CrossRef CAS PubMed.
- M. D. Boamah, P. E. Ohno, F. M. Geiger and K. B. Eisenthal, Relative Permittivity in the Electrical Double Layer from Nonlinear Optics, J. Chem. Phys., 2018, 148, 222808 CrossRef.
- P. E. Ohno, H.-f. Wang and F. M. Geiger, Second-order Spectral Lineshapes from Charged Interfaces, Nat. Commun., 2017, 8, 1032 CrossRef PubMed.
- S. W. Ong, X. L. Zhao and K. B. Eisenthal, Polarization of Water Molecules at a Charged Interface: Second Harmonic Studies of the Silica/Water Interface, Chem. Phys. Lett., 1992, 191, 327–335 CrossRef CAS.
- X. Zhao, S. Ong, H. Wang and K. B. Eisenthal, New Method for Determination of Surface pKa using Second Harmonic Generation, Chem. Phys. Lett., 1993, 214, 203–207 CrossRef CAS.
- Y. Liu, C. Y. Yan, X. L. Zhao and K. B. Eisenthal, Surface potential of charged liposomes determined by second harmonic generation, Langmuir, 2001, 17, 2063–2066 CrossRef CAS.
- J. P. Fitts, X. Shang, G. W. Flynn, T. F. Heinz and K. B. Eisenthal, Electrostatic Surface Charge at Aqueous/α-Al2O3 Single-Crystal Interfaces as Probed by Optical Second-Harmonic Generation, J. Phys. Chem. B, 2005, 109, 7981–7986 CrossRef CAS PubMed.
- R. Araya, J. Jiang, K. B. Eisenthal and R. Yuste, The Spine Neck Filters Membrane Potentials, Proc. Natl. Acad. Sci. U. S. A., 2006, 103, 17961–17966 CrossRef CAS PubMed.
- P. L. Hayes, J. N. Malin, D. S. Jordan and F. M. Geiger, Get Charged Up: Nonlinear Optical Voltammetry for Quantifying the Thermodynamics and Electrostatics of Metal Cations at Aqueous/Oxide Interfaces, Chem. Phys. Lett., 2010, 499, 183–192 CrossRef CAS.
- P. L. Hayes, E. H. Chen, J. L. Achtyl and F. M. Geiger, An Optical Voltmeter for Studying Cetyltrimethylammonium Interacting with Fused Silica/Aqueous Interfaces at High Ionic Strength, J. Phys. Chem. A, 2009, 113, 4269–4280 CrossRef CAS PubMed.
- J. L. Achtyl, R. R. Unocic, L. Xu, Y. Cai, M. Raju, W. Zhang, R. L. Sacci, I. V. Vlassiouk, P. F. Fulvio, P. Ganesh, D. J. Wesolowski, S. Dai, A. C. T. van Duin, M. Neurock and F. M. Geiger, Aqueous Proton Transfer across Single-layer Graphene, Nat. Commun., 2015, 6, 6539 CrossRef CAS PubMed.
- C. Macias-Romero, I. Nahalka, H. I. Okur and S. Roke, Optical Imaging of Surface Chemistry and Dynamics in Confinement, Science, 2017, 25, 784–788 CrossRef PubMed.
- Y.-C. Wen, S. Zha, X. S. Liu, S. Yang, P. Guo, G. Shi, H. Fang, Y. R. Shen and C. Tian, Unveiling Microscopic Structures of Charged Water Interfaces by Surface-Specific Vibrational Spectroscopy, Phys. Rev. Lett., 2016, 116, 016101 CrossRef PubMed.
- H.-f. Wang, Sum Frequency Generation Vibrational Spectroscopy (SFG-VS) for Complex Molecular Surfaces and Interfaces: Spectral Lineshape Measurement and Analysis Plus Some Controversial Issues, Prog. Surf. Sci., 2016, 91, 155–182 CrossRef CAS.
- H. Wang, E. C. Y. Yan, E. Borguet and K. B. Eisenthal, Second Harmonic Generation From the Surface of Centrosymmetric Particles in Bulk Solution, Chem. Phys. Lett., 1996, 259, 15–20 CrossRef CAS.
- G. Gonella, C. Lutgebaucks, A. G. F. de Beer and S. Roke, Second Harmonic and Sum-Frequency Generation from Aqueous Interfaces Is Modulated by Interference, J. Phys. Chem. C, 2016, 120, 9165–9173 CAS.
- A. C. McGeachy, N. Dalchand, E. R. Caudill, T. Li, M. Dogangun, L. L. Olenick, H. Chang, J. A. Pedersen and F. M. Geiger, Interfacial Electrostatics of Poly(vinylamine hydrochloride), Poly(diallyldimethylammonium chloride), Poly-L-lysine, and Poly-L-Arginine Interacting with Lipid Bilayers, Phys. Chem. Chem. Phys., 2018 10.1039/c7cp07353d.
- R. B. Best, X. Zhu, J. Shim, P. E. Lopes, J. Mittal, M. Feig and A. D. MacKerell Jr, Optimization of the Additive CHARMM All-atom Protein Force Field Targeting Improved Sampling of the Backbone ϕ, ψ and Side-chain χ1 and χ2 Dihedral Angles, J. Chem. Theory Comput., 2012, 8, 3257–3273 CrossRef CAS PubMed.
- J. B. Klauda, R. M. Venable, J. A. Freites, J. W. O'Connor, D. J. Tobias, C. Mondragon-Ramirez, I. Vorobyov, A. D. MacKerell Jr and R. W. Pastor, Update of the CHARMM All-atom Additive Force Field for Lipids: Validation on Six Lipid Types, J. Phys. Chem. B, 2010, 114, 7830–7843 CrossRef CAS PubMed.
- K. Vanommeslaeghe, E. Hatcher, C. Acharya, S. Kundu, S. Zhong, J. Shim, E. Darian, O. Guvench, P. Lopes and I. Vorobyov, CHARMM General Force Field: A Force Field for Drug-like Molecules Compatible with the CHARMM All-atom Additive Biological Force Fields, J. Comput. Chem., 2010, 31, 671–690 CAS.
- R. M. Venable, Y. Luo, K. Gawrisch, B. Roux and R. W. Pastor, Simulations of Anionic Lipid Membranes: Development of Interaction-specific Ion Parameters and Validation using NMR Data, J. Phys. Chem. B, 2013, 117, 10183–10192 CrossRef CAS PubMed.
- S. Jo, J. B. Lim, J. B. Klauda and W. Im, CHARMM-GUI Membrane Builder for Mixed Bilayers and Its Application to Yeast Membranes, Biophys. J., 2009, 97, 50–58 CrossRef CAS PubMed.
- J. C. Phillips, R. Braun, W. Wang, J. Gumbart, E. Tajkhorshid, E. Villa, C. Chipot, R. D. Skeel, L. Kale and K. Schulten, Scalable Molecular Dynamics with NAMD, J. Comput. Chem., 2005, 26, 1781–1802 CrossRef CAS PubMed.
- P. Eastman, M. S. Friedrichs, J. D. Chodera, R. J. Radmer, C. M. Bruns, J. P. Ku, K. A. Beauchamp, T. J. Lane, L.-P. Wang and D. Shukla, OpenMM 4: A Reusable, Extensible, Hardware Independent Library for High Performance Molecular Simulation, J. Chem. Theory Comput., 2012, 9, 461–469 CrossRef PubMed.
- M. S. Friedrichs, P. Eastman, V. Vaidyanathan, M. Houston, S. Legrand, A. L. Beberg, D. L. Ensign, C. M. Bruns and V. S. Pande, Accelerating Molecular Dynamic Simulation on Graphics Processing Units, J. Comput. Chem., 2009, 30, 864–872 CrossRef CAS PubMed.
- T. Darden, D. York and L. Pedersen, Particle mesh Ewald: An N
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log(N) Method for Ewald Sums in Large Systems, J. Chem. Phys., 1993, 98, 10089–10092 CrossRef CAS.
log(N) Method for Ewald Sums in Large Systems, J. Chem. Phys., 1993, 98, 10089–10092 CrossRef CAS. - A. B. Dahlin, P. Jonsson, M. P. Jonsson, E. Schmid, Y. Zhou and F. Hook, Synchronized Quartz Crystal Microbalance and Nanoplasmonic Sensing of Biomolecular Recognition Reactions, ACS Nano, 2008, 2, 2174–2182 CrossRef CAS PubMed.
- E. Guzman, F. Ortega, M. G. Prolongo, V. M. Starov and R. G. Rubio, Influence of the Molecular Architecture on the Adsorption onto Solid Surfaces: Comb-like Polymers, Phys. Chem. Chem. Phys., 2011, 13, 16416–16423 RSC.
- T. Inagaki, S. Aono, H. Nakano and T. Yamamoto, Like-Charge Attraction of Molecular Cations in Water: Subtle Balance between Interionic Interactions and Ionic Solvation Effect, J. Phys. Chem. B, 2014, 118, 5499–5508 CrossRef CAS PubMed.
- A. Y. Kostritskii, D. A. Kondinskaia, A. M. Nesterenko and A. A. Gurtovenko, Adsorption of Synthetic Cationic Polymers on Model Phospholipid Membranes: Insight from Atomic-Scale Molecular Dynamics Simulations, Langmuir, 2016, 32, 10402–10414 CrossRef CAS PubMed.
- N. BenTal, B. Honig, R. M. Peitzsch, G. Denisov and S. McLaughlin, Binding of Small Basic Peptides to Membranes Containing Acidic Lipids: Theoretical Models and Experimental Results, Biophys. J., 1996, 71, 561–575 CrossRef CAS.
- S. V. Solomatin, M. Greenfeld and D. Herschlag, Implications of Molecular Heterogeneity for the Cooperativity of Biological Macromolecules, Nat. Struct. Mol. Biol., 2011, 18, 732–734 CAS.
- J. Y. Kim, M. Mosior, L. A. Chung, H. Wu and S. McLaughlin, Binding of Peptides with Basic Residues to Membranes Containing Acidic Phospholipids, Biophys. J., 1991, 60, 135–148 CrossRef CAS PubMed.
- F. Torrens, G. Castellano, A. Campos and C. Abad, Negatively Cooperative Binding of Melittin to Neutral Phospholipid Vesicles, J. Mol. Struct., 2007, 834, 216–228 CrossRef.
- A. Katchalsky, J. Mazur and P. Spitnik, Polybase Properties of Polyvinylamine, J. Polym. Sci., 1957, 23, 513–532 CrossRef CAS.
- J. Vondrasek, P. E. Mason, J. Heyda, K. D. Collins and P. Jungwirth, The Molecular Origin of Like-Charge Arginine–Arginine Pairing in Water, J. Phys. Chem. B, 2009, 113, 9041–9045 CrossRef CAS PubMed.
- G. Tesei, M. Vazdar, M. R. Jensen, C. Cragnell, P. E. Mason, J. Heyda, M. Skepo, P. Jungwirth and M. Lund, Self-association of A Highly Charged Arginine-rich Cell-Penetrating Peptide, Proc. Natl. Acad. Sci. U. S. A., 2017, 114, 11428–11433 CrossRef CAS PubMed.
- M. Vazdar, E. Wernersson, M. Khabiri, L. Cwiklik, P. Jurkiewicz, M. Hof, E. Mann, S. Kolusheva, R. Jelinek and P. Jungwirth, Aggregation of Oligoarginines at Phospholipid Membranes: Molecular Dynamics Simulations, Time-Dependent Fluorescence Shift, and Biomimetic Colorimetric Assays, J. Phys. Chem. B, 2013, 117, 11530–11540 CrossRef CAS PubMed.
- Z. Wu, Q. Cui and A. Yethiraj, Why Do Poly-Arg and Poly-Lys Organize Lipids Differently? Insights from Coarse-grained and Atomistic Simulations, J. Phys. Chem. B, 2013, 117, 12145–12156 CrossRef CAS PubMed.
- N. W. Schmidt, A. Mishra, G. H. Lai, M. Davis, L. K. Sanders, D. Tran, A. Garcia, K. P. Tai, P. B. McCray, A. J. Ouellette, M. E. Selsted and G. C. L. Wong, Criterion for Amino Acid Composition of Defensins and Antimicrobial Peptides Based on Geometry of Membrane Destabilization, J. Am. Chem. Soc., 2011, 133, 6720–6727 CrossRef CAS PubMed.
- N. J. Gleason, V. V. Vostrikov, D. V. Greathouse and R. E. Koeppe, Buried Lysine, But Not Arginine, Titrates and Alters Transmembrane Helix tilt, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 1692–1695 CrossRef CAS PubMed.
- L. B. Li, I. Vorobyov and T. W. Allen, The Different Interactions of Lysine and Arginine Side Chains with Lipid Membranes, J. Phys. Chem. B, 2013, 117, 11906–11920 CrossRef CAS PubMed.
- M. Vazdar, J. Vymetal, J. Heyda, J. i. Vondrášek and P. Jungwirth, Like-charge Guanidinium Pairing from Molecular Dynamics and Ab Initio Calculations, J. Phys. Chem. A, 2011, 115, 11193–11201 CrossRef CAS PubMed.
- M. Vazdar, F. Uhlig and P. Jungwirth, Like-charge Ion Pairing in Water: An Ab Initio Molecular Dynamics Study of Aqueous Guanidinium Cations, J. Phys. Chem. Lett., 2012, 3, 2021–2024 CrossRef CAS.
- I. Vorobyov and T. W. Allen, The Electrostatics of Solvent and Membrane Interfaces and the Role of Electronic Polarizability, J. Chem. Phys., 2010, 132, 185101 CrossRef.
- D. J. Bonthuis and R. R. Netz, Beyond the Continuum: How Molecular Solvent Structure Affects Electrostatics and Hydrodynamics at Solid-Electrolyte Interfaces, J. Phys. Chem. B, 2013, 117, 11397–11413 CrossRef CAS PubMed.
- T. Ishiyama, D. Terada and A. Morita, Hydrogen-Bonding Structure at Zwitterionic Lipid/Water Interface, J. Phys. Chem. Lett., 2016, 7, 216–220 CrossRef CAS PubMed.
- P. Jedlovszky and M. Mezei, Orientational Order of the Water Molecules Across a Fully Hydrated DMPC Bilayer: A Monte Carlo Simulation Study, J. Phys. Chem. B, 2001, 105, 3614–3623 CrossRef CAS.
- B. Ding and Z. Chen, Molecular Interactions between Cell Penetrating Peptide Pep-1 and Model Cell Membranes, J. Phys. Chem. B, 2012, 116, 2545–2552 CrossRef CAS PubMed.
- L. Soblosky, A. Ramamoorthy and Z. Chen, Membrane Interaction of Antimicrobial Peptides using E. coli Lipid Extract as Model Bacterial Cell Membranes and SFG Spectroscopy, Chem. Phys. Lipids, 2015, 187, 20–33 CrossRef CAS PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c8sc00804c |
| ‡ ACM, ERC, and DL contributed equally to this work. |
| This journal is © The Royal Society of Chemistry 2018 |