Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Identifying key descriptors in surface binding: interplay of surface anchoring and intermolecular interactions for carboxylates on Au(110)†
Christopher R.
O'Connor‡
 a,
Fanny
Hiebel‡
a,
Wei
Chen
bc,
Efthimios
Kaxiras
bc,
Robert J.
Madix
b and
Cynthia M.
Friend
a,
Fanny
Hiebel‡
a,
Wei
Chen
bc,
Efthimios
Kaxiras
bc,
Robert J.
Madix
b and
Cynthia M.
Friend
 *ab
*ab
aDepartment of Chemistry and Chemical Biology, Harvard University, Cambridge, MA 02138, USA. E-mail: friend@fas.harvard.edu
bSchool of Engineering and Applied Sciences, Harvard University, Cambridge, MA 02138, USA
cDepartment of Physics, Harvard University, Cambridge, MA 02138, USA
First published on 12th March 2018
Abstract
The relative stability of carboxylates on Au(110) was investigated as part of a comprehensive study of adsorbate binding on Group IB metals that can be used to predict and understand how to control reactivity in heterogeneous catalysis. The binding efficacy of carboxylates is only weakly dependent on alkyl chain length for relatively short-chain molecules, as demonstrated using quantitative temperature-programmed reaction spectroscopy. Corresponding density functional theory (DFT) calculations demonstrated that the bidentate anchoring geometry is rigid and restricts the amount of additional stabilization through adsorbate-surface van der Waals (vdW) interactions which control stability for alkoxides. A combination of scanning tunneling microscopy (STM) and low-energy electron diffraction (LEED) shows that carboxylates form dense local islands on Au(110). Complementary DFT calculations demonstrate that adsorbate–adsorbate interactions provide additional stabilization that increases as a function of alkyl chain length for C2 and C3 carboxylates. Hence, overall stability is generally a function of the anchoring group to the surface and the inter-adsorbate interaction. This study demonstrates the importance of these two important factors in describing binding of key catalytic intermediates.
Introduction
Heterogeneous catalysis is key to ensuring sustainability in chemical transformations.1 Accordingly, there is a drive to develop principles for designing efficient catalytic processes. One approach to establishing such principles is the creation of a database of key properties (“descriptors”) that can be related to catalytic performance;2–6 for example, binding energies of key intermediates to specific materials. While the so-called Materials Genome Initiative7–9 seeks a limited set of key descriptors for complex materials design processes, it is important to understand the underlying factors that contribute to descriptors, such as binding energy.Carboxylate species are an important class of molecules that are both reactive intermediates and also potential poisons in oxidative processes. For example, carboxylates are intermediates in the oxidation of alcohols and olefins, yielding both carboxylic acids and CO2, and electrochemical reduction of CO2.10–27 Carboxylate intermediates also strongly bind to surfaces so as to block sites.17,22–24 For example, carboxylates formed in over-oxidation of alcohols block subsequent formation of the key alkoxide intermediates; thus, suppressing activity.17 Because of the broad importance of carboxylates in oxidation catalysis, we have systematically investigated them to develop a hierarchy of binding strength and also to provide a more detailed understanding of the factors that dictate their stability. This investigation is part of the development of a database for key intermediates on Group IB metals (Cu, Ag and Au), following on our prior studies of alkoxides.28–33 Herein, binding of carboxylates to Au(110) is investigated because of the broad interest in it as a selective oxidation catalyst.34–40
Creation of carboxylates on Au(110) is facile because organic acids generally react with adsorbed oxygen atoms15,41,42 by an acid–base mechanism as illustrated for carboxylic acids:
| 2RCOOH(g) + O(a) → 2RCOO(a) + H2O(g) | (1) |
The carboxylic acids do not react with clean metallic Au; thus, the surface concentration of the carboxylates formed is entirely controlled by the initial coverage of adsorbed oxygen and all oxygen can be removed as water to solely produce the carboxylate species at a specific surface coverage.41,42 Furthermore, carboxylates adsorbed on Au are also proton acceptors, so that they can react with other gas phase acids exposed to the surface, providing a means of evaluating the relative binding strength of various carboxylates. Indeed, the relative gas phase acidities of reactants qualitatively predict the stability of reaction intermediates.28
| R′COOH(g) + RCOO(a) → R′COO(a) + RCOOH(g) | (2) |
This competition can be described by a series of steps, the first of which is known from measured gas-phase acidities:
| RCOO′H(g) + RCOO(g)− → R′COO(g)− + RCOOH(g), Δ(ΔHacid) | (3) |
| R′COO(g)− → R′COO(a), ΔHads(R′COO(g)−) | (4) |
| RCOO(a) → RCOO(g)−, −ΔHads(RCOO(g)−) | (5) |
It follows that gas phase acidity is an accurate predictor of the competitive binding only if the energetic difference in bonding of the adsorbed conjugate bases to the surface is negligible and that adsorbate bonding is effectively ionic due to the anionic nature of adsorbates.28
Prior studies demonstrated that acetate forms condensed islands on Au(110) due to net attractive interactions between adsorbed species.43 Hence, these intermolecular interactions must be considered along with surface-adsorbate binding in evaluating overall stability of the carboxylates. Carboxylates, including acetate and formate, are more strongly bound than their alkoxide counterparts, ethoxy and methoxy, on Au, raising questions regarding the factors that contribute to this stronger binding. The primary anchoring bond, surface structure, intermolecular interactions and noncovalent interactions between the surface and the pendant alkyl group can all contribute to overall binding.
In this study the experimental hierarchy of binding stability for saturated carboxylates on Au(110) was determined through a series of adsorbate displacement experiments. Saturated carboxylates have a similar stability with only a small stabilization associated with longer chains. DFT calculations demonstrate that the bidentate geometry causes rigid binding which restricts further stabilization through adsorbate-surface van der Waals (vdW) interactions. Scanning tunneling microscopy (STM) and low-energy electron diffraction studies show that carboxylates form dense local islands; further, DFT calculations demonstrate that adsorbate–adsorbate vdW interactions play a pivotal role in determining carboxylate stability by increasing stabilization for longer chain carboxylates. Hence, this study refines the understanding of vdW interactions in determining the stability of intermediates.
Methods
Experimental
Temperature-programmed reaction spectroscopy and low-energy electron diffraction (LEED) experiments were performed under ultrahigh vacuum conditions in a chamber with a base pressure < 3.0 × 10−10 Torr. Temperature programmed experiments were performed using a triple filter Hiden quadrupole mass spectrometer (QMS, HAL-Hiden/3F). During all temperature programmed experiments, a −100 V bias was applied to the sample to prevent possible electron-stimulated reactions. A heating rate of 5 K s−1 was used for all experiments. LEED experiments were performed using Perkin-Elmer Phi Model 15-120 LEED Optics. In a separate chamber, scanning tunneling microscopy was performed with an Omicron VT-STM under ultra-high vacuum of base pressure P < 1.0 × 10−10 mbar, using commercial mechanically cut PtIr tips purchased from Veeco.Separate Au(110) crystals were prepared for the reactivity14 and STM35 measurements according to procedures described previously. Controlled amounts of atomic oxygen were deposited using ozone in established procedures.17,41 For STM experiments, the coverage of adsorbed oxygen was calculated by counting the oxygen atoms in zigzag chains and the top layer gold atoms in a given area; for temperature programmed experiments, the coverage of adsorbed oxygen was calibrated by the integrated O2 signal due to atomic oxygen recombination above 500 K for the saturation coverage of 1 ML.44
Experiments were performed on Au(110) covered with 0.05 ML adsorbed atomic oxygen, hereafter referred to as O/Au(110). The liquid organics were purified according to procedures described previously and the gas phase vapor was leaked in the chamber while monitoring the rise in pressure of the chamber.31,32 Temperature programmed experiments were performed with each reactant to identify its signature products and displacement reactions were preformed to determine the relative binding stability of selected pairs of carboxylates as described in the (ESI†). The quantitative analysis of the temperature programmed reaction data was performed as described in the ESI.†
Computational details
DFT calculations were performed using the Vienna ab initio simulation package (VASP).45 The projector augmented wave (PAW) method46 was used with a plane-wave basis set (kinetic energy cutoff 400 eV) and the PBE exchange-correlation functional.47 Dispersion interactions were approximated with the Tkatchenko–Scheffler method.48The Au(110) supercell was built out of 5 atomic layers with the two bottom layers constrained to their bulk positions and more than 10 Å of vacuum layer above the adsorbates. The bulk positions were adapted depending on whether dispersion interactions were included or not (lattice constant of 4.11 Å with and 4.16 Å without dispersion correction, which is close to the reported experimental value 4.08 Å).49 Laterally, a 4 × 4 (4 × 2) periodicity with respect to the Au(110)-(1 × 1) surface was used, with a 3 × 7 × 1 (7 × 7 × 1) Gamma-centered k-point mesh when isolated molecules (initial adsorption geometry exploration, namely top, bidentate top, bidentate bridge and chelating, and dense layers) were considered. Unconstrained atoms were relaxed to a force threshold of 0.01 eV Å−1.
Results and discussion
Displacement reactions to determine the relative stability of the carboxylates
Reaction products and their peak temperatures were first determined for each of the carboxylates studied—propanoate, trifluoroacetate, acetate and formate. All the carboxylates produce CO2; however, there are other signature products at different temperatures (Table 1), enabling the determination of the amounts of specific carboxylates present based on the temperature and magnitude of signature product evolution. In all cases, the signature products and the peak temperatures were determined using temperature programmed reaction after exposure of 0.05 ML of atomic oxygen on Au(110) to an excess of the carboxylic acid at 300 K, yielding 0.10 ML of the carboxylate. All adsorbed atomic oxygen is removed as water under these conditions. The coverage was held fixed to avoid coverage-dependent variation in the temperature for product evolution. The methodology is exemplified here by acetic acid/trifluoroacetic acid pair; data for other acid pairs are provided in the ESI (Fig. S1–S3; Table S1†).| Organic acid (adsorbed carboxylate) | Characteristic reaction products | Product peak temperature (K) |
|---|---|---|
| CH3CH2COOH (CH3CH2COO(a)) | CH2CH2, CO2 | 550 |
| CF3COOH (CF3COO(a)) | CF3, CO2 | 590 |
| CH3COOH (CH3COO(a)) | CH3, CO2 | 580 |
| HCOOH (HCOO(a)) | HCOOH, CO2 | 350 |
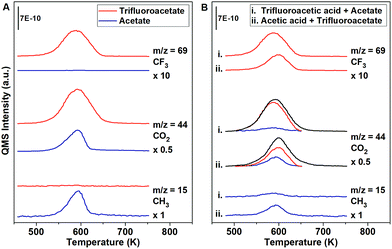
A pure layer of acetate (0.1 ML) decomposed to CO2 (m/z = 44) and CH3 (m/z = 15) at 580 K (Fig. 1A, blue). In separate experiments, trifluoroacetate (0.1 ML) decomposed to CO2 (m/z = 44) and CF3 (m/z = 69) at 590 K (Fig. 1A, red). The differences in the temperatures for decomposition and the differences in the signature products provides the basis for the quantitative determination of the amounts of trifluoroacetate and acetate in the displacement experiments. Since acetate and trifluoroacetate yield CO2 (m/z = 44) at overlapping temperatures, the unique evolution of CF3 (m/z = 69) from adsorbed trifluoroacetate at 590 K and CH3 (m/z = 15) from acetate at 580 K were used to quantify the relative amounts of adsorbed trifluoroacetate or acetate, respectively (eqn (6)–(8)).
| CF3COOH + CH3COO(a) ⇌ CF3COO(a) + CH3COOH | (6) |
| CH3COO(a) → CH3(g) + CO2(g) | (7) |
| CF3COO(a) → CF3(g) + CO2(g) | (8) |
Nearly complete displacement of acetate by trifluoroacetate is demonstrated by performing competition experiments (Fig. 1B), demonstrating that trifluoroacetate has a distinctly larger binding energy to the surface than acetate. By performing the experiments in both orders of adsorption, kinetic factors are ruled out. The exposure of excess trifluoroacetic acid to 0.10 ML of adsorbed acetate leads to nearly complete displacement, based on the predominance of CF3 evolution at 590 K and the absence of CH3 at 580 K (Fig. 1B, i). The exposure of excess acetic acid to 0.10 ML of adsorbed trifluoroacetate leads to partial displacement as evidenced by the evolution of both CF3 at 590 K and CH3 at 580 K (Fig. 1B, ii). The nearly complete displacement of acetate by trifluoroacetate when exposed to trifluoroacetic acid and limited displacement of trifluoroacetate by acetate when exposed to acetic acid clearly demonstrates that trifluoroacetate is more stable than acetate. The effect was observed for both orders of displacement, showing that this is a thermodynamic, not a kinetic, effect.
The selectivity of the decomposition of trifluoroacetate and acetate was determined to be constant up to 0.10 ML of carboxylate, within experimental error, so CF3 and CH3 can be used to quantify the presence of trifluoroacetate and acetate, respectively. The deconvolution of the measured CO2 peak is performed for acetate and trifluoroacetate by using the measured CH3 and CF3 signals according to the procedure described in the ESI.†
A hierarchy of binding efficacy was established using this displacement method (Table 2). Generally, longer alkyl chain lengths lead to somewhat stronger binding, which is qualitatively similar to alkoxide binding.30–32 Likewise, the stabilities of the carboxylates generally increase with the gas phase acidity of their conjugate acid (Table 2), with trifluoroacetic acid being the exception. Specifically, the gas phase acidities of trifluoroacetic acid (ΔHacid = 1351 KJ mol−1) and propanoic acid (ΔHacid = 1454 KJ mol−1) indicate that trifluoroacetate should bind much more strongly than propanoate, which is not in agreement with the experiments. A similar effect of fluorination was observed in the relative stabilities of trifluoroethoxy vs. ethoxy and propoxy on Au(111) and was attributed to repulsive interactions between the fluorine atoms and the surface, that decreased the heat of adsorption of the trifluoroethoxy relative to what is expected based on gas phase acidity.30 Nonetheless, there appears to be a general trend between the chemical structure of carboxylates and the relative binding stability of the carboxylates, consistent with previous studies on silver,28 gold,30,31 copper32 and anatase TiO2.51
| Conjugate base | Gas phase aciditya (KJ mol−1) | Probe reaction | Exp. Kb | |
|---|---|---|---|---|
| a Gas phase acidity (taken from the NIST database)50 is defined as ΔH for BH(g) → B(g)− + H(g)+ (KJ mol−1). b Equilibrium constant is determined at 260 K for formate/acetate and 300 K for other pairs. | ||||

|
Propanoate | 1454 ± 12 | CH3COO(a) + CH3CH2COOH → CH3COOH + CH3CH2COO(a) | 4 |
| Trifluoroacetate | 1351 ± 17 | CF3COO(a) + CH3CH2COOH → CF3COOH + CH3CH2COO(a) | 2 | |
| CH3COO(a) + CF3COOH → CH3COOH + CF3COO(a) | 2 | |||
| Acetate | 1459 ± 9 | CH3COO(a) + CH3COOH ↔ CH3COOH + CH3COO(a) | 1 | |
| Formate | 1444 ± 12 | CH3COO(a) + HCOOH ← CH3COOH + HCOO(a) | 0.9 | |
If the difference of enthalpies of adsorption between the two carboxylate anions could be determined, the equilibrium constant for the competition of two species could be determined quantitatively from the gas phase acidity difference (assuming their entropies of adsorption are nearly equal). In fact, if the entropies and energies of adsorption of the ions are nearly the same, the gas phase acidity can be used as a qualitative evaluation of relative binding stability; however, this is not always the case, and, though the gas phase acidity may give the trends in stability, it cannot be expected to yield accurate values for the equilibrium constants determined here. The difference of entropic contributions of adsorption can be empirically approximated52 but the energy of adsorption of the gas phase anions cannot be determined accurately, so the gas phase acidity can serve only as a guide for the relative binding stability. Exceptions may occur.
Determination of equilibrium constants
To quantitatively evaluate the relative binding of various carboxylates, it is necessary to determine the equilibrium constants (eqn (2)) for competitive binding. To this end, a new method for determining equilibrium constants that uses sequential dosing of different carboxylic acids was developed that probes the kinetics of the displacement reactions to determine the equilibrium constant (Table 2). This method was required because introducing a gaseous mixture of two carboxylic acids resulted in undesirable side reactions.Briefly, if R′COOH is exposed to the surface above its desorption temperature but below the temperature at which RCOO(a) decomposes, the rate of displacement of RCOO(a) is:
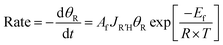 | (9) |
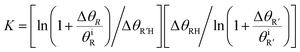 | (10) |
The equilibrium constants for various pairs of carboxylic acids were determined using this method (Table 2), as described in detail in the ESI.† The validity of the kinetic model used was established by accurately predicting the relative surface concentration of acetate and propanoate resulting from a well-defined increase in the acetic acid exposure to adsorbed propanoate (Fig. S4†). These results establish a quantitative basis for evaluating the relative binding efficacies of different carboxylates.
As the length of the alkyl chain increases, the surface stability of the carboxylate slightly increases, as demonstrated by the series of formate, acetate and propanoate (Table 2). Note that the reliability of the equilibrium constants is confirmed by the consistency among the measurements made for the competitions involving trifluoroacetic, acetic and propanoic acid. A similar, but stronger, dependence has been reported for adsorbed alkoxide species on gold surfaces30,31 that was explained by increasing adsorbate-surface vdW interactions as a function of alkyl chain length. The stronger dependence of binding strength on alkyl chain length for alkoxides is illustrated by comparison of the equilibrium constant for the methanol/ethanol competition, which is 5 in favor of ethoxy binding on Au(110),31 compared to the equilibrium constant of ∼1 for the formic acid/acetic acid pair measured here. A similarly weaker dependence for the carboxylates of increasing chain length relative to analogous alkoxide pairs is measured in all cases. A key question is why there is a weaker dependence on alkyl chain length for the carboxylates.
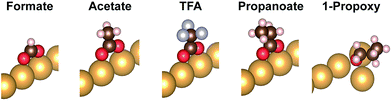
Carboxylate adsorbate-surface interactions
DFT calculations that include vdW corrections were performed to elucidate the origin of the relative stability of isolated carboxylates on Au(110) including formate, acetate, trifluoroacetate and propanoate (Fig. 2). Prior studies of alkoxides on Au and Cu demonstrated the importance of including vdW corrections. The anchoring of acetate on Au(110) was previously investigated in detail43 and the bidentate top configuration was significantly more stable than either the monodentate or bridge configurations. The same anchoring configuration was obtained for other carboxylates in the homologous series (Fig. S5, S6†). Adsorption within the troughs was also tested for propanoate and found to be less stable than the bridging configuration (Fig. S7†). The stability of isolated carboxylates was quantified according to the reaction: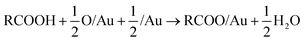 | (11) |
| E(rxn) (eV) | ||
|---|---|---|
| (PBE) | (PBE + vdw) | |
| a The reaction energy of 1-propoxy was included as a reference to demonstrate the stronger effect of vdW interactions for alkoxides. | ||
| Propanoate | −0.85 | −1.04 |
| Trifluoroacetate | −0.97 | −1.14 |
| Acetate | −0.82 | −0.99 |
| Formate | −0.89 | −1.01 |
| 1-Propoxy | −0.22 | −0.64 |
These differences are the consequence of differences in the binding to the surface of the carboxylates vs. the alkoxides (Table 4). The computed geometries of the carboxylates reveal that (1) methyl-surface distances are much larger than for alkoxides (they do not vary much among the carboxylates), and (2) at most small geometry changes are induced by vdW contributions. The possible molecular rotations bringing the carbon groups closer to the surface have been evaluated in detail (Fig S8; Table S2†). The robustness of the bidentate top adsorption geometry is so strong that any stabilization from increased adsorbate-surface vdW interactions is counterbalanced by energy loss from non-optimal anchoring geometry.
| h C0 (Å) | h C1 (Å) | h C2 (Å) | C0C1C2 angle (°) | ||
|---|---|---|---|---|---|
| a h Cn is the methyl group-surface distance for the nth group, starting from the carboxyl group C0. b 1-Propoxy heights are given with respect to the (111) microfacet. | |||||
| Propanoate | (PBE) | 2.74 | 4.26 | 4.94 | 115.4 |
| (PBE + vdW) | 2.74 | 4.26 | 4.94 | 115.5 | |
| Trifluoroacetate | (PBE) | 2.74 | 4.31 | ||
| (PBE + vdW) | 2.74 | 4.30 | |||
| Acetate | (PBE) | 2.74 | 4.25 | ||
| (PBE + vdW) | 2.74 | 4.25 | |||
| Formate | (PBE) | 2.73 | |||
| (PBE + vdW) | 2.72 | ||||
| 1-Propoxyb | (PBE) | 2.77 | 3.38 | 4.91 | 112.3 |
| (PBE + vdW) | 2.79 | 3.26 | 4.78 | 111.9 | |
Carboxylate adsorbate–adsorbate interactions
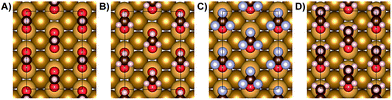
Previous work demonstrated that acetate forms dense, self-assembled 2-D islands on Au(110) due to intermolecular interactions,43 suggesting that adsorbate–adsorbate interactions are likely to contribute to the stability of carboxylates in general. The adsorbate-induced “deconstruction” of the surface occurs even for extremely low acetate coverages, indicating a strong intermolecular attraction. In fact, STM experiments determined that the formation of dense c(2 × 2) islands occurs for trifluoroacetate and is accompanied by reconstruction of the gold surface from 1 × 2 to 1 × 1, similar to acetate (Fig. 3A, B). In particular, the same type of elongated feature is observed at low coverage (Fig. 3A) and a bimodal distribution of high and low domains at saturation coverage (Fig. 3B). Nucleation mechanisms associated with those features have been discussed previously in the case of acetate43 and are beyond the scope of this study. Likewise, the same molecular ordering is observed for formate and propanoate at saturation coverage (0.25 ML) based on LEED experiments (Fig. S9†), providing a guideline for further simulations including inter-adsorbate interactions. The bright protrusions observed for 0.19 ML trifluoroacetate on Au(110) are 39 ± 4 pm taller than the darker protrusions and are attributed to minor structural disorder that can be removed by mild annealing (Fig. S10†).The effect of adsorbate–adsorbate interactions on the stability of carboxylates on Au(110) is determined by comparing the calculated interface energy (E(interface)) of isolated carboxylates versus densely-packed species in a c(2 × 2) molecular arrangement (Fig. 4; Table 5; Fig. S11†). The method for calculating the interface energy is similar to the one used to describe acetate43 and is detailed in the ESI.†
In the absence of vdW interactions (PBE), the close packing associated with condensed islands is destabilizing for all carboxylates studied, as signified by the positive interface energy change, ΔE(interface) (Table 5; Fig. S11†). Furthermore, the interface energy change per adsorbate is essentially independent of the alkyl chain length, although the effect of the electron-rich CF3 group in trifluoroacetate is marginally more destabilizing. Although the energy difference per adsorbate is small, there are 4 adsorbates per supercell which makes the energy differences significant for condensed islands of carboxylates (Fig. 4).
Inclusion of vdW interactions for the condensed (2 × 2) layers leads to stabilization and improves the agreement between theory and experiment (Table 5). The overall stabilities (E(reaction) + ΔE(interface)) of formate and acetate are essentially the same and the propanoate is most strongly bound, in agreement with experiment (Table 2). The outlier is trifluoroacetate, which is predicted to have a similar overall stability as propanoate (Table 5; Fig. S11†), whereas in experiment propanoate binding is favored over trifluoroacetate (Table 2). Although the overall stability is similar for propanoate and trifluoroacetate, the underlying factors contributing to the stability are different. The primary binding of the carboxylate functionality to the surface is stronger for trifluoroacetate, 1.14 eV; whereas the primary binding of the propanoate is lower, 1.05 eV. On the other hand, the propanoate gains more stability from the inter-adsorbate interaction, ΔE(interface) = 0.10 eV. Hence, the overall binding is a combination of different effects. It is possible, even likely, that errors in the calculated energies for these two effects combine to yield a similar overall stability even though these two carboxylates have different binding efficacies.
Although the DFT calculations are fairly accurate for comparing the stability of carboxylate because of their similar adsorption geometry, errors in the relative binding energies could still potentially be as large as several tens of meV. Based on the equilibrium constant measurements, the difference in free energy between the most stable carboxylate, propanoate, and the least stable carboxylate, formate, is 0.04 eV. Hence, the calculations and the results, are in general agreement with the experimental measurements. Nevertheless, the accuracy of the DFT calculations is not sufficient to quantitatively predict the energetic differences. Further, the DFT calculations do not take into account the role of entropy in the displacement experiments which could have a minor but possibly significant contribution in determining the displacement trends. We therefore focus on the qualitative effects of the vdW interaction and inter-adsorbate interaction on the stability of each adsorbate.
The overall hierarchy of stability for carboxylates depends on their condensation into islands, rendering longer-chain carboxylates more stable as shown for assembly of alkanethiols on Au(111) for carbon chains up to ten carbons.53 Accordingly, adsorbate–adsorbate stabilization calculated for trifluoroacetate is the same as for acetate, consistent with a driving force for trifluoroacetate to form dense c(2 × 2) molecular domains at low coverage and in agreement with the STM results that are similar to those for acetate. The attraction occurs despite the higher electron density that could lead to larger repulsive coulombic interactions.
The effect of carboxylate islanding is not unique to gold43,54 but rather has been shown to occur generally on metal surfaces, including: Cu,55–59 Ag,60 Al,60 Ni61,62 and Pd.63,64 Therefore, we anticipate that the effect of intermolecular interactions on carboxylate stability demonstrated herein would be a necessary consideration to carboxylate-metal systems.
Conclusions
Experimental work determined that carboxylate species, while strongly bound to the surface, have a much weaker dependence of stability on alkyl chain length compared to alkoxides. DFT calculations suggest that the rigid bidentate structure limits the influence of adsorbate-surface vdW interactions on carboxylate stability, accounting for this weak dependence. A second important factor in determining the stability of carboxylates are adsorbate–adsorbate interactions that drive condensation of the carboxylates into condensed islands on Au(110). Even for chains as short as acetate and trifluoroacetate, these interactions are sufficiently strong to drive the “deconstruction” of the Au(110) surface so the condensed (2 × 2) structure forms. The effect of adsorbate–adsorbate interactions on carboxylate stability demonstrated here is likely universal for bidentate carboxylate binding on metallic substrates due to the ubiquitous observation of carboxylate islanding on metal surfaces. The anchoring geometry controls the relative influence of adsorbate-surface and adsorbate–adsorbate vdW interactions which independently can control intermediate stability. These studies further demonstrate that complexity, such as formation of condensed phases, must be taken into account in building up an understanding of the binding of key intermediates and poisons on surfaces. Hence, a combination of experimental measurement and theoretical calculations are required to develop a complete picture.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported as part of the Integrated Mesoscale Architectures for Sustainable Catalysis (IMASC), an Energy Frontier Research Center (EFRC) funded by the US Department of Energy (DOE), Office of Science, Basic Energy Sciences under award no. DE-SC0012573. The computations in this paper were run on the Odyssey cluster supported by the FAS Division of Science, Research Computing Group at Harvard University.References
- A. T. Bell, D. R. Gates and M. R. Thompson, Basic Research Needs: Catalysis for Energy, U. D. o. Energy Report PNNL-17214, Pacific Northwest National Laboratory, Richland, WA, 2008 Search PubMed.
- J. Hattrick-Simpers, C. Wen and J. Lauterbach, Catal. Lett., 2014, 145, 290–298 CrossRef.
- J. J. de Pablo, B. Jones, C. L. Kovacs, V. Ozolins and A. P. Ramirez, Curr. Opin. Solid State Mater. Sci., 2014, 18, 99–117 CrossRef.
- J. K. Norskov and T. Bligaard, Angew. Chem., Int. Ed. Engl., 2013, 52, 776–777 CrossRef CAS PubMed.
- Z. K. Liu, Chin. Sci. Bull., 2014, 59, 1619–1623 CrossRef.
- C. Qian, T. Siler and G. A. Ozin, Small, 2015, 11, 64–69 CrossRef CAS PubMed.
- M. L. Green, C. L. Choi, J. R. Hattrick-Simpers, A. M. Joshi, I. Takeuchi, S. C. Barron, E. Campo, T. Chiang, S. Empedocles, J. M. Gregoire, A. G. Kusne, J. Martin, A. Mehta, K. Persson, Z. Trautt, J. Van Duren and A. Zakutayev, Appl. Phys. Rev., 2017, 4, 011105 Search PubMed.
- A. Jain, S. P. Ong, G. Hautier, W. Chen, W. D. Richards, S. Dacek, S. Cholia, D. Gunter, D. Skinner, G. Ceder and K. A. Persson, APL Mater., 2013, 1, 011002 CrossRef.
- A. Jain, K. A. Persson and G. Ceder, APL Mater., 2016, 4, 053102 CrossRef.
- X. Liu, B. Xu, J. Haubrich, R. J. Madix and C. M. Friend, J. Am. Chem. Soc., 2009, 131, 5757–5759 CrossRef CAS PubMed.
- J. C. F. Rodriguez-Reyes, C. M. Friend and R. J. Madix, Surf. Sci., 2012, 606, 1129–1134 CrossRef CAS.
- L. Zhou and R. J. Madix, J. Phys. Chem. C, 2008, 112, 4725–4734 CAS.
- X. Liu, A. Klust, R. J. Madix and C. M. Friend, Appl. Phys. Rev., 2007, 111, 3675–3679 CAS.
- X. Deng, B. K. Min, X. Liu and C. M. Friend, J. Phys. Chem. B, 2006, 110, 15982–15987 CrossRef CAS PubMed.
- D. A. Outka and R. J. Madix, J. Am. Chem. Soc., 1987, 109, 1708–1714 CrossRef CAS.
- B. Xu, X. Liu, J. Haubrich, R. J. Madix and C. M. Friend, Angew. Chem., Int. Ed. Engl., 2009, 48, 4206–4209 CrossRef CAS PubMed.
- S. Karakalos, B. Zugic, K. J. Stowers, M. M. Biener, J. Biener, C. M. Friend and R. J. Madix, Surf. Sci., 2016, 652, 58–66 CrossRef CAS.
- J. A. Rodriguez, S. D. Senanayake, D. Stacchiola, P. Liu and J. Hrbek, Acc. Chem. Res., 2014, 47, 773–782 CrossRef CAS PubMed.
- R. Burch, Phys. Chem. Chem. Phys., 2006, 8, 5483–5500 RSC.
- M. Aresta and A. Dibenedetto, Dalton Trans., 2007, 2975–2992, 10.1039/b700658f.
- M. A. Barteau, M. Bowker and R. J. Madix, J. Catal., 1981, 67, 118–128 CrossRef CAS.
- T. A. Nijhuis, T. Visser and B. M. Weckhuysen, Angew. Chem., Int. Ed. Engl., 2005, 44, 1115–1118 CrossRef CAS PubMed.
- J. T. Carneiro, J. A. Moulijn and G. Mul, J. Catal., 2010, 273, 199–210 CrossRef CAS.
- N. R. Blake and G. L. Griffin, J. Phys. Chem., 1988, 92, 5697–5701 CrossRef CAS.
- X. Y. Lv, G. Lu, Z. Q. Wang, Z. N. Xu and G. C. Guo, ACS Catal., 2017, 7, 4519–4526 CrossRef CAS.
- J. T. Feaster, C. Shi, E. R. Cave, T. Hatsukade, D. N. Abram, K. P. Kuhl, C. Hahn, J. K. Nørskov and T. F. Jaramillo, ACS Catal., 2017, 7, 4822–4827 CrossRef CAS.
- Y. Fang and J. C. Flake, J. Am. Chem. Soc., 2017, 139, 3399–3405 CrossRef CAS PubMed.
- M. A. Barteau and R. J. Madix, Surf. Sci., 1982, 120, 262–272 CrossRef CAS.
- S. W. Jorgensen and R. J. Madix, Surf. Sci, 1983, 130, L291–L293 CrossRef CAS.
- J. C. Rodriguez-Reyes, C. G. Siler, W. Liu, A. Tkatchenko, C. M. Friend and R. J. Madix, J. Am. Chem. Soc., 2014, 136, 13333–13340 CrossRef CAS PubMed.
- S. Karakalos, Y. Xu, F. Cheenicode Kabeer, W. Chen, J. C. Rodriguez-Reyes, A. Tkatchenko, E. Kaxiras, R. J. Madix and C. M. Friend, J. Am. Chem. Soc., 2016, 138, 15243–15250 CrossRef CAS PubMed.
- Y. Xu, W. Chen, E. Kaxiras, C. M. Friend and R. J. Madix, J. Phys. Chem. B, 2018, 122, 555–560 CrossRef PubMed.
- F. Cheenicode Kabeer, W. Chen, R. J. Madix, C. M. Friend and A. Tkatchenko, J. Phys. Chem. C, 2017, 121, 27905–27914 CAS.
- N. Zheng and G. D. Stucky, Chem. Commun., 2007, 3862–3864, 10.1039/b706864f.
- D. I. Enache, J. K. Edwards, P. Landon, B. Solsona-Espriu, A. F. Carley, A. A. Herzing, M. Watanabe, C. J. Kiely, D. W. Knight and G. J. Hutchings, Science, 2006, 311, 362–365 CrossRef CAS PubMed.
- D. A. Outka and R. J. Madix, Surf. Sci., 1987, 179, 351–360 CrossRef CAS.
- B. Xu, X. Liu, J. Haubrich and C. M. Friend, Nat. Chem., 2010, 2, 61–65 CrossRef CAS PubMed.
- T. Hayashi, K. Tanaka and M. Haruta, J. Catal., 1998, 178, 566–575 CrossRef CAS.
- E. Tebandeke, C. Coman, K. Guillois, G. Canning, E. Ataman, J. Knudsen, L. R. Wallenberg, H. Ssekaalo, J. Schnadt and O. F. Wendt, Green Chem., 2014, 16, 1586–1593 RSC.
- J. Liu, F. Wang, T. Xu and Z. Gu, Catal. Lett., 2009, 134, 51–55 CrossRef.
- C. G. F. Siler, T. Cremer, J. C. F. Rodriguez-Reyes, C. M. Friend and R. J. Madix, ACS Catal., 2014, 4, 3281–3288 CrossRef CAS.
- T. Cremer, C. G. Siler, J. C. Rodriguez-Reyes, C. M. Friend and R. J. Madix, J. Phys. Chem. Lett., 2014, 5, 1126–1130 CrossRef CAS PubMed.
- F. Hiebel, B. Shong, W. Chen, R. J. Madix, E. Kaxiras and C. M. Friend, Nat. Commun., 2016, 7, 13139 CrossRef CAS PubMed.
- J. M. Gottfried, K. J. Schmidt, S. L. M. Schroeder and K. Christmann, Surf. Sci., 2003, 525, 184–196 CrossRef CAS.
- G. Kresse and J. Furthmüller, Phys. Rev. B, 1996, 54, 11169–11186 CrossRef CAS.
- G. Kresse and D. Joubert, Phys. Rev. B, 1999, 59, 1758–1775 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- A. Tkatchenko and M. Scheffler, Phys. Rev. Lett., 2009, 102, 073005 CrossRef PubMed.
- C. Kittel, Introduction To Solid State Physics, Wiley, 2004 Search PubMed.
- NIST Chemistry WebBook, NIST Standard Reference Database Number 69, ed. P. J. Linstrom and W. G. Mallard, National Institute of Standards and Technology, Gaithersburg, MD, 20899, 2016, DOI:10.18434/T4D303.
- T. L. Silbaugh, J. S. Boaventura and M. A. Barteau, Surf. Sci., 2016, 650, 64–70 CrossRef CAS.
- C. T. Campbell and J. R. Sellers, J. Am. Chem. Soc., 2012, 134, 18109–18115 CrossRef CAS PubMed.
- E. Mete, M. Yortanli and M. F. Danisman, Phys. Chem. Chem. Phys., 2017, 19, 13756–13766 RSC.
- H. Noda, L.-J. Wan and M. Osawa, Phys. Chem. Chem. Phys., 2001, 3, 3336–3342 RSC.
- M. D. Marcinkowski, C. J. Murphy, M. L. Liriano, N. A. Wasio, F. R. Lucci and E. C. H. Sykes, ACS Catal., 2015, 5, 7371–7378 CrossRef CAS.
- M. Bowker, S. Poulston, R. A. Bennett, P. Stone, A. H. Jones, S. Haq and P. Hollins, J. Mol. Catal. A: Chem., 1998, 131, 185–197 CrossRef CAS.
- S. M. York, S. Haq, K. V. Kilway, J. M. Phillips and F. M. Leibsle, Surf. Sci., 2003, 522, 34–46 CrossRef CAS.
- B. G. Frederick, Q. Chen, F. M. Leibsle, M. B. Lee, K. J. Kitching and N. V. Richardson, Surf. Sci., 1997, 394, 1–25 CrossRef CAS.
- H. Iwai, M. Tobisawa, A. Emori and C. Egawa, Surf. Sci., 2005, 574, 214–218 CrossRef CAS.
- Y. T. Tao, J. Am. Chem. Soc., 1993, 115, 4350–4358 CrossRef CAS.
- A. R. Alemozafar and R. J. Madix, J. Phys. Chem. B, 2004, 108, 14374–14383 CrossRef CAS.
- M. Nowicki, A. Emundts, J. Werner, G. Pirug and H. P. Bonzel, Surf. Rev. Lett., 2000, 07, 25–36 CrossRef CAS.
- M. Bowker, C. Morgan and J. Couves, Surf. Sci., 2004, 555, 145–156 CrossRef CAS.
- E. Hansen and M. Neurock, J. Phys. Chem. B, 2001, 105, 9218–9229 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available: Supporting experimental methods and supporting discussion are included in the supplementary information. See DOI: 10.1039/c7sc05313d |
| ‡ Co-first authors had equal contributions to the work. |
| This journal is © The Royal Society of Chemistry 2018 |