Open Access Article
Open Access ArticlePore closure in zeolitic imidazolate frameworks under mechanical pressure†
Sebastian
Henke
 *a,
Michael T.
Wharmby‡
*a,
Michael T.
Wharmby‡
 b,
Gregor
Kieslich
b,
Gregor
Kieslich
 c,
Inke
Hante
d,
Andreas
Schneemann§
c,
Inke
Hante
d,
Andreas
Schneemann§
 c,
Yue
Wu
c,
Yue
Wu
 e,
Dominik
Daisenberger
b and
Anthony K.
Cheetham
e,
Dominik
Daisenberger
b and
Anthony K.
Cheetham
 e
e
aAnorganische Chemie, Fakultät für Chemie & Chemische Biologie, Technische Universität Dortmund, Otto-Hahn-Str. 6, 44227 Dortmund, Germany. E-mail: sebastian.henke@tu-dortmund.de
bDiamond Light Source Ltd., Harwell Science & Innovation Campus, Didcot, Oxfordshire OX11 0DE, UK
cLehrstuhl für Anorganische und Metallorganische Chemie, Technische Universität München, Lichtenbergstr. 4, 85748 Garching, Germany
dLehrstuhl für Anorganische Chemie II, Fakultät für Chemie & Biochemie, Ruhr-Universität Bochum, Universitätsstraße 150, 44801 Bochum, Germany
eDepartment of Materials Science and Metallurgy, University of Cambridge, 27 Charles Babbage Road, Cambridge, CB3 0FS, UK
First published on 4th January 2018
Abstract
We investigate the pressure-dependent mechanical behaviour of the zeolitic imidazolate framework ZIF-4 (M(im)2; M2+ = Co2+ or Zn2+, im− = imidazolate) with high pressure, synchrotron powder X-ray diffraction and mercury intrusion measurements. A displacive phase transition from a highly compressible open pore (op) phase with continuous porosity (space group Pbca, bulk modulus ∼1.4 GPa) to a closed pore (cp) phase with inaccessible porosity (space group P21/c, bulk modulus ∼3.3–4.9 GPa) is triggered by the application of mechanical pressure. Over the course of the transitions, both ZIF-4 materials contract by about 20% in volume. However, the threshold pressure, the reversibility and the immediate repeatability of the phase transition depend on the metal cation. ZIF-4(Zn) undergoes the op–cp phase transition at a hydrostatic mechanical pressure of only 28 MPa, while ZIF-4(Co) requires about 50 MPa to initiate the transition. Interestingly, ZIF-4(Co) fully returns to the op phase after decompression, whereas ZIF-4(Zn) remains in the cp phase after pressure release and requires subsequent heating to switch back to the op phase. These variations in high pressure behaviour can be rationalised on the basis of the different electron configurations of the respective M2+ ions (3d10 for Zn2+ and 3d7 for Co2+). Our results present the first examples of op–cp phase transitions (i.e. breathing transitions) of ZIFs driven by mechanical pressure and suggest potential applications of these functional materials as shock absorbers, nanodampers, or in mechanocalorics.
Introduction
Flexible metal–organic frameworks (MOFs) have attracted considerable attention in recent years. Their unique responsive properties suggest applications in gas storage and separations, chemical sensing, catalysis, and targeted drug release.1–4 Some flexible MOFs show displacive structural transitions in response to external stimuli, particularly the sorption of guest molecules.1,5–7 Such materials can maintain their intra-framework connectivity while reversibly switching between an open, or large pore form, and a narrow, or closed pore form. The most prominent example from this class of materials is MIL-53 (MIL = Matériaux de l'Institut Lavoisier; M(OH)(bdc); bdc2− = 1,4-benzenedicarboxylate), which shows a very large breathing effect upon gas adsorption (e.g. CO2) and can be prepared with a variety of different metal ions (M3+ = Al3+, Cr3+, etc.).5–8The guest-responsive structural flexibility of several MOFs has been thoroughly investigated and is well documented. The intrinsic structural response of such flexible frameworks to mechanical pressure, however, is relatively unexplored.9–17 This is surprising because flexible MOFs with pressure driven phase transitions are not only of interest for applications as shock absorbers, nanodampers, and supramolecular nanosprings, but might also lead to applications in mechanocalorics.18–25
To the best of our knowledge, examples of breathing phase transitions¶ of MOFs in response to extrinsic mechanical pressure have only been reported for materials of the MIL-53/MIL-47 family (MIL-47 = M(O)(bdc); M4+ = V4+).20–28 All of these frameworks exhibit a winerack-like structure composed of infinite metal-hydroxide or metal-oxide chains, which are crosslinked by linear dicarboxylates (e.g. bdc2− or fumarate) to generate lozenge-shaped channels (sra topology). Under the influence of mechanical pressure the large pore phase of these frameworks transforms to a closed pore phase, whereby the lozenge-shaped channels contract, resulting in a highly anisotropic structural change – under pressure, the long diagonals of the channels expand, while the short diagonals contract.
Here, we report on the high pressure structural behaviour of zeolitic imidazolate frameworks (ZIFs) of the ZIF-4 family and describe an almost isotropic, displacive structural transition under mechanical pressure. ZIF-4(Zn) (1, Zn(im)2 with im− = imidazolate) is a microporous MOF composed of ZnN4 tetrahedra interconnected by im− linkers in the four-connected cag topology.29,301 features a number of unusual properties: it transforms into an amorphous state when heated to about 300 °C and then converts to a non-porous phase with the zni topology on further heating; it can also be melted at temperatures of about 600 °C, and quenched to form ZIF glasses.31–36
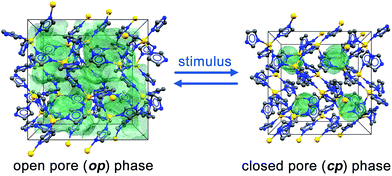
Recently, we reported that 1 also undergoes a reversible phase transition at lower temperatures. The open pore (op) phase of 1 transforms to a closed pore (cp) phase upon cooling the material below 140 K under vacuum (Fig. 1).37 This cp phase features the same topology (cag) and connectivity as the original op phase; however, the unit cell contracts almost isotropically by about 23%. In this breathing process, all im− linkers in the material undergo a concerted rotation, which results in a 3D inward folding of the framework, leading to a drastic reduction of the pore volume (from 39% to 9% of the crystal volume, see ESI†). The small pores remaining in the cp phase are isolated and hence inaccessible to any guest molecule. The thermodynamic driving force for the phase transition is the higher enthalpic stability of the cp phase, which arises from attractive dispersion interactions between the molecular building units, which move closer to each other in the cp phase.37 At higher temperature the op phase is stabilised by vibrational entropy.
Encouraged by our previous findings, we have now investigated the high pressure behaviour of 1 as well as its isostructural cobalt-based derivative ZIF-4(Co)38 (Co(im)2, 2) via high pressure, synchrotron powder X-ray diffraction and mercury intrusion experiments. Breathing phase transitions triggered by comparatively low mechanical pressures are apparent for both ZIF materials, extending the family of MOFs, which show mechano-switching behaviour, to ZIFs.
Results and discussion
To investigate the structural behaviour of 1 and 2 as a function of mechanical pressure, we conducted high pressure powder X-ray diffraction (HP-PXRD). The experiments were performed at beamline I15, Diamond Light Source (Oxon., UK) using a monochromatic X-ray beam with a wavelength of 0.41334 Å and membrane diamond anvil cells (mDACs) for the high pressure environment. Prior to the experiment, the ZIF samples were thoroughly evacuated at 130 °C under dynamic vacuum to ensure complete activation. Absence of any adsorbed guest molecules was verified by elemental and thermogravimetric analyses as well as IR spectroscopy of the powder samples (Fig. S15 and S16†). In addition, 1H NMR spectroscopy was carried out on evacuated samples digested in DMSO-d6/DCl/D2O. Residual organic solvents could not be detected by 1H NMR spectroscopy (Fig. S17 and S18†). For HP-PXRD measurements, the samples were loaded into mDACs under an inert atmosphere inside an Ar-filled glove box with an alkali halide internal pressure standard (NaCl for 1 and KBr for 2). Fluorinert FC-70, which is too large to penetrate into the micropores of 1 and 2, was used as a pressure transmitting fluid. Diffraction data were collected from ambient pressure up to about 2–3 GPa. The HP-PXRD patterns were analysed by structure-less Pawley refinement (see ESI† for further details).391 and 2 are isostructural at ambient pressure and the diffraction patterns are in accordance with the op phase of 1 reported previously (orthorhombic, Pbca, a = 15.50051(15) Å, b = 15.52013(14) Å, c = 18.05823(17) Å, V = 4344.27(7) Å3; see Fig. 2).37 Upon increasing hydrostatic pressure, 1 rapidly undergoes a phase transition to a new phase, which goes to completion by about 75 MPa (Fig. 2 and S4†). The corresponding PXRD pattern is similar, but not identical, to the diffraction pattern of the established low temperature cp phase of 1 (orthorhombic Pbca, a = 14.26686(9) Å, b = 14.28427(8) Å, c = 16.41270(11) Å, V = 3344.77(4) Å3).37 The pattern recorded at ∼75 MPa is more complex and features additional Bragg peaks, which led us to the conclusion that the high pressure cp phase of 1 differs from the established low temperature cp phase. Additional Bragg peaks in the pattern suggest a distortion of the structure from the orthorhombic to a monoclinic lattice. We tried to fit the PXRD pattern in monoclinic settings based on the most symmetric monoclinic subgroups (space groups P21/b11, P121/c1 or P1121/a) of the original orthorhombic structure (space group Pbca).|| The best fit to the experimental data was found for the monoclinic setting in P121/c1, with lattice parameters similar to the ones for the low temperature cp phase (Table 1 and Fig. 3). Hence, we conclude that the high pressure cp phase of 1 is indeed similar to the low temperature cp phase, but it involves a small shear element as indicated by a β angle of 91.55(3)°. It is noteworthy that the unit cell volume of the monoclinic high pressure cp phase of 1 is slightly larger (V = 3457(7) Å3) than the unit cell volume of the orthorhombic low temperature cp phase (V = 3345(7) Å3), which might originate from higher vibrational entropy at ambient temperature (HP-PXRD experiment) compared to at 80 K (variable temperature PXRD experiment).40 Nevertheless, the unit cell volume reduces by about 21% over the pressure-induced phase transition.
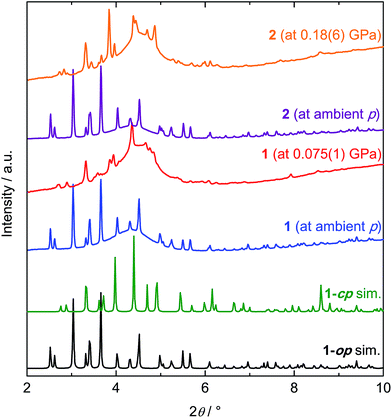 | ||
| Fig. 2 Collection of PXRD patterns of 1 and 2 recorded at ambient pressure (blue and purple) and at high pressure (orange and red). Diffractograms were recorded using a monochromatic X-ray beam with λ = 0.41334 Å. Simulated diffraction patterns for the room temperature op and low temperature cp phases of 1 (taken from ref. 37) are shown for comparison (black and green). The broad hump in the background of the experimental patterns is attributed to diffuse scattering from the pressure transmitting fluid. The patterns have been normalised and offset vertically for clarity. | ||
| Compound | 1-op | 1-cp | 2-op | 2-cp |
| p/GPa | ∼10−4 | 0.075(10) | ∼10−4 | 0.18(6) |
| a/Å | 15.502(3) | 14.235(12) | 15.440(2) | 13.981(9) |
| b/Å | 15.524(2) | 14.874(18) | 15.5102(18) | 15.045(13) |
| c/Å | 18.079(3) | 16.33(2) | 18.082(2) | 16.636(15) |
| α/° | 90 | 90 | 90 | 90 |
| β/° | 90 | 91.55(3) | 90 | 90.761(11) |
| γ/° | 90 | 90 | 90 | 90 |
| V/Å3 | 4350.9(13) | 3457(7) | 4330.1(9) | 3499(5) |
| S.G. | Pbca | P21/c | Pbca | P21/c |
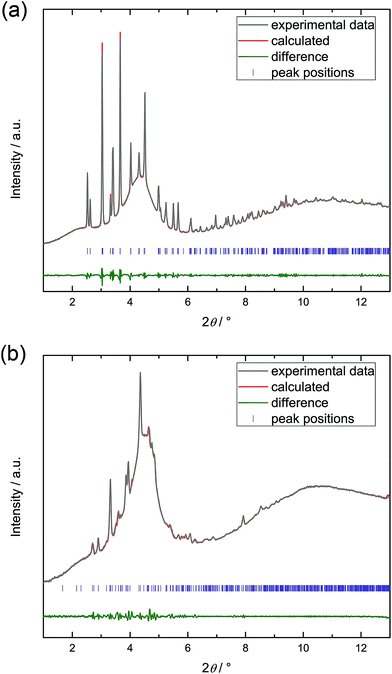 | ||
| Fig. 3 Pawley fit to the diffraction patterns of compound 1 recorded at ambient pressure (a) and at 0.075(10) GPa (b). Diffractograms were recorded using a monochromatic X-ray beam with λ = 0.41334 Å. The very broad peak (centered at ∼4.4°) underneath the Bragg peaks is attributed to the diffuse scattering from the pressure transmitting fluid FC-70. Crystallographic parameters are listed in Table 1. | ||
Further increasing the mechanical pressure results in a monotonic contraction of the cp phase, which is apparent by the shifting of the Bragg peaks to higher 2θ angles (Fig. S4†). In this process the reflections also get much broader, finally resulting in a largely amorphised material at ∼1 GPa. We note that the amorphisation of 1 seems to be irreversible since the largely amorphised material does not recover its original crystalline state after returning to ambient pressure (see ESI†). This observation deviates from previous findings by Bennett et al., who reported reversible amorphisation of 1 under mechanical pressure.32 The reason for this difference may be that we compressed 1 to a maximum pressure of about 2 GPa in the HP-PXRD experiment, while Bennett et al. compressed the material only to about 1 GPa. The higher maximum pressure of our experiment may result in irreversible structure collapse, while the amorphisation is reversible if a pressure of 1 GPa is not exceeded.
Also in contrast to our findings, Bennett et al. did not observe the op–cp phase transition of 1 in their previous HP-PXRD study.32 In their experiment the material remained in the op phase before amorphisation. The origin of the different phase behaviour in the previous study might be either incomplete sample evacuation or adsorption of moisture from the atmosphere during sample preparation, both of which could impede the observation of the op–cp transition. We have already shown that, in contrast to guest-free 1, DMF-containing 1 (op form) does not transform to the cp form upon cooling to cryogenic temperatures.37 It therefore seems natural that the presence of even small amounts of guests could also prevent the op–cp transition under the stimulus of mechanical pressure (see ESI† for further details).
As anticipated, the cobalt-derivative 2 behaves similarly to 1, transforming from the op phase to a cp phase under the influence of mechanical pressure (Fig. 2 and S5†). However, the pressure required to complete the transition is significantly higher (∼180 MPa). The pattern of the high pressure phase of 2 is also similar to the reference pattern of the low temperature cp phase of 1, but can again only be fitted with a monoclinic unit cell in the subgroup P21/c (see ESI† for details). The unit cell volume of 2 decreases by ∼19% at the op–cp transition. Increasing the mechanical pressure further leads to significant peak broadening and finally an irreversible transformation to a largely amorphous material at pressures in the range from 1–3 GPa (Fig. S5†). Table 1 presents the crystallographic data of the op and cp phases as determined by structure-less Pawley refinement for both compounds.
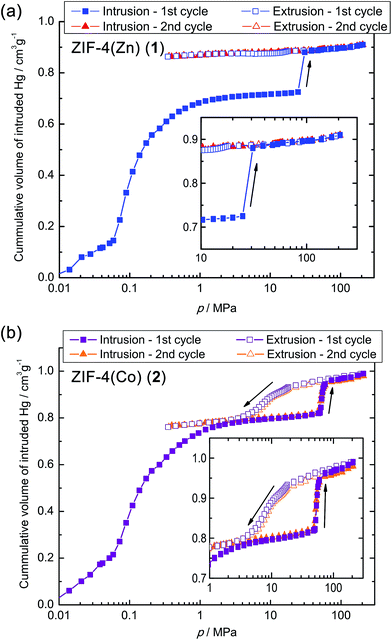
In order to obtain more information about the unusual op–cp phase transitions of both ZIF-4 derivatives in the pressure region below 200 MPa, mercury intrusion experiments were carried out. Mercury is a non-wetting liquid that cannot penetrate into micropores and acts as a hydrostatic pressure transmitting fluid. Hence, mercury intrusion experiments are ideally suited for the investigation of pressure-driven breathing transitions in microporous solids, resulting in an abrupt, large contraction.20–26 Sharp steps in the intrusion curve can be directly assigned to phase transitions involving a density change (i.e. volume change) of the material under study. Advantageously, in the lower pressure range (1–200 MPa), which is of interest here, mercury intrusion experiments allow a significantly better pressure resolution than HP-PXRD experiments.
The mercury intrusion experiments were performed on freshly activated and finely ground powders of 1 and 2 in the pressure range from 10−3 to about 210 MPa (Fig. 4). Samples for these experiments were prepared in an Ar-filled glove box to prevent any adsorption of moisture in the guest-free ZIFs. Up to a pressure of about 1 MPa, mercury intrusion is associated with filling of the inter-particle voids of the loose crystalline powder. Beyond this point, the ZIF microcrystals are totally surrounded by mercury and increasing pressure is then applied hydrostatically to the sample.
A sharp step in the mercury intrusion curve of 1 is visible at a surprisingly low pressure of about 28 MPa. This step cannot be attributed to the ingress of mercury into the compound's pores, since according to the Washburn equation,41 the step would indicate an effective pore diameter (d) of 40–50 nm (see ESI†). The pores of 1, however, lie well within the microporous range (d < 2 nm). The measured volume change ΔVmeas at the step of the intrusion curve is directly proportional to the decrease in unit cell volume or the increase in sample density at the phase transition. ΔVmeas amounts to 0.16 cm3 g−1 for 1, which is close to the value expected for the op–cp phase transition (ΔVcalc = 0.169 cm3 g−1; based on the change in unit cell volume determined from HP-PXRD). Hence, the prominent step in the intrusion curve can directly be ascribed to the op–cp phase transition of 1. Noticeably, the subsequent mercury extrusion branch does not show any steps, which indicates that the op–cp phase transition is irreversible and that 1 remains in the contracted cp phase upon decompression. Consequently, a successive second intrusion–extrusion cycle does not show any steps associated with a phase transition.
Noticeably, the threshold pressure for the op–cp transition, indicated by the mercury intrusion curve (∼28 MPa), is significantly lower than that expected on the basis of the HP-PXRD experiment (phase transition completed at ∼75 MPa). This variation most likely originates from the different pressure transmitting medium (FC-70 vs. mercury) used in the complementary experiments (HP-PXRD vs. mercury intrusion). Large variations of the threshold pressure as a function of the pressure transmitting fluid (i.e. silicone oil vs. mercury) were also observed for the large pore to closed pore phase transitions of MIL-53-type materials.23,24,26 For these materials, the use of silicone oil as pressure transmitting fluid resulted in a much higher threshold pressure compared to the use of mercury. This phenomenon was explained by a partial penetration of the chain ends of the silicone oil molecules into the pore opening of the MIL-53-type materials. In our HP-PXRD experiments we used Fluorinert FC-70 as pressure transmitting fluid. Similar to silicone oil, FC-70 might also partially penetrate the pore apertures of the microporous ZIF-4(M) compounds, which results in a shift of the op–cp transition to higher pressures compared to the use of mercury. Since mercury is a non-wetting fluid, however, the mercury intrusion data are expected to yield information on the intrinsic thermodynamic behaviour of the microporous material under study.
For reasons of comparison to other mechano-switchable MOFs (i.e. MIL-53/MIL-47-type compounds) we calculated the work (Wtrans) done on the system during the op–cp phase transition on the basis of the mercury intrusion curves (see ESI† for details).**Wtrans amounts to only ∼4.4 J g−1 for compound 1. Highlighting the pronounced flexibility of 1, this value is slightly lower than the work computed for the highly flexible MIL-53(Al) (∼6.6 J g−1) and significantly lower than the work calculated for other MIL-53 derivatives (∼14 J g−1 for MIL-53(Cr) and ∼33 J g−1 for MIL-47(V); all values were computed on the basis of mercury intrusion data).21,22,28
Interestingly, 2 shows a different behaviour. Again a sharp step for the op–cp transition is apparent in the intrusion curve (Fig. 4), but, at a higher pressure of about 50 MPa (compared to 28 MPa for 1). This pressure would correlate with an effective pore diameter of about 20 nm, which again cannot be attributed to a filling of the micropores present in 2 (see ESI†). The volume change ΔVmeas at the step of the intrusion curve amounts to 0.15 cm3 g−1, which again is in good agreement with the value expected for the op–cp phase transition (ΔVcalc = 0.162 cm3 g−1; based on the change in unit cell volume determined from HP-PXRD). Wtrans is ∼7.3 J g−1 (see ESI†), which is almost twice as large as for 1 due to the significantly higher phase transition pressure of 2. Surprisingly, compound 2 undergoes the inverse cp–op phase transition at pressures below 20 MPa, which is apparent as a shallow but distinct step during extrusion. The inverse transition is complete at a rather low pressure of only about 4 MPa, which gives rise to a very large hysteresis (width ∼46 MPa). However, the fact that the entire volume change associated with the transition is reversible demonstrates that the phase transition is indeed completely reversible for 2. A successive intrusion–extrusion cycle further underlines the reversibility of the op–cp transition of 2 under the conditions of the mercury intrusion experiment. The second cycle is virtually identical to the first cycle, except for the interparticle penetration at low pressures. A hysteretic phase behaviour as a function of an external variable (e.g. mechanical pressure, gas pressure, temperature) is typical for such kind of flexible MOFs and has also been observed for mechanical pressure-driven structural changes of the carboxylate-based MIL-53(Cr) and MIL-47(V) materials.20,21 Taking into account the results of the mercury intrusion and the HP-PXRD experiments, we can conclude that the op–cp phase transition of 2 is reversible at least if the maximum pressure is limited to about 210 MPa. At a certain threshold pressure the compound amorphises and if a pressure of about 2–3 GPa is achieved (as in the HP-PXRD experiment), this amorphisation is irreversible.
On the basis of linear fits to the mercury intrusion data, the bulk moduli (K) of the op and cp phases of 1 and 2 can be estimated (see ESI†). We found very low bulk moduli for the op phases of both materials (K = 1.42 GPa for 1-op and K = 1.40 GPa for 2-op), which reflects the exceptionally high flexibility and compressibility of the op phases of both materials. These values are even lower than the bulk modulus reported for the highly flexible large pore phase of MIL-53(Cr) (K ∼1.8–2.0 GPa (ref. 28 and 42)) and also lower than previously reported for 1 (K = 2.6 GPa, determined from HP-PXRD data;32K = 2.41 GPa, determined via ab initio calculations43). The bulk moduli of the contracted cp phases are considerably larger (K = 4.88 GPa for 1-cp and K = 3.31 GPa for 2-cp), which arises due to their higher densities and very low porosities.
Since both ZIF-4(M) materials are isostructural, the different properties of their metal cations (Zn2+vs. Co2+) must account for their different high pressure behaviour. The ionic radii of tetrahedrally coordinated Zn2+ and Co2+ are very similar (Shannon radii:44 0.74 Å for Zn2+ and 0.72 Å for Co2+), which results in almost identical unit cell parameters and unit cell volumes of their op phases (see Table 1). However, both metal ions feature markedly different electronegativities45 (1.65 for Zn and 1.88 for Co) and specific electron configurations (3d10 for Zn2+vs. 3d7 for Co2+). We hypothesise that the bonding of the im− linkers to the Zn2+ centres of compound 1 can solely be described by σ-bonding, while the 3d7 electron configuration of Co2+ strongly suggests the presence of additional ligand-to-metal π-bonding for compound 2. The π-bonding in 2 results qualitatively in stronger imidazolate–metal bonds compared to 1, where π-bonding is absent. Furthermore, the higher electronegativity of Co suggests more covalent (directional) ligand-to-metal bonding for 2, while in 1 these bonds are more ionic (non-directional) as a consequence of the lower electronegativity of Zn.
The pressure dependent phase behaviour of 1 and 2 directly reflects these fundamental chemical differences between their respective metal ions. It is evident that the phase transition from the op to the cp phase is associated with very significant distortions of the MN4 tetrahedra and the M–im–M bonding angles (see ESI, Tables S1 and S2†). As a consequence of the more covalent and directional ligand-to-metal bonds, a higher mechanical pressure (∼50 MPa) is needed to initiate the op–cp phase transition in 2, while compound 1 requires a much lower pressure (∼28 MPa). Advanced density functional theory calculations could shed light on the influence of the ligand-to-metal bonding on the high pressure phase behaviour of these compounds. These complex calculations (open shell nature of the 3d7 Co2+ system), however, are beyond the scope of this work.
Nonetheless, the irreversibility of the op–cp transition of 1 in the mercury intrusion experiment (maximum pressure ∼210 MPa) is surprising, because it was found that the op phase is entropically favoured over the cp phase at ambient temperature and pressure.37 To verify the results from the mercury intrusion experiments, we performed an additional ex situ pressurisation experiment. A finely ground powder of freshly evacuated 1 was pelletized in a conventional pellet press (see ESI† for details) using a uniaxial pressure of ∼190 MPa for about 10 min. After pressure release the obtained pellet was finely ground again and the material analysed by PXRD. The majority of the peaks in the diffraction pattern of pelletized 1 can be assigned to the cp phase, while some material remains in the op phase (Fig. S14†). We ascribe this to pressure inhomogeneities in the simple pelletizing experiment (uniaxial compression) compared to the previous mercury intrusion and HP-PXRD studies (hydrostatic compression). Notably, most of the contracted cp phase of the pelletized sample can be returned to the op phase by heating the sample to 130 °C for 8 h under vacuum. This finding strongly suggests that the op–cp phase transition is also reversible for 1, but returning to the op phase requires a significant energy barrier to be overcome.
In fact, the inverse cp–op transition of 2 also involves a large energy barrier which gives rise to the very large hysteresis (width ∼46 MPa) in the mercury intrusion experiment. Hence, we postulate that the lack of the cp–op transition upon decompression of 1 at ambient temperature originates from a similarly large pressure hysteresis. Thus, the cp phase of 1 is kinetically trapped after decompression at ambient temperature. However, the fact that the op phase of 1 can be recovered by heating the material to 130 °C clearly evidences that this phase is thermodynamically favoured over the cp phase at ambient pressure. For thermodynamic reasons (Clausius–Clapeyron relation), the threshold pressures for the op–cp transition (as well as for the reverse cp–op transition) will shift to lower values if the temperature is decreased or to higher values if the temperature is increased. Hence, if the mercury intrusion experiments could be done at 130 °C the op–cp transition should be directly reversible for compound 1 as well.
The strong influence of the metal cation on the material's mechanical phase behaviour suggests various chemical ways for a systematic fine-tuning of these properties. In the future, solid solution compounds containing both metal ions (Zn2+ and Co2+) in varying ratios or even other dopant cations, such as Fe2+, should be investigated.1,46–49 Moreover, we anticipate that these ZIFs, as well as the related MIL-53/MIL-47 materials, could be very interesting materials for applications in mechanocalorics. We demonstrated that the molar entropy change, ΔSm, for the low temperature op–cp phase transition of 1 amounts to about 60 J K−1 mol−1.37 If we assume a similar ΔS for the pressure-driven op–cp transition, a gravimetric ΔSg of approx. 300 J K−1 kg−1 can be expected. This value is very high, even in comparison to current benchmark materials in the field of mechanocalorics (ΔSg ∼100–150 J K−1 kg−1).19 In future studies we aim to investigate the mechanocaloric properties of these materials in detail.
Conclusions
Our findings add the first group of ZIF materials to the small family of highly flexible MOFs that show breathing phase transitions under a stimulus of mechanical pressure. Open pore to closed pore phase transitions with a contraction of about 19–21% of the crystal volume are apparent for ZIF-4(Zn) and ZIF-4(Co). The metal ion, and thus the nature of ligand-to-metal bonding, plays a crucial role, not only for the phase transition pressure, but also for the immediate reversibility and repeatability of the process. For ZIF-4(Co), the transition is directly reversible upon decompression (at least if pmax ≤ 210 MPa), while the phase transition is irreversible upon decompression for ZIF-4(Zn) but can be reversed via heating the material to 130 °C. This discovery proposes novel applications of these microporous ZIFs as shock absorbers (ZIF-4(Zn); irreversible transition) and nanodampers or in mechanocalorics (ZIF-4(Co); reversible transition). Our results further suggest there may exist similar breathing phase transitions in other ZIFs – a property so far mainly demonstrated by carboxylate-based MOFs.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We thank Diamond Light Source for the allocation of beamtime at I15 (EE12370). SH acknowledges the Alexander von Humboldt Foundation and the DFG Priority Program 1928 COORNETs for funding. The authors thank Wayne Skelton-Hough for assistance with mercury intrusion measurements.Notes and references
- A. Schneemann, V. Bon, I. Schwedler, I. Senkovska, S. Kaskel and R. A. Fischer, Chem. Soc. Rev., 2014, 43, 6062 RSC
.
- S. Horike, S. Shimomura and S. Kitagawa, Nat. Chem., 2009, 1, 695 CrossRef CAS PubMed
.
- G. Férey and C. Serre, Chem. Soc. Rev., 2009, 38, 1380 RSC
.
- Z. Chang, D. H. Yang, J. Xu, T. L. Hu and X. H. Bu, Adv. Mater., 2015, 27, 5432 CrossRef CAS PubMed
.
- C. Serre, F. Millange, C. Thouvenot, M. Noguès, G. Marsolier, D. Louër and G. Férey, J. Am. Chem. Soc., 2002, 124, 13519 CrossRef CAS PubMed
.
- C. Serre, S. Bourrelly, A. Vimont, N. A. Ramsahye, G. Maurin, P. L. Llewellyn, M. Daturi, Y. Filinchuk, O. Leynaud, P. Barnes and G. Férey, Adv. Mater., 2007, 19, 2246 CrossRef CAS
.
- A. M. Walker, B. Civalleri, B. Slater, C. Mellot-Draznieks, F. Cora, C. M. Zicovich-Wilson, G. Roman-Perez, J. M. Soler and J. D. Gale, Angew. Chem., Int. Ed., 2010, 49, 7501 CrossRef CAS PubMed
.
- F. Millange, N. Guillou, R. I. Walton, J.-M. Grenèche, I. Margiolaki and G. Férey, Chem. Commun., 2008, 4732 RSC
.
- P. Serra-Crespo, E. Stavitski, F. Kapteijn and J. Gascon, RSC Adv., 2012, 2, 5051 RSC
.
- K. J. Gagnon, C. M. Beavers and A. Clearfield, J. Am. Chem. Soc., 2013, 135, 1252 CrossRef CAS PubMed
.
- P. Serra-Crespo, A. Dikhtiarenko, E. Stavitski, J. Juan-Alcañiz, F. Kapteijn, F.-X. Coudert and J. Gascon, CrystEngComm, 2015, 17, 276 RSC
.
- J. Im, N. Yim, J. Kim, T. Vogt and Y. Lee, J. Am. Chem. Soc., 2016, 138, 11477 CrossRef CAS PubMed
.
- S. A. Moggach, T. D. Bennett and A. K. Cheetham, Angew. Chem., Int. Ed., 2009, 48, 7087 CrossRef CAS PubMed
.
- A. J. Graham, D. R. Allan, A. Muszkiewicz, C. A. Morrison and S. A. Moggach, Angew. Chem., Int. Ed., 2011, 50, 11138 CrossRef CAS PubMed
.
- A. J. Graham, J. C. Tan, D. R. Allan and S. A. Moggach, Chem. Commun., 2012, 48, 1535 RSC
.
- A. J. Graham, A. M. Banu, T. Duren, A. Greenaway, S. C. McKellar, J. P. Mowat, K. Ward, P. A. Wright and S. A. Moggach, J. Am. Chem. Soc., 2014, 136, 8606 CrossRef CAS PubMed
.
- S. C. McKellar, A. J. Graham, D. R. Allan, M. I. Mohideen, R. E. Morris and S. A. Moggach, Nanoscale, 2014, 6, 4163 RSC
.
- A. Kitanovski, U. Plaznik, U. Tomc and A. Poredoš, Int. J. Refrig., 2015, 57, 288 CrossRef
.
- L. Manosa and A. Planes, Adv. Mater., 2017, 29, 1603607 CrossRef PubMed
.
- I. Beurroies, M. Boulhout, P. L. Llewellyn, B. Kuchta, G. Férey, C. Serre and R. Denoyel, Angew. Chem., Int. Ed., 2010, 49, 7526 CrossRef CAS PubMed
.
- P. G. Yot, Q. Ma, J. Haines, Q. Yang, A. Ghoufi, T. Devic, C. Serre, V. Dmitriev, G. Férey, C. Zhong and G. Maurin, Chem. Sci., 2012, 3, 1100 RSC
.
- P. G. Yot, Z. Boudene, J. Macia, D. Granier, L. Vanduyfhuys, T. Verstraelen, V. Van Speybroeck, T. Devic, C. Serre, G. Ferey, N. Stock and G. Maurin, Chem. Commun., 2014, 50, 9462 RSC
.
- J. Rodriguez, I. Beurroies, T. Loiseau, R. Denoyel and P. L. Llewellyn, Angew. Chem., Int. Ed., 2015, 54, 4626 CrossRef CAS PubMed
.
- P. G. Yot, L. Vanduyfhuys, E. Alvarez, J. Rodriguez, J.-P. Itié, P. Fabry, N. Guillou, T. Devic, I. Beurroies, P. L. Llewellyn, V. Van Speybroeck, C. Serre and G. Maurin, Chem. Sci., 2016, 7, 446 RSC
.
- P. Ramaswamy, J. Wieme, E. Alvarez, L. Vanduyfhuys, J.-P. Itié, P. Fabry, V. Van Speybroeck, C. Serre, P. G. Yot and G. Maurin, J. Mater. Chem. A, 2017, 5, 11047 CAS
.
- J. Rodriguez, I. Beurroies, M. V. Coulet, P. Fabry, T. Devic, C. Serre, R. Denoyel and P. L. Llewellyn, Dalton Trans., 2016, 45, 4274 RSC
.
- P. G. Yot, K. Yang, V. Guillerm, F. Ragon, V. Dmitriev, P. Parisiades, E. Elkaïm, T. Devic, P. Horcajada, C. Serre, N. Stock, J. P. S. Mowat, P. A. Wright, G. Férey and G. Maurin, Eur. J. Inorg. Chem., 2016, 2016, 4424 CrossRef CAS
.
- A. V. Neimark, F.-X. Coudert, C. Triguero, A. Boutin, A. H. Fuchs, I. Beurroies and R. Denoyel, Langmuir, 2011, 27, 4734 CrossRef CAS PubMed
.
- Y. Q. Tian, Y. M. Zhao, Z. X. Chen, G. N. Zhang, L. H. Weng and D. Y. Zhao, Chem.–Eur. J., 2007, 13, 4146 CrossRef CAS PubMed
.
- K. S. Park, Z. Ni, A. P. Cote, J. Y. Choi, R. Huang, F. J. Uribe-Romo, H. K. Chae, M. O'Keeffe and O. M. Yaghi, Proc. Natl. Acad. Sci. U. S. A., 2006, 103, 10186 CrossRef CAS PubMed
.
- T. D. Bennett, A. L. Goodwin, M. T. Dove, D. A. Keen, M. G. Tucker, E. R. Barney, A. K. Soper, E. G. Bithell, J. C. Tan and A. K. Cheetham, Phys. Rev. Lett., 2010, 104, 115503 CrossRef PubMed
.
- T. D. Bennett, P. Simoncic, S. A. Moggach, F. Gozzo, P. Macchi, D. A. Keen, J. C. Tan and A. K. Cheetham, Chem. Commun., 2011, 47, 7983 RSC
.
- T. D. Bennett, J. C. Tan, Y. Yue, E. Baxter, C. Ducati, N. J. Terrill, H. H. Yeung, Z. Zhou, W. Chen, S. Henke, A. K. Cheetham and G. N. Greaves, Nat. Commun., 2015, 6, 8079 CrossRef CAS PubMed
.
- T. D. Bennett, S. Cao, J. C. Tan, D. A. Keen, E. G. Bithell, P. J. Beldon, T. Friscic and A. K. Cheetham, J. Am. Chem. Soc., 2011, 133, 14546 CrossRef CAS PubMed
.
- M. R. Ryder and J. C. Tan, Dalton Trans., 2016, 45, 4154 RSC
.
- R. Gaillac, P. Pullumbi, K. A. Beyer, K. W. Chapman, D. A. Keen, T. D. Bennett and F. X. Coudert, Nat. Mater., 2017, 16, 1149 CrossRef CAS PubMed
.
- M. T. Wharmby, S. Henke, T. D. Bennett, S. R. Bajpe, I. Schwedler, S. P. Thompson, F. Gozzo, P. Simoncic, C. Mellot-Draznieks, H. Tao, Y. Yue and A. K. Cheetham, Angew. Chem., Int. Ed., 2015, 54, 6447 CrossRef CAS PubMed
.
- Y.-Q. Tian, Z.-X. Chen, L.-H. Weng, H.-B. Guo, S. Gao and D. Y. Zhao, Inorg. Chem., 2004, 43, 4631 CrossRef CAS PubMed
.
- G. S. Pawley, J. Appl. Crystallogr., 1981, 14, 357 CrossRef CAS
.
- B. Fultz, Prog. Mater. Sci., 2010, 55, 247 CrossRef CAS
.
- H. Giesche, Part. Part. Syst. Charact., 2006, 23, 9 CrossRef
.
- Q. Ma, Q. Yang, A. Ghoufi, G. Férey, C. Zhong and G. Maurin, Dalton Trans., 2012, 41, 3915 RSC
.
- J.-C. Tan, B. Civalleri, A. Erba and E. Albanese, CrystEngComm, 2015, 17, 375 RSC
.
- R. D. Shannon, Acta Crystallogr., Sect. A: Cryst. Phys., Diffr., Theor. Gen. Crystallogr., 1976, 32, 751 CrossRef
.
- A. L. Allred, J. Inorg. Nucl. Chem., 1961, 17, 215 CrossRef CAS
.
- I. Schwedler, S. Henke, M. T. Wharmby, S. R. Bajpe, A. K. Cheetham and R. A. Fischer, Dalton Trans., 2016, 45, 4230 RSC
.
- F. Nouar, T. Devic, H. Chevreau, N. Guillou, E. Gibson, G. Clet, M. Daturi, A. Vimont, J. M. Greneche, M. I. Breeze, R. I. Walton, P. L. Llewellyn and C. Serre, Chem. Commun., 2012, 48, 10237 RSC
.
- H. Deng, C. J. Doonan, H. Furukawa, R. B. Ferreira, J. Towne, C. B. Knobler, B. Wang and O. M. Yaghi, Science, 2010, 327, 846 CrossRef CAS PubMed
.
- H. Zhang, S. Hwang, M. Wang, Z. Feng, S. Karakalos, L. Luo, Z. Qiao, X. Xie, C. Wang, D. Su, Y. Shao and G. Wu, J. Am. Chem. Soc., 2017, 139, 14143 CrossRef CAS PubMed
.
Footnotes |
| † Electronic supplementary information (ESI) available: Experimental details; synthetic procedures; supplementary data analyses; additional PXRD, thermal and elemental analyses as well as IR and 1H NMR spectroscopy data. See DOI: 10.1039/c7sc04952h |
| ‡ Present address: Deutsches Elektronen-Synchrotron (DESY), Notkestr. 85, 22607 Hamburg, Germany. |
| § Present address: Sandia National Laboratories, Livermore, CA 94551-0969, USA. |
| ¶ In the MOF literature, the term breathing has not only been used for phase transitions that result in large changes of accessible pore volume upon gas or guest adsorption, but also for related transitions triggered by other stimuli, such as temperature or mechanical pressure. The term breathing is used here to underline the huge differences in unit cell volume (density) and accessible pore space between the two involved phases. |
| || We use the extended Hermann–Mauguin Symbols here to illustrate the relationship between the monoclinic settings and the original orthorhombic setting (space group Pbca). The unconventional monoclinic settings P21/b11 and P1121/a can be converted to the standard setting P21/c (extended symbol P121/c1) by permuting the crystallographic axes (see ESI† for details). |
| ** Obviously, Wtrans depends on the actual phase transition pressure. The phase transition pressure, however, varies as a function of the utilised pressure transmitting fluid. In the following discussion, we only compare values of Wtrans, which have been determined on the basis of mercury intrusion data, to ensure their direct comparability. |
| This journal is © The Royal Society of Chemistry 2018 |