Open Access Article
Open Access ArticleMachine learning for the structure–energy–property landscapes of molecular crystals†
Félix Musil‡
 *a,
Sandip De‡
*a,
Sandip De‡ *a,
Jack Yang
*a,
Jack Yang b,
Joshua E. Campbell
b,
Joshua E. Campbell b,
Graeme M. Day
b,
Graeme M. Day b and
Michele Ceriotti
b and
Michele Ceriotti a
a
aNational Center for Computational Design and Discovery of Novel Materials (MARVEL), Laboratory of Computational Science and Modelling, Institute of Materials, Ecole Polytechnique Federale de Lausanne, Lausanne, Switzerland. E-mail: felix.musil@epfl.ch; sandip.de@epfl.ch
bSchool of Chemistry, University of Southampton, Highfield, Southampton, UK
First published on 12th December 2017
Abstract
Molecular crystals play an important role in several fields of science and technology. They frequently crystallize in different polymorphs with substantially different physical properties. To help guide the synthesis of candidate materials, atomic-scale modelling can be used to enumerate the stable polymorphs and to predict their properties, as well as to propose heuristic rules to rationalize the correlations between crystal structure and materials properties. Here we show how a recently-developed machine-learning (ML) framework can be used to achieve inexpensive and accurate predictions of the stability and properties of polymorphs, and a data-driven classification that is less biased and more flexible than typical heuristic rules. We discuss, as examples, the lattice energy and property landscapes of pentacene and two azapentacene isomers that are of interest as organic semiconductor materials. We show that we can estimate force field or DFT lattice energies with sub-kJ mol−1 accuracy, using only a few hundred reference configurations, and reduce by a factor of ten the computational effort needed to predict charge mobility in the crystal structures. The automatic structural classification of the polymorphs reveals a more detailed picture of molecular packing than that provided by conventional heuristics, and helps disentangle the role of hydrogen bonded and π-stacking interactions in determining molecular self-assembly. This observation demonstrates that ML is not just a black-box scheme to interpolate between reference calculations, but can also be used as a tool to gain intuitive insights into structure–property relations in molecular crystal engineering.
Introduction
Molecular crystals possess a diverse range of applications, including pharmaceutical,1,2 electronics3,4 and the food industry.5 The directed assembly of molecules into crystalline materials with targeted properties is a central goal of the active research field of crystal engineering. However, material design guided by empirical rules of self-assembly often exhibits inconsistent success, particularly for the crystallization of molecular solids, because it is generally impossible to predict the outcome of self-assembly that is directed by many competing, weak non-covalent intermolecular interactions. A typical example is the phenomenon of polymorphism in molecular crystals,6–8 whereby a given molecule can crystallize into different solid forms. This is a critical issue, especially for the pharmaceutical industry, where properties of molecules, such as dissolution rate, must be strictly controlled because they can be significantly affected by the presence of different polymorphs. Polymorphism also affects the opto-electronic performance of organic semiconductors, which are used in flexible electronic devices. To overcome these challenges, computational methods have been developed for crystal structure prediction (CSP) of organic molecules; over the past decade, CSP has been developed to the point where the experimentally-accessible polymorphs of small organic molecules can be predicted with reasonable success, as demonstrated by a series of CSP blind tests.9 Recently, CSP has been combined with property prediction to produce energy–structure–function maps that describe the diversity of structures and properties available to a given molecule.10,11 Hence, structure prediction methods are gaining increasing attention in the field of computer-guided materials design.12–14Despite these successes, it is clear that CSP is far from having demonstrated its full potential. First, the delicate balance between non-covalent interactions15–17 and entropic and quantum fluctuations18,19 call for a very precise description of the inter-molecular potential, in order to determine the cohesive energies of different polymorphs with predictive accuracy. An important observation from CSP studies on many organic molecules is that the landscapes of possible crystal structures usually contain large numbers of structures separated by small lattice energy differences.20 Thus, it is also important to be able to assess the stabilities of many structures at an affordable computational cost. Second, to guide the discovery of functional materials, one often needs to evaluate optical and electronic properties that can only be calculated at a quantum mechanical level of theory. Finally, in contrast to other fields of molecular science such as nano-clusters21,22 and biomolecules,23,24 little attention has been paid to the development of automatic analysis methods to rationalize the potential energy landscape and the structure–property relations in molecular crystals. Heuristic classifications of polymorphs based on the analysis of packing types25 or of hydrogen bond (H-bond) patterns26 are useful as they provide intuitive rules that can guide synthetic chemists in the design of crystallization protocols that yield the desired products. However, they lack transferability, and risk biasing the design of new materials based on outdated or partly irrelevant prior knowledge.
In the past few years, machine learning (ML) techniques have become increasingly popular in the field of atomic-scale modelling, as a way to interpolate between first-principles calculations of both energy27–33 and properties34–37 of atomistic structures, as well as classifying recurrent structural motifs in an atomistic simulation.38–40 In this paper we discuss how a recently-developed ML framework can be used alongside more traditional CSP methods, accelerating the prediction of stability and properties of the meta-stable structures of molecular crystals, as well as developing a data-driven classification scheme that provides useful insight into the packing motifs and structure–property relations. We use, as benchmark systems, pentacene (see Fig. 1a) and two azapentacene (see Fig. 1b and c) isomers, recently studied as possible organic semiconductors by CSP methods.11 We demonstrate how Gaussian Process Regression (GPR) based on the SOAP-REMatch kernel41,42 is capable of estimating the relative energetics of predicted crystal structures, and the transfer integrals that enter the evaluation of charge mobilities, both to high levels of accuracy. Using the same kernel to characterize the similarity between structures, we also introduce a data-driven classification scheme that highlights families of structures on each CSP landscape and helps to clarify how introducing nitrogen substitutions in pentacene modifies the overall crystal packing landscape.
Methods
A benchmark database of structures and properties
We focus our present investigation on the lattice energies and charge mobility landscapes of three polyaromatic molecules: pentacene and two azapentacenes (5A and 5B), as depicted in Fig. 1. Pentacene is one of the most studied polyaromatic hydrocarbons, with promising electronic properties for organic semiconductor applications as a hole transporter. Without strong, directional intermolecular interactions, pentacene favours herringbone packing in crystalline phases, where molecules are arranged with a tilted edge-to-face arrangement in which neighbouring molecules interact via C–H⋯π interactions. Generally, a co-facial π-stacking arrangement is preferable for crystalline organic semiconductors since it maximises the intermolecular charge transfer integrals.43 Winkler and Houk44 suggested introducing a symmetric and complementary nitrogen substitution pattern along the long edges of the pentacene molecule to encourage hydrogen-bonding into a sheet-like packing in the crystal of the resulting azapentacene (molecule 5A, Fig. 1b), with the intention of increasing charge mobilities by promoting π-stackings. We have also studied molecule 5B (Fig. 1c) to further investigate if an irregular nitrogen substitution pattern would be less likely to promote sheet-like molecular arrangements in the crystal structure of this molecule.Full details of the crystal structure and transport property predictions for these three molecules were presented in ref. 11, and are summarized for completeness in the ESI.† In brief, crystal structures were generated by quasi-random sampling45 in a range of space groups, followed by lattice energy minimization with DMACRYS46 using an empirically parameterized exp-6 force field model (W99 (ref. 47)) combined with atomic multipolar electrostatics derived from a distributed multipole analysis (DMA).48
Besides this well-established semi-empirical model for predicting lattice energies, we also computed single-point energies of all the structures using density functional theory (DFT), with an expansion of Kohn–Sham orbitals in plane waves and the generalized-gradient-approximation density functional PBE,49 including Grimme's D2 dispersion corrections,50 as implemented in Quantum ESPRESSO.51 Further details of the DFT calculations are given in the ESI.†
The crystal packings of the predicted structures were classified into one of the categories typically used in describing polyaromatic hydrocarbon crystal packing:25,52 herringbone, where all molecules adopt a tilted edge-to-face arrangement; sandwich-herringbone, in which pairs of coplanar molecules pack in a herringbone manner; γ, which features stacks of coplanar molecules; and sheet-like, where all molecules are coplanar. A fifth category, slipped-γ, was added in our previous publication11 describing gamma structures in which the lateral offset between stacked molecules is so large that there is little π–π contact along the stack of molecules. The classification was performed using an in-house algorithm based on a set of heuristic rules, by calculating the relative orientations of molecules in a sphere surrounding a central reference molecule in a given crystal, as described in ref. 11.
As discussed in the ESI,† charge mobility calculations for molecular crystals were performed based on a hopping model in which the essential ingredient is the calculation of the transfer integral (TI) tij that describes the intermolecular electronic coupling between nearby molecular dimers in a given crystal structure. To gather enough data for ML purposes, we computed TIs (hole transport in the pentacene and electron transport in the azapentacenes) for all the symmetry-independent dimer geometries extracted from an extended list of predicted crystal structures up to an energetic cutoff of 20, 15 and 20 kJ mol−1 above the predicted global minimum for pentacene (564 crystal structures), 5A (594 structures) and 5B (936 structures), respectively.
Here, we investigate the predicted lattice energy landscapes – the low energy crystal structures, relative lattice energies (lattice energies of each structure relative to the lattice energy of the global minimum) and TIs – of pentacene and these two azapentacene isomers.
Gaussian process regression
Gaussian Process Regression (GPR) machine-learning schemes are based on a kernel function that is meant to represent the correlations between the properties one wants to predict. In other terms, a kernel function should assess the similarity among the sampled data, in this case, the structural similarities between pairs of molecular crystal structures or dimers. These kernels can then be applied to predict properties such as the energies of new structures based on their similarities to reference structures of known energies, or to classify structural patterns amongst a set of structures. The quantification of the similarity between atomic structures is the key element to achieve both accurate predictions and a meaningful classification.41,53,54The SOAP-REMatch kernel
The SOAP-REMatch kernel41 measures the structural similarity between crystal structures by combining the local similarity measures given by the SOAP (Smooth Overlap of Atomic Positions) kernel, that can be used to compare local atomic environments χ, i.e. spherical regions centered around each atom in a structure.42 The similarity Cij(A,B) between the local environments χAi and χBj of the crystal structures A and B is provided by the following SOAP kernel function:
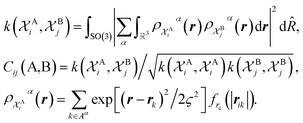 | (1) |
The kernel is built as the rotationally-averaged squared overlap of the smooth atom densities 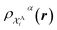 , which are in turn constructed as the superposition of Gaussian functions of width ς centered on the atoms of chemical species α that are found in each of the two structures, with positions rik relative to the i-th particle; frc is a cutoff function that selects smoothly the atoms within a radius rc from the central atom. In practice, the kernel can be computed more effectively based on a spherical harmonics decomposition of the two densities.42 In order to extract a single similarity measure from the matrix of pairwise environment similarities C(A,B), the REMatch kernel was used, which combines the similarity information from the local kernels into a global similarity measure by highlighting the pairs of local environments that exhibit the highest degree of structural similarity. For this purpose, the similarity between structure A and B is given by the weighted sum over the elements of C(A,B) where the weights are evaluated using a technique borrowed from optimal transport theory,55
, which are in turn constructed as the superposition of Gaussian functions of width ς centered on the atoms of chemical species α that are found in each of the two structures, with positions rik relative to the i-th particle; frc is a cutoff function that selects smoothly the atoms within a radius rc from the central atom. In practice, the kernel can be computed more effectively based on a spherical harmonics decomposition of the two densities.42 In order to extract a single similarity measure from the matrix of pairwise environment similarities C(A,B), the REMatch kernel was used, which combines the similarity information from the local kernels into a global similarity measure by highlighting the pairs of local environments that exhibit the highest degree of structural similarity. For this purpose, the similarity between structure A and B is given by the weighted sum over the elements of C(A,B) where the weights are evaluated using a technique borrowed from optimal transport theory,55
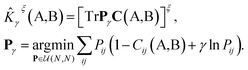 | (2) |
The optimal combination is obtained by searching the space of doubly stochastic matrices 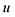 (N,M) which minimizes the discrepancy between matching pairs of environments, regularized using the information entropy of the weight matrix
(N,M) which minimizes the discrepancy between matching pairs of environments, regularized using the information entropy of the weight matrix 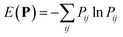 . The parameter ξ affects the sensitivity of the kernel and γ enables switching between a strict and broad selection of best matching pairs of local environment (see ref. 41 for more detail).
. The parameter ξ affects the sensitivity of the kernel and γ enables switching between a strict and broad selection of best matching pairs of local environment (see ref. 41 for more detail).
We choose the SOAP kernel as the basis of our measure of atomic structure similarity because it can be applied to both molecules and solids,56 and it combines a detailed and systematic description of atomic structures with a large degree of adaptability through its hyper-parameters. Finally, note that, given a positive-definite kernel between samples A and B, it is possible to define a kernel-induced distance57 that can be used for clustering or dimensionality reduction
D(A,B)2 = ![[K with combining circumflex]](https://www.rsc.org/images/entities/i_char_004b_0302.gif) γξ(A,A) + γξ(A,A) + ![[K with combining circumflex]](https://www.rsc.org/images/entities/i_char_004b_0302.gif) γξ(B,B) − 2 γξ(B,B) − 2![[K with combining circumflex]](https://www.rsc.org/images/entities/i_char_004b_0302.gif) γξ(A,B). γξ(A,B).
| (3) |
Property prediction
We model the property y of an atomic structure A using the Gaussian process framework58 and the SOAP-REMatch kernel. The property y is decomposed into the sum of a continuous function of the atomic configuration f(A) and an additive Gaussian noise ε ∼![[scr N, script letter N]](https://www.rsc.org/images/entities/char_e52d.gif) (0,σn2) of zero mean and variance σn2 associated to the measure of y:
(0,σn2) of zero mean and variance σn2 associated to the measure of y:| y = f(A) + ε. | (4) |
We further restrict the noiseless part of the property y to be a Gaussian process with zero mean and covariance function k(A,X) where A and X are atomic structures and k is a kernel function. Therefore, f belongs to a distribution over continuous functions for which every sample of the input space, i.e. atomic structures, is associated with a normally distributed random variable. The prediction model for property y becomes the mean over the possible functions conditioned by the input structure A, the set of training atomic structures {Xi,yi} ∀ i = 1, …, n and the model's hyper-parameters and is given by:
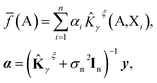 | (5) |
![[K with combining circumflex]](https://www.rsc.org/images/entities/b_char_004b_0302.gif) γξ]ij =
γξ]ij = ![[K with combining circumflex]](https://www.rsc.org/images/entities/i_char_004b_0302.gif) γξ(Xi,Xj). This model function is identical to the Kernel Ridge Regression model59 but this formulation (i) provides a probabilistic interpretation to the regularization hyper-parameter σn and (ii) allows the optimization of some hyper-parameters of the model (assuming Gaussian priors) by using the resulting log marginal likelihood and its derivatives. For instance, σn has been optimized following this method when predicting lattice energies.
γξ(Xi,Xj). This model function is identical to the Kernel Ridge Regression model59 but this formulation (i) provides a probabilistic interpretation to the regularization hyper-parameter σn and (ii) allows the optimization of some hyper-parameters of the model (assuming Gaussian priors) by using the resulting log marginal likelihood and its derivatives. For instance, σn has been optimized following this method when predicting lattice energies.
To rigorously assess the predictive power of our technique, we train GPR models on subsets of the molecular crystal datasets and compare our predictions with the reference data using K-fold cross-validation and the Mean Absolute Error (MAE), the Root Mean Square Error (RMSE), the supremum error (SUP) and the coefficient of determination (R2) metrics.
Structural classification
The SOAP-REMatch kernel provides a metric to quantify the structural similarities/distances (see eqn (2) and (3)) among the N atomic configurations in a database. However, this inherently high-dimensional information is not readily interpretable. In this work, two complementary approaches are applied to convey this information in an easily-visualizable form.The first approach involves building a two-dimensional “map” of the structural landscape, where each point corresponds to one of the structures in the database and the Euclidean distances between points is an approximation to the distances provided by the SOAP-REMatch kernel. We use sketch-map,60 a dimensionality reduction technique that aims to generate a low-dimensional projection of the data in which the proximity between structures is represented as faithfully as possible. The selection of the relevant length scales is achieved by tuning the parameters A, B, a, b and σmap (see ref. 61 for a complete discussion). The sketch-maps that we report in this work are labeled using the notation σmap-A_B-a_b.
The second approach uses the HDBSCAN*62 clustering technique to identify automatically the main structural motifs, i.e. regions with a dense agglomeration of samples within the dataset. HDBSCAN* has a single intuitive hyper-parameter, the minimal size of a cluster, which was set to approximately 1% of the dataset size to discard configurations that belong to sparsely-populated regions that do not correspond to a recurring structural motif. Given the quasi-random scheme used to enumerate locally stable polymorphs, no quantitative picture of the free energy of the landscape can be inferred from the clustering. Nevertheless, the presence of dense regions signals the possibility for the molecule to form many variations on the theme of a given packing pattern, and can be combined with information on lattice energies and charge mobilities to infer structure–property relations.
Results & discussion
The form of the SOAP-REMatch kernels is general, and rather agnostic to the nature of the system. However, it contains many hyperparameters that can be tuned at will. The spread of the smooth Gaussians determines how important are small displacements of the atoms; the entropy regularization determines how much the combination of environments departs from a purely additive form.56 The performance of the kernels and the outcome of unsupervised structural classifications are relatively insensitive to the value of most of these hyperparameters. The accuracy of cross-validated predictions provides an estimate of the generalization error of our models, i.e. the error for previously unseen data, which we used to optimize the performance of GPR for different systems. We found that a Gaussian width of ς = 0.3 Å and a regularization γ = 2 provide the best performance for all the systems we considered.The cutoff radius of the environment has the most significant influence on prediction performance and on the outcomes of the ML analysis. It also lends itself to a physical interpretation, since it determines the scale on which structural similarity is assessed. Although long-range electrostatics contribute significantly to the total lattice energies of crystalline structures, we found that a relatively short-range cutoff of rc = 5 Å is sufficient to obtain remarkably accurate predictions of the reference lattice energies. This finding suggests that the most important differences in electrostatic interactions between competing crystal structures of a given molecule are those between nearest-neighbour molecules. It is important to note that the lattice energies were calculated using a pairwise additive force field, so the lattice energies lack contributions from polarization. Although we also observed excellent performance when predicting DFT energies, that contain full electrostatic responses, the slight degradation of the prediction accuracy suggests that a longer cutoff, or explicit treatment of the electrostatic terms, might be beneficial when learning energies that contain long-range many-body effects.
While the “best” kernel for property prediction can be determined objectively based on the cross-validation error, it is more difficult to formulate objective criteria to optimize the parameters when a kernel is to be used for determining structural motifs, or generating low-dimensional maps of the crystal structure landscape. We found that by starting from the best parameters for energy prediction, and modifying the cutoff radius to select different chemical features, e.g. H-bonds and CH⋯π interactions, it is possible to change the representation of the structures in a predictable way. This turns out to be insightful, as we discuss below for the pentacene, 5A and 5B databases.
Pentacene
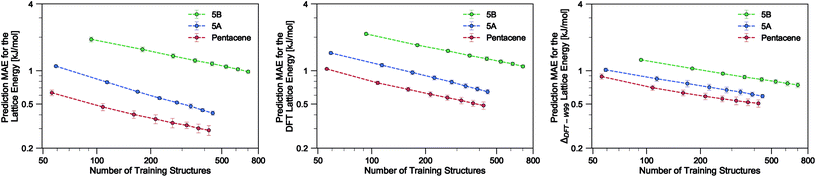
Using the SOAP-REMatch kernel with the hyper-parameters γ = 2, ς = 0.3 Å, rc = 5 Å, the force field relative lattice energies of the pentacene crystals can be predicted with an accuracy of MAE = 0.29 ± 0.03 kJ mol−1 and R2 = 0.979 using 75% of the dataset (see Table 1). The learning curve for pentacene (see Fig. 2) shows a polynomial convergence of the error with respect to the training set size, indicating that the accuracy of the method can be improved systematically.| Dataset | MAE [kJ mol−1] | RMSE [kJ mol−1] | R 2 |
|---|---|---|---|
| Pentacene (W99) | 0.29 ± 0.03 | 0.49 ± 0.08 | 0.979 |
| Pentacene (DFT) | 0.48 ± 0.04 | 0.68 ± 0.04 | 0.984 |
| Pentacene (Δ) | 0.51 ± 0.04 | 0.70 ± 0.06 | 0.96 |
| 5A (W99) | 0.41 ± 0.02 | 0.59 ± 0.04 | 0.967 |
| 5A (DFT) | 0.64 ± 0.03 | 0.91 ± 0.07 | 0.930 |
| 5A (Δ) | 0.59 ± 0.03 | 0.85 ± 0.06 | 0.85 |
| 5B (W99) | 0.98 ± 0.03 | 1.31 ± 0.03 | 0.877 |
| 5B (DFT) | 1.09 ± 0.03 | 1.44 ± 0.04 | 0.870 |
| 5B (Δ) | 0.74 ± 0.04 | 1.00 ± 0.05 | 0.83 |
Errors in the absolute lattice energies calculated with the W99 + DMA force field are, on average, about 15 kJ mol−1 when compared to benchmark experimental values,63 which is 1.2 to 4 times larger than the error associated with dispersion-corrected DFT. However, these errors are largely systematic and so much of the error cancels in the evaluation of relative lattice energies. Thus, W99 + DMA has been shown to be reliable in ranking the relative lattice energies in CSP studies on a large set of organic molecules64 and was validated for this study by reproducing the known crystal structures of pentacene and an aza-substituted tetracene as global minima on their CSP landscapes.11
In the present study, using only a small fraction (5%) of the pentacene dataset for training, one can already very accurately reproduce the lattice energies calculated using the W99 + DMA force field, with a MAE below 1 kJ mol−1 in the machine learned lattice energy predictions. The pentacene lattice energy landscape is dominated by the repulsion–dispersion contribution to intermolecular interactions and the above findings suggest that the predictions from the SOAP-REMatch kernel are robust in describing the relative thermodynamic stabilities of crystals of such non-polar molecules. The small fraction of structures required for training suggests that this approach could be used to reduce the cost of obtaining energy estimates at a higher level of theory, such as dispersion-corrected DFT, by performing training on a small number of high-level reference calculations. To verify this hypothesis we computed single-point dispersion-corrected DFT energies for each of the structures, which were then learned using the same kernel. As shown in Fig. 2, even though predictions are slightly less accurate, a ML model that uses just 50 training points can predict the DFT relative stability of different phases with a sub-kJ mol−1 error, opening the way to the use of more accurate energetics in large-scale CSP studies.
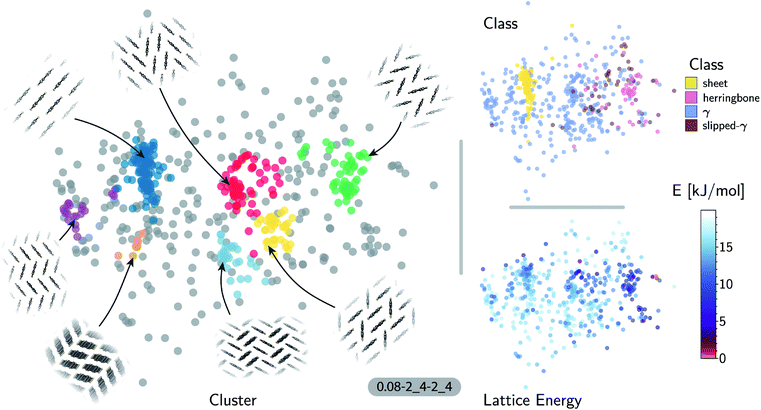
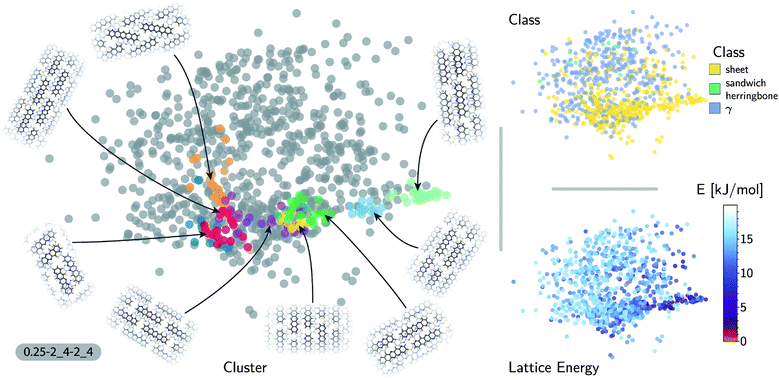
The accuracy of the lattice energy predictions suggests that the SOAP-REMatch kernel captures structural features that are strongly coupled with polymorph stability. This makes it well-suited as the basis of unsupervised-learning strategies to rationalize the structural diversity within this dataset, and to provide a meaningful and data-driven classification of the main structural patterns. Fig. 3 shows a sketch-map representation of the pentacene dataset color-coded according to the relative lattice energy (bottom right), a heuristic classification scheme developed in the previous publication on CSP of azapentacenes11 (top right) and the clusters detected by HDBSCAN* based on the kernel-induced metric (left).
The ‘islands’ on the sketch-map indicate the presence of distinct structural motifs (Fig. 3). The HDBSCAN* technique identifies seven clusters among which two match clearly the herringbone and sheet heuristic classes. The correspondence between a classification based on unsupervised data analysis and one based on a well-established understanding of the behavior of π-stacked system provides a cross-validation of the two approaches. The combination of SOAP-REMatch kernels, sketch-map and clustering is capable of recognizing well-known stacking patterns, and vice versa these heuristic classes have a clear correspondence in the structure of the crystal structure landscape.
Cases in which the two classifications differ are similarly insightful. For example, γ packing is defined by a stacking column of molecules along their short axis, while neighboring columns could be tilted with respect to this reference stacking direction. The HDBSCAN* clustering shows that this broadly-defined grouping overlooks the existence of several well-defined clusters of ‘mixed’ character, that differ by the tilting pattern between neighboring molecules, making it possible to identify e.g. structures that are (i) closer to a sheet-like packing, e.g. the orange island shown in Fig. 3 where one nearest-neighbor column is parallel whereas another neighboring column is tilted, or (ii) further from a sheet-like packing, e.g. the purple island shown in Fig. 3 where all nearest-neighbor columns are tilted with respect to each other. The slipped-γ packing, on the other hand, does not correspond to a clear-cut group of structures, encompassing a sparse set of configurations that populate different portions of the map. Inspection of these structures, informed by the mapping and the automatic classifications, reveals that this heuristic class is not well-suited to rationalize packing in pentacene.
Clustering techniques like HDBSCAN*, which work in the high dimensional space, are also useful to complement non-linear projections based on the similarity matrix, making it possible to recognize the distortions brought about by the projection and develop a better understanding of the actual structure of the similarity matrix. For instance, small groups of structures such as the one on the lower right of the sketch-map might appear like a cluster because of the projection, while clusters such as the green and red ones might not seem fully homogeneous. Nevertheless, a careful inspection of these groups of structures (see the ESI† for an interactive exploration of the sketch-maps) confirms that clusters detected by HDBSCAN* are indeed structurally homogeneous while the group on the lower right corresponds to complex variations and distortions of the herringbone pattern which do not show an obvious common structural pattern.
The quality of energy predictions based on SOAP-REMatch kernels for the predicted polymorphs of pentacene is remarkable, and the automatic classification based on kernels provides more fine-grained insights into the structural diversity in the lattice energy landscape compared to the heuristic classifications. To verify how these observations generalize to different classes of molecular crystals, we also considered the case of the two azapentacene isomers 5A and 5B.
Azapentacene 5A
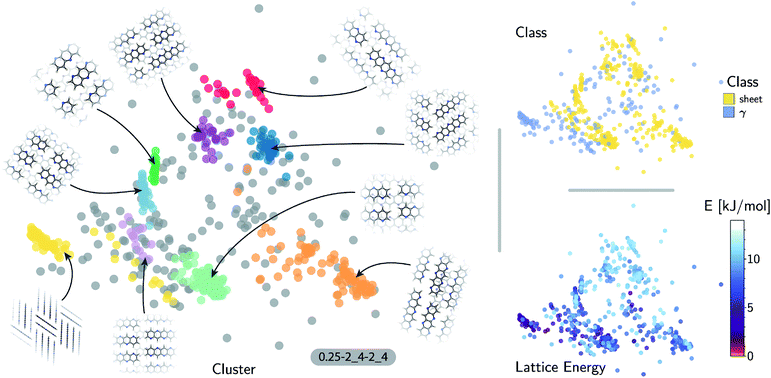
The quality of the lattice energy predictions for the 5A dataset is comparable to the pentacene dataset (see Table 1 and Fig. 2), showing similar accuracy (MAE = 0.41 ± 0.02 kJ mol−1 and R2 = 0.967 for predicting W99 energies, and MAE = 0.64 ± 0.03 kJ mol−1 and R2 = 0.930 for DFT predictions) and trends in the learning curves. However, to reach 1 kJ mol−1 accuracy we need at least twice as many training samples compared to pentacene. This can be rationalized by the introduction of stronger intermolecular electrostatic interactions involving the polar nitrogen atoms, which leads to the formation of CH⋯N H-bonds and the formation of molecular sheets. The presence of significant electrostatics as well as the dispersion interactions between arene rings results in a more complex lattice energy surface than that of pentacene, where dispersion interactions dominated and electrostatic contributions were small. The greater structural complexity of the landscape is reflected in the eigenvalue spectrum of the kernel matrix, which decays more slowly than in the case of pentacene (see ESI†). The intrinsic high dimensionality of the configurational landscape is also reflected in the failure of sketch-map to yield a particularly informative representation, even though HDBSCAN* clusters show some rough correspondence to the heuristic sheet and γ classes (see ESI†).The main difference between configurations, which is apparent by visual inspection, consists in the different arrangements of CH⋯N H-bonds between molecules within each sheet. In order to focus our investigation on such patterns, without the confounding information associated with the relative arrangement of molecules in adjacent sheets, we use a kernel with a cutoff radius of 3 Å, which is sufficient to identify H-bonds but is insensitive to inter-sheet correlation, given that the typical distance between sheets is about ∼3.5 Å. The outcome of this analysis is shown in Fig. 4. The HDBSCAN* automatic classification identifies nine main structural patterns, eight of which are sub-classes of the sheet motif. Representative structures for a few of these clusters (see Fig. 4) show that although a wide range of H-bond arrangements are possible within sheets, only a handful emerge as well-defined packing patterns. A single well-defined cluster that does not correspond to variations on the sheet stacking is also present and identified, corresponding to the γ heuristic class, while other patterns are detected as background/outliers by HDBSCAN*.
The fact that the overwhelming majority of structures can be traced to a sheet motif, despite using a CSP protocol that is designed to sample as widely as possible the most-likely packing patterns for a given molecule, as demonstrated in the case of pentacene, underscores the fact that the nitrogen substitution favors the sheet stacking patterns and inhibits other kinds of structural motifs. However, we find relatively poor correlation between structural similarity and lattice energy (see Fig. 4, bottom right) when the kernel is tuned to disregard inter-layer correlations. This reflects the fact that in-sheet H-bonding is not the sole factor determining the stability of packing. This is an example of the insight that can be obtained by combining supervised and unsupervised ML analysis of the configurational landscape of molecular materials.
Azapentacene 5B
Our results on the learning of lattice energies of the 5B dataset are satisfactory, but not as good as those observed for pentacene and 5A datasets (Table 1 and Fig. 2); we reach an accuracy of about 2 kJ mol−1 with 100 training points and 1 kJ mol−1 accuracy with 75% of the dataset. Not only are the absolute errors larger, but also the slope of the learning curve is smaller, showing that it is difficult to improve the accuracy by simply including more structures in the training set.The difficulty in learning can be traced to a higher inherent dimensionality of the dataset, as evidenced by the slow decay of the kernel eigenvalue spectrum (see ESI†). The structural basis of this greater complexity can be understood by performing an HDBSCAN* analysis and inspecting the sketch-map representation of the dataset. Even when using a 3 Å cutoff for the kernel, the sketch-map representation of the similarity matrix does not show clear ‘islands’, i.e. recurring structural patterns (see Fig. 5), suggesting the presence of a glassy structural landscape in which many distinct patterns can be formed.65 Indeed, even though HDBSCAN* finds 8 clusters that can be described as sheet-like (see a few representative structures in Fig. 5), they correspond to less than 20% of the structures, and the majority of the database (760 samples) is too sparse to be partitioned into well-defined clusters.
This variety of complex and diverse stacking patterns that do not seem to fit into specific arrangements can be traced to the irregular substitutions of carbon atoms by nitrogen atoms, that determines a transition from a structure-seeker energy landscape to a glassy energy landscape.65 The relatively poor performance when learning lattice energies can then be understood in terms of the presence of a large number of distinct structural motifs that require a larger training set size in comparison to pentacene and 5A, which on the contrary are characterized by combinations of relatively few easy-to-rationalize and easy-to-learn stacking and H-bond patterns. Similar performance is observed when learning DFT energetics, with MAE and RMSE errors about 0.1 kJ mol−1 higher than learning the W99 lattice energies.
An alternative strategy for learning the DFT lattice energies is to use the W99 results as a baseline and to apply ML to predict the difference between the baseline and DFT. This approach was applied to all three molecules (Table 1 and Fig. 2). For pentacene and 5A and when using 75% of structures for training, the resulting errors are essentially the same as when learning the DFT lattice energies directly. For smaller train set sizes and for 5B, instead, this approach considerably improves the accuracy. This indicates that W99 baselining does reduce the intrinsic variance of the learning targets: given that W99 energies are an inevitable byproduct of the W99-based structure search, it is a good idea to use them as a starting point to compute more accurate lattice energies. It is however clear that the difference between W99 and DFT is a function that is as difficult to learn as the DFT or W99 energy itself, so the asymptotic accuracy is not improved much – contrary to what is observed e.g. when using a ML model to predict exact-exchange corrections to DFT, where the use of a baseline can improve the predictions by almost an order of magnitude.56,66
Mobility prediction
Charge mobility is a key performance indicator for these set of molecular crystals considering their possible application to organic electronics. Therefore, being able to predict the hole (for pentacene) or electron (azapentacenes) mobility in putative crystal structures from CSP at a reasonable computational cost could accelerate property-driven design of functional organic semiconductors. However, contrary to the lattice energy for which bond-order expansions and additive energy models have been very successful, the charge mobility is commonly estimated through the computation of transfer integrals between pairs of molecules, each of which requires a rather demanding electronic structure calculation. The simulation protocol requires the collection from all crystal structures on the landscape of a structural database of all unique dimers within a specified distance cutoff, which are then used to calculate the corresponding TI values.Rather than trying to directly predict the charge-carrier mobility of a given crystal structure, we thus decided to apply our ML framework to predict the value of TIs within dimers, which is the most computationally demanding part of the mobility calculation. Given that the molecules are rigid, and that the value of the TIs depends primarily on the relative intermolecular orientation, we use a simplified version of the SOAP similarity that does not require the computation of several overlap kernels for each dimer. We introduce a virtual atom situated at the center of mass of each dimer, which is used as the center of a single SOAP environment used to define the similarity between two dimers A and B. We set the environment cutoff to 10 Å, so that it encompasses the entirety of the two molecules, giving a complete information on the geometry of the dimer. We found that the accuracy of the resulting ML model obtained with this procedure is comparable to an optimized SOAP-REMatch model while being much faster to compute.
Given the total pool of dimer configurations for each system, one needs to question what is the most efficient strategy to obtain a given level of accuracy with the minimum computational effort. We considered two different strategies to determine the training structures (for which electronic structure calculations need to be performed) and the test structures (for which one would want to just use ML predictions). As the simplest possible method we considered a random selection of dimers as training references. As a second approach, we built a training set that simultaneously maximizes structural diversity while explicitly computing the value of the TI for unusual, outlier structures for which a ML prediction may fail. We do this by using the farthest point sampling (FPS) algorithm,61,67 a greedy optimization strategy that iteratively selects data points that are most diverse from the already-selected training data.
We then used the similarity kernel of the training set to learn the TI values and perform predictions for the remaining dimers, within the GPR framework as described in Section 2.2.2, using the hyper-parameters ξ = 3 and σn = 5 × 10−4 throughout. Fig. 6 shows the trend of the MAE, RMSE and SUP in prediction when the training set was increased systematically from 10% to 80% of the full set, while predicting on the remaining dimers. All systems show similar trends. The RMSE is consistently about a factor of 2 larger than the MAE, which indicates a heavy-tailed distribution of errors (for a Gaussian distribution  ).
).
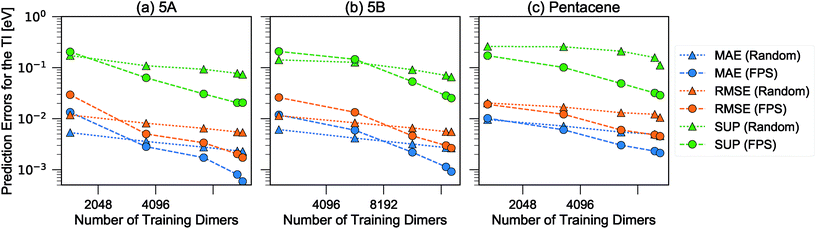 | ||
| Fig. 6 Learning curves for the errors in predicting TI when selecting training dimers using a random or FPS strategy. MAE, RMSE and SUP errors are defined in the text. | ||
There is a very substantial difference in the training curves between the random and the FPS selection of the training set. Similarly to what has been observed with isolated molecules,56 a small training set size with random selection provides better MAE, since more training points are concentrated in the densely-populated portions of the structural landscape. The SUP error, however, shows that this improved MAE comes at the price of larger errors coming from the outlier structures. As the training set size is increased, the FPS learning curves decay much faster, and quickly outperform the random selection. On the one hand, this is due to the greater diversity of the training set which, for a given size, provides a relatively uniform coverage of the landscape. On the other hand, outlier configurations that may be hard to predict are computed explicitly, and so only “easy” configurations are left in the test set. Far from being an artifact of the FPS training set construction, this second element is a useful feature that can be used in a practical setting, since the selection can be performed based only on the structures. Being able to focus explicit simulations on “difficult” structures makes it possible to achieve the best overall accuracy for a given investment of computer time.
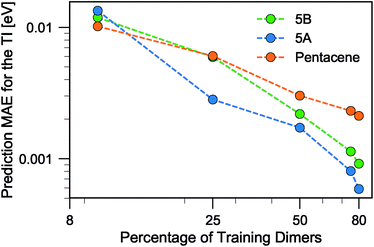
When discussing the absolute accuracy of predictions, one should keep in mind that the values of the TIs spread across several orders of magnitudes. Even when wavefunction-based methods, which are more accurate than the DFT-based method used here, were used to evaluate TIs, one could still observe errors of the order of 5–10 meV compared to high-level reference values,68,69 this indicates the intrinsic challenge in accurately predicting TIs. Here, it can be seen that this level of accuracy to predict DFT-derived TIs is easily achieved with about 10% of the dimer configurations, particularly if using a random selection. Using a FPS selection and increasing the training set size to about 25%, one can achieve more reliable predictions, with a MAE of about 3 meV for 5A dimers, and about 7 meV for 5B and pentacene (see Fig. 7). It is easy to see that the accuracy of predictions could be improved further. For instance, one could compute baseline values of the transfer integrals by a semiempirical method,30,56 or pre-select dimers with negligible TIs to reduce the computational expense. However, the present results already show that it is possible to use a straightforward ML protocol to reduce by a factor of 4–10 (depending on the desired level of accuracy) the cost of thoroughly screening all structures on a CSP landscape in terms of their charge carrier mobilities.
Conclusions
Statistical learning methods have demonstrated an accuracy on par with state-of-the-art electronic structure theory when constructing potentials for relatively simple materials56,70–75 or when predicting the properties of small isolated molecules.31,56,76–79 Here we have shown that sub-kJ mol−1 accuracy can also be obtained when predicting reference energies for the stability of different polymorphs of molecular crystals (relative lattice energies). Not only can we reproduce the energetics computed using an empirical atom–atom potential, but also predict accurately energies obtained at the dispersion-corrected DFT level. The possibility of interpolating between a few high-end reference calculations could improve the reliability of crystal structure prediction, while minimising the added computational cost.The combination of lattice energy predictions and unsupervised classification of the predicted structures can also be used to provide insights into the most important packing motifs available to the molecule during crystallization. For instance, we have shown that automatic clustering of pentacene structures identifies motifs that can be easily related to heuristic structural classifications, while capturing finer details and being fully data-driven. A similar analysis of nitrogen substituted pentacenes 5A and 5B confirmed that a regular substitution leads to regular H-bond patterns within the sheets, while an asymmetric substitution leads to less robust H-bonding patterns and a generally glassy potential energy landscape. At the same time, comparing energy predictions and structural classification showed clearly that H-bonding alone is not sufficient to characterize the lattice energies of 5A and 5B, but inter-sheet arrangements also need to be properly accounted for. This observation is an example of how an analysis based on machine-learning, when built around an easily-interpretable descriptor of molecular similarity, makes it possible to validate or disprove the interpretation of crystal packing in terms of a certain type of interactions.
Machine-learning can also be used to predict properties other than polymorph stability. Given that the polyaromatic compounds studied here are relevant for molecular electronics, we chose as an example the calculation of charge mobility. In order to build a model that minimizes the investment of CPU time needed to achieve a quantitative prediction for the large numbers of crystal structures found on CSP landscapes, we focused on the bottleneck of the calculation, which is the evaluation of electronic transfer integrals between pairs of adjacent molecules. Because of their origin in the electronic structure of interacting molecules, there is no simple form for the relationship between the intermolecular arrangement and these transfer integrals. We have tested Gaussian process regression using the SOAP descriptor of dimer structures to see if an inexpensive method can be trained using a small subset of dimers from a crystal structure landscape. Despite the fact that transfer integrals vary over several orders of magnitude, we showed that our ML scheme could predict their value at a level of accuracy comparable to that of the electronic structure reference using only 10% of the dimer configurations – corresponding to a potential 90% reduction of the computational effort associated with the screening of crystal structures for their charge mobility.
From faster, more accurate assessment of phase stability and the prediction of complex material properties, to the formulation and verification of hypotheses regarding structure–property relations, we believe that the machine-learning framework presented here could greatly advance the role of crystal structure and property prediction methods in the discovery of functional molecular materials.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
F. M. and S. D. were supported by the NCCR MARVEL, funded by the Swiss National Science Foundation. M. C. acknowledges funding by the European Research Council under the European Union's Horizon 2020 research and innovation programme (grant agreement no. 677013-HBMAP). G. M. D., J. Y. and J. E. C. acknowledge funding by the European Research Council under the European Union's Seventh Framework Programme (FP/2007-2013)/ERC (grant agreement number 307358, ERC-stG-2012-ANGLE).References
- P. Vishweshwar, J. A. McMahon, M. L. Peterson, M. B. Hickey, T. R. Shattock and M. J. Zaworotko, Chem. Commun., 2005, 4601–4603 RSC.
- N. K. Duggirala, M. L. Perry, Ö. Almarsson and M. J. Zaworotko, Chem. Commun., 2016, 52, 640–655 RSC.
- S. R. Forrest, Nature, 2004, 428, 911 CrossRef CAS PubMed.
- M. Muccini, Nat. Mater., 2006, 5, 605 CrossRef CAS PubMed.
- D. C. Hodgkin, J. Pickworth, J. H. Robertson, K. N. Trueblood, R. J. Prosen and J. G. White, et al. , Nature, 1955, 176, 325–328 CrossRef CAS PubMed.
- J. Bernstein, Nat. Mater., 2005, 4, 427 CrossRef CAS PubMed.
- L. Yu, Acc. Chem. Res., 2010, 43, 1257 CrossRef CAS PubMed.
- J. Bauer, S. Spanton, R. Henry, J. Quick, W. Dziki, W. Porter and J. Morris, Pharm. Res., 2001, 18, 859 CrossRef CAS.
- A. M. Reilly, R. I. Cooper, C. S. Adjiman, S. Bhattacharya, A. D. Boese, J. G. Brandenburg, P. J. Bygrave, R. Bylsma, J. E. Campbell, R. Car, D. H. Case, R. Chadha, J. C. Cole, K. Cosburn, H. M. Cuppen, F. Curtis, G. M. Day, R. A. DiStasio, A. Dzyabchenko, B. P. Van Eijck, D. M. Elking, J. A. Van Den Ende, J. C. Facelli, M. B. Ferraro, L. Fusti-Molnar, C. A. Gatsiou, T. S. Gee, R. De Gelder, L. M. Ghiringhelli, H. Goto, S. Grimme, R. Guo, D. W. Hofmann, J. Hoja, R. K. Hylton, L. Iuzzolino, W. Jankiewicz, D. T. De Jong, J. Kendrick, N. J. De Klerk, H. Y. Ko, L. N. Kuleshova, X. Li, S. Lohani, F. J. Leusen, A. M. Lund, J. Lv, Y. Ma, N. Marom, A. E. Masunov, P. McCabe, D. P. McMahon, H. Meekes, M. P. Metz, A. J. Misquitta, S. Mohamed, B. Monserrat, R. J. Needs, M. A. Neumann, J. Nyman, S. Obata, H. Oberhofer, A. R. Oganov, A. M. Orendt, G. I. Pagola, C. C. Pantelides, C. J. Pickard, R. Podeszwa, L. S. Price, S. L. Price, A. Pulido, M. G. Read, K. Reuter, E. Schneider, C. Schober, G. P. Shields, P. Singh, I. J. Sugden, K. Szalewicz, C. R. Taylor, A. Tkatchenko, M. E. Tuckerman, F. Vacarro, M. Vasileiadis, A. Vazquez-Mayagoitia, L. Vogt, Y. Wang, R. E. Watson, G. A. De Wijs, J. Yang, Q. Zhu and C. R. Groom, Acta Crystallogr., Sect. B: Struct. Sci., Cryst. Eng. Mater., 2016, 72, 439–459 CAS.
- A. Pulido, L. Chen, T. Kaczorowski, D. Holden, M. A. Little, S. Y. Chong, B. J. Slater, D. P. Mcmahon, B. Bonillo, C. J. Stackhouse, A. Stephenson, C. M. Kane, R. Clowes, T. Hasell, A. I. Cooper and G. M. Day, Nature, 2017, 543, 657–664 CrossRef CAS PubMed.
- J. E. Campbell, J. Yang and G. M. Day, J. Mater. Chem. C, 2017, 5, 7574–7584 RSC.
- A. Jain, S. P. Ong, G. Hautier, W. Chen, W. D. Richards, S. Dacek, S. Cholia, D. Gunter, D. Skinner, G. Ceder and K. A. Persson, APL Mater., 2013, 1, 011002 CrossRef.
- A. White, MRS Bull., 2012, 37, 715–716 CrossRef.
- G. Pizzi, A. Cepellotti, R. Sabatini, N. Marzari and B. Kozinsky, Comput. Mater. Sci., 2016, 111, 218–230 CrossRef.
- A. M. Reilly and A. Tkatchenko, Phys. Rev. Lett., 2014, 113, 055701 CrossRef PubMed.
- S. L. Price, CrystEngComm, 2004, 6, 344–353 RSC.
- F. Curtis, X. Wang and N. Marom, Acta Crystallogr., Sect. B: Struct. Sci., Cryst. Eng. Mater., 2016, 72, 562–570 CAS.
- J. Nyman and G. M. Day, CrystEngComm, 2015, 17, 5154–5165 RSC.
- M. Rossi, P. Gasparotto and M. Ceriotti, Phys. Rev. Lett., 2016, 117, 115702 CrossRef PubMed.
- G. M. Day, J. Chisholm, N. Shan, W. D. S. Motherwell and W. Jones, Cryst. Growth Des., 2004, 4, 1327–1340 CAS.
- D. Wales, Energy landscapes: Applications to clusters, biomolecules and glasses, Cambridge University Press, 2003 Search PubMed.
- S. De, A. Willand, M. Amsler, P. Pochet, L. Genovese and S. Goedecker, Phys. Rev. Lett., 2011, 106, 225502 CrossRef PubMed.
- A. L. Ferguson, A. Z. Panagiotopoulos, P. G. Debenedetti and I. G. Kevrekidis, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 13597–13602 CrossRef CAS PubMed.
- M. Ceriotti, G. A. Tribello and M. Parrinello, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 13023–13028 CrossRef CAS PubMed.
- G. R. Desiraju and A. Gavezzotti, Acta Crystallogr., Sect. B: Struct. Sci., 1989, 45, 473 CrossRef.
- M. C. Etter, J. C. MacDonald and J. Bernstein, Acta Crystallogr., Sect. B: Struct. Sci., 1990, 46, 256 CrossRef.
- J. Behler and M. Parrinello, Phys. Rev. Lett., 2007, 98, 146401 CrossRef PubMed.
- A. P. Bartók, M. C. Payne, R. Kondor and G. Csányi, Phys. Rev. Lett., 2010, 104, 136403 CrossRef PubMed.
- D. Jasrasaria, E. O. Pyzer-Knapp, D. Rappoport and A. Aspuru-Guzik, 2016, http://arxiv.org/abs/1608.05747.
- R. Ramakrishnan, P. O. Dral, M. Rupp and O. A. von Lilienfeld, J. Chem. Theory Comput., 2015, 11, 2087–2096 CrossRef CAS PubMed.
- G. Ferré, T. Haut and K. Barros, J. Chem. Phys., 2017, 146, 114107 CrossRef PubMed.
- F. A. Faber, A. Lindmaa, O. A. von Lilienfeld and R. Armiento, Phys. Rev. Lett., 2016, 117, 135502 CrossRef PubMed.
- A. Seko, H. Hayashi, K. Nakayama, A. Takahashi and I. Tanaka, Phys. Rev. B: Condens. Matter Mater. Phys., 2017, 95, 1–10 CrossRef.
- M. de Jong, W. Chen, R. Notestine, K. Persson, G. Ceder, A. Jain, M. Asta and A. Gamst, Sci. Rep., 2016, 6, 34256 CrossRef CAS PubMed.
- E. O. Pyzer-Knapp, K. Li and A. Aspuru-Guzik, Adv. Funct. Mater., 2015, 25, 6495–6502 CrossRef CAS.
- J. Carrete, W. Li, N. Mingo, S. Wang and S. Curtarolo, Phys. Rev. X, 2014, 4, 011019 Search PubMed.
- S. Kim, A. Jinich and A. Aspuru-Guzik, J. Chem. Inf. Model., 2017, 57, 657–668 CrossRef CAS PubMed.
- R. Nussinov and H. J. Wolfson, Proc. Natl. Acad. Sci. U. S. A., 1991, 88, 10495–10499 CrossRef CAS.
- F. Pietrucci and W. Andreoni, Phys. Rev. Lett., 2011, 107, 085504 CrossRef PubMed.
- P. Gasparotto and M. Ceriotti, J. Chem. Phys., 2014, 141, 174110 CrossRef PubMed.
- S. De, A. P. Bartók, G. Csányi and M. Ceriotti, Phys. Chem. Chem. Phys., 2016, 18, 13754–13769 RSC.
- A. P. Bartók, R. Kondor and G. Csányi, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 184115 CrossRef.
- E. F. Valeev, V. Coropceanu, D. A. da Silva Filho, S. Salman and J.-L. Bredas, J. Am. Chem. Soc., 2006, 128, 9882–9886 CrossRef CAS PubMed.
- M. Winkler and K. Houk, J. Am. Chem. Soc., 2007, 129, 1805 CrossRef CAS PubMed.
- D. H. Case, J. E. Campbell, P. J. Bygrave and G. M. Day, J. Chem. Theory Comput., 2016, 12, 910 CrossRef CAS PubMed.
- S. L. Price, M. Leslie, G. W. A. Welch, M. Habgood, L. S. Price, P. G. Karamertzanis and G. M. Day, Phys. Chem. Chem. Phys., 2010, 12, 8478–8490 RSC.
- D. E. Williams, J. Comput. Chem., 2001, 22, 1154–1166 CrossRef CAS.
- A. Stone and M. Alderton, Mol. Phys., 2002, 100, 221–233 CrossRef.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- S. Grimme, J. Comput. Chem., 2006, 27, 1787–1799 CrossRef CAS PubMed.
- P. Giannozzi, S. Baroni, N. Bonini, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli, G. L. Chiarotti, M. Cococcioni, I. Dabo, A. D. Corso, S. de Gironcoli, S. Fabris, G. Fratesi, R. Gebauer, U. Gerstmann, C. Gougoussis, A. Kokalj, M. Lazzeri, L. Martin-Samos, N. Marzari, F. Mauri, R. Mazzarello, S. Paolini, A. Pasquarello, L. Paulatto, C. Sbraccia, S. Scandolo, G. Sclauzero, A. P. Seitsonen, A. Smogunov, P. Umari and R. M. Wentzcovitch, J. Phys.: Condens. Matter, 2009, 21, 395502 CrossRef PubMed.
- L. Loots and L. J. Barbour, CrystEngComm, 2012, 14, 300–304 RSC.
- A. Sadeghi, S. A. Ghasemi, B. Schaefer, S. Mohr, M. A. Lill and S. Goedecker, J. Chem. Phys., 2013, 139, 184118 CrossRef PubMed.
- S. De, F. Musil, T. Ingram, C. Baldauf and M. Ceriotti, J. Cheminf., 2016, 9, 6 Search PubMed.
- M. Cuturi, in Advances in Neural Information Processing Systems 26, ed. C. J. C. Burges, L. Bottou, M. Welling, Z. Ghahramani and K. Q. Weinberger, Curran Associates, Inc., 2013, pp. 2292–2300 Search PubMed.
- A. P. Bartok, S. De, C. Poelking, N. Bernstein, J. Kermode, G. Csanyi and M. Ceriotti, Sci. Adv., 2017, 3, e1701816 CrossRef PubMed.
- C. Berg, J. Christensen and P. Ressel, Harmonic Analysis on Semigroups, 1984, pp. 86–143 Search PubMed.
- C. E. Rasmussen and C. K. I. Williams, Gaussian processes for machine learning, World Scientific Publishing Company, 2006, vol. 14, pp. 69–106 Search PubMed.
- C. Saunders, A. Gammerman and V. Vovk, Proceedings of the 15th International Conference on Machine Learning, 1998, pp. 515–521 Search PubMed.
- M. Ceriotti, G. A. Tribello and M. Parrinello, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 13023–13028 CrossRef CAS PubMed.
- M. Ceriotti, G. A. Tribello and M. Parrinello, J. Chem. Theory Comput., 2013, 9, 1521–1532 CrossRef CAS PubMed.
- R. J. G. B. Campello, D. Moulavi, A. Zimek and J. Sander, ACM Transactions on Knowledge Discovery from Data, 2015, vol. 10, pp. 1–51 Search PubMed.
- J. Nyman, O. S. Pundyke and G. M. Day, Phys. Chem. Chem. Phys., 2016, 18, 15828 RSC.
- G. M. Day, W. D. S. Motherwell and W. Jones, Cryst. Growth Des., 2005, 5, 1023–1033 CAS.
- S. De, B. Schaefer, A. Sadeghi, M. Sicher, D. G. Kanhere and S. Goedecker, Phys. Rev. Lett., 2014, 112, 083401 CrossRef.
- R. Ramakrishnan, P. O. Dral, M. Rupp and O. A. von Lilienfeld, J. Chem. Theory Comput., 2015, 11, 2087–2096 CrossRef CAS PubMed.
- D. J. Rosenkrantz, R. E. Stearns, I. Philip and M. Lewis, SIAM J. Comput., 1977, 6, 563–581 CrossRef.
- A. Pershin and P. G. Szalay, J. Chem. Theory Comput., 2015, 11, 5705–5711 CrossRef CAS PubMed.
- A. Kubas, F. Hoffmann, A. Heck, H. Oberhofer, M. Elstner and J. Blumberger, J. Chem. Phys., 2014, 140, 104105 CrossRef PubMed.
- V. L. Deringer and G. Csányi, Phys. Rev. B: Condens. Matter Mater. Phys., 2017, 95, 094203 CrossRef.
- W. J. Szlachta, A. P. Bartók and G. Csányi, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 90, 104108 CrossRef.
- T. Morawietz, V. Sharma and J. Behler, J. Chem. Phys., 2012, 136, 064103 CrossRef PubMed.
- N. Artrith, T. Morawietz and J. Behler, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 153101 CrossRef.
- G. C. Sosso, G. Miceli, S. Caravati, J. Behler and M. Bernasconi, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 174103 CrossRef.
- M. Gastegger, J. Behler and P. Marquetand, Chem. Sci., 2017, 8, 6924–6935 RSC.
- M. Gastegger, C. Kauffmann, J. Behler and P. Marquetand, J. Chem. Phys., 2016, 144, 194110 CrossRef PubMed.
- M. Hirn, S. Mallat and N. Poilvert, Multiscale Model. Simul., 2017, 15, 827–863 Search PubMed.
- K. Yao, J. E. Herr and J. Parkhill, J. Chem. Phys., 2017, 146, 014106 CrossRef PubMed.
- M. Rupp, A. Tkatchenko, K.-R. Müller and O. A. von Lilienfeld, Phys. Rev. Lett., 2012, 108, 058301 CrossRef PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c7sc04665k |
| ‡ These authors contributed equally to this work. |
| This journal is © The Royal Society of Chemistry 2018 |