Quantum optical emulation of molecular vibronic spectroscopy using a trapped-ion device

Abstract

Molecules are one of the most demanding quantum systems to be simulated by quantum computers due to their complexity and the emergent role of quantum nature. The recent theoretical proposal of Huh et al. (Nature Photon., 9, 615 (2015)) showed that a multi-photon network with a Gaussian input state can simulate a molecular spectroscopic process. Here, we present the first quantum device that generates a molecular spectroscopic signal with the phonons in a trapped ion system, using SO₂ as an example. In order to perform reliable Gaussian sampling, we develop the essential experimental technology with phonons, which includes the phase-coherent manipulation of displacement, squeezing, and rotation operations with multiple modes in a single realization. The required quantum optical operations are implemented through Raman laser beams. The molecular spectroscopic signal is reconstructed from the collective projection measurements for the two-phonon-mode. Our experimental demonstration will pave the way to large-scale molecular quantum simulations, which are classically intractable, but would be easily verifiable by real molecular spectroscopy.

---

1 Introduction

It is believed that a boson sampling computer would demonstrate quantum supremacy and be less demanding of resources than a universal quantum computer.¹ Serious experimental endeavors have been reported to realize the small-scale version only in photonic systems.^2–7 Recently, it has been suggested that Gaussian boson sampling^8,9 can simulate molecular spectroscopy: this particular problem is also expected to reveal the excellence of quantum computing.^10,11 In the case of molecular vibronic spectroscopy, there are vibrational transitions between the nuclear manifolds belonging to the two electronic states of a molecule,^10,12 as shown in Fig. 1a. 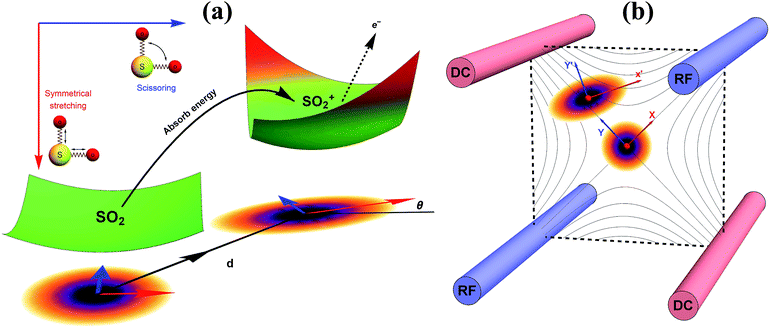Upon the electronic transition, a molecule undergoes structural deformation, vibrational frequency changes, and rotation of the normal modes; within a harmonic approximation of the electronic potential energy surfaces, these are equivalent to the displacement (D̂), squeezing (Ŝ) and rotation (R̂) operations in quantum optics, respectively. The (mass-weighted) normal coordinates of the initial (Q) and final (Q′) states are related linearly as Q′ = UQ + d, where U is called the Duschinsky rotation matrix and d is the displacement vector of the multidimensional harmonic oscillators in the mass-weighted coordinate, the corresponding dimensionless displacement vector α for the quantum optical operation is used later.¹² As a result, the molecule performs a multi-mode Bogoliubov transformation¹³ between the (vibrational) boson operators of the initial and final electronic states.^10,11 The probability distribution regarding a given molecular vibronic transition frequency (ω_v) at zero Kelvin, which is the Franck–Condon profile, is read as Fermi’s golden rule for a unitary Gaussian operator Û_Dok,^10,12,14where , 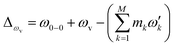with the k-th being the vibrational frequency (ω′_k) of a molecule in the final electronic state (ω_k belongs to the initial electronic state). The constant off-set frequency ω_0–0, which includes the electronic transition and zero-point vibrational transition, is set to be zero here without losing the generality. |0〉 = |0₁,…, 0_M〉 and |m〉 = |m₁,…, m_M〉 are the initial and final M-dimensional Fock states, respectively.

Fig. 1 A pictorial description of the photoelectron spectroscopy of SO₂ and the trapped-ion simulator. (a) The photoelectron process of SO₂ → SO₂⁺. The molecule is initially at the vibrational ground state of the symmetrical stretching and scissoring modes. After absorbing a photon, an electron is removed from the molecule and the molecule finds a new equilibrium structure for SO₂⁺, where the new potential energy surface is displaced, squeezed, and rotated from the original one. The transition of SO₂⁻ → SO₂ can be described in a similar manner. (b) The trapped-ion simulator performing Gaussian transformation for molecular vibronic spectroscopy. The two vibrational modes of SO₂ are mapped to the two radial modes (X and Y) of a single trapped-ion. The photoelectron process is simulated by applying a series of quantum optical operations, which are implemented by Raman laser beams (see section C in ESI†). Generally, the photoelectron process of more complicated molecules with N vibrational modes can be mapped to the collective motional modes of the N ions with similar operations by the Raman laser beams.

Doktorov et al.¹⁴ decomposed Û_Dok in terms of the elementary quantum optical operators as follows:

Û_Dok = D̂_N(α)Ŝ^†_N(ζ′)R̂_N(U)Ŝ_N(ζ) (2)

where D̂_N, Ŝ_N and R̂_N are the N-mode operators of displacement, squeezing and rotation¹⁵ (see also section A in the ESI†); 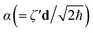is a (dimensionless) molecular displacement vector, and 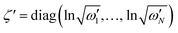are the diagonal matrices of the squeezing parameters, and U is a unitary rotation matrix. The actions of the quantum optical operators are defined in ref. 15. Therefore, the sequential operations of the quantum optical operators in eqn (2) in the vacuum state and the measurement using a Fock basis, as in eqn (1), can simulate the Franck–Condon profile.¹⁰

The process of molecular vibronic spectroscopy can be understood as a modified boson sampling with Gaussian input states, such as thermal and squeezed vacuum states. Gaussian boson sampling, which is classified as a classically hard problem from a computational complexity perspective,^8,9 requires more quantum optical operations on top of beam splitting and phase shifting operations for standard boson sampling. Boson sampling, however, is challenging in an optical system^2–5 because of the difficulties in preparing the initial states: single Fock states for original boson sampling and squeezed coherent states for molecular simulation. Non-optical boson sampling devices, such as trapped-ion devices^16,17 and superconducting circuits,¹⁸ have been suggested theoretically for the scalable boson sampling machine to overcome the difficulties of optical implementation in preparing the single photon states. Moreover, these non-optical devices can handle the squeezed states with relative ease. In this article, we present the first quantum simulation of molecular vibronic spectroscopy with the particular example of photoelectron spectroscopy of sulfur dioxide (SO₂).^19,20

2 Experimental implementation

Fig. 1b schematically illustrates the quantum optical operations of eqn (2) in the trapped-ion device for the molecular vibronic spectroscopy of SO₂. Our trapped-ion simulation is performed using a single ¹⁷¹Yb⁺ ion confined in the 3-dimensional harmonic potential generated by the four-rod trap. The two vibrational modes of the molecule are mapped to the two radial phonon modes (X and Y) of an ion, with the trap frequencies ω_X = (2π) 2.6 MHz and ω_Y = (2π) 2.2 MHz. After the mapping of the Hilbert space between the real molecule and simulator is established, the molecular spectroscopy is simulated through the following procedure: (i) the ion is first initialized to the motional ground state, (ii) the quantum optical operations in eqn (2) are then sequentially applied, and (iii) finally, the vibronic spectroscopy is constructed using the collective projection measurements (see ESI section D†) on the transformed state.

Accordingly, for the first step of the molecular spectroscopy simulation, we prepare the ion in the ground state |n_X = 0, n_Y = 0〉 by Doppler cooling and resolved sideband cooling methods.^21,22 Next, we perform the required displacement, squeezing, and rotation operations by converting the molecular parameters to the corresponding device parameters. The molecular parameters, α, ζ′, U and ζ, can be obtained via conventional quantum chemical calculations with the available program packages (e.g., ref. 23). See section B in the ESI† for the details of the parameter conversion for SO₂.

The quantum optical operations (displacement D̂, squeezing Ŝ, and rotation R̂), which preserve the phase coherence amongst themselves, are implemented by the σ⁺-polarized Raman laser beams from a pico-second pulse laser with a wavelength of 375 nm (see section C in the ESI†). In the trapped-ion experiment, the quantum optical operations with the desired parameters can be performed by controlling the applied laser frequency, duration, intensity, and phase. With different Raman laser configurations (see section C in the ESI†), we can realize the displacement, squeezing, and rotation operations, respectively.^24,25Fig. 2a shows the performance of the experimental displacement 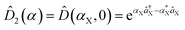and squeezing 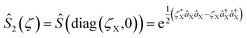operations, where a_X and a^†_X are the annihilation and creation operators of the bosonic mode X, respectively. The amount of displacement α and the squeezing parameter ζ are controlled by the duration of the corresponding Raman beams with rates of 0.042 μs⁻¹ and 0.004 μs⁻¹, respectively. We examine the trapped-ion implementation of the rotation operation 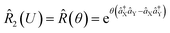between modes X and Y with two sets of initial states, as indicated in Fig. 2b. The rotation angle θ is also controlled by the duration of the operation with a rate of 0.005 rad μs⁻¹. The oscillations in Fig. 2b of the initial state |n_X = 1, n_Y = 0〉 (orange and green) are two times slower than those from state |1,1〉 (blue, black, and red), as expected. We note that at t = 157 μs, the near zero probability of 〈1,1|R̂|1,1〉 originates from the Hong–Ou–Mandel interference.²⁵

Fig. 2 The trapped-ion demonstration of the quantum optical operations; D̂, Ŝ, and R̂. (a) The displacement α = (α_X,0) (red) and squeezing ζ = diag(ζ_X,0) (blue) of mode X are controlled by the duration of the Raman laser beams. The insets show the measured phonon distributions for α_X = 0.5 and the squeezing parameter of ζ_X = 0.5. (b) The evolution of the rotation operation between mode X and Y. The ion is first prepared in state |n_X = 1, n_Y = 0〉 (orange and green) and |1,1〉 (blue, black and red), then we apply the rotation operation, finally measuring the corresponding Fock state population via the collective projection measurement method. Here, all the operations are implemented by Raman laser beams. The dots represent the experimental data and the lines are obtained by fitting. The error bars represent a 95% confidence level.

Fig. 3a depicts a scheme for reconstructing the spectroscopy at zero Kelvin from the output measurements of the trapped-ion simulator. The transition intensities from the ground state to the excited states are aligned according to the transition frequencies. Fig. 3b illustrates the transition between the two-dimensional Fock spaces resulting from the two-dimensional harmonic oscillators. Finally, we perform the collective quantum-projection measurement of the final state |n_X, n_Y〉 advanced from the measurement scheme of ref. 26 and 27: first, we transfer the population of a target state |n_X, n_Y〉 to the |0,0〉 state by a sequence of π-pulse transitions. Then, we measure the state population by applying three sequential fluorescence detections combined with the uniform red sideband technique (see section D in the ESI†). Our quantum projection measurement is limited by the imperfection of the state transfer and the fluorescence detection efficiency. We plot the fidelity of the collective projection measurement of the |n_X, n_Y〉 state in Fig. 3c. Based on the fidelity analysis, we perform measurement-error corrections for the experimental raw data (see section E in the ESI† for detailed information).

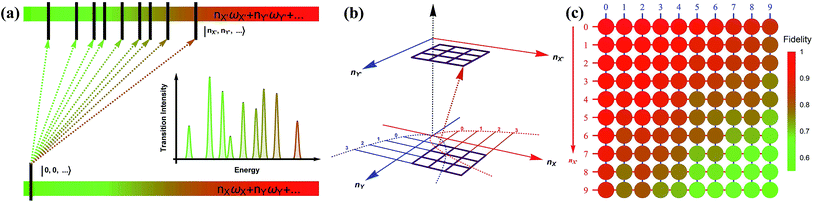Fig. 3 The construction scheme for the Franck–Condon profile of the photoelectron process with the trapped-ion simulator. (a) A generic diagram for the molecular transition process at T = 0 K. The lower bar indicates the initial state and the upper bar shows the final states after the process. The vibronic spectroscopy is constructed by measuring the transition probabilities from |n_X = 0, n_y = 0,…〉 to |n_X′,n_Y′,…〉. (b) The transition process of a molecule in the two-dimensional Fock space. The process begins with the lower plane and ends at the upper plane. The points in the grid represent the phonon number states. The transition probability is obtained by the collective projection measurements of the two phonon modes (see section D in the ESI†). (c) The fidelity analysis of the collective projection measurements. The fidelity of measuring the transition probability of the state |n_X′, n_Y′〉 is experimentally examined from |0,0〉 to |9,9〉. The fidelity is measured by applying the measurement sequence twice, starting from |0,0〉 to |n_X′, n_Y′〉, and then bringing back to |0,0〉. The square root of the remaining population represents the fidelity.

3 Results

Finally, we simulate the photoelectron spectroscopies of SO₂ and SO₂⁻, in which a single electron is removed from the molecule during the photon absorption process, with our trapped-ion quantum simulator. Owing to the symmetry of the molecules, we use only two vibrational modes of sulfur dioxide, which show mixing of the vibration modes with respect to the final vibrational coordinates,²⁰ in our quantum simulation for the molecular spectra; the remaining vibrational mode does not contribute to the overall spectral shape because SO₂ does not deform along the remaining (non-totally-symmetric) vibrational mode during the vibronic transition.

Fig. 4 presents the photoelectron spectra, SO₂ → SO₂⁺ and SO₂⁻ → SO₂, obtained from our trapped-ion quantum simulation; these are compared with the theoretical classical calculations. Fig. 4 shows good agreement between the theory calculations and the trapped-ion simulations of the two photoelectron processes of sulfur dioxide, and the required molecular parameters are described in the figure caption. In Fig. 4a, the photoelectron spectroscopy of SO₂ is dominated by the ω′₂ transitions due to the significant large displacement along the second mode: α = (−0.026,1.716). The photoelectron spectroscopy of SO₂⁻ in Fig. 4b shows tiny combination bands of the first and second modes regardless of the dominant contribution of the first mode (α = (1.360,−0.264)). We note that the observation of the tiny band combinations indicates reliable performance of the trapped-ion simulation.

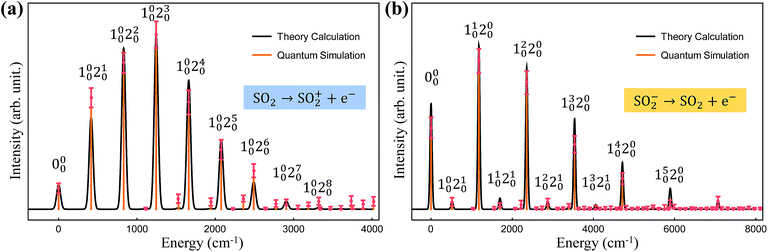Fig. 4 The trapped-ion simulation of the photoelectron spectra of SO₂ and SO₂⁻ with measurement-error correction. The two vibrational frequencies of the harmonic potentials for SO₂⁺, SO₂, and SO₂⁻ are (1112.7, 415.0), (1178.4, 518.9) and (989.5, 451.4) cm⁻¹, respectively. (a) The displacement vector α is (−0.026, 1.716) and the rotation angle θ is 0.189. (b) The displacement vector α is (1.360, −0.264) and the rotation angle θ is 0.065. The theoretical lines are intentionally broadened by convoluting with a Gaussian function with a width of 50 cm⁻¹ (ref. 20) for comparison. Here Nⁱ₀ denotes the i-phonon excitation on the N-th mode from the vibrational ground state |0〉, and accordingly, 0⁰₀ located at the off-set energy ω_0–0 = 0.

4 Conclusions

As the first demonstration of quantum simulation for molecular vibronic spectroscopy, our trapped-ion device shows excellent performance at a small-scale after the error-correction scheme in section E of the ESI.† In the near future, we expect many mode implementation for large-scale molecular simulation, where the multi-modes can be mapped to the local vibrational modes or collective normal modes of many ions in a single trap. The quantum optical operations demonstrated using a single ion will be directly applied for large-scale simulation. This would be useful in concluding the quantum supremacy of boson sampling with the Gaussian states. The molecular simulations in trapped-ion devices and the real molecular spectroscopic signals can be compared as a certification protocol for large-scale Gaussian boson sampling, which cannot be verified classically because of the #P-hardness (cf. Neville et al.²⁸ and Clifford²⁹ for the classical effort to reach the classical limit of the original boson sampling problem).^9–11 In closing, we would like to comment on the possible extension of the quantum simulation of molecular vibronic spectra, which is currently in preparation: (i) one could possibly go beyond the Condon approximation, i.e. the coordinate dependence of the transition dipole moment, by introducing an additional phase to the input Gaussian states; (ii) the anharmonic problem, which is more challenging, can be incorporated in the molecular process, for example with Morse-oscillators.^30,31 Moreover, we may adapt the quantum simulation of the spin-boson model³² or many-body bosonic-fermionic systems³³ for further vibronic simulation beyond the Born–Oppenheimer approximation.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was supported by the National Key Research and Development Program of China under Grants No. 2016YFA0301900 (No. 2016YFA0301901) and the National Natural Science Foundation of China Grants 11374178 and 11574002. JH acknowledges the support from the Basic Science Research Program through the National Research Foundation of Korea (NRF) funded by the Ministry of Education, Science and Technology (NRF-2015R1A6A3A04059773 and NRF-2017R1A4A1015770).

References

1. S. Aaronson and A. Arkhipov, Proceedings of the 43rd annual ACM symposium on Theory of computing – STOC’11, 2011, p. 333.
2. J. B. Spring, B. J. Metcalf, P. C. Humphreys, W. S. Kolthammer, X.-M. Jin, M. Barbieri, A. Datta, N. Thomas-Peter, N. K. Langford, D. Kundys, J. C. Gates, B. J. Smith, P. G. R. Smith and I. A. Walmsley, Science, 2013, 339, 798–801.
3. M. A. Broome, A. Fedrizzi, S. Rahimi-Keshari, J. Dove, S. Aaronson, T. C. Ralph and A. G. White, Science, 2013, 339, 794–798.
4. A. Crespi, R. Osellame, R. Ramponi, D. J. Brod, E. F. Galvao, N. Spagnolo, C. Vitelli, E. Maiorino, P. Mataloni and F. Sciarrino, Nat. Photonics, 2013, 7, 545–549.
5. M. Tillmann, B. Dakic, R. Heilmann, S. Nolte, A. Szameit and P. Walther, Nat. Photonics, 2013, 7, 540–544.
6. N. Spagnolo, C. Vitelli, M. Bentivegna, D. J. Brod, A. Crespi, F. Flamini, S. Giacomini, G. Milani, R. Ramponi, P. Mataloni, R. Osellame, E. F. Galvao and F. Sciarrino, Nat. Photonics, 2014, 8, 615–620.
7. J. Carolan, J. D. A. Meinecke, P. J. Shadbolt, N. J. Russell, N. Ismail, K. Wörhoff, T. Rudolph, M. G. Thompson, J. L. O’Brien, J. C. F. Matthews and A. Laing, Nat. Photonics, 2014, 8, 621–626.
8. A. P. Lund, A. Laing, S. Rahimi-Keshari, T. Rudolph, J. L. O’Brien and T. C. Ralph, Phys. Rev. Lett., 2014, 113, 100502.
9. S. Rahimi-Keshari, A. P. Lund and T. C. Ralph, Phys. Rev. Lett., 2015, 114, 060501.
10. J. Huh, G. G. Guerreschi, B. Peropadre, J. R. McClean and A. Aspuru-Guzik, Nat. Photonics, 2015, 9, 615–620.
11. J. Huh and M.-H. Yung, 2016, arXiv:1608.03731.
12. H.-C. Jankowiak, J. L. Stuber and R. Berger, J. Chem. Phys., 2007, 127, 234101.
13. S. L. Braunstein, Phys. Rev. A, 2005, 71, 1–4.
14. E. V. Doktorov, I. A. Malkin and V. I. Man’ko, J. Mol. Spectrosc., 1977, 64, 302–326.
15. X. Ma and W. Rhodes, Phys. Rev. A, 1990, 41, 4625–4631.
16. H. K. Lau and D. F. V. James, Phys. Rev. A, 2012, 85, 059905.
17. C. Shen, Z. Zhang and L. M. Duan, Phys. Rev. Lett., 2014, 112, 050504.
18. B. Peropadre, G. G. Guerreschi, J. Huh and A. Aspuru-Guzik, Phys. Rev. Lett., 2016, 117, 140505.
19. M. Nimlos and G. Ellison, J. Phys. Chem., 1986, 90, 2574–2580.
20. C.-L. Lee, S.-H. Yang, S.-Y. Kuo and J.-L. Chang, J. Mol. Spectrosc., 2009, 256, 279–286.
21. C. Monroe, D. M. Meekhof, B. E. King, W. M. Itano and D. J. Wineland, Phys. Rev. Lett., 1995, 75, 4714–4717.
22. C. Roos, T. Zeiger, H. Rohde, H. C. Nägerl, J. Eschner, D. Leibfried, F. Schmidt-Kaler and R. Blatt, Phys. Rev. Lett., 1999, 83, 4713–4716.
23. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16 Revision A.03, Gaussian Inc., Wallingford CT, 2016.
24. D. M. Meekhof, C. Monroe, B. E. King, W. M. Itano and D. J. Wineland, Phys. Rev. Lett., 1996, 76, 1796–1799.
25. K. Toyoda, R. Hiji, A. Noguchi and S. Urabe, Nature, 2015, 527, 74–77.
26. M. Um, J. Zhang, D. Lv, Y. Lu, S. An, J.-N. Zhang, H. Nha, M. S. Kim and K. Kim, Nat. Commun., 2016, 7, 11410.
27. J. Zhang, M. Um, D. Lv, J.-N. Zhang, L.-M. Duan and K. Kim, 2016, arXiv:1611.08700.
28. A. Neville, C. Sparrow, R. Clifford, E. Johnston, P. M. Birchall, A. Montanaro and A. Laing, Nat. Phys., 2017, 4270.
29. P. Clifford and R. Clifford, 2017, arXiv:1706.01260v1.
30. F. Iachello and M. Ibrahim, J. Phys. Chem. A, 1998, 102, 9427.
31. D. G. Olivares, B. Peropadre, J. Huh and J. J. Garcá-Ripoll, 2016, arXiv:1611.08101v1.
32. A. Lemmer, C. Cormick, D. Tamascelli, T. Schaetz, S. F. Huelga and M. B. Plenio, 2017, arXiv:1704.00629.
33. A. Mezzacapo, J. Casanova, L. Lamata and E. Solano, Phys. Rev. Lett., 2012, 109, 200501.

---

Footnote

† Electronic supplementary information (ESI) available: Trapped ion implementation of quantum optical operations, an experiment detection scheme, and experimental data error analysis. See DOI: 10.1039/c7sc04602b

---