Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Conservation of direct dynamics in sterically hindered SN2/E2 reactions
Eduardo
Carrascosa†
 ,
Jennifer
Meyer
,
Jennifer
Meyer
 ,
Tim
Michaelsen
,
Martin
Stei
and
Roland
Wester
,
Tim
Michaelsen
,
Martin
Stei
and
Roland
Wester
 *
*
Institut für Ionenphysik und Angewandte Physik, Universität Innsbruck, Technikerstraße 25, 6020 Innsbruck, Austria. E-mail: roland.wester@uibk.ac.at; Tel: +43 512 507 52620
First published on 13th November 2017
Abstract
Nucleophilic substitution (SN2) and base-induced elimination (E2), two indispensable reactions in organic synthesis, are commonly assumed to proceed under stereospecific conditions. Understanding the way in which the reactants pre-orient in these reactions, that is its stereodynamics, is essential in order to achieve a detailed atomistic picture and control over such processes. Using crossed beam velocity map imaging, we study the effect of steric hindrance in reactions of Cl− and CN− with increasingly methylated alkyl iodides by monitoring the product ion energy and scattering angle. For both attacking anions the rebound mechanism, indicative of a direct SN2 pathway, is found to contribute to the reaction at high relative collision energies despite being increasingly hindered. An additional forward scattering mechanism, ascribed to a direct E2 reaction, also contributes at these energies. Inspection of the product energy distributions confirms the direct and fast character of both mechanisms as opposed to an indirect reaction mechanism which leads to statistical energy redistribution in the reaction complex. This work demonstrates that nonstatistical dynamics and energetics govern SN2 and E2 pathways even in sterically hindered exchange reaction systems.
Introduction
One of the central characteristics that make bimolecular nucleophilic substitutions (SN2) central in organic synthesis is its stereospecific character.1 In the simplest approximation, the SN2 reaction is assumed to proceed in a collinear fashion, following a three step mechanism: first, the attacking anion approaches the neutral molecule through a long-range attractive ion–dipole interaction. The second step is the formation of an intermediate complex which follows the well known Walden inversion. Finally, the leaving group exits this complex and the final product is formed. The inversion of configuration that occurs during this mechanism is often used in synthetic chemistry to control the formation of specific isomeric compounds.For many decades significant effort has been devoted to understanding the efficiency of SN2 reactions under different conditions and if the proposed collinear attack is universally valid. For that purpose, studies on isolated gas phase reactions appear as an optimal approach. The simplest gas phase nucleophilic substitution reactions between a halide ion and a methyl halide (X− + CH3Y) present a minimum energy path resembling a double minimum structure separated by a transition state barrier, which is usually submerged with respect to the reactants' energy.2 According to classical statistical models, such as Rice–Ramsperger–Kassel–Marcus (RRKM) theory or transition state theory, the energy available in SN2 reactions is randomized among the dense bath of internal degrees of freedom of the intermediate complex through intramolecular vibrational relaxation.3 However, early theoretical studies already proposed the occurrence of stereodynamical effects, nonstatistical energy distributions for reaction products and vibrational mode-selective rate enhancement in model X− + CH3Y reactions.4–7 These results were reinforced by experimental studies that demonstrated a different effect of translational and internal energy on the reaction kinetics of such systems.8,9 Very recent high-level theoretical studies have identified rovibrational mode specificity in model SN2 reactions, thus contradicting the predictions of statistical models.10–13 All these findings have emphasized the importance of carefully considering the timescales for atomic and intramolecular motions along the reaction coordinate in SN2 processes.14–16
Experimentally, crossed beam velocity map imaging studies on X− + CH3Y systems have provided evidence of the direct and fast character of SN2 reaction pathways such as the direct rebound mechanism, as opposed to a rapid energy randomization.17–19 In addition, alternative entrance channel geometries such as X–H or X–Y bonded pre-reaction complexes have been identified.10,20,21 For some reactions, such entrance channels have been shown to promote either the formation of new product channels22 or to cause a dramatic change in the reaction stereodynamics.18,23 While the anionic attack on methyl halides (CH3Y) can only lead to nucleophilic substitution, reactions with methyl-substituted halides can also follow base-induced elimination, E2. Very recently, we have demonstrated this latter reaction to follow a direct forward scattering mechanism irrespective of the identity of the attacking anion and leaving group.24 Complementary theoretical calculations have shown this mechanisms to be a fast process (≈400 fs) that occurs predominantly at high impact parameter collisions.
One key question is if steric substitution may limit the nonstatistical effects observed in X− + CH3Y type reactions, that is if energy randomization among the large number of internal degrees of freedom may dominate over reorientation and mode-specific coupling effects in reactions with highly methylated halides.25 While many theoretical studies have focused on characterizing the effect of steric substitution on the barrier heights of SN2 and E2 reactions,26–29 computational reaction dynamics studies by means of trajectory calculations are needed in order to investigate the time-dependent steric and rovibrational mode specific effects governing both the branching ratio between SN2 and E2 pathways and their intrinsic collision patterns. Studying such factors is even more relevant in systems where nonstatistical effects may govern the reaction outcome, as shown for model nucleophilic substitutions. Further, trajectory calculations can provide important information to laboratory data by assigning experimental scattering angle and velocity ranges to specific reaction products.
To date, computational work on the intrinsic SN2/E2 reaction dynamics has been scarce. Only recently, “on the fly” classical dynamics simulations have been performed on F− + CH3CH2I at one specific collision energy.24 While this method does not require computing the full potential energy surface for these systems, it is limited by the long computational time needed to acquire reasonable statistics of reactive trajectories. This can be circumvented by the construction of full-dimensional ab initio potential energy surfaces followed by quasiclassical trajectory simulations on them.18,30 While the complexity of the above-mentioned systems makes the construction of analytical potential energy surfaces demanding, promising progress has been reported very recently.31
Experimentally, Bierbaum, Gronert and coworkers have reported a net reaction rate decrease of several X− + RY reactions with increasingly complex neutral reactants, thereby observing a clear relative preference for the E2 pathway as a function of methyl substitution,32–36 in agreement with our last scattering experiments.24 While the studies of Bierbaum and Gronert have provided important structure–energy relations, monitoring the way in which the reactants approach and exchange energy has remained elusive.
The goal of this work is to determine how methyl substitution affects the stereodynamics and energy partitioning in such ion–molecule reactions. We specifically focus on the well-established direct rebound SN2 mechanism. For this purpose, we have studied the reactive scattering of Cl− and CN− ions with stepwise methylated alkyl iodides at single collision conditions. Both anions have a low proton affinity and have been shown to disfavour the formation of pre-reaction complexes.17,37,38 Our aim is to investigate the effect of steric hindrance on direct reaction channels.
Table 1 summarizes the SN2 and E2 reaction exothermicities and transition state energies for the systems investigated in this work. If compared to the non-substituted Cl− + CH3I and CN− + CH3I reactions, the SN2 mechanisms in Cl− + CH3CH2I, Cl− + (CH3)2CHI and CN−/NC− + CH3CH2I also show transition state barriers very near to the reactant energy. In contrast, all anti-E2 reactions present positive transition state barriers, although the barrier heights are lower than the lowest relative collision energy studied in the present work (0.4 eV). Thus, all reaction channels presented in Table 1 are energetically accessible given the experimental conditions.
| Reaction | ΔrH (SN2) | ΔrH (E2) | E TS (SN2) | E TS (anti-E2) |
|---|---|---|---|---|
| (1) Cl− + CH3I | −0.55 | — | −0.08 | — |
| (2) Cl− + CH3CH2I | −0.67 | +0.07 | −0.01 | +0.28 |
| (3) Cl− + (CH3)2CHI | −0.68 | +0.07 | −0.02 | +0.10 |
| (4) NC− + CH3I | −1.98/−1.05 | — | −0.21/−0.03 | — |
| (5) NC− + CH3CH2I | −2.00/−1.16 | −0.65/+0.01 | −0.05/+0.10 | +0.14/+0.29 |
We report on a series of gas phase angle- and energy differential cross section measurements of the five reactions listed in Table 1 and show that direct substitution and elimination dynamics persist even when complex neutral partners are involved.
Results
The velocity distributions of product I− ions from reactions (1)–(5) (see Table 1) are presented in Fig. 1 and 2. Each velocity image consists of 30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000–40
000–40![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 ion events and is depicted in the center of mass frame. The scattering results for the reaction of Cl− with increasingly methylated alkyl iodides are depicted in Fig. 1. The red and white circles drawn in each velocity distribution indicate the kinematic limits for the SN2 and E2 reactions, respectively. The kinematic limit is given by the sum of relative collision energy (Erel) and reaction exothermicity (−ΔrH, see Table 1).
000 ion events and is depicted in the center of mass frame. The scattering results for the reaction of Cl− with increasingly methylated alkyl iodides are depicted in Fig. 1. The red and white circles drawn in each velocity distribution indicate the kinematic limits for the SN2 and E2 reactions, respectively. The kinematic limit is given by the sum of relative collision energy (Erel) and reaction exothermicity (−ΔrH, see Table 1).
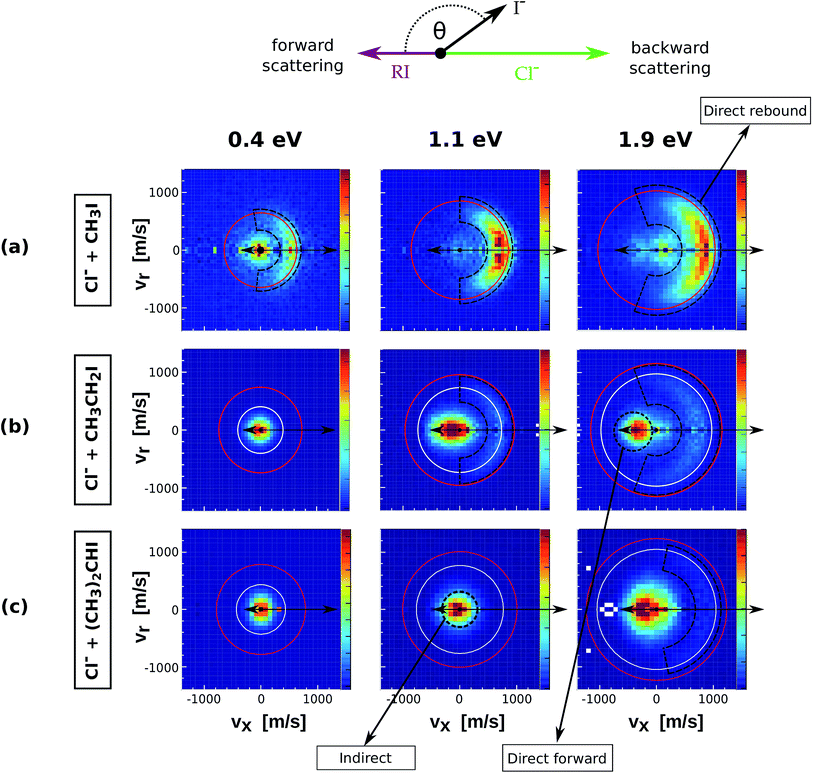 | ||
| Fig. 1 Center of mass velocity distributions of I− ions produced from the reactions Cl− + CH3I (a), Cl− + CH3CH2I (b) and Cl− + (CH3)2CHI (c). The images present measurements at three different relative collision energies. The arrows depicted above the images illustrate the schematic Newton diagram for the reaction systems, showing the relative direction of the reactant velocities in the center of mass frame and defining forward and backward scattering of the product ion. The red and white rings mark the maximum product ion velocity for the respective SN2 and E2 processes, given by energy and momentum conservation. The black dashed regions define the three main mechanistic features that can be distinguished. The data presented for Cl− + CH3I correspond to a new set of measurements using an improved version of the instrument compared to the initial study.17 | ||
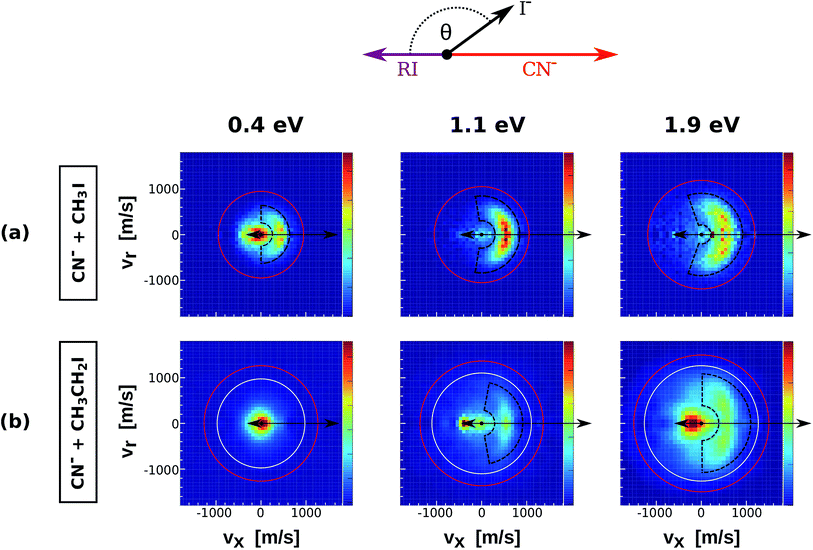 | ||
| Fig. 2 Center of mass I− velocity distributions from the reactions CN− + CH3I (a) and CN− + CH3CH2I (b). The depicted red and white circles mark the kinematic limits for SN2 and E2 reactions. The black dashed areas represent the region of direct backward scattered events. The image for CN− + CH3I at 1.1 eV has been presented in a recent publication.38 | ||
The upper row presents the velocity distributions of I− ions from the reaction of Cl− + CH3I at 0.4 eV, 1.1 eV and 1.9 eV. The velocity map at the lowest Erel shows distinct isotropic and backward scattering of the product I− ions relative to the incoming CH3I molecules. Isotropic scattering has been associated with the formation of an intermediate complex with a lifetime longer than its rotational period, while backward scattering of the product ion resembles the commonly accepted collinear nucleophilic substitution mechanism.14 This latter mechanism strongly dominates at increasing Erel, with a third distinct feature appearing at 1.9 eV, which has been previously ascribed to a roundabout mechanism.17 It is worth noting that only isotropic scattering was observed at Erel = 0.4 eV in a previous study on the same system.17 The current experimental data recorded at increased velocity resolution are in very good agreement with previous theoretical predictions.37
The product velocity images for Cl− + CH3CH2I (Fig. 1b) present a different dynamical picture. At low Erel almost all I− events are scattered isotropically around the center of mass with near-zero velocity. At increasing Erel both direct backward and forward scattering features appear. Backward scattered events have a considerably higher velocity than forward scattered events, in many cases appearing above the kinematic limit for E2 products, a fact that reinforces the assignment of these direct backward scattered ions to an SN2 mechanism. A considerable fraction of reactions occur via a forward scattering mechanism, whose relative abundance increases with the degree of methylation. This scattering pattern has been very recently observed in a series of different reactions with substituted alkyl halides and has been assigned as a fingerprint of E2 reactions.24 It cannot be excluded that a fraction of SN2 events also occurs via forward scattering, as has been shown for similar anion–molecule systems.20,22 However, forward scattering in SN2 reactions has been found to be intimately related to a favoured X–H bonded pre-reaction geometry.18 Due to the low proton affinity of both Cl− and CN− and the absence of such a mechanism in Cl− + CH3I and CN− + CH3I we expect the contribution of forward SN2 events to be negligible for the systems discussed here. The forward scattered ions show a very narrow range of product angles at 1.1 eV and 1.9 eV, in contrast to the broad angular distributions of backward scattered events.
For the Cl− + (CH3)2CHI reaction (Fig. 1c) isotropic scattering dominates at 0.4 eV and 1.1 eV, whereas forward scattering is the predominant feature at 1.9 eV. In contrast to Cl− + CH3CH2I, backward scattering is only observed at this latter collision energy. Although barely visible in the velocity map, its presence is demonstrated in the corresponding internal energy distribution (Fig. 4, lower panel), where a backward contribution with maximum at ≈1.1 eV can be distinguished. Again, a considerable fraction of these events is scattered with velocities above the kinematic limit for E2, reinforcing the ascription of this mechanism to direct nucleophilic substitution.
Fig. 2 depicts the velocity and scattering angle distributions of I− products from the reactions CN− + CH3I (a) and CN− + CH3CH2I (b) as a function of Erel. Due to the extremely low reaction rate of CN− + (CH3)2CHI,36 it was not possible to extract statistically meaningful experimental results for this system. The depicted kinematic limits for substitution and elimination correspond to the approach of the C-atom of the CN− ion to the neutral reactant. The scattering features of the velocity images from CN− + CH3CH2I are very similar to the ones observed in Cl− + CH3CH2I, with dominant isotropic scattering at low Erel and an increase of direct backward scattered events at higher energies. Again, a steric inhibition of this mechanism is observed if compared to CN− + CH3I. Forward scattering emerges at 1.1 eV in the same way as in reactions of Cl− with substituted alkyl iodides. Compared to the previous systems, the backward scattered events in CN− + CH3I and CN− + CH3CH2I show lower product velocities, indicating a significant energy partitioning into product internal degrees of freedom.
Discussion
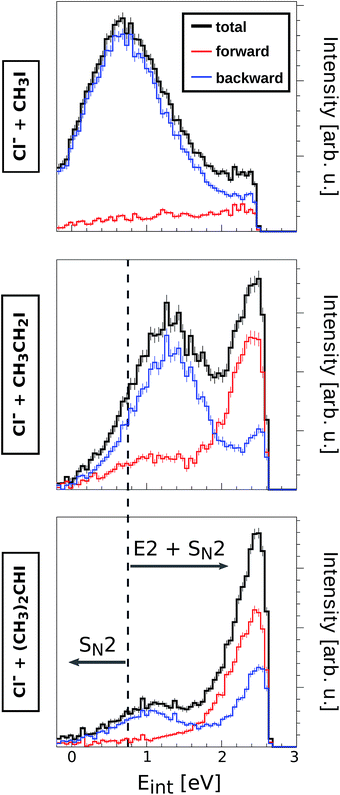
In order to quantify the effect of methylation on the relative intensity of the direct backward SN2 mechanism, Fig. 3 compares the fraction of direct rebound events for reactions (1)–(5). The fractions have been obtained by defining specific velocity and scattering angle regions for the direct rebound events. These are marked by the black dashed areas shown in Fig. 1 and 2. As the velocity distribution of direct backward events varies depending on reaction system and collision energy, the areas have been defined independently for each velocity image. More details are given in the Methods section.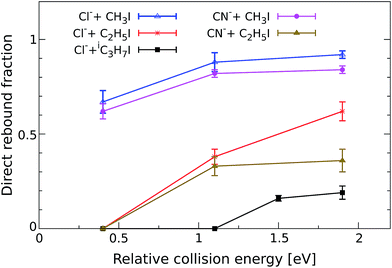 | ||
| Fig. 3 Normalized yield of reactive direct rebound events as a function of Erel. The yield represents the fraction of total scattering events that fall inside the velocity range of direct rebound scattering, which is marked by the corresponding dashed black area in Fig. 1 and 2. Error bars reflect a convolution of counting statistics and the uncertainties associated with the specific velocity and angle cut. The values for the reaction CN− + CH3I have been taken from a recent publication.38 | ||
As a general trend, the fraction of backward scattered events is shown to decrease at lower Erel and with increasing steric hindrance at the central carbon. Reactions of both Cl− and CN− with methylated alkyl iodides show no direct rebound at 0.4 eV, whereas the contribution is considerable at this energy in Cl− + CH3I and CN− + CH3I. Although less predominant than for the non-methylated reactions, backward scattering opens up at 1.1 eV in reactions with CH3CH2I and at 1.5 eV for Cl− + (CH3)2CHI, as confirmed by an additional measurement at this energy. Remarkably, more than half of the reactive collisions follow the direct rebound mechanism for Cl− + CH3CH2I and CN− + CH3CH2I at 1.9 eV. At the same Erel the contribution of this pathway in Cl− + (CH3)2CHI amounts to 0.15, which is a significant fraction considering the bulkiness of the neutral reactant. It is worth noting that the reported fraction only represents the amount of direct backward SN2 events. As shown in Fig. 1 and 2 the forward scattering channel at higher collision energies is also a direct mechanism that has been recently ascribed to an E2 reaction.24 Thus, direct scattered products account for the dominating fraction of reactive events at these energies. This demonstrates that direct dynamics still prevail in reactions with highly substituted alkyl iodides.
The direct backward SN2 mechanism is known to occur at timescales below 1 ps, i.e. considerably faster than intramolecular vibrational redistribution. However, it is important to analyze to what extent steric substitution affects the timescale of the reaction and thus the energy partitioning to the corresponding neutral product. For this purpose, a detailed inspection of the product internal energy distributions (Eint) has been carried out for reactions (1)–(5) at all studied collision energies. Fig. 4 depicts three selected product Eint distributions from reactions of Cl− with CH3I, CH3CH2I and (CH3)2CHI at Erel = 1.9 eV.
E int represents the amount of initially available energy that is partitioned into product internal degrees of freedom. It can be expressed as Eint = (Erel + (−ΔrH)) − Ekin, with Ekin being the sum of product ion and neutral translational energies. Long-lived intermediate complexes will favour the initial energy to be redistributed among the product internal degrees of freedom (large Eint), whereas short-lived complexes can result in efficient coupling to product ion translation (small Eint). By extracting the mean of the internal energy for direct rebound events (low Eint distributions of blue curves in Fig. 4), the corresponding fractions of initial energy partitioned into product internal excitation are obtained for the direct backward SN2 mechanism (fEint(bkw), Table 2). The relative error of these fractions is 10–15% and is dominated by the corresponding uncertainty in Erel.
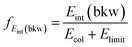 . The relative errors for the fractions are dominated by the uncertainty in Erel, which amounts to 10–15% in all cases
. The relative errors for the fractions are dominated by the uncertainty in Erel, which amounts to 10–15% in all cases
| 0.4 eV | 1.1 eV | 1.9 eV | |
|---|---|---|---|
| Cl− + CH3I | 0.10 | 0.20 | 0.29 |
| Cl− + CH3CH2I | — | 0.41 | 0.51 |
| Cl− + (CH3)2CHI | — | — | 0.42 |
| CN− + CH3I | 0.79 | 0.68 | 0.69 |
| CN− + CH3CH2I | — | 0.88 | 0.81 |
Among the reactions involving Cl−, only Cl− + CH3I shows direct backward scattering at 0.4 eV. This mechanism is significantly direct, with only 10% of the initial energy being partitioned into internal excitation. At increasing Erel, the fraction of energy partitioning increases, reaching nearly 30% at 1.9 eV. These data are in good agreement with a measurement performed earlier.41 A higher amount of energy is dissipated in form of internal excitation in the reactions Cl− + CH3CH2I and Cl− + (CH3)2CHI, however this fraction does not exceed 60% in any case. Strikingly, at high Erel direct backward SN2 events show slightly less energy partitioning in Cl− + (CH3)2CHI reactions than in Cl− + CH3CH2I reactions. This hints to very similar intermediate complex lifetimes and energy transfer in this direct process, irrespective of the degree of methyl substitution. A much higher product internal excitation is observed in reactions with CN−, possibly due to the strong coupling of the initial energy to the C–N bond vibration. Similar to the reactions with Cl−, the energy partitioning increases from CN− + CH3I to CN− + CH3CH2I. Overall, these results show that the energy partitioning for the direct SN2 mechanism at high Erel is not significantly affected by adding methyl substituents to the neutral reactant. This finding demonstrates the nonstatistical character of these SN2 processes, as fast energy transfer dominates over energy randomization through slow intramolecular vibrational redistribution even in reaction systems with a higher density of states at the intermediate complex than in previously studied reactions.7,8 Thus, the threshold between nonstatistical and statistical dynamics is not bridged by stepwise methyl substitution but likely has to involve either higher molecular complexity in form of large substituents on the central carbon or a different type of binding interaction.
Given the similarities in reaction dynamics and energetics of the direct SN2 channel for reactions (1)–(5), it can be predicted that this mechanism evolves through a collinear entrance channel complex irrespective of the neutral reactant. This would be in consonance with the low proton affinity of both Cl− and CN− ions, and with the observation of a very broad range of scattering angles as indicator of low impact parameter collisions. For such an approach geometry to occur, it is very likely that reactant preorientation takes place and steers the reaction towards the formation of a collinear and short-lived intermediate complex, as predicted for similar systems.4,17 This is supported by the results presented in Table 2, which show that the energy partitioning does not strongly depend on the substitution pattern. In this regard, the results presented here lay the ground for high level trajectory calculations to be performed in order to add a time-dependent atomistic understanding of the detailed stereodynamics involved in such sterically hindered SN2 reactions.
Conclusion
This work presents experimental reactive scattering results for a series of SN2/E2 ion–molecule reactions with stepwise methylated alkyl iodides. We focus on the direct backward SN2 mechanism and find that this pathway still occurs at high collision energies in reactions of Cl− and CN− with methylated alkyl iodides. Direct SN2 is even favoured both over base-induced elimination and alternative SN2 pathways at energies above 1 eV. Analysis of the scattering images and the energy partitioning into internal degrees of freedom shows that both SN2 and E2 mechanisms remain direct irrespective of the degree of methyl substitution. The prevailing of such an exchange process is likely related to a stereodynamical effect preorienting the reactants towards a collinear geometry. This study provides the first demonstration of prevailing direct dynamics and nonstatistical energy coupling in SN2/E2 reactions with substituted alkyl halides and shows the capability of crossed beam velocity map imaging to study steric effects in complex organic systems.Methods
Experimental procedure
Our experiment combines a crossed beam arrangement with a velocity map imaging (VMI) spectrometer to study the reactive scattering dynamics of the above-mentioned systems at single collision conditions. The whole apparatus operates in pulsed mode at a repetition rate of 20 Hz. The technical details have been reported elsewhere.42,43 The arrangement consists of three differentially pumped chambers. For the generation of reactant Cl− and CN− ions, low concentration mixtures of CH3Cl and CH3CN in argon are supersonically expanded into a first chamber through a homebuilt piezoelectric valve and exposed to a discharge between two electrodes. The resulting ions are extracted and mass-selected using a Wiley–McLaren type time-of-flight spectrometer.44 Electrostatic lenses and deflectors guide the ions into an octupole radiofrequency ion trap in which a specific ion mass is stored for tenths of milliseconds. During this time the ions undergo non-reactive collisions with nitrogen buffer gas molecules, thereby reducing their kinetic energy spread. The typical full width at half maximum (FWHM) of the ions' kinetic energy lies in the range of 100–150 meV. After extraction the ions are guided and focused into the interaction region of a third chamber containing a velocity map imaging spectrometer. Here, the ions are crossed at a 60° angle with a pulsed supersonic molecular beam, which consists of a low concentration of reactant gas seeded in helium. The neutral gas pulse is generated from a second piezoelectric valve and has a duration of ≈200 μs. The mean velocity of the neutral molecules used in this work is typically in the range of 1200–1300 m s−1. The velocity was probed via electron impact ionization of the respective neutral beam and subsequent imaging of the CH3I+/CH3CH2I+/(CH3)2CHI+ product velocity. The measured velocity and angular spreads (FWHM) of the neutral beam are typically 220–240 m s−1 and 1.5–2.5 degree, respectively. In order to avoid clustering, the temperature of the neutral beam nozzle is kept at 70 °C and both the backing pressure and reactant concentration of the gas mixture are minimized.Some of the collisions generate product I− ions, which are extracted normal to the scattering plane by pulsing on the electrodes of the VMI spectrometer. They travel through a drift tube until hitting a microchannel plate, thereby triggering an electron cascade that finally impacts on a phosphor screen. The position and time of the generated light are recorded by a CCD Camera and a photomultiplier, respectively. The accumulated product ion impact positions in the laboratory frame are transformed into a velocity vector in the center of mass frame, resulting in the type of images shown in Fig. 1 and 2. In the case of Cl− the reactive scattering experiments have been performed without discriminating 35Cl− and 37Cl− prior to the reactive collision. Therefore, 1/4 of the product events are assumed to come from reactions with 37Cl. The Newton diagrams have been corrected accordingly in order to resemble the accurate center-of-mass velocity.
In order to obtain the branching ratios for the direct SN2 mechanism shown in Fig. 3, appropriate cuts along the product velocity and scattering angle were performed for each velocity image. Thereby, two main assumptions have been made: first, it is assumed that all direct backward scattered events arise from the direct rebound SN2 mechanism. Although we have shown that a minor fraction of products from E2 reactions can also follow this scattering pattern in F− + CH3CH2I,24 this should represent a negligible fraction of the total direct backward scattered events. Second, it is assumed that the whole direct backward distribution is inside the cut when changes to the scattering angle or velocity limits do not cause significant changes in the total ion yield inside the range. This is demonstrated below.
By monitoring the number of counts as a function of different angle and velocity cuts, general trends can be obtained. Fig. 5 shows example scans along the scattering angle (a) and minimum total velocity (b) of the product I− ion for Cl− + CH3CH2I at 1.1 eV. Fig. 5a shows the evolution of ion intensity as a function of scattering angle (θ) cut for a fixed cut on the minimum total velocity (vtotmin) of 500 m s−1. The cut on the maximum total velocity (vtotmax) is set to 950 m s−1. A steep increase in ion intensity is observed from 170° to 90°, which is the region that contains the backward scattered events. The “plateau” from 90° to 60° marks the outer limit of the scattering angle distribution for the direct SN2 mechanism, after which the ion intensity rises again due to the contribution of forward scattered events. Fig. 5b depicts the dependence of ion intensity on vtotmin for a fixed scattering angle cut of 70°. We observe a similar steep increase with decreasing vtotmin, followed by a slight “plateau” from 600 m s−1 to 400 m s−1. After that, the second increase corresponds to the contribution of the forward scattered events. A second “plateau” below 100 m s−1 becomes apparent, indicating that all product events are inside the cut range.
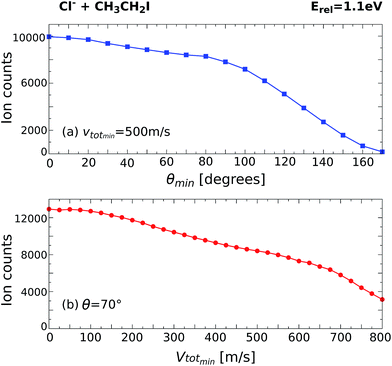 | ||
| Fig. 5 Scans along the product I− scattering angle (a) and minimum total velocity (b) cuts for the reaction Cl− + CH3CH2I at Erel = 1.1 eV. | ||
The beginning of the flat regions along the scans define the velocity and scattering angle limits of this mechanism. The range chosen for each image is represented by the black dashed areas in Fig. 1 and 2. The approximate uncertainty of these values is given by θ ± 10° for the scattering angle cut and vtotmin ± 50 m s−1 for the velocity cut. The vertical error bars in the branching ratios of Fig. 3 result from convoluting these two uncertainties.
Theoretical calculations
The electronic structure calculations have been performed at the MP2/aug-cc-pVDZ level of theory and using the Wadt and Hay relativistic effective core potential (ECP) to represent the iodine core electrons.45 All the transition states have been located using the Quadratic Synchronous Transit (QST2) path approximation. The vibrational frequencies were inspected for all considered structures, which allowed the assessment of the zero point energy corrections. All calculations were performed using the Gaussian 09 program package.46Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors thank the Austrian Science Fund (FWF) for financial support under project P25956-N20. E. C. acknowledges support by the DOC-fellowship of the Austrian Academy of Science.References
- M. B. Smith and J. March, March's Advanced Organic Chemistry: Reactions, Mechanisms and Structure, John Wiley & Sons, 2007 Search PubMed.
- M. L. Chabinyc, S. L. Craig, C. K. Regan and J. I. Brauman, Science, 1998, 279, 1882–1886 CrossRef CAS PubMed.
- W. Olmstead and J. Brauman, J. Am. Chem. Soc., 1977, 99, 4219–4228 CrossRef CAS.
- W. L. Hase and Y. J. Cho, J. Chem. Phys., 1993, 98, 8626–8639 CrossRef CAS.
- W. L. Hase, Science, 1994, 266, 998–1002 CAS.
- S. T. Graul and M. T. Bowers, J. Am. Chem. Soc., 1994, 116, 3875–3883 CrossRef CAS.
- L. Sun, K. Song and W. L. Hase, Science, 2002, 296, 875–878 CrossRef CAS PubMed.
- A. A. Viggiano, R. A. Morris, J. S. Paschkewitz and J. F. Paulson, J. Am. Chem. Soc., 1992, 114, 10477–10482 CrossRef CAS.
- L. A. Angel and K. M. Ervin, J. Phys. Chem. A, 2001, 105, 4042–4051 CrossRef CAS.
- I. Szabó and G. Czakó, Nat. Commun., 2015, 6, 5972 CrossRef PubMed.
- C. Hennig and S. Schmatz, Phys. Chem. Chem. Phys., 2016, 18, 19668–19675 RSC.
- I. Szabó and G. Czakó, J. Chem. Phys., 2016, 145, 134303 CrossRef PubMed.
- Y. Wang, H. Song, I. Szabó, G. Czakó, H. Guo and M. Yang, J. Phys. Chem. Lett., 2016, 7, 3322–3327 CrossRef CAS PubMed.
- J. Xie, R. Otto, J. Mikosch, J. Zhang, R. Wester and W. L. Hase, Acc. Chem. Res., 2014, 47, 2960–2969 CrossRef CAS PubMed.
- I. Szabó and G. Czakó, J. Phys. Chem. A, 2015, 119, 3134–3140 CrossRef PubMed.
- J. Xie and W. L. Hase, Science, 2016, 352, 32–33 CrossRef CAS PubMed.
- J. Mikosch, S. Trippel, C. Eichhorn, R. Otto, U. Lourderaj, J. X. Zhang, W. L. Hase, M. Weidemüller and R. Wester, Science, 2008, 319, 183–186 CrossRef CAS PubMed.
- M. Stei, E. Carrascosa, M. A. Kainz, A. Kelkar, J. Meyer, I. Szabó, G. Czakó and R. Wester, Nat. Chem., 2016, 8, 151–156 CAS.
- J. Meyer and R. Wester, Annu. Rev. Phys. Chem., 2017, 68, 333–353 CrossRef CAS PubMed.
- J. Zhang, J. Mikosch, S. Trippel, R. Otto, M. Weidemüller, R. Wester and W. L. Hase, J. Phys. Chem. Lett., 2010, 1, 2747–2752 CrossRef CAS.
- I. Szabó, B. Olasz and G. Czakó, J. Phys. Chem. Lett., 2017, 8, 2917–2923 CrossRef PubMed.
- R. Otto, J. Brox, S. Trippel, M. Stei, T. Best and R. Wester, Nat. Chem., 2012, 4, 534–538 CrossRef CAS PubMed.
- J. Mikosch, J. Zhang, S. Trippel, C. Eichhorn, R. Otto, X. Sun, W. de Jong, M. Weidemüller, W. Hase and R. Wester, J. Am. Chem. Soc., 2013, 135, 4250–4259 CrossRef CAS PubMed.
- E. Carrascosa, J. Meyer, J. Zhang, M. Stei, T. Michaelsen, W. L. Hase, L. Yang and R. Wester, Nat. Commun., 2017, 8, 25 CrossRef PubMed.
- A. A. Viggiano and A. J. Midey, J. Phys. Chem. A, 2000, 104, 6786–6790 CrossRef CAS.
- F. M. Bickelhaupt, J. Comput. Chem., 1999, 20, 114–128 CrossRef CAS.
- P. Bento, M. Sola and F. M. Bickelhaupt, J. Chem. Theory Comput., 2008, 4, 929–940 CrossRef PubMed.
- K. M. Conner and S. Gronert, J. Org. Chem., 2013, 78, 8606–8613 CrossRef CAS PubMed.
- P. R. Rablen, B. D. McLarney, B. J. Karlow and J. E. Schneider, J. Org. Chem., 2014, 79, 867–879 CrossRef CAS PubMed.
- I. Szabó, A. G. Csaszar and G. Czakó, Chem. Sci., 2013, 4, 4362–4370 RSC.
- V. Tajti and G. Czakó, J. Phys. Chem. A, 2017, 121, 2847–2854 CrossRef PubMed.
- C. H. DePuy, S. Gronert, A. Mullin and V. M. Bierbaum, J. Am. Chem. Soc., 1990, 112, 8650–8655 CrossRef CAS.
- S. Gronert, Chem. Rev., 2001, 101, 329–360 CrossRef CAS PubMed.
- S. Gronert, Acc. Chem. Res., 2003, 36, 848–857 CrossRef CAS PubMed.
- J. M. Garver, Y.-r. Fang, N. Eyet, S. M. Villano, V. M. Bierbaum and K. C. Westaway, J. Am. Chem. Soc., 2010, 132, 3808–3814 CrossRef CAS PubMed.
- J. M. Garver, N. Eyet, S. M. Villano, Y. Zhibo and V. M. Bierbaum, Int. J. Mass Spectrom., 2011, 301, 151–158 CrossRef CAS.
- J. Zhang, U. Lourderaj, R. Sun, J. Mikosch, R. Wester and W. L. Hase, J. Chem. Phys., 2013, 138, 114309 CrossRef PubMed.
- E. Carrascosa, M. Bawart, M. Stei, F. Linden, F. Carelli, J. Meyer, W. D. Geppert, F. A. Gianturco and R. Wester, J. Chem. Phys., 2015, 143, 184309 CrossRef CAS PubMed.
- D. R. Lide, CRC Handbook of Chemistry and Physics, CRC Press, 84th edn, 2003 Search PubMed.
- NIST, NIST Chemistry WebBook, NIST Standard Reference Database Number 69, National Institute of Standards and Technology, Gaithersburg MD, 20899, 2015 Search PubMed.
- M. Kowalewski, J. Mikosch, R. Wester and R. de Vivie-Riedle, J. Phys. Chem. A, 2014, 118, 4661 CrossRef CAS PubMed.
- S. Trippel, M. Stei, R. Otto, P. Hlavenka, J. Mikosch, C. Eichhorn, U. Lourderaj, J. X. Zhang, W. L. Hase, M. Weidemüller and R. Wester, J. Phys.: Conf. Ser., 2009, 194, 012046 CrossRef.
- R. Wester, Phys. Chem. Chem. Phys., 2014, 16, 396–405 RSC.
- W. C. Wiley and I. H. McLaren, Rev. Sci. Instrum., 1955, 26, 1150–1157 CrossRef CAS.
- W. R. Wadt and P. J. Hay, J. Chem. Phys., 1985, 82, 284–298 CrossRef CAS.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, Ö. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09 Revision A.02, Gaussian Inc., Wallingford CT, 2009 Search PubMed.
Footnote |
| † Present address: School of Chemistry, The University of Melbourne, 3010 Parkville (VIC), Australia. |
| This journal is © The Royal Society of Chemistry 2018 |