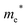Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Computer-aided design of metal chalcohalide semiconductors: from chemical composition to crystal structure†
Daniel W.
Davies
 a,
Keith T.
Butler
a,
Keith T.
Butler
 *a,
Jonathan M.
Skelton
*a,
Jonathan M.
Skelton
 a,
Congwei
Xie
b,
Artem R.
Oganov
a,
Congwei
Xie
b,
Artem R.
Oganov
 cde and
Aron
Walsh
cde and
Aron
Walsh
 *fg
*fg
aCentre for Sustainable Chemical Technologies, Department of Chemistry, University of Bath, Claverton Down, Bath BA2 7AY, UK. E-mail: k.t.butler@bath.ac.uk
bScience and Technology on Thermostructural Composite Materials Laboratory, International Center for Materials Discovery, School of Materials Science and Engineering, Northwestern Polytechnical University, Xian, Shaanxi 710072, Peoples Republic of China
cInternational Center for Materials Discovery, School of Materials Science and Engineering, Northwestern Polytechnical University, Xian, Shaanxi 710072, Peoples Republic of China
dSkolkovo Institute of Science and Technology, 3 Nobel Street, Moscow Region 143026, Russia
eMoscow Institute of Physics and Technology, Dolgoprudny, Moscow Region 141700, Russia
fDepartment of Materials Science and Engineering, Yonsei University, Seoul 03722, Korea. E-mail: a.walsh@imperial.ac.uk
gDepartment of Materials, Imperial College London, Exhibition Road, London SW7 2AZ, UK
First published on 4th December 2017
Abstract
The standard paradigm in computational materials science is INPUT: STRUCTURE; OUTPUT: PROPERTIES, which has yielded many successes but is ill-suited for exploring large areas of chemical and configurational hyperspace. We report a high-throughput screening procedure that uses compositional descriptors to search for new photoactive semiconducting compounds. We show how feeding high-ranking element combinations to structure prediction algorithms can constitute a pragmatic computer-aided materials design approach. Techniques based on structural analogy (data mining of known lattice types) and global searches (direct optimisation using evolutionary algorithms) are combined for translating between chemical composition and crystal structure. The properties of four novel chalcohalides (Sn5S4Cl2, Sn4SF6, Cd5S4Cl2 and Cd4SF6) are predicted, of which two are calculated to have bandgaps in the visible range of the electromagnetic spectrum.
I. Introduction
The past decade has seen the emergence of many databases for computed materials properties from quantum mechanical calculations.1–7 This has made it possible to virtually screen through enormous amounts of data in the search for promising materials for energy applications such as photovoltaics,8–10 solar fuels,11–15 and thermoelectrics.16–18 Furthermore, these databases are facilitating the move towards more predictive materials design using data-mining, machine learning, and other statistical techniques to reveal hitherto undiscovered trends and rules.19–29 In order to search for Earth-abundant materials for energy applications, it is important to move beyond known materials and extend screening criteria to new compositions and structures.There are vast areas of unexplored chemical space for inorganic compounds.30 Such a space is intractable to high-throughput first-principles computation, even with tremendous advances in computing power and algorithms. As such, a different approach is required to efficiently explore the search space – one that is less computationally demanding overall, but sufficiently accurate.
One modern tool that is providing impressive leaps forward in this area is machine learning (ML), a subfield of artificial intelligence that involves statistical algorithms whose performance improves with experience. A growing infrastructure of ML tools has enabled its application to complex problems in many areas of chemistry and materials science.6,20,21 This includes the development of models that relate system descriptors to desirable properties in order to reveal structure–property relationships,31 the prediction of the likelihood of a composition to adopt a given crystal structure,32 and the use of quantum-mechanics results as training data to extrapolate and discover new materials at a fraction of the computational cost.29,33
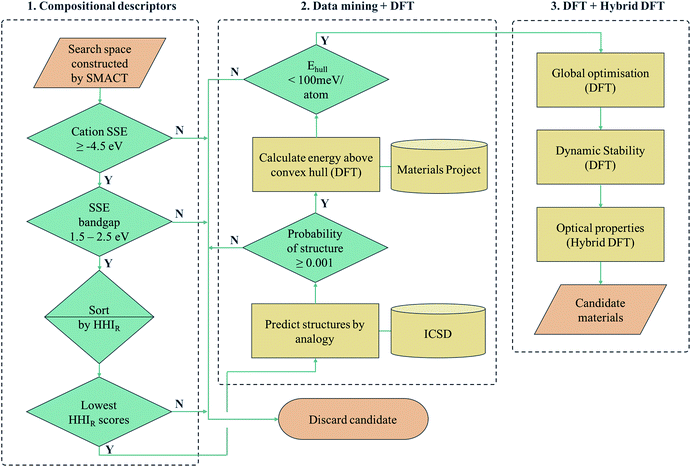
Another approach is to apply a hierarchy of screening steps, based on pre-existing methods, whereby the fact that accuracy is low in initial steps is counteracted by the idea that as the size of the search space that can be screened is so large, the chance of finding a promising material at the end of the process remains high. Here we present one such workflow incorporating simple chemical descriptors, data mining from public databases, density functional theory (DFT) calculations and global structure searching algorithms (Fig. 1) to translate from a compositional search space to compounds predicted to have target properties by quantum-mechanical calculations.
We employ a multi-stage screening approach in a search for new photoactive semiconductors. While metal oxides combine many attractive properties for energy materials (e.g. chemical stability and low cost), they usually have bandgaps too large to absorb a significant fraction of sunlight. The formation of multi-anion compounds offers a route to modifying the electronic structure, so we consider all ternary metal chalcohalides, (i.e., AxByCz with B = [O, S, Se, Te] and C = [F, Cl, Br, I]). As a target application, we search for materials for solar fuel generation, specifically for photoelectrochemical water splitting, where a set of well-defined screening criteria enables us to quickly narrow down the search space. Our searching methodology is built on already established and freely available materials design tools (SMACT, PYMATGEN and USPEX) and can be adapted to search for different classes of materials, in a wide range of contexts of technological interest.
II. Results
II.I. AxByCz compositional screening
There exist various compositional descriptors that enable the low-cost filtering of chemical space. One such tool is the solid-state energy (SSE) scale,34 which can be used to estimate the positions of the valence band maxima (VBM) and conduction band minima (CBM) of a semiconductor with respect to the vacuum level using solely the identity of the constituent ions. We employ the SSE scale to carry out our compositional screening (see Computational methods section for details).First, the SMACT code30 is used to narrow down the ternary compound search space of roughly 32 million compositions to the chalcohalide search space of 161![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 compositions. The SSE scale is then used to screen for suitable bandgaps and band-edge positions. The A cations are restricted to those with a SSE higher than the water reduction potential (approximately 4.5 V in relation to the vacuum at pH = 0) and the bandgap window was set to 1.5–2.5 eV. The latter criterion is set to a value range higher than the free energy for water dissociation (1.2 eV), in order to compensate for the combination of loss mechanisms found in practical devices that mean a bandgap as large as 2.2 eV could be required.35,36 This results in in 7676 candidate AxByCz compositions with unique x, y, z stoichiometries.
000 compositions. The SSE scale is then used to screen for suitable bandgaps and band-edge positions. The A cations are restricted to those with a SSE higher than the water reduction potential (approximately 4.5 V in relation to the vacuum at pH = 0) and the bandgap window was set to 1.5–2.5 eV. The latter criterion is set to a value range higher than the free energy for water dissociation (1.2 eV), in order to compensate for the combination of loss mechanisms found in practical devices that mean a bandgap as large as 2.2 eV could be required.35,36 This results in in 7676 candidate AxByCz compositions with unique x, y, z stoichiometries.
Next, we sort the candidates by the sustainability of their constituent elements based on the Herfindahl–Hirschman Index for elemental reserves (HHIR).37 The HHIR includes factors such as geopolitical influence over materials supply and price, and for a given composition can be obtained as the weighted average over the constituent elements. At this stage, because stoichiometry is variable, we consider the mean value for each AxByCz chemical system. The six most sustainable chemical systems according to this scale are SnxSyXz, CdxSyXz and TixSyXz, where X = [Cl, F]. Of these, the Sn- and Cd-containing compositions are selected and Ti3+ compounds are excluded due to the d1 electronic configuration being linked to fast electron–hole recombination, and, more practically, the well-known challenges for electronic-structure modelling due to the high correlation.38
The HHIR scores of ZnxSyXz and CdxSeyXz are the next lowest in the ranking, making these the next most sustainable according to this scale. This is because Zn and Se have higher HHIR scores than Ti and S respectively. These systems could be of interest for future studies in the same spirit, particularly the Zn-containing compositions due to their low toxicity. This rapid screening process based on composition alone constitutes the first phase of our overall procedure (part 1 of Fig. 1).
II.II. From chemical composition to crystal structure
Although compositional screening is a key initial step in materials exploration, the precision with which physical properties can be predicted from chemical composition alone is limited. In order to move to the next level of accuracy and make quantitative predictions, we must introduce a three-dimensional model of the arrangement of atoms in space. To our knowledge, no compounds of the compositions identified by our screening process have yet been reported, so the crystal structures must be predicted. Crystal structure prediction is a long-standing challenge in materials science,39 due to the large number of degrees of freedom (lattice vectors and internal coordinates) and poor scaling with increasing system complexity.We combine two machine learning approaches for generating candidate crystal structures from chemical composition, viz. (1) analogy with known crystal structures reported in crystallographic databases, and (2) direct global crystal structure searching. The first approach has a much lower computational cost, exploiting data on existing compounds, and we use this step to assess the metastability of a candidate composition. Those compounds that fall within an acceptable window of metastability are then passed to the second method, which is a more rigorous search of configurational space and allows for new structure types to be adopted.
For crystal structure prediction by analogy, we adopt the structure substitution algorithm developed by Hautier et al.,40 as implemented in the PYMATGEN framework.41 In this method, a combination of ions are substituted onto lattice sites in known structures from the Inorganic Crystal Structure Database (ICSD).42 Each ion substitution is associated with a certain probability, which comes from a statistical model trained on the compounds that already exist in the ICSD. If the overall probability for a given set of substitutions is above a certain threshold, it is added to a list of possible structures. This substitution process is performed on each known crystal structure in the database.
For each S-for-O of the four compositions, the candidate crystal structures are locally optimized using DFT calculations and the structure with the lowest energy per atom selected. Fig. 2 illustrates this process for one of the structures suggested by the algorithm for the CdxSyClz chemical system. In this case, the structure suggested is based on Hg5O4Cl2 due to the high probabilities associated with both Cd-for-Hg and S-for-O substitutions. Table 2 contains the chemical formulae of the four compounds deemed to be the most stable as a result of this process, along with the formulae of their parent structures in the ICSD. We next assess the thermodynamic stability of the candidate materials.
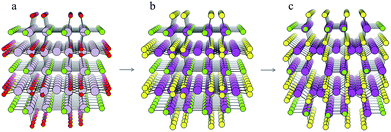 | ||
| Fig. 2 Illustration of the process of crystal structure prediction by ion substitution into existing lattice types. The Hg5O4Cl2 structure (a) is identified as a candidate structure for the CdxSyClz chemical system. The Hg2+ (grey balls) and O2− ions (red balls) are replaced by Cd2+ (purple balls) and S2− ions (yellow balls), respectively, to produce the Cd5S4Cl2 structure (b). Forces on the ions are then minimised using DFT with the PBEsol functional43 to produce the relaxed structure (c). | ||
II.III. Thermodynamic metastability
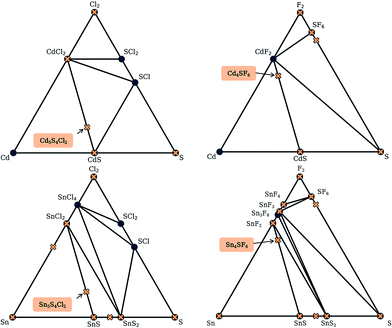
By calculating the total energies of all the competing phases of a chemical system, one can construct an energy – composition phase diagram and assess the stability of a given compound with respect to polymorphic transformations and phase separation. By creating a bounding surface between the lowest energy phases of each composition, a convex hull is constructed above which metastable compounds fall. A key value of interest for assessing the metastability of a compound is this energy above this convex hull (Ehull).Fortunately, the existence of databases of DFT total energies have all but eliminated the need for carrying out calculations for all phases of a given chemical system. Instead, one can perform calculations on new compounds using identical parameters to those used for the data in a given database, thus allowing for direct comparison of energies. Similarly, one can use the energy values in a database to construct a phase diagram and identify where on the diagram the new phase would appear. In doing so, the set of polymorphs and decomposition products that require explicit calculation can be identified. We note that it is standard to calculate such convex hulls based on internal energies, which neglect finite temperature contributions to the free energy of a compound.
Here, we use the Materials Project database to construct phase diagrams using the PYMATGEN code,41 and hence identify decomposition products. As mentioned above, and as depicted in the phase diagrams in Fig. 3, it is not necessary to consider competing polymorphs as no compounds have yet been reported for these compositions. As can be seen from Table 2, all of the values of Ehull for the structures predicted by analogy lie between 18 and 97 meV per atom. Hence, all the compounds can formally be described as thermodynamically metastable at 0 K, but does this rule out their existence?
Metastable materials exist and are ubiquitous in both nature and technology. This includes obvious examples such as diamond vs. the lower energy allotrope of carbon, graphite, as well as classes of materials such as zeolites and metal–organic frameworks.44 It was recently estimated by Sun et al. that around half of all known inorganic materials are metastable.25 Whether or not the value of Ehull is enough to predict the likelihood of successful synthesis of a material is a question that has yet to be answered. In the same work by Sun et al., it was shown that the likelihood of existence drops off exponentially as Ehull increases. The exact rate of the drop depends on the chemistry of the system. We use 100 meV per atom as a guiding principle for the maximum Ehull, as this criteria covers approximately 90% of compounds in the Materials Project database that represent fully-characterised structures in the ICSD. The four structures found by analogy all fall within this metastability window, so they are all carried forward to the global structure searching stage.
II.IV. Global structure search
The structure from analogy approach provides an attractive route to obtaining sensible crystal structures with reasonable energies, however it does not provide a rigorous route to obtaining the true ground state. Finding the true global ground state structure for a given chemical composition is one of the outstanding problems of theoretical chemistry. Whilst exhaustive searching of parameter space is the only way to find a guaranteed global minimum structure, this approach quickly becomes impractically expensive for even simple chemical systems. Global searching, based on evolutionary algorithms offer a solution to this problem and have had enormous success in discovering new ground state crystal structures. Here we use USPEX to apply an evolutionary algorithm and perform a global structure search.For each of the four compositions, the global structure search algorithm45,46 yields a different crystal structure to that found by analogy with known structures (Fig. 4). For each of the structures generated by the global search, there is no way in which the data-mining algorithm could have arrived at the same result. This is an intrinsic limitation of the data-mining approach, as it relies on a database of known structures and it is therefore incapable of predicting new structure types. Three of the four compounds adopt structure types that have not yet been reported, disregarding those with fractional occupancy on some lattice sites. The remaining compound, Cd5S4Cl2, adopts the same structure type as Li5BiO5.47 However, this substitution is rejected by the structure prediction algorithm on the basis that the resulting formula is not charge neutral – the structure we find is partially inverted in terms of anion/cation occupancy.
 | ||
| Fig. 4 Crystal structures of the four candidate compositions as predicted by analogy through data mining of other structures and by a first-principles global structure search algorithm. | ||
The values of Ehull for the structures predicted by global structure search are also shown in Table 2, and are universally lower than those found by analogy. While the structural analogy procedure is limited by the diversity of known structure types, the global structure search approach is restricted only by the structural complexity (number of formula units) included in the search. A holistic assessment of performance in the context of high-throughput screening must however also take into account time and resources: the data-mining algorithm takes only a few minutes to run on a desktop computer, while the global structure searching requires a supercomputing resource where around 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 CPU hours were needed for each material.
000 CPU hours were needed for each material.
In addition to thermodynamic stability, another factor that cannot be ignored is dynamic stability, to ensure that the crystal structures are true local minima (and not saddle points) on the potential energy surface. Finite-displacement calculations were carried out to obtain the vibrational (phonon) frequencies of each of the compounds, and no negative-frequency (imaginary) phonon modes were found at the zone centre (Γ point) for any of the structures. Full details of this analysis can be found in the ESI.†
II.V. Crystal structures and bonding environments
Table 1 contains the space groups and lattice parameters of the four minimum energy compounds identified at the end of the screening process.| Compound | Space group | a (Å) | b (Å) | c (Å) | Formula units per cell |
|---|---|---|---|---|---|
| Sn5S4Cl2 | Pma2 | 17.529 | 5.771 | 5.817 | 2 |
| Sn4SF6 | R3 | 8.615 | 8.615 | 9.528 | 3 |
| Cd5S4Cl2 | Cm | 14.507 | 4.212 | 15.631 | 2 |
| Cd4SF6 |
R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m m |
3.832 | 3.832 | 37.148 | 3 |
Having established promising compositions and their candidate structures, we next go on to perform quantitative analyses of the detailed electronic structure of these materials.
II.VI. Optoelectronic properties
The most critical property for any light-harvesting material, whether for photovoltaic or solar fuel applications, is the bandgap (Eg). Indeed, the screening procedure we have employed thus far relies on making initial estimates of Eg at an early stage, before considering structure or stability. The calculations required to accurately predict bandgaps are significantly more computationally demanding than those which can satisfactorily predict equilibrium geometry.The first-principles values of Eg are presented in Table 2 alongside the bandgaps estimated using the SSE scale. Two of the compounds found by the screening procedure, Cd5S4Cl2 and Cd4SF6, have bandgaps in the visible range of 2.75 and 2.15 eV, respectively. Sn5S4Cl2 has a bandgap of 0.9 eV, which is better suited for solar cell or thermoelectric applications. This is encouraging, given the small set of compounds that have been brought through to this stage of the screening process and the qualitative nature of the SSE metric employed to screen the bandgaps.
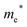 and
and 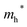 ) are also displayed
) are also displayed
| Compound | Parent | E analogyhull (meV per atom) | E globalhull (meV per atom) | E SSEg (eV) | E g (eV) | EA (eV) | IP (eV) | ||
|---|---|---|---|---|---|---|---|---|---|
| a When only polar surfaces could be found, a dipole correction term was added to the calculation of the surface dipole, which yields upper and lower bounds to the EA and IP values (see Computational methods section). | |||||||||
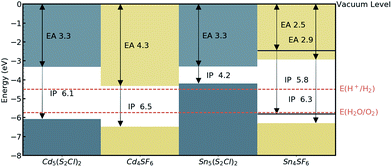
| Sn5S4Cl2 | Hg5 (O2Cl)2 | 96.5 | 61.8 | 2.0 | 0.91 | 3.30 | 4.21 | 0.50 | 0.40 |
| Sn4SF6 | Hg4OF6 | 51.8 | 46.7 | 2.0 | 3.36 | 2.45–2.94a | 5.81–6.30a | 0.86 | 2.01 |
| Cd5S4Cl2 | Hg5 (O2Cl)2 | 83.5 | 50.2 | 1.9 | 2.75 | 3.33 | 6.08 | 0.18 | 2.58 |
| Cd4SF6 | Cd4F6O | 18.2 | 18.0 | 1.9 | 2.15 | 4.33 | 6.48 | 0.25 | 2.00 |
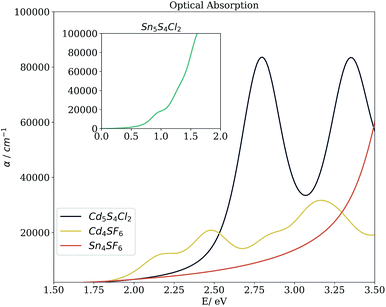
Beyond the bandgap, quantum-mechanical calculations can also provide access to optical absorption spectra via computation of the complex dielectric function. Fig. 5 shows the simulated spectra of the four compounds of interest. The Cd compounds display moderate absorption in the visible region, indicating their potential for use as solar fuel or photovoltaic materials. Of the two, Cd4SF6 absorbs photons with energy across more of the visible range but quite weakly, suggesting that thicker layers would be needed in a device. Meanwhile, Cd5S4Cl2 absorbs more strongly but at a higher energy, so would be suited to incorporation into a tandem solar cell.
The absolute band edge positions are also calculated using surface (non-polar slab) models of the four materials. The CBM position is the negative of the electron affinity (EA), and as indicated in Table 2, the EA values are all <4.5 eV. This indicates that as well as having promising bandgaps, the two Cd-based compounds have potential for use in photoelectrochemical water splitting applications, with VBM and CBM positions that bridge the water oxidation and reduction potentials, enabling the redox reaction. For Sn4SF6, no slab without an overall dipole could be found, so we instead report a likely range for the EA and IP values after applying a dipole correction in the slab calculation (see Computational methods section). This material also bridges these energies, but has too wide a band gap, while the other Sn-containing compound, Sn5S4Cl2, has an appropriate EA, but too small a bandgap, as has already been discussed. This is summarised in the energy band alignment diagram, Fig. 6.
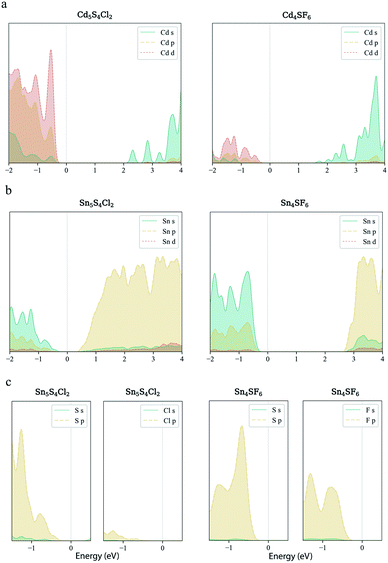
Finally, carrier effective mass (m*) is a quantity that can also provide preliminary insight into the performance of a semiconducting material, with smaller m* values being more desirable as this quantity is inversely proportional to conductivity. The two Cd-containing compounds have lower 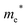 values than the Sn-containing compounds (Table 2). This is a result of the metallic s-states forming the lower conduction band in the former case which give higher dispersion than the more directional metallic p-states in the latter (Fig. 7a and b). The
values than the Sn-containing compounds (Table 2). This is a result of the metallic s-states forming the lower conduction band in the former case which give higher dispersion than the more directional metallic p-states in the latter (Fig. 7a and b). The  values are in general much higher, with the sulphur and halide p-states dominating the upper valence band. One notable exception is Sn5S4Cl2 with a value of 0.40 me. This is a result of strong hybridisation between the Sn s and S p orbitals which form a two-dimensional Sn–S network along which carriers can transport without encountering a Cl atom (Fig. 4). This is possible due to the Sn2+ oxidation state, which results in the Sn s orbitals remaining occupied. In the case of Sn4SF6, no such Sn–S network exists and S p states dominate the VBM, while F p states also contribute (Fig. 7c).
values are in general much higher, with the sulphur and halide p-states dominating the upper valence band. One notable exception is Sn5S4Cl2 with a value of 0.40 me. This is a result of strong hybridisation between the Sn s and S p orbitals which form a two-dimensional Sn–S network along which carriers can transport without encountering a Cl atom (Fig. 4). This is possible due to the Sn2+ oxidation state, which results in the Sn s orbitals remaining occupied. In the case of Sn4SF6, no such Sn–S network exists and S p states dominate the VBM, while F p states also contribute (Fig. 7c).
The calculated band structure of Sn5S4Cl2 reveals the presence of multiple band extrema (“multi-valley”), a sought-after feature in the design of thermoelectric materials.48 Furthermore, the effective number of extrema is increased by the presence of multiple bands within a few kBT in energy of each other at the R, T, S and U points in the Brillouin zone (see ESI Fig. S4†).
III. Conclusion
We have introduced a hierarchical screening procedure and used it to search through a large space of over 161![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 compositions to identify promising candidate photoactive semiconductors. Using our approach, which relies on compositional descriptors and exploits existing data, first-principles calculations were carried out on a subset of compounds in order to establish thermodynamic stability, and global structure searching was employed for the most promising candidates. This procedure has enabled us to identify four new chalcohalide compounds, two of which, Cd5S4Cl2 and Cd4SF6, have bandgaps in the visible range and good absorption properties for solar fuel applications. Further detailed investigation into the electronic structure of these materials show that effective electron and hole conduction should be possible. The approach constitutes a computer-aided materials design procedure that employs existing knowledge in a targeted manner in order to traverse the vast chemical hyperspace.
000 compositions to identify promising candidate photoactive semiconductors. Using our approach, which relies on compositional descriptors and exploits existing data, first-principles calculations were carried out on a subset of compounds in order to establish thermodynamic stability, and global structure searching was employed for the most promising candidates. This procedure has enabled us to identify four new chalcohalide compounds, two of which, Cd5S4Cl2 and Cd4SF6, have bandgaps in the visible range and good absorption properties for solar fuel applications. Further detailed investigation into the electronic structure of these materials show that effective electron and hole conduction should be possible. The approach constitutes a computer-aided materials design procedure that employs existing knowledge in a targeted manner in order to traverse the vast chemical hyperspace.
IV. Computational methods
IV.I. Compositional screening
Construction of the search space and subsequent screening based on SSE and HHIR is carried out with Python 3 on a desktop computer using the SMACT library, which is publicly available online at http://github.com/WMD-group/SMACT. First, the compositional search space of ternary chalcohalides is constructed using the SMACT package: the stoichiometry maximum is set to 8 and only those compositions which pass both the charge neutrality and electronegativity balance tests form part of the initial search space. Every possible combination of AxByCz is generated with B = [O, S, Se, Te] and C = [F, Cl, Br, I]. All known oxidation states of all elements in each combination are considered and charge neutrality is assessed by| xqA + yqB + zqC = 0 | (1) |
The SSE scale34 is used to limit the A cations to those with a SSE higher than the water reduction potential and the bandgap window was set to 1.5–2.5 eV. The SSE provides information on valence and conduction bands on the basis of the Frontier orbitals of the constituent ions. It reflects ionisation potential of an anion (filled electronic states) and electron affinity of a cation (empty electronic states). The energies of 40 elements were originally fitted from a test set of 69 closed-shell binary inorganic compounds, and now the SSE values for 94 elements are available.50 The bandgap (Eg) can then be estimated from the tabulated SSE values as
| ESSEg = SSEcation − SSEanion | (2) |
For multicomponent systems, the limiting SSE values are used.
IV.II. Crystal structure prediction by analogy
We use the structure substitution algorithm developed by Hautier et al.,40 as implemented in the PYMATGEN framework41 with a probability threshold of 0.001. For a given composition the procedure is carried out for each common oxidation state of the metal (e.g. for SnxsyClz both Sn(II) and Sn(IV) must be considered).IV.III. Crystal structure prediction by global searching
Global crystal structure searches are carried out for each of the candidate compositions using the same stoichiometries as the lowest energy crystal structures from the prediction by analogy. This step is only carried out if a structure found by analogy falls within the defined “metastability window” of 100 meV per atom. Using the evolutionary structure prediction algorithm USPEX,45,46 we perform global structure searches for the candidate compositions. No constraints are imposed on the shape or volume of the unit cell, but the search is restricted to one (11 atoms per cell) and two (22 atoms per cell) formula units for each of the four compositions. In the evolutionary optimisation procedure, the first generation contains 80 randomly generated structures, and the succeeding generations (each with 60 structures) are produced by random (20%), heredity (50%), permutation (10%), soft-mutation (10%), and lattice mutation (10%) operations as described elsewhere.46IV.IV. First-principles calculations
All first principles calculations are carried out using Kohn–Sham DFT with a projector-augmented plane wave basis51 as implemented in the Vienna Ab initio Simulation Package (VASP).52,53Absolute electron energies (IP and EA values) are calculated by generating 2D slab models of low Miller index, non-polar surfaces of the crystal structures. Hybrid DFT (HSE06 functional) is used to calculate the surface dipole, D, which is the difference between the average electrostatic potential in the slab and that in the vacuum level. The VBM and CBM positions from the bulk calculations can then be used to calculated the true VBM and CBM positions. These are simply the differences between D and VBMbulk, and D and CBMbulk, respectively. Convergence with respect to slab thickness and vacuum distance was achieved within two repeat layers and 15 Å respectively, in all cases. When no non-polar surfaces could be found for a material, a dipole–dipole correction, as implemented in the VASP code, was added to the potential. This leads to an upper and lower limit of the potential in the vacuum level, and hence an upper and lower limit to D.
Carrier effective masses are calculated using band structures generated from hybrid DFT (HSE06 functional) calculations. The SeeKpath code60 is used to generate a suitable path through the Brillouin zone, which is sampled at a resolution of 0.01 Å−1 between each k-point. In order to calculate effective masses, a parabola is fit to all points from the minimum (maximum) of the CBM (VBM) to the points kBT higher (lower).
V. Data access statement
The SMACT package can be accessed from https://github.com/WMD-group/SMACT. Screening results from these calculations may be reproduced using the Python code available on-line from https://github.com/WMD-group/SMACT/tree/master/examples. Optimised structures are available on-line from https://github.com/WMD-group/Crystal_structures/Chalcohalides. All other data may be obtained from the authors on request.Conflicts of interest
There are no conflicts to declare.Acknowledgements
DWD gratefully acknowledges support from the Engineering and Physical Sciences Research Council (EPSRC) via the Centre for Doctoral Training in Sustainable Chemical Technologies (grant no. EP/L016354/1). Calculations were carried out on the Balena HPC cluster at the University of Bath, which is maintained by Bath University Computing Services. Some of the calculations were also carried out on the UK national Archer HPC facility, accessed through membership of the UK Materials Chemistry Consortium, which is funded by EPSRC grant no. EP/L000202. JMS is supported by the EPSRC (grant no. EP/K004956/1 and EP/P007821/1)References
- J. Hill, G. Mulholland, K. Persson, R. Seshadri, C. Wolverton and B. Meredig, MRS Bull., 2016, 41, 399–409 CrossRef CAS.
- W. Setyawan and S. Curtarolo, Comput. Mater. Sci., 2010, 49, 299–312 CrossRef.
- W. Setyawan, R. M. Gaume, S. Lam, R. S. Feigelson and S. Curtarolo, ACS Comb. Sci., 2011, 13, 382–390 CrossRef CAS PubMed.
- D. D. Landis, J. S. Hummelshøj, S. Nestorov, J. Greeley, M. Dulłak, T. Bligaard, J. K. Nørskov and K. W. Jacobsen, Comput. Sci. Eng., 2012, 14, 51–57 CrossRef.
- A. Jain, S. P. Ong, G. Hautier, W. Chen, W. D. Richards, S. Dacek, S. Cholia, D. Gunter, D. Skinner, G. Ceder and K. A. Persson, APL Mater., 2013, 1, 011002 CrossRef.
- J. E. Saal, S. Kirklin, M. Aykol, B. Meredig and C. Wolverton, JOM, 2013, 65, 1501–1509 CrossRef CAS.
- The NoMaD Repository, http://nomad-repository.eu/.
- L. Yu, R. S. Kokenyesi, D. A. Keszler and A. Zunger, Adv. Energy Mater., 2013, 3, 43–48 CrossRef CAS.
- T. Krishnamoorthy, H. Ding, C. Yan, W. L. Leong, T. Baikie, Z. Zhang, M. Sherburne, S. Li, M. Asta, N. Mathews and S. G. Mhaisalkar, J. Mater. Chem. A, 2015, 3, 23829–23832 CAS.
- Y. Hinuma, T. Hatakeyama, Y. Kumagai, L. A. Burton, H. Sato, Y. Muraba, S. Iimura, H. Hiramatsu, I. Tanaka, H. Hosono and F. Oba, Nat. Commun., 2016, 7, 11962 CrossRef CAS PubMed.
- I. E. Castelli, D. D. Landis, K. S. Thygesen, S. Dahl, I. Chorkendorff, T. F. Jaramillo and K. W. Jacobsen, Energy Environ. Sci., 2012, 5, 9034–9043 CAS.
- I. E. Castelli, T. Olsen, S. Datta, D. D. Landis, S. Dahl, K. S. Thygesen and K. W. Jacobsen, Energy Environ. Sci., 2012, 5, 5814–5819 CAS.
- Y. Wu, P. Lazic, G. Hautier, K. Persson and G. Ceder, Energy Environ. Sci., 2013, 6, 157–168 CAS.
- I. E. Castelli, F. Hüser, M. Pandey, H. Li, K. S. Thygesen, B. Seger, A. Jain, K. A. Persson, G. Ceder and K. W. Jacobsen, Adv. Energy Mater., 2015, 5, 1400915 CrossRef.
- M. Pandey, A. Vojvodic, K. S. Thygesen and K. W. Jacobsen, J. Phys. Chem. Lett., 2015, 6, 1577–1585 CrossRef CAS PubMed.
- C. Toher, J. J. Plata, O. Levy, M. de Jong, M. Asta, M. B. Nardelli and S. Curtarolo, Phys. Rev. B, 2014, 90, 174107 CrossRef.
- T. D. Sparks, M. W. Gaultois, A. Oliynyk, J. Brgoch and B. Meredig, Scr. Mater., 2016, 111, 10–15 CrossRef CAS.
- A. Faghaninia, G. Yu, U. Aydemir, M. Wood, W. Chen, G.-M. Rignanese, S. Jeffrey, G. Hautier and A. Jain, Phys. Chem. Chem. Phys., 2017, 19, 6743–6756 RSC.
- C. C. Fischer, K. J. Tibbetts, D. Morgan and G. Ceder, Nat. Mater., 2006, 5, 641–646 CrossRef CAS PubMed.
- G. Hautier, C. C. Fischer, A. Jain, T. Mueller and G. Ceder, Chem. Mater., 2010, 22, 3762–3767 CrossRef CAS.
- G. Pilania, C. Wang, X. Jiang, S. Rajasekaran and R. Ramprasad, Sci. Rep., 2013, 3, 2810 CrossRef PubMed.
- B. Meredig, A. Agrawal, S. Kirklin, J. E. Saal, J. W. Doak, A. Thompson, K. Zhang, A. Choudhary and C. Wolverton, Phys. Rev. B, 2014, 89, 094104 CrossRef.
- O. Isayev, D. Fourches, E. N. Muratov, C. Oses, K. Rasch, A. Tropsha and S. Curtarolo, Chem. Mater., 2015, 27, 735–743 CrossRef CAS.
- P. V. Balachandran, J. Theiler, J. M. Rondinelli, T. Lookman and A. P. Sutton, Sci. Rep., 2015, 5, 13285 CrossRef CAS PubMed.
- W. Sun, S. T. Dacek, S. P. Ong, G. Hautier, A. Jain, W. D. Richards, A. C. Gamst, K. A. Persson and G. Ceder, Sci. Adv., 2016, 2, e1600225 Search PubMed.
- G. Pilania, A. Mannodi-Kanakkithodi, B. P. Uberuaga, R. Ramprasad, J. E. Gubernatis and T. Lookman, Sci. Rep., 2016, 6, 19375 CrossRef CAS PubMed.
- J. Lee, A. Seko, K. Shitara, K. Nakayama and I. Tanaka, Phys. Rev. B, 2016, 93, 115104 CrossRef.
- W. Chen, J.-H. Pöhls, G. Hautier, D. Broberg, S. Bajaj, U. Aydemir, Z. M. Gibbs, H. Zhu, M. Asta, G. J. Snyder, B. Meredig, M. A. White, K. Persson and A. Jain, J. Mater. Chem. C, 2016, 4, 4414–4426 RSC.
- T. Moot, O. Isayev, R. W. Call, S. M. McCullough, M. Zemaitis, R. Lopez, J. F. Cahoon and A. Tropsha, Materials Discovery, 2016, 6, 9–16 CrossRef.
- D. W. Davies, K. T. Butler, A. J. Jackson, A. Morris, J. M. Frost, J. M. Skelton and A. Walsh, Chem, 2016, 1, 617–627 CAS.
- A. Pulido, L. Chen, T. Kaczorowski, D. Holden, M. A. Little, S. Y. Chong, B. J. Slater, D. P. McMahon, B. Bonillo, C. J. Stackhouse, A. Stephenson, C. M. Kane, R. Clowes, T. Hasell, A. I. Cooper and G. M. Day, Nature, 2017, 543, 657–664 CrossRef CAS PubMed.
- A. O. Oliynyk, E. Antono, T. D. Sparks, L. Ghadbeigi, M. W. Gaultois, B. Meredig and A. Mar, Chem. Mater., 2016, 28, 7324–7331 CrossRef CAS.
- F. A. Faber, A. Lindmaa, O. A. von Lilienfeld and R. Armiento, Phys. Rev. Lett., 2016, 117, 135502 CrossRef PubMed.
- B. D. Pelatt, R. Ravichandran, J. F. Wager and D. A. Keszler, J. Am. Chem. Soc., 2011, 133, 16852–16860 CrossRef CAS PubMed.
- T. Bak, J. Nowotny, M. Rekas and C. Sorrell, Int. J. Hydrogen Energy, 2002, 27, 991–1022 CrossRef CAS.
- B. A. Pinaud, J. D. Benck, L. C. Seitz, A. J. Forman, Z. Chen, T. G. Deutsch, B. D. James, K. N. Baum, G. N. Baum, S. Ardo, H. Wang, E. Miller, T. F. Jaramillo, J. A. Turner and H. N. Dinh, Energy Environ. Sci., 2013, 6, 1983 CAS.
- M. W. Gaultois, T. D. Sparks, C. K. H. Borg, R. Seshadri, W. D. Bonificio and D. R. Clarke, Chem. Mater., 2013, 25, 2911–2920 CrossRef CAS.
- B. J. Morgan and P. A. Madden, Phys. Rev. B, 2012, 86, 035147 CrossRef.
- S. M. Woodley and R. Catlow, Nat. Mater., 2008, 7, 937–946 CrossRef CAS PubMed.
- G. Hautier, C. Fischer, V. Ehrlacher, A. Jain and G. Ceder, Inorg. Chem., 2011, 50, 656–663 CrossRef CAS PubMed.
- S. P. Ong, W. D. Richards, A. Jain, G. Hautier, M. Kocher, S. Cholia, D. Gunter, V. L. Chevrier, K. A. Persson and G. Ceder, Comput. Mater. Sci., 2013, 68, 314–319 CrossRef CAS.
- Karlsruhe, Inorganic Crystal Structure Database, 2016, http://icsd.cds.rsc.org Search PubMed.
- J. P. Perdew, A. Ruzsinszky, G. I. Csonka, O. A. Vydrov, G. E. Scuseria, L. A. Constantin, X. Zhou and K. Burke, Phys. Rev. Lett., 2008, 100, 136406–136414 CrossRef PubMed.
- C. H. Hendon, K. T. Butler, A. M. Ganose, Y. Román-Leshkov, D. O. Scanlon, G. A. Ozin and A. Walsh, Chem. Mater., 2017, 29, 3663–3670 CrossRef CAS PubMed.
- A. R. Oganov and C. W. Glass, J. Chem. Phys., 2006, 124, 244704 CrossRef PubMed.
- C. W. Glass, A. R. Oganov and N. Hansen, Comput. Phys. Commun., 2006, 175, 713–720 CrossRef CAS.
- C. Greaves and S. Katib, Mater. Res. Bull., 1989, 24, 973–980 CrossRef CAS.
- G. Tan, L.-D. Zhao and M. G. Kanatzidis, Chem. Rev., 2016, 116, 12123–12149 CrossRef CAS PubMed.
- L. Pauling, J. Am. Chem. Soc., 1932, 54, 3570–3582 CrossRef CAS.
- B. D. Pelatt, R. S. Kokenyesi, R. Ravichandran, C. B. Pereira, J. F. Wager and D. A. Keszler, J. Solid State Chem., 2015, 231, 138–144 CrossRef CAS.
- G. Kresse and D. Joubert, Phys. Rev. B, 1999, 59, 1758–1775 CrossRef CAS.
- G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50 CrossRef CAS.
- G. Kresse and J. Furthmüller, Phys. Rev. B, 1996, 54, 11169 CrossRef CAS.
- S. P. Ong, S. Cholia, A. Jain, M. Brafman, D. Gunter, G. Ceder and K. A. Persson, Comput. Mater. Sci., 2015, 97, 209–215 CrossRef.
- A. Togo, L. Chaput, I. Tanaka and G. Hug, Phys. Rev. B, 2010, 81, 174301 CrossRef.
- J. M. Skelton, S. C. Parker, A. Togo, I. Tanaka and A. Walsh, Phys. Rev. B, 2014, 89, 205203 CrossRef.
- A. Togo, L. Chaput and I. Tanaka, Phys. Rev. B, 2015, 91, 094306 CrossRef.
- A. V. Krukau, O. A. Vydrov, A. F. Izmaylov and G. E. Scuseria, J. Chem. Phys., 2006, 125, 224106 CrossRef PubMed.
- L. Yu and A. Zunger, Phys. Rev. Lett., 2012, 108, 068701 CrossRef PubMed.
- Y. Hinuma, G. Pizzi, Y. Kumagai, F. Oba and I. Tanaka, Comput. Mater. Sci., 2017, 128, 140–184 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c7sc03961a |
| This journal is © The Royal Society of Chemistry 2018 |