Chemistry topics posing incommensurate difficulty to students with low math aptitude scores

Vanessa Rosa; Scott E. Lewis

doi:10.1039/C8RP00115D

View PDF VersionPrevious ArticleNext Article

DOI: 10.1039/C8RP00115D (Paper) Chem. Educ. Res. Pract., 2018, 19, 867-884

Chemistry topics posing incommensurate difficulty to students with low math aptitude scores

Vanessa Rosa and Scott E. Lewis *
Department of Chemistry, University of South Florida, USA. E-mail: slewis@usf.edu

Received 25th April 2018 , Accepted 28th May 2018

First published on 28th May 2018

Abstract

The identification of students at risk for academic failure in undergraduate chemistry courses has been heavily addressed in the literature. Arguably one of the strongest and most well-supported predictors of undergraduate success in chemistry is the mathematics portion of the SAT (SAT-M), a college-entrance, standardized test administered by the College Board. While students scoring in the bottom quartile of the SAT-M (herein referred to as at-risk) perform significantly worse on first-semester chemistry assessments, little is known of the topics on which these students differentially struggle. The purpose of this study is to provide insight as to which first-semester chemistry topics present an incommensurate challenge to at-risk students. Students were identified as either at-risk or not at-risk via SAT-M scores. Students’ assessment responses were collected across four semesters of first-semester chemistry courses at a large, public university (N = 5636). At-risk students struggled consistently across all topics but disproportionately with mole concept and stoichiometry. Analyzing the trend in topics suggests that the struggles of at-risk students are not entirely attributable to topics that rely heavily on algorithms or algebraic math. Moreso, at-risk students found to have performed well on mole concept and stoichiometry went on to perform similarly as their not at-risk peers. The results support an instructional emphasis on these topics with reviewed literature offering promising, practical options to better serve at-risk students and broaden representation in the sciences.

Introduction

The promotion of safer, healthier, more-educated communities with strong economic growth is highly correlated to investment in science, technology, engineering, and mathematics (STEM) education (National Science Board, 2018). To maximize this investment, stakeholders are challenged to efficiently produce a knowledgeable workforce large enough to support the growing demand for scientists and engineers. Opportunities to improve efficiency exist in ensuring students receive equitable primary, secondary and post-secondary preparation in science and mathematics enabling the growth and diversification of students in the sciences and engineering. One such opportunity is to prevent the loss of students in post-secondary introductory chemistry, which is described as a gateway course required for many degree programs within science and engineering (Tai et al., 2005). In this course, students enter with various degrees of preparation in areas which have been related to success (e.g. math preparation). Students with lower degrees of preparation have been labeled as academically at-risk. The early identification and provision of aid to at-risk students offers an opportunity to minimize student attrition and increase participation in STEM.

The number of articles observed in the literature relating to the identification of at-risk students in chemistry is significant. However, the literature lacks detail as to the topics on which at-risk students struggle disproportionately when compared to their peers. These details are necessary to better understand the challenges at-risk students face and improve efforts directed toward their success. Therefore, this investigation seeks to characterize the topics on which students identified as at-risk most incommensurately struggle. The results of this study are presented with the intent that doing so will provide the information necessary to move beyond sourcing new ways to predict student failure and, instead, find the topics on which effective design, delivery, and assessment will result in the greatest learning and achievement gains. By providing lessons tailored toward meaningful student comprehension on the topics which impact at-risk students the most, the potential to provide equitable outcomes in introductory chemistry may be realized.

Identifying at-risk students in chemistry

The early identification of students at risk of poor academic performance (e.g., performance on examinations, course completion, or final grades) in chemistry has encompassed the vast majority of published work on this population of students since the 1970's (Kotnik, 1974; Meckstroth, 1974; Wartell, 1974). The list of predictors used to identify at-risk students in chemistry includes a variety of demographic, affective and cognitive traits. Considered demographic predictors include students’ gender (Andrews and Andrews, 1979; Spencer, 1996), age (Wagner et al., 2002), years in college (Spencer, 1996), and race or ethnicity (Spencer, 1996). Adaptive or affect-related qualities were also identified as predictors including self-efficacy (Chan and Bauer, 2014; Vincent-Ruz et al., 2018), chemistry competency beliefs (Vincent-Ruz et al., 2018), study habits (Ye et al., 2016), chosen undergraduate major (Spencer, 1996), test anxiety and emotional satisfaction (Chan and Bauer, 2014), and self-reflective or metacognitive accuracy (Potgieter et al., 2010).

Measures of cognitive traits via standardized pre-admissions testing such as the math component of the SAT (herein referred to as SAT-M) and, to a lesser extent, the American College Test (ACT) have been historically well-referenced and are considered a reasonably strong predictor for at-risk chemistry students (Coley, 1973; Pickering, 1975; Andrews and Andrews, 1979; Ozsogomonyan, 1979; Rixse and Pickering, 1985; Spencer, 1996; Wagner et al., 2002; Lewis and Lewis, 2007; Shields et al., 2012; Hall et al., 2014; Ye et al., 2016). Three major foci of the SAT-M were identified by the College Board as the mastery of linear equations and systems, quantitative literacy via problem-solving and data analysis, and the manipulation of complex questions (College Board, 2018a). Following its establishment, students’ scores on SAT-M were correlated with introductory chemistry course grades (transformed into a numerical scale) with values ranging from 0.42 to 0.51 (Pederson, 1975; Ozsogomonyan, 1979; Rixse and Pickering, 1985). Other considerations included pretest measures of prior knowledge in math and/or chemistry (Wagner et al., 2002; Hailikari and Nevgi, 2010) and measures of cognitive ability such as formal thought (Lewis and Lewis, 2007) or spatial ability (Lubinski, 2010).

Despite evidence of SAT-M relating to student performance in chemistry, studies began to converge on the idea that within ranges of SAT-M scores students ultimately received a wide variety of grades in chemistry courses. Andrews and Andrews (1979) concluded that students scoring high on the SAT-M are not guaranteed to pass, yet students with low scores are strongly predicted to perform poorly in chemistry. Spencer (1996) explored demographic and other background variables (years in college, ethnicity, gender, and major) for the extent these variables influence the relationship between SAT-M and academic performance in chemistry. Insufficient evidence of interactions was found, except students who declared majors in chemistry over-performed the expected outcome based on SAT-M, leading to the finding that the relationship of SAT-M with chemistry performance was consistent across the background variables (Spencer, 1996).

As SAT-M is well-established to serve as an identifier for students at academic risk in first-semester chemistry courses, the next logical distinction to be made is where along the range of SAT-M scores should the cutoff for at-risk students exist? Lewis and Lewis (2007) used a regression of SAT-M and SAT-V (verbal section) related to a cumulative final exam to identify combinations of student scores on SAT-M and SAT-V that were predicted to score in the bottom 30% on the cumulative exam. This study found that scoring below 500 on both sub-scores, or other combinations where a higher score on one measure could be offset by a lower score on the other, identified a cohort of students who scored below the threshold 70.5% of the time. More recent studies report accuracy in identifying students at risk of low academic performance in college chemistry as the bottom quartile in SAT-M of each semester's cohort (Shields et al., 2012; Hall et al., 2014; Ye et al., 2016). In this study, students scoring in the bottom quartile of their semester's cohort will be classified as at-risk. Combined, these studies present a compelling and consistent argument for the use of SAT-M scores to predict performance in first-semester chemistry. None of the studies address which aspects of a student's cognitive ability, specifically those essential for success in college chemistry, are predicted by the SAT-M. With regard to how the SAT-M predicts success in chemistry courses, the standing assumption has been that students entering college with lower SAT-M perform poorly in introductory chemistry owing primarily to a lack of quantitative skills.

Assisting at-risk students in chemistry

The research literature on identifying at-risk students or relating cognitive, affective or behavioral measures to student performance in chemistry often includes prescriptive suggestions for assisting at-risk students. A common suggestion is the assignment of a prerequisite course or remedial course in mathematics or chemistry (Coley, 1973; Pickering, 1975; Donovan and Wheland, 2009; Hailikari and Nevgi, 2010). The evaluation of cohorts following prerequisite courses in mathematics may be problematic as they create alternative cohorts of students eligible to enroll in the chemistry coursework that follows. In-class suggestions include adopting more frequent and higher quality study habits (Ye et al., 2016) or self-regulation to promote intellectual engagement with coursework (Potgieter et al., 2010). The in-class suggestions are resultant from the findings within the literature but were not explicitly evaluated within the same literature.

The research literature also includes examples of evaluating interventions designed to aid at-risk students. Mason and Verdel (2001) identified at-risk students as those voluntarily participating in university-sponsored retention improvement programs that sought to aid minority students, first-generation students and student-athletes. A group of 36 at-risk students was divided with 17 students attending a traditional large lecture and 19 students attending a small lecture class. Both groups received lecture-based instruction and dedicated time for individual or group work. The results showed that the students in the large lecture class outperformed the students in the small lecture class though there was insufficient evidence to make a case of statistical significance.

Another example is an evaluation of the Science Advancement through Group Engagement program (Hall et al., 2014). The program was available to students scoring in the bottom quartile of the SAT-M and included extracurricular work with learning specialists, teaching assistants, and class-related group-work over four semesters including two semesters of introductory chemistry and two of organic chemistry. The evaluation found that among at-risk students enrolled in the program, 68% completed their coursework through organic chemistry as compared to those not involved with the program (27%) and historical student records of retention (29%) with female students and students of underrepresented minority groups most benefiting from the program.

There is also a well-established body of literature evaluating interventions designed to aid all students in a setting, where the observed benefits likely extend to at-risk students within the setting. Meta-analyses of cooperative learning in chemistry (Warfa, 2015; Apugliese and Lewis, 2017) and active learning in STEM (Freeman et al., 2014) indicate a consistent positive effect of these pedagogical techniques on student performance overall. Prior work (Lewis and Lewis, 2008) explicitly investigated the impact of a peer-led guided inquiry pedagogy to mediate the relationship between SAT-M and student performance in chemistry. It was found that the pedagogy improved the average academic performance for students regardless of their SAT-M score, but had no significant impact on the relationship between SAT-M and student performance in chemistry, thus it did not ameliorate the differential performance between at-risk students in comparison to the rest of the cohort.

Purpose of the study

Despite a wide literature base showing a consistent predictive ability of SAT-M to identify at-risk students, none of the studies report the chemistry topics where at-risk students disproportionately struggle or succeed. As a result, both the design of prescriptive suggestions and interventions are without an evidence base on the chemistry topics to target. Further, evaluations of interventions in the form of pedagogical change or extracurricular support have shown benefits for all students at the setting including at-risk students, but there is a lack of evidence that the differential performance of at-risk students has been remedied. This study seeks to characterize these topics to inform efforts to aid at-risk students. The investigation will be guided by two principal research questions:

(1) Which topics most consistently pose differential difficulty for at-risk students, where differential performance is measured by the difference between at-risk students and the remainder of the cohort?

(2) How critical are the identified topics with differential difficulty to student success within introductory chemistry, particularly among at-risk students?

Methods

Research setting

This study was conducted at a large public research university in the southeastern United States. At this setting, multiple classes of first-semester chemistry courses were offered each semester and each class was attended by 200 to 240 students. The classes were coordinated with a common textbook, learning objectives, syllabus, and grading scheme. The textbook used for the classes was “Chemistry: A Molecular Approach” (Tro, 2014). Students attended the regular lectures twice a week and problem-solving peer leading sessions (Gosser et al., 2006; Lewis, 2011) once a week. Tests consisted of three interim tests (15% each of their grades) and an ACS final, cumulative exam (25%). This ACS exam was the 2015 First Term General Chemistry Exam available from the ACS Examinations Institute (Examinations Institute, 2015). The three interim tests were common across all classes but differ from semester to semester; the ACS exam was common across all classes and all semesters. Grades were also determined by three effort-based measures (10% each) characterized as performance on in-class clicker questions used in the regular lecture setting, attending and participating in peer leading sessions and online homework assignments. Eight online homework assignments were assigned throughout the semester using the Sapling Learning online homework system and were common to all classes.

The format of the tests consisted of multiple-choice questions developed by the instructors from a list of common learning objectives and a series of true/false questions, the latter following the Measure of Linked Concepts format to emphasize the links across topics in the course (Ye et al., 2015). While no two interim tests for the responses collected from Fall and Spring semesters of 2016 and 2017 were identical, each set of tests were written from the same list of learning objectives (presented in the Appendix) and administered to students throughout the semester in roughly equal intervals of time. Tests 1–3 for both semesters were scored out of a total of 158 points; 7 points for each of the 20 multiple choice question and 3 points for a correct response to each of the 6 true-or-false question or 1 point for selecting unsure (in an attempt to reduce chance guessing). Students’ final ACS exam scores were calculated from the percent correct achieved on the ACS exam multiplied by a total of 250 points. For comparisons, all test and exam scores reported herein are formatted as a percentage of possible points earned. Each semester had 78 items from interim assessments that were unique to that semester and 70 items from the summative ACS exam that were common across all semesters.

Identifying at-risk students

To describe which students may be at academic risk, data was collected from Spring 2016 through Fall 2017 and quartiles for the SAT-M scores within each semester were determined. In March 2016, the College Board revised the math portion of the SAT test, termed “new SAT” to include a greater emphasis on skills related to college-readiness and eliminate the penalty for selecting incorrect answers (College Board, 2018b). Although concordance tables between new SAT and old SAT scores are available (College Board, 2016), the decision was made to analyze the scores separately. At the research setting, data collected in Spring and Fall 2016 semesters have a strong majority of old SAT scores, while data collected in Spring and Fall 2017 semesters have a strong majority of new SAT scores. Analyses within each semester include only students who completed the same version of the SAT (e.g. old or new) and each threshold for identifying at-risk students was set on a relative scale for each semester rather than combining the SAT-M scores of the entire population to set a common threshold for at-risk students across all terms. For clarity in presentation, data from each semester is referred to only as SAT-M throughout the results and discussion. Students with data from the alternative SAT (e.g. a Fall 2017 student with old SAT scores) was considered as missing data (addressed later). Thus the analyses investigates the role of both old SAT and new SAT in exploring trends in topics where at-risk students disproportionately struggle.

Across the four semesters, a total of 5636 students enrolled in first-semester general chemistry of which 3789 (67.2%) had SAT-M scores and 4957 (88.0%) took the ACS exam. Scores at or below each semester's bottom quartile (25th percentile) for the SAT-M provided the cutoff for which 1023 students were determined as at-risk (see Table 1 where N is the total population of students, n indicates the number of students within a subgroup, M is the mean, SD the standard deviation, and percentiles indicated for the 25th, 50th, and 75th of each semester's cohort). Students of the Spring cohorts entered with lower average SAT-M scores than that of their Fall peers. Additionally, differences in SAT-M scores and assessment performance between the not at-risk and at-risk cohorts in Spring semesters are less pronounced than in the Fall. These differences further support the use of a relative scale for each semester to identify students at risk of low performance.

Table 1 Descriptive statistics for SAT-M and ACS for the entire cohort

SAT-M (score)
Measures		Spring 2016	Fall 2016	Spring 2017	Fall 2017
N		902	1983	757	1994
n		619	1462	389	1319
M ± S.D.		536 ± 66	581 ± 76	542 ± 67	614 ± 67
Percentiles	25th (at-risk)	490	530	500	570
	50th	530	580	530	610
	75th	570	630	585	660

ACS (percent)
Measures		Spring 2016	Fall 2016	Spring 2017	Fall 2017
N		902	1983	757	1994
n		690	1794	624	1849
M ± S.D.		54.2 ± 16.0	57.3 ± 17.8	50.5 ± 16.5	55.0 ± 17.4
Percentiles	25th	42.9	42.9	37.1	41.4
	50th	52.9	57.1	48.6	54.3
	75th	67.1	71.4	61.4	68.6

Students’ final grades, assessment performance, and a linear regression were used to explore the predictive validity of the bottom quartile of the SAT-M for students at academic risk in this setting. Fig. 1 provides a Sankey diagram demonstrating the various grade levels achieved by students having scored within each of the four quartiles on the SAT-M. Of the 333 students earning lower grades (D, F, or W), 43.8% (n = 146) of these students were at-risk; in contrast, of the 1355 students earning the highest grade (A), only 9.9% (n = 134) of these students were at-risk.


	Fig. 1 Grade level distributions for students within four quartiles of SAT-M score.

As 70% of the students’ grades were comprised of assessment scores (three tests at 15% each and the ACS exam at 25%), average assessment scores of students comprising each quartile are presented in Fig. 2. This figure demonstrates relatively low assessment performance for students comprising the bottom quartile across all semesters. One-way ANOVA and post hoc analyses support that each quartile performed significantly differently (with an adjusted threshold of p < 0.0125) from each other, suggesting SAT-M is a consistent predictor of assessment performance in students of first-semester chemistry. Among those who finished in the bottom quartile on the ACS Exam (N = 675), more than half (N = 348; 51.6%) were also in the bottom quartile on SAT-M.


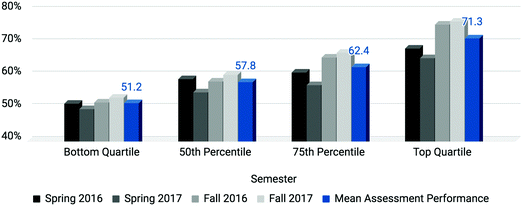	Fig. 2 Mean assessment performance by quartile suggests SAT-M is an adequate predictor of assessment outcomes for first-semester chemistry students.

To describe the impact of SAT-M on academic performance in the class, linear regression was calculated to predict mean ACS exam score (percent) performance based on SAT-M scores (scored from 200–800 points) for each semester, with the results shown in Table 2. Overall, ACS exam score was predicted to improve by 11% for every 100 points scored on the SAT-M for students of Spring semesters and 13–14% for students of the Fall semesters. The strength of the linear relationship between these measures, as estimated by correlation (r, equal to square root of R² in Table 2) ranges from 0.43 to 0.57 and is approximately equal to values observed in the literature between SAT-M scores and cumulative chemistry assessments, which range from 0.26 to 0.61 (Pederson, 1975; Ozsogomonyan, 1979; Rixse and Pickering, 1985; McFate and Olmstead III, 1999; Lewis and Lewis, 2007).

Table 2 Regression suggests SAT-M is an adequate predictor of low academic performance in chemistry

Semester	df	F	p	R ²	Equation
Spring 2016	(1, 474)	120	<0.0001	0.203	ACS = −3.196 + 0.108 (SAT-M)
Fall 2016	(1, 1335)	637	<0.0001	0.323	ACS = −19.659 + 0.132 (SAT-M)
Spring 2017	(1, 352)	78.1	<0.0001	0.182	ACS = −6.453 + 0.106 (SAT-M)
Fall 2017	(1, 1250)	513	<0.0001	0.291	ACS = −30.139 + 0.141 (SAT-M)

In summary, SAT-M scores have a significant linear relationship with chemistry assessments at the research setting. Additionally, students with SAT-M scores in the bottom quartile are more likely to receive a D or F grade or withdraw from the course and score substantially lower than other quartiles on average assessment scores. As a result, the decision to characterize students in the bottom quartile of SAT-M as at-risk was supported by the data collected in this research setting.

Students of underrepresented minorities are more often at-risk

Of the 3789 students entering the university with an SAT-M score, 44.2% self-identified as White in ethnicity (herein ethnicity refers to race or ethnicity), 22.5% as Hispanic/Latino, 12.3% as Black/African American, and 12.8% as Asian and 8.2% as an ethnicity with less than 5% representation (Native American or Alaska Native, Native Hawaiian or Other Pacific Islander) or an unknown ethnicity. The percent of students belonging to a particular ethnicity split by each semesters’ not at-risk and at-risk student groups are shown in Table 3.

Table 3 Students of underrepresented minorities more consistently comprise a greater percentage of the overall at-risk student cohort than that of the not at-risk cohort (in bold)

Ethnicity	Spring 2016		Fall 2016		Spring 2017		Fall 2017
Ethnicity	Not	At-risk	Not	At-risk	Not	At-risk	Not	At-risk
N	461	158	1067	395	277	112	961	358
a Native Hawaiian/other Pacific Islander or Native American or Alaska Native.
White	46.6%	43.7%	45.9%	41.0%	47.7%	36.6%	44.1%	40.2%
Hispanic/Latino	24.1%	22.2%	20.0%	28.9%	20.9%	23.2%	21.2%	24.9%
Black/African American	14.1%	21.5%	9.8%	13.9%	9.7%	25.9%	9.7%	16.8%
Asian	8.7%	7.6%	15.3%	11.4%	10.5%	7.1%	16.1%	9.2%
Ethnicities less than 5%^a or unknown	6.5%	5.1%	9.0%	4.8%	11.2%	7.1%	8.8%	8.9%

Amongst ethnicities with greater than 5% representation, students having self-identified as either Black/African American, or Hispanic/Latino comprised a greater percentage of the at-risk group than that of the not at-risk group with only one exception: Hispanic/Latino comprise a greater percentage of the not at-risk group in Spring 2016. These results suggest preparation in secondary-school mathematics, using SAT-M as a proxy, is not equitably achieved by students of underrepresented minorities (URMs) in the sciences, which includes students identifying as Black/African American, Hispanic/Latino (National Science Foundation, 2007). This result also corresponds with national trends in the US where the average SAT-M score for Black/African American students is 462 and Hispanic/Latino students is 489, each below the overall national average of 527 (College Board, 2017). The higher than expected percentage of Black/African American or Hispanic/Latino students in the at-risk group suggests aiding at-risk students has potential for increasing retention and improving the diversity of students who complete undergraduate degrees in chemistry and potentially other STEM fields. An analysis of URM performance is not within the scope of this article, but the commonality between at-risk students by SAT-M and URM is worth noting as efforts to aid at-risk students are likely to aid URM students as well.

Treatment of missing data

The primary analyses to follow occur with the 2979 (52.9%) of students who have both an SAT-M score and completed all assessments (three interim and one ACS final). Of these 2979 students with complete data, 753 (25.3%) were identified as having scored within the bottom quartile of the SAT-M and are herein referred to as the at-risk cohort. Students without SAT-M scores, ACS exam scores or any of the three interim assessments were considered separately within the missing data analysis are discussed later. Students who were missing an individual item (e.g. left a question blank) on a particular assessment but otherwise completed the assessment were assumed to have been unable to answer that particular question and thus their response was treated as an incorrect response. The university's Institutional Review Board reviewed the research protocol and approved this research as a review of educational records in accordance with institutional and local regulations.

Assessment items scored and mapped onto major topics

Assessment items from interim tests (N = 78 for each semester, N_total = 312) for the four semesters were written from a common list of learning objectives. A list of major topics was created to map onto learning objectives in such a way that learning objectives of similar topic matter were combined. All assessment items from two semesters, interim (N = 156) and ACS (N = 70), were then mapped onto the topic list by each author via an iterative process. The percent agreement was calculated and the discrepancies were reviewed creating revisions to the topics list. This process was iteratively continued until a topic list was generated that resulted in 89.8% agreement between the authors with the remaining discrepancies discussed to reach a consensus. This resulted in a list of 16 major topics that were mapped onto learning objectives (see Appendix). All remaining interim assessment items were then mapped onto the 16 major topics by a single author.

As a check on the consistency in which items could be assigned topics, two instructors at the research setting were provided the refined topic list and independently assigned items from differing semesters. The percent agreements between these instructors and the researchers were 83% and 80% (Cohen's Kappa 0.86 and 0.83; Gwet's AC1 0.86 and 0.84 respectively) (Cohen, 1960; Gwet, 2014). These values are interpreted as strong levels of agreement and suggest topics are distinct enough to provide consistent assignment of assessment items. The 16 major topics are arranged in order of teaching sequence at the setting and are followed by both distinctive, two-letter codes and frequencies on interim semester assessments in Table 4. Topic frequencies with an N < 3 (bold and italicized) were removed from all following analyses. Note that later topics such as Lewis structure, molecular shapes and valence bond theory were occasionally covered after the last interim assessment and therefore were only tested on the ACS exam. For the ACS Exam, the following topics had fewer than three items per topic: reactions in solution (RS), redox reactions (RR), changes in energy (CQ) and properties of light (PL).

Table 4 Topics in order of teaching sequence followed by two-letter codes and frequencies

#	Topics (codes)	Spring 2016	Fall 2016	Spring 2017	Fall 2017
1	Structure of the Atom (SA)	2	5	4	6
2	The Mole Concept (MC)	3	7	5	7
3	Nomenclature and Models of Bonding (NM)	8	9	6	4
4	Stoichiometry (ST)	3	7	4	6
5	Molarity (MR)	2	3	4	4
6	Reactions in Solution (RS)	1	3	7	7
7	Redox Reactions (RR)	3	3	3	3
8	The Gas Laws (GL)	9	8	7	5
9	Changes in Enthalpy (CH)	7	4	9	4
10	Changes in Energy (CQ)	4	3	6	5
11	Properties of Light (PL)	5	7	3	5
12	Electron Configurations (EC)	11	10	5	14
13	Periodic Trends (PT)	5	6	3	4
14	Lewis Structures (LS)	9	0	7	0
15	Molecular Geometry (MG)	1	0	0	0
16	Valence Bond Theory (VB)	0	0	2	0

Mean topic difficulties (P) for the interim (Spring 2016, ‘17, Fall ‘16, and ‘17) and ACS exam assessments were calculated for each semester as the percent correct of assessment items belonging to each topic (see Fig. 3). Here, the interim average represents the average difficulty for all interim assessment items related to a particular topic. The ACS average represents the same for those assessment items on the ACS exam. The overall average (in blue) represents the interim average plus the ACS average divided by 2 thereby giving equal weight to each source of assessment items. Overall, students appear to have experienced a wide range of topic difficulties over the four semesters. ACS assessment topics (dashed, gray line) appear to have greater topic difficulties than topics measured within interim assessments (dotted, gray line). The topics on which students performed with the least difficulty were the structure of the atom (SA; P = 78.65%), properties of light (PL; P = 76.50%), and reactions in solution (RS; P = 69.40%). Molecular geometry (MG; P = 38.50%), only tested on the ACS exam, posed a particularly notable difficulty to students overall. Other topics on which students encountered moderate difficulty include redox reactions (RR; P = 55.43%), changes in enthalpy (CH; P = 56.32%), and molarity (MR; P = 59.70%).


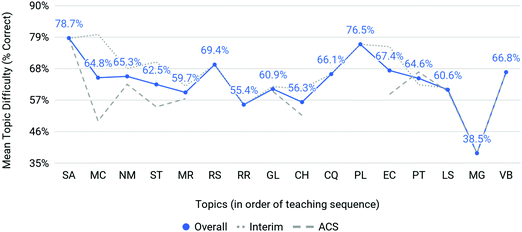	Fig. 3 A wide range of mean topic scores were observed on interim and ACS exams overall. The data presented in Fig. 3, and ensuing figures, represents categorical data on the x-axis (major topics). The choice was made to represent this data in a line graph to visually emphasize the relationship among the interim, ACS and overall averages across topic and it is not meant to portray continuity in performance between topics.

To explore the topics on which at-risk students most disproportionately struggled, mean topic scores were calculated for at-risk and not at-risk students. Differences between the groups’ mean topic scores were measured via effect size (Cohen's d) to control for the variability within the scores (Cohen, 1988). Effect size represents a standardized measure of the differential performance between the two groups where a positive number indicates the not at-risk group outperformed the at-risk group. A d = 0.2, 0.5, and 0.8 are described as having small, medium, and large effect sizes, respectively.

Results

At-risk students are challenged disproportionately on mole concept and stoichiometry assessment items

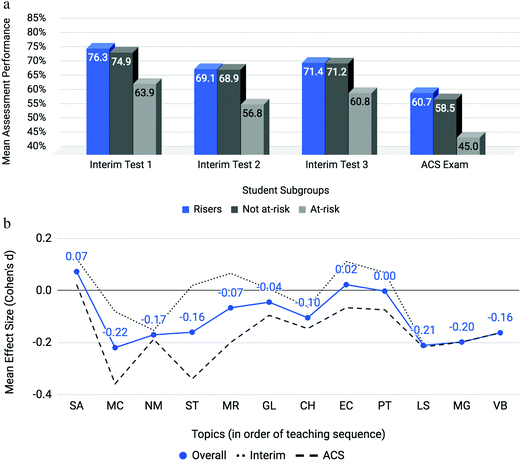
Mean effect sizes averaged across four semesters for both interim and ACS assessments are provided in Fig. 4. Interim, ACS and overall averages used the same approach as above with Cohen's d as the metric of differential performance (Cohen, 1988). Molecular geometry (MG) and valence bond theory (VB) were only assessed in the ACS exam. The effect sizes for the topics of the gas laws (GL) and electron configurations (EC) diverge when comparing interim (dotted line) to ACS (dashed line) assessments. All topics featured at least an effect size between small and medium which indicates that at-risk students struggle on all first-semester chemistry topics when compared to the not at-risk cohort; however, larger effect sizes on particular topics identify areas of particular concern. Two topics emerge as posing the most disproportionate and consistent challenge to at-risk students: mole concept (MC) and, to a greater extent, stoichiometry (ST) with medium to large effect sizes of 0.60 and 0.70, respectively. To determine the consistency of differential performance on mole concept and stoichiometry within the data, each semester was analyzed separately (results are described in the Appendix). It was found that stoichiometry was a relative peak in each of the four semesters and mole concept was a relative peak in three of the four semesters. The consistent differential performance found for these topics across each semester discounts the possibility that the differential performance observed is a result of random noise within the data.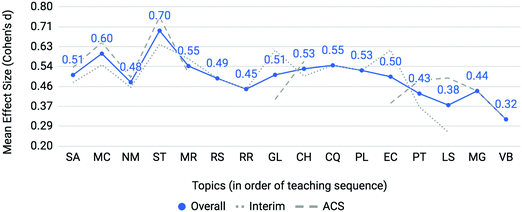


	Fig. 4 Mole Concept (MC) and Stoichiometry (ST) are topics posing incommensurate difficulty to students with low math aptitude scores.

Mole concept and stoichiometry are essential to student success

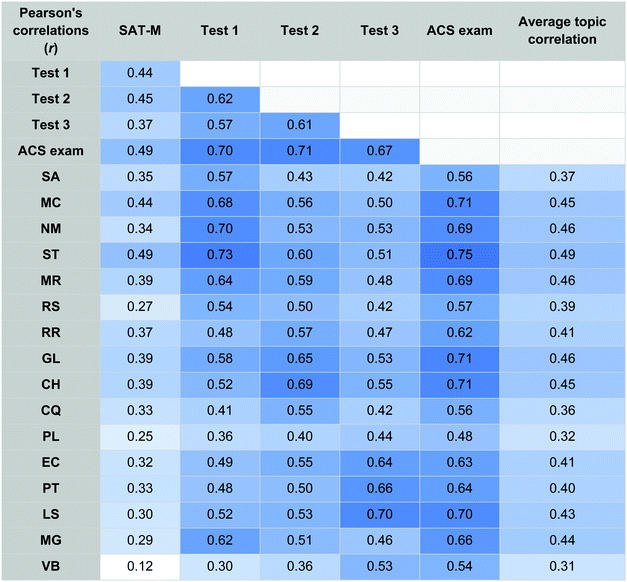
To determine the degree to which the SAT-M may measure a student's potential performance on the topics of mole concept and stoichiometry as compared to other topics, correlations for each topic to the SAT-M, interim and summative assessments were computed in Table 5. Conditional formatting presenting as various shades of blue in Table 5 emphasize larger effect sizes (darker shades blue) from smaller effect sizes (lighter shades of blue). Also included in Table 5 is Average Topic Correlation which was found by correlating the topic in the row with each other topic and then computing the average of those correlations.

Table 5 Pearson's correlation values for topic scores, the SAT-M, and assessments

The topics of mole concept (MC; r = 0.44) and stoichiometry (ST; r = 0.49) are moderately correlated with students’ SAT-M score; and are slightly higher than the correlation of SAT-M with other topics. ACS exam scores are highly correlated with the topics of stoichiometry (ST; r = 0.75), mole concept (MC), gas laws (GL), and changes of enthalpy (CH) each with values of r = 0.71. The topics of mole concept and stoichiometry are also among the topics with the strongest relation with student success in other topics; stoichiometry had the highest correlation with all other topics (ST; r = 0.49) and the topics of mole concept (MC; r = 0.45), molarity (MR; r = 0.46), gas laws (GL; r = 0.46), and changes in enthalpy (CH; r = 0.45) were also strongly related. The remaining topics had correlations between 0.31 and 0.41 suggesting an overall interconnected nature of the topics or a common skill set needed to succeed.

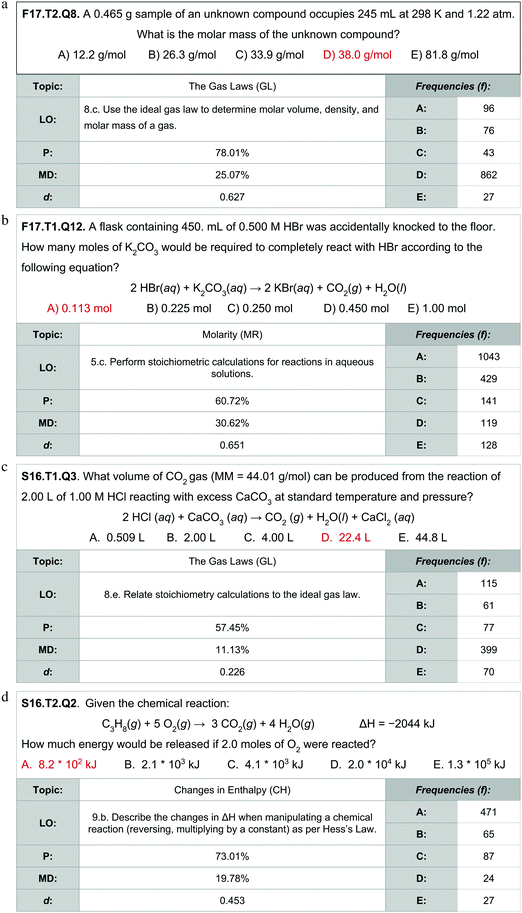
Upon reviewing assessment items and learning objectives, examples of applied forms of stoichiometry and mole concept appears in subsequent topics. Assessment items from interim exams were identified that explicitly relied on applied forms of stoichiometry and mole concept within subsequent topics. Exploring the differential performance indicates that the recurrence of stoichiometry and mole topics can partially explain some differential performance observed in later topics. Four exemplary items of this point are described in Fig. 5a–d; for copyright reasons items from the ACS Exam were explicitly not included as exemplars. Each figure includes the assessment item with the correct answer in red, the assigned learning objective (LO), percent correct (P), the differential between the percent of not at-risk versus at-risk students answering correctly (MD) and the effect size (d).


	Fig. 5 (a) Interim assessment item on mole concept in gas laws. (b) Interim assessment item on stoichiometry in molarity. (c) Interim assessment item on stoichiometry in gas laws. (d) Interim assessment item on stoichiometry in changes in enthalpy.

Two of these assessment items (Fig. 5a and b) have effect sizes greater than 0.6; commensurate with the effect sizes observed for mole concept and stoichiometry overall and above the average effect sizes for gas laws and molarity, respectively (see Fig. 4). Two other assessment items (Fig. 5c and d) still feature a differential performance of 0.226 and 0.453, respectively, but are below the overall average observed for their respective topics. By item analysis reveals considerable variation among the differential performance metric that is evened out by the topic score. Individually, each item could be impacted by various features. The item in Fig. 5c, for example, may have less differential owing to students selecting 22.4 L as the standard molar volume of a gas rather than performing the intended operation and with at-risk students disproportionately using this heuristic. Systemic investigation of by-item features that relate to differential performance can provide additional insight but was considered beyond the scope of the current investigation.

At-risk students achieving proficiency in mole concept and stoichiometry performed equitably or surpassed their not at-risk peers

To further explore whether the topics of mole concept and stoichiometry are essential to success for at-risk students, a subgroup of at-risk students who performed well in these topics was identified. This subgroup is termed “Risers” and was identified as at-risk students who scored better than 65% on the interim and ACS assessment items for either the mole concept or stoichiometry topics. If stoichiometry and mole concept were topics imperative to the success of at-risk students, students achieving proficiency on these topics would be expected to have higher academic outcomes than their peers within the at-risk student group. The mean SAT-M score of risers was 499, close to the mean SAT-M score for the at-risk group overall at 488 and considerably below the not at-risk students 598. The academic performance of risers surpassed not only that of their at-risk peers but was quite similar to that of the not at-risk students (see Fig. 6a). Risers were compared to not at-risk students by topic to determine if the result is only related to their performance on mole concept and stoichiometry. The results are shown in Fig. 6b where a positive value indicates not at-risk performed higher than the risers. Overall, the differential performance across topics tended to be proximate to zero, suggesting equal performance between the groups, or negative, indicating the risers scored higher on those topics. These results suggest that at-risk students proficient on stoichiometry or mole concept succeed in the course at a comparable rate as the rest of the cohort and further supports the importance of these topics for at-risk student performance.


	Fig. 6 (a) At-risk students proficient in mole concept and stoichiometry (Risers) perform similarly to the not at-risk cohort. (b) Topic performance of at-risk students proficient in mole concept and stoichiometry (Risers).

Explorations of the missing data

The above analyses focus on the 2979 students, 52.9% of the overall cohort, with complete data (incoming SAT-M score and completion of all interim and ACS assessments). Students with missing data were analyzed, where possible, to investigate the extent the key finding, that at-risk students disproportionately struggle with mole concept and stoichiometry, was applicable. Among those who had either taken the alternative version of SAT-M (e.g. a Fall 2017 student taking the old SAT-M) or had not taken the SAT-M there were 890 students, 15.8% of the overall cohort, with ACT scores and complete data on all interim and ACS assessments. In the US system, the ACT serves as a nationally available alternative to the SAT, and also features a mathematics component score (ACT-M). To determine whether at-risk students could be identified using ACT-M scores, concordance tables published by the College Board in 2016 provided a conversion between scores of the two standardize math aptitude tests. These conversions were developed using the equipercentile concordance method in which scores from each test were found to share the same percentile rank (College Board, 2016). For example, scores found at the 75th percentile nationally for the SAT-M correspond to the same percentile for converted scores on the ACT-M. The bottom quartile of ACT-M scores for this group of 890 students ranges between 20 to 23 depending on the semester. Referencing the College Board's concordance tables, SAT-M scores corresponding to these scores are between 510 and 570. As the bottom quartile for SAT-M scores at this setting is between 490 and 570, students defined as at-risk by either relative SAT-M or ACT-M performance appear reasonably comparable. At-risk students, among those without SAT scores, were then defined as those in the bottom quartile of the ACT-M and mean effect sizes measuring differential performance is presented in Fig. 7. The topics of mole concept and stoichiometry share the highest effect sizes observed indicating these topics also comprise the greatest differential between students in the bottom quartile ACT-M scores compared to the top three quartiles. With this measure, however, mole concept is observed as having a greater contribution to the difficulty of at-risk students than that of stoichiometry. Thus the finding of differential performance on these topics appears to extend to the cohort of students without SAT scores but with ACT scores.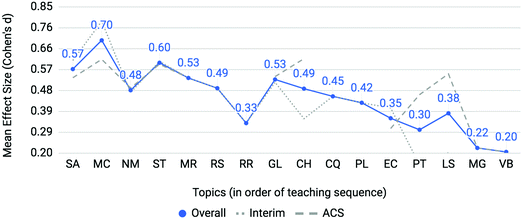


	Fig. 7 Trends related to disproportionate topic difficulty for at-risk students are consistent with students of lower ACT-M scores.

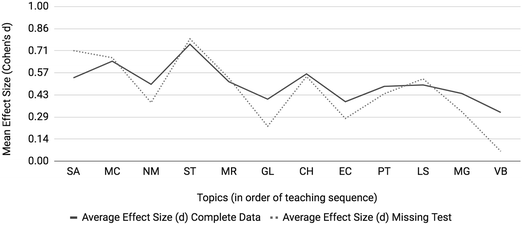
Another source of missing data are students who missed one or more of the interim assessments but did take the ACS assessment. Among those with SAT-M or ACT-M scores, there were 575 students, 10.2% of the cohort, who missed one or more of the interim assessments but completed the ACS assessment. Reasons for missing an interim assessment are varied and include scheduling conflicts, ailments or emergencies and students were provided an alternative exam at a later date in these situations. Owing to the alternative interim assessments, the analysis focused on differential performance by topic on the ACS assessment and used either SAT-M when available or ACT-M to classify at-risk students. The results (see Appendix) found that mole concept and stoichiometry topics provided the largest differential performance between at-risk and not at-risk students mirroring the results for the larger cohort.

The remaining sources of missing data includes students who did not take the ACS exam, 530 students or 9.4% of the cohort, and those who did not have SAT or ACT scores, 662 students or 11.7%. The ACS exam was required for successful completion of the course and students who did not take this exam either withdrew from the course, stopped attending the course or in rare cases arranged to complete the exam in a following semester. Among this group, the amount of interim assessments completed is inconsistent which prevents an exploration of differential topic performance. More descriptively, the students in each group (at-risk or not) that took the first test are not the same as those who took the second test and therefore a comparison across topics using the interim assessments would not be appropriate. Finally, there was no way to identify an at-risk cohort among the 11.7% of students who did not have SAT or ACT scores so the key finding could not be explored for this group either. That said, the differential performance by topic was consistent among the three groups: those with complete test scores and SAT scores, those with complete test scores and ACT scores but no SAT scores, and those who completed the ACS exam while missing one or more interim assessments. Combined these three groups represent 78.9% of the overall cohort.

Discussion

Of the overall cohort comprised of 5636 students, the primary analyses presented in this article reflect a consistent group of 2979 students entering first-semester chemistry with SAT-M scores and having completed all interim and ACS assessments items within their respective semesters. 753 at-risk students demonstrated differences in mean performance on all topics in introductory chemistry in comparison to not at-risk students. The mean difficulties (average percent correct) for students overall suggest reasonable performance on assessment items related to the topics of mole concept (MC) and stoichiometry (ST); each with respective means of 64.84% and 62.49% (see Fig. 3), however, these topics also featured the largest differential in performance between at-risk as compared to not at-risk students. The effect sizes between these two groups are medium to large with d = 0.60 for mole concept and d = 0.70 for stoichiometry (see Fig. 4) across four semesters of data. This finding was also consistent among those with missing data where applicable trends could be explored. This differential performance indicates these topics present consistent and significant challenges to students with low SAT-M scores.

Stoichiometry is not only the topic most correlated to performance on the ACS exam but is also the topic most correlated with SAT-M and other topic scores (see Table 5). Explorations of other topics with medium effect sizes such as molarity (MR; d = 0.53), gas laws (GL; d = 0.51), and changes of enthalpy (CH; d = 0.51) revealed mole concept and stoichiometry may partially explain the differential performance observed within these topics (see Fig. 5a–d). At-risk students demonstrating a proficiency of 65% or higher on assessment items of either mole concept or stoichiometry assessment items far outperformed their peers with comparable SAT-M scores in the at-risk cohort. Additionally, these proficient at-risk students performed either equitably or exceeded that of the not at-risk cohort (top three quartiles of the SAT-M) on both interim and ACS assessments (see Fig. 6a and b). The results reflect the findings of Tai et al. (2006) who found students’ self-report of time spent on stoichiometry in high school was varied and had the strongest relationship with first-semester chemistry grades among a set of other chemistry topics.

The research literature offers promising instructional techniques for promoting students’ understanding of stoichiometry. Kimberlin and Yezierski (2016) developed, implemented and evaluated two inquiry lessons to promote understanding of stoichiometry concepts. One lesson involved using particulate models and questions to elicit and address students’ common incorrect ideas regarding mole ratios. The other lesson targets the interpretation between symbolic, algorithmic and macroscopic descriptions of stoichiometry. The lessons were implemented in five high (secondary) schools introductory chemistry courses and were evaluated using a pre/post implementation of conceptual stoichiometry tests. Comparing the post-test to the pre-test, statistically significant gains with a large effect size were observed. These findings provide potential paths forward toward improving students understanding of stoichiometry concepts. Coupled with the findings presented here on the differential performance of at-risk students on stoichiometry topics, it is hypothesized that the effective implementation of such activities could promote the success of at-risk students. That said, Cacciatore and Sevian (2009) found that an inquiry laboratory experiment on stoichiometry led to improved performance on stoichiometry questions but not on indirect applications of stoichiometry, making the transfer of knowledge still an important hurdle to realizing this hypothesis.

Returning to the aforementioned hypothesis that low SAT-M performance would foreshadow a lack of quantitative skills, which is responsible for differential performance, the results are arguably more nuanced. First, mole concept and stoichiometry as they are articulated here include more than just algebraic manipulation. In particular, these topics rest on both proportional reasoning and the translation between mathematical and symbolic representations, with the latter serving as the language for communicating chemistry concepts (Taber, 2013). The difficulty in translation from symbolic to mathematical representations matches a common trend observed in the literature base exploring students’ problem-solving strategies in chemistry where students can apply algorithmic strategies to assessment items but are unable to meaningfully transfer their understanding to more conceptual or unique scenarios of the topic (Niaz and Robinson, 1992; Bunce, 1993; Nakhleh, 1993; Mason et al., 1997). The results here suggest that this issue may be particularly pronounced among students with low SAT-M. Second, other topics in the course reliant on more direct algebraic manipulation such as gas laws, changes of energy, and properties of light had differentials closer to the average of observed topics. In summation, at-risk students had pronounced challenges with topics that rely on quantitative reasoning and an emphasis on chemical formulas or reactions (mole concept and stoichiometry) but not as pronounced among topics that rely on quantitative reasoning with lesser emphasis on chemical formula or reactions (gas laws and properties of light).

The communicated need for more interdisciplinary cooperation between mathematics and chemistry instruction has been advocated (Wright and Chorin, 2000) as the role of mathematics in supporting quantitative elements of chemistry becomes increasingly relevant (Witten, 2005). As mentioned in the introduction of this article, one suggestion observed with regard to ensuring incoming chemistry students possess necessary skills in mathematics is the assignment of prerequisite courses in mathematics (Donovan and Wheland, 2009) based on incoming metrics such as high school GPA, math ACT, or SAT-M scores. In a study investigating math reasoning with and without a chemistry context, chemistry students were provided paired sets of chemistry and mathematics assessment items (Scott, 2012). Chemistry assessment items were related to the topics of mole concept and stoichiometry and mathematics assessment items were designed to measure student ability in the quantitative reasoning skills necessary to solve the chemistry assessment items without a chemistry context. The study found that success on the mathematics assessment items often did not transfer to paired, chemistry items in which similar quantitative reasoning skill sets are utilized. As the author states, “Since the mathematics questions are analogous to the chemistry questions, any practice at one should transfer some improved ability at the other; however, this does not appear to translate from mathematics to chemistry.” (Scott, 2012, p. 336). In consideration of this study and our own results, the simple placement of a prerequisite course in mathematics seems unlikely to ameliorate differential performance within chemistry, though it is possible that a collaboratively designed preparatory course in math and chemistry may resolve the lack of transferability between the content matter of the two disciplines.

The focus on topic averages rather than analyses of individual assessment items or the process by which students answer these items is a limitation of this work. While the intent of the article was to elucidate the topics on which at-risk and first-semester chemistry students overall most struggle, efforts to aid at-risk students would benefit by further characterizing the tasks on which students most struggle in chemistry. Carrying out this work may be achieved via item analysis and qualitative investigations to offer additional insight into efforts towards supporting at-risk students. Alternatively, explorations as to the learning progressions of students formulating concepts fundamental to stoichiometry are limited and could be further explored via repeated measures using surveys, interviews or assessments to measure student solution strategies or self-reflective explanations of said strategies. Characterizing such a learning progression may provide a framework on which educators can better assess and design learning experiences to facilitate high conceptual understanding of these topics (Talanquer, 2009; Duschl et al., 2011) and promote the success of at-risk students.

An additional limitation of this work is that the data collection was limited to one institution and is reliant on closed-ended assessments and potentially the sequencing of topics in this curriculum. With this acknowledgement, it remains uncertain the extent that at-risk students would struggle on these topics at varying institution types, assessment methods and curricula. Further studies into the performance of at-risk students are needed to substantiate a more generalizable claim and can also clarify whether proficiency in mole concept and stoichiometry is predictive of student success in general chemistry as this would establish greater need still for effectively designed lessons and assessments on these fundamental topics with evaluations that explicitly consider at-risk students. Such studies may have the potential to reduce attrition and promote inclusion of both students of inequitable pre-college math preparation and students of underrepresented minorities.

Conclusion

This study presents a trend towards the characterization of topics on which at-risk students (as comprised by students having scored relatively in the bottom quartile of each semester's cohort on the math component of SAT or ACT) most disproportionately struggle: the mole concept and stoichiometry. This trend for at-risk student struggle with these two topics was observed along two academic years (2016–2017) across four semesters of data. The results call attention to an emphasis on these topics to achieve the goal of an equitable class setting that is responsive to a range of incoming student preparations. This attention is further warranted given the correlations of these topics to success in the course overall and the presence of these topics in subsequent topics such as molarity, gas laws and thermodynamics. Additionally, at-risk students who were successful on these topics had similar assessment performance as the not at-risk cohort. The existing research literature offers potential avenues toward promoting student success on these topics which can serve as a fruitful area of future research. The methodology presented herein provides a path for future research to better understand other sources of inequitable success within chemistry courses. Finally, students of the at-risk cohort were also comprised of a greater number of students having self-identified as Black/African American and Hispanic/Latino and thus studies aimed at improving at-risk student outcomes have potential for ameliorating both differences observed amongst students of differential math preparation and towards diversification of STEM careers.

Conflicts of interest

There are no conflicts to declare.

Appendix

Coding list

The following major topics were the result of the iterative coding scheme and include the learning objectives that were affiliated with each major topic. The learning objectives were used to craft the exams.

(1) Structure of the Atom (SA):

(a) Describe the structure of the atom in terms of the placement and charge of protons, neutrons and electrons.

(b) Describe the structure of the atom in terms of the number of protons, neutrons and electrons given mass number and chemical identity or atomic number.

(d) Relate isotope abundance to the average atomic mass of an element.

(2) The Mole Concept (MC):

(a) Define mole and relate it to number of units.

(b) Differentiate empirical formula and molecular formula.

(d) Convert between mass, mole and number of atoms for any compound.

(e) Given a chemical formula, solve for the mass percent of each element in a compound.

(3) Nomenclature & Models of Bonding (NM):

(a) Describe the reason chemical bonds are stable and differentiate covalent and ionic bonds in terms of electron placement.

(b) Classify chemicals as atomic elements, molecular elements, molecular compounds or ionic compounds.

(d) Name covalent and ionic compounds including ionic compounds with transition metals and polyatomic ions.

(4) Stoichiometry (ST):

(a) Balance a chemical equation, given an unbalanced chemical equation.

(b) Given the mass of any compound and given a chemical reaction, solve for the mass of any other compound in the reaction.

(c) Given the mass of two reactants in a chemical reaction, solve for the mass produced of any product, determine which reactant is limiting and determine the mass remaining of the excess reactant.

(d) Given two of the three: percent yield, theoretical yield and actual yield, or a means to determine two of the three, solve for the third.

(5) Molarity (MR):

(a) Given two of the three: molarity, mol, volume of solution, be able to solve for the missing variable.

(b) Perform calculations for solution dilutions using M₁V₁ = M₂V₂.

(6) Reactions in Solution (RS):

(a) Define strong electrolyte, weak electrolyte, and nonelectrolyte.

(b) Classify ionic and molecular compounds as strong, weak, or nonelectrolytes.

(d) Determine the Reactions in Solution of ionic compounds in water.

(e) Given two ionic compounds that are dissolved in water, predict the possible products and identify if a precipitate forms.

(f) Given two ionic compounds that are dissolved in water, write a molecular equation, ionic equation and net ionic equation and identify spectator ions.

(7) Oxidation–Reduction (or Redox) Reactions (RR):

(a) Define and identify: reduction, oxidation, reducing agent, oxidizing agent and redox reactions.

(b) Assign oxidation numbers to any compound.

(8) The Gas Laws (GL):

(a) Define pressure in terms of molecular collisions.

(b) Use the ideal gas law to solve for any missing variable.

(d) Define and use mole fraction and partial pressure for a mixture of gases (Dalton's law).

(e) Relate stoichiometry calculations to the ideal gas law.

(f) Define standard temperature and pressure (STP) and molar volume at STP.

(g) Identify the three central parts of kinetic molecular theory and relate the theory to the observations in the simple gas laws.

(h) Interpret graphical representations of distributions of molecular speeds.

(i) Demonstrate the conceptual relationships between molar mass, temperature and the root mean square velocity of molecules.

(j) Given any two of molar mass, temperature, and root mean square speed, be able to calculate the third.

(k) Define mean free path, diffusion, and effusion.

(l) Use Graham's Law and the effusion rate or time of a known substance to solve for the rate, time, or molar mass of another substance.

(9) Changes in Enthalpy (CH):

(a) Relate mass of a compound in a reaction, enthalpy change of a reaction and energy change of a reaction.

(b) Describe the changes in ΔH when manipulating a chemical reaction (reversing, multiplying by a constant) as per Hess's Law.

(d) Relate ΔH of a reaction to heats of formation, ΔH_f.

(e) Write or identify a formation reaction for a compound from elements in the standard state (e.g. corresponds to the value for ΔH_f).

(10) Changes in Energy (CQ):

(a) Define kinetic energy, potential energy, chemical energy and state function.

(b) Describe the first law of thermodynamics and use it to model energy changes.

(c) Given three of the four: energy, mass, specific heat and change in temperature, or a means to solve three of the four, determine the value for the missing variable.

(d) Define the concept heat capacity and relate it to specific heat capacity and molar heat capacity.

(e) Define enthalpy, exothermic reaction, and endothermic reaction.

(f) Perform calorimetry calculations relating mass of a reactant to change in temperature of surrounding water.

(11) Properties of Light (PL):

(a) Define the term quantum mechanical model.

(b) Characterize the different regions of the electromagnetic spectrum.

(d) Relate energy, frequency and wavelength conceptually and mathematically.

(e) Relate amplitude to intensity conceptually and mathematically.

(f) Calculate and relate the concepts of threshold frequency, binding energy and kinetic energy of an ejected electron in the photoelectric effect.

(g) Define the terms emission spectrum and absorption spectrum.

(h) Relate deBroglie wavelength to mass and velocity conceptually and mathematically.

(i) Explain the term complementary properties and the specific example in Heisenberg's uncertainty principle.

(j) Define probability density and contrast deterministic with indeterminacy.

(k) Solve for the energy and wavelength associated with electron transitions in a Hydrogen atom and explain the relationship with the Bohr Model.

(12) Electron Configurations and Quantum Numbers (EC):

(a) Describe the purpose of each of the four quantum numbers and use the rules that define allowable sets of quantum numbers.

(b) Know the shapes of s, p, d, and f orbitals and the relationship to quantum numbers.

(d) Define and apply the Aufbau principle and Hund's rule.

(e) Describe an orbital filling diagram for any element on the periodic table.

(f) Relate orbital filling diagrams, electron configurations and quantum numbers.

(g) Determine number of valence electrons and core electrons for any atom on the periodic table.

(h) Determine the expected electron configuration for any atom on the periodic table (complete configuration and noble gas abbreviation).

(i) Know and understand that an electron configuration shows the number of electrons that occupy particular orbitals in atoms and is the basis for chemical reactivity.

(j) Write electron configurations of ions.

(k) Define and make predictions for diamagnetic and paramagnetic.

(13) Periodic Trends (PT):

(a) Define the term periodic property.

(b) Define the term degenerate as it applies to orbitals.

(d) Describe the trends in atomic radii on the periodic table and relate the observed trends to the structure of the atom.

(e) Relate the radius of an atom to an ion of the same element.

(f) Describe the trends in ionization energy on the periodic table and relate the observed trends to the structure of the atom.

(g) Predict the expected trends in successive ionization energies.

(h) Define electron affinity.

(i) Describe what is meant by metallic character and relate it to trends on the periodic table.

(14) Lewis Structures (LS):

(a) Define and provide examples of ionic, covalent and metallic bonds and differentiate between them based on physical properties.

(b) Represent any atom with a Lewis structure.

(d) Use Lewis structures to represent ionic compounds containing main group elements.

(e) Relate bond order to bond energy and bond length.

(f) Know that Lewis structures are simple predictors of how atoms combine to form ionic compounds and molecules.

(g) Define and describe the trends in electronegativity.

(h) Determine if a bond is considered covalent, polar covalent or ionic, given values for electronegativity and indicate the direction of the dipole.

(i) Use the formula for dipole moment and percent ionic character.

(j) Understand the resonance concept and relate it to relative bond strength and length.

(k) Solve for the formal charge of any atom in a Lewis structure and use formal charge to determine plausibility of a Lewis structure.

(l) Describe structures that are exceptions to the octet rule including odd-electron species, incomplete octets and expanded octets.

(m) Understand trends in bond length and bond energy and the relationship between bond length and bond energy.

(15) Molecular Geometry (MG):

(a) Understand the premise to VSEPR theory, particularly the role played by electron groups.

(b) Determine the electron geometry and molecular geometry for any Lewis structure.

(d) Determine the polarity of a bond, molecule, or ion given electronegativity values.

(16) Valence Bond Theory (VB):

(a) Describe the principles of valence bond theory.

(b) For any Lewis structure, predict hybridization and number of sigma and pi bonds.

(d) Describe the relationship between hybridization and bond type.

(e) Define bonding, antibonding and nonbonding orbitals.

(f) Use molecular orbital theory to determine the bond order for diatomic molecules given the MO diagram.

Effect sizes of topic scores by semester

Fig. 8 provides effect sizes comparing mean topic scores of not at-risk and at-risk students as determined from interim and ACS exams by semester. Not all topics were included in analyses for each semester's interim exams as a few topics did not have 3 or more assessment items with which to complete the analysis. In the U.S. system, the traditional academic year has a fall and spring semester. For the course first-semester General Chemistry the fall and spring semester cohorts have notably different profiles. In comparison to fall semester cohorts, spring semester tends to have lower overall SAT-M scores (see Table 1) and lower differential performance (Fig. 8). Across each semester, stoichiometry (ST) has the highest differential performance among all topics on the overall average. Demarcating by interim and ACS shows a consistent trend of stoichiometry having among the highest differential with the interim tests in Spring 2017 as the only exception. Mole concept (MC) also features a consistent relative peak for three of the four semesters, with the exception of Spring 2016 owing to the interim test items from that semester. The exploration by semester offers an indication of the consistency of the finding for differential performance on stoichiometry and mole concept.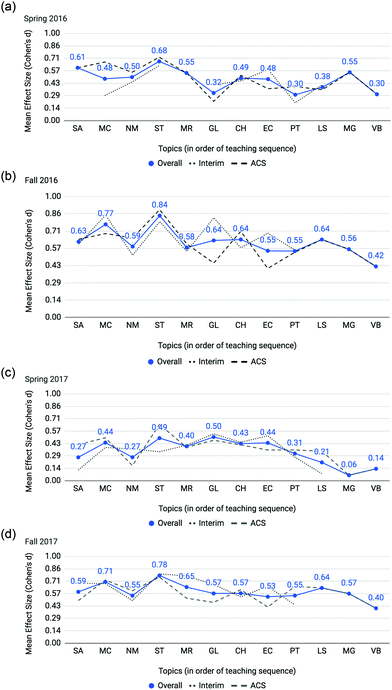


	Fig. 8 (a) Spring 2016. (b) Fall 2016. (c) Spring 2017. (d) Fall 2017. Effect sizes comparing mean topic scores of not at-risk and at-risk students on interim and ACS exams.

Results of additional missing data analyses

Missing data were analyzed to determine the extent possible the key finding was applicable to those with different sources of missing data. A frequency count of the different sources of missing data are presented in Table 6. The first data row in the table, SAT-M with All Tests, comprise the original cohort analyzed. The fourth data row in the table represents students without SAT scores but with ACT scores and complete test scores and these students were analyzed as a separate group. The second and fifth data rows, combined, represent students with SAT or ACT who took the summative assessment but missed an interim assessment; this group was analyzed separately as well in the text and below.

Table 6 Frequencies of students within each subgroup of the overall cohort

Semester		Spring 2016	Fall 2016	Spring 2017	Fall 2017	Total	Percent of cohort (%)
SAT-M	All tests	416	1189	269	1105	2979	52.9
	Missed test; took ACS	60	148	85	147	440	7.8
	No ACS score	143	125	35	67	370	6.6

No SAT-M; took ACT-M	All tests	99	304	122	365	890	15.8
	Missed test; took ACS	17	40	29	49	135	2.4
	No ACS score	37	28	55	40	160	2.8

Neither SAT nor ACT	All tests	82	98	78	148	406	7.2
	Missed test; took ACS	16	15	41	35	107	1.9
	No ACS score	32	36	43	38	149	2.6

Total students enrolled		902	1983	757	1994	5636	100.0

As mentioned 575 students (10.2% of the cohort) with SAT or ACT who took the summative (ACS) exam but missed an interim exam were analyzed separately. At-risk and not at-risk were identified using SAT or ACT (if SAT was not available) and their performance was compared on the ACS exam by topic. The results are presented as the dashed line in Fig. 9 and are consistent with those who have complete data (solid line in Fig. 9, also the solid line in Fig. 4).


	Fig. 9 Mean effect sizes between students with complete data and students missing tests.

Acknowledgements

Partial support for this work was provided by the National Science Foundation's Improving Undergraduate STEM Education (IUSE) program under DUE-1432085 and Florida-Georgia Louis Stokes Alliance for Minority Participation Bridge to the Doctorate award HRD-1612347. Any opinions, findings, and conclusions or recommendations expressed in this material are those of the authors and do not necessarily reflect the views of the National Science Foundation.

References

Andrews M. H. and Andrews L. J., (1979), First-Year Chemistry Grades and SAT-M Scores, J. Chem. Educ., 56(4), 231–232.
Apugliese A. and Lewis S. E., (2017), Impact of instructional decisions on the effectiveness of cooperative learning in chemistry through meta-analysis, Chem. Educ. Res. Pract., 18(1), 271–278.
Bunce D. M., (1993), Introduction: Symposium: Lecture and learning: Are they compatible? J. Chem. Educ., 70, 179–180.
Cacciatore K. L. and Sevian H., (2009), Incrementally Approaching an Inquiry Lab Curriculum: Can Changing a Single Laboratory Experiment Improve Student Performance in General Chemistry? J. Chem. Educ., 86, 498–505.
Chan J. Y. K. and Bauer C. F., (2014), Identifying At-Risk Students in General Chemistry via Cluster Analysis of Affective Characteristics, J. Chem. Educ., 91, 1417–1425.
Cohen J., (1960), A coefficient of agreement for nominal scales, Educ. Psychol. Meas., 20, 37–46.
Cohen J., (1988), Statistical Power Analysis for the Behavioral Sciences, Hillsdale: Lawrence Erlbaum Associates.
Coley N. R., (1973), Prediction of success in general chemistry in a community college, J. Chem. Educ., 50, 613.
College Board, (2016), Concordance SAT Suite of Assessments [online], available at: https://collegereadiness.collegeboard.org/pdf/higher-ed-brief-sat-concordance.pdf [accessed 24 May 2018].
College Board, (2017), SAT Suite of Assessments Annual Report [online], available at: https://reports.collegeboard.org/pdf/2017-total-group-sat-suite-assessments-annual-report.pdf [accessed 22 May 2018].
College Board, (2018a), Inside the Test - Math [online], available at: https://collegereadiness.collegeboard.org/sat/inside-the-test/math [accessed 24 May 2018].
College Board, (2018b), Compare SAT Specifications [online], available at: https://collegereadiness.collegeboard.org/sat/inside-the-test/compare-old-new-specifications [accessed 24 May 2018].
Donovan W. J. and Wheland E. R., (2009), Comparisons of success and retention in a general chemistry course before and after the adoption of a mathematics prerequisite, Sch. Sci. Math., 109, 371–382.
Duschl R., Maeng S. and Sezen A., (2011), Learning progressions and teaching sequences: a review and analysis, Stud. Sci. Educ., 47, 123–182.
Examinations Institute of the American Chemical Society Division of Education, (2015), First-Term General Chemistry Exam, Milwaukee, WI: University of Wisconsin–Milwaukee.
Freeman S., Eddy S. L., McDonough M., Smith M. K., Okoroafor N., Jordt H. and Wenderoth M. P., (2014), End of lecture: active learning increases student performance across the STEM disciplines, Proc. Natl. Acad. Sci. U. S. A., 111, 8410–8415.
Gosser D. K., Strozak V. and Cracolice M. S., (2006), Peer-Led Team Learning: General Chemistry, 2nd edn, Upper Saddle River, NJ: Prentice Hall.
Gwet K. L., (2014), Handbook of inter-rater reliability: the definitive guide to measuring the extent of agreement among raters, Gaithersburg, MD: Advanced Analytics, LLC.
Hailikari T. K. and Nevgi A., (2010), How to Diagnose At-risk Students in Chemistry: the case of prior knowledge assessment, Int. J. Sci. Educ., 32, 2079–2095.
Hall D. M., Curtin-Soydan A. J. and Canelas D. A., (2014), The Science Advancement through Group Engagement Program: Leveling the Playing Field and Increasing Retention in Science, J. Chem. Educ., 91(1), 37–47.
Kimberlin S. and Yezierski E., (2016), Effectiveness of Inquiry-Based Lessons Using Particulate Level Models To Develop High School Students’ Understanding of Conceptual Stoichiometry, J. Chem. Educ., 93(6), 1002–1009.
Kotnik J., (1974), What is being done to help the underprepared student? J. Chem. Educ., 51, 165–167.
Lewis S. E., (2011), Retention and Reform: An Evaluation of Peer-Led Team Learning, J. Chem. Educ., 88, 703–707.
Lewis S. E. and Lewis J. E., (2007), Predicting at-risk students in general chemistry: comparing formal thought to a general achievement measure, Chem. Educ. Res. Pract., 8, 32–51.
Lewis S. E. and Lewis J. E., (2008), Seeking Effectiveness and Equity in a Large College Chemistry Course: An HLM Investigation of Peer-Led Guided Inquiry, J. Res. Sci. Teach., 45, 794–811.
Lubinski D., (2010), Spatial ability and STEM: a sleeping giant for talent identification and development, Pers. Indiv. Differ., 49, 344–351.
Mason D. and Verdel E., (2001), Gateway to success for at-risk students in a large-group introductory chemistry class, J. Chem. Educ., 78, 252.
Mason D. S., Shell D. F. and Crawley F. E., (1997), Differences in problem-solving by nonscience majors in introductory chemistry on paired algorithmic-conceptual problems, J. Res. Sci. Teach., 34(9), 905–923.
McFate C. and Olmsted III J., (1999), Assessing student preparation through placement tests, J. Chem. Educ., 76, 562.
Meckstroth W. H., (1974), A chemistry course for underprepared students, J. Chem. Educ., 51, 329.
Nakhleh M. B., (1993), Are our students conceptual thinkers or algorithmic problem solvers? J. Chem. Educ., 69, 191.
National Science Board, (2018), Science and Engineering Indicators 2018, Alexandria, VA: National Science Foundation (NSB-2018-1).
National Science Foundation, (2007), Women, Minorities, and Persons with Disabilities in Science and Engineering, Arlington, VA: National Science Foundation, Division of Science Resources Statistics.
Niaz M. and Robinson W. R., (1992), From ‘algorithmic mode’ to ‘conceptual Gestalt’ in understanding the behavior of gases: an epistemological perspective, Res. Sci. Technol. Educ., 10, 53–64.
Ozsogomonyan A., (1979), Predictors of General Chemistry Grades, J. Chem. Educ., 56(3), 173–175.
Pederson L. G., (1975), The Correlation of Partial and Total Scores of the SAT of the College Entrance Examination Board with Grades in Freshman Chemistry, Educ. Psychol. Meas., 35, 509–511.
Pickering M., (1975), Helping the high risk freshman chemist, J. Chem. Educ., 52, 512.
Potgieter M., Ackermann M. and Fletcher L., (2010), Inaccuracy of self-evaluation as additional variable for prediction of students at risk of failing first-year chemistry, Chem. Educ. Res. Pract., 11, 17–24.
Rixse J. S. and Pickering M., (1985), Freshman chemistry as a predictor of future academic success, J. Chem. Educ., 62, 313.
Scott F. J., (2012), Is mathematics to blame? An investigation into high school students’ difficulty in performing calculations in chemistry, Chem. Educ. Res. Pract., 13, 330–336.
Shields S. P., Hogrebe M. C., Spees W. M., Handlin L. B., Noelken G. P., Riley J. M. and Frey R. F., (2012), A transition program for underprepared students in General Chemistry: diagnosis, implementation and evaluation, J. Chem. Educ., 89, 995–1000.
Spencer H. E., (1996), Mathematical SAT test scores and college chemistry grades, J. Chem. Educ., 73, 1150.
Taber K. S., (2013), Revisiting the chemistry triplet: drawing upon the nature of chemical knowledge and the psychology of learning to inform chemistry education, Chem. Educ. Res. Pract., 14(2), 156–168.
Tai R. H., Sadler P. M. and Loehr J. F., (2005), Factors influencing success in introductory college chemistry, J. Res. Sci. Teach., 42, 987–1012.
Tai R. H., Ward R. B. and Sadler P. M., (2006), High School Chemistry Content Background of Introductory College Chemistry Students and Its Association with College Chemistry Grades, J. Chem. Educ., 83, 1703.
Talanquer V., (2009), On Cognitive Constraints and Learning Progressions: the case of “structure of matter”, Int. J. Sci. Educ., 31, 2123–2136.
Tro N. J., (2014), Chemistry: A Molecular Approach, Boston, Columbus: Pearson Education.
Vincent-Ruz P., Binning K., Schunn C. D. and Grabowski J., (2018), The effect of math SAT on women's chemistry competency beliefs, Chem. Educ. Res. Pract., 19, 342–351.
Wagner E. P., Sasser H. and DiBiase W. J., (2002), Predicting students at risk in general chemistry using pre-semester assessments and demographic information, J. Chem. Educ., 79, 749.
Warfa A. R. M., (2015), Using cooperative learning to teach chemistry: a meta-analytic review, J. Chem. Educ., 93(2), 248–255.
Wartell M. A., (1974), Chemistry and the educationally disadvantaged student, J. Chem. Educ., 51, 116.
Witten G. Q., (2005), Designing a mathematics course for chemistry and geology students, Educ. Stud. Math., 58(1), 1–19.
Wright M. and Chorin A., (2000), Mathematics and Science. National Science Foundation Report [online], available at: http://www.nsf.gov/pubs/2000/mps0001/mps0001.txt [accessed 29 March 2018].
Ye L., Oueini R. and Lewis S. E., (2015), Developing and implementing an assessment technique to measure linked concepts, J. Chem. Educ., 92(11), 1807–1812.
Ye L., Shuniak C., Oueini R., Robert J. and Lewis S., (2016), Can they succeed? Exploring at-risk students’ study habits in college general chemistry, Chem. Educ. Res. Pract., 17, 878–892.