Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Optimum catalyst selection over continuous and discrete process variables with a single droplet microfluidic reaction platform†
Lorenz M.
Baumgartner‡
 a,
Connor W.
Coley‡
a,
Connor W.
Coley‡
 a,
Brandon J.
Reizman
a,
Kevin W.
Gao
ab and
Klavs F.
Jensen
a,
Brandon J.
Reizman
a,
Kevin W.
Gao
ab and
Klavs F.
Jensen
 *a
*a
aDepartment of Chemical Engineering, Massachusetts Institute of Technology, 77 Massachusetts Avenue, Cambridge, MA 02139, USA. E-mail: kfjensen@mit.edu
bDepartment of Chemical and Biomolecular Engineering, University of California Berkeley, Berkeley, CA 94702, USA
First published on 11th April 2018
Abstract
A mixed-integer nonlinear program (MINLP) algorithm to optimize catalyst turnover number (TON) and product yield by simultaneously modulating discrete variables—catalyst types—and continuous variables—temperature, residence time, and catalyst loading—was implemented and validated. Several simulated case studies, with and without random measurement error, demonstrate the algorithm's robustness in finding optimal conditions in the presence of side reactions and other complicating nonlinearities. This algorithm was applied to the real-time optimization of a Suzuki–Miyaura cross-coupling reaction in an automated microfluidic reaction platform comprising a liquid handler, an oscillatory flow reactor, and an online LC/MS. The algorithm, based on a combination of branch and bound and adaptive response surface methods, identified experimental conditions that maximize TON subject to a yield constraint from a pool of eight catalyst candidates in just 60 experiments, considerably fewer than a previous version of the algorithm.
1 Introduction
Drug research and development is a complex process that is estimated to require an average of more than 13 years and $1.8 billion to bring a single product to market.1 Because of high attrition rates in the clinical phases, an average of about ten entering preclinical candidates are needed for one successful launch.2 Lead compounds entering the preclinical development phase undergo toxicological and pharmacological characterizations requiring the production of larger material amounts than in earlier discovery stages. The ability to efficiently scale-up compound production from the sub-100 mg scale to the multigram scale is critical to bridge this gap between initial discovery and development. The optimization of reactions conditions to improve target values such as product yield, throughput, or chemical costs is a necessity to do so economically.To increase the likelihood of finding the true global optimum, it is beneficial to consider the synergistic effects of discrete variables, e.g., catalyst identity, and continuous variables, e.g., temperature. However, the inherent combinatorial nature of selecting reaction conditions presents a challenge to the secondary goal of minimizing the material usage and experimental time. For example, Murray et al.3 estimate that when considering multiple discrete and continuous variables, the testing of millions of combinations might be required to exhaustively screen one typical transition metal catalyzed reaction. Fortunately, such an enormous effort is rarely necessary because this “curse of dimensionality” can be mitigated by the use of optimization algorithms. Even without encoding prior chemical knowledge, chemical synthesis can be amenable to standard optimization techniques because response surfaces are often relatively smooth and well-behaved.4
The experimental conditions (“factors”) that influence the optimization objective can be classified as either discrete variables or continuous variables. For the screening of discrete variables like choice of catalyst or solvent, high throughput experimentation (HTE) equipment has been employed.5,6 A typical HTE optimization approach is to carry out a pre-defined screen at one or two temperature settings exploring a large variety of reagent combinations and/or concentration levels. Combinations of different solvents, catalyst ligands, or coupling partners with varying concentrations can be mixed on microtiter plates containing typically up to 1536 wells. These plates can then be incubated for the desired reaction time and temperature before each sample is analyzed, e.g., with rapid UPLC analysis.7 Because experiments are performed in parallel batch reactions, studying the effects of temperature and reaction time requires running a separate plate for each setting, which increases the effort required to run screening experiments prior to scale-up. Often, multiple iterations are performed to improve upon prior results by further studying successful conditions. Recently, HTE has been combined with continuous flow techniques to access more extreme pressure and temperature conditions.8 An alternative approach to discrete variable optimization is the genetic algorithm deployed by Kreutz et al. to evolve a catalyst system for the oxidation of methane.9
The effects of different reaction conditions can be efficiently studied with microfluidic reaction platforms, which generally offer the advantages of ease of automation, reproducibility, and low material consumption.10–12 Continuously operating microfluidic reaction systems are useful tools for studying the effects of continuous variables such as temperature, reaction time, or reagent concentrations. Flow also enables conditions less accessible with conventional batch methods, e.g., operating at elevated pressures and at temperatures above solvents' atmospheric boiling points. However, material and time is lost while waiting for the system to reach steady state, which requires about three residence times as a rule of thumb. Another disadvantage is that continuously-operating systems tend to be less effective at screening discrete variables because reagents are usually delivered by manually primed syringe pumps or single feed HPLC pumps.12,13 This issue can be addressed by performing reactions in droplets separated by a carrier fluid. Acting as continuously mixed micro-batch reactors, individual droplets can have compositions independent of each other allowing the study of different solvents or catalysts. Recently, this approach has enabled the screening of heterogeneous photocatalysts suspended in droplets.14
The integration of all elements into a system that is controlled by a central computer allowing real-time reaction optimization was first demonstrated by Krishnadasan and Brown for the spectral optimization of CdSe quantum dots.15 Over the last decade, this paradigm has been applied to many reaction systems in fine chemical and pharmaceutical synthesis. For example, McMullen and Jensen optimized the yield and the throughput of a Knoevenagel condensation reaction by varying residence time and temperature.16 Holmes et al. optimized the yield of a particular kinase inhibitor through computer control of flow rates, reagent equivalents, and reaction temperature.17 Considering 14 input variables, Houben et al. demonstrated the multitarget optimization of a target particle size and full conversion for a emulsion copolymerization process.18 These and many additional examples are well-reviewed elsewhere.13,19,20
Model-based optimization strategies with continuously operating microfluidic reaction systems allow the efficient scale-up of reactions because the intrinsic kinetic parameters can be determined in the absence of heat and mass transfer limitations. Employing such a strategy, McMullen and Jensen successfully used a kinetic model to optimize and scale-up a Diels–Alder reaction by a factor of 500.21 Several studies have used similar closed-loop optimization strategies for the determination of kinetic parameters.22,23
In the absence of a kinetic model and little prior knowledge of the reaction chemistry, the use of “black box” optimization strategies is very popular. The properties of black box algorithms and their application to real-time optimization platforms are summarized by Reizman and Jensen.13 One of the earliest black box algorithms, the Nelder–Mead simplex method,24 uses a series of evolving simplices (a generalization of triangles or tetrahedrons to higher dimensions) to iteratively select experimental conditions. This local search strategy is simple to implement and does not require the approximation of a gradient, but can have difficulties converging depending on the initialization and how the optimization problem is posed.25 Modified versions of the original Nelder–Mead simplex have been implemented into continuous flow optimization platforms.16,26–29
Another popular black box optimization strategy is the Stable Noisy Optimization by Branch and Fit (SNOBFIT) algorithm, whose implementation is facilitated through the availability of convenient and flexible software packages.30 Combining global and local search by branching and local fits, SNOBFIT selects experimental conditions both around local optima and in unexplored areas of the experimental region. Because of this exploratory behavior, convergence can be slow in the case of reaction systems with smooth and well-behaved response surfaces.16 SNOBFIT has been applied for reaction optimization in several microfluidic optimization systems.15–17,31,32
In comparison to simplex variants or SNOBFIT, gradient based black box optimization can offer faster convergence.16 The implementation into a microfluidic optimization platform has been demonstrated for three variants by Moore and Jensen.33 In order to maximize the objective function value, gradient-based algorithms select conditions along a trajectory. For example, a factorial design surrounding an initial point can be used to estimate the gradient direction in which the objective function increases most rapidly. Though offering fast convergence in the absence of local optima, gradient based methods can be complicated by irregularities in the response surface and experimental noise. Gradient calculation can also require a significant number of experiments, particularly when a large number of factors are considered.
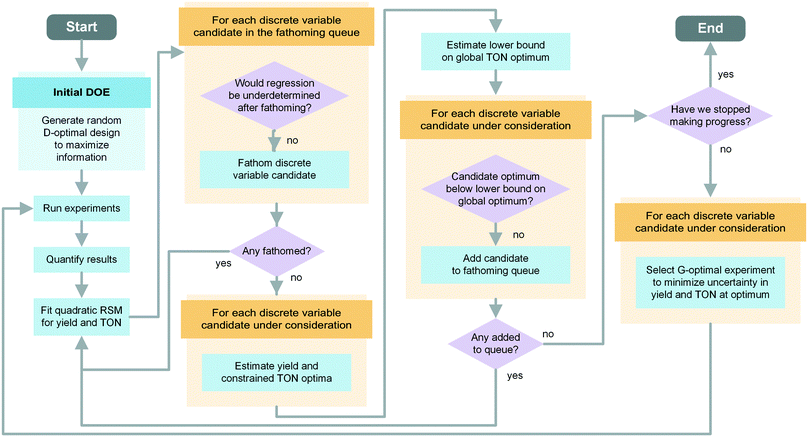
Our group developed an optimization algorithm for the simultaneous optimization of discrete and continuous variables posed as a mixed integer nonlinear programming (MINLP) problem. It is based on sequential adaptive response surface methodology (ARSM) coupled with optimal design of experiments.34 For the experimental implementation, we employed a microfluidic reaction platform equipped with a liquid handler for sequential experimentation in microliter droplets, allowing straightforward and automated manipulation of discrete and continuous variables.34,35 The platform is capable of conducting a broad range of medicinally-relevant chemical reactions including standard C–N and C–C couplings, biphasic reactions and multistep reactions.36 Coley et al. demonstrated that an optimized photocatalytic reaction could be transferred to continuous flow synthesis without measurable loss in performance.37 This shows that conditions determined with this platform are amenable to scale-up with flow synthesis because the heat and mass transfer rates are easier to match in flow than in batch. Experiments are run sequentially and analyzed by online LC/MS. The chromatograms from one experiment can be automatically analyzed and used to inform the conditions of the next experiment. This closed-loop optimization has previously been demonstrated for the simultaneous optimization over temperature, residence time, reagent concentration, and one discrete variable: (a) solvent type in an alkylation reaction35 and (b) catalyst type in several Suzuki–Miyaura reactions.34
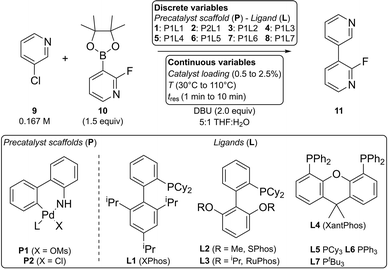
In this paper we present a new version of that MINLP optimization algorithm which exhibits significantly faster convergence. We validate its performance by maximizing catalyst turnover number (TON) subject to a minimum reaction yield constraint by varying temperature, residence time, catalyst concentration, and catalyst identity in simulated and experimental case studies. For experimental validation, we select an exemplary Suzuki–Miyaura cross-coupling reaction due to its important role in organic synthesis as a C–C bond forming reaction.39–41 In the last decade, it has been become more popular to perform cross-coupling reactions in flow using homogeneous catalysts.42,43 The development of dialkylbiarylphosphine ligands and palladacycle precatalysts has enabled the coupling of more difficult substrates44 and the utilization of unstable boronic acids,45,46 respectively. However, because the relationships between reaction parameters are usually complicated, empirical optimization—using a few pre-defined conditions and selecting the best—is commonly employed.34 Here, we combine our automated reaction platform and new MINLP algorithm to demonstrate the closed-loop optimization of the Suzuki–Miyaura cross-coupling of 3-chloropyridine and 2-fluoropyridine-3-boronic acid pinacol ester. The new algorithm has also been successfully applied to the optimization of a photocatalytic decarboxylative coupling, described in a separate publication.38
2 Methods
2.1 Optimization algorithm
We explain the optimization approach and its execution with our new algorithm. The re-derivation of a quadratic response surface model suitable for approximating the kinetics of a general bi-molecular reaction is provided in the ESI.†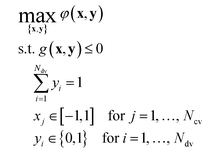 | (1) |
In the simulated and experimental demonstrations, we select catalyst TON (efficient use of catalyst) as the primary optimization objective while ensuring that the yield exceeds a certain minimum product yield (efficient reagent use, simpler purification). For a general bi-molecular reaction A + B → R catalyzed by a transition metal complex with concentration Ccat, the objective function can be defined by eqn (2) assuming a closed system with a constant reaction volume. The product yield is calculated based on the initial concentration of A, CA0 with eqn (3).
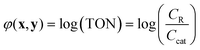 | (2) |
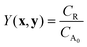 | (3) |
The nonlinear constraint function g(x,y) ≤ 0 is defined by eqn (4).
| g(x,y) = log(γ·Y*) − log(Y(x,y)) | (4) |
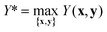 | (5) |
The parameter γ can take values in the range [0,1] and defines the trade-off between the importance of TON and product yield Y. For instance, if γ = 0.9, the optimum condition is required to have at least 90% of the maximum yield Y*. The global optimum yield Y* is estimated by solving eqn (5) subject to the same constraints on x and y as eqn (1).
In the absence of a physical model describing the system behavior, it is common to approximate continuous variable effects using a response surface methodology (RSM) introduced by Box and Hunter.47 In the simplest case, a fractional or full-factorial design of experiments is used to generate data, which is then regressed using a simple linear or quadratic model to estimate the relationships between continuous experimental factors and identify optimal experimental regions. To rapidly optimize more complex systems, Box introduced sequential RSM,48 which involves constructing a response surface model around a proposed optimum, testing the optimum experimentally, and updating the model iteratively. Further improvement is offered by coupling sequential RSM with adaptive RSM (ARSM), which splits the experimental space into subregions. Regional optima are compared against a common threshold to determine whether subregions can be disregarded in the optimum search.49,50 Convergence of ARSM can be accelerated by using more efficient optimal design of experiments51 instead of standard designs such as central composite52 or Box Behnken.53 To solve a MINLP problem with both continuous and discrete variables (as in eqn (1)), sequential ARSM can be integrated with a global search strategy such as branch and bound (B&B).54,55
In our optimization problem, the branches of the search tree represent specific discrete variable choices selected from a pool of possible candidates (e.g., a set of catalyst types). To gradually reduce the number of discrete variables under consideration, the algorithm tries to “fathom” poor-performing branches. To determine whether a candidate is performing far enough below the estimated optimum to disregard it, we use a response surface model to estimate the constrained objective function optimum for each discrete variable choice in the pool. Next, we select the discrete variable choice that provides the highest objective function value as the global optimum and estimate its uncertainty based on the overall model goodness of fit. We fathom a branch from the optimization problem if its estimated optimum is smaller than the lower bound on the global optimum. Updating the response surface model and fathoming branches of the tree after each batch of experiments allows us to focus experimental effort on conditions that are more likely to be close to the global optimum.
In the initialization phase, the algorithm selects a D-optimal design with diversified factor settings to carry out an efficient initial scan of the variable space. For this purpose, an evenly spaced 11-level full factorial design with all discrete variable combinations is generated. From this pool of experimental settings the algorithm picks a set of Nparam + Nextra experiments using a D-optimality criterion. This results in a selection of diversified settings that maximize the information that can be extracted from a set of experiments, as measured by the determinant of the Fisher information matrix. Although only Nparam experiments would be necessary to fit the Nparam parameters of the response surface model, including Nextra additional experiments provides a more reliable fit and enables uncertainty quantification. The experiments are carried out in a randomized order and evaluated.
After entering the refinement phase, the response surface model parameters are fitted using a weighted least squares regression, with weights equal to each experiment's HPLC yield. The algorithm uses the two models – one for TON and one for yield – to predict the yield optimum and constrained TON optimum for every discrete variable candidate. The best results from all of the observed discrete variable candidates constitute the global optima. Next, the optimization proceeds by determining one new G-optimal experiment per discrete variable candidate; G-optimality is defined to minimize the uncertainty of the model at the predicted global yield and TON optima. These experiments are run and the response surface models are regressed.
Starting with the second iteration of the refinement phase, the algorithm checks if discrete variable candidates can be added to the initially empty fathoming queue. The fathoming queue contains the discrete variables that have been removed from the pool of candidates considered for new experiments and are waiting to be removed from the model. The associated experiments are still used to fit the response surface until the candidate is fathomed. To determine whether any discrete variables should be added to the fathoming queue, a hypothesis test is performed for each candidate. The lower bound of the 99% confidence interval of the global optimum is estimated using a two-sided t-test. If the predicted constrained optimum TON of a discrete variable is below this lower bound, the data suggest that it is unlikely for that discrete variable to be used under the optimal conditions. The algorithm adds that candidate to the fathoming queue and returns to the beginning of the loop to re-fit the response surfaces.
After updating the response surfaces, the algorithm checks if any candidates from the fathoming queue can be removed (in the order of addition). This is necessary to avoid an ill-posed regression, as removing discrete variables will decrease both the number of fitting parameters and the number of data points used for fitting. To do so, the algorithm constructs a proposed experimental design matrix Xcheck and calculates its pseudorank using a finite tolerance (e.g., 0.02) to reflect the fact that experiments with highly similar conditions should be considered identical if they are similar to within physical precision. If the calculated pseudorank exceeds the number of fitting parameters by at least one, the discrete variable candidate is fathomed. This means that the discrete variable is no longer considered for further experiments, the corresponding model parameters are removed, and the associated experimental data are no longer used to fit the models. After the fathoming of a variable, the algorithm returns to the beginning of the loop to fit the new response surfaces. In the case that no variables were fathomed, the algorithm proceeds with estimating the constrained TON and yield optima.
If no discrete variable was added to the fathoming queue after the hypothesis test, the optimization procedure checks the convergence criterion. Convergence is satisfied when a certain number of iterations have elapsed (e.g., 4) without making progress, where progress is defined by an improvement in the experimental constrained TON optimum (e.g., of at least 1%). Every time a discrete variable candidate is sent to the fathoming queue or is fathomed, the countdown is reset. If this criterion is not satisfied, then the algorithm proposes the next set of G-optimal experiments and waits for them to be executed and analyzed.
2.2 Simulation of coupling reaction test cases
We first assess the algorithm's performance by applying it to simulated reaction data. For this purpose, the five simulation cases employed by Reizman56 were used to characterize the convergence behavior and robustness in finding the global optimum. This analysis provides insight into how the semi-empirical quadratic model accounts for unknown effects, such as the influence of side reactions, catalyst deactivation, and experimental noise.Using the catalyst concentration Ccat, the temperature T, the reaction time tres and the catalyst type i as input variables, the resulting product concentrations of the five simulation cases were calculated with rate equations according to Scheme 1.
 | ||
| Scheme 1 Simulation cases. The robustness of the algorithm was assessed against the presence of two global optima, side reactions, and catalyst deactivation at higher temperatures. | ||
For all simulation cases, the initial reagent concentrations were kept constant at CA0 = 0.167 M and CB0 = 0.250 M. The kinetic constant for the product formation was defined by AR = 3.1 × 107 L1/2 mol−3/2 s−1 and EAR = 55 kJ mol−1. An overview of each catalyst's effect on the activation energy EAi is given in Table 1.
| Catalyst | Case 1 | Case 2 | Case 3/4 | Case 5 |
|---|---|---|---|---|
| 1 (T < 80 °C) | 0 | 0 | 0 | −5.0 |
| 1 (T ≥ 80 °C) | 0 | 0 | 0 | −5.0 + 0.3 (T − 80) |
| 2 | 0.3 | 0 | 0.3 | 0.7 |
| 3 | 0.3 | 0.3 | 0.3 | 0.7 |
| 4 | 0.7 | 0.7 | 0.7 | 0.7 |
| 5 | 0.7 | 0.7 | 0.7 | 0.7 |
| 6 | 2.2 | 2.2 | 2.2 | 2.2 |
| 7 | 3.8 | 3.8 | 3.8 | 3.8 |
| 8 | 7.3 | 7.3 | 7.3 | 7.3 |
Simulation case 1 represents the basic bi-molecular reaction A + B → R. Catalyst 1 has the lowest activation energy posing the best choice out of the eight catalyst candidates. Test case 2 introduces a challenge to the search by also setting EA2 to the lowest value, resulting in a response surface with two equivalent global optima. Simulation case 3 is used to study the effect of the competing side reaction B → S1 yielding the undesired side product S1. This can occur, for instance, in the case of a temperature activated deboronation of boronic acids employed in Suzuki–Miyaura reactions.57 The dependence on higher temperatures is reflected by the relatively high activation energy of EAS1 = 100 kJ mol−1. In test case 4, we add the consecutive reaction B + R → S2 to form the undesired side product S2, which could represent over addition. Case 5 simulates the same reaction as the first case, but the ideal catalyst is subject to deactivation at temperatures exceeding 80 °C.
The algorithm and the simulated reaction cases were implemented in Matlab. Using eight catalysts candidates as discrete variables, the continuous variable space was defined with a temperature range of 30 °C to 110 °C and a reaction time in the range of 1 min to 10 min. Further, the catalyst concentration was varied from 0.835 mM to 4.175 mM which corresponds to a molar concentration of 0.5 mol% to 2.5 mol% with respect to the limiting reagent A concentration. The D-optimal design of the initialization phase was carried out with Nexp = Nparam + Nextra = 24 + 3 = 27. The yield criterion γ of the constraint function (eqn (4)) was set to 0.9, 0.95 and 0.98 for different runs. The algorithm was set to be terminated after four iterations without improvement using a critical improvement percentage of 1%. The effect of noise was simulated by increasing or decreasing the product concentration determined with the kinetic equations by a random, uniformly distributed percentage with an extrema of ±0.5%, ±1.0%, and ±2.0%. This reflects the experimental uncertainty that may be introduced during quantification. We perform ten simulated optimization runs for each test case and algorithm setting.
2.3 Experimental validation with a Suzuki–Miyaura coupling
To validate the new optimization algorithm in practice, we demonstrate the optimization of a Suzuki–Miyaura cross-coupling reaction for the conditions summarized in Scheme 2.The yield criterion was set to γ = 0.9 to prioritize TON optimization at the expense of yield. To provide greater confidence that the true optimum would be found, the number of extra experiments was conservatively increased from 3 to 15. A critical improvement percentage of 1% and a number of six iterations without improvement were selected as convergence criteria.
Individual stock solutions of the eight precatalyst combinations 1–8, 3-chloropyridine 9 with naphthalene as an internal standard and the boronic acid ester 10 were prepared in THF under nitrogen atmosphere. Together with vials containing the pure solvents water and THF, solutions were placed in the liquid handler (Gilson GX-241) rack under argon atmosphere during the optimization run. Glass syringes used for online injection of base and quench solutions were primed and mounted on the syringe pumps (Harvard Apparatus PHD Ultra). Protocols of stock solution preparation are provided in the ESI.†
The optimization campaign was carried out with a slightly modified version of the fully automated microfluidic reaction platform used by Coley et al.37 Matlab (The MathWorks, Inc., ver. R2016a) and Labview (National Instruments, ver. 16.0f2) were used to control all hardware and execute the optimization routine. A list of components, a detailed flow chart, and protocols for the system operation are provided in the ESI.†
The liquid handler prepares a reaction mixture of 40 μL by aspirating and mixing the five components by agitation inside the needle. The mixed solution is subsequently injected into a 15 μL sample loop. Before every reaction, four 15 μL THF rinse droplets are injected upstream of the liquid handler injection module and pushed through the system by the carrier gas syringe. After completion of the rinse process, the valve position is switched in order to transfer the droplet into the system. The droplet is moved to the reactor inlet T-junction where a base solution volume of 3.5 μL is injected, resulting in a DBU concentration of 0.333 M (2 equiv.) and a 5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ratio of THF
1 ratio of THF![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) water by volume. Next, the droplet is oscillated inside the reactor for the desired residence time range of 1 min to 10 min. A photodetector is used to reverse the direction of the carrier gas flow every time the liquid phase reaches the reactor inlet or outlet. The system is pressurized with 6.9 bar (100 psig) positive pressure using nitrogen. Controlled by two cartridge heaters and a fan, the reactor temperature is set between 30 °C and 110 °C. In order to stop the reaction, a quench solution consisting of a 1
water by volume. Next, the droplet is oscillated inside the reactor for the desired residence time range of 1 min to 10 min. A photodetector is used to reverse the direction of the carrier gas flow every time the liquid phase reaches the reactor inlet or outlet. The system is pressurized with 6.9 bar (100 psig) positive pressure using nitrogen. Controlled by two cartridge heaters and a fan, the reactor temperature is set between 30 °C and 110 °C. In order to stop the reaction, a quench solution consisting of a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 mixture of water
1 mixture of water![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) acetone by volume is injected at the reactor outlet. Using a second 6-way valve, the droplet in the 1.7 μL sample loop is partially transferred to the LC/MS system. The analysis is performed with a reversed-phase column using a UV detector for quantitative analysis and a mass spectrometer for mass verification. Automatically integrated peak areas are written to an Excel sheet and imported using Matlab. Details about the calibration method are available in the ESI.†
acetone by volume is injected at the reactor outlet. Using a second 6-way valve, the droplet in the 1.7 μL sample loop is partially transferred to the LC/MS system. The analysis is performed with a reversed-phase column using a UV detector for quantitative analysis and a mass spectrometer for mass verification. Automatically integrated peak areas are written to an Excel sheet and imported using Matlab. Details about the calibration method are available in the ESI.†
We conducted a second campaign for the same reaction using the previous MINLP algorithm and the experimental procedure for Suzuki–Miyaura cross-coupling optimization published by Reizman et al.34
3 Results and discussion
We discuss the simulation and experimental results of the algorithm introduced in this paper (MINLP 2) and compare them to results obtained with the previous algorithm (MINLP 1) published by Reizman et al.34 Detailed results are available in the ESI.†3.1 Simulation results
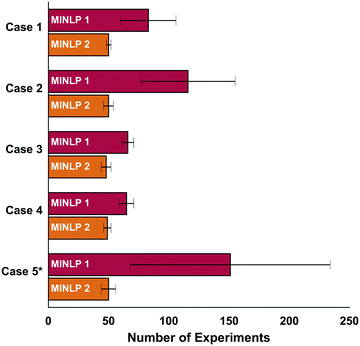
The new optimization algorithm (MINLP 2) determined optimal conditions with about 50 experiments for every case in the absence of noise and for γ = 0.9 (Fig. 2). MINLP 2 required 30% fewer experiments on average than MINLP 1 for the cases 1, 3 and 4. For the simulation cases 2 and 5 the number of experiments is 60% lower on average.The initialization phase of MINLP 1 is comprised of two fractional factorial designs amounting to 32 experiments. In comparison, the algorithm MINLP 2 uses a D-optimal design with 27 experiments allowing it to enter the refinement phase with fewer experiments. This permits the algorithm to utilize the experimental results by fitting the model and directing the search towards the optimum at an earlier point in the optimization run.
In addition, the slower convergence of MINLP 1 can be attributed in large part to the different fathoming procedure. In contrast to the algorithm presented in this paper, MINLP 1 fits the model to the entire data set including experiments from already-fathomed variables. However, poorly performing catalysts that have been removed from consideration may not follow the same reactivity trend as high performing catalysts, so their inclusion in the response surface fitting may decrease the accuracy of the model fit. This leads to an artificially high uncertainty at the global optimum and, in turn, to an overly conservative lower bound that slows down fathoming and convergence. This extremely cautious lower bound also explains why MINLP 1 requires a considerably larger number of experiments to converge in the case 5 and 2. For instance, in case 5, temperature affects the candidate catalysts in different ways, so including fathomed candidates in the fit may increase model error. Slow convergence is also observed for case 2 due to the large discrepancy between the two optimal catalysts and the six inferior ones.
Table 2 shows that the average conditions and response values determined with both algorithms match the true global optima for the first two simulation cases very accurately. Both algorithms also identified the correct optima with a slightly lower accuracy in the presence of side reactions in the cases 3 and 4. For simulation case 5, neither algorithm was able to determine the optimal catalyst in more than three out of ten trials and the average conditions and response values do not match the true optimum.
| Optimum | Cat. | T | t res | C cat | Yield | TONa |
|---|---|---|---|---|---|---|
| — | — | [°C] | [min] | [mol%] | [%] | — |
| a TON: average value ± sample standard deviation. b Catalyst 1 selected in 2/10 trials, catalysts 2–5 selected 8/10 trials. c Catalyst 1 selected in 3/10 trials, catalysts 2–5 selected 7/10 trials. | ||||||
| Case 1 | 1 | 110.0 | 10 | 0.500 | 90.4 | 180.7 |
| MINLP 1 | 1 | 110.0 | 10 | 0.500 | 90.4 | 180.9 ± 0.3 |
| MINLP 2 | 1 | 110.0 | 10 | 0.500 | 90.4 | 180.8 ± 0 |
| Case 2 | 1, 2 | 110.0 | 10 | 0.500 | 90.4 | 180.7 |
| MINLP 1 | 1, 2 | 110.0 | 10 | 0.500 | 90.4 | 180.8 ± 0.1 |
| MINLP 2 | 1, 2 | 110.0 | 10 | 0.500 | 90.4 | 180.7 ± 0 |
| Case 3 | 1 | 81.8 | 10 | 1.594 | 55.6 | 34.9 |
| MINLP 1 | 1 | 81.1 | 10 | 1.650 | 55.2 | 33.5 ± 1 |
| MINLP 2 | 1 | 81.5 | 10 | 1.573 | 55.3 | 35.2 ± 0.9 |
| Case 4 | 1 | 110.0 | 2.1 | 1.596 | 38.1 | 23.9 |
| MINLP 1 | 1 | 107.0 | 3.1 | 1.670 | 37.6 | 23.1 ± 2.5 |
| MINLP 2 | 1 | 109.9 | 2.2 | 1.602 | 38.1 | 23.8 ± 0.5 |
| Case 5 | 1 | 80.0 | 10 | 0.500 | 93.8 | 187.6 |
| MINLP 1 | 1b | 104.0 | 10 | 0.604 | 88.6 | 149.4 ± 16 |
| MINLP 2 | 1c | 100.6 | 10 | 0.647 | 90.3 | 147.6 ± 32 |
The quality of the response surface model fit depends on the underlying assumption that the nonlinear effects of temperature are independent of the catalyst candidate. Because this requirement is fulfilled, the kinetic behavior of the simulation cases 1 to 4 can be approximated. In contrast, case 5 violates this assumption because increasing temperatures above 80 °C causes a negative effect on the TON for the first catalyst, but a positive one for the other seven candidates. These adverse effects cannot be captured because the model parameters for nonlinear temperature effects are fitted to data from all catalyst candidates. This results in a poor regression illustrated by the discrepancy between true and predicted optima in Table 2. Optimization in presence of such diverse catalyst behavior would require expanding the model with additional parameters at the cost of more experiments.
The simulation of noise levels 0.0%, 0.5%, 1.0%, and 2.0% with γ = 0.9, 0.95, and 0.98 reveal that the number of experiments required for MINLP 2 to converge remained roughly constant at about 50 experiments. For cases 1 to 4, the algorithm identifies the optimum correctly in 90% of the simulation runs. This share was only 35% for simulation case 5. Failing to identify the optimal catalyst in the majority of runs, the algorithm selected the second best catalyst instead. More detailed information about the noise study are available in the ESI.† These results show that the presence of noise makes it more difficult for the algorithm to identify the true optimum over a range of settings for γ. However, this effect certainly also depends on how easily different catalyst choices can be differentiated relative to the noise level.
We can conclude from the simulation results that an experimental optimization campaign should also converge faster with MINLP 2 compared to MINLP 1. If dependencies between continuous and discrete variables match the assumption of our quadratic model, the algorithm should be able to fit the response surface correctly. As more experiments are performed around the optimum, the response surface fit will be increasingly biased toward this region which, in a small enough neighborhood, is guaranteed to be linear.
3.2 Experimental optimization campaign results
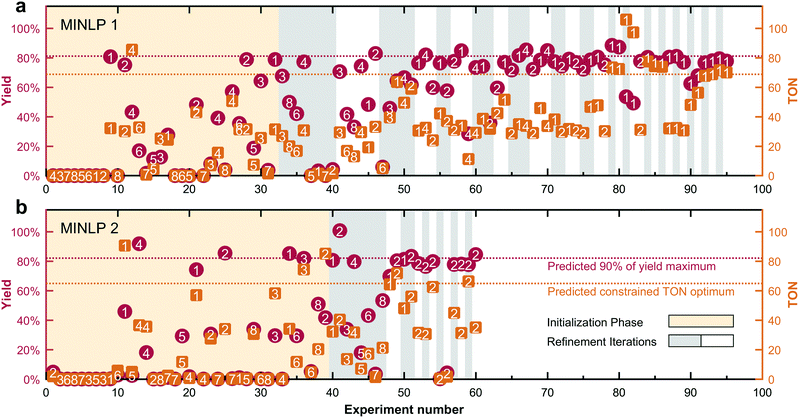
Fig. 3 shows that the significantly faster convergence of MINLP 2 in the simulated test cases extends to the experimental optimization. The optimization of the Suzuki–Miyaura cross-coupling (cf.Scheme 2) only required 60 experiments to converge, equivalent to a reduction of 37% compared to the previous MINLP 1.Each vertical pair of markers indicates the TON (orange square) and yield (red circle) measured by HPLC for each experiment along the x-axis. The algorithms both pick diverse conditions during the initialization phase (orange background). In the subsequent refinement phase (alternating grey/white backgrounds for each iteration), the algorithms converge to their final predictions. The optimum TON and 90% yield threshold predicted by the model are indicated by horizontal dashed lines. Both algorithms narrow the precatalyst–ligand combination pool down to the first two candidates. The refinement phase is significantly faster with MINLP 2, requiring one third as many experiments as MINLP 1. The optimal candidates ultimately chosen by MINLP 1 and MINLP 2 are P1L1 and P2L1, respectively.
The experimental optimization progress (Fig. 3) resembles simulation case 2 in which the presence of two superior and six inferior catalyst candidates lead to a slow convergence of MINLP 1. The data also let us highlight another difference in the fathoming procedures. This is the ability of MINLP 1 to take already fathomed discrete variables back into consideration. For example, candidate 4 is readmitted to the pool in experiment number 60 after having been fathomed two iterations earlier. In combination with the overly conservative lower bound on the global optimum, this feature is most likely responsible for the much larger number of iterations and slower convergence of algorithm MINLP 1 compared to MINLP 2.
Fig. 4 shows the details of the selected experimental conditions. The majority of experiments were conducted using the high performing precatalyst combinations 1 (P1L1) and 2 (P2L1). Product yields above 60% were only recorded for the precatalyst–ligand combinations 1–4. The low number of experiments performed using low-performing catalysts illustrates how the branch and bound approach leads to a more efficient search by disregarding less active discrete variable candidates in the course of the campaign. We can explain the higher activities of ligands L1–L3 because they belong to the family of dialkylbiarylphosphines having enhanced activity for the coupling of heteroaryl chlorides such as 9.44 The higher performance of catalyst combinations with ligand L1 (XPhos) compared to L2 (SPhos), L3 (RuPhos) and L6 (PPh3) matches the results of Bruno et al.46 and Reizman et al.34
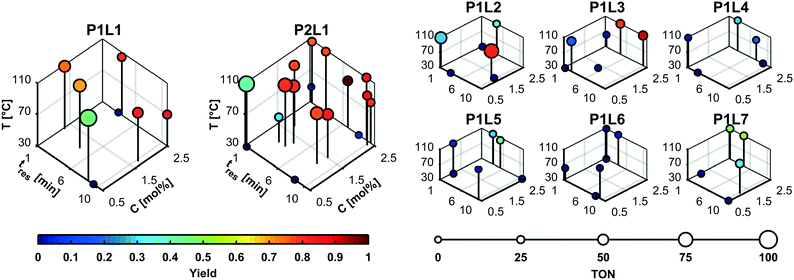 | ||
| Fig. 4 MINLP 2 experimental conditions. The majority of experiments were conducted using the high performing precatalyst combinations P1L1 and P2L1. Detailed data for both algorithms are included in the ESI.† | ||
Although temperatures of 110 °C clearly led to high yield and TON, it is noteworthy that the highest yield was recorded at only 90 °C. This suggests that the competing decay of the boronic acid ester 10 through hydrolysis and subsequent deboronation limits the yield close to the upper temperature limit. Another explanation could be the presence of a secondary reaction consuming the product 11. However, no significant side products were observed by LC/MS to suggest that the coupling product reacted further.
Table 3 shows that the optimal catalyst loadings determined by the two algorithms are quite similar. However, MINLP 2 determined slightly shorter residence times and a lower temperature for the TON optimum with P2L1. The algorithm MINLP 1 selected the other precatalyst but with the same XPhos ligand, P1L1. Because the differences between optima are as small as the sample standard deviations, we can conclude from Table 3 that the validated TONs and yields are equivalent within experimental error. Although the two algorithms chose different catalyst/ligand species, both XPhos precatalysts form the same active catalyst Pd(0)–XPhos under basic conditions. The tendency of P1 to be more stable in solution46 does not seem to offer a noticeable advantage in this reaction. The finding that both optima are equivalent is consistent with the notion that this experimental optimization resembles simulation case 2.
| Optimum | Optimum TON (γ = 0.9) | Maximum yield | ||
|---|---|---|---|---|
| Algorithm | MINLP 1 | MINLP 2 | MINLP 1 | MINLP 2 |
| Catalyst | P1L1 | P2L1 | P1L1 | P2L1 |
| T | 104 °C | 96 °C | 94 °C | 95 °C |
| t res | 10 min | 7.9 min | 10 min | 8.5 min |
| C cat | 1.2 mol% | 1.3 mol% | 2.3 mol% | 2.5 mol% |
| Model prediction and 99% confidence interval | ||||
|---|---|---|---|---|
| Yield | 81% | 82% | 90% | 91% |
| 99% | [78%, 84%] | [68%, 87%] | [86%, 95%] | [78%, 107%] |
| TON | 69 | 65 | 38 | 36 |
| 99% | [66, 71] | [54, 78] | [36, 40] | [31, 43] |
| Validated average and sample standard deviation (5 repeats) | ||||
|---|---|---|---|---|
| Yield | 88% ± 2% | 90% ± 1% | 91% ± 3% | 92% ± 2% |
| TON | 73 ± 2 | 70 ± 1 | 40 ± 1 | 37 ± 1 |
4 Conclusion
The mixed integer nonlinear program algorithm introduced by this paper was used to optimize the catalyst turnover number with a nonlinear constraint on the product yield by selecting one out of eight discrete catalyst candidates and manipulating the three continuous process variables temperature, residence time, and catalyst concentration. Our optimization strategy uses sequential adaptive response surface methodology in combination with optimal design of experiments and the global search strategy branch and bound. For this purpose, the kinetic behavior of a general bi-molecular reaction is approximated with a semi-empirical quadratic response surface model derived using a power law approach. Updating the response surface model and disregarding less active catalyst candidates after every batch of experiments allows us to focus experimental effort on conditions that are more likely to be close to the global optimum.Several simulation cases demonstrated the algorithm's robustness in finding the global optimum in presence of side reactions, experimental noise, and two equivalent global optima while exhibiting a distinctly faster convergence behavior in comparison to our previous algorithm. The experimental optimization of a Suzuki–Miyaura cross-coupling reaction was conducted with an automated reaction platform using 40 μL reaction solution per experimental setting. In agreement with our simulation study, our algorithm required only 60 experiments to determine optimum conditions, which amounts to a 37% reduction compared to the previous version.
Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
We thank the Novartis Center for Continuous Manufacturing for funding this research. We thank Hsiao-Wu Hsieh at Novartis (NIBR) for analytical chemistry support and Yiming Wang at the Buchwald Research Group at MIT for the catalyst synthesis. C. W. C. thanks the National Science Foundation Graduate Research Fellowship Program for support under Grant No. 1122374.References
- S. M. Paul, D. S. Mytelka, C. T. Dunwiddie, C. C. Persinger, B. H. Munos, S. R. Lindborg and A. L. Schacht, Nat. Rev. Drug Discovery, 2010, 9, 203 CrossRef CAS PubMed.
- J. P. Hughes, S. Rees, S. B. Kalindjian and K. L. Philpott, Br. J. Pharmacol., 2011, 162, 1239–1249 CrossRef CAS PubMed.
- P. M. Murray, S. N. Tyler and J. D. Moseley, Org. Process Res. Dev., 2013, 17, 40–46 CrossRef CAS.
- K. W. Moore, A. Pechen, X.-J. Feng, J. Dominy, V. J. Beltrani and H. Rabitz, Phys. Chem. Chem. Phys., 2011, 13, 10048–10070 RSC.
- J. R. Schmink, A. Bellomo and S. Berritt, Aldrichimica Acta, 2013, 46, 71–80 Search PubMed.
- A. B. Santanilla, E. L. Regalado, T. Pereira, M. Shevlin, K. Bateman, L.-C. Campeau, J. Schneeweis, S. Berritt, Z.-C. Shi, P. Nantermet, Y. Liu, R. Helmy, C. J. Welch, P. Vachal, I. W. Davies, T. Cernak and S. D. Dreher, Science, 2015, 347, 49–53 CrossRef PubMed.
- C. J. Welch, X. Gong, W. Schafer, E. C. Pratt, T. Brkovic, Z. Pirzada, J. F. Cuff and B. Kosjek, Tetrahedron: Asymmetry, 2010, 21, 1674–1681 CrossRef CAS.
- D. Perera, J. W. Tucker, S. Brahmbhatt, C. J. Helal, A. Chong, W. Farrell, P. Richardson and N. W. Sach, Science, 2018, 359, 429–434 CrossRef CAS PubMed.
- J. E. Kreutz, A. Shukhaev, W. Du, S. Druskin, O. Daugulis and R. F. Ismagilov, J. Am. Chem. Soc., 2010, 132, 3128–3132 CrossRef CAS PubMed.
- R. L. Hartman, J. P. McMullen and K. F. Jensen, Angew. Chem., Int. Ed., 2011, 50, 7502–7519 CrossRef CAS PubMed.
- K. F. Jensen, AIChE J., 2017, 63, 858–869 CrossRef CAS.
- M. B. Plutschack, B. Pieber, K. Gilmore and P. H. Seeberger, Chem. Rev., 2017, 117(18), 11796–11893 CrossRef CAS PubMed.
- B. J. Reizman and K. F. Jensen, Acc. Chem. Res., 2016, 49, 1786–1796 CrossRef CAS PubMed.
- B. Pieber, M. Shalom, M. Antonietti, P. H. Seeberger and K. Gilmore, Angew. Chem., Int. Ed. DOI:10.1002/anie.201712568.
- S. Krishnadasan, R. J. C. Brown, A. J. deMello and J. C. deMello, Lab Chip, 2007, 7, 1434–1441 RSC.
- J. P. McMullen and K. F. Jensen, Org. Process Res. Dev., 2010, 14, 1169–1176 CrossRef CAS.
- N. Holmes, G. R. Akien, A. J. Blacker, R. L. Woodward, R. E. Meadows and R. A. Bourne, React. Chem. Eng., 2016, 1, 366–371 CAS.
- C. Houben, N. Peremezhney, A. Zubov, J. Kosek and A. A. Lapkin, Org. Process Res. Dev., 2015, 19, 1049–1053 CrossRef CAS PubMed.
- V. Sans and L. Cronin, Chem. Soc. Rev., 2016, 45, 2032–2043 RSC.
- D. Fabry, E. Sugiono and M. Rueping, React. Chem. Eng., 2016, 1, 129–133 CAS.
- J. P. McMullen and K. F. Jensen, Org. Process Res. Dev., 2011, 15, 398–407 CrossRef CAS.
- J. S. Moore and K. F. Jensen, Angew. Chem., Int. Ed., 2014, 53, 470–473 CrossRef CAS PubMed.
- K. C. Aroh and K. F. Jensen, React. Chem. Eng., 2018, 3, 94–101 CAS.
- J. A. Nelder and R. Mead, Comput. J., 1965, 7, 308–313 CrossRef.
- M. H. Wright, Pitman Res. Notes Math. Ser., 1996, 191–208 Search PubMed.
- J. P. McMullen, M. T. Stone, S. L. Buchwald and K. F. Jensen, Angew. Chem., 2010, 122, 7230–7234 CrossRef.
- A. J. Parrott, R. A. Bourne, G. R. Akien, D. J. Irvine and M. Poliakoff, Angew. Chem., Int. Ed., 2011, 50, 3788–3792 CrossRef CAS PubMed.
- V. Sans, L. Porwol, V. Dragone and L. Cronin, Chem. Sci., 2015, 6, 1258–1264 RSC.
- D. Cortés-Borda, K. V. Kutonova, C. Jamet, M. E. Trusova, F. Zammattio, C. Truchet, M. Rodriguez-Zubiri and F.-X. Felpin, Org. Process Res. Dev., 2016, 20, 1979–1987 CrossRef.
- W. Huyer and A. Neumaier, ACM Trans. Math. Softw., 2008, 35, 9 CrossRef.
- R. A. Skilton, A. J. Parrott, M. W. George, M. Poliakoff and R. A. Bourne, Appl. Spectrosc., 2013, 67, 1127–1131 CrossRef CAS PubMed.
- N. Holmes, G. R. Akien, R. J. D. Savage, A. J. Blacker, B. A. Taylor, R. L. Woodward, R. E. Meadowse and R. A. Bourne, React. Chem. Eng., 2016, 1, 96–100 CAS.
- J. S. Moore and K. F. Jensen, Org. Process Res. Dev., 2012, 16, 1409–1415 CrossRef CAS.
- B. J. Reizman, Y.-M. Wang, S. L. Buchwald and K. F. Jensen, React. Chem. Eng., 2016, 1, 658–666 CAS.
- B. J. Reizman and K. F. Jensen, Chem. Commun., 2015, 51, 13290–13293 RSC.
- Y.-J. Hwang, C. W. Coley, M. Abolhasani, A. L. Marzinzik, G. Koch, C. Spanka, H. Lehmann and K. F. Jensen, Chem. Commun., 2017, 53, 6649–6652 RSC.
- C. W. Coley, M. Abolhasani, H. Lin and K. F. Jensen, Angew. Chem., 2017, 129, 9979–9982 CrossRef.
- H.-W. Hsieh, C. W. Coley, L. M. Baumgartner, K. F. Jensen and R. I. Robinson, Org. Process Res. Dev., 2018 DOI:10.1021/acs.oprd.8b00018.
- A. Suzuki, Angew. Chem., Int. Ed., 2011, 50, 6722–6737 CrossRef CAS PubMed.
- N. Schneider, D. M. Lowe, R. A. Sayle, M. A. Tarselli and G. A. Landrum, J. Med. Chem., 2016, 59, 4385–4402 CrossRef CAS PubMed.
- A. Bruneau, M. Roche, M. Alami and S. Messaoudi, ACS Catal., 2015, 5, 1386–1396 CrossRef CAS.
- T. Noel and S. L. Buchwald, Chem. Soc. Rev., 2011, 40, 5010–5029 RSC.
- D. Cantillo and C. O. Kappe, ChemCatChem, 2014, 6, 3286–3305 CrossRef CAS.
- R. Martin and S. L. Buchwald, Acc. Chem. Res., 2008, 41, 1461–1473 CrossRef CAS PubMed.
- T. Kinzel, Y. Zhang and S. L. Buchwald, J. Am. Chem. Soc., 2010, 132, 14073–14075 CrossRef CAS PubMed.
- N. C. Bruno, M. T. Tudge and S. L. Buchwald, Chem. Sci., 2013, 4, 916–920 RSC.
- G. E. Box and J. S. Hunter, Ann. Math. Stat., 1957, 195–241 CrossRef.
- G. E. Box, J. R. Stat. Soc. Ser. C Appl. Stat., 1957, 6, 81–101 Search PubMed.
- G. G. Wang, Z. Dong and P. Aitchison, Eng. Optim., 2001, 33, 707–733 CrossRef.
- G. G. Wang, J. Mech. Des. N. Y., 2003, 125, 210–220 CrossRef.
- A. Alaeddini, A. Murat, K. Yang and B. Ankenman, Qual. Reliab. Eng. Int., 2013, 29, 799–817 CrossRef.
- G. E. Box and K. Wilson, in On the Experimental Attainment of Optimum Conditions, Springer, 1992, pp. 270–310 Search PubMed.
- G. E. Box and D. W. Behnken, Technometrics, 1960, 2, 455–475 CrossRef.
- P. Belotti, C. Kirches, S. Leyffer, J. Linderoth, J. Luedtke and A. Mahajan, Acta Numer., 2013, 22, 1–131 CrossRef.
- C. A. Floudas and C. E. Gounaris, J. Glob. Optim., 2009, 45, 3–38 CrossRef.
- B. J. Reizman, PhD Thesis, Massachusetts Institute of Technology, 2015 Search PubMed.
- N. Miyaura and A. Suzuki, Chem. Rev., 1995, 95, 2457–2483 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available: Details of the experimental setup, simulation and experimental data, and analytical methods. See DOI: 10.1039/c8re00032h |
| ‡ These authors contributed equally to this work. |
| This journal is © The Royal Society of Chemistry 2018 |