A hierarchical approach to chemical reactor engineering: an application to micro packed bed reactors†
Stefano
Rebughini‡
 ab,
Mauro
Bracconi‡
ab,
Mauro
Bracconi‡
 a,
Anthony G.
Dixon
a,
Anthony G.
Dixon
 *b and
Matteo
Maestri
*b and
Matteo
Maestri
 *a
*a
aLaboratory of Catalysis and Catalytic Processes, Dipartimento di Energia, Politecnico di Milano, via La Masa 34, 20156, Milano, Italy. E-mail: matteo.maestri@polimi.it
bDepartment of Chemical Engineering, Worcester Polytechnic Institute, Worcester, MA, 01609 USA. E-mail: agdixon@wpi.edu
First published on 8th January 2018
Abstract
Hierarchical modeling is applied for the investigation of micro packed bed reactors. This method allows for the use of Computational Fluid Dynamics (CFD) simulations in the analysis of representative complex geometries, where a full-scale CFD simulation of the entire reactor is not possible. Detailed and computationally demanding analyses are used to study a selected number of conditions and phenomena. Then, lumped parameters are derived from CFD results by means of engineering correlations. These parameters are incorporated in simplified reactor models based on macroscopic conservation equations. We provide evidence for the potential of the approach by using as a show-case a micro packed bed reactor in the context of highly exothermic selective oxidation processes. This reactor configuration consists of catalytic particles packed in the channels of a honeycomb matrix, which is expected to strongly enhance the radial heat transfer. In particular, we first focus on the analysis of energy transfer mechanisms by CFD and their interpretation via a 1D model and we provide an assessment of existing correlations with respect to the unconventional configuration (2 mm channel equivalent diameter and 0.8 mm sphere diameter). These correlations are then implemented in a pseudo-continuous (i.e. macroscopic) 2D model to allow for a systematic investigation of the capabilities of the micro packed bed reactor in dealing with the selective oxidation of o-xylene to phthalic anhydride. We found that due to the enhanced radial heat transfer micro packed bed reactors allow for quasi-isothermal operations, thus extending the range of operating conditions possible without occurring in adverse thermal behavior of the reactor. On a more general basis, we prove that the hierarchical approach to chemical reactor engineering is an effective tool to bring the application of fundamental modeling at a level of complexity relevant to full-scale applications, otherwise not possible because of the impractical computational costs.
1. Introduction
Fundamental multiscale modeling is considered as a promising numerical methodology to design and investigate the novel reactor technologies.1 However, in the case of complex reactor geometries (e.g. micro packed bed reactors), its application is hampered by the high and unaffordable computational cost. In fact, the complexity of the geometry and the accurate description of the transport phenomena require a very detailed computational domain, which leads to an enormous number of cells. As a result, the analysis and design of these reactors is still based on conventional reactor models, based on macroscopic balance equations of mass, energy and momentum (e.g. 2D pseudo-homogeneous, 1D heterogeneous).2 On one hand, the solutions of these macroscopic models are computationally accessible. On the other hand, they strongly rely on lumped parameters and empirical correlations for the description of the transport phenomena occurring in the reactor. This description is not directly related to physically accessible phenomena and is often based on an experimental investigation for specific operating conditions. The application of these correlations (typically developed for conventional and well-established reactor geometries) would require dedicated experimentations to assess their reliability for novel reactor configurations.In previous work,3 Maestri and co-workers proposed a hierarchical modeling approach as an effective route to overcome this problem, thus enabling a practical implementation of the fundamental multiscale modeling approach. It consists of using detailed computationally demanding methods – based on computational fluid dynamics simulations (CFD) of the reactor geometry – to first study a selected and limited number of conditions. Then, CFD analysis is used for the derivation of lumped parameters and correlations to be adopted in macroscopic reactor modeling. In particular this approach has been successfully applied to assess the application of gas-to-solid heat and mass transport correlations derived for packed beds in the context of micro packed bed reactors.3 In this work, we extend the application of the hierarchical approach to the full-scale simulation of a micro-channel packed bed reactor with external heat transport in order to rate its performance with respect to that of a traditional multi-tubular reactor.
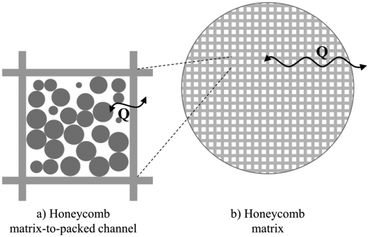
A micro packed bed reactor is a configuration suggested by Vervloet et al.4 to enhance the heat transfer properties of a conventional packed bed reactor and to increase the catalytic load per reactor volume of a structured reactor (e.g., honeycomb reactor).
Fig. 1 shows the schematic representation of this reactor configuration, which consists of small spherical catalytic particles packed into the channel of a metallic honeycomb matrix.5 The advantage of this reactor configuration would be two-fold. On one side, the honeycomb matrix is expected to show the enhanced heat transfer performance.6 In fact, as demonstrated by Groppi and Tronconi,7 the metallic connected solid matrix allows for quasi-isothermal operation of highly exothermic processes (e.g. oxidation of methanol to formaldehyde and epoxidation of ethylene) because of the improved effective radial conductivity. On the other side, the catalyst load per reactor volume is similar to conventional packed bed reactors. Indeed, the overall load of active catalyst per unit reactor volume in a micro packed bed reactor is 0.3–0.4 v/v, which is more similar to typical catalytic loads of industrial packed bed reactors (0.4–0.5 v/v) than those of structured reactors (typically ∼0.1 v/v for honeycomb reactors). As such, this reactor configuration, in principle, could enable quasi-isothermal operation of selective oxidation reactions while keeping a catalytic load per reactor volume similar to conventional packed bed reactors. Here, we first extend the previous analysis3 used for particle-to-gas energy and mass transport, to the assessment of existing correlations for the description of the external heat transfer phenomena. All these hierarchically derived correlations are then implemented in a steady-state pseudo-continuous 2D model for the full-scale simulation of the micro packed bed reactor. This hierarchical model, which is less computationally demanding than CFD simulations, is then used to investigate the performances of the reactor configuration for the selective oxidation of o-xylene to phthalic anhydride.2
This study demonstrates how the hierarchical modeling approach can be applied to investigate in detail the capabilities of novel reactor geometries, by enabling the use of CFD insights at a level of complexity otherwise not accessible because of the unbearable computational cost. It also proves that CFD can be employed to assess and screen existing correlations, thus enabling a rational derivation or selection of the most adequate one with respect to the particular set of operating conditions and reactor geometry. In particular, a CFD resolved-particle model of a single packed channel of a micro packed bed reactor is used to provide simulations of heat transfer, against which existing heat transfer correlations are evaluated using a 1D heat transfer model. The best results are then incorporated into a 2D effective continuum reactor model for o-xylene partial oxidation to phthalic anhydride.
2. Methods and models
In this section, we present the models used to hierarchically analyze micro packed bed reactors. In particular, we present the CFD model used to analyze the heat transfer phenomena and the 1D model used to interpret the CFD results. We also report the 2D model of the micro packed bed reactor. Details on the notation are reported in the ESI† (section 2).2.1. Multi-region computational fluid dynamics
The CFD simulations are performed by using the chtMultiRegionSimpleFoam solver available in the OpenFOAM framework,8 modeling the transport of heat and momentum in the fluid and the heat transport in the solid. The solid properties are reported in Table 1. Moreover, the thermo-physical properties of the ideal gas are evaluated according to the NIST-JANAF thermochemical tables.9 The generation of the packed bed is carried out with the Discrete Element Method (DEM) implemented in the open source code LIGGGHTS.10 Spherical particles are randomly placed in a square section tubular domain subject to the action of the gravity field. For each of these particles a force balance is formulated and solved taking into account the interactions among particles and between the particles and the tube wall, until the velocity of all the particles is virtually zero, which corresponds to mechanical equilibrium. The packed bed of spheres is created using the Standard Tessellation Language (STL). Moreover, the particle data are also used to find the contact point positions, which are replaced by bridges, following the methodology proposed in ref. 11 and 12. The computational grid for the fluid and solid domain is generated by using the cut-cell approach implemented in the snappyHexMesh utility of OpenFOAM.8 A mesh-independent solution is reached using a background mesh with a cell size equal to dp/10 and a refinement up to 3 levels has been done around the gas–solid interface to properly describe the temperature gradients and fluxes, as shown in Fig. 2.| Catalyst properties | ||
|---|---|---|
| Thermal conductivity | 1.5 | W m−1 K−1 |
| Density | 2100 | kg m−3 |
| Specific heat at constant pressure | 925 | J kg−1 K−1 |
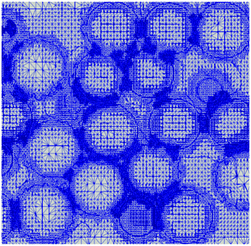 | ||
| Fig. 2 Insight of the computational grid used for CFD simulations with the mesh discretization in both fluid and solid domain. | ||
Given the low Reynolds numbers considered in the simulations, prism layers were not created near the walls.13 At the fluid–solid interface the boundary conditions for the heat diffusion fluxes suggested by Murthy and Mathur14 are adopted. Non-slip and Neumann boundary conditions are applied at the walls for velocity and pressure, respectively. The CFD simulations are performed by keeping constant the temperature of the channel walls and with the operating conditions and reactor geometries reported in Tables 2 and 3, respectively.
| Operating conditions | ||
|---|---|---|
| Feed temperature | 293 | K |
| External temperature | 295 | K |
| Outlet pressure | 1 | atm |
| Feed gas species | Air | |
| Reynolds numbers | 70–220 | |
| D p (mm) | D c (mm) | L (mm) | N |
|---|---|---|---|
| 0.6 | 2.0 | 8.0 | 3.33 |
| 0.6 | 2.5 | 8.0 | 4.17 |
| 0.6 | 3.0 | 8.0 | 5.00 |
2.2. Pseudo-homogeneous 1D model for heat transfer in a single channel of the honeycomb
The single packed channel of the honeycomb matrix is described by using a pseudo-homogeneous 1D model: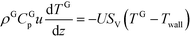 | (1) |
In eqn (1)ρG is the gas density, u the flow velocity, CGp the specific heat at constant pressure for the gas phase, TG the temperature of the gas phase, Twall the honeycomb matrix temperature, SV the specific heat exchange area between the packed channel and the honeycomb matrix and U is the overall heat transfer coefficient. The operating conditions have been selected to ensure constant gas properties in the channel, thus eqn (1) can be re-written as:
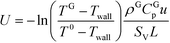 | (2) |
The temperature at the reactor inlet (T0) and at the reactor outlet (TG) in eqn (2) are estimated directly from the CFD simulations as mixing-cup average:15
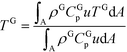 | (3) |
2.3. 2D model of micro packed bed reactors
The full-scale modeling of the micro packed bed reactor is based on a steady-state pseudo-continuous 2D reactor model. It describes a single externally cooled reactor tube loaded with a cylindrical honeycomb matrix with square channels, which are packed with spherical particles. This model is an extension of the model of Groppi and Tronconi7 successfully adopted to describe honeycomb reactors (i.e. no particles in the channel). In our model, the single packed channel is described through a 1D pseudo-homogeneous model which takes into account the heat exchange with the honeycomb matrix. The mass balance and the energy balance for the single channel are reported in eqn (4) and (5), respectively: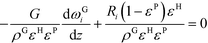 | (4) |
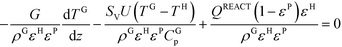 | (5) |
In eqn (4) and (5)G is the specific mass flow rate, ρG the gas density, εH the void fraction of the honeycomb matrix, and εP the void fraction of the packed channel. In eqn (4)ωGi is the mass fraction of the i-th species in the gas phase and Ri the reaction rate for the i-th species. In eqn (5)TG is the temperature of the gas phase, TH the temperature of the honeycomb matrix, CGp is the specific heat at constant pressure for the gas phase, SV specific the heat exchange area between the packed channel and the honeycomb matrix, QREACT the reaction heat and U the overall heat transfer coefficient. The size of the pellets adopted in the micro packed bed reactors results in negligible internal transport limitations due to the very small characteristic diffusion length.
The following boundary conditions at the reactor inlet (z = 0) are applied for eqn (4) and (5), respectively:
| ωGi(z = 0) = ωG,0i | (6) |
| TG(z = 0) = TG,0 | (7) |
The axial dispersion is neglected due to the high Péclet number. The gas-phase homogeneous reactions and radiative heat transfer are negligible, as reported in ref. 2 and 16.
The honeycomb matrix is described as a continuum17 consisting of a static, thermally connected solid phase.7 The heat balance for the honeycomb matrix is given by the following equation:
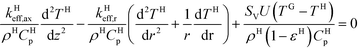 | (8) |
In eqn (8)ρH and CHp are the density and the specific heat at constant pressure of the honeycomb matrix, respectively. kHeff,ax and kHeff,r are the axial and radial thermal conductivity of the honeycomb matrix. The boundary conditions applied to eqn (8) are:
Inlet conditions at z = 0:
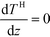 | (9) |
Outlet conditions at z = L:
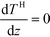 | (10) |
Symmetry condition at r = 0:
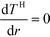 | (11) |
Wall conditions at r = R:
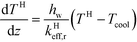 | (12) |
In eqn (12)Tcool is the coolant temperature and hw is the wall heat transfer coefficient between the honeycomb matrix and the external coolant.
In this 2D model, the solid properties are considered constant and reported in Table 4. The thermo-physical properties of the ideal gas are evaluated by using the OpenSMOKE++ library.18
| Packed bed2 | Micro packed bed | |
|---|---|---|
| Tube diameter (cm) | 2.54 | 2.54 |
| Particle diameter (cm) | 0.4 | 0.08 |
| CPSI/wall thickness | (not required) | 50/25 |
| Length (m) | 3.0 | 1.42 |
| Specific mass flow rate (kg m−2 s−1) | 1.3 | 0.45 |
| Catalyst conductivity (W m−1 K−1) | 1.5 | 1.5 |
| Support conductivity (W m−1 K−1) | (not required) | 100 |
The partial differential equations (PDEs) characterizing this model are solved by using the method of lines.19 The axial and radial reactor lengths are split into a suitable number of grid points and in each point the spatial derivatives are approximated by the Euler backward differentiation method. Thus, the PDEs problem is converted into a Differential Algebraic Equations (DAEs) system. The DAE system is solved by using the OpenSMOKE++ library, whose integrator can exploit the tridiagonal block structure of the Jacobian and which resulted in very efficient and robust convergence.18
3. Result and discussion
We start by assessing correlations from the literature for the estimation of the thermal lumped parameters of the 2D macroscopic model presented in section 2. In particular, as shown in Fig. 1, these parameters are related to two different mechanisms of energy transfer:a) Heat exchange between the single packed channel and the honeycomb matrix (Fig. 1a), accounted for by an overall heat transfer coefficient (U) in eqn (5) and (8);
b) Heat transfer within the honeycomb matrix (Fig. 1b), represented by axial (kHeff,ax) and radial (kHeff,r) effective thermal conductivities in eqn (8);
First, we apply the hierarchical modeling approach to derive these lumped parameters. Then, these parameters are implemented in the 2D model, which is used to analyze the behavior of micro packed bed reactors during selective oxidation processes.
For the effective thermal conductivities, we rely on the previous investigation of Groppi and Tronconi for a honeycomb matrix.20 Thus, the following correlations for the axial and radial effective thermal conductivity are employed:
| kHeff,ax = kH(1 − εH) | (13) |
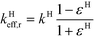 | (14) |
The correlations above result from a theoretical analysis of the heat conduction in the unit square cell of the honeycomb matrix and they have been applied to investigate the heat transfer phenomena in externally cooled monolith reactors. They have been validated by using experimental results7,17,21,22 and with 3D simulations of the honeycomb structure.23 Therefore, these correlations are a reliable description of the heat transfer within the honeycomb matrix and we implement them in the 2D model of micro packed bed reactors.
3.1. Hierarchical analysis: heat exchange between the single packed channel and the honeycomb matrix
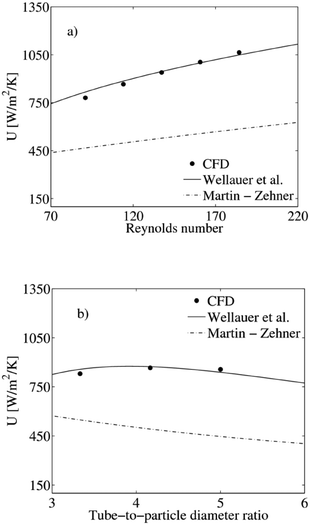
Correlations for the description of the heat exchange between the single packed channel and the honeycomb matrix are not available in literature. In fact, as reported in Rebughini et al.,3 the flow in the channels of the micro packed bed is characterized by a laminar flow regime at low Reynolds numbers (70 < Re < 220) due to the small dimensions of the spherical particles and the channels. Also, the tube-to-particle diameter ratio (3 < N < 6) is lower than the typical value of conventional packed bed reactors. Therefore, the literature correlations for the overall heat transfer coefficients of conventional packed bed cannot be directly applied to the micro packed bed geometry. In this view, we use the hierarchical methodology3 to screen and possibly refine existing correlations for the description of overall heat transfer coefficient at the particular conditions of the micro packed bed reactors.The hierarchical analysis of this heat transfer phenomenon is performed as follows. First, we describe the heat transfer in the micro packing by means of CFD simulations (high hierarchy model) of a single channel of the honeycomb matrix packed with spherical particles. Temperature contours for a tube-to-particle ratio of 4.1 and two different Reynolds numbers are reported Fig. 3. Then, the CFD calculated profiles are analyzed with the 1D pseudo-homogeneous model (low hierarchy model) to estimate the overall heat transfer coefficients by exploiting eqn (1) and (2). These values are now compared with the ones obtained from literature correlations derived for conventional packed bed reactors. We select the correlation proposed by Martin–Zehner,24,25 widely adopted for the description of packed beds,26 and the correlation by Wellauer et al.,27 derived for externally cooled packed bed reactor working at low Reynolds numbers. This condition is close to the one of micro-packed bed reactor, where the small dimension of the pellet employed leads to low Reynolds numbers.
 | ||
| Fig. 3 Contours of temperature on a mid-tube plane through the bed for a tube-to-particle ratio of 4.17 and Reynolds number equal to 110 (a) and 180 (b). | ||
The Martin–Zehner24,25 correlation consists of the wall heat transfer coefficient (hw) estimated with Martin and Nilles24 correlation coupled with the formula of Zehner and Schlünder25 for the effective radial thermal conductivity (kHeff,r). Wellauer et al.27 proposed alternative methods for the evaluation of the wall heat transfer coefficient and of the effective radial thermal conductivity derived in the context of low Reynolds number flows. The equations involved in this correlation are reported in the ESI† (section 1). The combination of these two expressions is based on the Biot number (Bi) as suggested by Dixon28 with eqn (15).
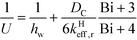 | (15) |
The prediction of the overall heat transfer coefficient of the correlations of Martin–Zehner24,25 and Wellauer et al.27 show large deviations, up to 300 W m−2 K−1, in the range of operating conditions of micro packed bed reactors, as shown in Fig. 4. In this case, we found out that the values estimated with the correlation of Wellauer et al.27 are more similar to the CFD-based results, such as in the range of ±10 W m−2 K−1, than those evaluated with the Martin–Zehner24,25 correlation. This difference can be ascribed to the flow regime and the operating conditions used to derive the literature correlations. In particular, in terms of flow regime, the correlation of Martin–Zehner24,25 has been proposed to describe industrial packed bed reactors, which operate at high Reynolds numbers. Instead, Wellauer et al.27 proposed their correlation to describe externally cooled packed bed reactor working at low Reynolds numbers. The micro packed bed reactors are characterized by Reynolds numbers between 30 and 130, which are around the ones investigated in the derivation of the correlation of Wellauer et al.27 Moreover, in terms of reactor geometry, the Martin–Zehner24,25 correlation describes packed bed with higher tube-to-particle diameter ratio than those represented by the correlation of Wellauer et al.27 Thus, the correlation suggested by Wellauer et al.27 can better reproduce the CFD-based results because it has been derived from experiments with tube-to-particle diameter ratios similar to those of micro packed bed reactors. The heat exchange between the packed channel and the honeycomb matrix in a micro packed bed reactor can be described by using the correlation suggested by Wellauer et al.27 The accuracy of the conventional models is guaranteed since the results of the CFD analysis allows for selecting the empirical correlation which properly accounts for the geometries and operating conditions of the investigated reactor.
3.2. Show-case: oxidation of o-xylene to phthalic anhydride
We apply the hierarchically derived model of the micro packed bed reactor to demonstrate the potential of the approach in the assessment of the performances of the micro packed bed configuration in the context of a highly exothermic reaction, such as the partial oxidation of o-xylene to phthalic anhydride.This process is industrially carried out in multi-tubular reactors cooled by molten salts. The reaction pathways that lead to the total combustion products are more activated and more exothermic than the ones responsible for phthalic anhydride production. Thus, the temperature control is crucial to ensure high selectivity to the desired product (phthalic anhydride). The kinetic parameters and the rate expressions are taken from Froment et al.,2 more details can be found in the ESI† (section 3). Fig. 5 shows the temperature profile obtained in the classical reactor configuration (parameters in Table 4) compared to the one evaluated in a micro-packed bed reactor.
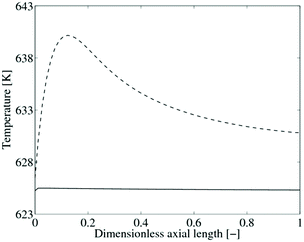 | ||
| Fig. 5 Temperature axial profile for the packed bed reactor (dashed line) and the micro packed bed reactor (solid line). | ||
The operating conditions for the micro packed reactor have been selected to guarantee to the micro packed bed the same Gas Hourly Space Velocity (GHSV) and the same pressure drop as the packed bed reactor. Moreover, the comparison between these two reactor configurations is performed by considering an o-xylene-to-air feed molar ratio of 0.009 and a coolant temperature of 625 K, which are the typical industrial conditions as reported by Froment et al.2
The packed bed configuration is characterized by a hot spot in the temperature profile. Instead, the micro packed bed reactor results in an almost isothermal profile. This different behavior depends on the amount of heat removed in the two reactor configurations. In fact, the heat extracted from the packed bed is initially lower than the heat generated by the reaction. Once the temperature difference between the reactor and the coolant becomes sufficient, the heat is properly removed decreasing the temperature in the reactor. This opposite behavior generates the hot-spot in the packed bed. On the contrary, the metallic honeycomb matrix of the micro packed bed increases the heat removal, which enables the quasi-isothermal operation of this configuration. This is due to the high overall heat transfer coefficient of the micro packed bed which allows for a large heat exchange even in presence of a small (<10 K) temperature difference between the reactor and the coolant. The overall heat transfer coefficient relies on three different contributions in series: the heat transfer between the packed bed and the solid matrix of the honeycomb, the heat conduction in the metallic matrix and the heat exchange between the monolith and the coolant. A tight fitting of the honeycomb in the reactor tube enables a perfect contact between the monolith and the tube wall. The radial heat transfer is strongly promoted by the metallic structure of the honeycomb through the conduction mechanism, when the contribution of the heat transfer between the packed bed and the solid matrix is sufficiently high. The proper design of the micro packed bed is pivotal to provide an intense gas to matrix heat transfer boosting the heat exchange phenomena by means of the conduction in the solid.
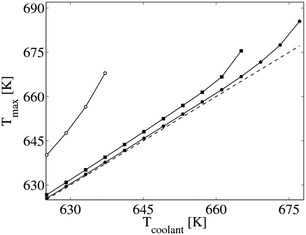
This results in an enhanced radial heat transfer in the micro packed bed allowing for a wider range of operating conditions. This is illustrated in Fig. 6 where the maximum temperature for both configurations is reported as a function of the coolant temperature. In the packed bed reactor, a coolant temperature higher than 637 K leads to a thermal loss of the reactor caused by the intensification of the combustion reactions to COx resulting in a dramatic decrease of the selectivity coupled to an uncontrolled increment of the temperature. On the contrary, the coolant temperature for the micro packed bed reactor can be increased up to 677 K keeping the maximum temperature in the reactor lower than 685 K, when the external heat transfer resistance between the monolith and the coolant is negligible. This behavior depends on the increased radial heat transfer, which allows for better heat removal and enables a quasi-isothermal operation of the reactor, even with the same catalytic load adopted in the packed bed reactor.
The previous analysis has been carried out with an optimal contact between the monolith and the tube. We also analyzed the effect of the presence of a gas gap between the honeycomb and the tube wall or the onset of fouling on the surface between the tube and the coolant. These phenomena introduce additional thermal resistances which reduce the heat performances of the reactor. Despite this, even considering an external heat transfer value of 700 W m−2 K−1,20 the behavior of the reactor is poorly affected as shown in Fig. 6 (full square symbols). The maximum temperature difference between the gas and the coolant remains below 10 K and the quasi-isothermal operating condition in the reactor are kept. The runaway is predicted at 669 K due to the lower heat flux between the monolith and the coolant. However, this is still a major improvement in the thermal behavior with respect to the conventional packed bed. Moreover, the increased heat removal affects the selectivity and yield to the desired product (phthalic anhydride) of the reactor. Fig. 7 reports calculated selectivity, yield, and conversion for the micro packed bed reactor as a function of the coolant temperature in the case of negligible external heat transfer resistance. It is shown that increasing the coolant temperature the conversion of o-xylene increases too but also reduces the selectivity to phthalic anhydride, which is the typical behavior of this reaction scheme (see ESI† section 3). Thus, an optimal temperature for the operation of the reactor is observed leading to a maximum of the phthalic anhydride molar yield. Fig. 7 shows that this value is 0.695 and it corresponds to a constant coolant temperature of 661 K. In particular, this value is slightly higher that the yield of industrial multi-tubular packed bed reactors (0.690)2 and quite similar to the value of 0.696 that can be obtained with an isothermal reactor. Moreover, the micro packed bed reactor enables a more stable operativity of the reactor strongly decreasing the hot-spot temperature and increasing the robustness to temperature variations in the reactor. Focusing our attention on the temperature profiles inside the reactors, despite the similar yield values between the multi-tubular packed bed and the micro packed bed rector, the second one is almost isothermal (Tmax–Tcool < 1.5 K). This analysis relies on the adequacy of the correlation used for the description of the heat transfer in the micro packed bed reactor. Fig. 8 shows the effect of two different correlations on the predicted temperature profile. Temperature differences between 2 and 18 K are experienced within the reactor due to the different estimation of the heat transfer coefficients. Above all, the Martin–Zehner correlation24,25 usually overpredicts the reactor temperature leading to an earlier runaway of the reactor at 661 K, clearly below the limit of 681 K obtained with the Wellauer method,27 which was selected using the hierarchical approach. The results obtained with the Martin–Zehner24,25 strongly underestimate the heat exchange masking the potential of micro packed bed reactors. In particular, the runaway of the reactor is predicted at lower temperatures, which actually correspond to the optimum of the yield evaluated using the Wellauer27 correlation. Thus, the selection of the correlation has a strong impact on the analysis of the reactor, hindering the operability of the reactor in these convenient conditions.
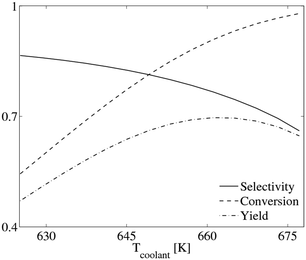 | ||
| Fig. 7 Effect of the coolant temperature on the o-xylene conversion, phthalic anhydride selectivity and phthalic anhydride yield for the micro packed bed reactor. | ||
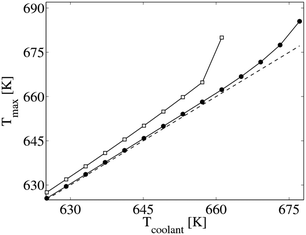 | ||
| Fig. 8 Correlation effect on the maximum temperature in the micro packed bed reactor as a function of the coolant temperature. Wellauer et al.27 solid line and full circular symbol. Martin–Zehner24,25 solid line and empty square symbol. | ||
Thus, the capabilities of the hierarchical modeling are evident being able to define the most adequate correlation with a reasonable computational effort.
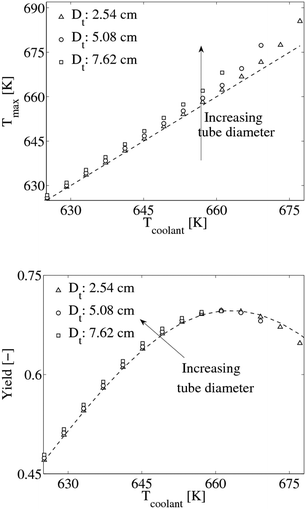
Our analysis demonstrates that the high heat removal of the honeycomb matrix allows a quasi-isothermal operation of the reactor. The connected solid matrix should also reduce the temperature radial gradients by the enhanced radial heat transfer, which allows for a significant increment of the reactor tube diameter. To better clarify this point, we performed a parametric analysis on the reactor geometry by increasing the tube diameter. In particular, Fig. 9 illustrates the maximum temperature and the yield as a function of the coolant temperature for different tube diameters. We observe that increasing the tube diameter slightly affects the maximum temperature in the reactor. In fact, Fig. 9 shows that the maximum temperature in the reactor increases while increasing the tube diameter. This is associated with the increased distance between the center of the reactor and the molten salts. Therefore, even with the enhanced heat transfer properties of the metallic matrix, the center of the reactor reaches higher temperature for higher tube diameter. Despite this trend in the temperature profile, increasing the tube diameter does not remarkably affect the reactor performance in terms of phthalic anhydride yield, which reaches the maximum value at 661 K for all the tube diameters investigated. In fact, even in the worst scenario of a tube diameter of 7.62 cm at a coolant temperature of 661 K, the micro packed bed is quasi-isothermal (Tmax–Tcool < 5.5 K).
On a more general basis, this analysis clearly demonstrates that the hierarchical modeling approach can be adopted to analyze complex reactor configurations, when fundamental CFD modeling is still limited by the impractical computational cost. In particular, the hierarchical modeling has been applied to investigate micro packed bed reactors by comparing them to multi-tubular packed bed reactors. Even if this comparison is based on a simplified kinetic scheme and on a limited number of operating conditions, this preliminary analysis shows that the micro packed bed reactors can be a suitable alternative to multi-tubular packed bed reactors.
4. Conclusions
We applied the hierarchical modeling approach to micro packed bed reactors aiming at the analysis of the heat exchange mechanism. First, the heat transfer properties in the single packed channel of this new reactor configuration were investigated by means of CFD simulations. Despite the unconventional dimensions, we found that the heat transfer phenomena in the packed channels rely on the same mechanisms as those occurring in conventional packed bed reactors. Therefore, we selected the most suitable state-of-the-art correlation to describe the heat transfer between the packed channel and the honeycomb matrix. We found out that the Wellauer27 correlation properly reproduces the micro packed bed behavior observed in the multiscale CFD simulations. Then, we investigated the capabilities of the whole micro packed bed reactor in dealing with the selective oxidation of o-xylene to phthalic anhydride. By implementing the correlation in a pseudo-continuous 2D model, the analysis of the entire reactor is carried out with a feasible computational cost and fully retaining the information recovered in the fundamental simulations. We found out that, at operating conditions similar to those used in an industrial packed bed reactor, the micro packed bed reactor is quasi-isothermal. This depends on the high heat transfer properties of the metallic honeycomb matrix, which enable a more effective and intense heat removal and, reducing the hot spot in the reactor and increasing the phthalic anhydride yield. We also investigated the reactor performance by changing the tube diameter and we found out that increasing the tube diameter does not remarkably affect the reactor performance in terms of phthalic anhydride yield. On a more general basis, the proposed analysis clearly shows that hierarchical modeling is a useful tool for the rational definition and/or assessment of the correlations of transport properties in novel reactor geometries.Conflicts of interest
There are no conflicts to declare.Acknowledgements
Computational time at CINECA (Bologna, Italy) is gratefully acknowledged.References
- M. P. Dudukovic, Science, 2009, 325, 698–701 CrossRef CAS PubMed.
- G. F. Froment, K. B. Bischoff and J. De Wilde, Chemical Reactor Analysis and Design, John Wiley & Sons, Incorporated, 3rd edn, 2010 Search PubMed.
- S. Rebughini, A. Cuoci and M. Maestri, Chem. Eng. J., 2016, 289, 471–478 CrossRef CAS.
- D. Vervloet, F. Kapteijn, J. Nijenhuis and J. R. Van Ommen, Catal. Today, 2013, 216, 111–116 CrossRef CAS.
- M. Iovane, R. Zennaro, P. Forzatti, G. Groppi, L. Lietti, E. Tronconi, C. G. Visconti, S. Rossini and E. Mignone, US Pat., 20120184631, 2012 Search PubMed.
- K. Pangarkar, T. J. Schildhauer, J. R. Van Ommen, J. Nijenhuis, F. Kapteijn and J. A. Moulijn, Structured packings for multiphase catalytic reactors, Ind. Eng. Chem. Res., 2008, 47(10), 3720–3751 CrossRef CAS.
- E. Tronconi and G. Groppi, Simulation of structured catalytic reactors with enhanced thermal conductivity for selective oxidation reactions, Catal. Today, 2001, 69, 63–73 CrossRef.
- H. G. Weller, G. Tabor, H. Jasak and C. Fureby, A tensorial approach to computational continuum mechanics using object-oriented techniques, Comput. Phys., 1998, 12, 620–631 CrossRef.
- M. W. J. Chase, NIST-JANAF Thermochemical Tables, American Inst. of Physics, 1998 Search PubMed.
- C. Kloss, C. Goniva, A. Hager, S. Amberger and S. Pirker, Pcfd, 2012, 12, 140–152 CrossRef.
- S. Rebughini, A. Cuoci and M. Maestri, Chem. Eng. Sci., 2016, 141, 240–249 CrossRef CAS.
- A. G. Dixon, M. Nijemeisland and E. H. Stitt, Comput. Chem. Eng., 2013, 48, 135–153 CrossRef CAS.
- S. A. Logtenberg, M. Nijemeisland and A. G. Dixon, Chem. Eng. Sci., 1999, 54, 2433–2439 CrossRef CAS.
- J. Y. Murthy and S. R. Mathur, J. Heat Transfer, 1998, 120, 583–591 CrossRef.
- R. K. Shah and A. L. London, Laminar flow forced convection in ducts: a source book for compact heat exchanger analytical data, Academic press, 1978 Search PubMed.
- G. Groppi and E. Tronconi, Chem. Eng. Sci., 2000, 55, 2161–2171 CrossRef CAS.
- G. Groppi and E. Tronconi, AIChE J., 1996, 42, 2382–2387 CrossRef CAS.
- A. Cuoci, A. Frassoldati, T. Faravelli and E. Ranzi, Comput. Phys. Commun., 2015, 192, 237–264 CrossRef CAS.
- J. H. Ferziger and M. Peric, Computational Methods for Fluid Dynamics, Springer, Berlin Heidelberg, 2001 Search PubMed.
- E. Tronconi, G. Groppi and C. G. Visconti, Curr. Opin. Chem. Eng., 2014, 5, 55–67 CrossRef.
- G. Groppi, A. Belloli, E. Tronconi and P. Forzatti, Chem. Eng. Sci., 1995, 50, 2705–2715 CrossRef CAS.
- E. Tronconi and G. Groppi, Study on the thermal behavior of structured plate-type catalysts with metallic supports for gas/solid exothermic reactions, Chem. Eng. Sci., 2000, 55, 6021–6036 CrossRef CAS.
- D. Schlereth and O. Hinrichsen, Ind. Eng. Chem. Res., 2014, 53, 11550–11556 CrossRef CAS.
- H. Martin and M. Nilles, Chem. Ing. Tech., 1993, 65, 1468–1477 CrossRef CAS.
- P. Zehner and E. U. Schlünder, Chem. Ing. Tech., 1970, 42, 933–941 CrossRef CAS.
- A. G. Dixon, Can. J. Chem. Eng., 2012, 90, 507–527 CrossRef CAS.
- T. Wellauer, D. L. Cresswell and E. J. Newson, in Chemical Reaction Engineering—Boston, American Chemical Society, 1982, vol. 196, pp. 41–527 Search PubMed.
- A. G. Dixon, Chem. Eng. Process., 1996, 35, 323–331 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available: Equations of Wellauer correlation, details on notation and symbols, kinetic scheme. See DOI: 10.1039/c7re00195a |
| ‡ These authors contributed equally to this work. |
| This journal is © The Royal Society of Chemistry 2018 |