Effect of metal doping on the visible light absorption, electronic structure and mechanical properties of non-toxic metal halide CsGeCl₃

Abstract

Non-toxic metal halide perovskites have become forefront for commercialization of the perovskite solar cells and optoelectronic devices. In the present study, for the first time we show that particular metal doping in CsGeCl₃ halide can considerably enhance the absorbance both in the visible and ultraviolet light energy range. We have carried out DFT based first principles calculations on Mn-doped and Ni-doped CsGeCl₃ halide. We investigate the detailed structural, optical, electronic and mechanical properties of all the doped compositions theoretically. The study of the optical properties shows that the absorption edge of both Ni and Mn-doped CsGeCl₃ is shifted toward the low energy region (red shift) relative to the pristine one. An additional peak is observed for both doped profiles in the visible light energy region. The study of the mechanical properties demonstrates that both the doped samples are mechanically stable and ductile as the pristine CsGeCl₃. The study of the electronic properties shows that the excitation of photoelectrons is easier due to the formation of intermediate states in Mn-doped CsGeCl₃. As a result Mn-doped CsGeCl₃ exhibits higher absorptivity in the visible region than the Ni-doped counterpart. A combinational analysis indicates that CsGe_1−xMn_xCl₃ is the best lead free candidate among the inorganic perovskite materials for solar cell and optoelectronic applications.

---

1. Introduction

Inorganic metal halide perovskite materials have been a topic of great interest in recent years due to their unique properties and applications. Metal halides hold great promise as solar cell material and have also shown outstanding performance in optoelectronics. Inorganic metal halides possess remarkable optoelectronic properties including high optical absorption, small carrier effective mass, tunable band gap, point defect, high charge carrier mobility and long charge diffusion.^1,2 The applications of these semiconductors are not limited to the branch of photovoltaics and optoelectronics; they have also a number of applications in photodetectors, LEDs (Light Emitting Diodes) and devices which are used for solar to fuel energy conversion.^3–6 Moreover, these semiconducting materials are inexpensive and abundant on earth. Due to this reason, the use of these materials in solar cells is convenient and more economical than the Si-based photovoltaic technology (PV-Technology).¹

The well known formula of metal halide perovskites is ABX₃ (where, A = a cation, B = a metal ion and X = a halogen anion). The majority of the materials which exhibit remarkable performances in this family contain lead (Pb). Therefore, the major concern for application of these materials in practice is the toxicity of Pb. In ambient conditions lead based metal halide perovskites decompose to PbI₂ which is harmful to the environment.^7–9 Hence, several theoretical and experimental studies have been carried out in recent years in the quest to find novel non-toxic perovskites by replacing lead with a non-toxic metal cation. Recently Roknuzzaman et al. carried out a detailed investigation on this group of materials by using theoretical methods to find a suitable lead free candidate.¹⁰ They performed a simulation study the structural, optical, electronic and mechanical properties of CsBX₃ (B = Ge, Sn and X = Cl, Br, I) semiconductors and compare their results with the lead containing semiconductors CsPbX₃ (X = Cl, Br, I). After a combinational analysis they suggest that Ge-based CsGeI₃ metal halide is the best lead free inorganic metal halide perovskite semiconductor for optoelectronic and solar cell applications. However, the study of the mechanical properties shows that the proposed sample is brittle in nature and hence unsuitable for real world application.

In 2016, Erdinc et al. studied the electronic, optical, thermodynamic and lattice dynamical properties of CsGeCl₃ semiconductor for both paraelectric and ferroelectric phases.¹¹ Another experimental and theoretical study suggests that CsGeCl₃ is a wide band gap semiconductor with an experimental band gap value of 3.67 eV.^12–15 Because of this large band gap value CsGeCl₃ metal halide is not perfect for solar cell application. However, an appropriate metal dopant in CsGeCl₃ can reduce the band gap to such extent which is suitable for the absorption of visible light energy. Therefore, in the present study we aim to dope with different transition metals the Ge-site of the CsGeCl₃ metal halide in order to extend its absorption spectra across all the range of the solar spectrum. We have studied the optical, electronic and mechanical properties of Ni and Mn-doped CsGeCl₃ by using a Density Functional Theory (DFT) based theoretical method to find a better candidate in this family for solar cell and optoelectronic applications than the previously proposed best lead free candidate CsGeI₃. Finally, a thorough comparison among the key properties of the metal doped CsGeCl₃ and pristine CsGeCl₃ with the CsGeI₃ metal halide is presented and discussed in details.

2. Theoretical methodology

The theoretical calculations are performed by using the Density Functional Theory (DFT) based plane wave pseudopotential approach.¹⁶ All the calculations are implemented by using the Cambridge Serial Total Energy Package (CASTEP) executed within the Material Studio-7.0.^17,25 In order to achieve the desired doping effect in pure cubic CsGeCl₃ metal halide, a 2 × 2 × 2 supercell is constructed which contains 40 atoms. As a result, the new chemical formula of CsGeCl₃ perovskite can be written as CsGe_1−xM_xCl₃ (x = 0.125 and M = Ni, Mn). Generalized Gradient Approximation (GGA) proposed by Perdew, Burke and Ernzerhof (PBE) is used for evaluating the exchange correlation energy.¹⁸ The wave function is expanded up to 350 and 500 eV plane wave cutoff energy for doped and pristine samples, respectively. For ensuring the criteria of convergence for both the electronic properties calculation and geometry optimization 3 × 3 × 3 k-points and 10 × 10 × 10 k-points have been used for doped and pure sample, respectively. For describing the electron ion interaction Vanderbilt type ultrasoft pseudopotential is used.¹⁹ BFGS (Broyden–Fletcher–Goldfarb–Shanno) relaxation scheme is used for optimizing the crystal structure.²⁰ The unit cell and atomic relaxations are performed as long as the residual forces are below 0.03 eV Å⁻¹.

Finite strain theory²¹ executed within the CASTEP module is used for evaluating the elastic constants of pristine and doped CsGeCl₃ metal halide. We set 0.003 as the maximum strain amplitude. Voigt–Reuss–Hill (VRH) averaging scheme²² is used for obtaining the polycrystalline mechanical parameters from the evaluated C_ij. The polycrystalline elastic moduli are calculated by using the equations given elsewhere.²³ The optical properties are calculated by using the CASTEP tool based on the standard DFT Kohn–Sham orbitals.²⁴ A scissor operator of 2.673 eV is applied in the calculation in order to compensate for the gap between the theoretical value (0.997 eV) and experimental value (3.67 eV) of the pure CsGeCl₃ band gap.

3. Results and discussion

3.1. Structural properties

Inorganic metal halide perovskite semiconductor CsGeCl₃ belongs to the space group Pm3̄m (221) with a cubic crystal structure.¹⁰ The unit cell consists of five atoms with only one formula unit. The fractional coordinates of the Cs, Ge and Cl atoms are (0, 0, 0), (0.5, 0.5, 0.5) and (0, 0.5, 0.5) with Wyckoff position 1a, 1b and 3c, respectively. The experimental lattice parameter and unit cell volume are listed in Table 1 with the theoretical values calculated in this study. For inserting impurities in CsGeCl₃ perovskite a supercell having size 8 times the unit cell of the pristine sample is constructed as shown in Fig. 1. The supercell of CsGeCl₃ contains 40 atoms including 8 Cs atoms, 8 Ge atoms and 24 Cl atoms. The impurities are inserted in pure CsGeCl₃ by replacing one Ge atom by Ni/Mn atom (substitutional doping) which corresponds to the doping concentration of about 12.5 atom%. The evaluated unit cell parameters of pristine and doped samples are tabulated in Table 1.

Table 1 The theoretical and experimental unit cell parameters of pristine and doped CsGeCl₃ perovskite

Properties	CsGeCl3			CsGe1−xNixCl3	CsGe1−xMnxCl3
	This study	Expt.^15	Calc.^10
a0 (Å)	5.317	5.434	5.314	5.258	5.269
V0 (Å^3)	150.31	160.45	150.10	145.36	146.27
B0 (GPa)	29.69	—	—	33.60	36.96

---

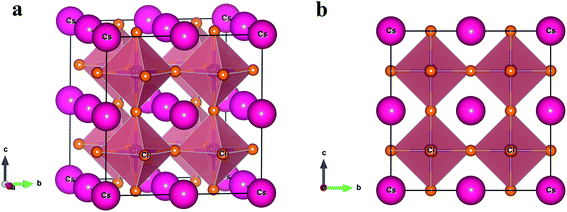Fig. 1 The crystal structure (2 × 2 × 2 supercell) of CsGeCl₃ metal halide. (a) Three dimensional and (b) two dimensional view.

3.2. Optical properties

In general, lead free (non-toxic) metal halide perovskites possess low reflectivity, high absorption coefficient and high optical conductivity compared to their lead containing counterpart. The study of optical properties is essential for discovering a suitable material in this family for the application in optoelectronic devices and solar cells. In this section of the paper the important optical parameters including absorption coefficient, reflectivity, real and imaginary part of dielectric constant and optical conductivity of pristine and Ni/Mn-doped CsGeCl₃ are analyzed and discussed in details.

The evaluated absorption profiles of pristine and doped CsGeCl₃ are illustrated in Fig. 2. The optical absorption coefficient is defined as the fraction of energy (wavelength) absorbed per unit length of the material and provides crucial information about the efficiency of optimum solar energy conversion of a material. Fig. 2(a) exhibits the photon energy dependent absorption coefficient of both pure and doped CsGeCl₃. According to the result, the absorption edge of both Ni and Mn-doped CsGeCl₃ is shifted toward the low energy region (red shift) relative to the pristine one. An additional peak is observed for both doped profiles in the low energy region. The absorption edge of Mn-doped CsGeCl₃ shifts more toward the lower energy region than Ni-doped CsGeCl₃. The pristine CsGeCl₃ shows no absorbance in the visible light region. The metal doping in pure CsGeCl₃ enhances the absorption coefficient to a great extent not only in the visible region but also in the ultraviolet region. For a better understanding of the light absorption feature of CsGeCl₃ in the visible region, the wavelength dependent absorption coefficient is presented in Fig. 2(b). As shown in Fig. 2(b) the Mn-doped CsGeCl₃ has a wider absorption area than the Ni-doped CsGeCl₃. The reason for the formation of the broadest absorption area in the Mn-doped sample will be discussed in details in the next section. In general, wide band gap semiconductors can absorb ultraviolet light of the solar spectrum which is only 4% of the total solar energy coming to the earth.²⁶ The visible light covers approximately 43% of the solar spectrum.²⁷ Therefore, the intrinsic CsGeCl₃ (band gap = 3.67 eV) is incapable to utilize the visible light energy for photovoltaic conversion. Hence, the prominent absorption in the visible region in the Mn-doped sample shows great promise for better utilization of the solar spectrum and may increase the solar cell efficiency.

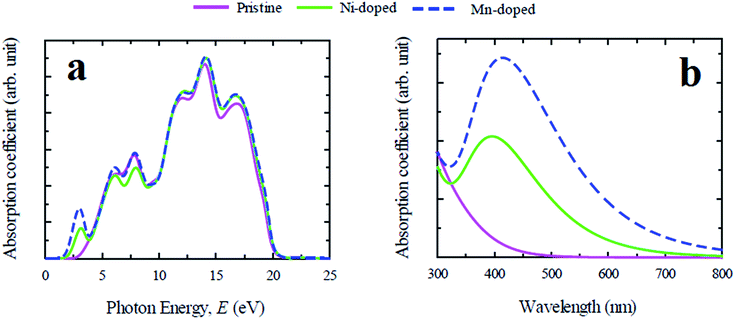Fig. 2 Calculated light absorption spectra of pure and metal doped CsGeCl₃ perovskite. (a) Photon energy dependent and (b) wavelength dependent absorption coefficient.

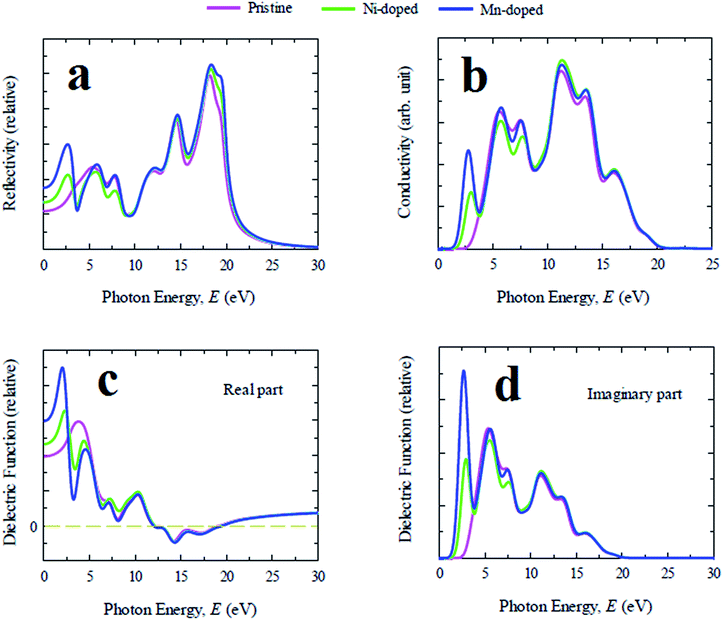
Reflectivity is one of the crucial optical properties of materials for photovoltaic applications and is defined as the amount of light energy reflected from the surface of a material with respect to the amount of light energy incident on the surface of the material. The reflectivity spectra of pristine and doped samples for photon energy up to 30 eV are illustrated in Fig. 3(a). CsGeCl₃ shows low reflectivity in the whole energy range of the solar spectrum. However, the reflectivity of all metal doped samples is nearly identical to the pristine one in the ultraviolet region. An additional peak is observed in the visible region for all doped samples whereas Mn-doped CsGeCl₃ has a stronger reflectivity in the low photon energy range than the Ni-doped sample. The dielectric function is characterized by the response of a material to the incident light energy. The charge carrier recombination rate and hence the overall performance of optoelectronic devices depends upon the static value of the dielectric function.²⁸ A material with high dielectric constant has relatively less charge carrier recombination rate. As a result the overall performance of optoelectronic devices is enhanced. The real and imaginary part of the evaluated dielectric function of pure and doped CsGeCl₃ are depicted in Fig. 3(c) and (d). It is evident that the Mn-doped sample shows relatively higher dielectric constant than the pure and Ni-doped CsGeCl₃. Therefore, in terms of dielectric constant Mn-doped CsGeCl₃ is a better candidate for solar cell and optoelectronic applications than the pristine one. Generally a material with a higher band gap exhibit lower dielectric constants.²⁹ Since metal doping in CsGeCl₃ decreases the band gap value (see Electronic properties section), the metal doped samples show a higher dielectric constant than the pure CsGeCl₃. As shown in Fig. 3(c) and (d) overall the dielectric profile (both real and imaginary part) of the metal doped samples is almost identical in the high energy region (ultraviolet zone) to that of the pure sample. An additional peak of the real part of the dielectric constant is observed in the visible light energy zone. The imaginary part of the dielectric constant of all the samples goes to zero above 19 eV while the real part reaches approximately unity. This result implies that both doped and pure CsGeCl₃ halide exhibit transparency with slight absorption in the high energy zone (above 19 eV) (it is also evident from the absorption coefficient graph [Fig. 2(a)]). The appearance of a sharp peak of the imaginary part of the dielectric constant of the metal doped sample in the visible region implies the occurrence of strong absorption in this region³⁰ which also justifies the result obtained from the absorption spectra of doped CsGeCl₃ [Fig. 2]. Therefore, the investigation of the dielectric constant of the pure and metal doped CsGeCl₃ suggests that both pristine and doped sample possess high transmissivity in the high energy region (above 19 eV) and metal doped samples possess nearly zero transmissivity in the visible region. This is the reason for high absorptivity of metal doped CsGeCl₃ (particularly Mn-doped CsGeCl₃) in the visible region. However, the study of the reflectivity spectra [Fig. 3(a)] shows that Mn and Ni-doped CsGeCl₃ have a slight higher reflectivity in the visible energy zone. Hence, further research should be conducted to reduce the reflectivity of the metal doped CsGeCl₃ in the visible region which may further increase the absorptivity as well as efficiency of the solar cells. The optical conductivity is also defined as the photoconductivity. The conductivity spectra of doped and pristine CsGeCl₃ are illustrated in Fig. 3(b) up to 25 eV light energy. The optical conductivity of the metal doped CsGeCl₃ is almost similar to that of the pure sample in the high energy region. A sharp peak appeared in the visible light energy zone for both doped profiles whereas the Mn-doped sample exhibits a larger photoconductivity than the Ni-doped sample. The appearance of the large photoconductivity in the visible region for the metal doped CsGeCl₃ is a consequence of its large absorptivity in the low energy region [Fig. 2].

Fig. 3 The simulated photon energy dependent (a) reflectivity, (b) conductivity, (c) real part of dielectric function and (d) imaginary part of dielectric function of pristine and transition metal doped CsGeCl₃.

3.3. Electronic properties

In order to explain the above optical features of the metal doped CsGeCl₃ halide, the basic electronic properties including band structure and density of states (DOS) of the studied samples are calculated and discussed in this section. Fig. 4 illustrates the electronic band structures of pristine and metal doped CsGeCl₃. The band structure diagram of the pure sample calculated using the single cell of CsGeCl₃ is depicted in Fig. 4(a). As shown in the figure the conduction band minimum and valence band maximum lies at R (k-point), indicating the direct band gap (0.97 eV) nature of pristine CsGeCl₃. This result is in accordance with the evaluated value of 0.978 eV by Roknuzzaman et al.¹⁰ implying the reliability of the present calculations. The band structure diagram illustrated in Fig. 4(b) is calculated by using the supercell (eight times) of CsGeCl₃. The computed band gap (direct) of pristine CsGeCl₃ is 0.997 eV showing a good agreement with the band gap value calculated using the single cell of CsGeCl₃. It is evident that the computed band gap value underestimates the experimentally evaluated band gap value 3.67 eV.¹⁵ The reason for this can be attributed to the well known limitation of GGA. The Local Density Approximation (LDA) and LDA + U methods also underestimate the band gap value. Sometimes Heyd–Scuseria–Ernzerhof (HSE) hybrid potential may provide a band gap value close to the experimental one, but it is also not valid for all of the materials. Partial correction of the theoretical band gap value relative to the experimental one can be achieved by using the GGA + U approach. However, we only focus on the variation of the band gap due to different metal doping in CsGeCl₃ and ignore the band gap error of the GGA approach. The band structure profile of metal doped CsGeCl₃ halide is illustrated in Fig. 4(c) and (d), respectively. It is evident that impurity states emerge within the band gap of Ni-doped sample, whereas intermediate states appear within the band gap of Mn-doped CsGeCl₃. In case of the Ni-doped sample [Fig. 4(c)], vacant states are formed over the Fermi level. The valence band is extended into the higher energy region. The extension of the valence band into the Fermi level can facilitate the transition of electrons from the valence band to the conduction band. However, the gap between the maximum of the valence band and the minimum of the conduction band is 1.10 eV which is larger than the band gap value of pristine CsGeCl₃ (0.997 eV). The enhancement of the band gap shows a contradiction with the optical absorbance of Ni-doped CsGeCl₃. Here, the shift of the Fermi level into the valence band can be defined as the negative Burstein shift. This broadening of the band gap can be ascribed to the phenomena known as Moss–Burstein effect.³¹ Therefore, ignoring the Moss–Burstein shift the band gap of the Ni-doped sample is reduced and causes the occurrence of absorbance in the visible region [Fig. 2(b)]. As shown in Fig. 4(d) in case of the Mn-doped CsGeCl₃ halide, an intermediate energy band appeared in the band gap. The energy gap between the valence band and the conduction band is 0.97 eV (similar to the pristine one) but the energy gap between the minimum of the conduction band and the top of the intermediate states is 0.29 eV which is much smaller than the band gap value of pure CsGeCl₃. Thus, the excitation of photo electrons is easier due to the formation of these intermediate states in the Mn-doped CsGeCl₃. As a result Mn-doped CsGeCl₃ exhibits a higher absorptivity in the visible region than the Ni-doped counterpart. It should also be noted that the band gap of the Mn-doped sample [Fig. 4(d)] is indirect and hence photons with this band gap energy can generate electron–hole pairs with the aid of phonons similar to silicon.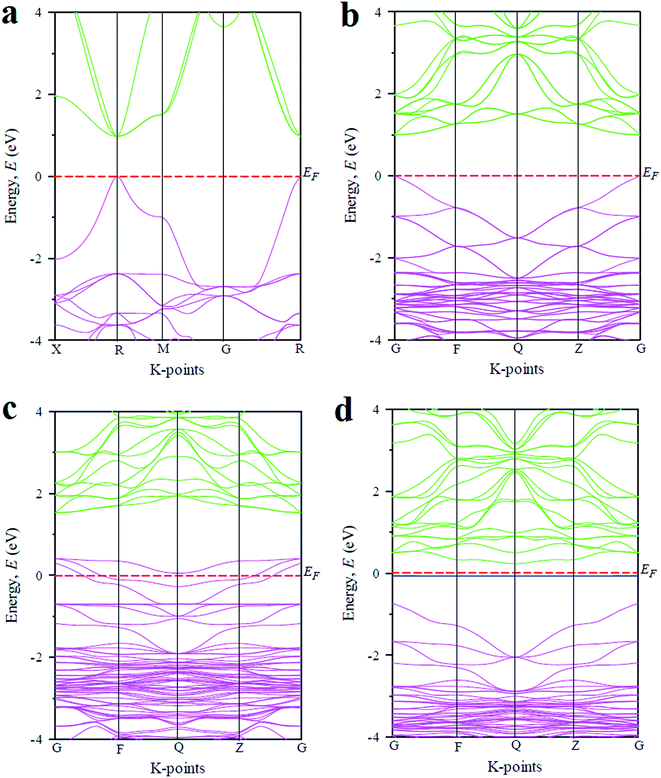

Fig. 4 The band structure diagram of CsGeCl₃ metal halide calculated by using (a) pure single cell, (b) pure supercell, (c) Ni-doped and (d) Mn-doped sample.

The total and partial density of states of pristine and doped CsGeCl₃ are depicted in Fig. 5. Fig. 5(a) illustrates the DOS profile of the pure sample. As shown in the figure the valence band is mostly composed of Cl-3p and Ge-4p orbitals with a small contribution of Cs-6s and Cs-5p orbitals. The conduction band mainly consists of Ge-4p orbital with a small contribution of Cs-6s and Cs-5p orbitals. After Ni doping in CsGeCl₃ a slight change is observed in the overall DOS profile as shown in Fig. 5(b). The composition of the valence band is almost similar to that of the pristine sample except for an extra peak which appeared in the total DOS due to the formation of dopant states (Ni-3d) in the valence band of CsGeCl₃. The composition of the conduction band is similar to the pristine one as no dopant peak is formed. A similar trend is observed for the Mn-doped sample as shown in Fig. 5(c). The conduction band slightly shifts toward the lower energy region. A flat peak is observed in the conduction band due to the formation of dopant states (Mn-3d) in the conduction band. Fig. 5(d) illustrates the change of the band gap due to the formation of new dopant states near the Fermi level. In case of Ni-doped CsGeCl₃ the impurity energy states are formed over the Fermi level and mixed with the valence band maximum. These impurity states can trap the photoexcited holes which reduce the recombination rate of electrons and holes.³² In case of Mn-doped CsGeCl₃ the impurity energy states appear in the middle of the band gap. These intermediate states reduce the energy which is necessary for electron transition to occur from the valence band to the conduction band. The valence electrons are first excited to the impurity energy states (intermediate band) and then excited to the conduction band by consuming the visible light energy. These results explain the red shift of the absorption spectra as shown in Fig. 2.

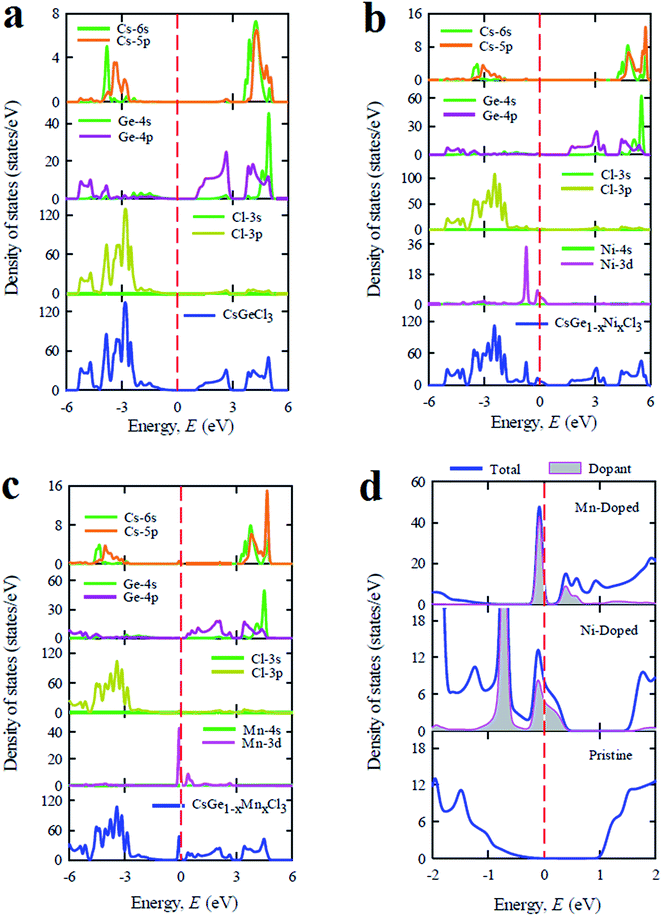Fig. 5 The total and partial density of states of CsGeCl₃ metal halide simulated by using (a) pure supercell, (b) Ni-doped sample, (c) Mn-doped sample and (d) dopant contribution at the Fermi level.

3.4. Mechanical properties

For ensuring the mechanical stability of the metal doped CsGeCl₃ halide the elastic constants of the doped phases are calculated and discussed in this section in details. The calculated elastic constants of pristine and doped CsGeCl₃ are tabulated in Table 2. It is evident that all the compositions fulfill the well established Born stability criteria³³ given as follows,

C₁₁ > 0, C₄₄ > 0, C₁₁ − C₁₂ > 0 and C₁₁ + 2C₁₂ > 0

Table 2 The evaluated elastic constants C_ij (GPa) and Cauchy pressure of pristine and doped CsGeCl₃ halide

Phase	C11	C12	C44	C12–C44
CsGeCl3	55.02	13.14	11.73	1.41
CsGe1−xNixCl3	54.16	14.60	13.36	1.24
CsGe1−xMnxCl3	56.68	14.36	13.33	1.03
CsGeCl3 (ref. 10)	54.93	13.08	11.99	—

---

Hence, both the doped phases are mechanically stable in nature. It is also evident that the calculated elastic constants of pristine CsGeCl₃ (by using supercell) agrees well with the available theoretical result bearing the reliability of the present investigation. The Cauchy pressure (C₁₂–C₄₄) is a useful parameter to predict the brittleness and ductility of materials. The negative (positive) value of this parameter indicates the brittle (ductile) nature of a compound.³⁰ The computed values of the Cauchy pressure of pristine and doped samples are positive [Table 2] implying that the doped samples are ductile as the pristine CsGeCl₃.¹⁰

By using the computed elastic constants the most important mechanical parameters of a compound such as the shear modulus G, bulk modulus B, Young’s modulus E, B/G ratio and Poisson’s ratio ν of pristine and doped samples are calculated and listed in Table 3. It is also evident from Table 3 that all the calculated mechanical parameters show good consistency with the theoretically calculated results. The bulk modulus is one of the essential mechanical parameter which gives an indication of the stiffness of a material. The calculated bulk modulus of all the composition is comparatively low indicating the flexibility of all the samples. The value of B is slightly increased after Ni and Mn doping. However, this lower value of B ensures that it will be easier to make thin films of Mn-doped CsGeCl₃ perovskite and hence suitable for solar cell applications. The shear modulus is used to calculate the plastic deformation of a material under external stress. As shown in Table 3 the value of G for all the samples is comparatively low. The value of G is slightly increased after Ni and Mn doping into CsGeCl₃. However, the lower value of the shear modulus implies that CsGe_1−xMn_xCl₃ is less rigid than the pristine sample and hence can be drawn into a desired shape. A similar trend is noticed for the Young’s modulus of all the compositions.

Table 3 The evaluated mechanical parameters of pristine and doped CsGeCl₃ halide

Phase	B (GPa)	G (GPa)	E (GPa)	ν	B/G
CsGeCl3	27.11	14.82	37.60	0.26	1.82
CsGe1−xNixCl3	27.78	15.63	39.48	0.26	1.77
CsGe1−xMnxCl3	28.46	16.05	40.53	0.26	1.77
CsGeCl3 (ref. 10)	27.03	15.02	38.02	0.27	1.80

---

The Poisson’s ratio is another useful parameter for explaining the bonding nature and plasticity of a material. The calculated value of ν for all the compositions is 0.26 implying the existence of a central force in all the samples.³⁴ However, all the samples should have predominant ionic feature as the value of ν is very close to the critical value of 0.25 which indicates an ionic crystal. The Poisson’s ratio is another useful indicator of ductility and brittleness of materials. The critical value for separating the ductility and brittleness of a material is 0.26.³⁵ Surprisingly the computed value of ν of all the samples is exactly 0.26 thus implying the ductile nature of all the compositions. The ratio between bulk modulus and shear modulus is usually known as Pugh’s ratio which is also used to predict the failure mode of a material. In this case, the critical value for separating the ductility and brittleness of a material is 1.75.³⁶ As shown in Table 3 all the studied compositions are ductile in nature as the value of B/G is greater than the critical value. The value of B/G is decreased after Ni and Mn doping in CsGeCl₃. However, the value of Pugh’s ratio of metal doped CsGeCl₃ perovskite is still greater than the critical value and hence should exhibited a ductile response as the pristine sample.

3.5. Environmentally-friendly perovskites

Among the lead free inorganic perovskite materials suitable for solar cell and optoelectronic applications CsGeI₃ perovskite compound is proposed to be the best candidate.¹⁰ Though the band gap of CsGeI₃ is suitable for the absorption of both visible and ultraviolet light energy of the solar spectrum, it is slightly brittle. Hence fabrication of solar cells using CsGeI₃ halide is difficult. On the other hand, CsGeCl₃ is ductile but possesses a large band gap which is not suitable for the absorption of visible light energy of the solar spectrum. Metal doping in CsGeCl₃ can solve this problem.

According to the present study, a small amount of Ni dopant in the Ge site of CsGeCl₃ can elevate the absorption in the visible region to a great extent. However, the Mn-doped CsGeCl₃ exhibits a very high absorption not only in the visible region but also in the ultraviolet region. The study of the mechanical properties shows that the proposed sample is ductile and possesses a low bulk modulus and hence it is possible to use it to make thin films. It also possesses high photoconductivity. The comparison among the key properties of pure and metal doped CsGeCl₃ with CsGeI₃ is presented in Table 4. From Table 4 it is clear that CsGe_1−xMn_xCl₃ is the best lead free candidate among the inorganic perovskite materials for solar cell and optoelectronic applications.

Table 4 Comparison of the key properties of pristine and doped CsGeCl₃ with those of CsGeI₃

Properties	CsGeCl3,^10 [this work]	CsGeI3 (ref. 10)	CsGe1−xNixCl3	CsGe1−xMnxCl3
Optical absorption	High in UV-region	High in UV-region	High in UV-region	High in UV-region
	Missing in visible region	Medium in visible region	Medium in visible region	High in visible region
Photoconductivity	Medium	High	Medium	High
Failure mode	Ductile	Brittle	Ductile	Ductile
Suitability for solar cells	Not good	Good	Better	Best

---

4. Conclusions

In summary, by using the density functional theory dependent ab initio method the optical, electronic and mechanical properties of metal doped CsGeCl₃ halide are investigated and discussed in details. The intrinsic CsGeCl₃ is incapable to utilize the visible light energy for photovoltaic conversion due to its large band gap energy 3.67 eV. The selection of suitable metal dopants in CsGeCl₃ halide can considerably enhance the absorbance and photoconductivity both in the visible and ultraviolet light energy range. However, due to the formation of an intermediate energy band the Mn-doped CsGeCl₃ exhibits a higher absorptivity and photoconductivity in the visible region than the Ni-doped counterpart. Hence, the prominent absorption in the visible region of Mn-doped sample shows great promise for better utilization of the solar spectrum and may increase the solar cell efficiency. The study of mechanical properties shows that the Mn-doped CsGeCl₃ is ductile and possesses a low bulk modulus. Therefore, it is also possible to make thin films by using CsGe_1−xMn_xCl₃. The comparison among the key properties of pure and metal doped CsGeCl₃ with the best known inorganic metal halide perovskite CsGeI₃ suggests that CsGe_1−xMn_xCl₃ is the best lead free candidate among inorganic perovskite materials for solar cell and optoelectronic applications.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was carried out in the Solid State Physics Research Laboratory, Department of Physics, Bangladesh University of Engineering and Technology, Dhaka, Bangladesh.

References

1. W. Zhang, G. E. Eperon and H. J. Snaith, Metal halide perovskites for energy applications, Nat. Energy, 2016, 1(6), 16048.
2. W.-J. Yin, T. Shi and Y. Yan, Unique properties of halide perovskites as possible origins of the superior solar cell performance, Adv. Mater., 2014, 26(27), 4653–4658.
3. Q. A. Akkerman, et al., Strongly emissive perovskite nanocrystal inks for high-voltage solar cells, Nat. Energy, 2017, 2(2), 16194.
4. G. E. Eperon, et al., Inorganic caesium lead iodide perovskite solar cells, J. Mater. Chem. A, 2015, 3(39), 19688–19695.
5. T. Krishnamoorthy, et al., Lead-free germanium iodide perovskite materials for photovoltaic applications, J. Mater. Chem. A, 2015, 3(47), 23829–23832.
6. P. Ramasamy, et al., All-inorganic cesium lead halide perovskite nanocrystals for photodetector applications, Chem. Commun., 2016, 52(10), 2067–2070.
7. A. Babayigit, et al., Assessing the toxicity of Pb-and Sn-based perovskite solar cells in model organism Danio rerio, Sci. Rep., 2016, 6, 18721.
8. G. E. Eperon, et al., The importance of moisture in hybrid lead halide perovskite thin film fabrication, ACS Nano, 2015, 9(9), 9380–9393.
9. A. Babayigit, et al., Toxicity of organometal halide perovskite solar cells, Nat. Mater., 2016, 15(3), 247.
10. M. Roknuzzaman, et al., Towards lead-free perovskite photovoltaics and optoelectronics by ab initio simulations, Sci. Rep., 2017, 7(1), 14025.
11. B. Erdinc, et al., Ab initio study of CsGeCl₃ compound in paraelectric and ferroelectric phases, Ferroelectrics, 2016, 494(1), 138–149.
12. D.-K. Seo, et al., Pressure-induced changes in the structure and band gap of CsGeX₃ (X= Cl, Br) studied by electronic band structure calculations, Inorg. Chem., 1998, 37(3), 407–410.
13. D. Huang, et al., First-principles prediction of a promising p-type transparent conductive material CsGeCl₃, Appl. Phys. Express, 2014, 7(4), 041201.
14. B. Erdinc, et al., Ab initio study of CsGeCl₃ compound in paraelectric and ferroelectric phases, Ferroelectrics, 2016, 494(1), 138–149.
15. L.-C. Tang, et al., First principles calculations of linear and second-order optical responses in rhombohedrally distorted perovskite ternary halides, CsGeX₃ (X= Cl, Br, and I), Jpn. J. Appl. Phys., 2009, 48(11R), 112402.
16. M. C. Payne, et al., Iterative minimization techniques for ab initio total-energy calculations: molecular dynamics and conjugate gradients, Rev. Mod. Phys., 1992, 64(4), 1045.
17. M. D. Segall, et al., First-principles simulation: ideas, illustrations and the CASTEP code, J. Phys.: Condens. Matter, 2002, 14(11), 2717.
18. J. P. Perdew, K. Burke and M. Ernzerhof., Generalized gradient approximation made simple, Phys. Rev. Lett., 1996, 77(18), 3865.
19. D. Vanderbilt, Soft self-consistent pseudopotentials in a generalized eigenvalue formalism, Phys. Rev. B: Condens. Matter Mater. Phys., 1990, 41(11), 7892.
20. T. H. Fischer and A. Jan, General methods for geometry and wave function optimization, J. Phys. Chem., 1992, 96(24), 9768–9774.
21. F. D. Murnaghan, Finite deformations of an elastic solid, Am. J. Math., 1937, 59(2), 235–260.
22. R. Hill, The elastic behaviour of a crystalline aggregate, Proc. Phys. Soc., London, Sect. A, 1952, 65(5), 349.
23. M. Z. Rahaman, M. A. Rahman and M. Abdur Razzaque Sarker, Prediction of a new transition metal oxide MgRhO₃ with SrTiO₃-type structure: Stability, structure and physical characteristics, Chin. J. Phys., 2017, 55(4), 1489–1494.
24. CASTEP GUIDE MATERIALS STUDIO 8.0, 2014.
25. Materials Studio CASTEP Manual Accelrys, 2010, available at http://www.tcm.phy.cam.ac.uk/castep/documentation/WebHelp/CASTEP.html.
26. W. Yu, J. Zhang and T. Peng, New insight into the enhanced photocatalytic activity of N-, C-and S-doped ZnO photocatalysts, Appl. Catal., B, 2016, 181, 220–227.
27. X. Zong, et al., Activation of photocatalytic water oxidation on N-doped ZnO bundle-like nanoparticles under visible light, J. Phys. Chem. C, 2013, 117(10), 4937–4942.
28. X. Liu, et al., A high dielectric constant non-fullerene acceptor for efficient bulk-heterojunction organic solar cells, J. Mater. Chem. A, 2018, 6(2), 395–403.
29. M. Roknuzzaman, et al., Insightinto lead-free organic–inorganic hybrid perovskites for photovoltaics and optoelectronics: A first-principles study, Org. Electron., 2018, 59, 99–106.
30. M. Z. Rahaman and M. A. Rahman, Investigation of the physical properties of two Laves phase compounds HRh₂ (H = Ca and La): A DFT study, Int. J. Mod. Phys. B, 2018, 32(12), 1850149.
31. E. Burstein, Anomalous optical absorption limit in InSb, Phys. Rev., 1954, 93(3), 632.
32. Z. Zhao and Q. Liu, Effects of lanthanide doping on electronic structures and optical properties of anatase TiO₂ from density functional theory calculations, J. Phys. D: Appl. Phys., 2008, 41(8), 085417.
33. M. Born, On the stability of crystal lattices. I., Mathematical Proceedings of the Cambridge Philosophical Society, Cambridge University Press, 1940, vol. 36, iss. 2.
34. B. G. Pfrommer, et al., Relaxation of crystals with the quasi-Newton method, J. Comput. Phys., 1997, 131(1), 233–240.
35. M. Z. Rahaman, M. L. Ali and M. A. Rahman, Pressure-dependent mechanical and thermodynamic properties of newly discovered cubic Na₂He, Chin. J. Phys., 2018, 56(1), 231–237.
36. S. F. Pugh, XCII. Relations between the elastic moduli and the plastic properties of polycrystalline pure metals, London, Edinburgh Dublin Philos. Mag. J. Sci., 1954, 45(367), 823–843.

---