Open Access Article
Open Access ArticleA multistep methodology for calculation of the tensile modulus in polymer/carbon nanotube nanocomposites above the percolation threshold based on the modified rule of mixtures
Yasser Zare a and
Kyong Yop Rhee*b
a and
Kyong Yop Rhee*b
aYoung Researchers and Elites Club, Science and Research Branch, Islamic Azad University, Tehran, Iran
bDepartment of Mechanical Engineering, College of Engineering, Kyung Hee University, Giheung, Yongin 446-701, Gyeonggi, Republic of Korea. E-mail: rheeky@khu.ac.kr; Fax: +82 31 202 6693; Tel: +82 31 201 2565
First published on 4th September 2018
Abstract
A multistep model is proposed for calculating the tensile modulus values of polymer/carbon nanotube (CNT) nanocomposites (PCNTs) based on the modified rule of mixtures, assuming a percolated network of nanoparticles. In the first step, the network of nanoparticles is considered as a new phase with a novel volume fraction and Young's modulus. Then, the volume fraction of the filler network in the PCNTs is correlated to the density of the network. Also, the percolation of the nanoparticles is related to the aspect ratio of the nanoparticles. Finally, a new model is proposed based on the modified rule of mixtures (the Riley model) of the properties of the filler network. The predictions of the proposed model are compared with experimental results and the roles of the nanoparticles and network properties in the modulus values of nanocomposites are determined. The proposed model presents acceptable predictions when compared with the experimental data. Moreover, the density and modulus of the filler network, as well as the aspect ratio and diameter of the nanoparticles was found to directly affect the moduli of the nanocomposites.
1 Introduction
Carbon nanotubes (CNTs) are an ideal reinforcing material that are used to obtain a high-modulus and conductive polymer nanocomposite, because of their great mechanical properties, good conductivity, nanoscale diameter and high aspect ratio.1–7 Previous studies have shown that CNTs have a Young's modulus of ca. 1000 GPa and a tensile strength of 10–50 GPa, which are much higher than those of conventional fibres, such as carbon fibers and other nanofillers such as clay and silica. To confirm an effective load transfer from a polymer matrix to CNTs, the interfacial bonding between the polymer matrix and the nanoparticles should be optimized to prevent the bonds breaking between the two materials. Also, the van der Waals attraction between the nanotubes causes the aggregation/agglomeration of CNTs in nanocomposites, which decreases the surface area of the nanofiller and disturbs the network structure. So, it is necessary to use some methods such as modification, functionalization and compatibilizing of CNTs to gain a uniform dispersion of nanoparticles in the polymer matrix and promote good interfacial interaction/adhesion between the polymer matrix and nanoparticles.3,8–10The electrical conductivity of polymer/CNT nanocomposites (PCNTs) can be increased through the formation of a filler network above the filler concentration, known as the percolation threshold.11–14 This means that significant conductivity of PCNTs is only obtained at or above the percolation threshold. Researchers have attempted to obtain a low percolation threshold in PCNTs by manipulating the material and processing parameters.15–17 In addition to the electrical percolation threshold, a substantial improvement in the tensile modulus has also been observed in polymer nanocomposites, which is known as mechanical percolation.18–21 In other words, a network of nanoparticles above a specific volume fraction (percolation) results in an important improvement in the mechanical properties. For example, the high shear modulus of reinforced films with cellulose whiskers has been explained by the percolation threshold of the filler.22 Although the mechanisms of the electrical and mechanical percolations are different, they are consistent in PCNTs.
From a theoretical point of view, the models for the critical conductivity of polymer nanocomposites are in the form of a power-law,23,24 as a function of the percolation volume fraction. Similarly, Ouali et al.25 proposed a model for the tensile modulus of conventional composites above the percolation threshold. Although this model has been extensively used for polymer nanocomposites in the previous work, it does not produce accurate results for the tensile modulus. There have been very few studies on the mechanical percolation of polymer nanocomposites in the literature, even though the percolation threshold is quickly reached in nanocomposites containing CNTs, due to the high aspect ratio of nanofillers.26–28 Therefore, it is necessary to study the effects of the filler network on the mechanical properties of PCNTs, such as the tensile modulus, because it directly affects the reinforcing role that CNTs play in polymer nanocomposites.
The modified rule of mixtures, first reported by Riley in 1976,29 produces inaccurate predictions for the tensile modulus of PCNTs (as discussed in the following sections), because it incorrectly assumes the role of the nanofiller aspect ratio. Also, this model does not incorporate the effect of the filler network in nanocomposites such as PCNTs above the percolation threshold. In this study, this model is modified and developed assuming a percolating network in PCNTs and a new model is proposed for calculating the tensile modulus of PCNTs containing a filler network. In the first step, a network of nanoparticles is considered as a new phase with a novel volume fraction that depends on the density of the network. Also, the aspect ratio of the network phase is assumed to have a value of 1, because it is considered as a sphere. Finally, the proposed model for the tensile modulus is presented by modification of the Riley model and incorporation of the new properties of the filler network. The predictions of the proposed model were compared with experimental results. Furthermore, the effects of some parameters, such as the network modulus and density, the nanofiller aspect ratio, the percolation volume fraction and diameter and the number of nanotubes per unit volume on the modulus of PCNTs were determined using the proposed model.
2 The proposed model
The high aspect ratio (the length per diameter) of CNTs, which produces a low percolation threshold, i.e. the networking of CNTs at a very low concentration in nanocomposites, is the main advantage of using CNT nanoparticles. The current study focuses on this specification of polymer CNT nanocomposites with nanoparticles/polymer nanocomposites. A network of nanoparticles can be considered as a new phase in PCNTs, which includes CNT nanoparticles and the polymer matrix among the nanotubes. In this condition, the volume fraction of the network can be expressed as:| ϕN = Aϕf | (1) |
ϕN = P![[small rho, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b7.gif) ϕf ϕf
| (2) |
![[small rho, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b7.gif) ” is the relative density of the 3D CNT network. Certainly, the exact value of the “P” parameter can be calculated using some techniques, such as morphological analysis. The “
” is the relative density of the 3D CNT network. Certainly, the exact value of the “P” parameter can be calculated using some techniques, such as morphological analysis. The “![[small rho, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b7.gif) ” parameter can be defined30 as:
” parameter can be defined30 as:
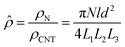 | (3) |
![[small rho, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b7.gif) ” can be expressed as:
” can be expressed as:
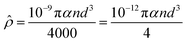 | (4) |
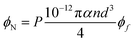 | (5) |
Moreover, the percolation threshold of CNTs can be related to the aspect ratio of the nanoparticles30 as:
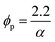 | (6) |
By substituting the above equation into eqn (5), “ϕN” can be defined as:
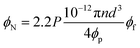 | (7) |
Riley modified the rule of mixtures for the tensile modulus of polymer nanocomposites assuming a modulus reduction factor (MRF) by including the aspect ratio of the nanofiller and the shear modulus of the polymer matrix29 as:
| E = Emϕm + MRFϕfEf | (8) |
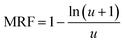 | (9) |
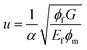 | (10) |
“ϕf” can be calculated by the weight fraction of the nanofiller in the nanocomposite (mf) as:
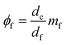 | (11) |
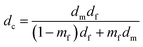 | (12) |
Now, the Riley model is modified and developed for PCNTs containing a filler network by assuming that the network of nanoparticles is a filler phase in the PCNTs. So, the characteristics of the whole filler network are considered as filler properties. The “ϕf” and “Ef” parameters in the Riley model are replaced by “ϕN” and “EN” parameters in the proposed model. Moreover, the aspect ratio of the filler network is considered to have a value of 1, because the network is assumed as being a sphere in the PCNTs. Also, the shear modulus of isotropic materials, such as the polymer matrix, can be defined as:
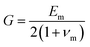 | (13) |
Assuming the properties of the filler network as the filler phase in PCNTs and α = 1 and G = 1 GPa in the Riley model, a new model can be proposed for calculating the tensile modulus of PCNTs above the percolation threshold as:
| E = Em(1 − ϕN) + MRFϕNEN | (14) |
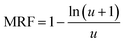 | (15) |
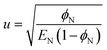 | (16) |
If the “ϕN” parameter in the above equations is substituted by eqn (5), the proposed model represents the properties of both the filler network and the nanoparticles. Furthermore, when “ϕN” is expressed by eqn (7), the proposed model shows the dependence of the modulus on the percolation threshold of the nanoparticles.
The relative modulus of PCNTs can also be expressed by:
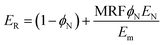 | (17) |
3 Results and discussion
The calculations made using the original Riley model and the proposed model were evaluated by comparing them against the experimentally determined moduli of some previously prepared samples. Fig. 1 shows the experimental data of the relative modulus and the model calculations for polyamide 6 (PA6)/CNTs from ref. 31, chitosan/multi-walled CNTs (MWCNTs) from ref. 32, PA6/MWCNTs from ref. 33, ultra-high molecular weight polyethylene (UWPE)/MWCNTs from ref. 34 and polyacrylonitrile (PAN)/MWCNTs from ref. 35. The calculations made using the original model gave the average values: νm = 0.4, Ef = 1000 GPa and α = 200. It is obvious that the calculated values from the Riley model are below those of the experimental values. As a result, the original model is not suitable for the calculation of the modulus value in PCNTs and the application of the model proposed in this study is thus justified.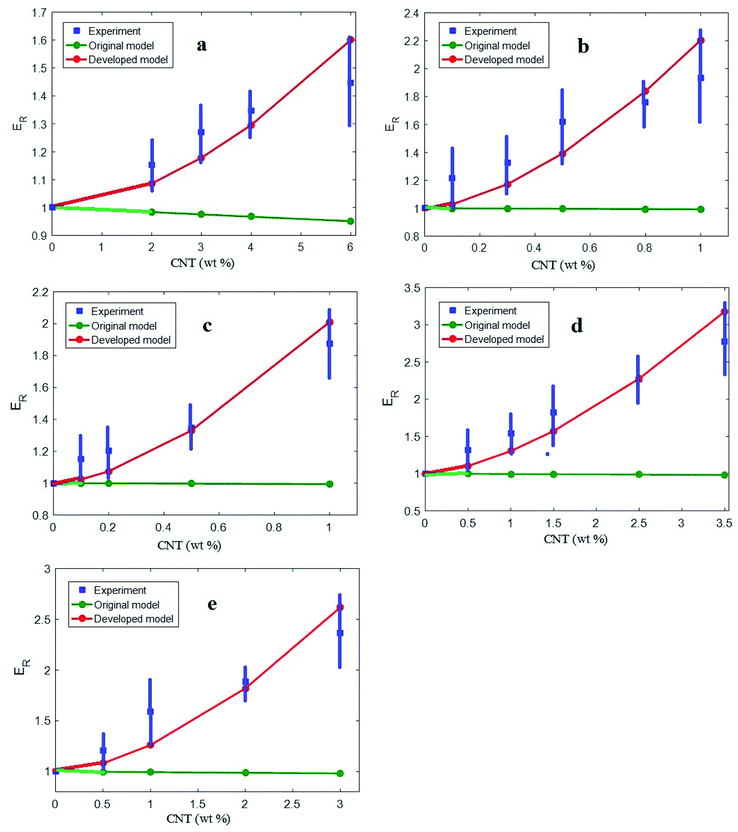 | ||
| Fig. 1 The experimental data and the calculations of the relative modulus using the original and proposed model for (a) PA6/CNTs,31 (b) chitosan/MWCNTs,32 (c) PA6/MWCNTs,33 (d) UWPE/MWCNTs34 and (e) PAN/MWCNTs.35 | ||
Good agreement is observed between the experimental values and the calculated values of the developed model for all samples at all filler concentrations, which validates the proposed model. In other words, although some deviation is observed between the experimental and theoretical data, the agreement between the calculations and experimental measurements is acceptable. Accordingly, the proposed model can be applied to predict the tensile modulus of PCNTs. Also, the good predicting power of the proposed model indicates that the reported samples contain CNT networks above the percolation threshold. It should be noted that the calculations of the developed model show high deviations from the experimental data at high CNT concentrations, because the CNT agglomerates at a high filler concentration weaken the modulus. However, the developed model cannot consider the agglomeration of nanoparticles. Therefore, it is suggested to apply the developed model at low CNT concentrations, which excludes the agglomerations. In addition, the proposed model is suitable for nanocomposites containing CNT networks above the percolation threshold. Since a low percolation threshold arises as a result of the high aspect ratio of nanoparticles, this model can properly predict the modulus in the samples containing high aspect ratio CNTs.
The best “A” and “EN” values can be calculated by fitting the proposed model to the experimental results. The best “A” obtained were 3, 16, 17, 5 and 10 for PA6/CNTs, chitosan/MWCNTs, PA6/MWCNTs, UWPE/MWCNTs and PAN/MWCNTs, respectively. Moreover, the calculated “EN” values were 4000, 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000, 14
000, 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500, 5500 and 9000 GPa for these samples, in that order. These calculations demonstrate that the best network is formed in the PA6/MWCNT sample, while PA6/CNTs has a poorly formed network. The predicted results are reasonable, because a strong network leads to a strong nanocomposite, while a poor network decreases the modulus of the nanocomposite sample. For example, the strong network of CNTs in the PA6/MWCNT sample results in an improvement in the modulus of 90% for 1 wt% of MWCNTs, but the weak network of nanoparticles only improves the modulus of the PA6/CNT sample by 50% for 6 wt% of MWCNTs. Therefore, the predicted values of the network are consistent with the improvement ranges of the modulus in the samples. Additionally, if the value of “P” is determined by looking at the material morphology in recorded images, it is possible to estimate the levels of “n”, “α” and “ϕp” using the proposed model. However, it is possible to evaluate the general properties of a network in different samples, such as the density and modulus, using the proposed model.
500, 5500 and 9000 GPa for these samples, in that order. These calculations demonstrate that the best network is formed in the PA6/MWCNT sample, while PA6/CNTs has a poorly formed network. The predicted results are reasonable, because a strong network leads to a strong nanocomposite, while a poor network decreases the modulus of the nanocomposite sample. For example, the strong network of CNTs in the PA6/MWCNT sample results in an improvement in the modulus of 90% for 1 wt% of MWCNTs, but the weak network of nanoparticles only improves the modulus of the PA6/CNT sample by 50% for 6 wt% of MWCNTs. Therefore, the predicted values of the network are consistent with the improvement ranges of the modulus in the samples. Additionally, if the value of “P” is determined by looking at the material morphology in recorded images, it is possible to estimate the levels of “n”, “α” and “ϕp” using the proposed model. However, it is possible to evaluate the general properties of a network in different samples, such as the density and modulus, using the proposed model.
Next, the roles of different parameters on the predicted modulus of PCNTs were plotted in the form of 3D and contour designs according to the proposed model. Fig. 2 shows the effects of the “A” and “EN” parameters on the predicted modulus with values of ϕf = 0.02 and Em = 2 GPa. The best modulus values were obtained using the highest “A” and “EN” values, as expected. As observed, the relative modulus increased to 2.8 at A = 11 and EN = 5000 GPa, while the relative modulus of 1 related to the modulus of the polymer matrix was observed at A < 4 and EN < 3000 GPa. So, high values of the “A” and “EN” parameters are required to achieve a high modulus value in PCNTs. The “A” parameter is a function of the relative density of the CNT network in the PCNT (eqn (1) and (2)). Obviously, a high network density results in a high level of reinforcement in the nanocomposites, because a denser network can bear a higher level of external stress. Also, a high “EN” value shows the formation of a strong network in the nanocomposite, which results in a high modulus.
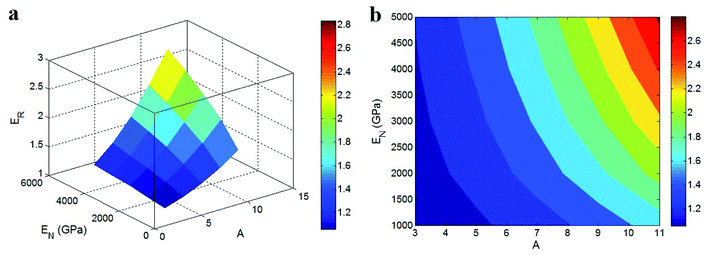 | ||
| Fig. 2 (a) 3D and (b) contour plots showing the relative modulus as a function of the “A” and “EN” parameters at ϕf = 0.02 and Em = 2 GPa. | ||
The percolation of nanoparticles in nanocomposites depends on the interaction between the nanoparticles and a percolated network with a strongly connected network has more desirable properties compared one with a poorly connected network. Moreover, a strong network can significantly reinforce the nanocomposites, because it has a much higher modulus than that of a polymer matrix. As a result, high values for both the “A” and “EN” parameters have been shown to logically improve the modulus of PCNTs, based on the proposed model.
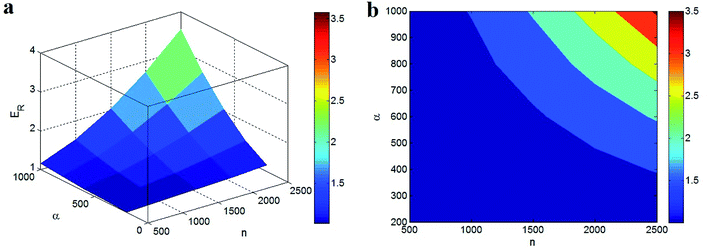
Fig. 3 also depicts the effects of the “n” and “α” parameters on the relative modulus of PCNTs using the proposed model with values of: ϕf = 0.02, Em = 2 GPa, Ef = 3000 GPa, d = 20 nm and P = 1000. Low modulus values were observed at low “n” and “α” values. In other words, the modulus value of a nanocomposite cannot be improve if n < 1500 and α < 700, under these conditions. However, the relative modulus value of the nanocomposite increases to 3.5 (a 250% improvement) at n = 2500 and α = 1000. These explanations demonstrate the important effects of the “n” and “α” parameters on the modulus value of PCNTs. When high “n” and “α” values are achieved by tuning the material and processing parameters, the modulus significantly improves to good values, while the poor “n” and “α” values result in an undesirable modulus value in nanocomposites.
These outputs from the proposed model are reasonable, because the “n” and “α” parameters directly affect the modulus of the nanocomposites. The “n” parameter representing the number of nanotubes in a unit volume of the network obviously affects the modulus value, because the number of nanotubes in the network determines the level of reinforcement. A high number of nanotubes in the network significantly reinforces the polymer matrix, whereas a poor “n” value has a negligible effect on the modulus of the nanocomposite. So, there is a direct influence of “n” on the modulus of PCNTs. Moreover, the high aspect ratio of nanotubes results in good reinforcement in the nanocomposites. As is known, long and thin nanotubes provide more interfacial area between the polymer matrix and nanoparticles, which results in a strong interfacial interaction.36–38 Therefore, the high aspect ratio of nanoparticles results in a large interfacial interaction between the polymer matrix and nanofiller, which facilitates the transfer of stress from the polymer matrix to the nanoparticles. Also, a high “α” value results in the breaking of the aggregates/agglomerates of the CNTs (or achievement of nanoscale in most cases) and good dispersion of the nanoparticles in the polymer matrix, which in turn results in an increase in the modulus. Therefore, the role of “α” in the modulus of nanocomposites in the proposed model is justified according to the values calculated for the interface/interphase between the polymer matrix and CNTs and the properties of the nanoparticles.39,40
Fig. 4 shows the effects of the “d” and “ϕp” parameters on the predicted relative modulus using the proposed model with values of: ϕf = 0.02, Em = 2 GPa, Ef = 3000 GPa, N = 400 and P = 1000. It is suggested that the relative modulus of nanocomposites is highly dependent on the “d” and “ϕp” parameters, because it changes from 1 to 10 for different values of these parameters. The modulus values of nanocomposites do not improve for the polymer matrix over wide ranges of the “d” and “ϕp” parameters, including low “d” and high “ϕp” values. So, low “d” and high “ϕp” values produce undesirable modulus values for polymer nanocomposites. However, an increase in the “d” value from about 25 nm and a decrease in the “ϕp” value from 0.003 results in some improvement in the modulus of nanocomposites. The best relative modulus of 10 is observed at d = 35 nm and ϕp = 0.001. So, a good nanocomposite modulus can be obtained with a thick layer of nanoparticles and a low percolation threshold. The thickness of the nanoparticles increases the density of the CNT network in the nanocomposites (eqn (4)), which reinforces the nanocomposites, as previously mentioned. In addition, a low percolation threshold accelerates the formation of the filler network in the nanocomposites for only a slight amount of nanofiller. On the other hand, a high percolation does not permit the nanoparticles to form a network at a low concentration of nanofiller and the network forms at a high nanoparticle content.
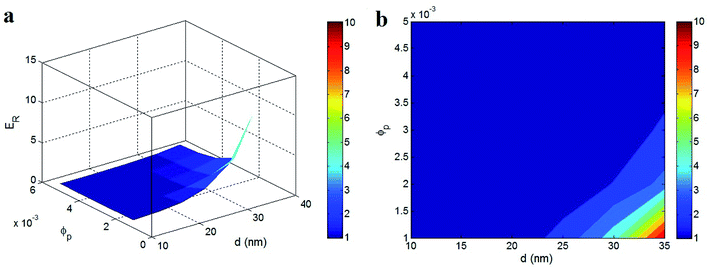 | ||
| Fig. 4 “ER” as a function of the “d” and “ϕp” parameters using the proposed model at values of ϕf = 0.02, Em = 2 GPa, Ef = 3000 GPa, N = 400 and P = 1000: (a) 3D and (b) contour plots. | ||
Since the modulus of nanocomposites considerably improves by the percolation of the nanoparticles, the inverse relationship between the modulus and the percolation is correct. Therefore, the observed effects of the “d” and “ϕp” parameters on the PCNT modulus are correct, which validates the proposed model for calculating the modulus of PCNTs containing a filler network. Now, the use of the proposed model to predict the values of the relative density of the CNT network and other parameters in PCNTs and replicate experimental tensile modulus values is promising. Therefore, the present modeling method can be helpful in the absence of accurate and practical methods for the determination of these parameters. Also, there is the potential to compare the network properties in different samples using the proposed model without undertaking morphological analysis.
4 Conclusions
The conventional model proposed by Riley for calculating the tensile modulus of polymer nanocomposites was modified and developed in various steps, assuming a percolated network of CNTs in PCNTs. A network of nanoparticles was considered as a filler phase with a new volume fraction and Young's modulus. Also, the volume fraction of the filler network and the percolation of nanoparticles were found to be dependent on the density of the network and the aspect ratio of the nanoparticles, respectively. The proposed model can be used to predict the modulus of PCNTs as a function of the properties of the nanoparticles and filler network. The predictions of the proposed model show an acceptable level of agreement with the experimental results of several samples from literature, while the original model cannot be used to calculate logical results for the modulus values of PCNTs. The relative modulus value was found to increase to 2.8 at A = 11 and EN = 5000 GPa, while it did not improve at A < 4 and EN < 3000 GPa. Thus, the “A” and “EN” parameters were found to have a positive effect on the modulus values of PCNTs. Moreover, the modulus of a nanocomposite did not increase at n < 1500 and α < 700, while the relative modulus improved by 250% at n = 2500 and α = 1000. These findings demonstrate the direct effect of the “n” and “α” parameters on the modulus values of PCNTs. The proposed model also shows that a thin layer of nanoparticles and high percolation threshold decreases the modulus values of polymer nanocomposites. Nevertheless, the best relative modulus value of 10 was observed at d = 35 nm and ϕp = 0.001. Therefore, a good modulus can be obtained with a thick layer of nanoparticles and a low percolation threshold.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the Basic Science Research Program through the National Research Foundation of Korea (NRF) funded by the Ministry of Education, Science and Technology (project number: 2018R1A2B5A02023190).References
- A. Rostami, H. Nazockdast and M. Karimi, Graphene induced microstructural changes of PLA/MWCNT biodegradable nanocomposites: rheological, morphological, thermal and electrical properties, RSC Adv., 2016, 6, 49747–49759 RSC.
- Y. Zare and K. Y. Rhee, A simple methodology to predict the tunneling conductivity of polymer/CNT nanocomposites by the roles of tunneling distance, interphase and CNT waviness, RSC Adv., 2017, 7, 34912–34921 RSC.
- W. Cai, M. Li, S. Wang, Y. Gu, Q. Li and Z. Zhang, Strong, flexible and thermal-resistant CNT/polyarylacetylene nanocomposite films, RSC Adv., 2016, 6, 4077–4084 RSC.
- T. Wu and B. Chen, Autonomous self-healing multiwalled carbon nanotube nanocomposites with piezoresistive effect, RSC Adv., 2017, 7, 20422–20429 RSC.
- T. Kaur and A. Thirugnanam, Tailoring in vitro biological and mechanical properties of polyvinyl alcohol reinforced with threshold carbon nanotube concentration for improved cellular response, RSC Adv., 2016, 6, 39982–39992 RSC.
- R. Razavi, Y. Zare and K. Y. Rhee, A two-step model for the tunneling conductivity of polymer carbon nanotube nanocomposites assuming the conduction of interphase regions, RSC Adv., 2017, 7, 50225–50233 RSC.
- A. Rostami, M. Masoomi, M. J. Fayazi and M. Vahdati, Role of multiwalled carbon nanotubes (MWCNTs) on rheological, thermal and electrical properties of PC/ABS blend, RSC Adv., 2015, 5, 32880–32890 RSC.
- A. Al-Kawaz, A. Rubin, N. Badi, C. Blanck, L. Jacomine, I. Janowska, C. Pham-Huu and C. Gauthier, Tribological and mechanical investigation of acrylic-based nanocomposite coatings reinforced with PMMA-grafted-MWCNT, Mater. Chem. Phys., 2016, 175, 206–214 CrossRef.
- A. Esbati and S. Irani, Effect of functionalized process and CNTs aggregation on fracture mechanism and mechanical properties of polymer nanocomposite, Mechanics of Materials, 2018 Search PubMed.
- A. H. Baferani, A. Katbab and A. Ohadi, The role of sonication time upon acoustic wave absorption efficiency, microstructure, and viscoelastic behavior of flexible polyurethane/CNT nanocomposite foam, Eur. Polym. J., 2017, 90, 383–391 CrossRef.
- Y. Zare and K. Y. Rhee, A simple model for electrical conductivity of polymer carbon nanotubes nanocomposites assuming the filler properties, interphase dimension, network level, interfacial tension and tunneling distance, Compos. Sci. Technol., 2018, 155, 252–260 CrossRef.
- J.-M. Zhu, Y. Zare and K. Y. Rhee, Analysis of the roles of interphase, waviness and agglomeration of CNT in the electrical conductivity and tensile modulus of polymer/CNT nanocomposites by theoretical approaches, Colloids Surf., A, 2018, 539, 29–36 CrossRef.
- N. Nikfar, Y. Zare and K. Y. Rhee, Dependence of mechanical performances of polymer/carbon nanotubes nanocomposites on percolation threshold, Phys. B, 2018, 533, 69–75 CrossRef.
- S. Maiti, N. K. Shrivastava and B. Khatua, Reduction of percolation threshold through double percolation in melt-blended polycarbonate/acrylonitrile butadiene styrene/multiwall carbon nanotubes elastomer nanocomposites, Polym. Compos., 2013, 34, 570–579 CrossRef.
- S. Maiti, S. Suin, N. K. Shrivastava and B. Khatua, Low percolation threshold in polycarbonate/multiwalled carbon nanotubes nanocomposites through melt blending with poly (butylene terephthalate), J. Appl. Polym. Sci., 2013, 130, 543–553 CrossRef.
- E. Garboczi, K. Snyder, J. Douglas and M. Thorpe, Geometrical percolation threshold of overlapping ellipsoids, Phys. Rev. E, 1995, 52, 819 CrossRef.
- R. Goyal, S. Samant, A. Thakar and A. Kadam, Electrical properties of polymer/expanded graphite nanocomposites with low percolation, J. Phys. D: Appl. Phys., 2010, 43, 365404 CrossRef.
- S. C. Baxter and C. T. Robinson, Pseudo-percolation: Critical volume fractions and mechanical percolation in polymer nanocomposites, Compos. Sci. Technol., 2011, 71, 1273–1279 CrossRef.
- Y. Zare and K. Y. Rhee, Development and modification of conventional Ouali model for tensile modulus of polymer/carbon nanotubes nanocomposites assuming the roles of dispersed and networked nanoparticles and surrounding interphases, J. Colloid Interface Sci., 2017, 506, 283–290 CrossRef PubMed.
- H.-x. Li, Y. Zare and K. Y. Rhee, The percolation threshold for tensile strength of polymer/CNT nanocomposites assuming filler network and interphase regions, Mater. Chem. Phys., 2018, 207, 76–83 CrossRef.
- R. Razavi, Y. Zare and K. Y. Rhee, A model for tensile strength of polymer/carbon nanotubes nanocomposites assuming the percolation of interphase regions, Colloids Surf., A, 2018, 538, 148–154 CrossRef.
- V. Favier, H. Chanzy and J. Cavaille, Polymer nanocomposites reinforced by cellulose whiskers, Macromolecules, 1995, 28, 6365–6367 CrossRef.
- L. Flandin, J. Cavaillé, G. Bidan and Y. Brechet, New nanocomposite materials made of an insulating matrix and conducting fillers: processing and properties, Polym. Compos., 2000, 21, 165–174 CrossRef.
- C. McClory, T. McNally, M. Baxendale, P. Pötschke, W. Blau and M. Ruether, Electrical and rheological percolation of PMMA/MWCNT nanocomposites as a function of CNT geometry and functionality, Eur. Polym. J., 2010, 46, 854–868 CrossRef.
- N. Ouali, J. Cavaillé and J. Perez, Elastic, viscoelastic and plastic behavior of multiphase polymer blends, Plast., Rubber Compos. Process. Appl., 1991, 16, 55–60 Search PubMed.
- Y. Zare and K. Y. Rhee, Development of a model for electrical conductivity of polymer graphene nanocomposites assuming interphase and tunneling regions in conductive networks, Ind. Eng. Chem. Res., 2017, 56(32), 9107–9115 CrossRef.
- Y. Zare and K. Y. Rhee, Prediction of tensile modulus in polymer nanocomposites containing carbon nanotubes (CNT) above percolation threshold by modification of conventional model, Curr. Appl. Phys., 2017, 17, 873–879 CrossRef.
- Z. Liu, W. Peng, Y. Zare, D. Hui and K. Y. Rhee, Predicting the electrical conductivity in polymer carbon nanotube nanocomposites based on the volume fractions and resistances of the nanoparticle, interphase, and tunneling regions in conductive networks, RSC Adv., 2018, 8, 19001–19010 RSC.
- Y. Zare and H. Garmabi, Analysis of tensile modulus of PP/nanoclay/CaCO3 ternary nanocomposite using composite theories, J. Appl. Polym. Sci., 2012, 123, 2309–2319 CrossRef.
- Y. Chen, F. Pan, Z. Guo, B. Liu and J. Zhang, Stiffness threshold of randomly distributed carbon nanotube networks, J. Mech. Phys. Solids, 2015, 84, 395–423 CrossRef.
- O. Meincke, D. Kaempfer, H. Weickmann, C. Friedrich, M. Vathauer and H. Warth, Mechanical properties and electrical conductivity of carbon-nanotube filled polyamide-6 and its blends with acrylonitrile/butadiene/styrene, Polymer, 2004, 45, 739–748 CrossRef.
- X. Cao, H. Dong, C. M. Li and L. A. Lucia, The enhanced mechanical properties of a covalently bound chitosan-multiwalled carbon nanotube nanocomposite, J. Appl. Polym. Sci., 2009, 113, 466–472 CrossRef.
- G.-X. Chen, H.-S. Kim, B. H. Park and J.-S. Yoon, Multi-walled carbon nanotubes reinforced nylon 6 composites, Polymer, 2006, 47, 4760–4767 CrossRef.
- A. Mierczynska, M. Mayne-L'Hermite, G. Boiteux and J. Jeszka, Electrical and mechanical properties of carbon nanotube/ultrahigh-molecular-weight polyethylene composites prepared by a filler prelocalization method, J. Appl. Polym. Sci., 2007, 105, 158–168 CrossRef.
- J. Ji, G. Sui, Y. Yu, Y. Liu, Y. Lin, Z. Du, S. Ryu and X. Yang, Significant improvement of mechanical properties observed in highly aligned carbon-nanotube-reinforced nanofibers, J. Phys. Chem. C, 2009, 113, 4779–4785 CrossRef.
- J. Wernik, B. Cornwell-Mott and S. Meguid, Determination of the interfacial properties of carbon nanotube reinforced polymer composites using atomistic-based continuum model, Int. J. Solids Struct., 2012, 49, 1852–1863 CrossRef.
- D. Liu, A. Pourrahimi, R. Olsson, M. Hedenqvist and U. Gedde, Influence of nanoparticle surface treatment on particle dispersion and interfacial adhesion in low-density polyethylene/aluminium oxide nanocomposites, Eur. Polym. J., 2015, 66, 67–77 CrossRef.
- Y. Zare, K. Y. Rhee and S.-J. Park, Predictions of micromechanics models for interfacial/interphase parameters in polymer/metal nanocomposites, Int. J. Adhes. Adhes., 2017, 79, 111–116 CrossRef.
- Y. Zare and K. Y. Rhee, Development of Hashin-Shtrikman model to determine the roles and properties of interphases in clay/CaCO 3/PP ternary nanocomposite, Appl. Clay Sci., 2017, 137, 176–182 CrossRef.
- Y. Zare and K. Y. Rhee, Dependence of Z Parameter for Tensile Strength of Multi-Layered Interphase in Polymer Nanocomposites to Material and Interphase Properties, Nanoscale Res. Lett., 2017, 12, 42 CrossRef PubMed.
| This journal is © The Royal Society of Chemistry 2018 |