Open Access Article
Open Access ArticleWidely used hardly known. An insight into electric and dynamic properties of formamidinium iodide†
K. Mencela,
P. Durlaka,
M. Rok a,
R. Jakubasa,
J. Baranb,
W. Medyckic,
A. Ciżman
a,
R. Jakubasa,
J. Baranb,
W. Medyckic,
A. Ciżman d and
A. Piecha-Bisiorek
d and
A. Piecha-Bisiorek *a
*a
aFaculty of Chemistry, University of Wrocław, F. Joliot-Curie 14, 50–383 Wrocław, Poland. E-mail: anna.piecha@chem.uni.wroc.pl; Fax: +48 713757270; Tel: +48 713757646
bInstitute of Low Temperature and Structure Research, PAS, Okólna 2, 50-422 Wrocław, Poland
cInstitute of Molecular Physics, Polish Academy of Science, M. Smoluchowskiego 17, 60-179 Poznań, Poland
dDivision of Experimental Physics, Wroclaw University of Science and Technology, Wybrzeże Wyspiańskiego 27, 50-370 Wrocław, Poland
First published on 24th July 2018
Abstract
The simple organic crystal formamidinium iodide (FAI) appeared to be a novel semiconducting material in a wide temperature range. The electric properties of FAI and the role of formamidinium cation (FA+) in the molecular mechanism of the solid-to-solid phase transitions (at 345 K (III → II) and 388 K (II → I)) were analysed. The creation of the ferroelastic domain structure in phases III and II was proved on the basis of observation under a polarizing microscope. Moreover, the molecular arrangement of dipolar organic FA+ was studied by 1H NMR (spin-lattice relaxation time) and vibrational spectroscopy supported by density functional theory. The theoretical results show a good agreement with the experimental data. The infrared spectrum in a harmonic approximation was calculated and a comparative vibrational analysis was performed. All used techniques showed that the prototypic phase I exhibits the feature of plastic phase.
Introduction
The use of perovskite in solar cells for the first time in history in 2009 by Kojima et al.1 opened the way to new dynamically developing applications of this material in the photovoltaic industry. In the course of progressive research on perovskite solar cells, new manufacturing methods of perovskite layers and tools have been developed which have contributed to an increase of power conversion efficiency (PCE) from 3.8% to more than 20%.2 As for the photoactive layer, organic–inorganic hybrids, described by the general formula RMX3, were applied (where R is an organic cation, M a metal, and X = Cl, Br, I). Such compounds appeared to be promising candidates for application in photovoltaics due to their excellent properties including a direct bandgap,3 a high absorption factor,4 a long lifetime of the carrier, high mobility, long-range charge transport, low trap densities and efficient charge collection at the contacts.5,6Methylammonium lead iodide (CH3NH3)PbI3 (MAPbI3), synthesized and characterized by Weber in 1978, appeared to be the best in this class of compounds. Apart from simplicity with which it can be obtained and low manufacturing costs, this compound's PCE is almost 20%.7–9 The success of MAPbI3 in the field of photovoltaics inspired researchers to attempt to create among others ultrasensitive photodetectors10,11 and ultrabright diodes emitting light12,13 by means of MAPbX3 (X = Cl, Br, I). In 2014 Koh et al.14 suggested that the MA+ cation should be replaced by the formamidinium one, NH2CH = NH2+ (FA+), in order to improve the efficiency. Research on FAPbI3 revealed a considerable advantage of this compound over the methylammonium analogue resulting mainly from a better thermal stability and smaller bandgap which enabled, among other things, a near-infrared absorption.15–21 Moreover, Rehmen et al.22 have proved that the carrier diffusion length of polycrystalline thin films of FAPbI3 reaches 3.1 μm while for MAPbI3 it is limited to hundreds of nanometres.23 An additional advantage of FAPbI3 is the lack of phase transition up to a temperature of 150 °C (in contrast to the methylammonium analogue); for this reason, the material in question seems to be much better suited for commercial use.24
The discovery of several solar cells based on FA+ in spite of considerable research on perovskite structures25,26 based in turn on FA+, physicochemical properties of the main precursor, formamidinium iodide (FAI), have not been well explored yet. Consequently, the knowledge of FAI's properties and crystal structure can lead to better understanding of the process of crystallization of perovskites based on FA+, and contribute to designing organic–inorganic perovskite materials of specific qualities.
Given the results presented by Petrov et al.,27 it seems that FAI undergoes two reversible phase transitions at about 346 K and 387 K, and is described by monoclinic symmetry (space group P21/c) in the room temperature phase. PXRD data gathered at different temperatures (along with thermal analysis) confirm the existence of orthorhombic and cubic phases at 358 K and 400 K, respectively (Scheme 1).
 | ||
| Scheme 1 The phase diagram for FAI.27 | ||
Experimental
Sample preparation
FAI (NH2CH = NH2+I−) was purchased from commercial sources (Aldrich; ≥98%) and used without further purification. Single crystals suitable only for optical measurements were obtained by recrystallization from an anhydrous ethanol solution at constant room temperature. The purity of the FAI was verified by XRD (see Fig. S1 in ESI†) and by elemental analysis. The mass percentages for FAI were: N 16.19% (16.29%); C 6.93% (6.98%); H 2.80% (2.93%). The values in parentheses are theoretical. Fig. 1 presents views of the sample as a powder (Fig. 1(a)) and crystals (Fig. 1(b)). Deuterated crystals were obtained by threefold recrystallization from a solution of (NH2CH = NH2+I−) in D2O (∼99.8%). In each step of the crystallization 2 g of FAI were dissolved in 50 ml of hot D2O. The estimated value of deuterium concentration in (ND2CH = ND2+I) from IR and Raman powder spectra is more than 90–92% for the protons attached to the nitrogen atoms (see Fig. S2a, ESI†).Thermal analysis
Differential scanning calorimetry (DSC) heating traces were obtained using a PerkinElmer model 8500 differential scanning calorimeter calibrated using n-heptane and indium in the temperature range 300–400 K.Thermogravimetric analysis (TGA) and differential thermal analysis (DTA) measurements were carried out using a Setaram SETSYS 16/18 instrument from 300 to 660 K with a ramp rate of 5 K min−1 under nitrogen (flow rate: 1 dm3 h−1).
Dilatometric measurements
Dilatometric measurements were performed using a Perkin Elmer TMA-7 thermomechanical analyser from 325 to 395 K with a scanning rate of 3 K min−1. The measurement was carried out on a powder sample as a pellet with height h = 3 mm.Dielectric measurements
The complex dielectric permittivity, ε* = ε′ − iε′′, was measured between 300 and 400 K using an Agilent E4980A Precision LCR Meter in the frequency range between 135 Hz and 2 MHz. The overall error for the real and imaginary parts of the complex dielectric permittivity was less than 5% and 10%, respectively. In the dielectric experiments, polycrystalline material was used in the form of pressed pellets. The diameter of the pellets was 13 mm, and the thickness was 0.75 mm. The overall error in the estimation of the real part of dielectric permittivity value was less than 5%. Gold electrodes were painted on both opposing faces of the pellets. The dielectric measurements were carried out in a controlled atmosphere (N2).DC conductivity
The DC conductivity was measured by a Keithley 6517D electrometer, between 300 and 410 K, with a ramp rate of 2 K min−1. Samples in the form of pellets (S = 20 mm2, d = 1 mm) were made from powder by milling the crystals for 1 min in an agate mortar. The powder at room temperature was uniaxially pressed in a cylindrical die with a diameter of 5 mm, under a 350 MPa compressing stress for 5 min. The surfaces of the pellet were coated with silver conductive paint (Electron Microscopy Sciences, 503).1H NMR
NMR measurements were performed with an ELLAB TEL-Atomic PS 15 spectrometer working at a frequency of 25 MHz. Spin-lattice relaxation times, T1, were measured using a saturation sequence of π/2 pulses followed by a variable time interval τ and a reading π/2 pulse. In the analysed temperature range (90–410 K), the recovery of magnetization was one-exponential. The temperature of the sample was adjusted by liquid nitrogen evaporation and was controlled by a UNIPAN 660 temperature controller operating with a Pt 100 sensor, providing extended temperature stability of better than 1 K. The errors in the measurements of T1 were estimated to be approximately 5%. Measurements of the proton NMR second moment (M2) were carried out with a wide-line ELLAB CW spectrometer operating at 28.2 MHz. M2 values were calculated by the numeral integration of the first derivative of an absorption line and corrected for the finite modulation amplitude.Optical measurements
Optical microscopy observation was carried out by using an Olympus BX53 combined with a LINKAM THM-600 heating/cooling stage, where the temperature was stabilized to within 0.1 K.IR measurements
The infrared spectra of FAI were recorded in a wide temperature range (from 298 to 400 K) in CsI pellets with a Bruker IFS-88 spectrometer in the wavenumber range of 4000–500 cm−1 with a resolution of 1 cm−1 (Fig. S2(b), ESI†). A SPECAC variable temperature cell (P/N 21.500) was used for high-temperature IR spectra measurements. The Grams/368 Galactic Industries program was used for numerical fitting of the experimental data. Gaussian functions were used for fitting the infrared bands. Powder Raman spectra were measured using a Jobin-Yvon Raman-U1000 spectrophotometer equipped with CCD and photomultiplier (PHT) detectors (Fig. S2(b), ESI†). The actual spectra were measured with PHT detector applying GAME laser (λ = 532 nm) with power equal to 450 mW for the exciting beam laser. The spectra were measured in the region between 3600 and 10 cm−1 with a resolution of 2 cm−1. The bands characteristic of the internal vibrations of FAI appear in the measured IR spectra. Proposed assignments (see Table S1†) were determined based on both: (i) theoretical analysis of harmonic IR wavenumbers for formamidine/formamide molecule and cation and (ii) experimental IR and Raman spectra of [FA][Fe(HCOO)3] and [FA][Co(HCOO)3].28Static density functional theory (DFT) calculations in the solid state
A series of full geometry and cell optimizations with the London-type empirical correction for dispersion interactions as proposed by Grimme,29 together with vibrational harmonic frequency calculations, were undertaken to localize the key stationary points on the potential energy surface (PES) of FAI in the solid state. For the calculations, the structural data were taken from Petrov's X-ray diffraction studies.27 The crystal structure at 290 K adopts monoclinic symmetry (P21/c) with cell dimensions a = 4.82116 Å, b = 13.7763 Å, c = 7.011310 Å and β = 98.063° and four formula units in the unit cell (Z = 4). Calculations were performed using the CRYSTAL09 program,30,31 utilizing the DFT method with B3LYP hybrid functional32–35 with two shrinking factors (5, 5) to generate a commensurate grid of k-points in reciprocal space, following the Monkhorst–Pack method.36 Calculations were carried out with the consistent Gaussian basis sets of a triple-zeta valence with polarization quality for solid-state calculations (pob_TZVP_2012) as proposed by Peintinger, Vilela Oliveira and Bredow.37 In addition for the iodine atom, the large core effective core pseudopotential (HAYWLC) proposed by Hay and Wadt coupled with the basis set suitable for use with their large core pseudopotentials has been used.38,39 Calculations of the vibrational frequencies for FAI were performed in CRYSTAL09 at the Γ-point and the data were visualized using the ChemCraft40 and J-ICE41 programs (Fig. S2(c), ESI†).Localised basis set calculations in the gas phase
A series of geometry optimizations, together with vibrational harmonic frequencies calculations, were undertaken to localise the key stationary points on the PES of the complex of FAI in the gas phase. Calculations were performed using the Gaussian 09 package,42 utilizing the Møller–Plesset43 correlation energy correction level truncated at the second order (i.e. MP2), and at DFT levels B3LYP32–35 all coupled with the aug-cc-pVDZ basis set.44,45 The aug-cc-pVDZ-PP46–48 basis set was used for the iodine atom.Results and discussion
Thermal analysis
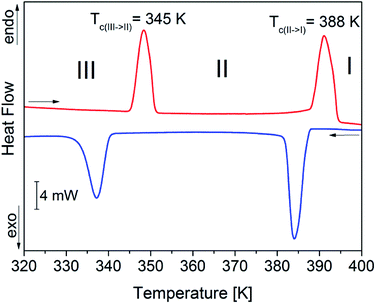
In order to verify the sequence of phase transitions in FAI reported by Petrov et al.,27 the DSC method was applied (see Fig. 2). FAI undergoes two reversible phase transitions at 345/341 K (heating/cooling) from phase III to II and at 388/387 K from phase II to I. It should be noted that the shape of thermal anomalies and the presence of thermal hysteresis indicate the discontinuous nature of these structural transformations. Moreover, the heat anomalies are accompanied by significant values of entropy changes, which are ΔS(III→II) = 9 J mol−1 K−1 and ΔS(II→I) = 10 J mol−1 K−1, suggesting an ‘order–disorder’ mechanism. FAI reveals also very high thermal stability among amine hydrohalides which is ca. 520 K (see Fig. S3, ESI†). The estimated entropy of melting (ΔSmelting ≈ 17 J mol−1 K−1) appeared to be comparable to the sum of entropy changes (ΔS(III→II) + ΔS(II→I)) for both transitions. It is characteristic for ionic crystals, exhibiting high-temperature plastic phase, where only one component (asymmetric cation) contributes to the resultant entropy changes at structural transitions.The appearance and reversibility of the solid-to-solid phase transitions were confirmed additionally by dilatometric measurements (as shown in Fig. S4, ESI†). In the vicinity of transition III → II the change in the crystal size varies in the threshold of 0.5%. In the case of the second phase transition II → I the change is significant (2%).
Dielectric properties
The temperature dependence of the real (ε′) and imaginary (ε′′) parts of the complex dielectric permittivity are presented in Fig. 3(a) and (b). The solid-to-solid phase transition from ordered (phase III) to semi-ordered (phase II) is pronounced as a jump in the real part, ε′, with a dielectric increment (Δε) which equals ca. 3. On the other hand, the transition from the semi-ordered (phase II) to orientationally disordered (phase I) is significant and accompanied by a rapid increase of ε′ and ε′′ near Tc = 388 K. It should be noted that the high value of ε′ at 2 MHz and the outline of the frequency dependency of the electric permittivity indicate that the dynamics of polar FA+ cations is fast and that the dielectric relaxation process is expected to appear at least in the microwave frequency region (f > 2 MHz).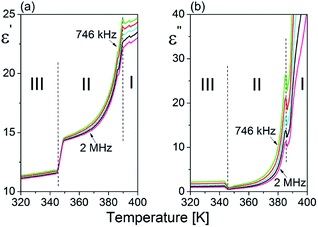 | ||
| Fig. 3 Temperature dependence of the (a) real (ε′) and (b) imaginary (ε′′) parts of the complex dielectric permittivity (ε*) measured for a powder sample of FAI upon heating. | ||
The conductivity effects are pronounced in all phases, as is shown in Fig. 4, and significantly enhanced at higher temperatures. In the ordered phase (III) the AC conductivity equals ca. 3.5 × 10−5 S m−1 (for 200 Hz) and increases up to 2 × 10−4 S m−1 at the highest frequency (2 MHz) (see Fig. 4(a)). In the semi-ordered phase (II) the AC conductivities are comparable with those obtained in phase III (Fig. 4(b)). While, in the high-temperature phase I, due to the overall molecular tumbling which occurs in the plastic phase, the AC conductivity rises abruptly (∼0.05–0.1 S m−1) and strong temperature dependence is observed (see Fig. 4(c)).
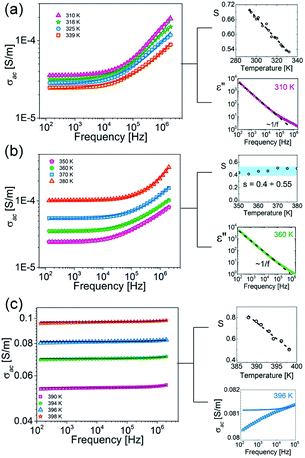 | ||
| Fig. 4 Frequency dependence of the AC conductivity [S m−1], on log–log scale, measured in (a) III, (b) II, (c) I solid phases at selected temperatures. | ||
The AC conductivity behaviours, in each phase, were analysed by using conductivity formalism, i.e. universal power law (UPL) predicted by Jonscher.49 According to this, the total conductivity σAC at angular frequency ω and temperature can be written as:
| σAC(ω) = ε0ε′′ω = σDC + Aωs | (1) |
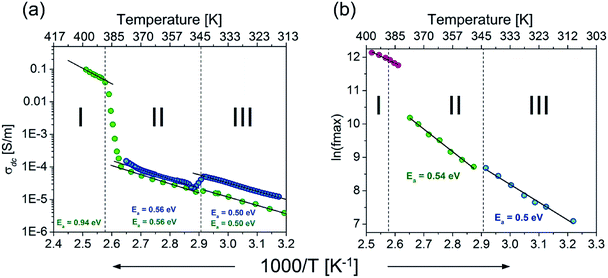
For all solid phases, the AC conductivities for different temperatures were fitted to eqn (1) and the parameters σDC, A and s were extracted from this analysis. Continuous lines in Fig. 4 represent the UPL fit at different temperatures. For temperatures above the II → I phase transition, towards low frequencies, f < 10 kHz, the conductivity starts to decrease again, reaching values below the DC plateau. This effect is presented in the right-hand plot in Fig. 4(c) at 396 K. This decrease is connected with blocking electrode effects, which is typical for ionic conductors.50,51 As is shown in the right-hand plots in Fig. 4(a) and (b), the usual ε′′ ∼ 1/f behaviour, arising from DC conductivity via the relation ε′′ = σAC/(2πfε0), and these effects are observed in all phases. In the case of phases III and I, the power exponent, s, decreases with temperature. For the semi-ordered phase (II) s is almost constant and varies between 0.4 and 0.55. These characteristics are typical for hopping charge transport on the basis of the correlated-barrier-hopping model:52 the charge transport between localized states due to hopping over the barrier can be found in many kinds of disordered matter and ionic conductors.53,54 Therefore, simultaneously with the dielectric measurements, the direct current conductivity, σDC, measurement was also carried out. The result of this experiment is depicted in Fig. 5 (blue colour). Also in Fig. 5, the temperature dependencies of σDC, obtained from fitting eqn (1) to experimental data from the alternating current measurements (green), are presented.
The plots were found to be linear and fitted using the Arrhenius equation:
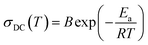 | (2) |
In the case of phase I, the measurement in the direct current manner was completely impossible due to very low values of the resistance. However, the very good agreement in the slope of the plots from DC and AC measurements in phases III and II would suggest that similar energy barriers should be obtained in phase I. The values of the barrier and values of conductivity suggest that the crystals possess semiconducting properties over all phases.
It is well known that the conductivity effect can be highly suppressed by the electric modulus representation of experimental data. Complex electric modulus can be used for analysing the dielectric behaviour of an insulating material, especially at high temperatures, where complex permittivity usually becomes very high due to electrode polarization and carrier transport. From the physical aspect, in materials where the electric displacement is constant, electric modulus corresponds to the relaxation of the electric field in the material.
The complex electric modulus (M*) is defined as the inverse of the complex relative permittivity ε* and is represented as:
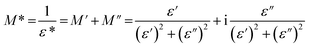 | (3) |
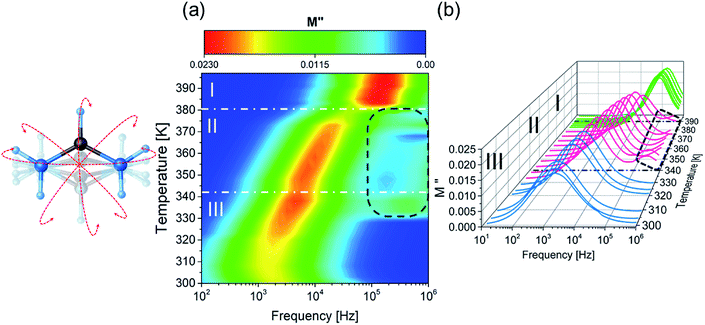
The imaginary part of electric modulus, calculated from eqn (3) for FAI crystals, is presented in Fig. 6. For the III and II phases, the maximum of M′′(f) is shifted towards lower frequencies with the temperature increasing, which indicates the rate of the relaxation process. The relaxation process in the low-temperature phase occurs at 320 K, and extends to the intermediate phase (II) (Fig. 6(a)). In addition, the second relaxation process occurs in this phase, as is shown in Fig. 6(b) as a dotted black line, but the maxima of the M′′ shift towards the higher region of frequency, above 1 MHz. The mechanism of the III → II phase transition may be described as an order–semiorder transition and the movement of polar FA+ cations is at least between two energetically equivalent positions.
This was confirmed by thermal analysis, according to the Boltzmann relation ΔS = R![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) N, where N is 2.9. In the high-temperature phase (I), the maxima of M′′ are practically frequency independent, which is probably due to the fact that the motions of dipolar groups are too fast to be detected with the used range of frequencies (1 MHz). Due to (i) the increasing number of energetically equivalent positions from phase II to I (N = 3.3) and (ii) the dielectric processes which shift towards higher frequencies, we can conclude that in this case, we deal with the semiordered-disordered type of transition. A similar observation was made for the typical plastic crystal of adamantane derivatives.55,56
N, where N is 2.9. In the high-temperature phase (I), the maxima of M′′ are practically frequency independent, which is probably due to the fact that the motions of dipolar groups are too fast to be detected with the used range of frequencies (1 MHz). Due to (i) the increasing number of energetically equivalent positions from phase II to I (N = 3.3) and (ii) the dielectric processes which shift towards higher frequencies, we can conclude that in this case, we deal with the semiordered-disordered type of transition. A similar observation was made for the typical plastic crystal of adamantane derivatives.55,56
The characteristic frequency associated with the relaxation process was determined from the peak of the imaginary part of the electric modulus. It can be seen that the characteristic frequency satisfies a linear dependence and hence fulfils the Arrhenius law:
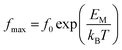 | (4) |
From the numerical fitting analysis, the activation energy of the relaxation process was calculated to be ca. 0.5 and 0.54 eV for phases III and II, respectively. It is worth noting that the activation energies for relaxation process and DC and AC conduction are in a good agreement. This suggests that similar energy barriers are involved in both the relaxation and conduction processes.
Optical properties
The thermal evolutions of the ferroelastic domain structure observed under a polarizing microscope are illustrated in Fig. 7. As-grown single crystals of FAI without any external strain in phase III are usually monodomain samples (see Fig. 7(a)). On the other hand, one can enforce the formation of the ferroelastic domain structure by pressing the sample perpendicular to the bc plane. The distortion of the crystal lattice during phase transition III → II leads to the appearance of plate-like ferroelastic domains which were observed in the bc plane (see Fig. 7(b)). In phase II the domain walls are inclined with respect to the a-axis at an angle of ca. 48°. Return to phase III generates new domain walls which intersect with ones characteristic of phase II at an angle of ca. 65° (see Fig. 7(c)).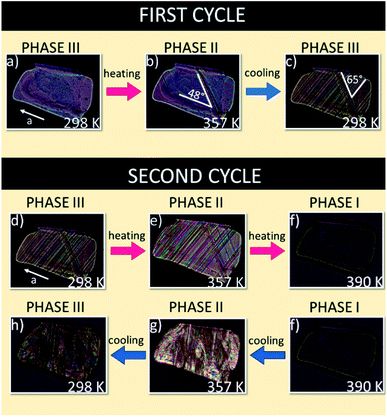 | ||
| Fig. 7 Evolution of the domain structure during heating and cooling scans for FAI sample seen in the bc plane. | ||
During the second cycle the phase transitions III → II at 345 K (Fig. 7(d and e)) and II → I at 388 K (Fig. 7(e and f) lead to the monodomain sample, prototypic phase I (see Fig. 7(f)). The following cooling of the sample, through the transition I → II, leads to a very complex picture of domain structure due to the enormous distortion of the crystal at 388 K (Fig. 7(f–h)). It should be emphasized that the thermal evolution of the domain structure confirms the presence of ferroic phase transitions at 345 and 388 K and that is in a good agreement with the X-ray diffraction results by Petrov et al.27 which postulated the change in the crystal symmetry from monoclinic, via orthorhombic to cubic.
The evolution of the ferroelastic domain structure with temperature transitions was presented in film F1 (ESI†). In the first heating cycle the transition from monoclinic phase III to orthorhombic phase II was recorded; then, we can see the cooling cycle and reversible transition to III phase. Next, upon second heating we can see the renewed transition from III phase to II phase and up to cubic phase (I). The last view presents the transition from phase I to phase III during the cooling scan.
Proton magnetic resonance studies (1H NMR)
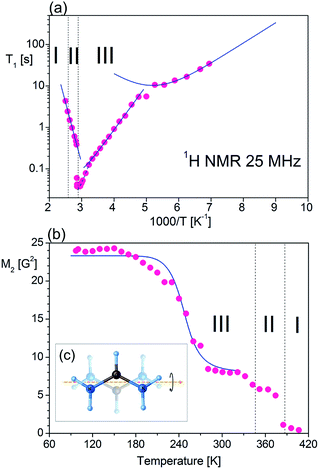
The measurement of the temperature dependence of the spin-lattice relaxation time (T1) of FAI was performed, as shown in Fig. 8(a). During heating (from T1 = 33.3 s at 144 K) one can observe that the relaxation time decreases continuously and forms characteristic minimum with T1min = 10.4 s at 190 K. Further heating of the sample leads to a sudden linear decrease of T1 (170 ms at 304 K) and then an even bigger slope appears down to T1 = 40 ms at 338 K. At Tc (III→II), T1 increases rapidly and becomes almost ten times longer (T1 = 384 ms at 352 K). Unfortunately, the expected local minimum of relaxation time has been obscured by the strong influence of both phase transitions on molecular dynamics of FA+. Therefore we may estimate the activation energies only for three slopes starting from low temperatures: 20.5 kJ mol−1, 39.7 kJ mol−1 and 56.4 kJ mol−1, respectively.For low-temperature relaxation minimum we fit the T1 data with the BPP-type equation:57
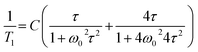 | (5) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(Ea/RT). The obtained molecular dynamics parameters were as follows: the activation energy Ea = 9.17 kJ mol−1, the correlation time τc0 = 1.1 × 10−11 s and the relaxation constant C = 1.07 × 107 s−2. These parameters indicate a small angle restricted librational motion of all the FA+ cations or some of them. Between 210 and 346 K (within phase III), the relaxation time T1 decreases linearly with temperature showing two different slopes with Ea of ca. 20.5 and 40 kJ mol−1 for the ranges 210–306 and 306–346 K, respectively. In turn, the phase transition at 346 K is accompanied by a drastic jump in T1 from 60 ms to 380 ms. Next, in phase II a significant increase in the Ea value up to 56 kJ mol−1 is observed. Visible increases in Ea values indicate the subsequent activation of various available rotational axes of the formamidinium cation, i.e. parallel to the N–N axes (within phase III) and above 346 K around the axes perpendicular to the N–N line. The temperature dependence of the second moment of the proton resonance lines, M2, of FAI is shown in Fig. 8(b).
exp(Ea/RT). The obtained molecular dynamics parameters were as follows: the activation energy Ea = 9.17 kJ mol−1, the correlation time τc0 = 1.1 × 10−11 s and the relaxation constant C = 1.07 × 107 s−2. These parameters indicate a small angle restricted librational motion of all the FA+ cations or some of them. Between 210 and 346 K (within phase III), the relaxation time T1 decreases linearly with temperature showing two different slopes with Ea of ca. 20.5 and 40 kJ mol−1 for the ranges 210–306 and 306–346 K, respectively. In turn, the phase transition at 346 K is accompanied by a drastic jump in T1 from 60 ms to 380 ms. Next, in phase II a significant increase in the Ea value up to 56 kJ mol−1 is observed. Visible increases in Ea values indicate the subsequent activation of various available rotational axes of the formamidinium cation, i.e. parallel to the N–N axes (within phase III) and above 346 K around the axes perpendicular to the N–N line. The temperature dependence of the second moment of the proton resonance lines, M2, of FAI is shown in Fig. 8(b).
Between 97 K and 150 K, the second moment has a plateau of about 24 G2. Above 150 K the M2 value continually decreases to about 8 G2 at 180 K showing the main reduction of 1H NMR line which occurs in this temperature range. Above 320 K the value of the second moment slowly decreases to 370 K where a sudden drop in the value of M2 is observed. It should be stressed that the complete reduction tends to the vanishing of the second moment and FAI becomes like a liquid. The theoretical calculation of the dipolar second moment M2 for the rigid structure obtained from XRD was derived by van Vleck:58
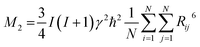 | (6) |
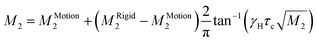 | (7) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(Ea/RT), and MRigid2 and MMotion2 are the second-moment values before and after the onset of a given motion, respectively. The reduction of the second moment has been fitted according to eqn (6) with Ea of 29.8 kJ mol−1 and correlation time of 3.2 × 10−12 s. Such high values of the fitting parameters indicate the process of breaking of hydrogen bonds before the possible reorientation motions of FA+. The detailed analysis of the M2 behaviour indicates that, during heating over phase III (mainly between 180 and 270 K), FA+ undergoes reorientations along the axis defining the centre of gravity of the cation (around the axis which is parallel to the N–N line as presented in Fig. 8(c)). Note that the reached value above 270 K is greater than 1/4 of the second-moment value before reduction (∼8 G2 instead of expected 6 G2). This fact suggests that the rotation of FA+ around the mentioned axis is not fully free and may be limited by stronger hydrogen bonds. The next small reduction of the M2 value (from 8 G2 to 6 G2) which occurs just before the first phase transition at 346 K indicates the breaking of the hydrogen bonds and the onset of the free rotation of the organic cations around the axis parallel to the N–N line. Approaching the phase transition at 388 K, the next sudden reduction of M2 is visible (the value of the second moment practically decays to a fractional value) suggesting the tumbling reorientations of the organic cations.
exp(Ea/RT), and MRigid2 and MMotion2 are the second-moment values before and after the onset of a given motion, respectively. The reduction of the second moment has been fitted according to eqn (6) with Ea of 29.8 kJ mol−1 and correlation time of 3.2 × 10−12 s. Such high values of the fitting parameters indicate the process of breaking of hydrogen bonds before the possible reorientation motions of FA+. The detailed analysis of the M2 behaviour indicates that, during heating over phase III (mainly between 180 and 270 K), FA+ undergoes reorientations along the axis defining the centre of gravity of the cation (around the axis which is parallel to the N–N line as presented in Fig. 8(c)). Note that the reached value above 270 K is greater than 1/4 of the second-moment value before reduction (∼8 G2 instead of expected 6 G2). This fact suggests that the rotation of FA+ around the mentioned axis is not fully free and may be limited by stronger hydrogen bonds. The next small reduction of the M2 value (from 8 G2 to 6 G2) which occurs just before the first phase transition at 346 K indicates the breaking of the hydrogen bonds and the onset of the free rotation of the organic cations around the axis parallel to the N–N line. Approaching the phase transition at 388 K, the next sudden reduction of M2 is visible (the value of the second moment practically decays to a fractional value) suggesting the tumbling reorientations of the organic cations.
Vibrational properties
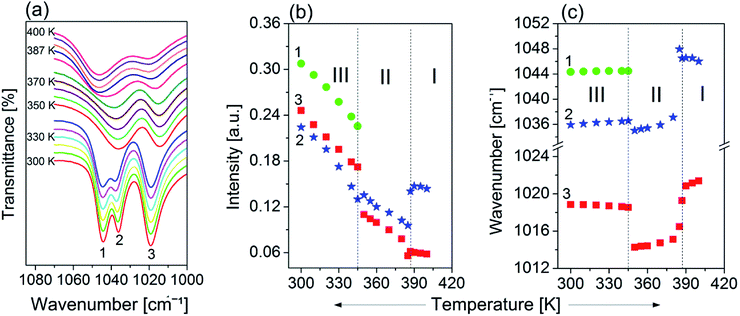
The infrared spectra of the powdered FAI sample in Nujol (300 and 400 K) CsI, Fluorolube and FIR at 300 K and the FT-Raman spectra at 300 K are presented in Fig. S2(b) (ESI†). The role of the FA+ cation in the molecular mechanism of the high-temperature phase transitions was also analysed by temperature-variable infrared spectroscopy. As the most prominent example of such a role, we present the temperature evolution of the bands in the IR spectra between 1080 and 1000 cm−1 (see Fig. 9(a)). Two well-separated components are distinguished at room temperature. One of them, at ca. 1019 cm−1 (marked as 3), is a well-shaped single band, while the other creates the characteristic doublet with the following band positions: 1044 cm−1 (1) and 1036 cm−1 (2). It should be noted that the nature of the observed changes for all three modes is similar and related to their intensity reductions when temperature increases (Fig. 9(b)). This tendency is well visible mainly over phase III, while the most remarkable anomalies are seen during the first phase transition at 345 K related to the change in the multiplicities of the higher-frequency band.As a consequence, only two broad and single bands are observed in phases II and III. Drastic changes are also observed regarding the positions of the selected peaks while being heated. As presented in Fig. 9(c), positions of the peaks 1, 2 and 3 change slightly with temperature over phase III; nevertheless at Tc (III → II) stepwise anomalies are observed for modes 2 and 3 which are related to shifting towards lower wavenumbers by almost 2 and 6 cm−1 respectively. As has already been mentioned, the mechanism of mode 1 vanishes during the III → II phase transition, whereas bands 2 and 3 shift towards higher frequencies over phases II and III, and experience another strong (discontinuous) change of their positions (Tc (II → I)), but this time towards the opposite direction.
It should be also emphasized that the changes in the band positions of selected vibrations during phase transitions are extraordinarily large and confirm the key role of FA+ in the order–disorder mechanism of these structural transformations.
Static calculations in the condensed and gas phase
Optimized and selected geometrical parameters together with the unit cell parameters at the DFT level with the B3LYP functionals with dispersion corrections are listed in Table 1, whereas the structure in the unit cell is presented in Fig. 10. The reliability of obtained results can be confirmed by comparison with the experimental data for the crystal of FAI published by Petrov and co-workers.27 The static calculations correctly predict that in this case, we have a confirmed occurrence of the intermolecular hydrogen bond N–H⋯I. The experimental (3.622 Å) and calculated (3.765 Å) values of distances between heavy atoms (N⋯I) in the hydrogen bridge are very similar and typical for weak hydrogen bonds. It is also important to add that these hydrogen contacts are quite nonlinear and values of the hydrogen bond angles are equal to 155.76° (exp.) and 150.41° (calc.). Taking the above into account, we cannot agree with the statement of previous authors27 that in FAI we deal with strong hydrogen bonds. In order to verify this issue, we have carried out simulations for isolated gas-phase FAI. The calculations clearly indicate that a strong hydrogen bond is formed in the complex, but it has completely different geometric parameters. Calculations at the MP2 and DFT method levels in the gas phase indicate that the distance between two heavy atoms (N⋯I) in the hydrogen bridge is 3.221 Å and 3.248 Å respectively and angles equal to about 151.52° and 153.02°, respectively. This distance is definitely shorter (ca. 0.401 Å) than in the crystal phase. This is strictly due to the crystal lattice structure and spatial volume occupied by the iodide anion. This fact contributes to the significant elongation of the hydrogen bond in the studied crystal.| Parameter | B3LYP/pob_TZVP_2012/(HAYWLC) | Exptl.27 |
|---|---|---|
| N–C | 1.307 | 1.301 |
| N–C | 1.312 | 1.309 |
| N–H | 1.015 | 0.899 |
| N–H | 1.017 | 0.901 |
| N–H | 1.013 | 0.899 |
| N–H | 1.014 | 0.900 |
| C–H | 1.083 | 0.950 |
| N–H | 2.751 | 2.772 |
| N⋯I | 3.765 | 3.622 |
| <N–C–N | 124.34 | 125.81 |
| <H–N–H | 118.95 | 120.03 |
| <H–N–H | 117.94 | 120.00 |
| <H–N–C | 121.97 | 120.37 |
| <H–N–C | 122.00 | 120.27 |
| <N–C–H | 118.28 | 117.13 |
| <N–C–H | 117.37 | 117.06 |
| <N–H⋯I | 150.41 | 155.76 |
| a | 4.442 | 4.821 |
| b | 15.656 | 13.776 |
| c | 7.575 | 7.011 |
| α | 90.00 | 90.00 |
| β | 102.48 | 98.06 |
| γ | 90.00 | 90.00 |
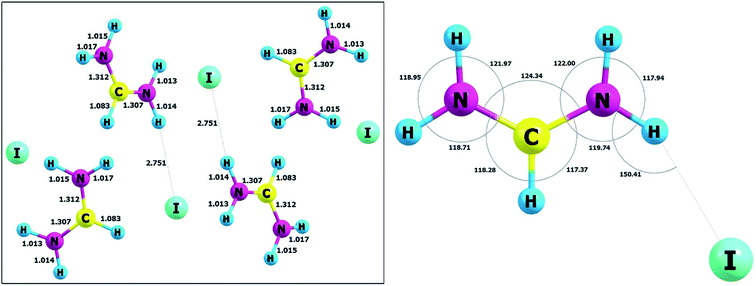 | ||
| Fig. 10 The unit cell and atom labelling (left) and molecular angles (right) of FAI crystal after optimization. | ||
However, in our opinion, the hydrogen bonds in FAI should be classified into the group of weak hydrogen bonds which, in turn, are strong enough to stabilize the entire crystal system. The static DFT calculations in the solid state also confirm that the FA+ cation and iodide anion form a tight ionic pair by a weak N–H⋯I hydrogen bond and create zigzag-like chains propagating toward [2 0 1] via strong N–H⋯I hydrogen bonds. The hydrogen-bonded chains are further packed in stacks along [1 0 0]. In our opinion, the creation of such specific chains of hydrogen bonds may induce the occurrence of the phenomenon of sigma cooperative type of hydrogen bonds. This effect promotes the increase in the strength of the hydrogen bonds themselves and, consequently, the strength of the interactions in the entire crystal structure. However, regardless of the philosophy of classifying the strength of hydrogen bonds, it can be concluded that these interactions have a very important role in stabilizing the crystal structure and are also very important for the phase transition mechanism.
One can expect the dispersion correction to have no influence on the chemical bonds. The most important influence of dispersion forces is on the values of the unit cell parameters as presented in Table 1.
For a and c lattice constants the dispersion correction is important and it reproduces values very well; on the other hand, a completely different picture is observed for the b parameter. For calculations with B3LYP density functional, the value of b parameter (15.656 Å) is too large in comparison to the experimental value of 13.776 Å.27 The large influence of the dispersion term on the b-axis parameter is probably due to the crystal structure of FAI and depends on the packing of hydrogen bond chains and the direction of interactions.
In standard ab initio calculations, the vibrational frequencies are calculated at the harmonic level. Selected harmonic vibrational frequencies from the static DFT simulations of FAI crystal and available experimental data (IR) together with tentative assignments are presented in Table S1.† Fig. S2(c) (ESI†) presents a comparison of experimental and calculated spectra of FAI crystal. As can be seen in Fig. S2(b) (ESI†), the theoretical spectrum is shifted towards higher frequencies by about 170–120 cm−1 or less, depending on the band. This is due to the harmonic approximation used for calculations; however, it should be noted that the shape of the bands has been very well reproduced. The approximation applied does not prevent proper band assignment. As normally expected, the frequencies calculated at the harmonic approximation are somewhat higher than experimental data, due chiefly to the neglect of anharmonicity. The vibrational analysis is very important since it proves the results from the theoretical simulation are correct. The infrared spectrum is very sensitive to structural changes during simulation especially for molecular systems with hydrogen bonds. Comparison of the experimental frequencies and those calculated at the DFT method level with the harmonic approximation shows only small differences for the characteristic molecular group; see Table S1 (ESI†). It should also be added that theoretical simulations were extremely helpful in identifying individual vibration contributions in the experimental spectrum and in assigning bands, especially for the νas(NH2)/νNH⋯I (3337/3336/3528 cm−1) molecular grouping bands and combination vibrations such as: νas(NCN) + δ(NH2) + δ(CH) or ρ(NH2) + δ(CH) + γ(CH). Our results also are in accordance with the experimental and theoretical work of Kucharska et al.28 considering the formamidinium cation [NH2–CH–NH2]+.
Conclusion
The main aim of the presented study was to analyse in detail the dynamic properties of dipolar formamidinium cations of FAI in a wide temperature range covering three phases, from ordered (monoclinic phase III) via partially disordered (orthorhombic phase II) to highly disordered (cubic phase I). FAI undergoes two reversible phase transitions at about 345 K (III → II) and 388 K (II → I). The observations of FAI under a polarizing microscope showed that the drastic symmetry breaking between monoclinic, orthorhombic and cubic phases is accompanied by the appearance of the ferroelastic domain structure in phases III and II, whereas phase I is a paraelastic prototypic phase. Thermal characteristics of FAI (DSC and dilatometric measurements) confirmed first-order character of both ferroic phase transitions with a clear ‘order–disorder’ feature.The results of AC conductivity measurements indicate unquestionably the semiconducting properties of FAI in a wide temperature range. Moreover, the AC conductivity reveals a dispersion process at low frequencies (between 135 Hz and 10 kHz) which obeys Jonscher's power law. The change in the exponent s in AC conductivity dispersion term (Aωs) makes the nature of the conductivity mechanism apparent as localized hopping of the charges which is a thermally activated process. Over phase I, the prominent effect of the DC conductivity is observed. It should be highlighted that dielectric properties mentioned above are related to the isotropic overall reorientational motion of ions and are characteristic of plastic crystals. The results of electric modulus derived from dielectric permittivity data provide information about the nature of dielectric relaxation and the same values of the activation energy as for AC and DC indicate that similar barriers are involved in both the relaxation and conduction processes.
The spin-lattice relaxation time (T1) of 1H NMR measurements showed that phases III and II are dominated by the rapid reorientation of the FA+ cations around the axis which is parallel to the N–N line, whereas in phase I the overall rotation of cations is evidenced. Dielectric response around 387 K and the entropy change effects for the both phase transitions and the melting as well as the M2 (1H NMR) values at high temperatures clearly indicate the plastic behaviour of phase I. The drastic changes in the motional state of the formamidinium moieties with temperature are reflected well in the infrared spectra around both phase transitions.
The static calculations in the condensed phase conducted at the DFT method level with B3LYP functionals with dispersion corrections reproduce very well the geometrical parameters together with the unit cell parameters and also proved to reproduce very well the infrared spectra of the studied system.
The isotopic effect in FAI ((NH2CH = NH2+I−) → (ND2CH = ND2+I−)) appeared to be weak; however, it is reflected in the temperature shift of Tc (III→II) by ca. +1 K whereas for Tc (II→I) by ca. +5 K. This suggests that the changes in the hydrogen bond configurations are essential in the molecular mechanism of phase transition (II → I) in spite of the fact that N–H⋯I hydrogen bonds are quite weak. Investigations of organic plastic materials allow for a deeper understanding of the interrelation between the crystal structure and the physicochemical properties of simple organic compounds. They are essential for designing new multi-functional materials based on simple precursors used in the synthesis of useful and important solar-cell systems.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors (Klaudia Mencel and Piotr Durlak) would like to gratefully acknowledge the Wroclaw Centre for Networking and Supercomputing (WCSS) for allocation of computer time on the BEM Cluster. The calculations also were performed at the Interdisciplinary Centre for Mathematical and Computational Modeling (ICM), Warsaw University under grant no. G60-18. Project supported by Wroclaw Centre of Biotechnology, programme the Leading National Research Centre (KNOW) for years 2014–2018.References
- A. Kojima, K. Teshima, Y. Shirai and T. Miyasaka, J. Am. Chem. Soc., 2009, 131, 6050–6051 CrossRef PubMed.
- R. Hamaguchi, T. Miyasaka, H. Kunugita, K. Ema, Y. Takeoka and M. Rikukawa, Chem. Commun., 2017, 53, 4366–4369 RSC.
- A. Kojima, M. Ikegami, K. Teshima and T. Miyasaka, Chem. Lett., 2012, 41, 397–399 CrossRef.
- Q. Chen, N. De Marco, Y. Michael, T. Song, C. Chen and H. Zhao, Nano Today, 2015, 10, 355–396 CrossRef.
- G. Xing, N. Mathews, S. S. Lim, N. Yantara, X. Liu, D. Sabba, M. Grätzel, S. Mhaisalkar and T. C. Sum, Nat. Mater., 2014, 13, 476–480 CrossRef PubMed.
- G. Xing, N. Mathews, S. Sun, S. S. Lim, Y. M. Lam, M. Graẗzel, S. Mhaisalkar and T. C. Sum, Science, 2013, 342, 344–347 CrossRef PubMed.
- H. S. Kim, C. R. Lee, J. H. Im, K. B. Lee, T. Moehl, A. Marchioro, S. J. Moon, R. Humphry-Baker, J. H. Yum, J. E. Moser, M. Grätzel and N. G. Park, Sci. Rep., 2012, 2, 1–7 Search PubMed.
- H. Zhou, Q. Chen, S. L. G. Li, T. B. Song, H. S. Duan, Z. Hong, J. You, Y. Liu and Y. Yang, Science, 2014, 345, 542–546 CrossRef PubMed.
- N. Ahn, D. Y. Son, I. H. Jang, S. M. Kang, M. Choi and N. G. Park, J. Am. Chem. Soc., 2015, 137, 8696–8699 CrossRef PubMed.
- M. I. Saidaminov, V. Adinolfi, R. Comin, A. L. Abdelhady, W. Peng, I. Dursun, M. Yuan, S. Hoogland, E. H. Sargent and O. M. Bakr, Nat. Commun., 2015, 6, 1–7 Search PubMed.
- Z. Lian, Q. Yan, Q. Lv, Y. Wang, L. Liu, L. Zhang, S. Pan, Q. Li, L. Wang and J. Sun, Sci. Rep., 2015, 5, 16563 CrossRef PubMed.
- H. Cho, S.-H. Jeong, M.-H. Park, Y.-H. Kim, C. Wolf, C.-L. Lee, J. H. Heo, A. Sadhanala, N. Myoung, S. Yoo, S. H. Im, R. H. Friend and T.-W. Lee, Science, 2015, 350, 1222–1225 CrossRef PubMed.
- L. M. Pazos, D. Credgington and N. Nanotechnol, Nat. Nanotechnol., 2014, 9, 687–692 CrossRef PubMed.
- T. M. Koh, K. Fu, Y. Fang, S. Chen, T. C. Sum, N. Mathews, S. G. Mhaisalkar, P. P. Boix and T. Baikie, J. Phys. Chem. C, 2014, 118, 16458–16462 CrossRef.
- C. C. Stoumpos, C. D. Malliakas and M. G. Kanatzidis, Inorg. Chem., 2013, 52, 9019–9038 CrossRef PubMed.
- G. E. Eperon, S. D. Stranks, C. Menelaou, M. B. Johnston, L. M. Herz and H. J. Snaith, Energy Environ. Sci., 2014, 7, 982–988 RSC.
- J. Huang, Y. Yuan, Y. Shao and Y. Yan, Nat. Rev. Mater., 2017, 2, 17042 CrossRef.
- J. Kim, N. Park, J. S. Yun, S. Huang, M. A. Green and A. W. Y. Ho-Baillie, Sol. Energy Mater. Sol. Cells, 2017, 162, 41–46 CrossRef.
- C. Li, Q. Guo, H. Zhang, Y. Bai, F. Wang, L. Liu, T. Hayat and A. Alsaedi, Nano Energy, 2017, 40, 248–257 CrossRef.
- F. Ma, J. Li, W. Li, N. Lin, L. Wang and J. Qiao, Chem. Sci., 2016, 8, 800–805 RSC.
- Y. Zhao, X. Xu, H. Zhang, J. Shi, L. Zhu and H. Wu, J. Power Sources, 2017, 359, 147–156 CrossRef.
- W. Rehman, R. L. Milot, G. E. Eperon, C. Wehrenfennig, J. L. Boland, H. J. Snaith, M. B. Johnston and L. M. Herz, Adv. Mater., 2015, 27, 7938–7944 CrossRef PubMed.
- S. D. Stranks, S. D. Stranks, G. E. Eperon, G. Grancini, C. Menelaou, M. J. P. Alcocer, T. Leijtens, L. M. Herz, A. Petrozza and H. J. Snaith, Science, 2014, 342, 341–344 CrossRef PubMed.
- J. W. Lee, D. J. Seol, A. N. Cho and N. G. Park, Adv. Mater., 2014, 26, 4991–4998 CrossRef PubMed.
- S. Pang, H. Hu, J. Zhang, S. Lv, Y. Yu, F. Wei, T. Qin, H. Xu, Z. Liu and G. Cui, Chem. Mater., 2014, 26, 1485–1491 CrossRef.
- A. I. Au, H. A. Evans, E. C. Schueller, S. R. Smock, G. Wu, R. Seshadri and F. Wudl, Inorganica Chim. Acta, 2017, 468, 280–284 CrossRef.
- A. A. Petrov, E. A. Goodilin, A. B. Tarasov, V. A. Lazarenko, P. V. Dorovatovskii and V. N. Khrustalev, Acta Crystallogr., 2017, E73, 569–572 CrossRef PubMed.
- E. Kucharska, J. Hanuza, A. Ciupa, M. Mączka and L. Macalik, Vib. Spectrosc., 2014, 75, 45–50 CrossRef.
- S. Grimme, J. Comput. Chem., 2006, 27, 1787–1799 CrossRef PubMed.
- R. Dovesi, V. R. Saunders, C. Roetti, R. Orlando, C. M. Zicovich-Wilson, F. Pascale, B. Civalleri, K. Doll, N. M. Harrison, I. J. Bush, P. D'Arco and M. Llunell, CRYSTAL09 User's Manual, University of Torino, Torino, 2009 Search PubMed.
- R. Dovesi, R. Orlando, B. Civalleri, C. Roetti, V. R. Saunders and C. M. Zicovich-Wilson, Z. Kristallogr., 2005, 220, 571–573 Search PubMed.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652 CrossRef.
- C. Lee, W. Yang and R. G. Parr, Phys. Rev. B, 1988, 37, 785–789 CrossRef.
- S. H. Vosko, L. Wilk and M. Nusair, Can. J. Phys., 1980, 58, 1200–1211 CrossRef.
- P. J. Stephens, F. J. Devlin, C. F. Chabalowski and M. J. Frisch, J. Phys. Chem., 1994, 98, 11623–11627 CrossRef.
- H. J. Monkhorst and J. D. Pack, Phys. Rev. B, 1976, 13, 5188–5192 CrossRef.
- M. F. Peintinger, D. V. Oliveira and T. Bredow, J. Comput. Chem., 2013, 34, 451–459 CrossRef PubMed.
- W. R. Wadt and P. J. Hay, J. Chem. Phys., 1985, 82, 284–298 CrossRef.
- P. J. Hay and W. R. Wadt, J. Chem. Phys., 1985, 82, 270–283 CrossRef.
- G. A. Adrienko, ChemCraft, http://www.chemcraftprog.com Search PubMed.
- P. Canepa, R. M. Hanson, P. Ugliengo and M. Alfredsson, J. Appl. Crystallogr., 2011, 44, 225–229 CrossRef.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. J. A. Montgomery, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, T. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gausian 09, Revision A.02, Gaussian, Inc., Wallingford CT, 2009 Search PubMed.
- C. Møller and M. S. Plesset, Phys. Rev., 1934, 46, 618–622 CrossRef.
- R. A. Kendall, T. H. Dunning and R. J. Harrison, J. Chem. Phys., 1992, 96, 6796–6806 CrossRef.
- D. E. Woon and T. H. Dunning, J. Chem. Phys., 1993, 98, 1358–1371 CrossRef.
- K. A. Peterson, B. C. Shepler, D. Figgen and H. Stoll, J. Phys. Chem. A, 2006, 110, 13877–13883 CrossRef PubMed.
- D. Feller, J. Comput. Chem., 1996, 17, 1571–1586 CrossRef.
- K. L. Schuchardt, B. T. Didier, T. Elsethagen, L. Sun, V. Gurumoorthi, J. Chase, J. Li and T. L. Windus, J. Chem. Inf. Model., 2007, 47, 1045–1052 CrossRef PubMed.
- A. K. Jonscher, Nature, 1977, 267, 673–679 CrossRef.
- S. R. Elliott and A. P. Owens, Philos. Mag. B, 1989, 60, 777–792 Search PubMed.
- T. Bauer, M. Köhler, P. Lunkenheimer, A. Loidl and C. A. Angell, J. Chem. Phys., 2010, 133, 144509 CrossRef PubMed.
- A. Ghosh, Phys. Rev. B, 1990, 42, 1388–1393 CrossRef.
- A. K. Jonscher, Dielectric relaxations in solids, Chelsea Dielectrics Press, London, 1983 Search PubMed.
- S. R. Elliott, Adv. Phys., 1987, 36, 135–217 CrossRef.
- M. Kosmowska, J. Tarasiewicz and M. J. Adamczyk, Chem. Phys. Lett., 2013, 579, 64–67 CrossRef.
- M. Kosmowska, J. Tarasiewicz and H. a. Kołodziej, J. Mol. Struct., 2012, 1016, 8–12 CrossRef.
- N. Bloembergen, E. M. Purcell and R. V. Pound, Phys. Rev., 1948, 73, 679–712 CrossRef.
- J. H. Van Vleck, Phys. Rev., 1948, 74, 1168–1183 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available: Thermal characterization (TGA-DTA), dilatometric and IR measurements. See DOI: 10.1039/c8ra03871f |
| This journal is © The Royal Society of Chemistry 2018 |