Open Access Article
Open Access ArticleWater wettability of graphene: interplay between the interfacial water structure and the electronic structure
Jian
Liu
 *a,
Chia-Yun
Lai
b,
Yu-Yang
Zhang
a,
Matteo
Chiesa
b and
Sokrates T.
Pantelides
ac
*a,
Chia-Yun
Lai
b,
Yu-Yang
Zhang
a,
Matteo
Chiesa
b and
Sokrates T.
Pantelides
ac
aDepartment of Physics and Astronomy, Vanderbilt University, Tennessee 37235, USA. E-mail: Jian.Liu@alumni.stonybrook.edu
bLaboratory for Energy and Nano-Sciences, Khalifa University of Science and Technology, Abu Dhabi, United Arab Emirates
cDepartment of Electrical Engineering and Computer Science, Vanderbilt University, Tennessee 37235, USA
First published on 8th May 2018
Abstract
Wetting phenomena are ubiquitous and impact a wide range of applications. Simulations so far have largely relied on classical potentials. Here, we report the development of an approach that combines density-functional theory (DFT)-based calculations with classical wetting theory that allows practical but sufficiently accurate determination of the water contact angle (WCA). As a benchmark, we apply the approach to the graphene and graphite surfaces that recently received considerable attention. The results agree with and elucidate the experimental data. For metal-supported graphene where electronic interactions play a major role, we demonstrate that doping of graphene by the metal substrate significantly alters the wettability. In addition to theory, we report new experimental measurements of the WCA and the force of adhesion that corroborate the theoretical results. We demonstrate a correlation between the force of adhesion and WCA, and the use of the atomic force microscope (AFM) technique as an alternative measure for wettability at the nanoscale. The present work not only provides a detailed understanding of the wettability of graphene, including the role of electrons, but also sets the stage for studying the wettability alteration mechanism when sufficiently accurate force fields may not be available.
Wetting phenomena are ubiquitous in a variety of practical issues, including adhesion,1 friction,2 interfacial thermal conductance (Kapitza conductance),3,4 to name just a few. Graphene has emerged as an important material for applications where water wettability plays a major role, e.g., as a lubricant,5 small-molecule gas sensor,6,7 desalination membrane,8,9 protective coating from electrochemical degradation,10 promotive coating for dropwise condensation,11etc. Among these applications, to wet or not to wet is the key problem.12,13 More recently, doping-induced tunable wettability was reported for graphene.14,15
Interactions between the wetting liquid and the solid it rests on are responsible for the wetting properties of a surface. The binding energy of individual molecules on the solid surface, obtained by quantum-mechanical calculations, has at times been used as an indicator of wettability.14,16 A better indicator, however, is the water contact angle (WCA), an experimentally easily accessible parameter that characterizes macroscopically a surface's wettability by water.17,18 Large WCA, >90°, signifies hydrophobic behavior, whereas small WCA, <90°, signifies hydrophilic behavior. The past few years have witnessed increasing efforts to understand the wetting mechanism of graphitic carbon surfaces. Theoretical calculations of WCAs of graphitic carbon surfaces have so far been done primarily using classical potentials, by constructing an analytical interaction potential between water and the solid surface based on interatomic Lennard-Jones potentials19–21 or classical molecular dynamics (CMD) simulations.19,22–29 In those pioneering studies with the work-of-adhesion approach, one first computes the work of adhesion of a water slab on a surface and then employs the Young-Dupré equation that relates the work of adhesion to the WCA.19,25–28 Alternatively, CMD can be sued to measures the shape of a water droplet on a surface and extract the WCA.22–24
Though these approaches have provided significant insights into wetting behavior,19,22–28 they depend on the availability of reliable classical potentials. The construction of such potentials becomes a difficult task when many atomic species are present. For example, the interplay between ions such as Ca2+, Mg2+, SO42−, Na+ and Cl− in saline water and calcite (CaCO3) surfaces is responsible for the wettability alteration for oil recovery.30,31 There are also cases, e.g., monolayers on metallic substrates, where explicit electron doping effects may play a major role, requiring electronic-structure calculations. While density functional theory (DFT) is the method of choice for predictive, atomic-scale calculations of interactions at the solid–water interface, the major difficulty lies in the limited time and length scales achievable by quantum MD (QMD) simulations.32 So far there exists only one report of QMD simulations of water nanodroplets, on graphene and hexagonal boron nitride monolayers.33
In this paper, we adopt the method based on the work of adhesion and the Young-Dupré equation, and employ an approximation that allows practical but sufficiently accurate DFT-based determination of the WCA. Benchmark calculations confirm that graphitic carbon surfaces are nonpolar and intrinsically hydrophilic, with their wettability determined by the dispersive interaction. The WCA gradually decreases with increasing number of graphene layers N, while a monolayer of adsorbed hydrocarbons is sufficient to render graphene hydrophobic, complementing similar results obtained using classical potentials.20,21,25,34 In the presence of a metal substrate, electronic structure comes into play and electron doping of the graphene sheet by the metal substrate alters the wettability of graphene. We report new WCA and AFM (atomic force microscopy) measurements for Cu-supported monolayer and multilayer graphene that further corroborate the theoretical results. Finally, we demonstrate a correlation between the force of adhesion and WCA, and the use of the AFM technique as an alternative measure for wettability at the nanoscopic scale.
Theory
Starting with the Young-Dupré equation,35 the work of adhesion Wadh is related to the surface tension γ of a two-phase interface (S-solid; L-liquid; V-vapor) byWadh = γSV + γLV − γSL = γLV(1 + cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ) θ) | (1) |
We note that γ in the Young-Dupré equation is the free energy per unit area when an interface is created.36–38Wadh then is the free energy difference when the two surfaces SV and LV are brought together to create the interface SL. Leroy et al. demonstrated through classical MD simulations that given the interaction between water and graphene, Wadh only weakly depends on the water model used.26 It is then clear from eqn (1) that an independent evaluation of Wadh immediately yields a value for the WCA if one uses the experimentally determined value for γLV (72.8 mJ m−2, independent of the surface as the solid phase is not involved),39 as is adopted throughout the present calculations.
The task of evaluating Wadh has so far been undertaken by classical MD simulations, primarily for carbon-based materials such as graphene and graphite for which accurate classical potentials are available. The enthalpy part of Wadh can be calculated directly from the total energies of the system with a water slab on and off the surface. For the entropy part, however, one must perform a series of calculations along a reversible thermodynamic integration path19,25–27 as the water slab is lifted off the surface (e.g. by the action of a phantom wall25). Implementing this methodology using QMD simulations is, however, currently impractical.
Nevertheless, we note that, for graphitic carbon surfaces, the entropic contribution to Wadh is a constant 33% of the enthalpic contribution, regardless of the number of graphene layers.25 We shall, therefore, implement the method by approximating Wadh as 67% of the energy of adhesion Eadh obtained via QMD simulations, for which only the two end states are involved. We will extend this approximation to hydrocarbon-contaminated surfaces and to graphene on metal substrates. The approach, therefore, represents a trade-off between accurate entropy calculations and introduction of explicit electronic-structure effects that are altogether absent in CMD, but are likely to be important, especially in the case of graphene on metal substrates. The present results set the stage for future evolution of the theory as computer performance increases.
Results
A quantitative determination of the WCA requires an accurate description of the water–graphene interaction in the first place. The level of sophistication depends on the choice of the density functional. The present calculations adopt the widely-used (for its general applicability) PBE functional.40 To properly account for the vdW interaction, the Grimme dispersion correction41 with a global scaling factor of 0.35 is used. To demonstrate the accuracy of our choice, we compare the binding energy of a water monomer on a free-standing graphene sheet with that calculated by the more sophisticated (but computationally impractical for subsequent WCA calculations) DFT-based random phase approximation (RPA),42 as shown in Fig. 1a. A close agreement is found.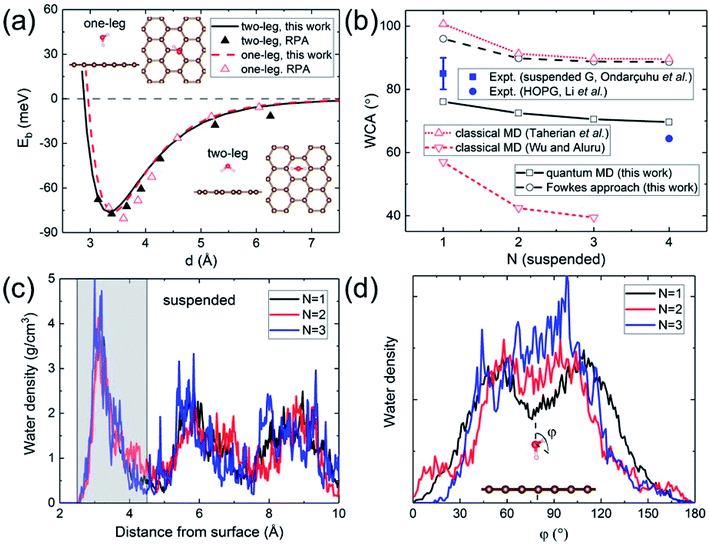 | ||
| Fig. 1 (a) Binding energy of a water monomer on suspended graphene surface. The solid and dashed curves show the results for the “two-leg” and “one-leg” configurations respectively calculated with the PBE-D (s = 0.35) functional, compared to the RPA benchmark results42 shown by triangles. The insets are the side and top views of the “one-leg” and “two-leg” structures. (b) Calculated WCA as a function of the number of graphene layers N. (c) Water density profile along the surface normal. The shaded area shows the first wetting layer. (d) Orientation angle distribution of water molecules in the first wetting layer. | ||
A hydrophilic WCA of 74° is then obtained for suspended monolayer graphene, compared to the measured value of 85° ± 5°.43 Given the approximations made, the agreement is satisfactory. The calculated WCA of suspended multilayer graphene gradually decreases as the number of graphene layers N is increased, in agreement with previous theoretical results,20,21,25 as shown in Fig. 1b. The trend of decreasing WCA as a function of the number of graphene layers is also in qualitative agreement with calculations using the empirical Fowkes approach.44–46 In the Fowkes approach, the interfacial tension γSL is divided into a polar (polar chemical bonds, e.g. hydrogen bonding) part and a nonpolar (dispersive or van der Waals) part. Wadh is then approximated by the geometric mean of the dispersive and polar component of the surface tension 2(γdLVγdSV)1/2 + 2(γpLVγpSV)1/2.47 For nonpolar surfaces the polar part vanishes, and therefore the wetting behavior of graphitic carbon surfaces is predominantly determined by the dispersive interaction with water molecules, as demonstrated experimentally by contact angle and surface energy measurements.48
The density and dipole moment profiles of water molecules near the surface are considered to have direct relevance on the WCA.49 In agreement with previous DFT theoretical results on the structure of water layers on graphene,50 we find that there is a depletion region of 2.5 Å adjacent to the surface, after which the first interfacial water layer rises sharply to its peak at around 3.15 Å, as shown in Fig. 1c. Furthermore, no significant electronic doping of graphene is induced from the wetting of a water slab, consistent with previous DFT total-energy and structural relaxation calculations.51 The orientation angle (defined as the angle between the H–O–H bisecting vector and the surface normal) distribution of water molecules in the first wetting layer (shaded area in Fig. 1c) reveals the nonpolar nature of graphitic carbon surfaces. As shown in Fig. 1d, water molecules in the first wetting layer preferably have their dipole moments pointing parallel to the surface (φ ∼ 90°). It is noteworthy that the distribution appears to be “bi-modal” for monolayer graphene and gradually merges into “unimodal” with increasing N.
The nonpolar nature of graphitic carbon surfaces in both dry and wet conditions is further manifested from a Mulliken population analysis52 at the electronic structure level. The ensemble average of Mulliken charges on carbon atoms in the topmost graphene surface 〈Q〉 are obtained for monolayer and multilayer graphene. For both “dry” and “wet” surfaces, these Mulliken charges are on average 4, equal to the valency of the carbon atoms regardless of the number of graphene layers. This demonstrates that the nonpolar nature is robust against water wetting, and therefore it is sufficient to describe the water–carbon interaction with the Lennard-Jones potential, as has been done in many prior classical MD simulations.19,22–28
To further test our calculations, we also investigated the effect of hydrocarbon contaminations. Due to the illusive effect of airborne hydrocarbon contaminants,21,53,54 graphitic carbon surfaces were often observed to be hydrophobic,55 while the water wettability of graphene has been reported to vary from “wetting transparency”56 and “wetting translucency”57 to “wetting opaqueness”58 (the graphene coating has no effect, partly alters, or completely dominates, respectively, the WCA of the underlying surface). Here we model hydrocarbons with a monolayer of methane CH4 (adsorbed on graphene). The contamination density is one-sixth of the graphene carbon atom density. We then study the water wettability of the contaminated graphene surface, which appears to be hydrophobic, as shown in Fig. 2b. The contaminated surface exhibits strong water repellency, as already manifested in the water density profile in Fig. 2b. This is in qualitative agreement with previous classical MD simulations,34,59 and demonstrates that in experiments care needs to be exercised to ensure that the samples are free of hydrocarbon contaminations. Indeed the WCA of Cu-supported graphene has been found to increase by 25° upon exposure to ambient air.53 The induced hydrophilic-to-hydrophobic wettability alteration arises from the weaker vdW interaction between hydrocarbons and water.
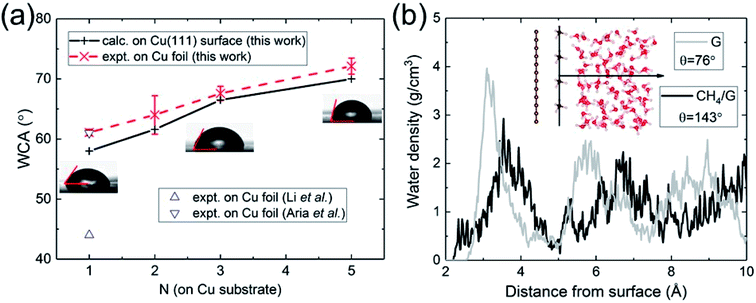 | ||
| Fig. 2 (a) Calculated and measured WCA as a function of the number of graphene layers N on Cu substrate. (b) Water density profile of graphene contaminated by hydrocarbons (CH4). | ||
Having validated the approach of predicting WCA from the energy of adhesion Eadh, we resolve outstanding issues of practical concern. We carried out WCA experiments on monolayer and multilayer graphene on Cu foil. The results of the present calculations and experimental data are in excellent agreement, as shown in Fig. 2a. For monolayer graphene on copper foil, there exists a spread of prior experimental data ranging from 44° (ref. 21) to 61°,60 while our measurement is close to its upper bound. We believe the spread can be partly attributed to the difference in the annealing procedures, which is related to the removal of residual hydrocarbons. Besides, the strain mismatch caused by the difference in thermal expansion between graphene (negative) and Cu (positive) could induce surface roughness, which influences the water wettability. Compared with suspended monolayer and multilayer graphene (Fig. 1b), the trend of WCA is reversed to be increasingly hydrophobic with increasing N. Cu-supported graphene is more hydrophilic with a WCA of 58° than suspended monolayer graphene. Since water completely wets Cu (111) surface, this demonstrates that the major part of the interaction with water is established by the topmost graphene surface.
In the presence of a metal substrate, the electronic structure comes into play. In addition to the dispersive interaction with water, a metal substrate could also effectively polarize graphene by electron redistribution and doping. Graphene can no longer be considered as nonpolar. As a result, the doped graphene interacts with water through not only dispersive but also polar forces. Indeed, in experiments the wettability of graphene could be tuned toward more hydrophilic by either electrical doping14 or chemical doping.15
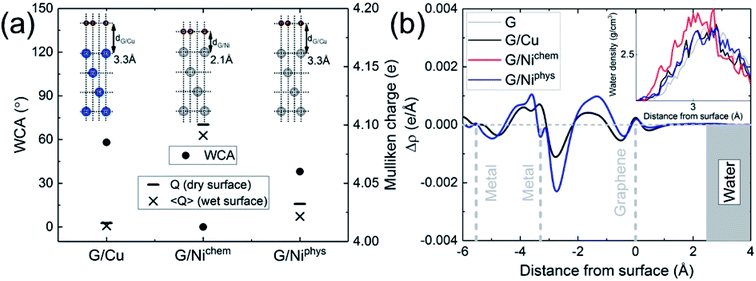
The electronic structure is naturally incorporated in our approach. In the presence of a metal substrate, previous DFT calculations have found a systematic increase in the adsorption energy of a water monomer.61 In order to further explore the role of electronic structure on the WCA of monolayer graphene on a metal substrate, we calculated the WCA for monolayer graphene on two different metal substrates, Cu (111) and Ni (111). The results are shown in Fig. 3a. For G/Cu (111), the natural substrate-graphene distance is 3.3 Å, and the calculated WCA is 58°. For G/Ni (111), two delicate competing binding mechanisms exist:62,63 a chemisorbed state at around 2.1 Å and a physisorbed state at around 3.3 Å. At its chemisorption state, complete wetting (θ = 0°) is predicted. The strong affinity for water is also manifested in the water density profile (inset of Fig. 3b).
It is noteworthy that G/Ni (111) at its physisorption state is more hydrophilic than G/Cu (111) with a WCA of 38°, albeit the substrate-graphene distances of the two systems are very close. Note that in the Grimme dispersion correction41 scheme, the same correction parameters are used for Cu and Ni. Also, as shown in the inset of Fig. 3b, water density profiles of the two systems are quite similar. Therefore, it is reasonable to expect that dispersive interactions in these two systems make similar contribution to Eadh. Clearly, the dispersive interaction alone cannot fully account for the difference in the water wettability (as much as 20°).
A closer examination reveals the effect of doping induced by the metal substrate. For all three metal-supported graphene studied in this work, the Mulliken charges on graphene are larger than 4 (the valency of carbon atom), indicating that electrons are transferred from the metal substrate to graphene. This is also manifested in the planar-averaged electron density difference 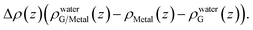 For example, the amount of charge transfer for G/Ni (111) at its physisorption state is estimated to be 0.003 e Å−2, while the corresponding Fermi level is 0.38 eV above the Dirac point (calculated from the projected density of states). The comparison between “dry” surface and “wet” surface suggests that the electron transfer is accomplished mainly from the metal substrate, i.e. water wetting does not alter the intrinsic charge transfer of metal-supported graphene. It is then clear that compared to G/Cu (111), G/Ni (111) at its physisorption state is more hydrophilic by 20°, which correlates with the more significant charge transfer (0.01 Mulliken charge e− per carbon atom), as shown in Fig. 3a. The charge transfer is further enhanced (0.08 Mulliken charge e− per carbon atom) for G/Ni (111) at its chemisorption state, which correlates again with an even pronounced water wettability (complete wetting).
For example, the amount of charge transfer for G/Ni (111) at its physisorption state is estimated to be 0.003 e Å−2, while the corresponding Fermi level is 0.38 eV above the Dirac point (calculated from the projected density of states). The comparison between “dry” surface and “wet” surface suggests that the electron transfer is accomplished mainly from the metal substrate, i.e. water wetting does not alter the intrinsic charge transfer of metal-supported graphene. It is then clear that compared to G/Cu (111), G/Ni (111) at its physisorption state is more hydrophilic by 20°, which correlates with the more significant charge transfer (0.01 Mulliken charge e− per carbon atom), as shown in Fig. 3a. The charge transfer is further enhanced (0.08 Mulliken charge e− per carbon atom) for G/Ni (111) at its chemisorption state, which correlates again with an even pronounced water wettability (complete wetting).
In terms of the empirical Fowkes approach, graphene is made effectively polar due to the electrostatic interaction induced by electronic redistribution. It is then immediately obvious that the water hydrophilicity of graphene is closely correlated with the amount of electrons transferred from the underlying metal substrate, as shown in Fig. 3a. The electron-transfer-induced polar interaction is therefore identified as being responsible for the difference in the water wettability of metal-supported graphene. Note that the surface tension of water has more polar component (51.0 mJ m−2) than dispersive component (20.8 mJ m−2). This suggests that doping provides an efficient way to alter the water wettability of graphene, as has been reported in experiments.14,15
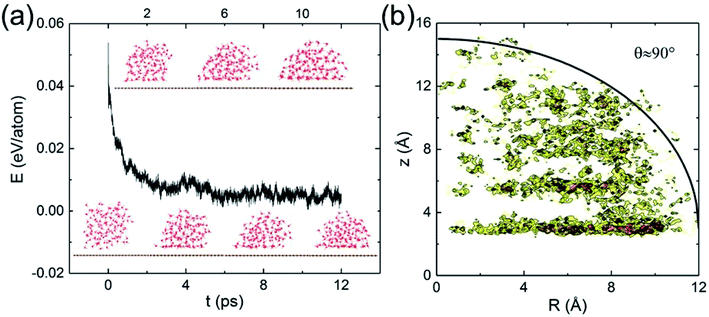
Classical MD simulations of nanodroplets to obtain the WCA are more common than the work-of-adhesion approach. For example, the interaction of a gas molecule with the surface of a water droplet is actively investigated recently.64,65 For a nanodroplet on a surface, such simulations entail a sizable uncertainty due to the line tension effect,20 while the simulation time required for equilibration is nanoseconds.24 Since there is only one reported QMD simulation of a nanodroplet,33 in which the WCA of graphene monolayer was found to be 87°, we performed such simulations to compare with the present results and check the inherent uncertainty. We find that a relatively long simulation time is required in order for the WCA to reach equilibrium.
The initial configuration of the droplet is taken from a cubic box of water having density 1 g cm−3 pre-equilibrated for 10 ps at 360 K. As shown in Fig. 4a, the WCA of monolayer graphene is not geometrically well-defined until 10 ps. Unable to determine a statistically significant boundary of the droplet, we estimate the WCA to be around 90°, close to that reported in ref. 33 (simulated with a different functional, and a longer simulation time). We believe the agreement is fortuitous. At the picosecond time scale and nanometer length scale, caution needs to be exercised to measure the WCA. The droplet simulation, on the other hand, makes no assumption on the entropy. Clearly, both the nanodroplet and work-of-adhesion approaches need more powerful computers to eliminate their current shortcomings and establish themselves as accurate methods for WCA calculations by QMD simulations.
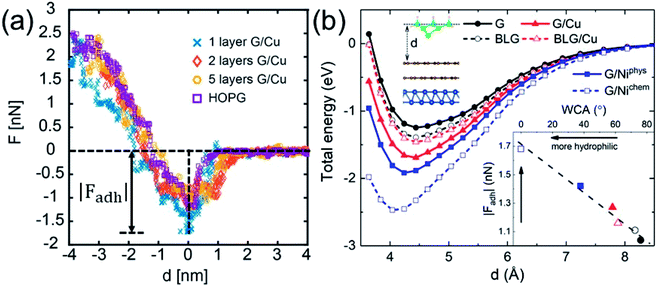
While WCA quantifies the water wettability of a surface on a macroscopic length scale, the force of adhesion |Fadh| (the attractive maximum of the force profile) measured/simulated by AFM provides an alternative measure on a nanoscopic scale.66–73 A relation between the two quantities is highly needed, since it enables the high-resolution characterization of wettability. For this purpose, we examine the correlation between WCA and |Fadh|. We have measured the force profiles exerted on Cu-supported monolayer and multilayer graphene, which exhibit a decreasing |Fadh| with increasing N, as shown in Fig. 5a. The trend of decreasing |Fadh| corresponds well with the decreasing hydrophilicity reported in Fig. 2a. Indeed, this correlation has been demonstrated experimentally over a wide variety of surfaces.74
The DFT-simulated AFM energy profiles are shown in the main panel of Fig. 5b (see Methods for technical details). The calculated energies (symbols in the main panel) are fitted to the Buckingham potential35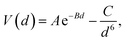 and the forces of adhesion |Fadh| are taken from the derivatives. In line with the AFM measurements in Fig. 5a, for Cu-supported graphene the DFT-simulated |Fadh| also exhibits a decreasing trend with increasing N (from filled triangle to empty triangle in Fig. 5b). This agreement is satisfactory, demonstrating that the simulated AFM technique (see Methods for details) provides a reliable representation of the AFM measurement.
and the forces of adhesion |Fadh| are taken from the derivatives. In line with the AFM measurements in Fig. 5a, for Cu-supported graphene the DFT-simulated |Fadh| also exhibits a decreasing trend with increasing N (from filled triangle to empty triangle in Fig. 5b). This agreement is satisfactory, demonstrating that the simulated AFM technique (see Methods for details) provides a reliable representation of the AFM measurement.
We further demonstrate the correlation between |Fadh| and WCA with the simulated AFM technique. As shown in the inset of Fig. 5b, a larger |Fadh| corresponds to a smaller WCA (more hydrophilic). Many trends found in WCA are faithfully reproduced by |Fadh|. For example, Cu-supported graphene is less hydrophilic with increasing N (from filled triangle to empty triangle), while this trend is reversed for free-standing graphene (from filled circle to empty circle). Also, chemisorbed Ni-supported graphene is much more hydrophilic than the physisorbed one (from empty square to filled square). With the established correlation, it is therefore feasible to characterize wettability with the AFM technique, which is particularly advantageous at the nanoscale. Another possible advantage of the AFM technique lies in its ability to quantify the affinity of strongly hydrophilic surfaces where WCA yields complete wetting.
Conclusions
The WCA is an economical measure of the water wettability of a surface. The absence of a suitable method to compute WCAs at the electronic-structure level has been troublesome for the iterative interplay of wettability between theory and experiment. Large uncertainties in the determination of WCAs prevail in both theory and experiment. By noting that the relative wettability is often of practical concern, we developed an approach that combines classical wetting theory with QMD simulations, allowing practical but sufficiently accurate determination of the WCA. The present work paves the way for studying wettability at the electronic-structure level from first principles, which is particularly suited when the electrostatic forces are determining such as in the electrowetting phenomenon75 and in the low-salinity waterflooding technique.76We have validated our approach with a case study on graphitic carbon surfaces. We have shown that due to their nonpolar nature, graphitic carbon surfaces are mildly hydrophilic and their wettability is completely determined by the dispersive interaction with water. The WCA gradually reduces with increasing number of graphene layers N, while a monolayer of adsorbed hydrocarbons is sufficient to render graphene hydrophobic. These findings are in agreement with previous theoretical calculations based on classical potential simulations and with experimental measurements. We then further resolve the outstanding issue regarding the intrinsic effect of electron doping on the wettability of metal-supported graphene. In addition to the dispersive interaction, we find that upon electron transfer graphene becomes polar, and therefore its interaction with the polar component of the surface tension of water is invoked. This further alters the water wettability of graphene to be strongly hydrophilic. We also find a correlation between the adhesion force and the WCA, demonstrating the feasibility of characterizing wettability with the AFM technique.
The gap between experiment and theory is still to be bridged and a great deal of work is required to resolve other existing controversies. For example, progress has been made to compute the wettability of 2D materials beyond graphene such as hexagonal boron nitride77,78 and molybdenum disulfide,79–82 where the development of universally accepted force fields is still in progress. The dependence of WCA on surface morphology at the nanoscale is also under active investigation.83–85 Finally, it was reported that the wettability of the calcite/oil/brine system depends on a variety of factors such as brine concentration86 and temperature.87 It has been proposed that ions present in seawater altering the surface charge of calcite is responsible for wettability alteration.30,88 We believe the present work opens the avenue to study such underlying mechanisms at the atomic scale in order to enhance oil recovery.
Methods
WCA simulation
Electronic structure calculations are performed in the basis of linear combinations of localized atomic orbitals, as implemented in the SIESTA package.89 A variationally optimized double-ζ polarized (DZP) basis set is used. After structural relaxations through total-energy and force calculations, DFT-based QMD simulations are performed. In order to correctly describe the density and diffusivity of liquid water at room temperature (with the PBE functional),90–92 an elevated temperature of 360 K is maintained by the Nosé–Hoover thermostat. For each MD simulation, a trajectory of 3 ps is used for production after an equilibration stage of 2 ps, with a time step of 0.5 fs. In the production stage, snapshots are taken every 10 fs. The simulation supercell contains 4 × 7 rectangular unit cells (112 C atoms for graphene, almost square surface) and 125 water molecules (pre-equilibrated in a cubic box). The initial positions and velocities of water molecules on multilayer graphene are generated from the final snapshot of monolayer simulations. Four layers are used to represent fcc metal (111) substrates, with the lattice constant adapted to the optimized in-plane lattice constant of graphene. Ghost orbitals93 are introduced to correct for the basis set superposition error wherever necessary.AFM force simulation
The AFM simulation is performed using DFT total-energy and force calculations with a 10-atom silicon tip. The four silicon atoms at the tip apex and the graphene layer are allowed to relax, while the six silicon atoms at the tip base and the substrate are held fixed. The tip is placed atop the hollow site of graphene at distance d. The Grimme dispersion correction41 is used to properly account for the vdW interaction.WCA measurement
A Kyowa DM-701 contact angle machine is used for the static contact angle (SCA) measurement and FAMAS (interface Measurement & Analyses System) is used to analyze the results. SCAs are measured at ambient conditions and all the samples are annealed in a vacuum oven at 80 °C for 24 hours. The average SCA values and standard deviations are calculated using 12 measurements.AFM force measurement
The AFM data are collected in ambient conditions in standard dynamic AFM,94i.e. in particular in amplitude modulation AFM, since it allows recovering the full force versus distance profile.53,95 In our experiments, the effective radius R was monitored in situ with the use of the critical amplitude Ac method that provides a functional relationship in dynamic AFM between the minimum free amplitude A0 required to reach the repulsive regime and R, i.e. R = 4.75 (Ac)1.1 as reported elsewhere96 was used here to monitor R throughout the experiments. The amplitude-phase distance data are converted into force F versus distance d profiles by employing the Sader–Jarvis–Katan algorithm.94,97,98 In this algorithm, the raw amplitude A and phase φ data comprise the input while the force F versus distance d profiles comprise the output. A Cypher AFM from Asylum Research and standard OLYMPUS cantilevers (AC160TS) with k ≈ 30 N m−1, Q ≈ 400, and f0 ≈ 280 kHz are used in all experiments. A total of 100 force profiles are reconstructed on each sample on at least 5 different locations within each sample.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported in part by the Gas Subcommittee Research and Development under Abu Dhabi National Oil Company (ADNOC) and by the McMinn Endowment at Vanderbilt University. Computations were carried out at the National Energy Research Scientific Computing Center, a DOE Office of Science User Facility supported by the Office of Science of the U.S. Department of Energy under Contract No. DE-AC02-05CH11231, and the Extreme Science and Engineering Discovery Environment (XSEDE), which is supported by National Science Foundation grant number ACI-1053575.References
- A. J. Meuler, J. D. Smith, K. K. Varanasi, J. M. Mabry, G. H. McKinley and R. E. Cohen, ACS Appl. Mater. Interfaces, 2010, 2, 3100 CrossRef CAS.
- J. G. Vilhena, C. Pimentel, P. Pedraz, F. Luo, P. A. Serena, C. M. Pina, E. Gnecco and R. Pérez, ACS Nano, 2016, 10, 4288 CrossRef CAS PubMed.
- N. Shenogina, R. Godawat, P. Keblinski and S. Garde, Phys. Rev. Lett., 2009, 102, 156101 CrossRef PubMed.
- B. Ramos-Alvarado, S. Kumar and G. P. Peterson, J. Phys. Chem. Lett., 2016, 7, 3497 CrossRef CAS.
- D. Berman, A. Erdemir and A. V. Sumant, Mater. Today, 2014, 17, 31 CrossRef CAS.
- F. Schedin, A. K. Geim, S. V. Morozov, E. Hill, P. Blake, M. I. Katsnelson and K. S. Novoselov, Nat. Mater., 2007, 6, 652 CrossRef CAS.
- O. Leenaerts, B. Partoens and F. M. Peeters, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77, 125416 CrossRef.
- D. Cohen-Tanugi and J. C. Grossman, Nano Lett., 2012, 12, 3602 CrossRef CAS.
- S. P. Surwade, S. N. Smirnov, I. V. Vlassiouk, R. R. Unocic, G. M. Veith, S. Dai and S. M. Mahurin, Nat. Nanotechnol., 2015, 10, 459 CrossRef CAS.
- R. K. S. Raman, P. C. Banerjee, D. E. Lobo, H. Gullapalli, M. Sumandasa, A. Kumar, L. Choudhary, R. Tkacz, P. M. Ajayan and M. Majumder, Carbon, 2012, 50, 4040 CrossRef.
- D. J. Preston, D. L. Mafra, N. Miljkovic, J. Kong and E. N. Wang, Nano Lett., 2015, 15, 2902 CrossRef CAS.
- J. Carrasco, B. Santra, J. Klimeš and A. Michaelides, Phys. Rev. Lett., 2011, 106, 026101 CrossRef.
- P. Guo, Y. Tu, J. Yang, C. Wang, N. Sheng and H. Fang, Phys. Rev. Lett., 2015, 115, 186101 CrossRef.
- G. Hong, Y. Han, T. M. Schutzius, Y. Wang, Y. Pan, M. Hu, J. Jie, C. S. Sharma, U. Müller and D. Poulikakos, Nano Lett., 2016, 16, 4447 CrossRef CAS.
- A. Ashraf, Y. Wu, M. C. Wang, K. Yong, T. Sun, Y. Jing, R. T. Haasch, N. R. Aluru and S. Nam, Nano Lett., 2016, 16, 4708 CrossRef CAS.
- X. Li, H. Qiu, X. Liu, J. Yin and W. Guo, Adv. Funct. Mater., 2016, 27, 1603181 CrossRef.
- A. Kozbial, Z. Li, J. Sun, X. Gong, F. Zhou, Y. Wang, H. Xu, H. Liu and L. Li, Carbon, 2014, 74, 218 CrossRef CAS.
- A. Kozbial, X. Gong, H. Liu and L. Li, Langmuir, 2015, 31, 8429 CrossRef CAS.
- B. Ramos-Alvarado, S. Kumar and G. P. Peterson, J. Chem. Phys., 2015, 143, 044703 CrossRef.
- C.-J. Shih, Q. H. Wang, S. Lin, K.-C. Park, Z. Jin, M. S. Strano and D. Blankschtein, Phys. Rev. Lett., 2012, 109, 176101 CrossRef PubMed.
- Z. Li, Y. Wang, A. Kozbial, G. Shenoy, F. Zhou, R. McGinley, P. Ireland, B. Morganstein, A. Kunkel and S. P. Surwade, Nat. Mater., 2013, 12, 925 CrossRef CAS PubMed.
- M. Khalkhali, N. Kazemi, H. Zhang and Q. Liu, J. Chem. Phys., 2017, 146, 114704 CrossRef.
- D. Sergi, G. Scocchi and A. Ortona, Fluid Phase Equilib., 2012, 332, 173 CrossRef CAS.
- J. Li and F. Wang, J. Chem. Phys., 2017, 146, 054702 CrossRef.
- F. Taherian, V. Marcon, N. F. A. van der Vegt and F. Leroy, Langmuir, 2013, 29, 1457 CrossRef CAS.
- F. Leroy, S. Liu and J. Zhang, J. Phys. Chem. C, 2015, 119, 28470 CrossRef CAS.
- V. Kumar and J. R. Errington, J. Phys. Chem. C, 2013, 117, 23017 CrossRef CAS.
- F. Taherian, F. d. r. Leroy and N. F. van der Vegt, Langmuir, 2013, 29, 9807 CrossRef CAS.
- W. W. Zhong, Y. F. Huang, D. Gan, J. Y. Xu, H. Li, G. Wang, S. Meng and X. L. Chen, Phys. Chem. Chem. Phys., 2016, 18, 28033 RSC.
- P. Zhang, M. T. Tweheyo and T. Austad, Colloids Surf., A, 2007, 301, 199 CrossRef CAS.
- S. J. Fathi, T. Austad and S. Strand, Energy Fuels, 2011, 25, 5173 CrossRef CAS.
- S. Meng, L. F. Greenlee, Y. R. Shen and E. Wang, Nano Res., 2015, 8, 3085 CrossRef CAS.
- H. Li and X. C. Zeng, ACS Nano, 2012, 6, 2401 CrossRef CAS PubMed.
- Y. Wu and N. Aluru, J. Phys. Chem. B, 2013, 117, 8802 CrossRef CAS.
- R. G. Mortimer, Physical chemistry, Elsevier Academic Press, 2008 Search PubMed.
- P. Roura and J. Fort, J. Colloid Interface Sci., 2004, 272, 420 CrossRef CAS.
- G. Whyman, E. Bormashenko and T. Stein, Chem. Phys. Lett., 2008, 450, 355 CrossRef CAS.
- R. Shuttleworth, Proc. Phys. Soc., London, Sect. A, 1950, 63, 444 CrossRef.
- N. Vargaftik, B. Volkov and L. Voljak, J. Phys. Chem. Ref. Data, 1983, 12, 817 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865 CrossRef CAS PubMed.
- S. Grimme, J. Comput. Chem., 2006, 27, 1787 CrossRef CAS.
- J. Ma, A. Michaelides, D. Alfe, L. Schimka, G. Kresse and E. Wang, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 033402 CrossRef.
- T. Ondarçuhu, V. Thomas, M. Nuñez, E. Dujardin, A. Rahman, C. T. Black and A. Checco, Sci. Rep., 2016, 6, 24237 CrossRef.
- D. K. Owens and R. Wendt, J. Appl. Polym. Sci., 1969, 13, 1741 CrossRef CAS.
- D. Y. Kwok and A. W. Neumann, Adv. Colloid Interface Sci., 1999, 81, 167 CrossRef CAS.
- A. Kozbial, Z. Li, C. Conaway, R. McGinley, S. Dhingra, V. Vahdat, F. Zhou, B. D'Urso, H. Liu and L. Li, Langmuir, 2014, 30, 8598 CrossRef CAS.
- F. M. Fowkes, Ind. Eng. Chem., 1964, 56, 40 CrossRef CAS.
- M. Annamalai, K. Gopinadhan, S. A. Han, S. Saha, H. J. Park, E. B. Cho, B. Kumar, A. Patra, S.-W. Kim and T. Venkatesan, Nanoscale, 2016, 8, 5764 RSC.
- C. Zhu, H. Li, Y. Huang, X. Zeng and S. Meng, Phys. Rev. Lett., 2013, 110, 126101 CrossRef.
- G. Cicero, J. C. Grossman, E. Schwegler, F. Gygi and G. Galli, J. Am. Chem. Soc., 2008, 130, 1871 CrossRef CAS.
- T. O. Wehling, M. I. Katsnelson and A. I. Lichtenstein, Appl. Phys. Lett., 2008, 93, 202110 CrossRef.
- R. S. Mulliken, J. Chem. Phys., 1955, 23, 1833 CrossRef CAS.
- C.-Y. Lai, T.-C. Tang, C. A. Amadei, A. J. Marsden, A. Verdaguer, N. Wilson and M. Chiesa, Carbon, 2014, 80, 784 CrossRef CAS.
- C. A. Amadei, C.-Y. Lai, D. Heskes and M. Chiesa, J. Chem. Phys., 2014, 141, 084709 CrossRef.
- A. Kozbial, F. Zhou, Z. Li, H. Liu and L. Li, Acc. Chem. Res., 2016, 49, 2765 CrossRef CAS.
- J. Rafiee, X. Mi, H. Gullapalli, A. V. Thomas, F. Yavari, Y. Shi, P. M. Ajayan and N. A. Koratkar, Nat. Mater., 2012, 11, 217 CrossRef CAS.
- C.-J. Shih, M. S. Strano and D. Blankschtein, Nat. Mater., 2013, 12, 866 CrossRef CAS.
- R. Raj, S. C. Maroo and E. N. Wang, Nano Lett., 2013, 13, 1509 CrossRef CAS.
- C. Mücksch, C. Rösch, C. Müller, C. Ziegler and H. M. Urbassek, J. Phys. Chem. C, 2015, 12496 CrossRef.
- A. I. Aria, P. R. Kidambi, R. S. Weatherup, L. Xiao, J. A. Williams and S. Hofmann, J. Phys. Chem. C, 2016, 120, 2215 CrossRef CAS.
- X. Li, J. Feng, E. Wang, S. Meng, J. Klimeš and A. Michaelides, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 085425 CrossRef.
- T. Olsen, J. Yan, J. J. Mortensen and K. S. Thygesen, Phys. Rev. Lett., 2011, 107, 156401 CrossRef.
- S. M. Kozlov, F. Viñes and A. Görling, J. Phys. Chem. C, 2012, 116, 7360 CrossRef CAS.
- Y. Zhao, H. Li and X. C. Zeng, J. Am. Chem. Soc., 2013, 135, 15549 CrossRef CAS PubMed.
- J. Zhong, Y. Zhao, L. Li, H. Li, J. S. Francisco and X. C. Zeng, J. Am. Chem. Soc., 2015, 137, 12070 CrossRef CAS PubMed.
- Y.-H. Chang, T. Olukan, C.-Y. Lai, S. Santos, T.-Y. Lin, H. Apostoleris, J. Font, V. Barcons and M. Chiesa, J. Phys. Chem. C, 2015, 119, 18267 CrossRef CAS.
- C. A. Amadei, C.-Y. Lai, M. J. Esplandiu, F. Alzina, C. D. Vecitis, A. Verdaguer and M. Chiesa, RSC Adv., 2015, 5, 39532 RSC.
- C.-Y. Lai, T. Olukan, S. Santos, A. Al Ghaferi and M. Chiesa, Chem. Commun., 2015, 51, 17619 RSC.
- A. Foster, A. Gal, Y. Lee, A. Shluger and R. Nieminen, Appl. Surf. Sci., 2003, 210, 146 CrossRef CAS.
- A. S. Foster, A. Gal, J. Airaksinen, O. Pakarinen, Y. Lee, J. Gale, A. Shluger and R. M. Nieminen, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 68, 195420 CrossRef.
- A. S. Foster, C. Barth, A. Shluger and M. Reichling, Phys. Rev. Lett., 2001, 86, 2373 CrossRef CAS PubMed.
- Y. Sugimoto, P. Pou, M. Abe, P. Jelinek, R. Pérez, S. Morita and O. Custance, Nature, 2007, 446, 64 CrossRef CAS.
- T. Fukuma, B. Reischl, N. Kobayashi, P. Spijker, F. F. Canova, K. Miyazawa and A. S. Foster, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 92, 155412 CrossRef.
- A. Rana, A. Patra, M. Annamalai, A. Srivastava, S. Ghosh, K. Stoerzinger, Y.-L. Lee, S. Prakash, R. Y. Jueyuan and P. S. Goohpattader, Nanoscale, 2016, 8, 15597 RSC.
- F. Mugele and J.-C. Baret, J. Phys.: Condens. Matter, 2005, 17, R705 CrossRef CAS.
- P. C. Myint and A. Firoozabadi, Curr. Opin. Colloid Interface Sci., 2015, 20, 105 CrossRef CAS.
- Y. Wu, L. K. Wagner and N. R. Aluru, J. Chem. Phys., 2016, 144, 164118 CrossRef.
- A. Kayal and A. Chandra, J. Chem. Phys., 2017, 147, 164704 CrossRef.
- A. Govind Rajan, V. Sresht, A. A. Pádua, M. S. Strano and D. Blankschtein, ACS Nano, 2016, 10, 9145 CrossRef CAS.
- B. Luan and R. Zhou, Appl. Phys. Lett., 2016, 108, 131601 CrossRef.
- F. Leroy, J. Chem. Phys., 2016, 145, 164705 CrossRef.
- M. Heiranian, Y. Wu and N. R. Aluru, J. Chem. Phys., 2017, 147, 104706 CrossRef.
- P. Zhao, Y. Huang, Y. Shen, S. Yang, L. Chen, K. Wu, H. Li and S. Meng, Nanoscale, 2017, 9, 3843 RSC.
- C. Q. Zhu, Y. R. Gao, Y. Y. Huang, H. Li, S. Meng, J. S. Francisco and X. C. Zeng, Nanoscale, 2017, 18240 RSC.
- A. A. Ali, A. Haidar, O. Polonskyi, F. Faupel, H. Abdulkhaliq, M. Veith and O. C. Aktas, Nanoscale, 2017, 14814 RSC.
- A. A. Yousef, S. H. Al-Saleh, A. Al-Kaabi and M. S. Al-Jawfi, SPE Reservoir Eval. Eng., 2011, 14, 578 CrossRef CAS.
- Y. Lu, N. F. Najafabadi and A. Firoozabadi, Energy Fuels, 2017, 31, 4989 CrossRef CAS.
- P. Zhang and T. Austad, Colloids Surf., A, 2006, 279, 179 CrossRef CAS.
- J. M. Soler, E. Artacho, J. D. Gale, A. García, J. Junquera, P. Ordejón and D. Sánchez-Portal, J. Phys.: Condens. Matter, 2002, 14, 2745 CrossRef CAS.
- M. Fernández-Serra and E. Artacho, J. Chem. Phys., 2004, 121, 11136 CrossRef.
- J. Wang, G. Román-Pérez, J. M. Soler, E. Artacho and M.-V. Fernández-Serra, J. Chem. Phys., 2011, 134, 024516 CrossRef.
- S. Y. Willow, X. C. Zeng, S. S. Xantheas, K. S. Kim and S. Hirata, J. Phys. Chem. Lett., 2016, 7, 680 CrossRef CAS.
- M. M. Szczȩśniak and S. Scheeiner, J. Chem. Phys., 1986, 84, 6328 CrossRef.
- A. J. Katan, M. H. Van Es and T. H. Oosterkamp, Nanotechnology, 2009, 20, 165703 CrossRef.
- S. Santos, C. A. Amadei, A. Verdaguer and M. Chiesa, J. Phys. Chem. C, 2013, 117, 10615 CrossRef CAS.
- S. Santos, L. Guang, T. Souier, K. Gadelrab, M. Chiesa and N. H. Thomson, Rev. Sci. Instrum., 2012, 83, 043707 CrossRef.
- J. E. Sader and S. P. Jarvis, Appl. Phys. Lett., 2004, 84, 1801 CrossRef CAS.
- C. A. Amadei, S. Santos, S. O. Pehkonen, A. Verdaguer and M. Chiesa, J. Phys. Chem. C, 2013, 117, 20819 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2018 |