Open Access Article
Open Access ArticlePressure-dependent branching in initial decomposition of gamma-valerolactone: a quantum chemical/RRKM study†
Lili Ye *,
Wei Li and
Fei Qi
*,
Wei Li and
Fei Qi
Key Laboratory for Power Machinery and Engineering of MOE, Shanghai Jiao Tong University, Shanghai 200240, P. R. China. E-mail: yell@sjtu.edu.cn
First published on 6th April 2018
Abstract
Recently, the potential of gamma-valerolactone (a cyclic ester, C5H8O2) as a bio-fuel and fuel additive has been highlighted. To unravel its chemical behavior in combustion, the reaction kinetics of initial decomposition of gamma-valerolactone (GVL) has been investigated theoretically by utilizing ab initio calculations and transition-state-theory based simulations. The effect of pressure on decomposition rates and, more importantly, on the branching fractions of major products has been explored. The potential energy surface was constructed at the CCSD(T)-F12/cc-pVDZ-f12 level based on B2PLYPD3/cc-pVTZ optimized geometries. Rate coefficients were obtained from the solution of RRKM/master-equations at a number of pressures (within the range of 7.6–76![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 torr). The isomerization of GVL to 4-pentenoic acid (4PA) followed by C–C bond fission to form allyl plus CH2COOH is confirmed to be the most important route in the initial decomposition of GVL. Aside from isomerization to 4PA, several other routes also occur with significant contributions, during which pressure was found to take a great role in their branching. At pressures above 760 torr, the concerted reactions to form CO + ethene + acetaldehyde and propene + 2-oxiranone account for over 50% of the overall decomposition at the higher temperature end. On the other hand, the “formally direct formation” of allyl + CH2COOH, which occurs via directly skipping the 4PA well, has a non-ignorable branching above 1400 K at low pressures. As opposed to GVL, the effect of pressure on the branching of 4PA consumption routes is very minor. It is hoped that the present study will establish a firm foundation for more comprehensive kinetic studies on GVL combustion in the future.
000 torr). The isomerization of GVL to 4-pentenoic acid (4PA) followed by C–C bond fission to form allyl plus CH2COOH is confirmed to be the most important route in the initial decomposition of GVL. Aside from isomerization to 4PA, several other routes also occur with significant contributions, during which pressure was found to take a great role in their branching. At pressures above 760 torr, the concerted reactions to form CO + ethene + acetaldehyde and propene + 2-oxiranone account for over 50% of the overall decomposition at the higher temperature end. On the other hand, the “formally direct formation” of allyl + CH2COOH, which occurs via directly skipping the 4PA well, has a non-ignorable branching above 1400 K at low pressures. As opposed to GVL, the effect of pressure on the branching of 4PA consumption routes is very minor. It is hoped that the present study will establish a firm foundation for more comprehensive kinetic studies on GVL combustion in the future.
1. Introduction
Concerns about the depletion of fossil fuels drive society to search for renewable and sustainable energy sources. Gamma-valerolactone (C5H8O2, Scheme 1), a cyclic ester readily obtainable from cellulosic biomass, exhibits the most important characteristics of an ideal sustainable liquid. Recently, its potential as a promising biofuel and fuel additive has been highlighted and it is attracting increasing attention from researchers.1,2 For this novel biomass-derived chemical, the ΔcHm,liqθ (standard molar enthalpy of combustion) value is −2.65 MJ mol−1, between the values of −1.37 MJ mol−1 for ethanol and −3.37 MJ mol−1 for methyl tert-butyl ether. Other important fuel properties of gamma-valerolactone (GVL) include a high boiling point, high density, high oxygen content and less formation of dangerous peroxides during combustion.1 Studies on the effect of GVL on diesel engine performance, fuel properties and exhaust emissions have recently been carried out.3,4 When blending GVL into diesel, an advantageous effect has been generally found on the physicochemical fuel properties and exhaust emissions such as NOx, CO, unburned hydrocarbons and smoke. In contrast to ethanol, GVL does not form an azeotrope with water. The easy removal of water by distillation results in a less energy demanding and cheaper process for its production from biomass.At present, the interest in GVL is mostly centered on its production routes from cellulose/lignocellulose and on the development of efficient catalysts for reactions thereof.5–10 As the key step in its production, the transformation of levulinic acid to GVL is normally achieved on noble-metal catalyst using H2. Lately, Xue et al.10 has synthesized zirconium-cyanuric acid coordination polymer for this conversion process, providing a new route for designing highly efficient catalysts. While the development of efficient catalysts has initiated numerous studies, investigation on its detailed combustion chemistry is just getting started. De Bruycker et al.11,12 studied the thermal decomposition of GVL through the combined techniques of experiment, theory and modeling. The experiments were performed in a tubular flow reactor from 873 K to 1073 K at 1275 torr. Thermodynamic and kinetic data were computed at the CBS-QB3 level for key reactions involved. Their study proposes that the isomerization of GVL to 4-pentenoic acid (4PA) followed by C–C fission forming allyl and carboxy methyl is an important route for the initial radical pool. Unfortunately, only rate coefficients of two barrier-characterized reactions were computed from theory, and the rate coefficients of direct bond fissions, especially the important C2–C3 fission in 4PA, were assigned from estimation. Furthermore, the rate coefficients were obtained simply at the high pressure limit for this pressure-dependent reaction, with no predictions being made for the falloff region. For the reasons above, an in-depth pressure-dependent kinetic study is expected to provide more systematic kinetic data and improve the performance of the De Bruycker model. Following the pyrolysis study, Sudholt et al.13 performed an oxidation experiment of GVL in a low pressure premixed flat flame at 50 torr, and a kinetic model of high temperature oxidation was extended from the pyrolysis model of De Bruycker et al.11
Kinetic modeling is a powerful tool in using fundamental reaction mechanism to evaluate the engine-relevant behaviors of fuels, such as ignition properties and pollutant emission. To accelerate the application of GVL as a practical fuel, the comprehensive reaction mechanism of GVL combustion needs to be explored in detail, and the core reactions involved must be provided with reliable kinetic data that covers various temperature and pressure conditions. To satisfy this purpose, the present work is dedicated to unravel the initial decomposition mechanism of GVL, and more importantly, to elucidate the effect of pressure on the branching of major decomposition products. This study is expected to lay a firm foundation for more comprehensive kinetic studies on GVL combustion in the future.
2. Theoretical methodologies
2.1. Electronic structure calculations
The characterization of C5H8O2 potential energy surface was performed by using a combination of explicitly correlated CCSD(T)-F12 (ref. 14 and 15) and density functional theory (DFT) methods. The geometric structures and rovibrational properties of reactant, intermediates, transition states and products were obtained by employing the B2PLYPD3 functional and the cc-pVTZ basis set. The B2PLYPD3 method requests the B2PLYP double hybrid functional combined with Grimme's D3BJ dispersion correction.16,17 Methods of this kind combine exact HF exchange with an MP2-like correlation to the DFT calculation, and have similar computational cost as MP2 rather than that of DFT. The connectivity of specific transition state to its adjacent local minima were generally examined through visualization of corresponding imaginary vibrational mode. For the ambiguous cases, the intrinsic reaction coordinate (IRC) calculations18 were also performed to ensure the correct connectivity of transition state to desired reactant and product. The DFT calculations were done with Gaussian09 program.19High level evaluations of single point energies were computed using the CCSD(T)-F12 method at cc-pVDZ-F12 basis set.20 The zero point energies were included from the B2PLYPD3/cc-pVTZ frequency analysis. Note that the CCSD(T)-F12/cc-pVTZ-f12 level was also tested for several species, and very small difference was found from the energies at cc-pVDZ-f12 (mostly within 0.5 kcal mol−1). Such small difference is presumed to improve the rate coefficients by only a very limited extent. Considering the notably higher expense of CCSD(T)-F12/cc-pVTZ-f12 calculations, we did not refine the entire potential energy surface using this level. The CCSD(T)-F12 calculations were done with the MOLPRO2015 program.21
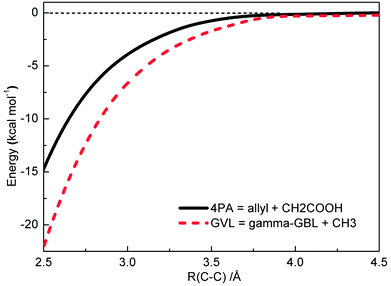
Direct bond fissions are usually barrierless reactions that have no well-defined saddle points along the reaction coordinate. In this work only the most possible direct bond fissions for each of GVL and 4PA were considered, namely, the C–C fission of GVL to lose the side methyl group and the C–C fission of 4PA to form allyl plus CH2COOH, respectively. For these two reactions, the multi-reference methods were employed for accurate description of the interaction potentials between the two reacting moieties. Specifically, the CASPT2(2e,2o)/cc-pVDZ method22 was used for the C–C bond fission of GVL to form γ-radical of gamma-butyrolactone (GBL) and methyl radical. The (2e,2o) active space simply consists of the two singly occupied radical orbitals. With the C–C fission of 4PA to form allyl plus CH2COOH, the CASPT2(6e,6o)/cc-pVDZ method was used, where the (6e,6o) active space consists of (2e,2o) for (π, π*) of C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O double bond, (2e,2o) for (π, π*) of C
O double bond, (2e,2o) for (π, π*) of C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C double bond and (2e,2o) for the two singly occupied carbon radical orbitals. The three pi electrons on C3H5 fragment become delocalized when the separation of two reacting fragments gets larger, and (6e,6o) was tested to be the minimal active space for this reaction. High level corrections for the interaction potentials were done with the MRCI method at cc-pVDZ and cc-pVTZ basis sets.23 The active spaces in MRCI calculations remained the same with those in CASPT2 calculations, and the Davidson correction was included in final MRCI energies. These multi-reference calculations were done with the MOLPRO2015 program package.21
C double bond and (2e,2o) for the two singly occupied carbon radical orbitals. The three pi electrons on C3H5 fragment become delocalized when the separation of two reacting fragments gets larger, and (6e,6o) was tested to be the minimal active space for this reaction. High level corrections for the interaction potentials were done with the MRCI method at cc-pVDZ and cc-pVTZ basis sets.23 The active spaces in MRCI calculations remained the same with those in CASPT2 calculations, and the Davidson correction was included in final MRCI energies. These multi-reference calculations were done with the MOLPRO2015 program package.21
2.2. RRKM/master equation analysis
The rate coefficients were calculated via the solution of the time-dependent RRKM/master equation using the MESS code.24,25 MESS is a newly developed master equation solver by Georgievskii et al., and it aims to effectively and simultaneously calculate temperature- and pressure-dependent rate coefficients for reaction systems with an arbitrary number of wells and bimolecular species. One distinguished feature of this code is the “well-merging” scheme for the treatment of rapidly equilibrated species. Specifically, when the rate of chemical interconversion between two species approaches or exceeds the internal energy relaxation rate, these two species will be combined into a new compound and the number of species in master equation simulations will be reduced accordingly by one. Another important feature of this code is the capture of rate coefficients for the so-called “formally direct” channels. The formally direct channels are those that traverse more than one transition state in a single elementary step, without stabilization into in-between wells. This type of channels is formally “direct” but mechanistically “indirect”. Rate coefficients of these channels are not the same as the effective rate coefficients that are derived from applying conventional quasi-steady-state assumption to the transient intermediate in a multi-step reaction scheme.For the present reaction system, the temperature covers a range of 800–2000 K at a list of pressures (7.6, 76, 760, 7600 and 76![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 torr) with Ar as the bath gas. The interaction between reactant and bath gas was described by the Lennard-Jones model potential. The (σ, ε) parameters were estimated to be σ = 5.87 Å and ε = 304 cm−1 for C5H8O2 from the group contribution method of Joback,26 and σ = 3.47 Å and ε = 79 cm−1 for Ar from recommendations by Hippler.27 The collision induced energy transfer was modeled with the single exponential down model, i.e., P(ΔE) = exp(−ΔE/α), where P is the probability and ΔE = Einitial − Efinal > 0 The average downwards energy transferred per collision was assumed to follow a temperature-dependent form, i.e., 〈ΔEdown〉 = 200 (T/300)0.85, which is estimated based on previous experience.28,29
000 torr) with Ar as the bath gas. The interaction between reactant and bath gas was described by the Lennard-Jones model potential. The (σ, ε) parameters were estimated to be σ = 5.87 Å and ε = 304 cm−1 for C5H8O2 from the group contribution method of Joback,26 and σ = 3.47 Å and ε = 79 cm−1 for Ar from recommendations by Hippler.27 The collision induced energy transfer was modeled with the single exponential down model, i.e., P(ΔE) = exp(−ΔE/α), where P is the probability and ΔE = Einitial − Efinal > 0 The average downwards energy transferred per collision was assumed to follow a temperature-dependent form, i.e., 〈ΔEdown〉 = 200 (T/300)0.85, which is estimated based on previous experience.28,29
For reactions with a pronounced chemical barrier, the conventional transition state theory was applied in RRKM/master equation analysis, with the transition state dividing surface fixed at the saddle point. Whereas for direct bond fission reactions, the location of optimal transition state normally varies with temperature. During the MESS simulations, the microcanonical variational transition state theory was employed for the minimization of rate constants along the reaction coordinate. Variational procedure for determining microcanonical rate coefficients is as follows. A range of dividing surfaces were selected at different positions along the reaction coordinate, and the sum of states was evaluated appropriate to the given energy and angular momentum at each position. The transition state was identified with the surface that provides the minimum sum of states. The high-pressure-limit rate coefficient is then obtained as the canonical average of the variationally determined microscopic rate coefficients over the Boltzmann population distribution. Eventually, it emerges that the transition state of a barrierless reaction varies with temperature, i.e., moving from larger separation between two fragments at low temperatures to smaller separation at high temperatures.
In addition, the rigid rotor harmonic oscillator (RRHO) approximation was used to deal with the vibrational degrees of freedom. Note that the RRHO frequencies were multiplied by a scale factor of 0.99 as a crude correction for the normal modes obtained from CASPT2 calculations. The internal torsions were treated as one-dimensional hindered rotors, and were removed from the RRHO analysis. The hindrance potentials of the hindered rotors were obtained through relaxed scan along the dihedral coordinate at an interval of 10 degrees, by using the B3LYP/6-311+G(d) level. Furthermore, the quantum tunneling effect, which has a potential to be important for H-transfer reactions at low temperatures, was incorporated using the asymmetric Eckart's potential.30
3. Results and discussion
3.1. Reaction mechanism
Fig. 1 displays the major reaction pathways occurring on the C5H8O2 potential energy surface for the initial decomposition of GVL, with the energy of GVL as the zero reference. Schematic structures of the transition states on this surface are shown in Fig. 2. Normal mode frequencies of the major stationary points are provided in Table S1 of the ESI.† Table 1 compares the relative enthalpies at 298 K calculated in this work with those by De Bruycker et al.12 using the CBS-QB3 method. As can be seen, there is generally a good consistency between the present predictions and the CBS-QB3 values for most of the stationary points or product sets, with exceptions of the three transitions states that characterize the forward conversion of 4PA, i.e., TS6, TS7 and TS8. For the three exceptions, the present evaluations are lower than the CBS-QB3 values by over 1.5 kcal mol−1. These three transition states all have very tight structures and consequently small entropies. Later kinetic analysis results will demonstrate that even an increase of 2 kcal mol−1 for energies of these transition states has little influential effect on the decomposition behavior.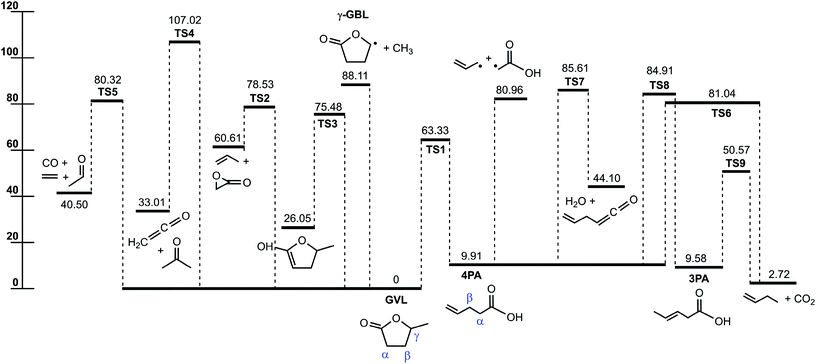 | ||
| Fig. 1 Potential energy profile for the initial decomposition of GVL. The energies (0 K, kcal mol−1) are calculated at the CCSD(T)-F12/cc-pVDZ-f12//B2PLYPD3/cc-pVTZ level. | ||
 | ||
| Fig. 2 Schematic structures of transition states on C5H8O2 potential energy surface at B2PLYPD3/cc-pVTZ level (Cartesian coordinates were provided in the ESI†). | ||
| Present work | CBS-QB3 (ref. 12) | |
|---|---|---|
| a The GVL enthalpy is set as the zero reference. The relative enthalpies of transition states are in parenthesis. | ||
| Gamma-valerolactone (GVL) | 0.0 | 0.0 |
| γ-GBL + CH3 | 89.81 | 90.78 |
| 4-Pentenoic acid (TS1) | 10.62 (63.37) | 12.18 (64.02) |
| C3H5 + CH2COOH | 82.49 | 83.13 |
C3H6 + cy(OCH2C)![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O (TS2) O (TS2) |
61.88 (79.50) | 62.11 (79.55) |
| 5-Methyl-4,5-dihydro-2-furanol (TS3) | 26.24 (75.41) | 25.08 (76.21) |
| CH2CO + CH3C(O)CH3 (TS4) | 35.15 (107.96) | 35.59 (107.98) |
| CO + C2H4 + CH3CHO (TS5) | 43.42 (81.56) | 45.87 (81.70) |
| C3H5CH2CO + H2O (TS7) | 46.54 (86.62) | 47.78 (88.15) |
| 3-Pentenoic acid (TS8) | 10.51 (85.97) | 10.27 (90.06) |
| 1-Butene + CO2 (TS6, TS9) | 4.17 (81.84, 50.99) | 5.26 (83.37, 51.36) |
For the initial decomposition of GVL, the lowest bond fission channel is demethylation via direct C–C bond cleavage to produce methyl and γ-radical of butyrolactone. Other direct bond fissions are not shown here because of the high bond dissociation energies. As presented in Fig. 1, the other five channels from GVL are all characterized by pronounced energy barriers. Among them, the most important one is the isomerization to 4-pentenoic acid (4PA) via the lowest barrier, TS1, with the energy of 63.33 kcal mol−1. In this reaction, one hydrogen atom at the methyl group is transferred to the ring oxygen via a four-membered ring transition state, leading to the ring-opening process. The present barrier height agrees satisfactorily with the CBS-QB3 value within 1 kcal mol−1. This transition state has an energy of similar magnitude to the 1,3-H shift reactions in ether systems, such as the decomposition of methyl ethyl ether into methanol plus ethene (65.2 kcal mol−1) and decomposition of ethyl tert-butyl ether into tert-butanol plus ethene (63.4 kcal mol−1).31
The next lowest barrier from GVL is TS3 for the keto–enol tautomerization reaction, where one hydrogen at the carbon atom α to the carbonyl group transfers to the oxygen atom in the carbonyl group. TS3 has a small entropy because of the tight ring structure, implying that this channel could not be important under current conditions. GVL can also proceed by several concerted reactions to lead to separate product species. These concerted reactions are (a) decomposition to propene plus 2-oxiranone via TS2 (78.53 kcal mol−1), (b) decarbonylation to form CO plus ethene plus acetaldehyde via TS5 (80.32 kcal mol−1), and (c) decomposition to acetone plus ketene (CH2CO) via TS4 (107.02 kcal mol−1). The former two molecular decomposition channels happen with barriers below the direct demethylation channel. The last channel producing acetone plus ketene occurs with a rather high energy barrier, so it can be neglected under current conditions.
4-Pentenoic acid is of special importance in GVL initial decomposition. For this intermediate, the most favored channel appears to be the reaction back to GVL at lower temperatures. The forward consumption of 4PA is expected to be dominated by the barrierless Cα–Cβ bond fission to form allyl plus the carboxymethyl radical (CH2COOH). The bond dissociation energy of Cα–Cβ (71.05 kcal mol−1) in this work agrees very well with 70.95 kcal mol−1 at the CBS-QB3 level. Other dissociation routes of 4PA include isomerization to 3-pentenoic acid (3PA), molecular decomposition to 1-butene plus CO2, and dehydration to form allylketene. These three routes are unlikely to play a major role as a result of two factors that take effect in the same direction. First, the barriers of these routes almost all lie above the Cα–Cβ bond fission energy, and second, they are entropically unfavored compared with direct bond fission process.
Quantum chemical calculations suggest that the most energetically favored route for GVL decomposition is isomerization to 4PA followed by C–C fission to form allyl plus CH2COOH. This route serves as an important source of initial radical pool in the thermal decomposition of GVL.
3.2. Reaction kinetics
Fig. 4 compares the high pressure limit rate coefficients of major channels for initial GVL decomposition. It is apparent that the isomerization to 4PA is the most favored channel except at the high temperature end. Available studies about similar systems are very limited, and only the rate parameters from De Bruycker et al. are illustrated for comparison.11 The present work shows an excellent agreement with the results from De Bruycker et al., particularly for the two channels forming CO + ethene + acetaldehyde and propene + 2-oxiranone (the two sets of results almost superpose each other). For these two channels, the discrepancy of rate coefficients is less than 30%. For the barrierless channel of γ-GBL + CH3, the present result and estimation by De Bruycker et al. agree well with each other below 1000 K. However, the latter exhibits a faster growth rate as the temperature increases and approximately triples the former at 2000 K. The inset in Fig. 4 illustrates the rate coefficients obtained via varying the transition state energies in a range of ±1 kcal mol−1. It can be seen that De Bruycker's estimations fall within the upper limit of variation below 900 K, but are still a factor of 2 larger than our predictions at the high temperature end. For this channel, the interaction energies and rovibrational frequencies of transition state configurations are assumed to be the largest source of uncertainty. Since relevant studies are very scarce, it is not easy to determine which set of data is more accurate. Fortunately, this channel plays only a minor contribution to the overall kinetics, as will be seen in later discussion. It is possible that kinetic modeling for high temperature pyrolysis of GVL under high pressure conditions could provide useful insight into the importance of this channel.
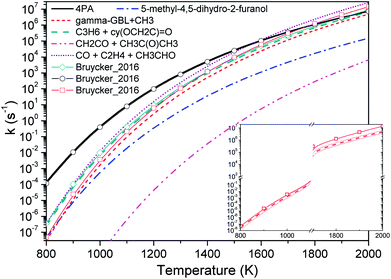 | ||
| Fig. 4 High pressure limit rate coefficients of major channels for GVL decomposition. Thin lines with symbols are from De Bruycker et al.:12 the green line with diamond and the black line with circle are from transition-state-theory calculations at CBS-QBS level; and the red line with square is from estimations. The inset shows varied rate coefficients within 1 kcal mol−1 of transition state energies for barrierless reaction GVL → γ-GBL + CH3. | ||
Regarding the keto–enol tautomerization, although it has the second lowest energy barrier, which is only next to the isomerization barrier, this channel is rather uncompetitive due to the small entropy of the transition state. Moreover, the channel leading to ketene plus acetone is never important under the current conditions.
Fig. 5 shows the high pressure limit rate coefficients of 4PA consumption occurring over the C5H8O2 surface. From this plot, the reaction back to GVL is the dominant channel at lower temperatures because of the enthalpic effect, whereas with temperature increasing the direct bond fission forming allyl plus CH2COOH quickly dominates the consumption of 4PA. H addition to the allyl radical generated from this channel accounts for part of the concentration of propene observed in earlier experimental studies.11,12 The other radical product CH2COOH will primarily generate methyl and CO2 via a two-step mechanism: first, intramolecular H-migration to intermediate CH3COO; second, C–C bond fission of CH3COO to final products. The C–O β-scission of CH2COOH to form CH2CO and OH is expected to be only a minor reaction, and this is in accordance with the fact that no ketenes were detected in related experiments.11,12 The remaining channels of 4PA, such as isomerization to 3PA and dehydration, are insignificant channels.
 | ||
| Fig. 5 High pressure limit rate coefficients of 4PA decomposition. The thin line with symbol represents estimations by De Bruycker et al.12 The varied rate coefficients of barrierless channel allyl + CH2COOH within 1 kcal mol−1 of transition state energies are shown by red dot lines. | ||
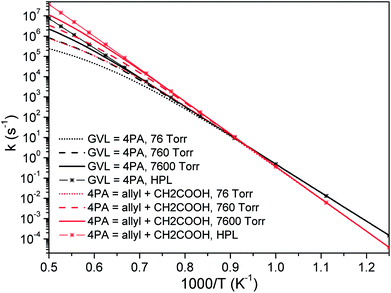 | ||
| Fig. 6 Pressure-dependent rate coefficients of two most important channels in initial decomposition of GVL: black, GVL → 4PA; red, 4PA → allyl + CH2COOH. | ||
According to De Bruycker et al.,12 radical chemistry tends to take over from molecular chemistry at high temperatures. This might lead the falloff regime of unimolecular decomposition rate coefficients, which locates just at high temperatures, to be seemingly unimportant. However, it should be noted that the branching fraction of primary decomposition products is quite sensitive to the pressure and the product distribution will certainly affect the subsequent transformation of the formed species.
Fig. 7 plots the branching ratios of major consumption channels for GVL (a–c) and 4PA (d–f) as a function of temperature at the pressures of 7.6, 760 and 76![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 Torr. All these panels suggest the great importance of the interconversion between GVL and 4PA, especially at lower temperatures. For GVL, the reactivity of the interconversion channel reduces gradually and the dominance covers a broader temperature range than the situation under high pressure conditions. The considerable amount of allyl + CH2COOH in panel (a) can be explained by the formally direct formation mechanism from the initial reactant. At low pressures the collisional stabilization effect is much less significant, so that a part of the excited 4PA* from GVL directly undergoes C–C bond fission to form allyl plus CH2COOH instead of first being stabilized into the stable 4PA well. As the pressure increases, more of excited 4PA* will be first deactivated via unreactive collisions before being reactivated to dissociate, and this leads to a reduced formation of allyl plus CH2COOH directly from GVL. Within the current investigated range, the well-skipping reaction of GVL cannot compete with its conversion to 4PA. Since any formed 4PA will rapidly dissociate into fragmented radicals at higher temperatures, the formation of allyl plus CH2COOH will be primarily from the reaction sequence GVL → 4PA → allyl + CH2COOH, rather than the well-skipping reaction.
000 Torr. All these panels suggest the great importance of the interconversion between GVL and 4PA, especially at lower temperatures. For GVL, the reactivity of the interconversion channel reduces gradually and the dominance covers a broader temperature range than the situation under high pressure conditions. The considerable amount of allyl + CH2COOH in panel (a) can be explained by the formally direct formation mechanism from the initial reactant. At low pressures the collisional stabilization effect is much less significant, so that a part of the excited 4PA* from GVL directly undergoes C–C bond fission to form allyl plus CH2COOH instead of first being stabilized into the stable 4PA well. As the pressure increases, more of excited 4PA* will be first deactivated via unreactive collisions before being reactivated to dissociate, and this leads to a reduced formation of allyl plus CH2COOH directly from GVL. Within the current investigated range, the well-skipping reaction of GVL cannot compete with its conversion to 4PA. Since any formed 4PA will rapidly dissociate into fragmented radicals at higher temperatures, the formation of allyl plus CH2COOH will be primarily from the reaction sequence GVL → 4PA → allyl + CH2COOH, rather than the well-skipping reaction.
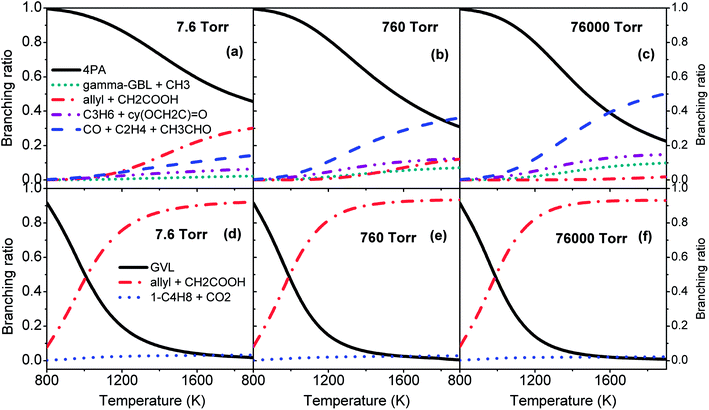 | ||
| Fig. 7 Branching ratios of major consumption channels for GVL (a–c) and 4PA (d–f) at various pressures. | ||
Additionally, the branching of the remaining decomposition channels is markedly enhanced at high pressures. Of the two concerted reactions, which form C3H6 + 2-oxiranone and CO + C2H4 + CH3CHO, respectively, the latter reaction is more favored than the former one because of the larger entropic effect.
The situation in the case of 4PA is quite different from that of GVL. From Fig. 7(d–f), the pressure has only a minor influence on the branching of the three major consumption channels. The branching of isomerization to GVL drops rapidly with temperature, while the branching of allyl + CH2COOH increases correspondingly. It has been mentioned earlier in Section 3.1 that the transition states of TS6, TS7 and TS8, which characterize the remaining consumption channels of 4PA, have lower energies than the CBS-QB3 energies by De Bruycker et al.,11 so it can be deduced that the contribution from these channels will be even smaller when using the CBS-QB3 parameters for kinetic evaluations.
In all, the upper panels in Fig. 7 demonstrates that the distribution of primary decomposition products is quite sensitive to the pressure, which will certainly affect the subsequent radical chemistry. The upper and lower panels combine to highlight the most important route in initial decomposition of GVL, that is, isomerization to 4PA followed by C–C bond fission into allyl + CH2COOH. However, although the C–C scission of 4PA and decomposition of CH2COOH are rather fast at higher temperatures, the radical chemistry of 4PA, such as H/CH3 addition, is also expected to be very competitive. In view of this fact, kinetic modeling should be a good way to examine the importance of the falloff regime of decomposition rates.
The calculated rate constants were fitted in the modified Arrhenius expressions, with the (A, n, E) parameters tabulated in Table 2.
| P (torr) | Reactions | A | n | E | Reactions | A | n | E |
|---|---|---|---|---|---|---|---|---|
a k = ATn![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−E/RT), with units of s−1, cal and mol. exp(−E/RT), with units of s−1, cal and mol. |
||||||||
| 7.6 | GVL → 4PA | 4.53 × 1081 | −19.9 | 101![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 470 470 |
4PA → GVL | 2.24 × 1077 | −19.5 | 88![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 823 823 |
| 76 | 7.09 × 1068 | −16.0 | 96![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 093 093 |
3.43 × 1064 | −15.6 | 83![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 434 434 |
||
| 760 | 5.96 × 1050 | −10.7 | 86![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 550 550 |
3.49 × 1046 | −10.3 | 73![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 942 942 |
||
| 7600 | 2.27 × 1032 | −5.3 | 75![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 996 996 |
1.49 × 1028 | −4.9 | 63![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 427 427 |
||
76![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
2.99 × 1018 | −1.3 | 67![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 715 715 |
1.99 × 1014 | −0.9 | 55![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 150 150 |
||
| ∞ | 1.62 × 109 | 1.4 | 62![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 040 040 |
1.07 × 105 | 1.8 | 49![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 474 474 |
||
| 7.6 | GVL → γ-GBL + CH3 | 1.06 × 1098 | −24.4 | 127![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 600 600 |
4PA → allyl + CH2COOH | 3.15 × 1087 | −21.3 | 110![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 470 470 |
| 76 | 4.86 × 1097 | −23.8 | 133![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 010 010 |
2.29 × 1084 | −20.0 | 113![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 130 130 |
||
| 760 | 6.35 × 1074 | −17.0 | 120![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 920 920 |
2.13 × 1058 | −12.4 | 98![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 005 005 |
||
| 7600 | 4.00 × 1054 | −11.1 | 110![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 190 190 |
7.31 × 1038 | −6.7 | 87![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 198 198 |
||
76![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
2.94 × 1037 | −6.1 | 100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 300 300 |
2.54 × 1024 | −2.5 | 78![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 687 687 |
||
| ∞ | 2.66 × 1024 | −2.3 | 92![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 431 431 |
3.57 × 1017 | −0.6 | 74![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 727 727 |
||
| 7.6 | GVL → allyl + CH2COOH | 1.28 × 10115 | −28.7 | 143![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 280 280 |
4PA → 1-C4H8+CO2 | 3.99 × 1084 | −20.9 | 109![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 670 670 |
| 76 | 3.35 × 10108 | −26.4 | 146![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 200 200 |
3.13 × 1077 | −18.5 | 109![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 940 940 |
||
| 760 | 3.72 × 1088 | −20.5 | 140![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 400 400 |
1.88 × 1049 | −10.3 | 92![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 999 999 |
||
| 7600 | 2.31 × 1058 | −11.7 | 126![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 610 610 |
1.61 × 1030 | −4.7 | 82![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 044 044 |
||
76![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
1.10 × 1025 | −2.2 | 108![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 970 970 |
1.01 × 1017 | −0.9 | 74![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 166 166 |
||
| ∞ | — | — | — | 1.47 × 109 | 1.3 | 69![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 408 408 |
||
| 7.6 | GVL → C3H6 + cy(OCH2C)![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O O |
6.33 × 1092 | −22.9 | 120![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 540 540 |
4PA → 3PA | 1.51 × 1082 | −20.9 | 104![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 290 290 |
| 76 | 1.82 × 1090 | −21.8 | 124![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 190 190 |
1.30 × 1088 | −21.9 | 115![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 060 060 |
||
| 760 | 3.89 × 1064 | −14.2 | 109![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 760 760 |
4.07 × 1070 | −16.4 | 109![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 110 110 |
||
| 7600 | 1.16 × 1044 | −8.2 | 98![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 538 538 |
5.77 × 1043 | −8.5 | 94![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 870 870 |
||
76![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
2.33 × 1027 | −3.4 | 88![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 805 805 |
3.59 × 1023 | −2.6 | 83![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 135 135 |
||
| ∞ | 5.01 × 1014 | 0.31 | 81![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 138 138 |
1.49 × 1012 | 0.7 | 76![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 261 261 |
||
| 7.6 | GVL → CO + C2H4 + CH3CHO | 2.84 × 1095 | −23.5 | 123![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 420 420 |
||||
| 76 | 1.78 × 1093 | −22.4 | 127![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 490 490 |
|||||
| 760 | 1.39 × 1068 | −15.0 | 113![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 740 740 |
|||||
| 7600 | 9.93 × 1046 | −8.8 | 102![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 340 340 |
|||||
76![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
1.77 × 1029 | −3.6 | 92![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 061 061 |
|||||
| ∞ | 1.27 × 1015 | 0.4 | 83![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 506 506 |
|||||
4. Conclusions
Detailed reaction kinetics of the initial decomposition of gamma-valerolactone (GVL) has been explored by combining quantum chemical calculations and RRKM/master equation analysis. The branching ratios of primary decomposition products has been determined at a variety of pressures. It has been found that GVL decomposes predominantly via isomerization to 4-pentenoic acid (4PA), except at high temperatures and elevated pressures where the channel to form CO plus ethene plus acetaldehyde has the largest branching. The channel to the formation of propene plus 2-oxiranone also has a nonnegligible contribution at high temperatures and moderate to high pressures. Interestingly, the formally direct formation of allyl plus CH2COOH from GVL has a considerable contribution at very low pressures, but shows a declining reactivity with the increasing pressure.4PA is an important intermediate in GVL decomposition. Subsequent consumption of this species occurs mainly through the direct cleavage of the allyl–carboxymethyl bond, except at low temperatures under which conversion back to the initial reactant is more likely to occur. In contrary to GVL, the branching of 4PA consumption is insensitive to the pressure. The present study has confirmed that the products of allyl and CH2COOH, which are crucial for the formation of initial radical pool, primarily come from the reaction sequence GVL → 4PA → allyl + CH2COOH. The well-skipping reaction only account for a small portion of their concentration.
Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
This work was supported by the Natural Science Foundation of China (Grants No. 51606122, 91541201). The authors are grateful to the technical support from the Center for High Performance Computing at Shanghai Jiao Tong University.References
- I. T. Horvath, H. Mehdi, V. Fabos, L. Boda and L. T. Mika, Green Chem., 2008, 10, 238–242 RSC.
- D. M. Alonso, S. G. Wettstein and J. A. Dumesic, Green Chem., 2013, 15, 584–595 RSC.
- M. Yang, Z. W. Wang, T. Z. Lei, L. Lin, X. F. He, T. Qi, X. F. Xin, Z. J. Li and J. Shi, J. Biobased Mater. Bioenergy, 2017, 11, 66–72 CrossRef CAS.
- A. Bereczky, K. Lukacs, M. Farkas and S. Dobe, Nat. Resour., 2014, 05, 177–191 Search PubMed.
- R. Yoshida, D. L. Sun, Y. Yamada, S. Sato and G. J. Hutchings, Catal. Commun., 2017, 97, 79–82 CrossRef CAS.
- S. H. Zhu, Y. F. Xue, J. Guo, Y. L. Cen, J. G. Wang and W. B. Fan, ACS Catal., 2016, 6, 2035–2042 CrossRef CAS.
- K. Yan, Y. Y. Yang, J. J. Chai and Y. Lu, Appl. Catal., B, 2015, 179, 292–304 CrossRef CAS.
- X. Tang, X. H. Zeng, Z. Li, L. Hu, Y. Sun, S. J. Liu, T. Z. Lei and L. Lin, Renewable Sustainable Energy Rev., 2014, 40, 608–620 CrossRef CAS.
- Z. Xue, F. Liu, J. Jiang, J. Wang and T. Mu, Green Chem., 2017, 19, 5041–5045 RSC.
- Z. Xue, J. Jiang, G. Li, W. Zhao, J. Wang and T. Mu, Catal. Sci. Technol., 2016, 6, 5374–5379 CAS.
- R. De Bruycker, H. H. Carstensen, M. F. Reyniers, G. B. Marin, J. M. Simmie and K. M. Van Geem, Combust. Flame, 2016, 164, 183–200 CrossRef CAS.
- R. De Bruycker, H. H. Carstensen, J. M. Simmie, K. M. Van Geem and G. B. Marin, Proc. Combust. Inst., 2015, 35, 515–523 CrossRef CAS.
- A. Sudholt, R. Tripathi, D. Mayer, P. A. Glaude, F. Battin-Leclerc and H. Pitsch, Proc. Combust. Inst., 2017, 36, 577–585 CrossRef CAS.
- T. B. Adler, G. Knizia and H.-J. Werner, J. Chem. Phys., 2007, 127, 221106 CrossRef PubMed.
- G. Knizia, T. B. Adler and H.-J. Werner, J. Chem. Phys., 2009, 130, 054104 CrossRef PubMed.
- S. Grimme, S. Ehrlich and L. Goerigk, J. Comp. Chem., 2011, 32, 1456–1465 CrossRef CAS PubMed.
- L. Goerigk and S. Grimme, J. Chem. Theory Comput., 2011, 7, 291–309 CrossRef CAS PubMed.
- K. Fukui, Acc. Chem. Res., 1981, 14, 363–368 CrossRef CAS.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. J. A. Montgomery, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, T. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian, Inc., Wallingford CT, 2013, vol. Revision D.01 Search PubMed.
- K. A. Peterson, T. B. Adler and H.-J. Werner, J. Chem. Phys., 2008, 128, 084102 CrossRef PubMed.
- H.-J. Werner, P. J. Knowles, G. Knizia, F. R. Manby and M. Schutz, in a package of ab initio programs, http://www.molpro.net., 2015, vol. version 2015.1 Search PubMed.
- P. Celani and H. J. Werner, J. Chem. Phys., 2000, 112, 5546–5557 CrossRef CAS.
- K. R. Shamasundar, G. Knizia and H.-J. Werner, J. Chem. Phys., 2011, 135, 054101 CrossRef CAS PubMed.
- Y. Georgievskii and S. J. Klippenstein, MESS, Argonne National Laboratory, 2016 Search PubMed.
- Y. Georgievskii, J. A. Miller, M. P. Burke and S. J. Klippenstein, J. Phys. Chem. A, 2013, 117, 12146–12154 CrossRef CAS PubMed.
- K. G. Joback, MPhil, Massachusetts Institute of Technology, 1984.
- H. Hippler, J. Troe and H. J. Wendelken, J. Chem. Phys., 1983, 78, 6709–6717 CrossRef CAS.
- L. Zhao, M. Xie, L. Ye, Z. Cheng, J. Cai, Y. Li, F. Qi and L. Zhang, Combust. Flame, 2013, 160, 1958–1966 CrossRef CAS.
- L. Ye, L. Xing, W. Yuan, Y. Li, L. Zhang and F. Qi, Proc. Combust. Inst., 2017, 36, 533–542 CrossRef CAS.
- C. Eckart, Phys. Rev., 1930, 35, 1303–1309 CrossRef CAS.
- K. Yasunaga, J. M. Simmie, H. J. Curran, T. Koike, O. Takahashi, Y. Kuraguchi and Y. Hidaka, Combust. Flame, 2011, 158, 1032–1036 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Cartesian coordinates of major species and transition states on C5H8O2 potential energy surface. See DOI: 10.1039/c8ra02204f |
| This journal is © The Royal Society of Chemistry 2018 |