Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
BxCyNz hybrid graphenylene: stability and electronic properties†
A. Freitas *a,
L. D. Machado
*a,
L. D. Machado a,
C. G. Bezerraa,
R. M. Tromera,
L. F. C. Pereira
a,
C. G. Bezerraa,
R. M. Tromera,
L. F. C. Pereira a and
S. Azevedob
a and
S. Azevedob
aDepartamento de Física, Universidade Federal do Rio Grande do Norte, 59072-970, Natal, RN, Brazil. E-mail: alilianefisica@yahoo.com.br
bDepartamento de Física, CCEN, Universidade Federal da Paraíba, Caixa Postal 5008, 58051-970, João Pessoa, PB, Brazil
First published on 10th July 2018
Abstract
Interest in hybrid monolayers with arrangements that differ from that of the honeycomb lattice has been growing. However, systematic investigations on the properties of these structures are still lacking. In this work, we combined density functional theory (DFT) and molecular dynamics (MD) simulations to study the stability and electronic properties of nanosheets composed of B, C, and N atoms arranged in the pattern of the carbon allotrope graphenylene. We considered twenty structures with varied atomic arrangements and stoichiometries, which we call BxCyNz hybrid graphenylenes. We calculated the formation energy for each arrangement, and found that it decreases as the number of B–C and N–C bonds decreases. We also found that the structure with minimum energy has stoichiometry B2CN and an atomic arrangement with BN and C stripes connected along the zigzag direction. Regarding the electronic properties, we found that all investigated structures are semiconductors, with band gaps ranging from 0.14 to 1.65 eV. Finally, we found that the optimized hybrid lattices presented pores of varied sizes and shapes. This diversity in pore geometry suggests that these structures might be particularly suited for molecular sieve applications.
1. Introduction
Over the last years two-dimensional (2D) materials have attracted considerable interest, especially those composed of sp2-hybridized atoms arranged in a honeycomb lattice, due to their novel properties and potential applications in many emerging technologies.1 Examples of already synthesized 2D materials include graphene and hexagonal boron-nitride (h-BN).2–5 Graphene is a zero-band-gap semiconductor, with high electron mobility at room temperature, high thermal conductivity, absorbs 2.3% of incident white light, and has mechanical properties that characterize it as a strong and flexible material.6–10 On the other hand, h-BN is a large-band-gap semiconductor (>4 eV), with mechanical properties similar to graphene, and exhibits high thermal and chemical stability.11–13 In this context, an interesting possibility consists in combining the properties of these two materials by replacing C atoms in the graphene lattice by B and N atoms, leading to the formation of BxCyNz hybrid monolayers,14–19 some of which have recently been synthesized.20,21 These structures typically present small energy gaps (<2 eV), which are intermediate between those found for graphene and h-BN. However, by tuning the atomic arrangements and stoichiometries (x, y, z), they can also present metallic and semi-metallic behavior.22–24 Due to this high diversity of energy band gaps, these materials have been regarded as ideal candidates for the next generation of nanoscale electronic devices.In addition to the above-mentioned honeycomb lattices, other two-dimensional arrangements of carbon, boron and nitrogen atoms have been suggested. To the best of our knowledge, these materials have been theoretically proposed and some of them have already been synthesized. Examples include graphynes,25–29 graphenylene,30,31 inorganic graphenylene (IGP),32–34 nitrogenated holey graphene (NHG),35–37 T-graphene,38 and others.39–41 First-principle calculations of structural optimization, phonon modes, and finite temperature molecular dynamics predict stability for all these structures. Investigations on these materials have also revealed promising mechanical, optical, and electronic properties for future technological applications. Among the cited examples, two of them have recently attracted a lot of attention and differ only by their chemical composition, graphenylene and IGP.
Graphenylene is a two-dimensional lattice of sp2-hybridized carbon atoms, which was first described by Balaban et al.42 This material is composed of six-membered rings (cyclohexatriene units) connected to four-membered rings, in a configuration with periodic pores of diameter 5.51 Å.30,31 This 2D structure is a semiconductor with a direct gap of 0.8 eV,30,31 which is promising for applications in semiconducting devices. Using simulations based on density functional theory, Brunetto et al.31 have shown that graphenylene can be formed spontaneously through a dehydrogenation process of porous graphene. Although the synthesis of graphenylene has not yet been achieved, porous graphene has already been obtained experimentally.43 Among the many possible applications of graphenylene, we point out the use of this structure as a molecular sieve: Song et al.30 and Zhu et al.44 have shown that graphenylene is a promising membrane for the separation of light gases, such as H2, N2, CO, CO2, and CH4, with remarkable high selectivity for H2. Hussain et al. has shown that graphenylene doped with alkali or alkaline earth metals, are promising materials for clean energy storage.45 Additionally, it was shown that graphenylene can be a good anode material for lithium-ion batteries.46
IGP, on the other hand, consists of B and N atoms arranged in a graphenylene lattice.32–34 Perim et al. performed ab initio calculations in order to investigate the structural and electronic properties of an IGP sheet.32 The authors found IGP to be stable in molecular dynamics simulations, and also found a cohesive energy only ∼6% smaller than that of h-BN. They also showed that, in the same way as graphenylene, IGP can be formed spontaneously through the dehydrogenation of porous BN (the BN analogue of porous graphene). IGP is an insulating material with large energy gap (≈4.10 eV), and possesses periodic pores of diameter 5.35 Å. DFT calculations performed by Xu et al. suggest that IGP could also be used as a molecular sieve for the separation of H2, N2, CO, and CO2 gases.48 Moreover, Perim et al.32 showed that the selective substitution of B and N atoms by C atoms in IGP significantly reduced the energy gap, changing its behavior from insulating to semiconducting. This result suggested the possibility of tuning the band gap of this material by changing its chemical composition.
Following the progress of investigations about honeycomb lattices, a natural development in the study of graphenylene monolayers is to consider the behavior of BxCyNz hybrid nanosheets. So far, to the best of our knowledge, no theoretical or experimental studies exist in the literature that may have systematically investigated such lattices. Bearing this motivation in mind, and also considering the growing interest in BxCyNz hybrid nanostructures, in the present contribution we employ first-principles calculations to investigate the structural stability and electronic properties of what we call BxCyNz hybrid graphenylenes, shown in Fig. 1. In the structures considered here, rather than substituting selected atoms, we consider well-defined patterns mixing carbon, boron, and nitrogen atoms in a graphenylene geometry.
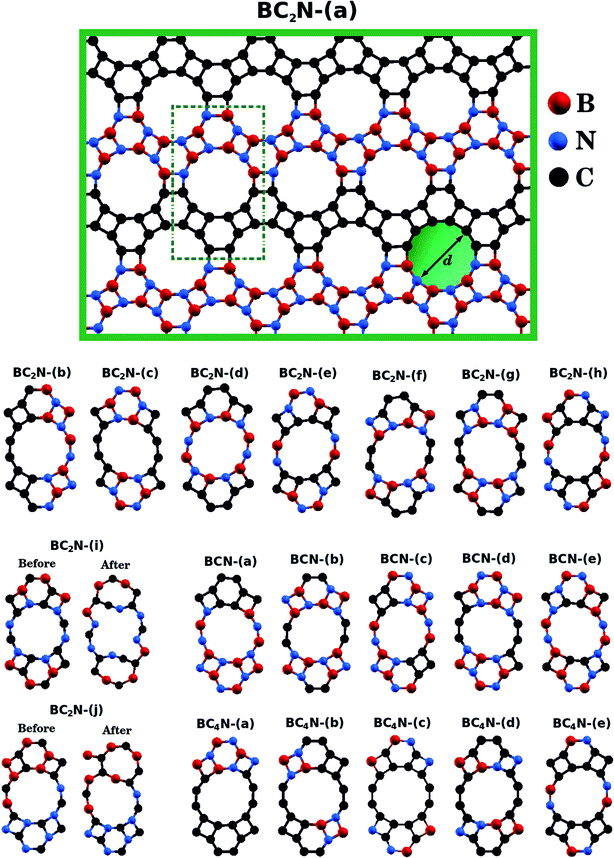 | ||
| Fig. 1 Illustration of the optimized BxCyNz hybrid graphenylenes with different atomic arrangements. | ||
2. Computational details and methods
First principles calculations were performed using density functional theory (DFT) within the generalized gradient approximation (GGA) for the exchange-correlation term,49,50 as implemented in the SIESTA code.51,52 A linear combination of numerical atomic orbitals was used to represent a double-ζ basis set with polarized functions (DZP). To modulate the strong interactions between electrons and core ions, we used the norm-conserving Troullier Martins pseudopotential53 in the Kleinman-Bylander factorized form.54 In order to ensure an accurate description of the charge density in real space and calculate the self-consistent Hamiltonian matrix elements, we have utilized a mesh cutoff of 150 Ry. For the systems investigated, we have observed that a 6 × 4 × 1 special k-points grid is enough to give the correct geometry and stability. Self-consistency is achieved when the maximum difference between the output and the input of each element of the density matrix, in a self-consistent field cycle, is smaller than 10−4 eV. The optimization of atomic positions was allowed to proceed until the force on each atom was less than 0.05 eV Å−1. We adopted a rectangular supercell (Fig. 1) and all calculations were performed at T = 0 K. The unit cell is repeated in the x and z directions, forming an infinite BxCyNz hybrid graphenylene sheet. A vacuum region of 20 Å was added along the y-axis to avoid artificial interaction between neighboring images.In order to estimate the energetic stability of the BxCyNz hybrid graphenylenes considered in this work, we calculate the formation energy EForm through a thermodynamic approach based on the prior determination of the chemical potentials of the atomic species involved in the synthesis reaction. The details of this approach are described in ref. 15 and 16. The formation energy is defined by the following expression
 | (1) |
| μBN = μB + μN and μCC = μC + μC, | (2) |
| EForm = (ETot − nBNμBN − nCCμCC)/nat. | (3) |
3. Results and discussion
Fig. 1 shows the relaxed structure of the BxCyNz hybrid graphenylenes with different stoichiometries (x, y, and z) investigated in this work. These structures are two-dimensional lattices of sp2-hybridized boron, carbon, and nitrogen atoms. They are formed by the fusion of four-membered and six-membered rings, resulting in a lattice with periodically distributed large pores. The nomenclature used to label the BxCyNz graphenylenes refers to the minimal molecular formulas BCN, BC2N or BC4N. In order to construct the BxCyNz graphenylenes, we considered a unit cell with 24 atoms (as indicated in Fig. 1 by a dashed rectangle) and different atomic arrangements. Thus, BxCyNz graphenylenes have different numbers of B–N, C–C, B–C and N–C bonds. The chosen atomic arrangements preclude the presence of energetically unfavorable B–B and N–N bonds.55 Some interesting features presented by the considered structures include: (i) the presence of (BN)x and Cy units of different sizes and forms; (ii) BN and C stripes connected along different directions; (iii) a high number of B–C and N–C bonds associated with a low number of B–N and C–C bonds (BC2N-(i) and BC2N-(j)).In this context we point out that, before the DFT optimization, the unit cell of all BxCyNz graphenylenes contained a circular pore of diameter d. However, our DFT optimization resulted in a substantial amount of structural stress, so that all final structures presented elliptical pores of varied shapes. In order to characterize the geometry of the pores, we measured the semi-major axis (a), the semi-minor axis (b), and calculated the eccentricity (ε) as
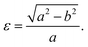 | (4) |
Values for 2a, 2b, and c are shown in Table 1. Out of all investigated structures, two (BC2N-(a), BC2N-(b)) retained pores of nearly circular shape (see Fig. 1). In these structures, each pore is half graphenylene and half IGP. Note that both graphenylene and IGP present circular pores. Conversely, notice that high eccentricity is strongly associated with multiple (BN)x and Cy components dispersed through the unit cell. It is worth noting that some elliptical pores found by us are similar to the ellipsoidal cross sections of BxCyNz hybrid nanotubes composed of diametrically opposed BN and C stripes, which were studied by Machado et al.56 and Guedes et al.57 On the other hand, for the BC2N-(i) and BC2N-(j) structures, which maximize the number of B–C and N–C bonds, we found extensive structural deformation. A two-dimensional lattice with non-graphenylene geometry arised as a result. From this, we conclude that maximizing the number of B–C and N–C bonds is not a favorable trend for BxCyNz hybrid graphenylenes.
| Structure x | EForm (eV/nT) | Rb | Wb | Rb/Wb | Eg (eV) | [2a][2b] (Å) | ε |
|---|---|---|---|---|---|---|---|
| BC2N-(a) | 0.08 | 32 | 4 | 8.0 | 1.06 | [5.61][5.51] | 0.19 |
| BC2N-(b) | 0.15 | 28 | 8 | 3.5 | 0.16 | [5.61][5.47] | 0.22 |
| BC2N-(c) | 0.16 | 28 | 8 | 3.5 | 1.65 | [5.76][5.02] | 0.49 |
| BC2N-(d) | 0.17 | 28 | 8 | 3.5 | 0.53 | [5.81][5.17] | 0.46 |
| BC2N-(e) | 0.19 | 24 | 12 | 2.0 | 0.50 | [5.54][5.24] | 0.32 |
| BC2N-(f) | 0.21 | 24 | 12 | 2.0 | 1.02 | [5.96][5.08] | 0.52 |
| BC2N-(g) | 0.30 | 20 | 16 | 1.3 | 0.86 | [5.92][5.21] | 0.47 |
| BC2N-(h) | 0.32 | 20 | 16 | 1.3 | 0.75 | [5.77][5.23] | 0.42 |
| BC2N-(i) | 0.56 | 9 | 22 | 0.4 | 1.30 | — | — |
| BC2N-(j) | 0.79 | 4 | 30 | 0.1 | 0.00 | — | — |
| BCN-(a) | 0.11 | 30 | 6 | 5.0 | 1.09 | [5.77][5.18] | 0.44 |
| BCN-(b) | 0.17 | 28 | 8 | 3.5 | 0.77 | [5.83][5.22] | 0.45 |
| BCN-(c) | 0.17 | 28 | 8 | 3.5 | 0.51 | [5.84][5.21] | 0.45 |
| BCN-(d) | 0.17 | 28 | 8 | 3.5 | 1.10 | [5.80][5.06] | 0.49 |
| BCN-(e) | 0.25 | 20 | 16 | 1.3 | 1.05 | [5.82][5.13] | 0.47 |
| BC4N-(a) | 0.11 | 30 | 6 | 5.0 | 0.74 | [5.80][5.09] | 0.48 |
| BC4N-(b) | 0.17 | 28 | 8 | 3.5 | 0.36 | [5.81][5.16] | 0.46 |
| BC4N-(c) | 0.23 | 24 | 12 | 2.0 | 0.72 | [5.60][5.39] | 0.27 |
| BC4N-(d) | 0.26 | 20 | 16 | 1.3 | 0.38 | [5.84][5.15] | 0.47 |
| BC4N-(e) | 0.37 | 28 | 8 | 3.5 | 0.14 | [5.83][5.22] | 0.45 |
The results presented in Fig. 1 and Table 1 suggest a possible application for the BxCyNz hybrid graphenylenes. Observe that the structures proposed present pores of diverse sizes, which are located in a range that is convenient for applications in gas separation. For instance, simulations have previously demonstrated that graphenylene membranes with pore size below 5.68 Å can separate H2 from CO2, CO, N2, and CH4 (in that investigation, pore size was controlled with strain).44 Other 2D membranes with diameters below this threshold have also displayed effective performance in H2 separation processes,30,48,58,59 further suggesting that hybrid graphenylenes could be used towards this end. Regarding the proposed structures with larger pores, some are located in a range that could be useful for the separation of different gases.44 Moreover, the varied pore shapes could prove useful in molecular sieves, as pores with roughly the same size and area can present different permeation ratios.47 Finally, further versatility could be attained by varying the polarity of the membrane, by selecting compositions with higher/lower fractions of B and N atoms. Polarity has been shown to influence both the selectivity and the permeance of IGP membranes; polarity may hinder or aid diffusion, depending on the gas composition.48 The great adaptability of hybrid graphenylenes suggests that particular pore sizes, shapes, and compositions could be selected to assemble sieves customized for varied gas separation tasks.
We also report in Table 1 the values of the formation energy for the BxCyNz hybrid graphenylenes. Additionally, we note that there is a relationship between EForm and the number, within the structure, of ‘regular’ chemical bonds, C–C and B–N, and ‘wrong’ chemical bonds, C–B and C–N. Thus, in order to quantify this effect, we define the ratio Rb/Wb, between the number of regular (Rb) and wrong (Wb) chemical bonds. The value of the ratio Rb/Wb, for each structure, is shown in Table 1. We notice an increase in the formation energy when the number of wrong bonds increases, i.e., when the ratio Rb/Wb decreases. This relationship has also been observed in other types of hybrid nanostructures with BxCyNz stoichiometry.15,16,60
Bearing this in mind, notice in Table 1 that the BC2N-(a) graphenylene with the highest possible ratio Rb/Wb, presents the lowest EForm. Therefore, it is the most stable structure. Following this line of thought, the BCN-(a) and BC4N-(a) monolayers are tied as the second most stable structures, since they present the second lowest EForm and the second highest Rb/Wb. Notice also that the difference between the Eform of these two structures and that of BC2N-(a) is only 0.03 eV/nat. The reason for the stability of these structures is found in their atomic arrangement, with BN and C stripes connected along the zigzag direction. In the case of the BC2N-(a) structure, where the width of the BN and C stripes are quite similar, we have a minimum amount of structural stress and a stable two-dimensional lattice. However, when the width of the BN and C stripes are different (BCN-(a) and BC4N-(a)), small deformations and pores with higher eccentricity appear in the lattice, slightly decreasing the stability. The most unstable structures are BC2N-(i) and BC2N-(j), which have the highest EForm (over 0.5 eV/nat above that of BC2N-(a)). Unsurprisingly, these configurations present the lowest Rb/Wb ratio, maximizing the number of B–C and N–C bonds. They are also the only two that present optimized lattices that completely differ from the initial graphenylene geometry.
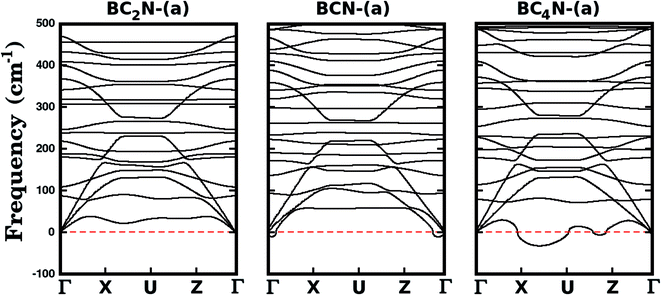
We further investigate the stability of the three most stable structures (BC2N-(a), BCN-(a), and BC4N-(a)) by calculating their phonon dispersion curves, presented in Fig. 2. Among the considered structures, BC2N-(a) is the only one that does not present imaginary frequencies (which are shown as negative values in Fig. 2), confirming its structural stability. Meanwhile, the presence of negative frequencies in the phonon dispersions of BCN-(a) and BC4N-(a) is an indication of possible structural instabilities. Furthermore, our prediction of structural stability based on the calculated phonon frequencies is in agreement with the calculated formation energies, with BC2N-(a) showing the lowest formation energy.
We also compare the formation energy of the BC2N-(a) graphenylene (which corresponds to the most stable structure) with the calculated formation energies for the BxCyNz hexagonal monolayers,14 which have already been experimentally observed.20,21 In order to do so, we re-calculate the formation energy for the BC2N-(a) using the chemical potentials of the BN and CC pairs (μBN and μCC) estimated for the BxCyNz hexagonal monolayers, as done by Azevedo et al.14 The most stable hexagonal monolayer estimated by those authors is the one which presents stoichiometry B3C2N3, with formation energy of 0.12 eV/nat. For comparison purposes, we found that the BC2N-(a) graphenylene presents a formation energy 0.5 eV/nat larger than B3C2N3.
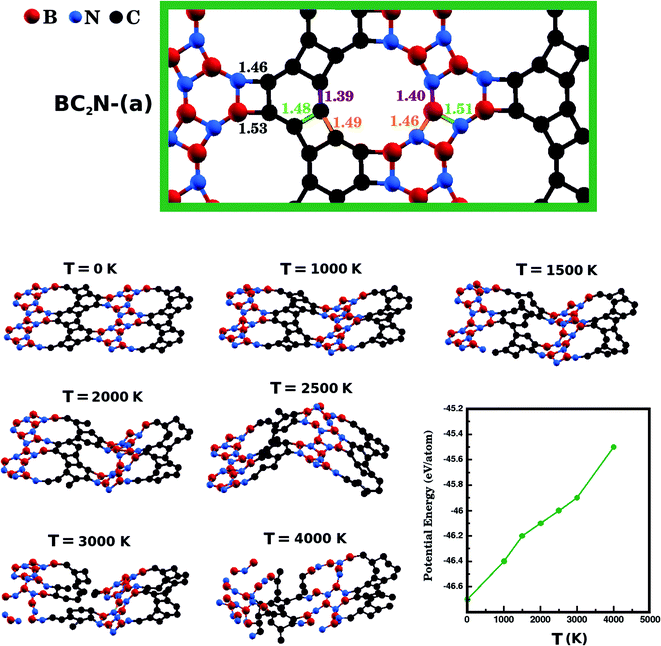
Next, we investigate the stability of the structure with lowest Eform, BC2N-(a), performing Ab Initio Molecular Dynamics (AIMD) simulations using the SIESTA code. We used a time step of 1 fs to evolve BC2N-(a) for 20 ps in the NPT ensemble. We also employed the Nosé-Hoover thermostat and the Parrinello–Rahman barostat to control the temperature and in-plane pressure components, respectively. In order to avoid relaxation of the system in the direction perpendicular to the plane, we kept the monolayers separated by a vacuum slab of fixed length (20 Å). Finally, we performed AIMD stability tests at six temperatures: 1000 K, 1500 K, 2000 K, 2500 K, 3000 K, and 4000 K. In Fig. 3, we present snapshots of BC2N-(a) after thermalization, at different temperatures. We also present a plot relating the converged potential energy with temperature, which displays the proportionality between these two quantities. For 1000 K the thermalization process caused few changes in the atomic structure of BC2N-(a). From 1500 K to 2500 K, we observed that the graphenylene lattice remained intact, in spite of the increasing amplitude of the out-of-plane vibrations. From 3000 K onwards we observed bond breakage, and at 4000 K changes to the initial arrangement of bonds were extensive. In summary, our AIMD simulations indicate that the BC2N-(a) hybrid graphenylene is able to withstand high temperatures and is, therefore, very stable.
Additionally, Brunetto et al.31 and Perim et al.32 have shown that graphenylene and IGP can be formed spontaneously through a dehydrogenation process of porous graphene and porous BN, respectively. Although the synthesis of graphenylene has not yet been achieved, porous graphene has already been obtained experimentally.43 Thus, graphenylene could be obtained experimentally by using an electron beam as a means of selectively removing the hydrogen atoms from a porous graphene sheet, through the so-called knock-on effect,61 thus causing a spontaneous conversion to a stable graphenylene sheet. In view of this, we suggest that the BxCyNz hybrid graphenylenes could also be obtained experimentally by removing the hydrogen atoms from a BxCyNz porous graphene sheet by the knock-on effect. The synthesis of BxCyNz porous graphene could be made using the same method for synthesis of BxCyNz hybrid hexagonal monolayers.20,21
We have also calculated the B–N, C–C, B–C, and N–C bond lengths in the relaxed structures of the BxCyNz hybrid graphenylenes. In the case of the most stable structure, BC2N-(a), we found three possible lengths for the C–C and B–N bonds. Specific values depend on the position in the lattice, since a bond can be part of a six-membered ring, of a four-membered ring, or can be shared by a six- and a four-membered ring (see Fig. 3). We measured C–C bond lengths of 1.39 Å, 1.49 Å, and 1.48 Å; and B–N bond lengths of 1.40 Å, 1.46 Å, and 1.51 Å, respectively. Similar results were also found in the literature for graphenylene and IGP, where, in both structures, there are three possible C–C and B–N bond lengths.30,32 The wrong bonds, B–C and N–C, measured ∼1.53 Å and 1.46 Å, respectively.
Let us now discuss the electronic properties of the BxCyNz hybrid graphenylenes. In Fig. 4 we present the calculated electronic band structure with 100 k-points along the Γ–X–Z direction. The calculated energy band gaps Eg are shown in the fifth column of Table 1. We found Eg values ranging from 0.14 to 1.65 eV. With the exception of the BC2N-(i) and (j), which are not BxCyNz hybrid graphenylenes, all the other structures behave as semiconductors, regardless of the atomic arrangement in the unit cell. It is interesting to note that the energy gap values of BxCyNz graphenylenes oscillate above or below the estimated energy gap for pristine graphenylene (0.86 eV (ref. 31)), and are always lower than the estimated gap value for IGP (4.10 eV (ref. 32)). These results indicate that the inclusion of B and N atoms in the porous lattice of the graphenylene, for the formation of the BxCyNz hybrid graphenylene, can increase or decrease the energy gap, but maintains the semiconducting behavior. This fact is associated with the presence of π-bonds and isolated electron pairs in the pz orbitals of nitrogen atoms in the hexagonal rings. Moreover, the direct gap of 1.06 eV for the BC2N-(a) is about half of the estimated gap for the most stable BxCyNz hexagonal monolayer, for which the gap is around 1.69 eV.14,15 Finally, we believe that our results for the energy gap of the BxCyNz hybrid graphenylenes may open new perspectives for applications of these structures in future electronic nanodevices.
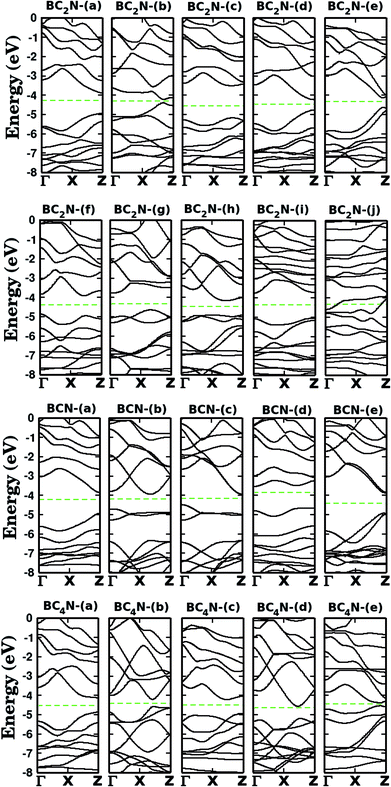 | ||
| Fig. 4 Calculated band structures for the monolayers shown in Fig. 1. The dashed line represents the Fermi level. | ||
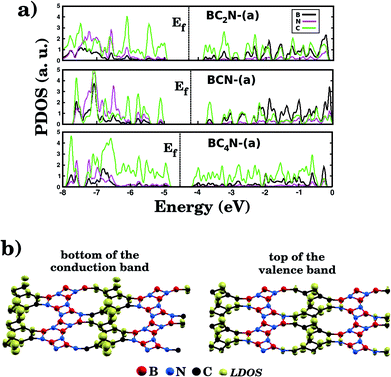
Fig. 5(a) shows the projected density of states (PDOS) for selected BxCyNz hybrid graphenylenes. We can infer from the PDOS that, in general, the contribution of the C atoms is more significant for electronic states near the Fermi energy Ef. The contribution of the B atoms is stronger for electronic states in the conduction band, while the contribution of the N atoms is more significant in the valence band. This behavior is also observed in other types of nanostructures with stoichiometry BxCyNz, such as hexagonal monolayers,23,24 nanotubes62,63 and nanocones.64 Additional calculations of the localized density of states (LDOS) for the BC2N-(a) structure, shown in Fig. 5(b), reveal that the bottom of the conduction band and the top of the valence band are associated with the pz orbitals of the C and N atoms, which is consistent with the results of the PDOS. For completeness, we show in Fig. 6 results of spin-polarization calculations, which reveal zero spin for all BxCyNz hybrid graphenylenes structures, which means the valence band is completely filled and that unpaired electrons are not available.
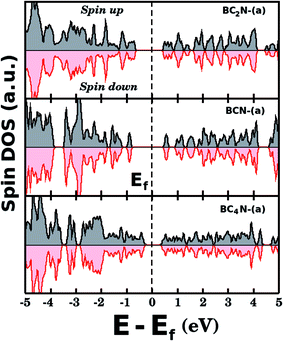 | ||
| Fig. 6 Densities of states (spin up and down) for selected BxCyNz hybrid graphenylenes. The total spin is zero for all investigated structures. | ||
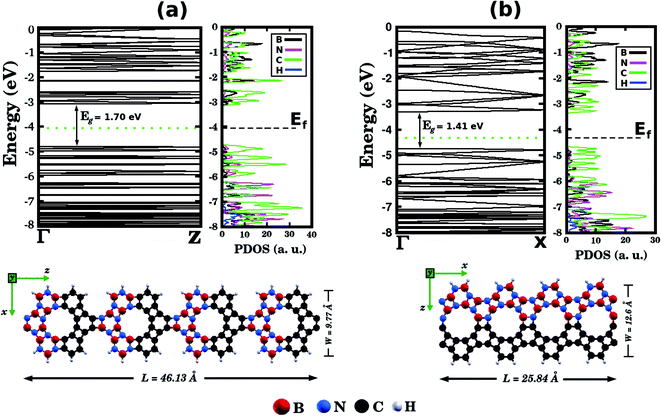
Before concluding, inspired by the recent work of Song et al.30 we performed first-principles calculations to probe electronic properties and structural stability of BxCyNz graphenylene nanoribbons, as illustrated in Fig. 7. These structures were constructed based on the atomic arrangement of BC2N-(a), which is the most stable structure among all BxCyNz hybrid graphenylenes. Thus, we considered nanoribbons composed of BN and C stripes, with either armchair (Fig. 7 (a)) or zigzag (Fig. 7(b)) symmetries. In particular, we notice that the BN and C stripes are perpendicular to the periodic direction in the armchair nanoribbon and parallel to the periodic direction in the zigzag nanoribbon. We found that the zigzag nanoribbon (total energy of −143.21 eV per atom) is more energetically favorable than the armchair one (total energy of −137.40 eV per atom). This result is associated with the fact that the zigzag nanoribbon presents a lower number of ‘wrong bonds’ (B–C and N–C) than the armchair one. Fig. 7 also shows the band structures of the studied nanoribbons. It can be seen that the zigzag nanoribbon exhibits a smaller energy gap Eg than the armchair one (a difference of 0.29 eV). However, both structures are semiconductors with an energy gap larger than that of the BC2N-(a) hybrid graphenylene. This result is similar to the one found for pristine graphenylene nanoribbons.30 Finally, from the corresponding PDOS shown in Fig. 7, it is possible to see that the electronic states near the Fermi level, which are responsible for the closing of the energy gap, are associated with carbon atoms.
4. Conclusions
In summary, we combined DFT calculations and AIMD simulations to investigate the stability and electronic properties of two-dimensional nanosheets, composed of B, C, and N atoms, with a geometry similar to that of graphenylene. We analyzed twenty structures with different atomic arrangements and stoichiometries, which we called BxCyNz hybrid graphenylenes. We found that the most stable structure is the one with stoichiometry BC2N, which maximizes the number of B–N and C–C bonds, and minimizes the number of B–C and N–C bonds. This behavior is similar to that found for BxCyNz hybrid honeycomb monolayers, for which the most stable structures also maximize the number of B–N and C–C bonds. Another interesting characteristic of the BC2N sheet is the atomic arrangement, with BN and C stripes connected along the zigzag direction. Regarding the structural properties, we found that the optimized structures of the BxCyNz hybrid graphenylene present elliptical pores with different eccentricities and chemical compositions, which makes these structures particularly suited for molecular sieves. Our calculations also showed that the electronic properties of the BxCyNz hybrid graphenylene are highly sensitive to the specific arrangement of B, C, and N atoms. We also found energy gaps ranging from 0.14 eV to 1.65 eV. Thus, all structures present semiconductor behavior, which may be interesting for the development of future electronic devices from these nanomaterials. Moreover, spin-polarized calculations demonstrated that none of the investigated structures exhibit magnetic behavior. Finally, we also investigated the electronic properties and the stability of BxCyNz graphenylene nanoribbons. Our results show that the zigzag nanoribbon is more energetically favorable than the armchair one, and both present semiconductor behavior. We believe that this work adds an important group of monolayers to the ever increasing family of hybrid monolayers which combine B, C, and N atoms.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We would like to thank the Brazilian Research Agencies CNPq, PNPD/CAPES and INCT of Space Studies for financial support. C. G. B., R. M. T. and L. F. C. P. acknowledge financial support from CAPES for the project “Physical properties of nanostructured materials” (Grant No. 3195/2014) via its Science Without Borders program. We are also grateful for the provision of computational resources by the High Performance Computing Center (NPAD) and the CLIMA cluster at UFRN, and the Laboratory of Computational Physics at UFPB.References
- G. R. Bhimanapati, Z. Lin, V. Meunier, Y. Jung, J. Cha, S. Das, D. Xiao, Y. Son, M. S. Strano, V. R. Cooper, L. Liang, S. G. Louie, E. Ringe, W. Zhou, S. S. Kim, R. R. Naik, B. G. Sumpter, H. Terrones, F. Xia, Y. Wang, J. Zhu, D. Akinwande, N. Alem, J. A. Schuller, R. E. Schaak, M. Terrones and J. A. Robinson, ACS Nano, 2015, 9, 11509–11539 CrossRef PubMed.
- A. H. C. Neto, F. Guinea, N. M. R. Peres, K. S. Novoselov and A. K. Geim, Rev. Mod. Phys., 2009, 81, 109–162 CrossRef.
- A. K. Geim, Science, 2009, 324, 1530–1534 CrossRef PubMed.
- D. Pacile, J. C. Meyer, C. O. Girit and A. Zettl, Appl. Phys. Lett., 2008, 92, 133107 CrossRef.
- C. H. Jin, F. Lin, K. Suenaga and S. Iijima, Phys. Rev. Lett., 2009, 102, 195505 CrossRef PubMed.
- S. D. Sarma, A. Shaffique, E. H. Hwang and R. Enrico, Rev. Mod. Phys., 2011, 83, 407–470 CrossRef.
- E. Gibney, Nature, 2015, 522, 274 CrossRef PubMed.
- X. Xu, L. F. C. Pereira, Y. Wang, J. Wu, K. Zhang, X. Zhao, S. Bae, C. T. Bui, R. Xie, J. T. L. Thong, B. H. Hong, K. P. Loh, D. Donadio, B. Li and B. Özyilmaz, Nat. Commun., 2014, 5, 3689 CrossRef PubMed.
- C. Lee, X. Wei, J. W. Kysar and J. Hone, Science, 2008, 321, 385–388 CrossRef PubMed.
- X. Ma and H. Zhang, Nanoscale Res. Lett., 2013, 8, 440 CrossRef PubMed.
- W. Han, L. Wu, Y. Zhu, K. Watanabe and T. Taniguchi, Appl. Phys. Lett., 2008, 93, 223103 CrossRef.
- Y. Miyamoto, M. L. Cohen and S. G. Louie, Phys. Rev. B, 1995, 52, 14971–14975 CrossRef.
- S. Azevedo, J. Kaschny, M. Caio and F. de Brito Mota, Eur. Phys. J. B, 2009, 67, 507–512 CrossRef.
- S. Azevedo and R. De Paiva, Europhys. Lett., 2006, 75, 126–132 CrossRef.
- S. Azevedo, M. Mazzoni, R. Nunes and H. Chacham, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 70, 205412 CrossRef.
- S. Azevedo, J. R. Kaschny, C. Castilho and F. B. Mota, Nanotechnology, 2007, 18, 495707 CrossRef PubMed.
- M. S. Mazzoni, R. W. Nunes, S. Azevedo and H. Chacham, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 073108 CrossRef.
- Y. Tateyama, T. Ogitsu, K. Kusakabe, S. Tsuneyuki and S. Itoh, Phys. Rev. B: Condens. Matter Mater. Phys., 1997, 55, R10161–R10164 CrossRef.
- I. M. Felix and L. F. C. Pereira, Sci. Rep., 2018, 8, 2737 CrossRef PubMed.
- L. Ci, L. Song, C. Jin, D. Jariwala, D. Wu, Y. Li, A. Srivastava, Z. F. Wang, K. Storr, L. Balicas, F. Liu and P. M. Ajayan, Nat. Mater., 2010, 9, 430–435 CrossRef PubMed.
- C. Huang, C. Chen, M. Zhang, L. Lin, X. Ye, S. Lin, M. Antonietti and X. Wang, Nat. Commun., 2015, 6, 7698 CrossRef PubMed.
- A. K. Manna and S. K. Pati, J. Phys. Chem. C, 2011, 115, 10842–10850 CrossRef.
- A. Freitas, S. Azevedo, M. Machado and J. R. Kaschny, Appl. Phys. A, 2012, 108, 185–193 CrossRef.
- A. Du, Z. Zhu, G. Lu and S. C. Smith, J. Am. Chem. Soc., 2009, 131, 1682–1683 CrossRef PubMed.
- D. Sundholm, L. N. Wirz and P. Schwerdtfeger, Nanoscale, 2015, 7, 15886–15894 RSC.
- W. S. Cranford, B. D. Brommer and J. M. Buehler, Nanoscale, 2012, 4, 7797–7809 RSC.
- Y. Jiao, A. J. Du, M. Hankel, Z. H. Zhu, V. Rudolph and S. C. Smith, Chem. Commun., 2011, 47, 11843–11845 RSC.
- S. W. Cranford and M. J. Buehler, Carbon, 2011, 49, 4111–4121 CrossRef.
- B. Mortazavi, M. Shahrokhi, T. Rabczuk and L. F. C. Pereira, Carbon, 2017, 123, 344–353 CrossRef.
- Q. Song, B. Wang, K. Deng, X. Feng, M. Wagner, J. D. Gale, K. Mullen and L. Zhi, J. Mater. Chem. C, 2013, 1, 38–41 RSC.
- G. Brunetto, P. A. S. Autreto, L. D. Machado, B. I. Santos, R. P. B. Santos and D. S. Galvão, J. Phys. Chem. C, 2012, 116, 12810–12813 CrossRef.
- E. Perim, R. Paupitz, P. A. S. Autreto and D. S. Galvão, J. Phys. Chem. C, 2014, 118, 23670–23674 CrossRef.
- R. Paupitz, C. E. Junkermeier, A. C. T. van Duin and P. S. Branicio, Phys. Chem. Chem. Phys., 2014, 16, 25515–25522 RSC.
- J. R. Feng and G. C. Wang, Comput. Mater. Sci., 2016, 111, 366–373 CrossRef.
- J. Mahmood, E. K. Lee, M. Jung, D. Shin, I. Y. Jeon, S. Jung, H. J. Choi, J. M. Seo, S. Y. Bae, S. D. Sohn, N. Park, J. H. Oh, H. J. Shin and J. B. Baek, Nat. Commun., 2015, 6, 6486 CrossRef PubMed.
- H. Sahin, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 92, 085421 CrossRef.
- B. Mortazavi, O. Rahaman, T. Rabczuk and L. F. C. Pereira, Carbon, 2016, 106, 1–8 CrossRef.
- Y. Liu, G. Wang, Q. Huang, L. Guo and X. Chen, Phys. Rev. Lett., 2012, 108, 225505 CrossRef PubMed.
- Z. Wang, X.-F. Zhou, X. Zhang, Q. Zhu, H. Dong, M. Zhao and A. R. Oganov, Nano Lett., 2015, 15, 6182–6186 CrossRef PubMed.
- L. F. C. Pereira, B. Mortazavi, M. Makaremi and T. Rabczuk, RSC Adv., 2016, 6, 57773–57779 RSC.
- M. Shahrokhi, B. Mortazavi and G. R. Berdiyorov, Solid State Commun., 2017, 253, 51–56 CrossRef.
- A. T. Balaban, C. C. Rentia and E. Ciupitu, Rev. Roum. Chim., 1968, 13, 231 Search PubMed.
- M. Bieri, M. Treier, J. Cai, K. Aït-Mansour, P. Ruffieux, O. Gröning, P. Gröning, M. Kastler, R. Rieger, X. Feng, K. Müllen and R. Fasel, Chem. Commun., 2009, 45, 6919–6921 RSC.
- L. Zhu, Y. Jin, Q. Xue, X. Li, H. Zheng, T. Wu and C. Ling, J. Mater. Chem. A, 2016, 4, 15015–15021 RSC.
- T. Hussain, M. Hankel and D. J. Searles, J. Phys. Chem. C, 2017, 121, 14393–14400 CrossRef.
- Y. X. Yu, J. Mater. Chem. A, 2013, 1, 13559–13566 RSC.
- D. Huailiang, L. Jingyuan, Z. Jing, S. Gang, L. Xiaoyi and Z. Yuliang, J. Phys. Chem. C, 2011, 115, 23261–23266 CrossRef.
- J. Xu, S. Zhou, P. Sang, J. Li and L. Zhao, J. Mater. Sci., 2017, 52, 10285–10293 CrossRef.
- W. Kohn and L. J. Sham, Phys. Rev. Lett., 1965, 140, A1133–A1138 Search PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef PubMed.
- D. Sánchez-Portal, P. Ordejón, E. Artacho and J. M. Soler, Int. J. Quantum Chem., 1997, 65, 453–461 CrossRef.
- J. M. Soler, E. Artacho, J. D. Gale, A. García, J. Junquera, P. Ordejón and D. Sánchez-Portal, J. Phys.: Condens. Matter, 2002, 14, 2745 CrossRef.
- N. Troullier and J. L. Martins, Phys. Rev. B: Condens. Matter Mater. Phys., 1991, 43, 1993–2006 CrossRef.
- L. Kleinman and D. M. Bylander, Phys. Rev. Lett., 1982, 48, 1425–1428 CrossRef.
- A. N. Andriotis, E. Richter and M. Menon, Phys. Rev. B: Condens. Matter Mater. Phys., 2016, 93, 081413 CrossRef.
- M. Machado, T. Kar and P. Piquini, Nanotechnology, 2011, 22, 205706 CrossRef PubMed.
- J. P. Guedes, F. B. Mota, S. Azevedo and C. M. C. Castilho, Eur. Phys. J. B, 2015, 88, 236 CrossRef.
- Y. Jiao, A. Du, M. Hankel, Z. Zhu, V. Rudolph and S. C. Smith, Chem. Commun., 2011, 47, 11843–11845 RSC.
- Z. Ma, X. Zhao, Q. Tang and Z. Zhou, Int. J. Hydrogen Energy, 2014, 39, 5037–5042 CrossRef.
- A. C. M. Carvalho, C. G. Bezerra, J. A. Lawlor and M. S. Ferreira, J. Phys.: Condens. Matter, 2014, 26, 015303 CrossRef PubMed.
- D. B. Williams and C. B. Carter, Transmission Electron Microscopy: A Textbook for Materials Science, 1996, Springer Search PubMed.
- S. Azevedo and J. R. Kaschny, Solid State Commun., 2013, 168, 11–14 CrossRef.
- H. Pan, Y. P. Feng and J. Lin, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 74, 045409 CrossRef.
- S. Azevedo and M. Machado, Nanotechnology, 2009, 20, 115709 CrossRef PubMed.
Footnote |
| † PACS numbers: 73.20.At, 73.20.Hb, 71.15.Mb. |
| This journal is © The Royal Society of Chemistry 2018 |