Which NICS method is most consistent with ring current analysis? Assessment in simple monocycles

Abstract

The aromaticity of benzene, Al₄²⁻ cluster, cyclopropane, borazine and planar cyclooctatetraene (COT) was analyzed according to different strategies based on nucleus-independent chemical shift (NICS) computations. The analysis of NICS-components evolution along the main molecular axis seems to be the most adequate and simplest strategy to predict the aromatic or antiaromatic character of the studied systems. Moreover, the analysis of the σ- and π-electron contributions to the out-of-plane component of NICS (NICS_zz) leads to the same qualitative and quantitative conclusions previously obtained by the analysis of the magnetically induced ring current densities.

---

Introduction

The aromaticity concept, introduced by August Kekulé in 1865, to rationalize the properties of benzene,^1,2 is commonly applied to analyze a great variety of molecules nowadays. Although aromaticity is not an experimentally measurable quantity, many indices from different criteria have been proposed to characterize and quantify it^3–9 (see references cited above for further details). Most of these indices were originally developed within the organic chemistry framework, but with increasing applications in inorganic chemistry.^3,6,10 One of these criteria, the magnetic one, is based on the fact that aromatic compounds sustain an induced ring current density in the presence of both a normal – to the molecular plane- and uniform magnetic field.^11–14

The magnetically induced ring current is analyzed through different strategies to assess (the degree of) aromaticity of a compound.^15,16 This analysis is performed on the computationally predicted property, since this ring current is solely manifested in NMR spectroscopy and measurements of magnetic anisotropy experimentally.^5,17 This inspired the introduction of the nucleus-independent chemical shifts (NICS), by far the most widely used index for assessing aromaticity, or antiaromaticity, in molecular systems. Schleyer and coworkers, in their pioneering work, defined NICS as “the negative of the absolute magnetic shielding”, further suggesting to compute it at the molecular center.¹⁸ This index became rapidly popular because of its easy computation in almost all quantum chemical packages. However, its indiscriminate use has often been criticized.^17,19–26 These criticisms have pointed to the validity of NICS being limited by spurious contributions from the in-plane tensor components, which are not related with the aromaticity phenomenon. To avoid these issues, different ways to analyze NICS have been suggested. For instance: to compute the property 1.0 ångström (Å) above the molecular plane NICS(1);²⁷ to evaluate the out-of-plane component of the NICS tensor (NICS_zz has been proven to be particularly sensitive to π-electron delocalization patterns);^28,29 to assess NICS-scans (providing an indication of the diamagnetic and paramagnetic ring currents)³⁰ and to compute the dissected NICS^31,32 (allowing the analysis of the orbital contributions to aromaticity or antiaromaticity). These, and other approaches, have contributed to improve NICS capability as an aromaticity descriptor. Consequently, suitable conclusions can be obtained when this magnetic response is analyzed in depth, even in problematic molecules.^20,33–35

Recently, Bultinck and coworkers showed that there is no simple one-to-one relationship that allows reconstructing current density maps from only NICS-values. These authors argue that NICS should not be used without an ab initio computed current density map, to adequately analyze aromaticity.³⁶ However, the use of NICS, independently of current densities, has become part of the standard practices of computational chemists and this is unlikely to change in the short term. We agree with preferably analyzing the current density, conjointly with NICS, to diagnose aromaticity, but we can also realize that NICS remains a simple method and widely used in the chemical community. In this context, it is paramount to find out which NICS aromaticity index, or strategy, is the most consistent one with ring current analysis. Different works have dealt with this problem; however, most of them have focused on benzene and derivatives. Some of these strategies have already been mentioned in the previous paragraph and others have been inspired by them. For example, we recently proposed the identification of the free of in-plane component NICS along the main molecular axis (FiPC-NICS), which allowed us to obtain characteristic patterns for aromatic, anti-aromatic and non-aromatic benchmark molecules.^22,34 Other more sophisticated approaches are those based on molecular dissected NICS^31,32 conjointly with their bi- or tri- dimensional plots.^34,37–41 It is also important to highlight that the quantitative relationship between shielding and ring current strengths has been rigorously analyzed in the past.^42–45 In these works, it is assumed that the wire carrying the ring current is circular and infinitely thin; thus, the induced magnetic field is easily determined from classical electrodynamics, using the Biot–Savart's law.⁴⁶ These studies conclude that the relationship between these two properties is not linear, due to the distance dependence of the induced magnetic field. However, the linear relationship is a good approximation, particularly considering that: the induced ring current, in a molecular ring, is not a perfect homogeneous circular current flowing through the molecular wire.

The main goal of this work is to evaluate how different methods based in NICS computations may provide similar pictures of the aromatic, or antiaromatic, character when compared to those obtained by the ring current analysis. The study focused on evaluating both the σ- and π-electrons contributions to the aromaticity in a set of five benchmark molecules: benzene, Al₄²⁻ cluster, cyclopropane, borazine and planar cyclooctatetraene. This selection was made because the (anti)aromatic character of these species has previously been thoroughly assessed by dissecting ring currents (σ- and π-electrons contributions),⁴⁷ providing us with the adequate data to be compared with our NICS computations. To our best knowledge, there are no available studies in the literature that systematically compare the information obtained from dissected currents with their NICS counterparts, which are the most sophisticated ways to analyze aromaticity according to these theoretical properties. Therefore, we expect that our research contributes to shorten the gap between both methods. It is important to mention that our conclusions are strictly applicable to monocycles. In the near future, we hope to extend this work to polycyclic molecules, where discrepancies between NICS and ring currents should be more notorious.^48–50

Computational details

All calculations reported in this work were done using Gaussian 09 computational package⁵¹ at the PW91/def2TZVP^52,53 level. This functional has been widely used for the calculation of magnetic properties in organic, inorganic and solid compounds, providing results comparable with experiments.^38,54–56 Vibrational frequency calculations were performed at the same level to effectively obtain a true-minimum on the potential energy surface (PES), with the exception of the planar COT, which has one imaginary frequency (156.1i cm⁻¹). NICS values were computed employing gauge including the atomic orbital (GIAO)⁴⁰ method and were dissected into their core, valence, σ and π contributions using the natural chemical shielding (NCS) analysis implemented in the NBO 6.0 program.^57,58 The size NICS plots are 10 × 10 Å with a step-size of 0.2 Å and were generated using the VisIt 2.10.0 program⁵⁹ and our own codes.^34,35,60

Results and discussion

Evaluation of NICS changes along the main molecular axis

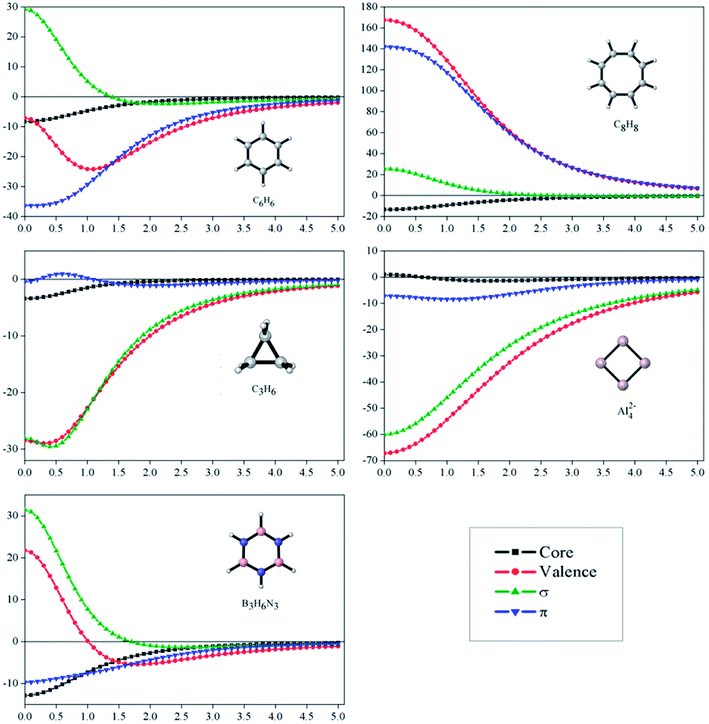
Let us start our discussion by analyzing how the plots NICS_out-plane vs. NICS_in-plane (−1/3 (σ_zz) vs. −1/3 (σ_xx + σ_yy)) allows to classify the studied systems as aromatic or antiaromatic (see Fig. 1). This strategy, named FiPC-NICS, was introduced as a simplification of the Stanger proposal (based on scanning NICS values over a distance and separating them into in-plane and out-of plane contributions) four years ago.³⁰ Its basis lies on the assumption that in-plane components are more sensitive to local induced fields arising from the core and localized (lone pairs and bonding) electrons. Thus, local magnetic fields should be of short-range, meaning that they should decay in small spatial intervals. In contrast, the out-of-plane component is expected to highlight the induced magnetic field due to cyclic delocalized electrons, as is the case of aromatic, and antiaromatic, systems. According to the FiPC-NICS plots (Fig. 1), the systems C₆H₆, Al₄²⁻, C₃H₆ and B₃H₆N₃ could be classified as aromatic, whereas the planar C₈H₈ molecule as antiaromatic; the main difference between aromatic and antiaromatic rings being that the former exhibits negative NICS_out-of-plane values, whereas the later exhibits positive NICS_out-of-plane values. Additionally, observing from top, the antiaromatic and aromatic curves have concave and convex slopes, respectively. Another important result of this analysis is to identify at which distance the in-plane components of NICS becomes zero. These distances are of 1.1, 3.0, 1.1, 1.3 and 1.1 Å for C₆H₆, Al₄²⁻, C₃H₆, B₃H₆N₃ and C₈H₈, respectively. This suggest that local contributions of NICS are negligible above 1.1, 1.3 and 3.0 Å for the aromatic hydrocarbons, the borazine and the Al₄²⁻ cluster, respectively. The larger distance in borazine (1.3 Å) and Al₄²⁻ cluster (3.0 Å) are explained by their peculiar local contributions. In borazine, the lone pairs on the nitrogen atoms, are known to exhibits local diatropic ring currents under magnetic perturbation, which are consequently expected to contribute to the NICS locally.^34,61 In the case of the Al₄²⁻ cluster, Sundholm and collaborators, based on total ring current analysis, predicted a doubly (π and σ) aromatic character.⁶² However, Fowler and collaborators showed that the π-electron exhibits a significant ring current when the molecule is perturbed by a parallel magnetic field, which implies mobility of the π-electron cloud, but not aromaticity.⁶³ FiPC-NICS prediction supports this finding (there is an important local magnetic contribution in Al₄²⁻, even at 3.0 Å). In the light of this analysis, FiPC-NICS shows to be a simple and adequate strategy to be used in the aromaticity scrutiny of a molecular system.

Fig. 1 (a) Analyzed molecules; (b) plots of the NICS_in-plane vs. NICS_out-plane to identify the FiPC-NICS for the systems studied in this work. C₆H₆ (black), Al₄²⁻ (blue), C₃H₆ (green), B₃H₆N₃ (red) and C₈H₈ (yellow).

Since isotropic NICS do not model (conceptually) Pople's ring currents,^12,64 we will now focus our attention on the out-of-plane component of the NICS tensor (commonly represented as NICS_zz), which was suggested by Fowler and Steiner in 2000 as an improved aromaticity index.^28,29 Although it was initially proposed to best represent cyclic π-electron delocalization, in general it should be sensitive to any current densities associated with the aromaticity phenomenon. With the aim of supporting this assumption, we analyzed the σ-, π- and core-electrons contributions to the NICS_zz. The main results are discussed in the next paragraphs.

Fig. 2 depicts profiles of the core-, σ- and π-electrons contributions to the NICS_zz for the set of the studied molecules, from the center of the ring and above up to 5.00 Å. Through these plots, it is possible to appreciate how important these contributions are at different distances from the molecular center. First, we focus our attention on the core-contributions, which could be an important source of errors in aromaticity predictions, according to NICS measures. For all systems, except for Al₄²⁻, core-contributions are important at the center of the molecules, being approximately −8.3, −3.4, −12.9 and −13.6 ppm for C₆H₆, C₃H₆, B₃H₆N₃ and C₈H₈, respectively. The values remain significant even above 1.0 Å for C₆H₆, B₃H₆N₃ and C₈H₈. This result deserves particular attention, because it is commonly assumed that at this distance the core- or local-contributions should be negligible. Consequently, NICS_zz(1.0) is used as an infallible index of aromaticity. Now, we will evaluate the σ- and π-contributions to the NICS_zz. The molecules C₆H₆, B₃H₆N₃ and C₈H₈ show a similar σ-pattern: the NICS_zz,σ values are significant and positive near the molecule. These are maximum at the molecular center (C₆H₆: 29.3, B₃N₃H₆: 31.5 and C₈H₈: 25.5 ppm) but decrease rapidly as they move away from the center. However, these values do not represent true antiaromaticity due to the absence of the characteristic long-range effect (vide infra). By contrast, the NICS_zz,σ values at the center of cyclopropane and Al₄²⁻are of −60.0 and −28.1 ppm, respectively. This indicates that these molecules are strongly σ-aromatic. In the case of π-contributions, these are significantly diatropic and paratropic on benzene and C₈H₈, respectively. This is consistent with the expected π-aromatic and π-antiaromatic character of these species. In cyclopropane, the π-contribution is insignificant, whereas in borazine and Al₄²⁻ it is marginal (less than a third than in benzene at the center), being in complete agreement again with what is expected for these molecules. Therefore, the profile analysis of the dissected NICS shows to be a good tool to interpret the magnetic molecular response, since it leads exactly to the same conclusions obtained by the induced ring currents analysis.

Fig. 2 Dissected NICS_zz (ppm) vs. distance (in Ångström) at PW91/def2TZVP level.

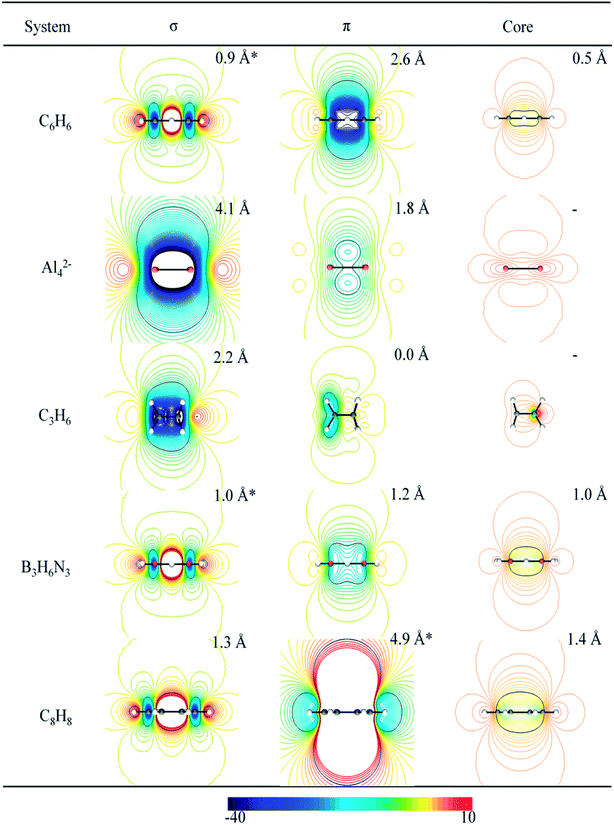
Evaluation of NICS_zz maps

The analysis of tridimensional shielding isosurfaces, also defined as iso-chemical shielding surfaces (ICSS), was proposed by Kleinpeter to quantify the influence of both the presence of functional groups (with multiple bonds) and the ring current effect of arenes, on the anisotropy of the chemical shielding.^40,41 In a similar way to the ICSS analysis, we and others have used contour lines of the z-component of the induced magnetic field (B^ind_z), which is equivalent to NICS_zz, to study the aromatic or antiaromatic character of clusters and molecules.^{22,34,38,60,65,66} Fig. 3 depicts selected planes (perpendicular to the molecular plane) containing isolines of the σ- and the π-electron contribution to NICS_zz, for the set of studied molecules. This plane is expected to contain the more characteristic anisotropic effects due to the presence of ring currents in aromatic and antiaromatic molecules. This is because diatropic and paratropic regions, inside and around the molecular rings, evolve in a direction perpendicular to the molecular plane in aromatic and antiaromatic compounds, respectively. This is consistent with both the ring current model and the shielding anisotropy concept.

Fig. 3 Contour lines of the σ, π and core-electron contributions to the NICS_zz (in a plane perpendicular to the molecules). The color scale is given in ppm and the distance (from the molecular center and along the z-axis) at which the isoline coincides with a value equal to +/−7 ppm is given in Ångström (Å).

The magnetic response of borazine has been previously analyzed according to ICSS,⁶¹ NICS-isosurfaces^67–69 and ring currents.⁶¹ In all these works the computed properties were compared with those of benzene. These studies disagree on the interpretation of some patterns emerging from the NICS analysis. For instance, the presence of a small paratropic transition zone around the center of borazine, absent in benzene, was attributed to a stronger localization of σ-electrons in borazine.⁶⁷ In contrast, Carion et al. attributed it to the fact that diatropic π-currents are quite strong and flow all over the cycle pathway in benzene, but they are smaller and localized in borazine, counteracting in different magnitudes with the paratropic effect of the σ-currents (similar in benzene and borazine).⁶¹ This apparent contradiction, between NICS and ring current analysis, disappears when we analyze the maps of NICS_zz,σ and NICS_zz,π (see Fig. 3). This leads us to the same conclusions obtained by Carion et al.: the shapes and signs of NICS_zz,σ-isolines predicts the presence of a paratropic σ-ring current, with a similar magnitude, in both benzene and borazine; whereas the shapes and signs of NICS_zz,π-isolines, predicts the presence of a strong diatropic π-ring current in benzene (long-range effect) and a weak diatropic π-ring current in borazine (short-range response). It is important to note that NICS_zz,σ-maps also suggest that σ-paratropic character is slightly higher in borazine than in benzene (we will return to this point later, where a detailed quantitative analysis based on these maps will be further discussed). For the case of Al₄²⁻, the shapes and signs of the NICS_zz-isolines also lead to the same conclusion obtained from ring current analysis. NICS_zz,σ and NICS_zz,π maps, suggest the presence of a strong diatropic σ-ring current and a weak diatropic π-ring current, respectively. The same consistency was found for the C₃H₆ and C₈H₈ systems. For the former, NICS-maps predicts a strong diatropic σ-ring current and an absence of π-ring currents while for the latter NICS-maps predicts a strong π-paratropic ring current (long-range effect) and an absent σ-ring current (short-range effect). In the last column, to the right of Fig. 3, the core contributions to NICS_zz are depicted. It is clearly shown that these contributions are of short-range nature (non-aromatic). However, in some cases, NICS_zz,core values are appreciable near the center of the ring: benzene, borazine and the planar COT present a value of −7 ppm at 0.5, 1.0 and 1.4 Å, respectively. This evidences the importance of considering the long-range response as an inherent quality of aromatic systems.

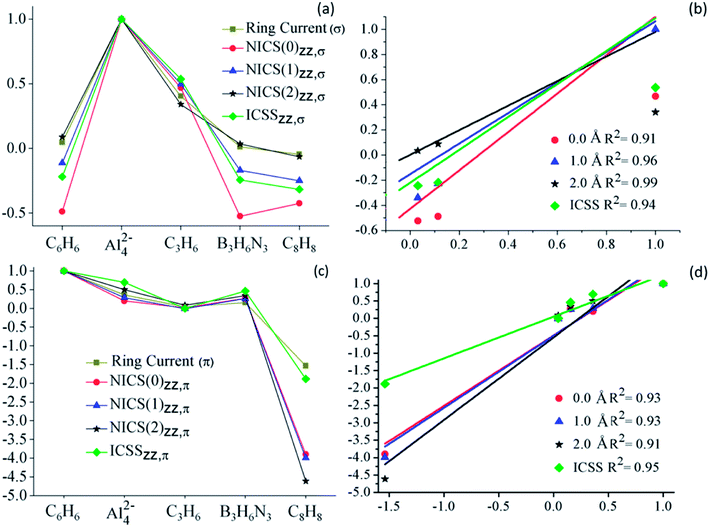
Quantifying aromaticity according to different approximations based on NICS_zz computations

In the previous paragraphs, we have shown that an adequate analysis of NICS can lead to the same qualitative picture about aromaticity obtained by ring current analysis. Now, we will evaluate the performance of the existing NICS_zz based strategies to quantify aromaticity in the set of the analyzed molecules. These values will be compared with the ring current strengths (RCS), also known as current susceptibilities, which are obtained by a numerical integration of the current flow parallel to the normal vector of the integration plane. RCS data were taken from ref. 47. For more details about calculations, we recommend reviewing this work and the references therein. NICS_zz were computed at three different distances (0.0, 1.0 and 2.0 Å) along the main molecular axis (z-axis in this case). The ICSS_zz corresponds to the distance from the molecular center, at which a selected NICS_zz-isoline (plotted in a plane perpendicular to the molecular plane) intersects the z-axis. It is important to note, that we used ICSS to identify these values, because these were obtained from the ICSS-maps. With the aim of comparing different systems, the isoline should have the same value. This value is defined arbitrarily; the only requirement is to be small enough to be out of the local contributions. In this case, we have assigned the value of +/−7.0 ppm, which fulfills the above-mentioned requirement for all the analyzed molecules. RCSs, as well as the quantities obtained from NICS_zz analysis, are depicted in Table 1. Correlations between NICS based strategies and RCS values are better appreciated through graphs (lines and scatter plots), as those depicted in Fig. 4.

Fig. 4 (a) Comparison between RCS_σ and different NICS_zz,σ (ppm) computations for the analyzed systems, (b) normalized RCS_σ vs. different NICS_zz,σ (ppm) computations; (c) comparison between RCS_π and different NICS_zz,π (ppm) computations for the analyzed systems, (d) normalized RCS_π vs. different NICS_zz,π (ppm) computations. Calculations were performed at PW91/def2TZVP level.

Table 1 Comparison of RCS with different NICS_zz computations, for the studied molecules

System	RCS^a [nA T^−1]		NICSzz [ppm]						ICSSzz
	σ	π	0.0 Å		1.0 Å		2.0 Å		σ	π
			σ	π	σ	π	σ	π
a Values taken from ref. 47.b Relative values, obtained by dividing the quantities by the value corresponding to the most aromatic system (according to the evaluated descriptor). These values will be used in Fig. 4.
C6H6	1.1 (0.05)^b	11.7 (1.00)	29.3 (−0.49)	−36.4 (1.00)	5.2 (−0.11)	−29.4 (1.00)	−2.3 (0.09)	−13.0 (1.00)	−0.9 (−0.22)	2.6 (1.00)
Al4^2−	24.0 (1.00)	4.2 (0.36)	−60.0 (1.00)	−7.2 (0.20)	−46.0 (1.00)	−8.4 (0.29)	−26.1 (1.00)	−6.5 (0.50)	4.1 (1.00)	1.8 (0.69)
C3H6	9.7 (0.40)	0.5 (0.04)	−28.1 (0.47)	−0.5 (0.01)	−22.9 (0.50)	0.2 (−0.01)	−8.9 (0.34)	−1.1 (0.08)	2.2 (0.54)	0.0 (0.00)
B3H6N3	0.3 (0.01)	1.8 (0.15)	31.5 (−0.53)	−9.7 (0.27)	7.8 (−0.17)	−7.6 (-)	−0.9 (0.03)	−4.4 (0.34)	−1.0 (−0.24)	1.2 (0.46)
C8H8	−1.1 (−0.05)	−18.0 (−1.54)	25.5 (−0.43)	141.9 (−3.90)	11.5 (−0.25)	117.4 (−3.99)	1.7 (−0.07)	60.0 (−4.62)	−1.3 (−0.32)	−4.9 (−1.88)

---

In Fig. 4, the different NICS-based descriptors are compared to the RCS, for the series of studied systems. Clearly, the descriptors based on both σ- and π-contributions of NICS_zz follow the same trend as their RCS counterparts, as observed in part (a) and (c) of the figure, respectively. This correlation is more evident in the scatter plots (part (b) and (d) of the Fig. 4). For these comparisons, both NICS based descriptors and RCS have been normalized, dividing them by the maximum (or minimum) value of RCS and ICSS (or NICS) property. All NICS_zz-descriptors have a good linear correlation with RSC. For σ-contributions the best and poorest correlation is shown for NICS_zz,σ(2.0) and NICS_zz,σ(0.0), R² = 0.99 and 0.91, respectively. While, for π-descriptors, the best and poorest correlation is shown for ICSS_zz,π and NICS_zz,π(2.0), R² = 0.95 and 0.91, respectively. These results clearly show that the out-of-plane component of NICS predicts the same trends of electronic delocalization as the ring current analysis does. Therefore, it is a good magnetic descriptor of aromaticity.

Concluding remarks

A detailed analysis of the nucleus-independent chemical shift (NICS) on the benzene, Al₄²⁻ cluster, cyclopropane, borazine and planar cyclooctatetraene leads to the same conclusion obtained by the analysis of ring currents regarding aromaticity. The aromatic, non-aromatic or antiaromatic character of these species is adequately predicted through the analysis of NICS evolution along the main molecular axis. This is due to the different effects that localized (non-aromatic) and delocalized contributions (aromatic or antiaromatic) have on the in-plane and out-of-plane components of NICS, respectively. As for the quantitative analysis, evaluating the σ- and π-electrons contributions to the out-of-plane component of NICS (NICS_zz) is the most adequate assessment, since core-electrons contributions are appreciable in most of the studied cases, specially near the molecular center.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors are grateful for the financial support of the grants: Universidad Andres Bello (DI-1365-16/RG).

References

1. A. Kekulé, Eur. J. Org. Chem., 1872, 162, 77–124.
2. F. A. Kekulé, Bull. Acad. R. Med. Belg., 1865, 19, 551–563.
3. F. Feixas, E. Matito, J. Poater and M. Sola, Chem. Soc. Rev., 2015, 44, 6434–6451.
4. J. Gomes and R. B. Mallion, Chem. Rev., 2001, 101, 1349–1384.
5. R. H. Mitchell, Chem. Rev., 2001, 101, 1301–1316.
6. M. K. Cyranski, T. M. Krygowski, A. R. Katritzky and P. v. R. Schleyer, J. Org. Chem., 2002, 67, 1333–1338.
7. A. T. Balaban, D. C. Oniciu and A. R. Katritzky, Chem. Rev., 2004, 104, 2777–2812.
8. T. M. Krygowski and M. K. Cyrański, Chem. Rev., 2001, 101, 1385–1420.
9. M. Randic, Chem. Rev., 2003, 103, 3449–3606.
10. P. v. R. Schleyer, Chem. Rev., 2001, 101, 1115–1118.
11. R. McWeeny, Mol. Phys., 1958, 1, 311–321.
12. J. A. Pople, Mol. Phys., 1958, 1, 175–180.
13. L. Pauling, J. Chem. Phys., 1936, 4, 673–677.
14. C. Kumar, H. Fliegl and D. Sundholm, J. Phys. Chem. A, 2017, 121, 7282–7289.
15. P. Lazzeretti, Prog. Nucl. Magn. Reson. Spectrosc., 2000, 36, 1–88.
16. D. Sundholm, H. Fliegl and R. J. F. Berger, Wiley Interdiscip. Rev. Comput. Mol. Sci., 2016, 6, 639–678.
17. P. Lazzeretti, Phys. Chem. Chem. Phys., 2004, 6, 217–223.
18. P. v. R. Schleyer, C. Maerker, A. Dransfeld, H. Jiao and N. J. R. v. E. Hommes, J. Am. Chem. Soc., 1996, 118, 6317–6318.
19. S. Pelloni, G. Monaco, P. Lazzeretti and R. Zanasi, Phys. Chem. Chem. Phys., 2011, 13, 20666–20672.
20. R. Islas, G. Martínez-Guajardo, J. O. C. Jiménez-Halla, M. Solà and G. Merino, J. Chem. Theory Comput., 2010, 6, 1131–1135.
21. Z. Badri, S. Pathak, H. Fliegl, P. Rashidi-Ranjbar, R. Bast, R. Marek, C. Foroutan-Nejad and K. Ruud, J. Chem. Theory Comput., 2013, 9, 4789–4796.
22. J. J. Torres-Vega, A. Vásquez-Espinal, L. Ruiz, M. A. Fernández-Herrera, L. Alvarez-Thon, G. Merino and W. Tiznado, ChemistryOpen, 2015, 4, 302.
23. S. Radenkovic and P. Bultinck, J. Phys. Chem. A, 2011, 115, 12493–12502.
24. R. Carion, B. Champagne, G. Monaco, R. Zanasi, S. Pelloni and P. Lazzeretti, J. Chem. Theory Comput., 2010, 6, 2002–2018.
25. P. Bultinck, S. Fias and R. Ponec, Chem.–Eur. J., 2006, 12, 8813–8818.
26. E. Steiner and P. W. Fowler, Phys. Chem. Chem. Phys., 2004, 6, 261–272.
27. P. v. R. Schleyer, H. Jiao, N. J. R. v. E. Hommes, V. G. Malkin and O. L. Malkina, J. Am. Chem. Soc., 1997, 119, 12669–12670.
28. E. Steiner, P. W. Fowler and L. W. Jenneskens, Angew. Chem., Int. Ed., 2001, 40, 362–366.
29. I. Cernusak, P. W. Fowler and E. Steiner, Mol. Phys., 2000, 98, 945–953.
30. A. Stanger, J. Org. Chem., 2006, 71, 883–893.
31. C. Corminboeuf, T. Heine and J. Weber, Phys. Chem. Chem. Phys., 2003, 5, 246–251.
32. T. Heine, P. v R. Schleyer, C. Corminboeuf, G. Seifert, R. Reviakine and J. Weber, J. Phys. Chem. A, 2003, 107, 6470–6475.
33. A. C. Castro, E. Osorio, J. O. C. Jiménez-Halla, E. Matito, W. Tiznado and G. Merino, J. Chem. Theory Comput., 2010, 6, 2701–2705.
34. J. J. Torres-Vega, A. Vásquez-Espinal, J. Caballero, M. L. Valenzuela, L. Alvarez-Thon, E. Osorio and W. Tiznado, Inorg. Chem., 2014, 53, 3579–3585.
35. J. J. Torres, R. Islas, E. Osorio, J. G. Harrison, W. Tiznado and G. Merino, J. Phys. Chem. A, 2013, 117, 5529–5533.
36. S. Van Damme, G. Acke, R. W. A. Havenith and P. Bultinck, Phys. Chem. Chem. Phys., 2016, 18, 11746–11755.
37. T. Heine, R. Islas and G. Merino, J. Comput. Chem., 2007, 28, 302–309.
38. G. Merino, T. Heine and G. Seifert, Chem.–Eur. J., 2004, 10, 4367–4371.
39. T. Heine, C. Corminboeuf and G. Seifert, Chem. Rev., 2005, 105, 3889–3910.
40. S. Klod, A. Koch and E. Kleinpeter, J. Chem. Soc., Perkin Trans. 2, 2002, 1506–1509.
41. S. Klod and E. Kleinpeter, J. Chem. Soc., Perkin Trans. 2, 2001, 1893–1898.
42. R. Gershoni-Poranne and A. Stanger, Chem.–Eur. J., 2014, 20, 5673–5688.
43. G. Monaco and R. Zanasi, J. Phys. Chem. A, 2014, 118, 1673–1683.
44. G. Monaco and R. Zanasi, Chem. Phys. Lett., 2013, 588, 247–252.
45. J. Juse and D. Sundholm, Phys. Chem. Chem. Phys., 1999, 1, 3429–3435.
46. D. C. Giancoli, Physics for scientists and engineers, Pearson Education International, 2008.
47. G. Monaco, R. Zanasi, S. Pelloni and P. Lazzeretti, J. Chem. Theory Comput., 2010, 6, 3343–3351.
48. J. Poater, M. Solà, R. G. Viglione and R. Zanasi, J. Org. Chem., 2004, 69, 7537–7542.
49. N. D. Charistos, A. G. Papadopoulos, T. A. Nikopoulos, A. Muñoz-Castro and M. P. Sigalas, J. Comput. Chem., 2017, 38, 2594–2604.
50. M. Solà, F. Feixas, J. O. C. Jiménez-Halla, E. Matito and J. Poater, Symmetry, 2010, 2, 1156–1179.
51. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, Farkas, J. B. Foresman, J. V Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Revis. C.01, Gaussian, Inc., Wallingford CT, 2010.
52. J. P. Perdew, J. A. Chevary, S. H. Vosko, K. A. Jackson, M. R. Pederson, D. J. Singh and C. Fiolhais, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 46, 6671.
53. J. P. Perdew, K. Burke and Y. Wang, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 16533.
54. N. Perez-Peralta, M. Contreras, W. Tiznado, J. Stewart, K. J. Donald and G. Merino, Phys. Chem. Chem. Phys., 2011, 13, 12975–12980.
55. S. T. Holmes, S. Bai, R. J. Iuliucci, K. T. Mueller and C. Dybowski, J. Comput. Chem., 2017, 38, 949–956.
56. F. Mauri, N. Vast and C. J. Pickard, Phys. Rev. Lett., 2001, 87, 85506.
57. J. A. Bohmann, F. Weinhold and T. C. Farrar, J. Chem. Phys., 1997, 107, 1173–1184.
58. E. D. Glendening, J. K. Badenhoop, A. E. Reed, J. E. Carpenter, J. A. Bohmann, C. M. Morales, C. R. Landis and F. Weinhold, NBO 6.0., Theoretical Chemistry Institute, University of Wisconsin, Madison, 2013.
59. H. Childs, E. Brugger, B. Whitlock, J. Meredith, S. Ahern, D. Pugmire, K. Biagas, M. Miller, C. Harrison, G. H. Weber, H. Krishnan, T. Fogal, A. Sanderson, C. Garth, E. W. Bethel, D. Camp, O. Rübel, M. Durant, J. M. Favre and P. Navrátil, in High Performance Visualization–Enabling Extreme-Scale Scientific Insight, 2012, pp. 357–372.
60. A. Vásquez-Espinal, R. Pino-Rios, L. Alvarez-Thon, W. A. Rabanal-León, J. J. Torres-Vega, R. Arratia-Perez and W. Tiznado, J. Phys. Chem. Lett., 2015, 6, 4326–4330.
61. R. Carion, V. Liégeois, B. Champagne, D. Bonifazi, S. Pelloni and P. Lazzeretti, J. Phys. Chem. Lett., 2010, 1, 1563–1568.
62. Y.-C. Lin, J. Jusélius, D. Sundholm and J. Gauss, J. Chem. Phys., 2005, 122, 214308.
63. R. W. A. Havenith and P. W. Fowler, Phys. Chem. Chem. Phys., 2006, 8, 3383–3386.
64. H. Fallah-Bagher-Shaidaei, C. S. Wannere, C. Corminboeuf, R. Puchta and P. v R. Schleyer, Org. Lett., 2006, 8, 863–866.
65. R. Islas, T. Heine and G. Merino, Acc. Chem. Res., 2012, 45, 215–228.
66. C. Corminboeuf, T. Heine, G. Seifert, P. von Ragué Schleyer and J. Weber, Phys. Chem. Chem. Phys., 2004, 6, 273–276.
67. R. Islas, E. Chamorro, J. Robles, T. Heine, J. C. Santos and G. Merino, Struct. Chem., 2007, 18, 833–839.
68. N. D. Charistos, A. G. Papadopoulos and M. P. Sigalas, J. Phys. Chem. A, 2014, 118, 1113–1122.
69. A. G. Papadopoulos, N. D. Charistos, K. Kyriakidou and M. P. Sigalas, J. Phys. Chem. A, 2015, 119, 10091–10100.

---