Pressure-induced phase transition of 4-aminobenzonitrile: the formation and enhancement of N–H⋯N weak hydrogen bonds

Abstract

A reversible pressure-induced structural phase transition of 4-aminobenzonitrile was found at about 0.3 GPa by conducting in situ high-pressure synchrotron angle-dispersive X-ray diffraction (ADXRD) experiments. The discontinuous changes of Raman modes at 0.2 GPa confirmed the occurrence of phase transition. In situ high-pressure Raman spectra indicated that the molecular arrangement and intermolecular interactions changed abruptly. The process of this phase transition continued up to about 1.0 GPa. When the pressure reached 1.1 GPa, the initial N–H⋯N interaction transformed into a new weak hydrogen bond, which was enhanced by further compression. The ab initio calculations and Hirshfeld surfaces were used to illustrate the above views. This study gives an example that demonstrates that the pressure can induce the formation of hydrogen bonds, which contributes to the development of supramolecular chemistry.

---

1 Introduction

The hydrogen bond is a common and important intermolecular interaction in biomolecules, inorganic materials, organic materials and hybrid compounds.^1–7 As a typical non-covalent interaction, the hydrogen bond can maintain the structural stability of supramolecular assembly and improve the functionality of materials.^8–12 According to the literature, hydrogen bonds are sensitive to pressure because the intermolecular distance can be reduced dramatically during contraction of the volume.^13–18 High pressure can make the hydrogen-bonded networks become distorted or rearranged.^19–23 Usually, combined with π-stacking, van der Waals force, electrostatic interactions and other effects, pressure-induced changes in hydrogen bonds can lead to changes in the arrangement of molecules, which can change the symmetry of the crystal structure.^24–27 Moreover, when the intermolecular interactions are altered by the pressure, several new properties of the material can be discovered.^28–32 Therefore, the formation and various changes of hydrogen bonds play a key role in studying the structures and properties of materials under high pressure.

At ambient conditions, 4-aminobenzonitrile (C₇H₆N₂) crystals are of monoclinic P2₁/c symmetry (phase I).³³ The amino group and the benzene ring of 4-aminobenzonitrile are almost co-planar with the dihedral angle of about 13°. Since the length of C–NH₂ bond is short, the amino group is substantially in a triangular conformation. As shown in Fig. 1, 4-aminobenzonitrile molecules are attached by N–H⋯N interactions almost along the c-axis. Due to the geometrical characteristics of the molecular arrangement, only one hydrogen atom on the amino group of 4-aminobenzonitrile is possible to form the N–H⋯N hydrogen bond with the nitrogen atom on the cyano group. The distance of H⋯N in this N–H⋯N interaction is 2.527 Å, which is just a little longer than that of regular weak hydrogen bonds.¹ Since the packing of molecules can be enhanced by accelerating pressure, it is very possible for 4-aminobenzonitrile to form N–H⋯N hydrogen bonds under high pressure. Sometimes, new hydrogen bonds may form after the original ones being broken by external pressure,^10,34,35 but it is rare to observe the formation of hydrogen bonds from other weak non-covalent interactions.

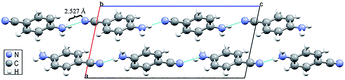Fig. 1 Crystal structure of 4-aminobenzonitrile under ambient conditions. The dash lines represent the N–H⋯N interactions between adjacent molecules.

Moreover, the crystal structure will change with the formation of new hydrogen bonds. Furthermore, the continuous increase of the pressure can enhance the intensity of the weak and medium D–H⋯A hydrogen bonds (D and A denote the donor and acceptor of the hydrogen bond respectively), resulting in an extension of the D–H distance.^36–38 Therefore, we took 4-aminobenzonitrile as an example to investigate its potential various changes of the N–H⋯N hydrogen bond and crystal structure by using in situ high-pressure Raman spectroscopy and synchrotron ADXRD combining with ab initio calculations in this study. As N–H⋯N hydrogen bonds widely exist in supramolecular materials,^1,25 the results of this study can provide some new ideas to understand the formation and enhancement of weak hydrogen bonds in the supramolecular assembly at high pressure.

2 Experimental section

The sample chamber with a diameter of 130 μm was pre-drilled in the center of a T301 steel sheet, which was placed in a symmetric diamond anvil cell (DAC). The commercial 4-aminobenzonitrile powder crystals (purity > 99%) were placed in the sample chamber for high-pressure Raman and ADXRD experiments. We measured the pressure through the ruby fluorescence measurement method³⁹ and used silicone oil as the pressure transmitting medium (PTM). A little silicone oil as PTM does not affect the sample's signal (Fig. S1†). The temperature conditions of the high-pressure experiments are maintained at room temperature.

Raman measurements were made by a micro Raman system assembled with a thermo-electrically cooled CCD (Synbority, Horiba Jobin Yvon), a spectrometer (iHR 550, Horiba Jobin Yvon) and a 671 nm excitation laser. The beamline with a 0.6199 Å wavelength beam of BL15U1 in Shanghai Synchrotron Radiation Facility (SSRF) was used for in situ high-pressure ADXRD experiments.⁴⁰ The CeO₂ standard was used for calibration. The Fit2D software was used to process the ADXRD patterns collected by the Mar345 detector.⁴¹ The ADXRD patterns were further analyzed by using Materials Studio 5.0 to obtain detailed information on the crystal structure of 4-aminobenzonitrile at high pressure. Ab initio calculations of the high-pressure crystal structure were performed by using the pseudopotential plane wave method in the CASTEP package. The generalized gradient approximation of Perdew–Burke–Ernzerhof exchange correlation^42–44 was used in the geometric optimization with a plane wave cutoff energy of 700 eV.

3 Results and discussion

In order to analyze the changes in the structure of 4-aminobenzonitrile crystals under high pressure, we performed in situ high-pressure synchrotron radiation ADXRD experiments. Fig. 2a depicts the ADXRD patterns of 4-aminobenzonitrile powder crystals at different pressures up to 2.0 GPa. All the diffraction peaks moved to higher angles as the pressure increased, indicating that the lattice spacing was decreased and the intermolecular distance was compressed. As shown in Fig. 3a, the compression ratio of the b-axis is largest during the compression of the unit cell below 0.2 GPa, while the compression ratio of the c-axis is significantly smaller than those of the a, b-axes, because the N–H⋯N interaction almost along the c-axis. When the pressure reached 0.3 GPa, three new diffraction peaks (marked by blue arrows in Fig. 2a) emerged, which were enhanced as the pressure increased continuously. This phenomenon indicates that the structural phase transition occurred at 0.3 GPa. When the pressure exceeded 0.9 GPa, the intensity of these new peaks was maintained, which means the phase transition was complete. As the pressure was elevated up to 6.2 GPa continuously, all the diffraction peaks moved to higher angles regularly, indicating the phase II was stable in this range of pressure (Fig. 2b). In Fig. S2 and Table S1,† the Pawley refinement of the diffraction pattern of 1.6 GPa shows that the possible structure of the new high-pressure phase (phase II) belongs to the P2 space group of monoclinic symmetry. At the beginning of this phase transition, these three new diffraction peaks were weak.^15,16 When the original crystal structure was destroyed, the crystal symmetry was lowered and the initial molecular arrangement was also changed.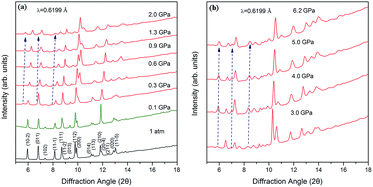

Fig. 2 Representative synchrotron XRD patterns of 4-aminobenzonitrile at high pressures: (a) from 1 atm to 2.0 GPa; (b) from 3.0 GPa to 6.2 GPa. The new peaks are marked by blue arrows.

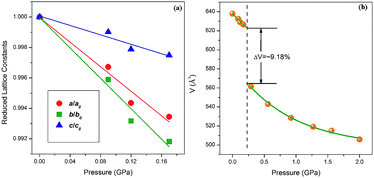Fig. 3 (a) Reduced lattice constants from ADXRD experiments, (b) unit cell volume as a function of pressure.

After further analysis, we obtained the evolution of the unit cell volume of 4-aminobenzonitrile crystals below 2 GPa (Fig. 3b). The results of the second-order Birch–Murnaghan equation fitting on the unit cell volume with compression were calculated by the free online program PASCal from http://pascal.chem.ox.ac.uk/:⁴⁵ V₀ = 638.19(5) ų, B₀ = 9.25(8) GPa, B′₀ = 4 (fixed) in the initial phase (phase I); V₀ = 567.74(6) ų, B₀ = 12.79(9) GPa, B′₀ = 4 (fixed) in the high-pressure phase (phase II). These parameters indicate that the compressibility of 4-aminobenzonitrile crystals is reduced after high-pressure phase transition.

For further studying the mechanism of this high-pressure phase transition, we investigated the high-pressure Raman spectra of 4-aminobenzonitrile powder crystals. The point group symmetry of the 4-aminobenzonitrile crystal is C_2h (2/m). The mechanical representation of this symmetry is

M = 45A_g + 45A_u + 45B_g + 45B_u

showing 3 acoustic modes

Γ_acoustic = A_u + 2B_u

and 177 optic modes

Γ_optic = 45A_g + 44A_u + 45B_g + 43B_u

Group-theoretical analysis of the vibrations shows that, among the 177 optical modes, the Raman-active modes belong to the 45A_g + 45B_g symmetry and the infrared-active modes belong to the 44A_u + 43B_u symmetry. Some of the Raman modes could not be observed in our experiments because of the weak intensities and limited splitting. The assignments for the Raman modes of 4-aminobenzonitrile are based on the reported literature (Table S2†).⁴⁶

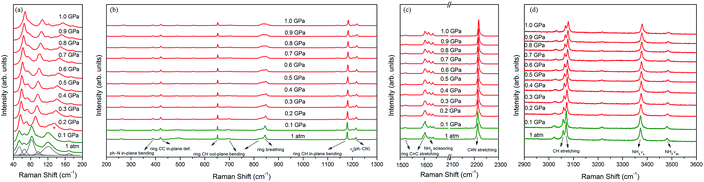
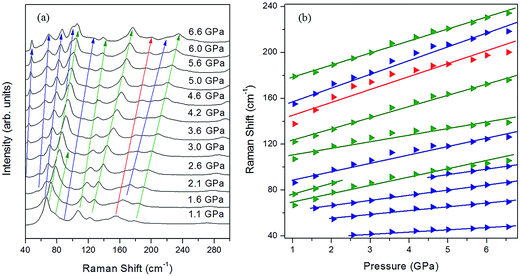
Fig. 4a depicts the changes in the external modes of the Raman spectra (40 to 200 cm⁻¹) in the pressure range from 0 to 1.0 GPa. At the ambient condition, the external modes consist of six peaks (54, 64, 82, 120, 169 and 98 cm⁻¹). As shown in Fig. 5a, the blue shifts of all the external modes during the compression indicate that the intermolecular interactions were enhanced, which was derived from the reduction of intermolecular distance.^18,47 When the pressure reached 0.2 GPa, the original six external modes changed to seven. This phenomenon indicates that the intermolecular interactions were changed. Meanwhile the crystal structure was likely to transform into in a lower symmetry phase.⁴⁸ Additionally, the external modes showed regular blue shifts after the phase transition below 1.0 GPa without abrupt changes.

Fig. 4 Raman spectra of 4-aminobenzonitrile from 1 atm to 1.0 GPa: (a) 40 cm⁻¹ to 200 cm⁻¹, the asterisk denotes the new Raman mode; (b) 200 to 1300 cm⁻¹; (c) 1500 to 2300 cm⁻¹; (d) 2900 to 3600 cm⁻¹.

Fig. 5 Raman shifts of 4-aminobenzonitrile from 1 atm to 1.0 GPa: (a) 40 cm⁻¹ to 200 cm⁻¹, (b) 200 to 1300 cm⁻¹, (c) 1500 to 2300 cm⁻¹, (d) 3010 to 3230 cm⁻¹, (e) 3370 to 3490 cm⁻¹.

The internal Raman modes can reflect the changes of molecular vibrations, which help to study the chemical environment around the molecular groups. From 1 atm to 1.0 GPa, the high-pressure Raman spectra of the 4-aminobenzonitrile powder crystals in the range of 200 to 1300 cm⁻¹, 1500 to 2300 cm⁻¹ and 2900 to 3600 cm⁻¹ are shown in Fig. 4b–d, respectively. The evolutions of Raman shifts of 4-aminobenzonitrile from 1 atm to 1.0 GPa in these regions are shown in Fig. 5b–e. From 1 atm to 0.2 GPa, most internal modes moved to the high frequency regions, indicating that the vibrations of most chemical groups on 4-aminobenzonitrile molecules were enhanced under high pressure.^49,50 The blue shifts of C–H and N–H stretching modes indicate the initial N–H⋯N interactions are even weaker than normal weak hydrogen bonds, which usually show red shifts under compression.³⁶ When the pressure reached 0.2 GPa, the ph–N in-plane bending, ring CC in-plane def., ring CH out-plane bending, ring breathing, ring CH in-plane bending, ν_s(ph–CN), C≡N stretching, NH₂ scissoring, ring C=C stretching, C–H stretching and N–H stretching modes showed slightly discontinuous shifts. This phenomenon indicates phase I and phase II have similar molecular arrangement and conformation. Thus, the changes of internal modes were weak at the beginning of this phase transition.^15,16 However, the blue shifts of these Raman modes indicate that each chemical group especially the benzene ring suddenly shrank. The increase of the vibrational frequency of CH in-plane bending mode reflects the reduction of dihedral angle between the amino group and benzene ring,⁴⁶ resulting from the planarity of molecular conformation under high pressure. The red shift of NH₂ scissoring mode and the blue shifts of C–H stretching and N–H stretching modes indicate that the C–H and N–H bonds were shortened and distorted in the process of phase transition.^51,52

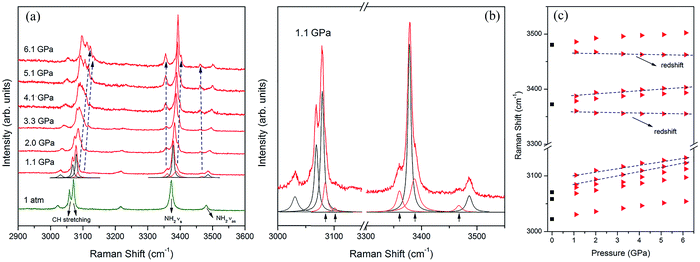
As the pressure was continuously increased up to 6.1 GPa, the new C–H and N–H stretching modes started separating at 1.1 GPa (Fig. 6a and b). Meanwhile several new external modes also emerged beyond 1.1 GPa (Fig. 8a), but the ADXRD patterns moved regularly to higher angles without abrupt changes in this pressure range (Fig. 2b). These results indicate the phase transition was completed at 1.1 GPa and the crystal structure was just contracted in the same symmetry as phase II at higher pressures up to 6.1 GPa. The newly generated C–H stretching modes indicate that the chemical environment surrounding the benzene ring changed. The blue shifts of these two new C–H stretching modes indicates that the C–H bonds on the benzene ring became shorter as the pressure was increased. The vibrational frequency of the C–H bonds was enhanced when the benzene ring shrank. It is noteworthy that three new N–H stretching modes emerged near the original N–H stretching modes, and the two of these new peaks showed red shifts as the pressure rose (Fig. 6c). According to reported literatures, these results indicate that new weak N–H⋯N hydrogen bonds formed in the high-pressure phase transition, and then these new hydrogen bonds were enhanced by further compression.^35,36,52 Meanwhile the splitting of N–H stretching modes is attributed to the lower symmetry in phase II, which is derived from distortion of amino groups in the formation of N–H⋯N hydrogen bonds. The formation of these new weak N–H⋯N hydrogen bonds also corresponds to the presence of several new external Raman modes in Fig. 7a. Since the red shifts of N–H stretching modes with the pressure was observed only after the phase transition (Fig. 6c) and the initial distance of H⋯N was longer than the empirical value of H⋯A of weak hydrogen bonds,¹ the N–H⋯N interaction at the ambient condition was weaker than the weak hydrogen bond. In addition, Raman spectra of 4-aminobenzonitrile at 1 atm and the released samples in Fig. S3† indicate this high-pressure phase transition is reversible. The diffraction peaks released from 20.3 GPa broadened but were substantially the same as the initial ones (Fig. S4†). This also demonstrates that this high-pressure phase transition is reversible in the 20.3 GPa pressure range.

Fig. 6 (a) Raman spectra of 4-aminobenzonitrile from 1.1 GPa to 6.1 GPa (2900 to 3600 cm⁻¹), (b) peak fitting and decomposition of Raman modes at 1.1 GPa, arrows mark the new Raman modes different from phase I, (c) pressure dependence of Raman shifts of 4-aminobenzonitrile from 1.1 GPa to 6.1 GPa (3000 to 3550 cm⁻¹), blue dash lines mark the new Raman modes different from phase I.

Fig. 7 (a) Raman spectra of 4-aminobenzonitrile from 1.1 GPa to 6.6 GPa (40 to 300 cm⁻¹). The red arrow marks the new Raman mode below 1.1 GPa, blue arrows mark the new Raman modes beyond 1.1 GPa, (b) pressure dependence of Raman shifts of 4-aminobenzonitrile from 1.1 GPa to 6.6 GPa (40 to 240 cm⁻¹). The red arrow marks the new Raman mode below 1.1 GPa, blue arrows mark the new Raman modes beyond 1.1 GPa.

Fig. 8 (a) Molecular structure of 4-aminobenzonitrile. (b) Hirshfeld surface for the structure of 4-aminobenzonitrile at 1 atm mapped with d_norm; (c) Hirshfeld surface for the calculated structure of 4-aminobenzonitrile at 0.9 GPa mapped with d_norm; (d) Hirshfeld surface for the calculated structure of 4-aminobenzonitrile at 6.0 GPa mapped with d_norm.

When the sample was subjected to high pressure, the lattice was compressed. Meanwhile the molecular packing was enhanced, leading to the gradual increase of the free energy. As the pressure shortened the distance between molecules, the abrupt changes of the molecular conformation and molecular arrangement of 4-aminobenzonitrile occurred to release the increasing free energy, leading to the phase transition of the crystal structure. When the phase transition occurred, the symmetry of the crystal was abruptly lowered, and the collapse of the volume was about 9.18% (Fig. 3b). At the same time, the amino group, the benzene ring and the cyano group on the 4-aminobenzonitrile molecules were suddenly contracted to adapt the tighter volume. The amino groups were slightly twisted with the distortion of N–H⋯N interactions. The new molecular arrangement shortened the distance of H⋯N between adjacent amino and cyano moieties, which led to the formation of new N–H⋯N weak hydrogen bonds. Then, as the pressure was increased continuously, N–H bonds of the new weak hydrogen bonds elongated, resulting in the red shifts of N–H stretching modes. This phenomenon confirms the previous analysis of the formation and enhancement of weak hydrogen bonds under high pressure.^35,36

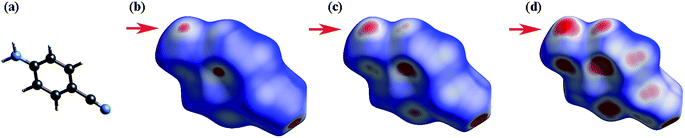
To understand the changes of the intermolecular interactions in 4-aminobenzonitrile crystals under high pressures, ab initio calculations were performed by using pseudopotential plane wave methods. The calculated crystal constants in Fig. S5a† have the similar compressibility with the ADXRD results. Although it is difficult to calculate the phase transition by geometric optimization, the second-order Birch–Murnaghan equation of the calculated results before and after 0.9 GPa are different (Fig. S5b†). This phenomenon is corresponding to the result that the phase transition was complete at about 1.0 GPa. Fig. 8b–d depict the Hirshfeld surfaces for 4-aminobenzonitrile at ambient pressure, 0.9 GPa and 6.0 GPa, respectively. The blue regions on the Hirshfeld surfaces reflect long contacts, whereas the red regions are corresponding to short contacts.⁵³ Fingerprint plots are also utilized to compare the changes in molecular packing in Fig. 9. The decreased maximum values of d_e between ambient pressure (2.435 Å) and 6.0 GPa (2.063 Å) indicate the long contacts are shortened under high pressure. The two “spikes” in these three plots represent N–H⋯N hydrogen bonds. The distance of N–H⋯N hydrogen bond was reduced quickly at 0.9 GPa, which is consistent with the formation of N–H⋯N hydrogen bond and the finish of the phase transition. In Fig. 9b, the single N–H⋯N hydrogen bond extends down to (d_i, d_e)=(0.88 Å, 1.28 Å), corresponding to a hydrogen-bonded distance of 2.16 Å. From 0.9 to 6.0 GPa, the decrease of the blue regions and increase of the red regions indicate the intermolecular contacts were shortened at high pressure. The region marked by the red arrow as shown in Fig. 8b is corresponding to the amino group. The obvious increase of red colour in this region from 0.9 GPa to 6.0 GPa (Fig. 9c and d) indicates the enhancement of the N–H⋯N hydrogen bond.

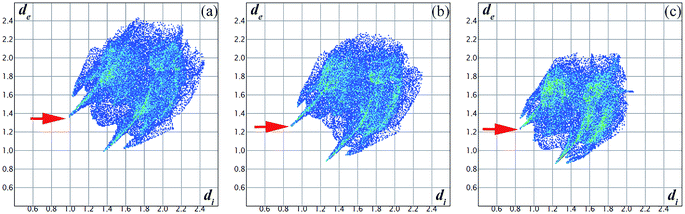Fig. 9 Fingerprint plots for 4-aminobenzonitrile at (a) ambient pressure, (b) 0.9 GPa and (c) 6.0 GPa.

4 Conclusions

In summary, we studied the crystal structure and hydrogen bonds of 4-aminobenzonitrile under high pressure by using DAC combined with in situ Raman and ADXRD experimental apparatuses. The crystal and molecular structure of 4-aminobenzonitrile was contracted as the pressure increased. When the pressure exceeded 0.2 GPa, a reversible phase transition of 4-aminobenzonitrile crystals occurred, which finished at about 1.1 GPa. The crystal symmetry was lowered and the molecular arrangement was abruptly changed, which led to the formation of new weak N–H⋯N hydrogen bonds. Moreover, these weak N–H⋯N hydrogen bonds were enhanced during further compression, which was confirmed by the calculated results. This study gives an example that the formation and enhancement of hydrogen-bonded interactions can be induced by external pressure, which is helpful in the field of supramolecular chemistry.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work is supported by “the Fundamental Research Funds for the Central Universities” (No. N162410002-21).

References

1. T. Steiner, Angew. Chem., Int. Ed., 2002, 41, 48–76.
2. L. J. Prins, D. N. Reinhoudt and P. Timmerman, Angew. Chem., Int. Ed., 2001, 40, 2382–2426.
3. R. P. Sijbesma, F. H. Beijer, L. Brunsveld, B. J. B. Folmer, J. H. K. K. Hirschberg, R. F. M. Lange, J. K. L. Lowe and E. W. Meijer, Science, 1997, 278, 1601–1604.
4. J. H. K. K. Hirschberg, L. Brunsveld, A. Ramzi, J. A. J. M. Vekemans, R. P. Sijbesma and E. W. Meijer, Nature, 2000, 407, 167–170.
5. Y. Liu, Y. Yu, J. Gao, Z. Wang and X. Zhang, Angew. Chem., Int. Ed., 2010, 49, 6576–6579.
6. Y. Abe, K. Harata, M. Fujiwara and K. Ohbu, Langmuir, 1996, 12, 636–640.
7. Q. Zeng, T. Yan, K. Wang, Y. Gong, Y. Zhou, Y. Huang, C. Q. Sun and B. Zou, Phys. Chem. Chem. Phys., 2016, 18, 14046–14054.
8. C. J. Pickard and R. J. Needs, Nat. Mater., 2008, 7, 775–779.
9. M. Somayazulu, J. Shu, C. Zha, A. F. Goncharov, O. Tschauner, H. Mao and R. J. Hemley, J. Chem. Phys., 2008, 128, 064510.
10. A. Olejniczak, K. Ostrowska and A. Katrusiak, J. Phys. Chem. C, 2009, 113, 15761–15767.
11. H. Shimizu, K. Nagata and S. Sasaki, J. Chem. Phys., 1988, 89, 2743–2747.
12. K. F. Dziubek and A. Katrusiak, J. Phys. Chem. B, 2008, 112, 12001–12009.
13. K. Wang, D. Duan, R. Wang, D. Liu, L. Tang, T. Cui, B. Liu, Q. Cui, J. Liu, B. Zou and G. Zou, J. Phys. Chem. B, 2009, 113, 14719–14724.
14. K. Wang, D. Duan, R. Wang, A. Lin, Q. Cui, B. Liu, T. Cui, B. Zou, X. Zhang, J. Hu, G. Zou and H. Mao, Langmuir, 2009, 25, 4787–4791.
15. T. Yan, K. Wang, X. Tan, K. Yang, B. Liu and B. Zou, J. Phys. Chem. C, 2014, 118, 15162–15168.
16. T. Yan, K. Wang, X. Tan, J. Liu, B. Liu and B. Zou, J. Phys. Chem. C, 2014, 118, 22960–22967.
17. D. R. Allan and S. J. Clark, Phys. Rev. Lett., 1999, 82, 3464–3467.
18. T.-R. Park, Z. A. Dreger and Y. M. Gupta, J. Phys. Chem. B, 2004, 108, 3174–3184.
19. E. V. Boldyreva, J. Mol. Struct., 2004, 700, 151–155.
20. A. K. Mishra, C. Murli and S. M. Sharma, J. Phys. Chem. B, 2008, 112, 15867–15874.
21. J. L. Kuo, M. L. Klein and W. F. Kuhs, J. Chem. Phys., 2005, 123, 134505.
22. A. F. Goncharov, V. V. Struzhkin, H. Mao and R. J. Hemley, Phys. Rev. Lett., 1999, 83, 1998–2001.
23. M. Bernasconi, P. L. Silvestrelli and M. Parrinello, Phys. Rev. Lett., 1998, 81, 1235–1238.
24. Q. Wang, T. Yan, K. Wang, H. Zhu, Q. Cui and B. Zou, J. Chem. Phys., 2015, 142, 244701.
25. M. Podsiadło, A. Olejniczak and A. Katrusiak, Cryst. Growth Des., 2017, 17, 2218–2222.
26. R. Gajda and A. Katrusiak, Cryst. Growth Des., 2011, 11, 4768–4774.
27. R. D. L. Johnstone, A. R. Lennie, S. F. Parker, S. Parsons, E. Pidcock, P. R. Richardson, J. E. Warren and P. A. Wood, CrystEngComm, 2010, 12, 1065–1078.
28. G. Xiao, Y. Cao, G. Qi, L. Wang, C. Liu, Z. Ma, X. Yang, Y. Sui, W. Zheng and B. Zou, J. Am. Chem. Soc., 2017, 139, 10087–10094.
29. Q. Zeng, K. Wang and Z. Bo, J. Am. Chem. Soc., 2017, 139, 15648–15651.
30. Y. Gu, K. Wang, Y. Dai, G. Xiao, Y. Ma, Y. Qiao and B. Zou, J. Phys. Chem. Lett., 2017, 8, 4191–4196.
31. L. Zhang, Q. Zeng and K. Wang, J. Phys. Chem. Lett., 2017, 8, 3752–3758.
32. S. Zhang, Y. Dai, S. Luo, Y. Gao, N. Gao, K. Wang, B. Zou, B. Yang and Y. Ma, Adv. Funct. Mater., 2017, 27, 1602276.
33. S. Merlino and F. Sartori, Acta Crystallogr., 1982, 38, 1476–1480.
34. K. Wang, J. Liu, K. Yang, B. Liu and B. Zou, J. Phys. Chem. C, 2014, 118, 18640–18645.
35. C. Murli, N. Lu, Z. Dong and Y. Song, J. Phys. Chem. B, 2012, 116, 12574–12580.
36. S. D. Hamann and M. Linton, Aust. J. Chem., 1976, 29, 1641–1647.
37. J. Joseph and E. D. Jemmis, J. Am. Chem. Soc., 2007, 129, 4620–4632.
38. Y. Dai, K. Wang, H. Yuan, X. Meng, K. Luo, D. Yu, J. Liu, X. Zhang, Y. Ma, Y. Tian and B. Zou, J. Phys. Chem. C, 2015, 119, 12801–12807.
39. H. Mao, P. Bell, J. W. Shaner and D. J. Steinberg, J. Appl. Phys., 1978, 49, 3276–3283.
40. L. Zhang, S. Yan, S. Jiang, K. Yang, H. Wang, S. He, D. Liang, L. Zhang, Y. He, X. Lan, C. Mao, J. Wang, H. Jiang, Y. Zheng, Z. Dong, L. Zeng and A. Li, Nucl. Sci. Tech., 2015, 26, 060101.
41. A. P. Hammersley, S. O. Svensson, M. Hanfland, A. N. Fitch and D. Hausermann, High Pres. Res., 1996, 14, 235–248.
42. G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11185.
43. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
44. S. Grimme, J. Comput. Chem., 2006, 27, 1787–1799.
45. M. J. Cliffe and A. L. Goodwin, J. Appl. Crystallogr., 2012, 45, 1321–1329.
46. C. Ma, W. M. Kwok, P. Matousek, A. W. Parker, D. Phillips, W. T. Toner and M. Towrie, J. Phys. Chem. A, 2002, 106, 3294–3305.
47. J. A. Ciezak, T. A. Jenkins, Z. Liu and R. J. Hemley, J. Phys. Chem. A, 2007, 111, 59–63.
48. H. Sahin, S. Tongay, S. Horzum, W. Fan, J. Zhou, J. Li, J. Wu and F. M. Peeters, Phys. Rev. B, 2013, 87, 165409.
49. O. Franco, I. Orgzall, W. Regenstein and B. Schulz, J. Phys.: Condens. Matter, 2006, 18, 1459–1472.
50. R. Rao, T. Sakuntala and B. K. Godwal, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 65, 054108.
51. S. Li, Q. Li, K. Wang, X. Tan, M. Zhou, B. Li, B. Liu, G. Zou and B. Zou, J. Phys. Chem. B, 2011, 115, 11816–11822.
52. P. Hobza and Z. Havlas, Chem. Rev., 2000, 100, 4253–4264.
53. P. A. Wood, J. J. Mckinnon, S. Parsons, E. Pidcock and M. A. Spackman, CrystEngComm, 2008, 10, 368–376.

---

Footnote

† Electronic supplementary information (ESI) available: The Raman spectra of 4-aminobenzonitrile and 4-aminobenzonitrile + silicone oil at 1 atm, the Pawley refinement of the diffraction pattern of 1.6 GPa, the assignments of the major Raman bands of 4-aminobenzonitrile, released Raman spectra and ADXRD patterns, reduced lattice constants and unit volume of calculated results. See DOI: 10.1039/c8ra00020d

---