Open Access Article
Open Access ArticleImpact of the acidic group on the hydrolysis of 2-dinitromethylene-5,5-dinitropyrimidine-4,6-dione†
Kuan Wanga,
Jian-Gang Chen *a,
Zhan-Bin Niea,
Zhao-Tie Liu
*a,
Zhan-Bin Niea,
Zhao-Tie Liu *ab,
Yueping Jic,
Bozhou Wangc,
Fengyi Liua,
Zhong-Wen Liua,
Wenliang Wang
*ab,
Yueping Jic,
Bozhou Wangc,
Fengyi Liua,
Zhong-Wen Liua,
Wenliang Wang a and
Jian Lu*c
a and
Jian Lu*c
aKey Laboratory of Applied Surface and Colloid Chemistry (Ministry of Education), School of Chemistry & Chemical Engineering, Shaanxi Normal University, Xi’an 710119, China. E-mail: jgchen@snnu.edu.cn; ztliu@snnu.edu.cn; Fax: +86-29-81530803; Fax: +86-29-81530802; Tel: +86-29-81530803 Tel: +86-29-81530802
bCollege of Chemistry and Chemical Engineering, Shaanxi University of Science & Technology, Xi’an, 710021, China
cState Key Laboratory of Fluorine & Nitrogen Chemicals, Xi’an Modern Chemistry Research Institute, Xi’an, 710065, China. E-mail: lujian204@263.net; Fax: +86-29-88291213; Tel: +86-29-88291213
First published on 10th April 2018
Abstract
The hydrolysis mechanism and the kinetics of using 2-dinitromethylene-5,5-dinitropyrimidine-4,6-dione (NMP) to prepare the representative insensitive energetic material 1,1-diamino-2,2-dinitroethylene (FOX-7) in a nitric–sulfuric acid system are systematically investigated via a density functional theory (DFT) method. The impact of the co-existing acidic group of HSO4− as well as the solvent effects of the mixed acids on the hydrolysis of NMP are elucidated and discerned, and the proposed catalysis and promotion of the hydrolysis of NMP with HSO4− are verified. The HSO4−-catalyzed hydrolysis pathway is more favorable than the direct pathway as well as the H2O-catalyzed hydrolysis, indicating that HSO4− may be a promising catalyst for the preparation of FOX-7 in a mixed acid system. The present study is expected to provide a better understanding of the hydrolysis of NMP, and will significantly help with better preparation of FOX-7 and other nitro-energetic materials.
1. Introduction
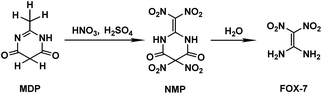
The special significance and importance of energetic materials in military affairs along with their severe defects and hazards leading to accidental casualties during production, transportation, storage and application have spurred numerous attempts to develop better substitutes, insensitive energetic materials (IEMs), for traditional materials.1–3 Due to its distinctly high threshold towards impact and friction along with its comparable explosiveness to the traditional energetic materials currently used, 1,1-diamino-2,2-dinitroethylene (FOX-7) has been suggested as a promising candidate as an IEM and has been extensively studied in recent years, including its synthesis method,2–6 molecular/crystal structure,7 thermodynamic properties,8 performance as an explosive,9 thermal decomposition10 and other characteristics.11 However, the synthesis mechanism for FOX-7 has been seldom reported. It is known that FOX-7 can be prepared from several nitrogen-containing compounds via a batch process in a nitric–sulfuric acid (mixed acid) system. When 2-methyl-4,6-dihydroxypyrimidine (MDP) is used as the reactant, the preparation process involves nitration of MDP followed by further hydrolysis of the nitration product of 2-dinitromethylene-5,5-dinitropyrimidine-4,6-dione (NMP).3–5 The preparation strategy for FOX-7 is shown in Scheme 1.Recently, we employed a density functional theory (DFT) method to elucidate the nitration of MDP in the mixed acids, in which a coexisting HSO4− induced/promoted nitration mechanism was presented, via which the formation of the key intermediate NMP was discerned.12 Such induction/promotion of HSO4− was also illustrated in the nitration of triazol-3-one (TO).13 Moreover, the impact of the solvent effects of the mixed acids on nitration was also studied.12 Koleva et al.14 suggested that formamide as well as dimethylsulfoxide (DMSO) may be used as a model solvent for the nitration in the mixed acids system. By comparing the calculated activation free energy (ΔG≠) in the formamide, DMSO, and gas phases, we found that the solvent effects on the nitration of MDP may be inapparent/weak.12 Based on such calculations, we suppose that the coexisting HSO4− may also assist the hydrolysis process of NMP. However, to the best of our knowledge, no detailed understanding is available on the hydrolysis of NMP in the mixed acid system.
The formation of NO2+ in mixed acids has been investigated for years, and can be expressed as HNO3 + H2SO4 → NO2+ + HSO4− + H2O.14–16 Then the hydrogen-bonding complex HSO4−·H2O may form, similar to the formation of HO·H2O,17 HO2·H2O,18 HNO3·H2O,19 H2SO4·H2O![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 20 or H2O·H2O
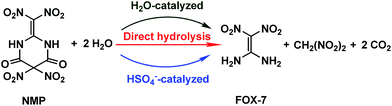
20 or H2O·H2O![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 21 in their corresponding systems, indicating that HSO4− as well as H2O may participate and play a noticeable role in the hydrolysis of NMP. The possible hydrolysis pathways for NMP in the mixed acids are presented in Scheme 2.
21 in their corresponding systems, indicating that HSO4− as well as H2O may participate and play a noticeable role in the hydrolysis of NMP. The possible hydrolysis pathways for NMP in the mixed acids are presented in Scheme 2.
In the present work, the hydrolysis of NMP in a mixed acid system is systematically investigated via a quantum chemistry method. Firstly, the hydrolysis mechanism is elucidated, via which the impact of the co-existing acidic group of HSO4− as well as the solvent effects of the mixed acids on the hydrolysis of NMP is demonstrated and understood. Secondly, the hydrolysis kinetics of NMP in the mixed acids are also studied, through which the proposed special promotion of HSO4− on the hydrolysis of NMP is verified. The present study is expected to provide a better understanding of the hydrolysis of NMP, and will significantly help with better preparation of FOX-7 and other nitro-energetic materials.
2. Theoretical methods
Most of the computational details in the geometry investigation in the present work are very similar to those in our recent report.12,13 The calculations were carried out using the Gaussian 09 software package.22 DFT-B3LYP/6-311G(d,p)23,24 has been used in similar systems.12,25–28 The accuracy of this method was evaluated and verified, as shown in the ESI (Table S1).† Thus, B3LYP/6-311G(d,p) was intentionally employed to optimize the geometries of the reactant complexes, transition states, intermediates and products of the hydrolysis of NMP. B3LYP/6-311G(d,p) was also used to compute the vibrational frequency, via which whether the obtained structures were those of the transition states or local minima points was verified, and based on which the zero-point vibrational energy (ZPE) was calculated. Intrinsic reaction coordinate (IRC)29 analysis was performed to ensure that the structure of every transition state obtained does connect the corresponding reactant and product. Additionally, the conductor-like polarizable continuum model (CPCM)30,31 was used to evaluate the solvent effect of the reaction medium.Based on the optimized geometries, the single-point energies of the first step in the direct hydrolysis of NMP in the formamide phase were estimated using DFT functions (B3LYP-D3,32,33 M06-2X-D3, M06-HF-D3, and BP86 with 6-311++G(3df,3pd)), double hybrid function B2PLYP/aug-cc-pvdz, and CCSD(T)/6-311G(d,p) so as to determine a suitable method (Table S2†). The accuracy of the B3LYP-D3/6-311++G(3df,3pd)//B3LYP/6-311G(d,p) and M06-2X-D3/6-311++G(3df,3pd)//B3LYP/6-311G(d,p) energies was gauged by comparison with the CCSD(T)/6-311G(d,p)//B3LYP/6-311G(d,p) and B2PLYP/aug-cc-pvdz//B3LYP/6-311G(d,p) energies of the first step in the direct hydrolysis of NMP in the formamide phase. It was found that the difference in the energy barrier was less than 0.5 kcal mol−1, indicating that the accuracy as well as the reliability of the former two methods is comparable to that of the latter two methods. Therefore, B3LYP-D3/6-311++G(3df,3pd)//B3LYP/6-311G(d,p) was intentionally used to calculate the single-point energies due to its relatively high efficiency.
All the kinetic calculations were performed using the VKLab program.34 The rate coefficients of conventional transition state theory were calculated with an asymmetric Eckart tunneling correction (TST/Eckart)35 for every elementary reaction in the titled reaction in the temperature range of 233–400 K.
3. Results and discussion
It has been reported that solvent effects in the mixed acid system may be fairly weak.12 Thus, the hydrolysis mechanism of NMP in the gas phase is mainly discussed in the present work though the solvent effect is also explored to understand the impact of the reaction medium on the titled hydrolysis system. Moreover, it is known that FOX-7 and 2,2-dinitromalonic acid (C(NO2)2(COOH)2, DMA) may be simultaneously produced during the hydrolysis of NMP. The experimental results2–6 show that DMA may further decompose after it is produced. This subsequent decomposition of DMA was also investigated besides the hydrolysis of NMP in the present work.3.1 Hydrolysis mechanism of NMP in the gas phase
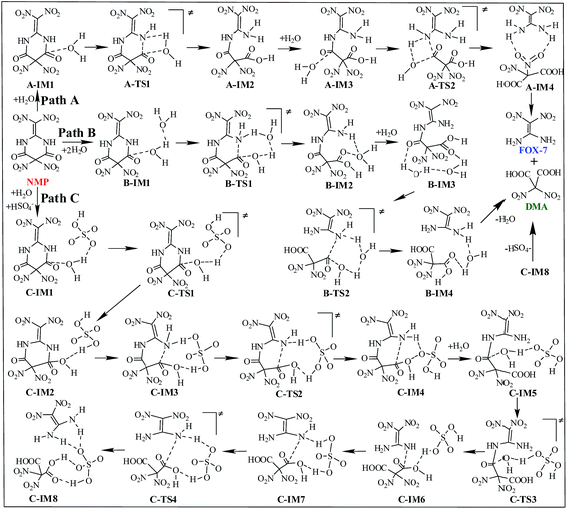
Three possible reaction paths are proposed and discussed based on the catalyst considered in the present work. The direct hydrolysis mechanism, in which no catalysis was taken into account, is denoted as path A. In view of the fact that the addition of water in the later synthesis stages may distinctly increase the yield of FOX-7,6 water may thus play an important role during the titled hydrolysis. The water-catalyzed hydrolysis pathway is denoted as path B. Herein, we propose that the coexisting acidic group of HSO4− may significantly promote/catalyze the hydrolysis of NMP. This HSO4−-catalyzed hydrolysis pathway is denoted as path C. A schematic depiction of the hydrolysis mechanism of NMP is shown in Scheme 3.The relative energies (ΔE) and free energies (ΔG) for all the possible hydrolysis paths are listed in Table 1.
| System | ΔE(g) | ΔG(g) | ΔG(f) | ΔG(d) |
|---|---|---|---|---|
| a The gas, formamide and DMSO phases are denoted as (g), (f), and (d), respectively. | ||||
| Path A | ||||
| NMP + 2H2O | 0.00 | 0.00 | 0.00 | 0.00 |
| A-IM1 + H2O | −7.95 | 1.73 | 3.48 | 3.36 |
| A-TS1 + H2O | 45.45 | 56.66 | 55.04 | 55.09 |
| A-IM2 + H2O | 1.69 | 11.72 | 9.69 | 9.73 |
| A-IM3 | −4.69 | 14.80 | 17.59 | 17.54 |
| A-TS2 | 42.47 | 63.48 | 62.61 | 62.68 |
| A-IM4 | −16.47 | −0.30 | −0.11 | −0.04 |
| FOX-7 + DMA | −9.35 | −2.20 | −7.30 | −7.24 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||
| Path B | ||||
| NMP + 2H2O + H2O | 0.00 | 0.00 | 0.00 | 0.00 |
| B-IM1 + H2O | −16.48 | 2.34 | 10.62 | 10.43 |
| B-TS1 + H2O | 28.54 | 50.26 | 47.21 | 49.24 |
| B-IM2 + H2O | −7.03 | 12.23 | 10.76 | 10.61 |
| B-IM3 | −14.98 | 14.69 | 22.78 | 23.55 |
| B-TS2 | 21.14 | 53.27 | 57.06 | 57.00 |
| B-IM4 | −31.32 | −3.16 | 2.93 | 2.01 |
| FOX-7 + DMA + H2O | −9.35 | −2.20 | −7.30 | −7.24 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||
| Path C | ||||
| NMP + 2H2O + HSO4− | 0.00 | 0.00 | 0.00 | 0.00 |
| C-IM1 + H2O | −45.49 | −22.22 | 4.40 | 4.06 |
| C-TS1 + H2O | −36.44 | −11.47 | 21.21 | 20.73 |
| C-IM2 + H2O | −36.38 | −12.05 | 20.90 | 20.53 |
| C-IM3 + H2O | −33.31 | −10.40 | 25.02 | 24.52 |
| C-TS2 + H2O | −34.56 | −11.02 | 23.79 | 23.27 |
| C-IM4 + H2O | −43.47 | −21.20 | 12.90 | 12.40 |
| C-IM5 | −32.41 | 1.37 | 28.16 | 27.82 |
| C-TS3 | −20.25 | 14.22 | 48.10 | 47.66 |
| C-IM6 | −44.71 | −11.69 | 12.64 | 12.72 |
| C-IM7 | −33.78 | 1.24 | 38.28 | 37.78 |
| C-TS4 | −34.52 | 0.68 | 37.47 | 37.00 |
| C-IM8 | −76.12 | −44.91 | −12.11 | −12.61 |
| FOX-7 + DMA + HSO4− | −9.35 | −2.20 | −7.30 | −7.24 |
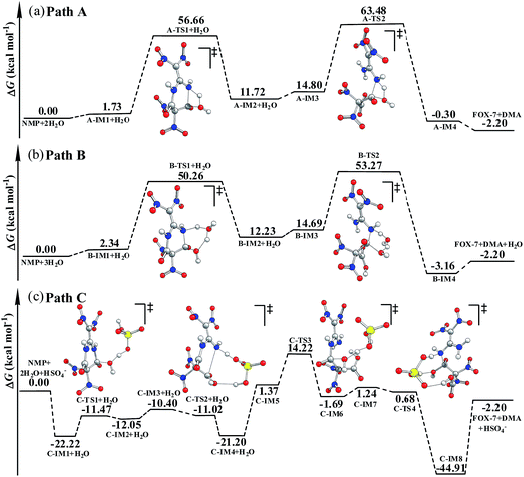
As shown in Fig. S4,† in the first hydrolysis step of NMP, a complex with one NMP molecule and one H2O molecule (A-IM1) forms after the H2O molecule approaches the C3 atom in NMP. Clearly, the stability of A-IM1 is higher than that of the sum of its monomers (ΔE = −7.95 kcal mol−1, as shown in Table 1). Meanwhile, the free energy of A-IM1 is higher than that of the sum of its monomers (ΔG = 1.73 kcal mol−1) possibly due to the contribution of entropy to the free energy. It is seen that though there is a distinct difference between ΔE and ΔG, ΔE≠ and ΔG≠ differ slightly in every elementary reaction during the hydrolysis of NMP. In the present work, the free energy is mainly discussed.
Starting from A-IM1, the bonds C3–N6 and O24–H26 may be undermined and completely break via a four-membered cyclic transition state A-TS1 in the first hydrolysis step. The ΔG≠ value associated with this step is 54.93 kcal mol−1. This is followed by A-IM2 being produced. Then A-IM2 may be transformed into A-IM3, which can be obtained after A-IM2 complexes with a second H2O. For the second hydrolysis step, a complex of FOX-7 and DMA, namely A-IM4, may be produced, also via a four-membered cyclic transition state A-TS2 with a ΔG≠ value of 49.68 kcal mol−1 (A-IM3 → A-IM4). Eventually, FOX-7 as well as DMA forms.
As shown in Fig. S5,† after two H2O molecules approach NMP, complex B-IM1 forms with the assistance of hydrogen bonds. Beginning with B-IM1, the first hydrolysis step of NMP occurs via an eight-membered cyclic transition state B-TS1 to produce the intermediate B-IM2. The ΔG≠ value associated with this step is 47.92 kcal mol−1. In this step, (one of) the O–H bonds in each H2O molecule break. Synchronously, the hydroxyl oxygen (O27) and H25 add to and finally bond with C3 and N6 in NMP, respectively. The first hydrolysis step of NMP may be realized after the formation of a new H2O molecule, indicating that H2O may catalyze the hydrolysis process. Then B-IM2 may easily be transformed into B-IM3. Similar to that in B-TS1, H2O may also catalyze the second hydrolysis step from B-IM3 to BIM4 via an eight-membered cyclic transition state B-TS2, in which the hydroxyl oxygen (O30) and H24 add to and bond with C1 and N5. The ΔG≠ value for this step is 38.58 kcal mol−1. Finally, complex B-IM4, which contains FOX-7, DMA and H2O, forms, indicating the completion of the hydrolysis.
As can be clearly seen in Fig. S6† and 1(c), after H2O·HSO4− approaches and combines with NMP, complex C-IM1 spontaneously forms. The free energy was found to decrease by 22.22 kcal mol−1. In view of the steric hindrance in the first hydrolysis step in path C, it is supposed that the addition of O25 in the hydroxyl group to C3 and that of H27 to N6 may occur separately, differing to that of the first hydrolysis step in path B. C-IM2 is formed via the transition state C-TS1 with a ΔG≠ value of 10.75 kcal mol−1, in which the addition of O25 to C3 may be aided by the H-abstracting process. After C-IM2 is transformed to C-IM3, the addition of H27 to N6 (C-IM3 → C-IM4) occurs in a barrierless way via an eight-membered transition state C-TS2, resulting in the formation of C-IM4.
In the second hydrolysis process, the addition of O27 in the hydroxyl group to C1 (C-IM5 → C-IM6) and that of H28 to N5 (C-IM7 → C-IM8) also occur separately. The ΔG≠ values associated with these two elementary reactions are 12.58 and −0.56 kcal mol−1, respectively. Eventually, FOX-7 as well as DMA is released from C-IM8.
Clearly, HSO4− acts as a temporary H-acceptor in both hydrolysis steps in path C. After the key intermediate (C-IM4/C-IM8) forms, HSO4− is released and recycled during the hydrolysis process. More importantly, as shown in Fig. 1, the potential energy surface of the HSO4−-catalyzed hydrolysis (path C) is much smoother than that of the direct hydrolysis (path A) and that of the H2O-catalyzed hydrolysis (path B). We thus believe that the coexisting HSO4− may effectively promote/catalyze hydrolysis of NMP. Moreover, it can be clearly seen that the activation free energy of the rate-determining step in path C (C-IM5 → C-IM6, 12.85 kcal mol−1) is much lower than that in path A (54.93 kcal mol−1) and path B (47.92 kcal mol−1). Such a dramatic decline in the free energy barrier clearly demonstrates the efficiency of the HSO4− catalyst. Here, we suppose that HSO4− may greatly assist and accelerate the breaking of the O–H bond in the water molecule as well as the H-transfer process, and thus effectively catalyze and promote hydrolysis of NMP.
It was observed that the yield of FOX-7 can be distinctly increased when water is added in the later stages of its preparation in the mixed acid system. Such an increase was also observed by Mandal et al.5 and Latypov et al.6 With the view that the catalysis of water is minimal during hydrolysis, the observed increase in the yield of FOX-7 may be predominantly derived from enhanced dissociation of the concentrated H2SO4 and the resulting increase in HSO4− in the hydrolysis system, in which, though the catalysis of water may also exist and play a role, the catalysis of HSO4− may be of the most importance during the hydrolysis process.
3.2 The decomposition mechanism of DMA in the gas phase
It was reported that CO2 as well as CH2(NO2)2 was detected during the decomposition of DMA.5,6 The decomposition mechanism of DMA was investigated. We suggest that HSO4− may also catalyze the decomposition of DMA. The optimized geometries and corresponding potential energy surfaces in the gas phase are shown in Fig. S7† and 2. Meanwhile, the schematic free energy diagrams of the direct decomposition in the gas phase are shown in Fig. S8 and S9.† The relative energies ΔE and free energies ΔG for the decomposition of DMA are listed in Table S3.†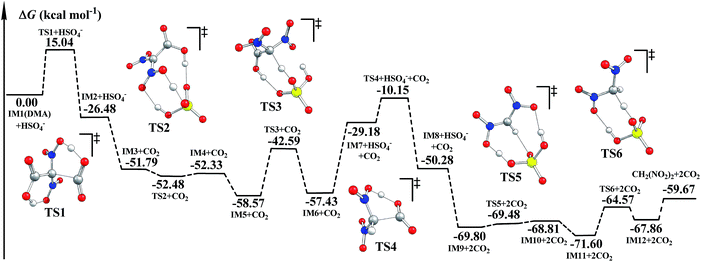 | ||
| Fig. 2 Potential energy surfaces for the decomposition of DMA calculated via B3LYP-D3/6-311++G(3df,3pd)//B3LYP/6-311G(d,p) in the gas phase. | ||
As shown in Fig. S7† and 2, during the H-transfer process (IM1 → IM2, H13 transfers from O12 to O7), a CO2 molecule is easily released from DMA (IM1). The ΔG≠ value for this step is merely 15.04 kcal mol−1, indicating that the breaking of C2–C3 may be assisted by H-transfer.
We supposed that after the intermediate IM7 (similar to IM1) forms via an H-transfer process, the second CO2 molecule may be easily released. The H atom may be transferred by two means during the formation of IM7: direct H-transfer and HSO4−-catalyzed H-transfer. It can be clearly seen that when IM7 was produced via the direct H-transfer process (IM3′ → IM4′(IM7), shown in Fig. S8†), ΔG≠ is up to 63.21 kcal mol−1. However, when IM7 was obtained the ΔG≠ value was merely 15.98 kcal mol−1. And the ΔG≠ value for the release of the second CO2 molecule (IM7 → IM8) is 19.03 kcal mol−1. Next, during the HSO4−-catalyzed H-transfer process (IM3 → IM6), CH2(NO2)2 may be produced after the H atom is transferred. Similarly, the H atom may also be transferred in two ways in the formation of CH2(NO2)2: the direct way and the HSO4−-catalyzed way. The ΔG≠ value for the direct one is 44.70 kcal mol−1 (IM11′ → IM12′, in Fig. S9†), while the ΔG≠ value for the HSO4−-catalyzed one (IM9 → IM12) is merely 7.39 kcal mol−1. Such severe declines in ΔG≠ clearly indicate that the formation of both IM7 (IM3 → IM6) and CH2(NO2)2 (IM9 → IM12) may be effectively catalyzed by the coexisting HSO4−. Additionally, since decomposition of DMA releases two molecules of CO2, we believe that decomposition of DMA may promote hydrolysis of NMP, and thus favor the generation of the targeted product FOX-7.
3.3 Solvation effects on the hydrolysis of NMP
Koleva14 suggested that formamide as well as DMSO can be used as the model solvent for theoretical investigation of the bulk solvent effects via CPCM30,31 on the nitration of benzene in the mixed acid system. Model solvents such as these along with the CPCM method were employed to evaluate the solvent effects on the hydrolysis of NMP in paths A to C. The bond lengths of the relevant species in paths A to C in the formamide (f) and DMSO (d) phases are shown in Fig. S10–S15.† The relevant free energies in paths A to C in both the formamide and DMSO phases are listed in Table 1.As shown in Fig. S4–S6 and S10–15,† it can be clearly seen that solvent effects impact slightly on the geometries of the species in the hydrolysis of NMP. As shown in Table S4,† it can be seen that the changes in ΔG≠ in the solvent phases differ obviously to those in the gas phase in paths A to C, though the ΔG≠ values are quite analogous to each other in the two solvent phases. The formamide phase was mainly chosen as a model to evaluate the solvent effects on the hydrolysis of NMP, in which the dipole moments for the rate-determining steps in paths A to C are calculated using the B3LYP/6-311G(d,p) method (as shown in Table 2) and discussed as follows.
| Path A system | μ | Path B system | μ | Path C system | μ |
|---|---|---|---|---|---|
| A-IM1 | 2.4 | B-IM1 | 4.2 | C-IM5 | 9.0 |
| A-TS1 | 5.8 | B-TS1 | 7.2 | C-TS3 | 6.4 |
The dipole moment of A-IM1 is 2.4 debye, calculated via B3LYP/6-311G(d,p). Identical dipole moments of A-IM1 were also obtained via B3LYP-D3/6-311G(d,p), M06-2X/6-311G(d,p), B3PW91/6-311G(d,p), and B3LYP/agu-cc-pvdz (as shown in Table S5†). Moreover, the dipole moment of A-TS1 is 5.8 debye, which is also similar to that obtained via the other four methods (Table S5†). This indicates that the B3LYP/6-311G(d,p) method is reliable, and thus it was mainly employed to calculate the dipole moments in the present work.
As shown in Table 1, the ΔG≠ value for the rate-determining step in the formamide phase is lower by 3.37 kcal mol−1 than that for the gas phase in path A. The B3LYP/6-311G(d,p) calculations shown in Table 2 indicate that the dipole moment of A-TS1 is much bigger than that of A-IM1. This implies that the solvent effect of formamide on A-TS1 is stronger than that on A-IM1, namely, the transition state A-TS1 may be better stabilized by formamide than A-IM1 is. Similarly, the solvent effect on B-TS1 may also be stronger than that on B-IM1 as the dipole moment of B-TS1 (μ = 7.2 debye) is larger than that of B-IM1 (μ = 4.2 debye). However, the dipole moment of C-TS3 (6.4 debye) is less than that of C-IM5 (9.0 debye), indicating that the stabilization of the solvent on C-TS3 is inferior to that on C-IM5. This may answer for the calculation that the ΔG≠ value in the formamide phase is higher by 7.06 kcal mol−1 than that in the gas phase.
More importantly, as shown in Table S4,† the ΔG≠ values for the rate-determining steps in formamide for paths A to C are 52.73, 38.81, and 19.84 kcal mol−1, respectively. Meanwhile, those in the gas phase are 54.93, 47.92, and 12.85 kcal mol−1. It is obvious that formamide may assist the hydrolysis process and thus significantly impact ΔG≠, indicating that the solvent effects in the mixed acid system may be notable and should not be ignored. Even so, HSO4−-catalyzed path C is still much more favorable than the other two paths (paths A and B), whenever hydrolysis occurs in the gas or formamide phase. Fortunately, since identical results are obtained in the gas and solvent phases, it is believed that the calculations for the titled reaction in the gas phase are reliable and acceptable. Interestingly, the activation free energies and optimized geometries of the relevant species for the decomposition of DMA in the gas, formamide, and DMSO phases are quite analogous (see Table S3 and Fig. S7, S16 and S17†). Thus calculation in the gas phase may be reliable as is that for the kinetics of hydrolysis of NMP in the mixed acid system.
3.4 Hydrolysis kinetics of NMP
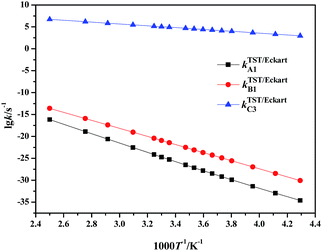 | ||
| Fig. 3 Calculated rate constants for the rate-determining steps in paths A to C via TST/Eckart in the temperature range 233–400 K. | ||
| Reactions | log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) A A |
n | Ea/R |
|---|---|---|---|
| A-IM1 → A-IM2 | 1.88 | 2.63 | 23![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 074 074 |
| A-IM3 → A-IM4 | −16.06 | 7.20 | 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 528 528 |
| B-IM1 → B-IM2 | 7.19 | 0.78 | 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 974 974 |
| B-IM3 → B-IM4 | 7.15 | 0.95 | 16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 201 201 |
| C-IM1 → C-IM2 | 9.75 | 0.61 | 3642 |
| C-IM3 → C-IM4 | 13.31 | −0.62 | 532 |
| C-IM5 → C-IM6 | 9.80 | 0.74 | 4599 |
| C-IM7 → C-IM8 | 13.83 | −0.31 | 269 |
It can be clearly seen that the calculated TST/Eckart rate constants for the rate-determining step in the HSO4−-catalyzed path C (kTST/EckartC3) are much larger than the corresponding values in the direct hydrolysis path A (kTST/EckartA1) and the H2O-catalyzed path B (kTST/EckartB1), as shown in Fig. 3. Thus the HSO4−-catalyzed path C may be the most dominant path for hydrolysis of NMP in the mixed acid system, indicating that path A as well as path B is unlikely to occur within the investigated temperature range.
Moreover, it can also be seen that the rate constants for every elementary reaction slowly increase with the increase in temperature in path C (in Table S6†), indicating that the rate constants are slightly impacted by the temperature. Therefore, to avoid loss of the targeted energetic material of FOX-7 and improve the safety of the mixed acid system, it is suggested that hydrolysis of NMP should be carried out at relatively low temperatures. Such a prediction is in good agreement with experimental observations.2
| νA = kA[NMP][H2O]2 | (1) |
| νB = kB[NMP][H2O]3 | (2) |
| νC = kC[NMP][HSO4−][H2O]2 | (3) |
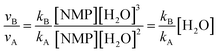 | (4) |
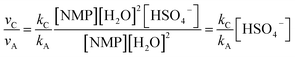 | (5) |
Thus the relative hydrolysis rate of NMP depends not only on the corresponding rate constants but also on the concentrations of H2O and HSO4−. HSO4− is able to be easily released in diluted acids. Based on our recent work,12 the overall formation rate of NMP can be expressed as eqn (6).
| vNMP = k[MDP][NO2+]4 | (6) |
It has been demonstrated that a higher acid concentration favours easier formation of NO2+ and faster production of the key intermediate NMP in the mixed acid system, which may promote the nitration of MDP, benefit the subsequent hydrolysis of NMP, and improve the production of FOX-7. Therefore, the acid concentration should be well balanced and optimized throughout the experiment. Latypov et al. reported that an appropriate concentration of H2SO4 in the mixed acids should be 93–97%.6 Moreover, they also found that adding a certain amount of water in the later reaction stages can improve the preparation of FOX-7. This has been proven well in our pilot-scale production of FOX-7 in the mixed acid system.
4. Conclusions
The hydrolysis of NMP in the mixed acid system was systematically investigated in the present work. Firstly, the hydrolysis mechanism in gas as well as in the solvent phase was elucidated via which the impact of the co-existing acidic group of HSO4− on the hydrolysis of NMP was discerned. HSO4−-catalyzed hydrolysis is more favorable than direct and H2O-catalyzed hydrolysis since HSO4− may dramatically decrease the free energy barrier and effectively promote the hydrolysis of NMP. Moreover, HSO4− can also effectively catalyze the decomposition of DMA in the mixed acid system. This may be an additional promotion of the hydrolysis of NMP which may be partly due to the release of CO2 shifting the chemical equilibrium of the system forward. Secondly, the hydrolysis kinetics of NMP were studied theoretically. Based on the effect of temperature on the TST/Eckart rate constants of the elementary reaction, it can be concluded that HSO4− may effectively accelerate the hydrolysis of NMP, and may thus act as a promising catalyst for the titled hydrolysis. Moreover, the concentration of HSO4− may significantly impact the hydrolysis rates. Thus the concentration of H2SO4 in the mixed acids should be optimized effectively and strictly controlled not only in the experimental preparation but also in the industrial production of FOX-7.Since the co-existing HSO4− may dramatically accelerate the nitration of MDP to form NMP, and effectively promote the following hydrolysis of NMP to produce FOX-7, we firmly believe that HSO4− may be a promising catalyst for the preparation of FOX-7 in the mixed acid system. A catalysis and promotion such as this is also believed to be effective in other nitration systems performed in mixed acids and thus is of especially great significance for better production of nitro-energetic materials.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors gratefully acknowledge the financial support from the National Natural Science Foundation of China (21327011 and 21776170), the Program for Changjiang Scholars and Innovative Research Team in University (IRT_14R33), the 111 Project (B14041), and the Fundamental Research Funds for the Central Universities (GK201603103 and 2016TS046).Notes and references
- N. V. Latypov, J. Bergman, A. Langlet, U. Wellmar and U. Bemm, Tetrahedron, 1998, 54, 11525–11536 CrossRef CAS.
- N. V. Latypov, U. Wellmar and A. Langlet, Method of preparing salts of dinitromethane, US Pat. No. 6,340,780 B1, 2002.
- H. Q. Cai, Y. J. Shu, H. Huang, B. B. Cheng and J. S. Li, J. Org. Chem., 2004, 69, 4369–4374 CrossRef CAS PubMed.
- H. Q. Cai, Y. J. Shu, W. F. Yu, J. S. Li and B. B. Cheng, Acta Chim. Sin., 2004, 62, 295–301 CAS.
- A. K. Mandal, U. Thanigaivelan, R. K. Pandey, S. Asthana, R. B. Khomane and B. D. Kulkarni, Org. Process Res. Dev., 2012, 16, 1711–1716 CrossRef CAS.
- N. V. Latypov, M. Johansson, E. Holmgren, E. V. Sizova, V. V. Sizov and A. J. Bellany, Org. Process Res. Dev., 2007, 11, 56–59 CrossRef CAS.
- (a) R. Gilardi, CCCD 127539, Cambridge Structural Database, Cambridge Crystallographic Data Center, Cambridge, UK, 1999; (b) D. E. Taylor, F. Rob, B. M. Rice, R. Podeszwa and K. Szalewicz, Phys. Chem. Chem. Phys., 2011, 13, 16629–16636 RSC; (c) Z. A. Dreger, A. I. Stash, Z. G. Yu, Y. S. Chen, Y. C. Tao and Y. M. Gupta, J. Phys. Chem. C, 2016, 120, 27600–27607 CrossRef CAS; (d) Q. L. Zhao, N. Liu, B. Z. Wang and W. L. Wang, RSC Adv., 2016, 6, 59784–59793 RSC.
- (a) G. Majano, S. Mintova, T. Bein and T. M. Klapötke, J. Phys. Chem. C, 2007, 111, 6694–6699 CrossRef CAS; (b) N. V. Muravyev, A. N. Pikina and V. G. Kiselev, J. Chem. Eng. Data, 2017, 62, 575–576 CrossRef CAS.
- (a) X. Fang and W. G. McLuckie, J. Hazard. Mater., 2015, 285, 375–382 CrossRef CAS PubMed; (b) A. Belaada, W. A. TRzciński, Z. Chylek and J. Paszula, Propellants, Explos., Pyrotech., 2017, 42, 1–8 CrossRef.
- (a) V. G. Kiselev and N. P. Gritsan, J. Phys. Chem. A, 2014, 118, 8002–8008 CrossRef CAS PubMed; (b) Z. A. Dreger, Y. C. Tao and Y. M. Gupta, J. Phys. Chem. C, 2016, 120, 11092–11098 CrossRef CAS.
- (a) H. X. Gao and J. M. Shreeve, Angew. Chem., Int. Ed., 2015, 54, 6335–6338 CrossRef CAS PubMed; (b) T. T. Vo and J. M. Shreeve, J. Mater. Chem. A, 2015, 3, 8756–8763 RSC.
- K. Wang, J.-G. Chen, B. Z. Wang, Y. P. Ji, F. Y. Liu, Z.-T. Liu, W. L. Wang, Z.-W. Liu, Z. P. Hao and J. Lu, RSC Adv., 2016, 6, 80145–80157 RSC.
- K. Wang, J.-G. Chen, B. Z. Wang, F. Y. Liu, Z.-T. Liu, Z.-W. Liu, W. L. Wang, J. Q. Jiang, Z. P. Hao and J. Lu, RSC Adv., 2015, 5, 25183–25191 RSC.
- G. Koleva, B. Galabov, B. Hadjieva, H. F. Schaefer III and P. V. R. Schleyer, Angew. Chem., Int. Ed., 2015, 54, 14123–14127 CrossRef CAS PubMed.
- N. C. Marziano, A. Tomasin, C. Tortato and J. S. Zaldivar, J. Chem. Soc., Perkin Trans. 2, 1998, 2, 1973–1982 RSC.
- F. Cacace, M. Attinà, G. D. Petris and M. Speranza, J. Am. Chem. Soc., 1990, 112, 1014–1018 CrossRef CAS.
- J. Gonzalez, J. M. Anglada, R. J. Buszek and J. S. Francisco, J. Am. Chem. Soc., 2011, 113, 3345–3353 CrossRef PubMed.
- T. L. Zhang, W. L. Wang, P. Zhang, J. Lu and Y. Zhang, Phys. Chem. Chem. Phys., 2011, 13, 20794–20805 RSC.
- J. Gonzalez and J. M. Anglada, J. Phys. Chem. A, 2010, 114, 9151–9162 CrossRef CAS PubMed.
- M. T. Sucarrat, J. S. Francisco and J. M. Anglada, J. Am. Chem. Soc., 2012, 134, 20632–20644 CrossRef PubMed.
- J. R. R. Verlet, A. E. Bragg, A. Kammrath, O. Cheshnovsky and D. M. Neumark, Science, 2005, 307, 93–96 CrossRef CAS PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, T. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Revision D.01, Gaussian, Inc., Wallingford, CT, 2010 Search PubMed.
- C. Lee, W. T. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789 CrossRef CAS.
- A. D. McLean and G. S. Chandler, J. Chem. Phys., 1980, 72, 5639–5648 CrossRef CAS.
- L. T. Chen, H. M. Xiao, J. J. Xiao and X. D. Gong, J. Phys. Chem. A, 2003, 107, 11440–11444 CrossRef CAS.
- L. T. Chen, H. M. Xiao and J. J. Xiao, J. Phys. Org. Chem., 2005, 18, 62–68 CrossRef CAS.
- L. X. Jin, W. L. Wang, D. D. Hu and S. T. Min, J. Phys. Chem. B, 2013, 117, 3–12 CrossRef CAS PubMed.
- K. Wang, J.-G. Chen, B. Z. Wang, J. Lu, W. L. Wang, F. Y. Liu, C. Zhou, P. Lian, Z.-W. Liu and Z.-T. Liu, Chem. J. Chin. Univ., 2015, 36, 531–538 CAS.
- C. Gonzales and H. B. Schlegel, J. Chem. Phys., 1989, 90, 2154–2161 CrossRef.
- V. Barone and M. Cossi, J. Phys. Chem. A, 1998, 102, 1995–2001 CrossRef CAS.
- M. Cossi, N. Rega, G. Scalmani and V. Barone, J. Comput. Chem., 2003, 24, 669–681 CrossRef CAS PubMed.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104–154119 CrossRef PubMed.
- S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456–1465 CrossRef CAS PubMed.
- W. T. Duncan, R. L. Bell and T. N. Truong, J. Comput. Chem., 1998, 19, 1039–1052 CrossRef CAS.
- (a) C. Eckart, Phys. Rev., 1930, 35, 1303–1309 CrossRef CAS; (b) B. C. Garrett and D. G. Truhlar, J. Phys. Chem., 1979, 83, 2921–2926 CrossRef CAS; (c) H. S. Johnston and J. Heicklen, J. Phys. Chem., 1962, 66, 532–533 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available: Calculated bond lengths (in Angstroms) of FOX-7 using multiple methods; the calculated single point energy and activation free energy (ΔG≠) using multiple methods for the first step in the direct hydrolysis of NMP in the formamide phase; the optimized geometries of reactant NMP; potential energy diagrams for the internal rotation of the dihedral angles in NMP; the optimized geometries of species in the direct hydrolysis of NMP calculated at the B3LYP/6-311G(d,p) level with the CPCM model in the gas, formamide, and DMSO phases; the optimized geometries of species in H2O catalyzed hydrolysis of NMP calculated at the B3LYP/6-311G(d,p) level with the CPCM model in the gas, formamide, and DMSO phases; the optimized geometries of species in HSO4−-catalyzed hydrolysis of NMP calculated at the B3LYP/6-311G(d,p) level with the CPCM model in the gas, formamide, and DMSO phases; the optimized geometries of species in HSO4−-catalyzed decomposition of DMA calculated at the B3LYP/6-311G(d,p) level in the gas, formamide, and DMSO phases; a schematic energy diagram of the corresponding direct decomposition process of DMA obtained in the gas phase; relative energies of species in the decomposition of DMA in the gas, formamide, and DMSO phases; the activation (free) energies for the hydrolysis paths A to C in the gas, formamide, and DMSO phases; the calculated dipole moments (μ, in debye) of the rate-determining step for direct hydrolysis path A using multiple methods; the calculated TST/Eckart rate constants (s−1) of each elementary reaction for hydrolysis of NMP in the temperature range of 233–400 K; structural and energetic information. See DOI: 10.1039/c7ra12605k |
| This journal is © The Royal Society of Chemistry 2018 |