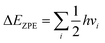Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Theoretical investigation on the ground state properties of the hexaamminecobalt(III) and nitro–nitrito linkage isomerism in pentaamminecobalt(III) in vacuo†
Jules Tshishimbi Muya *a,
Hoeil Chung
*a,
Hoeil Chung *a and
Sang Uck Lee
*a and
Sang Uck Lee *bc
*bc
aHanyang University, Department of Chemistry, Seoul, South Korea. E-mail: hoeil@hanyang.ac.kr; julescmuya.tmuya@gmail.com
bHanyang University, Department of Chemical & Molecular Engineering, Sangnok-gu, Ansan 426-791, Korea. E-mail: sulee@hanyang.ac.k
cHanyang University, Department of Bionanotechnology, Sangnok-gu, Ansan 426-791, Korea
First published on 16th January 2018
Abstract
Nitro–nitrito isomerization in Co(NH3)5NO22+ linkage isomers was investigated with a focus on the geometries, relative stabilities and chemical bonding using ωB97XD/6-31+G(d,p) to elucidate the photo-salient effect in [Co(NH3)5NO2]NO3Cl. Different techniques like atoms in molecules (AIM), electron localization function (ELF) and natural bonding orbital (NBO) were used to gain insight into the chemical bonds of the isomers and to identify the key factors influencing their relative stabilities. The study of the ground-state potential energy surface of [Co(NH3)5NO2]2+ reveals that the nitro/exo-nitrito isomerization reaction can proceed via the following two paths: (1) nitro → TS1 (38.16 kcal mol−1) → endo-nitrito → TS2 (9.68 kcal mol−1) → exo-nitrito and (2) nitro → TS3 (41.76 kcal mol−1) → exo-nitrito. Pathway (1) through endo-nitrito is the most likely isomerization mechanism because of a lower energy barrier than pathway (2). The intramolecular-resonance-assisted hydrogen bonds (N–H⋯O and N–H⋯N), the orientation of NO2, and the difference between Co–N and Co–O bond energies are identified as the key factors determining the relative stabilities of the linkage isomers. Co(NH3)63+ is less stable compared to Co(NH3)5NO22+ and undergoes a slight geometrical distortion from D3d to either D3 or S6 characterized by a stabilization energy of ∼750 cm−1 at CCSD(T)/6-31+G(d,p).
1. Introduction
Co complexes play various important roles in the chemistry of life processes and have been known for ages to impart blue color to ceramics.1,2 Considerable research effort has been made to understand the properties of Co complexes, particularly those derived from cobaltammines. Sakiyama et al.3 analyzed the electronic spectra of the hexaamminecobalt(III) complex cation in aqueous solution to obtain the spectral components attributed to the slight distortion from a regular octahedron around the central cobalt(III) ion and reported that the LC-BLYP/6-31G(d) optimized geometry of the complex in aqueous solution is a trigonally compressed octahedron under D3d. The influence of this reduction in the symmetry of [Co(NH3)6]3+ on its vibrational spectrum was also examined in the solid state.4 This trigonal deformation was reported to be sensitive to the environment of the complex.3 A crystallographic study of the binding of oxo-anions with cationic cobaltammine carried out by Sharma et al.5 revealed the presence of discrete [Co(NH3)6]3+ ions and mixed anions (e.g. Cl− and ClO3−, Br− and ClO3−, Cl− and ClO3−) which are stabilized by hydrogen bonding interactions and attractive electrostatic forces. The hexaamminecobalt(III) complex cation is a potential anion receptor5,6 widely used in structural biology to characterize biomolecules like DNA, RNA, and proteins7 and it is considered as a representative cationic Werner complex. It is worth mentioning that the works of Alfred Werner on cobaltammines led to a Nobel Prize in 1913,8 which formed the basis of modern transition-metal coordination complex chemistry, especially the linkage of atoms in transition metal compounds.Transition-metal linkage isomers have the same chemical composition, differing only in the nature of the metal–ligand connectivity.9 For example, when one ammonia in hexaamminecobalt(III) is substituted by a nitrite anion, nitro, endo-nitrito, and exo-nitrito isomers are formed (Fig. 1). Nitrite anion is an ambident ligand with electronic density delocalized on both N–O bonds, and both N and O atoms acting as alternative reactive sites. It can bind to the metal through N as well as through O, leading to linkage isomerism. The ambident reactivity of the nitrite ion was studied in detail by Tishkov et al.10 For instance, the cationic cobalt complex of formula [Co(NH3)5NO2]Cl2 exists as either the yellow-colored nitro isomer ([Co(NH3)5NO2]Cl2), where the nitro ligand is bound to Co through nitrogen, or the red-colored nitrito isomer ([Co(NH3)5ONO]Cl2), where the nitrito is bound to Co through one of the oxygen atoms11–16 Several research groups have focused their studies on metal linkage compounds due to their potential applications in medicinal therapy, photo-responsive materials, tunable optical materials, and molecular devices.11–13,17–26
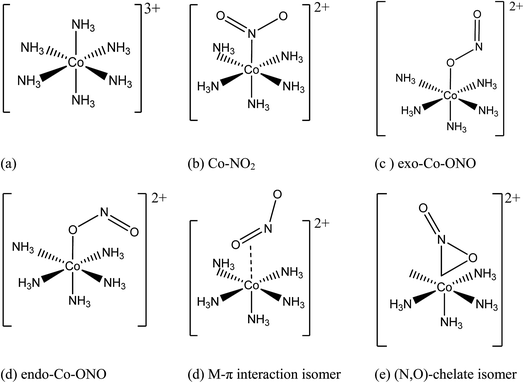 | ||
| Fig. 1 Initial geometries of: (a) hexaamminocobalt(III) cation, (b–c) N- and O-linked Co-complexes isomers, (d) M–π interaction Co-complex isomer, and (e) (N,O)-chelate Co-complex isomer. | ||
The transformation of the N-bonded nitro isomer to the less stable O-bonded nitrito isomer has already been extensively studied experimentally and the conversion was demonstrated to occur intramolecularly.13–16 The nitrito isomers of [Co(NH3)5ONO](NO3)2 and [Co(NH3)5ONO](NO3)Cl convert slowly to the respective nitro isomers [Co(NH3)5NO2](NO3)2 and [Co(NH3)5NO2](NO3)Cl when placed in a dark room.19 The base dependence of this linkage isomerization and the transformation of the nitrito in nitrito was also observed overnight by Jackson et al.27 in [Co(NH3)5ONO](ClO4) in solution using H1 NMR and UV-vis techniques. The reaction of the transformation of [Co(NH3)5ONO]2+ in [Co(NH3)5NO2]2+ in solution and in solid state was found to be accelerated by light.27–29 More detailed information related to the experiments describing the synthesis of [Co(NH3)5NO2]2+ and [Co(NH3)5ONO]2+ and the application of spectroscopic techniques to detect the nitrite bonding mode are provided elsewhere.27,29–32 Here we only recall that this transformation may pass through an intermediate endo-[Co(NH3)5ONO]2+. According to Ciofini,33 experimental data do not provide a better understanding of the nitro/nitrito transformation mechanism, and theoretical methods can help in the elucidation of this reaction mechanism. This solid-state intramolecular reaction changes the configuration of the [Co(NH3)5NO2]2+ complex cation alone at its site in the lattice, leaving the rest of the lattice unchanged9 and was reported to be autocatalytic or auto-inhibitory.24 In contrast to the dark condition, Naumov et al.22,23 reported that the [Co(NH3)5NO2](NO3)Cl crystal exhibits a forceful jump when exposed to UV light (referred to as the photo-salient effect). During this photo-isomerization process, [Co(NH3)5ONO]2+ was thought to serve as a local source of strains.24,25
The discovery of photo-induced leaping in [Co(NH3)5ONO](NO3)Cl crystals stimulated extensive research into its structural and photo-rearrangement properties.22,23,34,35 The design of dynamic molecular crystals with properties that can be controlled by applying an external stimulus is an important challenge in molecular materials science. Herein we investigate in detail the geometry, relative stability, and chemical bonding in the ground state of the hexaamminecobalt(III) cation and the nitro-/nitrito-pentaamminecobalt(III) linkage isomers (denoted as Co–NO2 and Co–ONO) in vacuo using ωB97XD/6-31+G(d,p). Knowledge of the structural and electronic properties of the nitro-/nitrito-pentaamminecobalt(III) linkage isomers is critical in the research of novel linked isomers with switchable optical properties. The main purpose of this study is the prediction of the pathway of the nitro-/nitrito-pentaamminecobalt(III) isomerization because the latter is the probable cause of the photo-salient effect in [Co(NH3)5ONO](NO3)Cl.
This study is organized as follows:
(1) First, the relative stability of Co(NH3)63+ having D3d symmetry in vacuo is analyzed using group theory and various quantum chemical methods. Contrary to literature reports, we found [Co(NH3)6]3+ to be unstable in D3d (possessing 6 imaginary frequencies) and it tends to distort towards either D3 or S6. [Co(NH3)6]3+ is compared to its analogous complexes e.g. [Ru(NH3)6]3+, [Cr(NH3)6]3+ and [Fe(NH3)6]2+ at B3LYP/LanL2DZ. This D3 geometry was afterwards used in an isodesmic reaction to compute the formation energies of [Co(NH3)5NO2]2+ isomers.
(2) Secondly, MP2, CCSD, B3LYP, B3LYP-D3, M062X, LC-BLYP, and ωB97XD methods are compared with CCSD(T). The ωB97XD and LC-BLYP methods gave good results approaching CCSD(T). Therefore, the subsequent analysis is performed using ωB97XD.
(3) Thirdly, the thermodynamics and kinetics of the Co(NH3)5NO22+ isomers are studied at the ωB97XD level, and two nitro/exo-nitrito isomerization reaction paths are identified: (1) nitro → TS1 (38.16 kcal mol−1) → endo-nitrito → TS2 (9.68 kcal mol−1) → exo-nitrito and (2) nitro → TS3 (41.76 kcal mol−1) → exo-nitrito. The most likely reaction is the one that follows pathway (1) because it is the lowest-energy path.
(4) Lastly, the nature of chemical bonding in the nitro- and nitrito linkage isomers is examined briefly to understand how atoms are held together and to identify key factors to justify their order of stabilities. Hydrogen bonds, orientation of atoms in ONO group, and difference in natural bonding orbital (NBO) energy between Co–N and Co–O bonds are identified as the key factors to explain the relative stabilities of linkage isomers.
We confirmed through this analysis that the reaction path (1) through endo-nitrito is the most likely isomerization mechanism causing photo-salient effect, because it is the lowest energy reaction path.
2. Computational details
Fig. 1 shows the initial geometric structures used herein for geometry optimization. The [Co(NH3)5NO2]2+ linkage isomers were constructed following the coordination modes proposed in literature.36,37 Fig. 1c and d display two O-bonded nitrito isomers with different spatial orientation of the atoms of the ONO group, denoted as exo-Co–ONO and endo-Co–ONO. Only singlet states were considered in the present study because octahedral Co(III) prefers the low-spin state, contrary to the Co(II) state.38–40 Comprehensive understanding of [Co(NH3)6]3+ and [Co(NH3)5NO2]2+ isomers requires state-of-the-art quantum chemical methods. All geometries were fully optimized and minima characterized by real vibrational modes at ωB97XD/6-31+G(d,p). Transition states were located using QST3 and IRC methods, followed by vibrational frequency analysis. All the minima energy values reported here are zero-point energy (ZPE) corrected using the expression:where h and νi stand for Plank's constant and the vibrational frequency of mode Qi, respectively.
CCSD(T) single-point calculations were performed based on CCSD optimized geometries to validate our methodology, and the structures and their relative energies were found to be similar to those obtained at ωB97XD. The dynamic correlation in D3d–Co(NH3)63+ was traited on the top of the CASSCF(2,2) method with the Multireference Averaged Coupled-Pair Functional (MRACPF) approach to evaluate the Pseudo-Jahn–Teller stabilization energy (PJTE). The dispersion energies in the complexes were evaluated as an electronic energy difference between B3LYP and B3LYP-D3. The latter is composed of three terms: Kohn–Sham B3LYP, pair-wise London dispersion and three-body dispersion energies. Several studies41,42 have indicated that transition metals can have important relativistic effects that require detailed research. The zero-order regularized approximation to the Dirac equation (ZORA)42 was employed to treat relativistic effects. The symmetry disruption in the D3d [Co(NH3)6]3+ was investigated using quantum mechanical calculations and group theory.43 Further, the D3d epikernels of [Co(NH3)6]3+ were compared with [Ru(NH3)6]3+, [Cr(NH3)6]3+ and [Fe(NH3)6]2+ epikernels at B3LYP/LanL2DZ. The accumulation of electron density at the bond critical point (BCP),44 electron localization function (ELF),45,46 and natural bond orbitals (NBO)47,48 were undertaken to obtain useful information on the electron density charge distribution and for the rationalization of chemical bonding. Most of the optimization calculations were performed using Gaussian 0949 for single reference methods, whereas orca50 program was employed for treatment of multireference and relativistic effects. Further optimization of the epikernels geometries of [Co(NH3)6]3+ (D3d, D3, S6, C2h) were carried out using B3LYP/TZP on TURBOMOLE51 and SVWN/TZP method including ZORA on Amsterdam Density Functional (ADF).52 Gaussview 5.0,53 chemcraft,54 Jmol 13.0,55 were used for visualization while AIM2000,56 and Multiwfn57 programs were employed to analyze the topology of the chemical bonding in nitro/nitrito linkage isomers.
3. Results and discussion
3.1 [Co(NH3)6]3+
| Methods | Co–N | PJT energy | H–L gaps | LF (symmetry) |
|---|---|---|---|---|
| BD(T) | 2.001 | 2.16 | 17.24 | — |
| CCSD(T) | 1.992 | 2.14 | 17.74 | — |
| MP2 | 1.973 | 2.43 | 17.79 | — |
| B3LYP | 2.013 | 1.75 | 6.28 | 75(e) |
| B3LYP-D3 | 2.004 | 1.77 | 6.24 | 78(e) |
| M062X | 2.022 | 2.04 | 10.89 | 106(e) |
| ωB97XD | 2.009 | 2.12 | 11.13 | 89(e) |
| LC-BLYP | 1.976 | 2.14 | 13.27 | 83(e) |
| Exp. [ref. 55] | 1.97 |
Our calculations show that D3d in vacuo is unstable contrary to what was reported elsewhere,3 in solid and aqueous media. Its optimized geometry is characterized by six imaginary modes of representations a1u, a2g, eg and eu at i167, i164, i101 and i90 cm−1 at ωB97XD/6-31+G(d,p) (i154, i150, i74 and i45 cm−1 at CCSD/6-31G(d)), respectively. A distortion with the D3 symmetry constraint yields a minimum energy characterized by the lowest vibrational mode of e symmetry located at 89 cm−1 at ωB97XD/6-31+G(d,p) (79 cm−1 at CCSD/6-31G(d)). The energy difference between the HOMO and LUMO is slightly increased to 17.74 eV at CCSD(T)/6-31+G(d,p) for D3. A further optimization of D3 and D3d geometries using B3LYP/TZP method as implemented in TURBOMOLE gives an energy difference of 1.54 kcal mol−1. The HOMO–LUMO gap in gas phase is 6.25 eV. The vibrational analysis is characterized by two imaginary frequency at i107.97 and i104.40 cm−1 of a1u and a2g representations, whereas a full optimization of the same geometry in D3d at the SVWN/TZP including the scalar and spin–orbit ZORA as implemented in ADF program reproduces six imaginary frequencies estimated about i137.99 (a1u), i137.90 (a2g), i54.56 (eg), i18.00 (eu) cm−1 confirming that D3d is not the true global minimum of [Co(NH3)6]3+.
The structural change between D3d and D3 in [Co(NH3)6]3+ is small (Fig. S2†). The distortion vector responsible of this symmetry breaking can be expressed as:62,63
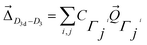 | (1) |
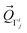 , and the subscript describes the irreducible representation of the vibrational mode.
, and the subscript describes the irreducible representation of the vibrational mode.
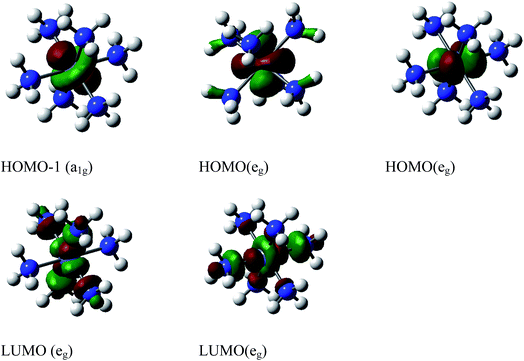
Our calculations show a significant contribution of the 1a1u imaginary mode of nearly 98.89% in the distortion vector (Fig. S3†). A further distortion of D3d along the imaginary vibrational mode a2g will lead to S6. The distortion of D3d–[Co(NH3)6]3+ along 1a1u vibrational mode acts essentially on H and destroys the center of symmetry. The full D3d symmetry group is broken because by destroying the inversion point, 1a1u will also remove the improper rotation axis (S6) and the dihedral plane. However, the imaginary modes show a rotation of hydrogen atoms. The free rotation of NH3 groups in octahedral symmetry observed in water solvent should not strictly be applicable to low symmetry complex. The decent in symmetry observed from D3d to its subgroup D3 can only arise from the Pseudo-Jahn–Teller (PJT) effect because the HOMO (eg)4 in D3d is fully occupied and cannot trigger a pure Jahn–Teller distortion according to group theory. The computed PJT energy caused by this vibronic coupling is about 742 cm−1 at ωB97XD/6-31+G(d,p) (∼750 cm−1 at CCSD(T)/6-31+G(d,p)). The Pseudo-Jahn–Teller computed at CASSCF(2,2)-MRCAPF/SVP is about 154 cm−1 at SVP. Krisloff et al.64 investigated the unphysical ground states of the multireference averaged coupled-pair functional and reported that CASSCF(2,2)-MRCAPF can provide unphysical solution in the avoided crossing or conical intersection and the instabilities can be removed by employing larger complete active spaces (CAS). Unfortunately, the latter is computationally more demanding. The molecular orbitals involved in this distortion mechanism require further investigation. The energy level of the valence molecular orbitals of the D3d geometry is listed in Table S1† and agree with the literature.65 The HOMOs are localized on the metal and are nonbonding pure d orbitals. The LUMOs have high contribution on the metal and nitrogen and are antibonding orbitals (Fig. S1†). The HOMO (eg) and HOMO-1 (a1g) derived from the reduction of t2g in Oh. To validate the use of ωB97XD, various DFT and MP2 methods were employed and compared with CCSD(T). The data obtained shown in Table 1 suggest ωB97XD and LC-BLYP could perform quite well with respect to CCSD(T). Therefore, the ωB97XD/6-31+G(d,p) method and the lowest D3 geometry are considered for further analysis on nitro-/nitrito-pentaamminecobalt(III) linkage isomers.
We have extended this study to other hexammines complexes analogs of Ru(III), Cr(III) and Fe(II) which were reported to have either D3d or D3 symmetries.3,58,65–74 [Ru(NH3)6]3+, [Cr(NH3)6]3+ and [Fe(NH3)6]2+ ions can be considered as octahedral in which the d orbital of the transition metal splits in t2g and eg. For comparison, the most popular functional for transition metal B3LYP was employed with LanL2DZ basis set for all atoms on the D3d symmetry of the low-spin states [1A1g: (t2g)6 (eg)0 ] and [2T2g: (t2g)5 (eg)0] of [Co(NH3)6]3+ and [Ru(NH3)6]3+, and high spin states [4T2g: (t2g)3 (eg)0] and [5T2g: (t2g)4 (eg)2] of [Cr(NH3)6]3+ and [Fe(NH3)6]2+. The Pseudo-Jahn–Teller energies obtained at B3LYP/LanL2DZ for the symmetry breaking of D3d towards either D3 or S6 are given in Table 2. D3 and S6 are higher ranking epikernels and are found as minima for all transition metal complexes studied in the present paper, whereas the lower ranking epikernel C2h is found to be a saddle point [Tables 2 and 3]. The difference in metal-N bonds between D3 and S6 is negligible (∼0.001 A). These findings are in good agreement with the epikernel principle.63 The Pseudo-Jahn–Teller distortion energies are considerably more important in Co- and Cr-complexes than Ru- and Fe-complexes. The M–N bonds distances listed in Table 2 computed at B3LYP/LanL2DZ are close to that obtained at high level of calculations.61,67–71 For instance, the Co–N bond evaluated about 2.037 at B3LYP/LanL2DZ is approaching that obtained by Rotzinger61 at CASSF-MP2(10,10)/6-31G(d) and CASSF(10,10)/6-31G(d) levels, estimated about 2.014 and 2.034. The D3 [Fe(NH3)6]2+ geometry was also predicted as minima by Pierloot et al.70 in their study on the performance of BP86, B3LYP and PBE0 with CASPT2 in the estimation of the relative energy of the high and low spins states of [Fe(H2O)6]2+, [Fe(NH3)6]2+ and [Fe(bpy)3]2+. According to the authors, DFT even in cases it does not provide accurate energetics, still provides high quality structure.
| State in D3d | C2h | D3d | RE |
|---|---|---|---|
| Co[1A1g] | i70(au), i50(bg) | i160(a1u), i155(a2g), i77(eg), i36(eu) | −1.60 |
| Ru[2A1g] | i52(au), i48(bg) | i106(a2g), i98(a1u), i23(eg) | 0.05 |
| Cr[4A1g] | i140(au), i114(bg), i92(bg), i60(bu) | i138(a1u), i134(a2g), i69(eg), i43(eu) | −0.13 |
| Fe[5A1g] | i51(eu), | i80(a1u), i67(a2g) | −0.33 |
Contrary to D3 symmetry which symmetry was mentioned by many researchers,61,70 S6 symmetry is proposed in the present paper for the first time as probable minima for [Co(NH3)6]3+, [Cr(NH3)6]3+, [Ru(NH3)6]3+ and [Fe(NH3)6]2+ in gas phase. Tables S2 and S3† compare B3LYP, ωB97XD and OPBE results of [Co(NH)3]63+ computed with ccpVtz basis sets to check the basis set dependency. The OPBE functional was suggested by Swart et al.72 to provide accurate geometries for several transition metal compounds. The relative energies of D3, S6 and C2h with respect to D3d computed with OPBE method lay in between ωB97XD and B3LYP. D3 is slightly more stable than S6 at different levels of calculations. The EOMCCSD/6-31+G(d,p) calculations from D3 optimized geometry show three bands at 114, 129, and 162 nm assigned to respectively ligand to ligand transition (4t1u → 5a1g), and ligand to metal charge transfer transitions (1a1u → 5eg and 4t1u → 5eg) which lie close to the greatest absorbance experimental value of about 195 nm reported by Goursot et al.65 They argue that the ab initio energy values of these charge transfer transitions are largely dependent on the basis set chosen. A similar transition was observed in [Ru(NH3)6]3+ UV-vis spectrum also arising from t1u and eg.73,74 Daul et al.74 investigated the electronic structure of [Ru(NH3)6]3+ using extended Huckel molecular orbitals method and reported that ammonia are rotating freely to keep an octahedral site symmetry. The d–d transitions in octahedral [Co(NH3)6]3+ and [Ru(NH3)6]3+ complexes are forbidden due to the presence of a center of inversion following Laporte rule75 which states that allowed transitions in centro-symmetric molecules should involve change in parity between gerade and ungerade orbitals. In real world, [Co(NH3)6]3+ and [Ru(NH3)6]3+ geometries are not frozen but thermally vibrating. The oscillator strength of the symmetry-forbidden d–d transition of the octahedral transition metal complexes, [Co(NH3)6]3+ and [Ru(NH3)6]3+, was evaluated theoretically by Saito et al.67 using B3PW91 functional with the effective core potential/basis set combination SDB-cc-pVTZ. The authors found that the oscillator strengths of 1A1 → 1T1g is considerably larger than that of the 1A1g → 1T2g in both complexes and arises from H3N–M–NH3 antisymmetric bending vibration. The metal ligand charge transfer (MLCT) was found larger in the Ru-complex than in its counterpart Co-complex. Multiconfigurational self-consistent-field (MCSCF) approaches are more efficient way one can use for diagnosticate the pseudo-Janh–Teller effect in D3d–[M(NH3)6]3+ (with M = Co, Fe, Cr, Ru).76 Symmetry plays a crucial role in Physics and Chemistry because the properties of molecular systems under symmetry transformation govern selection rules for molecular spectroscopy and interactions.77
3.2 [Co(NH3)5NO2]2+ and [Co(NH3)5ONO]2+
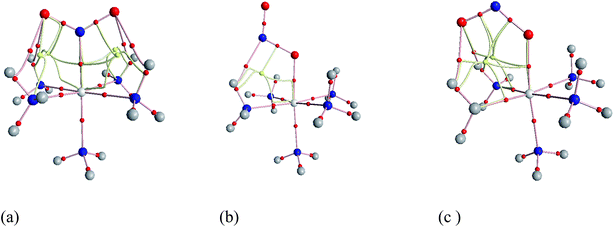
Geometries of [Co–NO2]2+ and [Co–ONO]2+ isomer compared to D3–[Co(NH3)6]3+. Fig. 3 shows the geometries of the ground states of O- and N-linked isomers and transition states computed at ωB97XD/6-31+G(d,p). A close inspection on the geometric structures shows that the substitution of ammonia by nitro or nitrito in [Co(NH3)6]3+ to form [Co(NH3)5NO2]2+ or [Co(NH3)5ONO2]2+ gives rise to the shrinking of Co–N bonds formed by NH3 positioned in the equatorial region with the concomitant elongation of the axial Co–NH3 bond. The NH3 ligands in the horizontal plane are apparently more strongly bound to Co than the axial NH3 ligands. In Co–NO2 (Fig. 3a), the bond length between Co and NO2 is 1.924 Å, which is 0.075 and 0.141 Å shorter than those in the Co–N bonds formed by equatorial and axial NH3. The Co–O bond length in the exo-ONO complex (Fig. 3b) is ∼0.03 Å shorter than that of the endo-ONO complex (Fig. 3c). The Co–NO2 and exo-Co–ONO geometries were also studied by Ciofini et al.33 at B3LYP/LanL2DZ level in order to clarify the intrinsic and environmental effects on the kinetic and thermodynamics of linkage isomerizasion in nitropentaamminecobalt(III) complex. The geometrical parameters of our Co–NO2 and Co–ONO complexes optimized at ωB97XD/6-31+G(d,p) are compared in Table S4† with B3LYP/Lanl2dz geometries obtained by Ciofini et al.33 and the available X-ray data.78,79 ωB97XD/6-31+G(d,p) performs better than B3LYP/Lanl2dz and the small difference observed between X-ray and the optimized geometries can be attributed to crystal environment.33 Boldyreva et al.80 found different geometrical parameters in the pentaamminenitrocobalt(III)chloride nitrate at 298 K and 150 K using X-ray spectroscopy characterized by Co–N, and N–O distances in the range of 1.959–1.989 and 1.206–1.222, and O–N–O and O–N–Co bonds angles of 123.1 and 117.8 degrees.
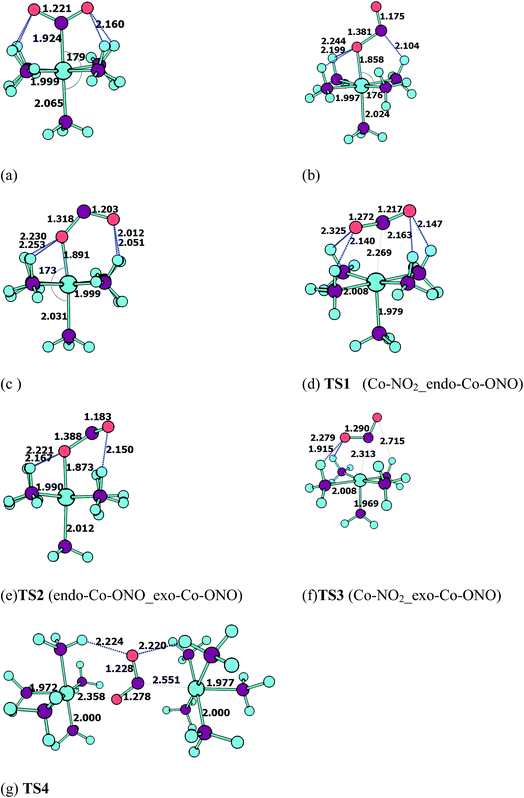 | ||
| Fig. 3 Equilibrium geometries (a–c) and transition states geometries (d–g) of Co(NH3)5NO22+ and Co(NH3)5ONO2+ isomers computed at ωB97XD/6-31+G(d,p). | ||
All these ωB97XD/6-31+G(d,p) optimized geometries comprise intramolecular hydrogen bonding (IHB) involving NO2 or ONO. The Co–NO2 complex has a O⋯H–N bond of 2.160 Å, which is 0.148 Å longer than the shortest O⋯H–N bond in the endo-Co–ONO complex. The exo-Co–ONO is characterized by two types of IHBs: N⋯H–N and O⋯H–N of 2.104 and 2.199–2.244 Å. The two N–O bonds that have the same bond lengths in the nitro-complex becomes unequal when the nitro is orientated in nitrito, and the difference between the bond lengths increases from the endo-nitrito to exo-nitrito complex, showing a decrease in the electron resonance character of the ONO atoms group. Electron delocalization around ONO was reported81 to enhance hydrogen bonds.
We have computed the IR spectra of nitro and nitrito complexes at B3LYP/6-31+G(d,p). Our calculations show a clear difference in vibrational frequencies between NO2 and ONO isomers in the region between 700–1700 cm−1 (Fig. 4). The vibrational modes which characterize the NO2 and ONO in Co–NO2 and Co–ONO complexes are listed in Table 4 and shown in Fig. 5. The deformation NO2 and ONO modes are well reproduced whereas our asymmetric N–O stretching modes are overestimated referring to Ciofini findings and experimental data.33
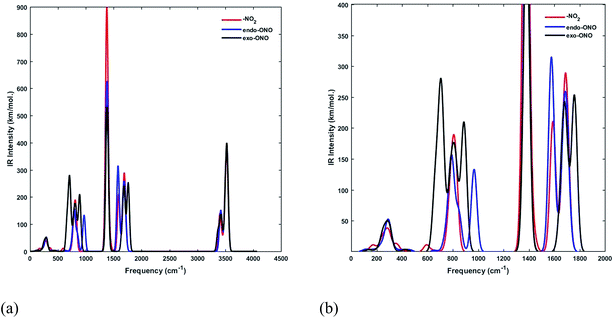 | ||
| Fig. 4 Superimposed IR spectra of Co–NO2 and Co–ONO complexes computed using a scaling factor of 0.9632 at B3LYP/6-31+G(d,p). | ||
| Co–NO2 | Endo-Co | Exo-Co–ONO | Assignment |
|---|---|---|---|
| a Theoretical values taken from ref. 33a.b Experimental data taken from ref. 33b. | |||
| 820(757a, 825b) | 880 (718a, 791b) | NO2 and ONO deformation | |
| 1367(1257a, 1315b) | 968 | Sym. NO2 stretching + NH3 defor. | |
| 1590(1466a, 1440b) | 1578 | 1759(1586a, 1460b) | Asym. NO2 and ONO stretching |
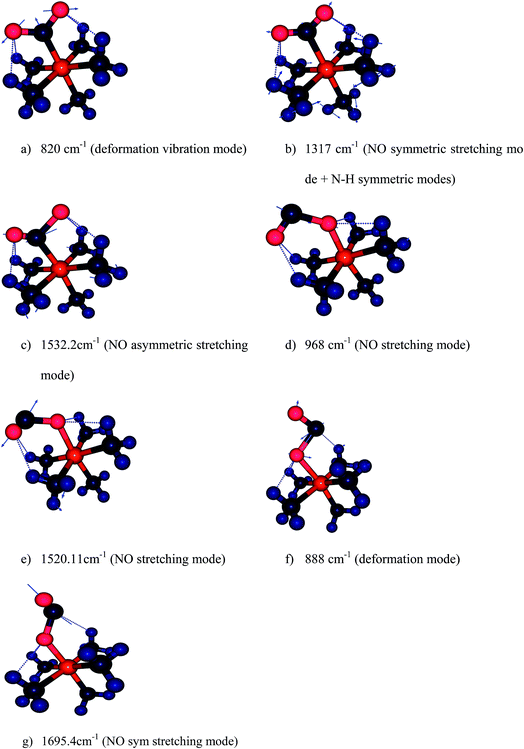 | ||
| Fig. 5 Harmonic vibration modes of NO2 and ONO in Co–NO2 (a–c), endo-Co–ONO (d–e) and exo-Co–ONO (f–g) computed at B3LYP/6-31+G(d,p). | ||
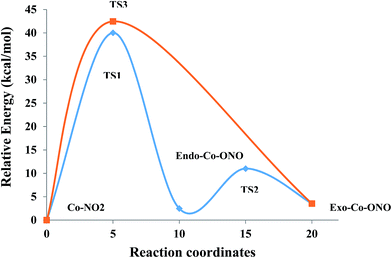
Transition states. Co–NO2 → endo-Co–ONO → exo-Co–ONO reaction mechanism describes the sequence of the elementary transformation of Co–NO2 complex in exo-Co–ONO via the endo-Co–ONO complex. TS1 (i569 cm−1 computed at ωB97XD/6-31+G(d,p)) and TS2 (i210 cm−1 ωB97XD/6-31+G(d,p)) depicted in Fig. 3d and e are predicted sequential transition states in this reaction path by intrinsic reaction coordinate (IRC) method. TS1 has a NO2 moiety detached from Co; the Co–N bond length is estimated to be about 2.27 Å, but still binds to four NH3 ligands through O⋯H–N hydrogen bonds ranging between 2.14 and 2.32 Å at ωB97XD/6-31+G(d,p). The TS1 geometry was reported as first-order saddle point with one imaginary vibrational mode located at i385 cm−1at B3LYP/LanL2DZ.33 Its geometrical parameters geometry computed at ωB97XD/6-31+G(d,p) and B3LYP/LanL2DZ are detailed in Table S4.† This transition state is difficult to detect experimentally.15 The structural geometry of TS2 (Co–O bond of 1.87 Å) is similar to that of exo-Co–ONO but differs with exo-Co-ONO by the orientation of N–O bonds, which lies in the horizontal plane to form N–O⋯H hydrogen bonds of 2.15 Å with ammonia computed at ωB97XD/6-31+G(d,p). Another transition state similar to TS1, denoted as TS3 (i506 cm−1) (Fig. 3f) was observed between Co–NO2 and exo-Co-ONO and was characterized by two O⋯H–N hydrogen bonds of 1.91 and 2.28 Å carried out at ωB97XD/6-31+G(d,p). The N–O (1.29 E) and N–Co (2.31 E) bonds in TS3 are slightly longer than that of TS1. The π-bonding coordination to the central metal observed in these activated complexes (TS1, TS3) was also suggested by Balt et al.,82 but the authors did not provide the geometries of transition states. The imaginary vibrational modes of these transitions states are shown in Fig. S4.† The displacements of atoms displayed in Fig. S4† indicate that the imaginary modes of TS1 and TS2 change the Co–O–N–O torsion angle and O–N–O bond angle, whereas in TS3, the imaginary frequency attempts to rotate NO2 atoms group. The change in TS3 between Co–NO2 and exo-Co-ONO is mediated when the nitro atoms group rotates such that N or O can form the Co–N or Co–O bond, respectively. TS4 represented in Fig. 3g (i95 cm−1) was proposed in ref. 83 and 84 as the activated complex to explain the nitro and nitrito interconversion in [Co(NH3)5NO2]NO3Cl through the intermolecular process. In TS4, two groups of Co(NH3)53+ are held together by the nitro and nitrito ligands through O⋯H–N hydrogen bonds of 2.220 and 2.224 Å, respectively.
Origin of mechanical motion in solids. The electronic spatial extents85 of [Co(NH3)5ONO2]2+ and [Co(NH3)5NO2]2+ were computed to gauge the increase in the size of those cations upon intramolecular conversion. The exo-Co-ONO has a larger electronic spatial extent than Co–NO2: these are estimated to be about 1556 and 1411 a.u., respectively (1451 for endo-Co–ONO). The effective size of the exo-Co-ONO isomer was evaluated to be 1.2 times greater than that of the NO2–Co.16,17 According to Boldyreva,24 the former is expected to play an important role in increasing the local pressure near the product in nitro and nitrito interconversion reaction in solids, and can be at the origin of the mechanical motion observed in crystals. Thus, it is important to first understand this isomerization reaction as this constitutes the fundamental process that triggers the photo-salient phenomenon in [Co(NH3)5NO2]NO3Cl.
Relative energy. Table 5 compares the relative energies of exo-Co-ONO and endo-Co-ONO complexes and their transitions states (TS1 and TS2) with respect to the Co–NO2 isomer at ωB97XD/6-31+G(d,p). According to the data listed in Table 5, the Co–NO2 complex is 1.32 and 3.39 kcal mol−1 lower than endo-Co-ONO and exo-Co-ONO complexes, respectively (1.12 and 2.00 kcal mol−1 at CCSD(T)/6-31G(d)) on the potential energy surface (PES). Noted that the relative energy of the exo-Co-ONO computed by Ciofini et al.33 is about 3.9 kcal mol−1 at B3LYP/LanL2DZ including ZPE corrections in gas phase. Thus, the nitro form is predicted to be the lowest isomer. The fact that the ωB97XD/6-31+G(d,p) energy ordering of isomers is reconfirmed by CCSD(T) (Table S5†) shows that the ωB97XD functional is an alternative method at an affordable cost for studying these linkage isomers. The dispersion energies in NO2–Co, endo-Co-ONO, and exo-Co-ONO isomers computed using dispersion-corrected B3LYP at 6-31+G(d,p) amount to −26.25, −25.43 and −24.95 kcal mol−1, respectively. The zero-order regular approximation (ZORA), a two-component form of the fully-relativistic Dirac equation used along with B3LYP at SVP, also indicates that Co–NO2 is the most stable isomer, followed by endo-Co-ONO. The difference in relative energies obtained using non-relativistic and relativistic method is small, ranging from 0.13 to 0.5 kcal mol−1.
| gs, TS | ΔE | ΔH | ΔG | ΔS | H–L |
|---|---|---|---|---|---|
| Co–NO2 | 0.00 | 0.00 | 0.00 | 0.00 | 8.68 |
| Endo-Co–ONO | 1.32 | 0.90 | 2.47 | −5.25 | 7.92 |
| Exo-Co–ONO | 3.39 | 3.58 | 3.53 | 0.17 | 7.64 |
| TS1 | 39.48 | 39.35 | 40.01 | −2.22 | — |
| TS2 | 11.00 | 10.95 | 11.00 | −0.16 | — |
| TS3 | 41.87 | 41.77 | 42.46 | −2.30 | — |
Binding energy. The binding energies of NH3 and NO2− to the metal in Co-complexes and the formation energy (FE) of complexes were obtained as electronic energy (E) difference between the most stable geometries of the products and reactants at ωB97XD/6-31+G(d,p) from the following equations:
| Co(NH3)3+5 + NH3 → Co(NH3)3+6 | (2) |
| Co(NH3)3+5 + NO−2 → Co(NH3)5NO2+2 | (3) |
| Co(NH3)3+6 + NO−2 → Co(NH3)5NO2+2 + NH3 | (4) |
| FE = E(Co(NH3)5NO22+) + E(NH3) − E(Co(NH3)63+) − ENO2− | (5) |
The heat of formation of Co(NH3)5NO22+ at 298 K calculated by means of the isodesmic reaction (eqn (5)) is −280.55 kcal mol−1. The binding energies of NO2 and NH3 to the metal Co were found to be about −343.49 and −61.70 kcal mol−1, showing that NO2 binds more strongly to Co than NH3 does. Thus, the Co(NH3)5NO22+ complex appears to be thermodynamically more stable than Co(NH3)63+.
HOMO–LUMO & transition states. In conceptual DFT formalism, the HOMO–LUMO gap energy is related to the kinetic stability. The NO2–Co complex in Table 4 has the largest HOMO–LUMO gap of 8.68 eV, followed by endo-Co-ONO with a HOMO–LUMO gap energy of 7.92 eV. The HOMO–LUMO of exo-Co-ONO is 0.28 eV lower than that of endo-Co-ONO at ωB97XD/6-31+G(d,p). Therefore, by considering the HOMO–LUMO gap energy, Co–NO2 appears to be kinetically more stable than ONO–Co complexes. For this purpose, two trajectories involving TS1 and TS2 transitions states were investigated by exploring the ground state potential energy surface of [Co(NH3)5NO2]2+: the trajectory from the Co–NO2 to endo-Co-ONO complex and that from the endo-Co-ONO to exo-Co-ONO complex. The mechanistic study of the intramolecular conversion reveals that the energy barrier for the intramolecular conversion of endo-Co-ONO in Co–NO2 (∼39 kcal mol−1) is 3.5 times larger than that of the interconversion between endo-Co-ONO and exo-Co-ONO. Our TS1 activation energy barrier carried out at ωB97XD/6-31+G(d,p) is 9 kcal mol−1 above the activation energies computed at B3LYP/LanL2DZ (5 kcal mol−1 at B3LYP/LanL2DZp) by Ciofini et al.33
Relative free energies. The relative free energies, enthalpies and entropies of the ground and transition states of the Co(NH3)5NO22+ isomers calculated at the ωB97XD/6-31+G(d,p) theory level provided in Table 5 suggest that a direct transformation from nitro to exo-Co-ONO required more energy than that required for the transformation via the intermediate endo-Co-ONO. The energy difference between the activated complexes TS1 and TS3 is about 2.39 kcal mol−1. endo-Co-ONO appears to be more structured (low relative entropy) than Co–NO2 and exo-Co-ONO. The entropic energy differences can be associated with the strength of the hydrogen bonding in these systems. Overall, the entropy differences in these complexes are quite small ranging from 0.2 to 5 cal mol−1 and do not significantly affect the relative stabilities of Co–NO2 and Co–ONO complexes and their transition states. Because of the large energy of the TS2 transition-state, the molecular conversion between nitro and endo-nitrito is predicted to be the slow step of the reaction and may determine the rate of the intramolecular conversion between the Co–NO2 and exo-Co-ONO complexes. The most likely reaction mechanism involves starting from Co–NO2 and then transforming into the endo-Co-ONO intermediate and finally into exo-Co-ONO:
| Co(NH3)5NO22+ → [Co(NH3)5NO22+]≠ (TS1) → endo-Co(NH3)5ONO2+ | (6) |
| endo-Co(NH3)5ONO2+→[Co(NH3)5NO22+]≠ (TS2) → exo-Co(NH3)5ONO2+ | (7) |
The pathway (1) proceeds through the higher-energy transition state (TS1), but yields the lower-energy nitrito conformer (endo-Co-ONO) (Fig. 6 and S5†). The second pathway (2) leads through the lower-energy transition (TS2), but yields a relatively higher-energy nitrito conformer (exo-Co-ONO). Therefore, the pathways (1) and (2) of the interconversion of Co–NO2 in exo-Co-ONO can be assumed to be respectively, the thermodynamically-favored and the kinetically-favored pathways (Fig. 6). TS4 and chelate structure (Fig. 1e) were also proposed as possible transition states.11 Our calculations show that the former (TS4, i95 cm−1) requires ∼233 kcal mol−1, while the chelate structure possesses several imaginary frequencies and relaxes towards TS2. However, the possibility of the reaction occurring via the TS4 state at standard conditions in gas phase is very low as the activation energy is too high. The reorientation of the NO2 ligand slightly changes the magnitude of the dipole moments from 10D in Co–NO2 to 11D in exo-Co–ONO (10D in endo-Co–ONO). With regards to the relative stabilities of linkage isomers, our results agree with previously reported experimental results,17,18 and these can justify the reorientation of the NO2 moiety in the [Co(NH3)5NO2]ClNO3 isomer upon UV irradiation to form the exo-[Co(NH3)5ONO]ClNO3 isomer and the slow conversion of the less stable exo-[Co(NH3)5ONO]ClNO3 complex into [Co(NH3)5NO2]ClNO3 in the dark. The fast conversion of endo-Co–ONO in the exo-Co–ONO conformer explains why the former has never been observed experimentally.
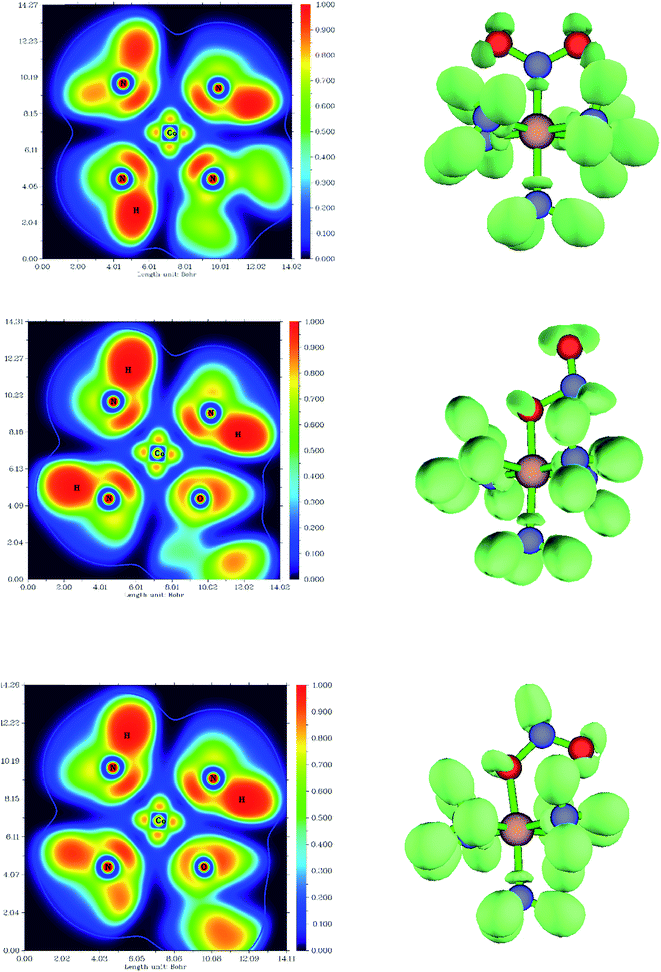
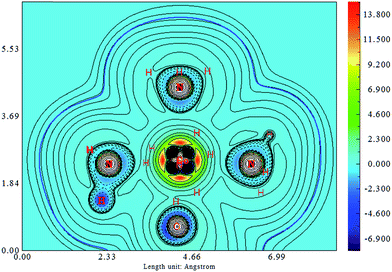
The difference in the electronic structure between Co–NO2, endo-Co–ONO and exo-Co–ONO is shown in Table S6.† The N–O Mayer bond order and electrons occupancies of Co–NO2 and Co–ONO complexes are given in Table 7. The two N–O bonds in nitro have a 1.50 Mayer bond order, whereas in endo-Co–ONO, they are about 1.16 and 1.67 and are nearly 1.91 and 0.98 in exo-Co–ONO. These computed bond orders show that the electron density charge is delocalized over the two N–O bonds in Co–NO2 giving both of them a partial double bond character, while the electron delocalization is diminishing in Co–ONO. The electronic density delocalization over N–O bonds diminishes the most when nitro is converted in exo-Co–ONO. These findings suggest that the electron resonance in these complexes assists intramolecular hydrogen bonds and can justify the ranking relative stabilities of isomers. The electrostatic attraction between the Co and O atoms was proposed as driving force of the linkage isomerization due to the fact that the O atoms are rich in electrons than N in NO2 ligand.91,92 Fig. 8 shows the ELF isosurfaces of nitro and nitrito complexes and their cut planes. The topologies of the molecular electron densities are similar, but a small difference can be noticed around ONO and NO2 (Table S7†). The N–H bond is of polar covalent type, while the bonds formed between Co and NH3 are of dative type, as indicated by the orientation of the lone pairs of electrons located on N. The ELF and electron density Laplacian cut planes (Fig. 8 and 9) clearly indicate the lone pair region of nitrogen and electron deficiency in Co that enable the NH3 donor ligand to form a dative bond.
| Bonds | Endo | Exo | Nitro |
|---|---|---|---|
| a O bound to Co in endo and exo-nitrito complexes.b LPs of N of nitro or nitrito. | |||
| H–N | 0.95(1.99) | 0.95 (1.99) | 0.96(1.99) |
| H3N–Co | 0.66(1.97) | 0.66 (1.97) | 0.67(1.97) |
| Co–O | 0.68(1.93) | 0.83 (1.92) | — |
| N–Co | — | — | 0.51(1.93) |
| O–N | 1.67(1.99, 1.99) | 1.91(2.00, 1.99) | 1.50(1.99, 1.99) |
| N–Oa | 1.16(1.98) | 0.98(1.99) | 1.50(1.99) |
| LP (O) | (1.97, 1.85) | (1.99, 1.82) | (1.97, 1.84, 1.44) |
| LP(O)a | (1.92, 1.70) | (1.93, 1.77) | (1.97, 1.84) |
| LP(N)b | (1.91) | (1.91) | — |
| LP(Co) | (1.98, 1.97, 1.97) | (1.97, 1.97, 1.97) | (1.98, 1.94, 1.97) |
4. Conclusion
The nitro–nitrito isomerization in Co(NH3)5NO22+ linkage isomers was investigated from a theoretical perspective using quantum chemical calculations at ωB97XD/6-31+G(d,p), emphasizing on the structural, thermodynamic, and chemical bonding properties of the isomers. This isomerization is fundamental for a better understanding of the photo-salient effect in [(NH3)5CoNO2]ClNO3. The Bader theory based on the partitioning of electron density, the electron localization function, and natural bond orbitals were used for chemical bonding analysis. Our computational study led to the following conclusions:(a) The nitrito/exo-nitrito isomerization reaction is predicted to occur via the following reaction pathway:
| Co(NH3)5NO22+ → [Co(NH3)5NO22+]≠ (TS1) → endo-Co(NH3)5ONO2+ | (8) |
(b) The intramolecular conversion on the ground-state potential energy surface of Co–NO2 between endo-Co–ONO and exo-Co–ONO complexes is kinetically controlled and that leading to the Co–NO2 complex formation is thermodynamically controlled.
(c) O⋯H–N and N⋯H–N intramolecular hydrogen bonds, orientation of the atoms of the ONO group, and the difference in Co–N and Co–O bond energies are identified as key factors determining the relative stabilities of the Co–NO2 and Co–ONO linkage isomers.
(d) Co(NH3)63+ is less stable compared to Co(NH3)5NO22+ and undergoes a slight geometry distortion from D3d to D3 characterized by a PJTE of 741 cm−1 at ωB97XD/6-31+G(d,p) (750 cm−1 at CCSD(T)/6-31+G(d,p)). It is worth noting that the hydrogen can freely rotate to keep the high octahedral symmetry.
The photo-isomerization of the [Co(NH3)5NO2]2+ complex is currently under investigation in our lab to determine the role of conical intersection and excited states in the UV-initiated intramolecular conversion of [Co(NH3)5NO2]NO3Cl.
Conflicts of interest
The authors declare that they have no conflict of interest.Acknowledgements
This research was supported by Korea Research Fellowship program and grants from the Basic Science Research Program funded by the Ministry of Science, ICT and Future Planning through the National Research Foundation of Korea (NRF-2015H1D3A1062502, NRF-2015R1C1A1A02036670, NRF-2015R1A2A2A01006445). JTM thanks Prof. Carol Parish for the support and permissions to use the facilities and computing resources of the University of Richmond and Dr Harry Ramanantoanina from the Paul Scherrer Institute in Switzerland for helpful discussion.References
- K. Czarnek, S. Terpiłowska and A. K. Siwicki, Cent. Eur. J. Immunol., 2015, 40, 236 CrossRef CAS PubMed.
- A. Werner, Über strukturisomere Salze der Rhodanwasserstoffsäure und der salpetrigen Säure, Ber. Dtsch. Chem. Ges., 1907, 40, 765 CrossRef CAS.
- H. Hiroshi Sakiyama, Y. Ishiyama and H. Sugawara, Spectrosc. Lett., 2017, 50, 111 CrossRef.
- N. N. Greenwood, Spectroscopic properties of inorganic and organometallic compounds, Burlington House, London, 1970, vol. 3, p. 501 Search PubMed.
- R. P. Sharma, R. Bala, R. Sharma and V. Ferreti, Inorg. Chim. Acta, 2005, 358, 3457 CrossRef CAS.
- R. P. Sharma, R. Bala, R. Sharma, K. K. Bhasin and R. K. Chadha, J. Coord. Chem., 2004, 57, 313 CrossRef CAS.
- S. Rudisser and I. Tinoco Jr, J. Mol. Biol., 2000, 295, 1211 CrossRef CAS PubMed.
- http://www.nobelprize.org/nobel_prizes/chemistry/laureates/1913/.
- D. A. Buckingham, I. I. Creaser and A. M. Sargeson, Inorg. Chem., 1970, 9, 655 CrossRef CAS.
- A. A. Tishkov, U. Schmidhammer, S. Roth, E. Riedle and H. Mayr, Angew. Chem., Int. Ed., 2005, 44, 4623 CrossRef CAS PubMed.
- F. Basolo and G. S. Hammaker, Inorg. Chem., 1962, 1, 1 CrossRef CAS.
- C. Buda, A. B. Kazi, A. Dinescu and T. R. Cundari, J. Chem. Inf. Model., 2005, 45, 965 CrossRef CAS PubMed.
- A. M. Heyns and D. de Waal, Spectrochim. Acta, Part A, 1989, 45, 905 CrossRef.
- O. Bortin, Acta Chem. Scand., 1968, 22, 2890 CrossRef CAS.
- M. Kubota and S. Ohba, Acta Crystallogr., 1992, B48, 627 CAS.
- H. Hohman, J. Chem. Educ., 1974, 51, 553 CrossRef.
- R. G. Pearson, P. M. Henry, J. G. Bergmann and F. Basolo, J. Am. Chem. Soc., 1954, 76, 5920 CrossRef CAS.
- I. Grenthe and E. Nordin, Inorg. Chem., 1979, 18, 1869 CrossRef CAS.
- V. Balzani, R. Ballardi, N. Sabbatin and L. Moggi, Inorg. Chem., 1968, 7, 1398 CrossRef CAS.
- D. A. Johnson and K. A. Pashman, Inorg. Nucl. Chem. Lett., 1975, 11, 23 CrossRef CAS.
- B. A. Zakharov, A. S. Marchuk and E. V. Boldyreva, CrystEngComm, 2015, 17, 8812 RSC.
- P. Naumov, S. Chandra Sahoo, B. A. Zakharov and E. V. Boldyreva, Dynamic Single Crystals: Kinematic Analysis of Photoinduced Crystal Jumping (The Photosalient Effect), Angew. Chem., Int. Ed., 2013, 52, 9990 CrossRef CAS PubMed.
- S. S. Chandra, M. K. Panda, N. K. Nath and P. Naumov, J. Am. Chem. Soc., 2013, 135, 12241 CrossRef PubMed.
- E. V. Boldyreva, A. A. Sidelnikov and N. Z. Lyakhov, Thermochim. Acta, 1985, 92, 109 CrossRef CAS.
- E. V. Boldyreva, Izv.Sib.Otd.Akad. Nauk USSR, Ser. chim. nauk, 1982, ch. 5, pp. 18–27 Search PubMed.
- M. Mares, D. A. Palmer and H. Kelm, Inorg. Chim. Acta, 1978, 27, 153 CrossRef CAS.
- W. G. Jackson, G. A. Lawrance, P. A. Lay and A. M. Sagerson, J. Chem. Educ., 1981, 58, 734 CrossRef CAS.
- V. Balzani, R. Ballardini, N. Sabbatini and L. Moggi, Inorg. Chem., 1968, 7, 1398 CrossRef CAS.
- W. H. Hohman, J. Chem. Educ., 1974, 51, 553 CrossRef CAS.
- D. Shriver, M. Weller, T. Overton, J. Rourke and F. Armstrong, Inorganic chemistry, Kindle Edition, 6th edn, 1995, p. 218 Search PubMed.
- G. Miessler, P. J. Fischer and D. A. Tarr, Inorganic Chemistry, Pearson, 5th edn, 2012, p. 333 Search PubMed.
- G. B. Kauffman, Coord. Chem. Rev., 1973, 11, 161 CrossRef CAS.
- (a) I. Ciofini and C. Adamo, J. Phys. Chem. A, 2001, 105, 1086 CrossRef CAS; (b) R. B. Penland, T. J. Lane and J. V. Quagliano, J. Am. Chem. Soc., 1956, 78, 887 CrossRef CAS.
- M. Behl and A. Lendlein, Soft Matter, 2007, 3, 58 RSC.
- (a) R. Medishetty, A. Husain, Z. Bai, T. Runčevski, R. E. Dinnebier, P. Naumov and J. J. Vittal, Angew. Chem., Int. Ed., 2014, 53, 5907 CrossRef CAS PubMed; (b) http://io9.gizmodo.com/how-internal-explosions-make-these-crystals-leap-around-1690643855.
- J. M. Cole, Chem. Soc. Rev., 2004, 33, 501 RSC.
- M. R. Warren, Photocrystallographic studies into linkage isomerism, PhD thesis, Chemistry, University of Bath, UK, 2011.
- F. A. Cotton and G. Wilkinson, Advanced Inorganic Chemistry, Wiley, New York, 5th edn, 1988, p. 731 Search PubMed.
- J. Kozhukh, M. A. Minier and S. J. Lippard, Inorg. Chem., 2015, 54, 418 CrossRef CAS PubMed.
- N. N. Greenwood and A. Earnshaw, Chemistry of the Elements, Pergamon Press Ltd, Oxford, England, 1984 Search PubMed.
- G. C. Bond, Phtinzm Mutak Rw., 2000, 44, 14C155 Search PubMed.
- J. Austchbach, J. Chem. Phys., 2012, 136, 150902 CrossRef PubMed.
- J. T. Muya, A. Ceulemans, G. Gopakumar and C. Parish, J. Phys. Chem. A, 2015, 119, 2015 Search PubMed.
- B. Richard, Atoms in Molecules: A Quantum Theory, Oxford Univ. Press, USA, 1994 Search PubMed.
- A. D. Becke and K. E. Edgecombe, J. Chem. Phys., 1990, 92, 5397 CrossRef CAS.
- A. Savin, O. Jepsen, J. Flad, O. K. Andersen, H. Preuss and H. G. von Schnering, Angew. Chem., Int. Ed. Engl., 1992, 31, 187 CrossRef.
- F. Weinhold and C. R. Landis, Discovering Chemistry with Natural Bond Orbitals, John Wiley & Sons, New Jersey, Hoboken, 2012, p. 319 Search PubMed.
- E. D. Glendening, C. R. Landis and F. Weinhold, J. Comput. Chem., 2013, 34, 1429 CrossRef CAS PubMed.
- M. J. Frisch, G. W. Trucks and H. B. Schlegel, et al., Gaussian 09, Revision D.01, Gaussian, Inc., Wallingford CT, 2009 Search PubMed.
- F. Neese, The ORCA program system, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 73 CrossRef CAS.
- F. Furche, R. Ahlrichs, C. Hättig, W. Klopper, M. Sierka and F. Weigend, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2014, 4, 91 CrossRef CAS.
- ADF, SCM, Theoretical Chemistry, Vrije Universiteit, Amsterdam, The Netherlands, 2017, http://www.scm.com Search PubMed.
- R. Dennington, T. Keith and J. Millam, GaussView, Version 5, Semichem Inc., Shawnee Mission, KS, 2009 Search PubMed.
- http://www.chemcraftprog.com.
- Jmol: an open-source Java viewer for chemical structures in 3D, http://www.jmol.org/.
- (a) F. Biegler-Konig, J. Schonbohm and D. Bayles, AIM2000 program A program to Analyze and visualize atoms in molecules, J. Comput. Chem., 2001, 22, 545 CrossRef; (b) AIM2000 homepage and software from, http://gauss.fh-bielefeld.de/aim2000.
- T. Lu and F. Chen, Multiwfn: A Multifunctional wavefunction analyzer, J. Comput. Chem., 2012, 33, 580 CrossRef CAS PubMed.
- D. W. Meek and J. A. Ibers, Inorg. Chem., 1970, 9, 465 CrossRef CAS.
- M. D. Newton, J. Phys. Chem., 1991, 95, 30 CrossRef CAS.
- B. S. Brunschwig, C. Creutz, D. H. Macartney, T.-K. Sham and N. Sutin, Faraday Discuss. Chem. Soc., 1982, 74, 113 RSC.
- F. P. Rotzinger, J. Chem. Theory Comput., 2009, 5, 1061 CrossRef CAS PubMed.
- J. T. Muya, T. Sato, M. T. Nguyen and A. Ceulemans, Chem. Phys. Lett., 2012, 543, 111 CrossRef CAS.
- A. Ceulemans, Group Theory Applied to Chemistry, Springer, 2013 Search PubMed.
- D. B. Krisloff, V. B. Oyeyemi, F. Libisch and E. A. Carter, J. Chem. Phys., 2014, 140, 024102 CrossRef PubMed.
- A. Goursot and E. Penigault, Chem. Phys., 1979, 38, 11–19 CrossRef CAS.
- B. S. Brunschwig, C. Creutz, D. H. Macartney, T.-K. Sham and N. Sutin, Faraday Discuss. Chem. Soc., 1982, 74, 113 RSC.
- K. Saito, Y. Eishiro, Y. Nakao, H. Sato and S. Sakaki, Inorg. Chem., 2012, 51, 2785 CrossRef CAS PubMed.
- H. C. Stynes and J. A. Ibers, Inorg. Chem., 1971, 10, 2304 CrossRef CAS.
- B. F. G. Johnson, Inorganic Chemistry of the transition elements, 1972, vol. 2, p. 517 Search PubMed.
- K. Pierloot and S. Vancoillie, J. Chem. Phys., 2006, 125, 124303 CrossRef PubMed.
- D. A. Fletcher, R. F. McMeeking and D. Parking, J. Chem. Inf. Comput. Sci., 1996, 36, 746 CrossRef CAS.
- M. Swart, J. Chem. Theory Comput., 2008, 4, 2057 CrossRef CAS PubMed.
- P. Castillo-Villalon, J. Ramırez, M.-J. Peltre, C. Louis and P. Massiani, J. Phys. Chem. B, 2003, 107, 8547 Search PubMed.
- C. Daul and A. Goursot, Inorg. Chem., 1985, 24, 3554 CrossRef CAS.
- O. Laporte and W. F. Meggers, J. Opt. Soc. Am., 1925, 11, 459 CrossRef CAS.
- M. J. Bearpark, L. Blancafort and M. A. Robb, Mol. Phys., 2002, 100, 1735 CrossRef CAS.
- D. J. Gross, Proc. Natl. Acad. Sci. U. S. A., 1996, 93, 14256 CrossRef CAS.
- F. A. Cotton and W. T. Edwards, Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem., 1968, 24, 474 CrossRef CAS.
- I. Grenthe and E. Nordin, Inorg. Chem., 1979, 18, 1869 CrossRef CAS.
- E. V. Boldyreva, J. Kivikoski and J. A. K. Howard, Acta Crystallogr., 1997, C53, 526 CAS.
- P. Gilli, V. Bertolasi, V. Ferretti and G. Gilli, J. Am. Chem. Soc., 2000, 122, 10405 CrossRef CAS.
- S. Balt, M. W. G. De Bolster, C. J. van Garderen, A. M. van Herk, K. R. Lammers and E. G. van der Velde, Inorg. Chim. Acta, 1985, 106, 43 CrossRef CAS.
- W. L. Jolly, The Synthesis and Characterization of Inorganic Compounds, 1970 Search PubMed.
- H. Leonhardt and A. Weller, Phys. Chem., 1961, 29, 277 CAS.
- H. Sabzyan and F. Taghavi, Phys. Chem. Res., 2014, 2, 41 Search PubMed.
- R. F. W. Bader, Chem. Rev., 1991, 91, 893 CrossRef CAS.
- M. Daszkiewicz, CrystEngComm, 2013, 15, 10427 RSC.
- X. Yu, H. Zhu and Y. Zeng, Int. J. Quantum Chem., 2016, 116, 1244 CrossRef CAS.
- O. E. Kasende, J. T. Muya, V. P. Nziko and S. Scheiner, J. Mol. Model., 2016, 22, 77 CrossRef PubMed.
- O. E. Kasende, A. Matondo, J. T. Muya and S. Scheiner, Int. J. Quantum Chem., 2017, 117, 157 CrossRef CAS.
- T. Kikkawa, S. Ohba, Y. Saito, S. Kamata and S. Iwata, Acta Crystallogr., 1987, B43, 83 CAS.
- M. Okuda, S. Ohba, Y. Saito, T. Ito and I. Shibuya, Acta Crystallogr., 1990, B46, 343 CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c7ra11603a |
| This journal is © The Royal Society of Chemistry 2018 |