Nanofluidic transport through humic acid modified graphene oxide nanochannels†
Tukhar Jyoti
Konch
a,
Raj Kumar
Gogoi
 a,
Abhijit
Gogoi
a,
Abhijit
Gogoi
 b,
Kundan
Saha
a,
Jumi
Deka
a,
K. Anki
Reddy
c and
Kalyan
Raidongia
b,
Kundan
Saha
a,
Jumi
Deka
a,
K. Anki
Reddy
c and
Kalyan
Raidongia
 *a
*a
aDepartment of Chemistry, Indian Institute of Technology Guwahati, Guwahati, Assam 781039, India. E-mail: k.raidongia@iitg.ernet.in
bDepartment of Mechanical Engineering, Indian Institute of Technology, Guwahati, Assam 781039, India
cDepartment of Chemical Engineering, Indian Institute of Technology, Guwahati, Assam 781039, India
First published on 28th June 2018
Abstract
The chemical similarity of graphene oxide (GO) and humic acid has been exploited to fine-tune the ionic and molecular transport properties of a lamellar GO membrane. Introduction of humic acid (in 10, 15 and 20%) is found to improve the nanofluidic transport characteristics, such as ionic mobility, molecular selectivity, diffusivity and permeability, of the GO membrane. Remarkably, the membrane prepared with 15% humic acid displayed superior proton mobility (μH = 1.04 × 10−4 cm2 V−1 s−1), in-plane diffusivity (D = 4.8 × 10−6 cm2 s−1), and cross-plane permeability (PL = 2.03 × 10−4 mm g cm−2 s−1 bar−1) to the pure GO and other composite membranes. The favorable nanofluidic characteristics of the 15% membrane are attributed to the larger effective heights of the 2D nanochannels, derived from the onset point of the surface charge governed ionic conductivity of the membranes. The activation energy of proton transport (∼0.07 to 0.1 eV) confirmed the occurrence of a Grotthuss-like hopping mechanism in all the GO–HA membranes. Introduction of humic acid into two-dimensional GO channels also improved the solution stability and mechanical robustness of the pristine GO membrane. The lamellar GO–HA membranes were also found to be suitable for energy harvesting applications such as direct methanol fuel cells and reverse electrodialysis. Remarkably, even after 72 hours exposure to electrolyte solutions, open circuit potentials up to 0.05 V, 0.21 V, and 0.12 V were found for the 10, 15, and 20% membranes, respectively.
Introduction
Fabrication of well-defined nanochannels in the sub-nanometer size regime is a matter of great importance as these channels provide access to interesting phenomena associated with biological nanochannels and promise technological breakthroughs in areas like water treatment, energy harvesting and molecular sieving.1–4 The major bottleneck in the study of sub-nanometer-size fluids is the limitation in device fabrication techniques. The traditional methods employed for this purpose are either of low-throughput or require highly expensive and sophisticated instrumentation.5–7 In order to overcome these shortcomings, molecularly thin nanochannels were prepared by self-assembling exfoliated layers of two-dimensional (2D) materials.8–14 The space between the layers of reconstructed-layered-materials forms a percolated network of two-dimensional nanochannels, providing a new platform to study ionic/molecular transport under sub-nanometer confinement. Thanks to the abundance of layered materials, and ease of preparation and scalability, reconstructed lamellar membranes also promise practical applications in areas like water desalination, molecular sieving, and energy storage and harvesting.15,16Even though layered material based lamellar membranes have several advantages over polymer and inorganic membranes, they are not free from drawbacks. The sub-nanometer-size pores of lamellar membranes that facilitate unprecedented ionic/molecular selectivity also impede molecular permeability. The natural choice to overcome the problem of low permeability is to increase the channels’ heights by applying spacers between the sheets.17–19 However, application of incompatible inert spacers could sacrifice the selectivity and robustness of the pristine membranes. Here, we have explored the possibility of tuning the transport characteristics of GO membranes without sacrificing their lamellar structure or altering the channels’ heights. Humic acid, a naturally occurring organic material, is applied here to tune the structure of GO nanochannels. With a structure chemically and physically similar to that of GO, humic acid causes an all-round improvement of the GO lamellar membrane.
Results and discussion
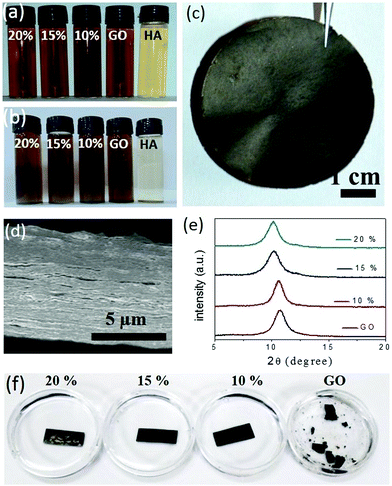
Humic acid, a decomposed product of organic biomass, is ubiquitous in a natural environment. The outstanding chemical functionalities of humic acid are known for more than 150 years, but these functionalities have not been applied much in advanced technologies due to uncertainties in its chemical structure. Recent studies demonstrated that the morphology and composition of humic acid are very similar to those of GO.20 Moreover, just like GO, humic acid produces conductive 2D sheets upon reduction.21,22 Based on their structural and chemical similarities, humic acid molecules are expected to perform as synergistic spacers in the GO membrane. Humic acid extracted from native soils following standard procedures was characterized with various spectroscopic techniques such as IR, UV-Vis, and fluorescence spectroscopy (Fig. S1, ESI†). X-ray photoelectron spectroscopy based analysis reveals the O/C ratio of purified humic acid samples to be 0.3 (Fig. S2a, ESI†), which was also supported by the EDX elemental quantification carried out under an electron microscope as shown in Fig. S2b (ESI†) (the O/C ratios were found to be in the 0.25 to 0.3 range). Similar to GO, humic acid forms homogeneous dispersions in neutral water and hence it can be easily mixed with GO into appropriate compositions. The GO sample used here was synthesized following modified Hummers’ method and characterized with electron and atomic force microscopy, see Fig. S3 (ESI†). The interactions between GO and humic acid can be visualized by studying the colloidal stability of the mixtures. In Fig. 1a, aqueous dispersions of GO and humic acid are compared with those of the mixtures (10, 15 or 20% humic acid with GO). While dispersions of humic acid started settling down after around 72 undisturbed hours, those of the mixtures remained unaltered for 60 days (Fig. 1b), suggesting the existence of favorable interactions between these two negatively charged nanomaterials. Composed of synergistic blends of aromatic and oxygenated carbon atoms, both humic acid and GO sheets are amphiphilic in nature. The surfactant-like properties of both these materials23–27 have been exploited to disperse hydrophobic nanomaterials like carbon nanotubes through π–π stacking.28,29 In the HA–GO dispersion, the aromatic segments of humic acid molecules are expected to interact with the hydrophobic regions of the GO surface through π–π stacking, projecting away the oxygen containing hydrophilic regions. As a result, the negative zeta potential of the humic acid and GO dispersions increases upon mixing (Fig. S4a, ESI†), which is attributed to the superior dispersibility of the mixtures in polar solvents like water. As the polarity of the medium was decreased by adding ethyl acetate and isopropanol, the HA–GO mixture agglomerated before pure GO and humic acid dispersions, as can be seen in Fig. S4b (ESI†). The existence of π–π stacking between the hydrophobic regimes of humic acid and the GO sheets was also verified through the fluorescence quenching experiment shown in Fig. S5 (ESI†). The purified humic acid samples display a characteristic emission spectrum (λexcitation = 320 nm and λemission = 470 nm) that originates from the conjugated carbon atoms (both aromatic and non-aromatic) bonded with various chromophores.30,31 Addition of GO not only quenched the fluorescence of the humic acid dispersion, but the extent of quenching was also found to be directly proportional to the amount of GO added. It supports the existence of definite interactions between the two materials, as GO is known to quench fluorophores through excited-state energy transfers via π–π stacking.20,32–34Similarly, upon vacuum filtration, except for pure humic acid, all other dispersions yielded freestanding membranes. Fig. 1c shows a digital photo of a composite membrane (GO–HA) obtained from the dispersion of 15% humic acid. The cross-sectional field emission electron microscopy (FESEM) examinations on the broken edges of the GO–HA membranes revealed the formation of densely packed lamellar structures. Under the electron microscopy examinations no large pores or agglomerated chunks of humic acid were observed. A characteristic cross-sectional FESEM image of the 15% GO–HA membrane is presented in Fig. 1d. The lamellar structures of the GO–HA membranes were also confirmed by the existence of characteristic (002) reflections in the XRD patterns (Fig. 1e). Addition of humic acid marginally increased the interlayer spacing, from 8.2 Å of GO to 8.8 Å, in the 20% GO–HA membranes. In order to test their solution stability, small pieces of the membranes (15 mm × 7 mm) were soaked in water for a prolonged time. As can be seen from Fig. 1f, the GO membrane started disintegrating within 3 days of soaking, but the GO–HA membranes remained unaltered for more than 60 days. The enhanced stability of the GO–HA membranes is attributed to the crosslinking of lamellar GO sheets by the humic acid molecules. During vacuum filtration, the humic acid modified GO sheets are forced into a tightly packed lamellar structure, providing a geometrically favourable situation for crosslinking interactions such as π–π stacking, H-bonding, and CH–π stacking. The existence of these interactions in the composite membranes is evident from the Fourier transform infrared (FTIR) spectra shown in Fig. S6 (ESI†). The π–π interaction weakens the double bond character of the aromatic rings, causing a red-shift of the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C stretching vibration band of humic acid35 from 1657 cm−1 to 1620 cm−1. Similar π–π interaction is also seen in the pure GO membranes. The weakening of the stretching vibrations of the C–H bond (2920–2850 cm−1) in the composite system as compared to those of humic acid and GO can be attributed to the CH–π interaction between the sheets.32,36 Likewise, in the O–H stretching regime, a decrease in peak intensity, broadening, and shifting of the peak position (from 3440 cm−1 to 3340 cm−1) indicate the occurrence of inter-molecular H-bonding between the hydrophilic functionalities of the two materials.37 The crosslinking effect of humic acid was further confirmed by studying the mechanical properties of the membranes. Fig. S7 (ESI†) shows that the tensile strength values of the membranes, determined from maximum loads lifted by rectangular strips (dimensions of 20 mm × 3 mm × 0.027 mm) before failure, improve with increasing humic acid content on them. The same trend is also followed by the bending stiffness values of the membranes, discussed in Fig. S8 (ESI†).
C stretching vibration band of humic acid35 from 1657 cm−1 to 1620 cm−1. Similar π–π interaction is also seen in the pure GO membranes. The weakening of the stretching vibrations of the C–H bond (2920–2850 cm−1) in the composite system as compared to those of humic acid and GO can be attributed to the CH–π interaction between the sheets.32,36 Likewise, in the O–H stretching regime, a decrease in peak intensity, broadening, and shifting of the peak position (from 3440 cm−1 to 3340 cm−1) indicate the occurrence of inter-molecular H-bonding between the hydrophilic functionalities of the two materials.37 The crosslinking effect of humic acid was further confirmed by studying the mechanical properties of the membranes. Fig. S7 (ESI†) shows that the tensile strength values of the membranes, determined from maximum loads lifted by rectangular strips (dimensions of 20 mm × 3 mm × 0.027 mm) before failure, improve with increasing humic acid content on them. The same trend is also followed by the bending stiffness values of the membranes, discussed in Fig. S8 (ESI†).
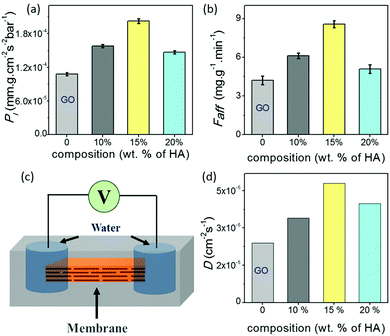
One of the most widely anticipated applications of reconstructed layered materials is in the water treatment processes. The requirements of ideal water purification membranes include chemical/mechanical robustness, high permeability and great selectivity. The solution stability and mechanical robustness of the GO–HA membranes are already described in Fig. 1f and Fig. S7 and S8 (ESI†), respectively. The next key is to improve permeability and selectivity, concurrently. With the intention to test permeability and selectivity, fixed volumes (3 ml) of aqueous dye solutions (200 ppm) were vacuum filtered through the composite membranes. From the “time” required to complete the filtration process, the permeabilities of the membranes were calculated by employing eqn (1).11
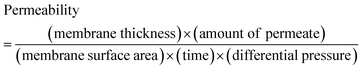 | (1) |
Data shown in Fig. 2a and b show the permeability of water molecules across the membrane in the vertical direction, where water molecules travel through long zig-zag channels. In lamellar membranes, the preferred movement of the molecules should be in the horizontal direction, i.e. in the plane of the sheets. In order to gain insights into their in-plane molecular diffusivity, rectangular strips of the membranes were encapsulated into freshly prepared polydimethylsiloxane (PDMS) elastomer. As shown in the schematic of Fig. 2c, liquid water was introduced into the channels through the holes cut out at both ends of the strip. The diffusion process was monitored by measuring the response current across the membranes after applying a voltage (0.5 volt) for 50 ms through the Ag/AgCl electrodes inserted into the droplets at regular intervals of 30 minutes. In the beginning, no current was observed; measurable ionic current was seen only when water molecules diffusing from both ends of the membranes met each other to complete the circuit. As the water molecules diffused into the other regions of the membranes, the current values started increasing with time and reached saturation when all the channels became completely hydrated (Fig. S11, ESI†). The time (t) taken by the water molecules to diffuse into the channels of the entire membrane reflects the characteristics of the channels in the respective membranes. Fig. 2d shows the diffusivity values (D) of the membranes calculated using Einstein's approximation for two dimensional diffusions, eqn (2).12
| x2 = 4Dt | (2) |
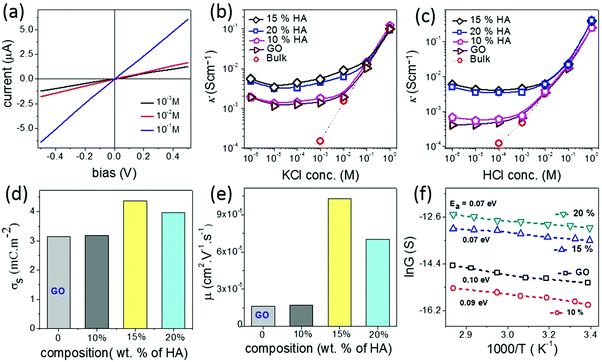
Another important characteristic of reconstructed lamellar membranes is their high nanofluidic ionic conductivity. Ionic currents through the 2D channels of the different GO–HA membranes were measured after exposing water soaked devices to aqueous KCl solutions of different concentrations. The slopes of the I–V curves (shown in Fig. 3a) measured after 7 hours of KCl soaking were normalized with the membranes’ dimensions to determine conductivity. The conductivity–concentration plots of Fig. 3b reveal that each membrane exhibits two distinct regimes of conductivity. At high concentrations, the conductivities of the devices vary linearly with concentration similar to those of bulk solutions. But, for concentrations below 10−2 M, the conductivity does not vary even for a four orders of magnitude change in the concentration. This typical characteristic of nanofluidic channels known as the surface-charge-governed ionic conductivity originates from the overlapping Debye layers of the channel walls under nanofluidic confinement. It not only confirms the formation of a percolated network of nanofluidic channels but also indicates the absence of large macropores. Moreover, the transition point (Ct), defined as the concentration at which the characteristics of ionic conductivity changes from bulk-like to surface-charge-governed, throws light on the effective dimensions of the nanochannel.38 From the conductivity versus concentration plots of Fig. 3b, the Ct values of the different membranes were determined from the intersection of the lines laid over the two distinct conductivity regimes as shown in Fig. S12 (ESI†). The effective channel heights (h) and Ct are connected through eqn (3).38
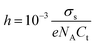 | (3) |
| Membrane | Effective channel height (nm) | Liquid permeability (mm g cm−1 s−1 bar−1) | Gas permeability (mm g cm−1 s−1 bar−1) | In-plane diffusivity (cm2 s−1) | Proton mobility (cm2 V−1 s−1) | Activation energy (eV) |
|---|---|---|---|---|---|---|
| GO | 1.54 | 1.0 × 10−4 | 2.6 × 10−7 | 2.4 × 10−6 | 1.6 × 10−5 | 0.10 |
| 10% | 1.60 | 1.5 × 10−4 | 8.3 × 10−7 | 3.4 × 10−6 | 1.7 × 10−5 | 0.09 |
| 15% | 2.19 | 2.0 × 10−4 | 1.0 × 10−6 | 4.8 × 10−6 | 1.0 × 10−4 | 0.07 |
| 20% | 1.99 | 1.4 × 10−4 | 7.3 × 10−7 | 3.9 × 10−6 | 7.0 × 10−5 | 0.07 |
Fig. 3b also reveals that in the surface-charge-governed regime the membranes with 15% and 20% humic acid contents showed ∼4 times higher ionic conductivity than the GO and 10% GO–HA membranes. In order to verify this unusual trend, the conductivities of the membranes were also measured with HCl solutions of similar concentrations. Here again, in the low concentration regime the 15% and 20% GO–HA membranes showed one order of magnitude higher ionic conductivity than the other membranes, see Fig. 3c.
The measured ionic conductivity of the channels is a product of surface charge density (equivalent to ionic concentration) and ionic mobility. To understand the unusual enhancement in the surface-charged-governed ionic conductivity of the 15% and 20% GO–HA membranes, it is important to determine one of these parameters, independently. The surface charge density of the channel walls was determined by employing an ion-exchange based method.13 In the first step, all the movable ions of the membranes were exchanged with Li+ by stirring a piece of the membrane (11 mm × 7 mm × 0.013 mm and 0.8 mg) with 10 ml of 2 M LiCl solution, for 24 hours. The excess Li+ ions were then removed by washing with excess water. The movable Li+ ions were then re-exchanged with H+, by stirring the membranes with 1 mM HCl solution for 20 hours. The total numbers of protons exchanged (Np) with Li+ ions were determined from the decrease in the conductivity value of the supernatant liquid, by considering the limiting conductances of HCl and LiCl as 425 Ω−1 and 115 Ω−1, respectively. The surface charge densities (σs) of the different membranes were determined from Np using eqn (4).
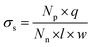 | (4) |
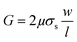 | (5) |
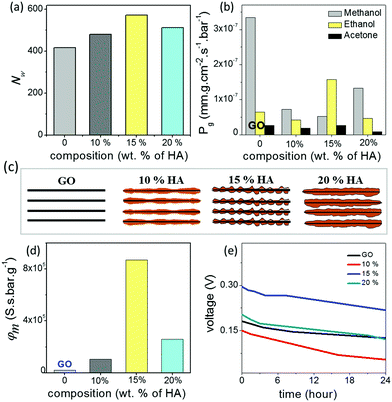
In order to understand the unusual behaviour of the 15% HA–GO membrane, the effective channel heights of the membranes are compared with their ionic mobility, molecular diffusivity and permeability values. The data listed in Table 1 clearly connect the superior mobility and diffusivity of the 15% GO–HA membrane to the larger effective channel height of the 2D nanochannels. In order to understand the origin of the larger effective channel height of the 15% membrane, HA–GO dispersions were investigated under a transmission electron microscope, which revealed that the surfaces of the GO sheets with 15% humic acid are more rough and uneven than those of the other compositions (Fig. S13, ESI†). The exact reason for the same is not known yet. This inhomogeneous coating of the sheets would create channels with non-uniform heights, having localized regions of slightly larger channels. These localized regions of the larger channels would not only provide additional spaces or pathways for ionic/molecular transportation but also reduce the viscosity of permeates in those regimes.41 However, it is worth mentioning that as long as the overlapping of Debye lengths occurs in the different regimes of the nanofluidic network the selectivity value of the membrane would not be compromised. In order to gain further insights into the nanofluidic transport of the humic acid modified GO nanochannels, the permeation of water molecules in the HA–GO membranes of different compositions was investigated through equilibrium molecular dynamics (MD) simulation. As both GO and humic acid possess similar chemical structures, representative structures of both these nanoflakes were constructed by locating hydroxyl and epoxy functional groups on the basal planes of aromatic carbon atoms (Fig. S14, ESI†); the carboxylic functional groups were placed at the edges of the aromatic networks by fixing the elementary compositions at C10O1(OH)1(COOH)0.5.42–44 The nanoflakes of GO and humic acids were arranged in space to get the GO–humic acid composite membrane of desired proportion (0, 10, 15 and 20% humic acids with GO) as shown in Fig. S15a–d (ESI†). The geometric parameters of the membrane were kept as H = 8 Å, W = 5 Å and D = 10 Å. After the construction of the layered GO membranes, each of the membranes was hydrated with a water box (dimensions: 147 × 102 × 64 Å3) containing 19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 894 water molecules, and the water molecules within 2 Å of the GO nanosheets were removed. A methylene blue (MB) solution box (4 MB molecules and 7745 water molecules in a box with dimensions of 147 × 102 × 32 Å3) was placed above and below the hydrated membrane. Equilibrium molecular dynamics (MD) simulations were performed to investigate the permeation of water molecules. The simulation setup is shown in Fig. S16 (ESI†). During the simulation no MB molecules permeated through any of the membranes. The details of the MD simulation are provided in the ESI.† Typically, when a water molecule travels from one end of the membrane to the other end, a water permeation event is counted. During the simulation, the 15% GO–HA membrane showed better permeability with 571 water molecules permeated, and for comparison the pure GO and the membranes with 10 and 20% humic acid displayed permeation of 416, 480 and 512 water molecules respectively. The permeabilities of water (Nw) through the different HA–GO membranes obtained as such are shown in Fig. 4a.
894 water molecules, and the water molecules within 2 Å of the GO nanosheets were removed. A methylene blue (MB) solution box (4 MB molecules and 7745 water molecules in a box with dimensions of 147 × 102 × 32 Å3) was placed above and below the hydrated membrane. Equilibrium molecular dynamics (MD) simulations were performed to investigate the permeation of water molecules. The simulation setup is shown in Fig. S16 (ESI†). During the simulation no MB molecules permeated through any of the membranes. The details of the MD simulation are provided in the ESI.† Typically, when a water molecule travels from one end of the membrane to the other end, a water permeation event is counted. During the simulation, the 15% GO–HA membrane showed better permeability with 571 water molecules permeated, and for comparison the pure GO and the membranes with 10 and 20% humic acid displayed permeation of 416, 480 and 512 water molecules respectively. The permeabilities of water (Nw) through the different HA–GO membranes obtained as such are shown in Fig. 4a.
The work here demonstrated that the interlayer spaces of GO membranes can be modified with humic acid to further improve their ionic conductivity, solution stability and mechanical robustness. Such improved membranes should be ideal for energy harvesting applications such direct methanol fuel cells (DMFCs) and reverse electrodialysis (RED). A major problem faced by traditional proton exchange membranes like Nafion in DMFC applications is their high methanol permeability, which leads to a crossover effect.45,46 In order to verify the prospects of GO–HA membranes in DMFC applications, the permeabilities of different solvent vapors through the membranes were studied by the gravimetric method. The rates of solvent evaporation from glass vials covered with the membranes 20 μm thick are shown in Fig. 4b. Interestingly, all the GO–HA membranes blocked methanol vapors much more effectively than the pure GO membrane (Fig. 4b). Typically, the membrane performance for DMFCs is evaluated by the selectivity value defined as the ratio of proton conductivity to methanol permeability.45,46 The bar diagrams shown in Fig. 4d clearly show that GO–HA membranes will be more preferred over GO membranes for DMFC applications. Similarly, the applicability of GO–HA membranes for RED was tested by measuring open circuit voltages obtained from the concentration differences of the electrolytes across the membranes.9,47 Devices comprising two compartments separated by GO–HA membranes were fabricated using freshly prepared PDMS elastomer are shown in Fig. S17 (ESI†). The compartments were filled with KCl solutions of different concentrations, 10−3 M in the low (CL) and 1 M in the high (CH) concentration chamber. The transmembrane potentials and diffusion currents were measured by inserting Ag/AgCl electrodes into the solutions. In Fig. 4e, the transmembrane potentials recorded as a function of time are shown for the different membranes, after 72 hours of experiment. Remarkably, even after the 3rd consecutive cycle (each cycle 24 hours long) the open circuit potentials due to the concentration gradient driven transport of cations across the membranes were calculated to be 0.125 V, 0.05 V, 0.21 V and 0.12 V, for the GO, 10%, 15% and 20% membranes respectively. In order to demonstrate the contribution of the HA–GO membranes to the measured cross-membrane potential, the experiment was repeated by replacing the HA–GO membranes with a commercial PTFE membrane (pore dimension 1 μm) and an insulating non-permeable plastic barrier. In both the cases, no open circuit voltage was observed (Fig. S18a and b, ESI†). Similarly, to exclude concentration gradient induced redox reactions at the electrode surface, the open circuit voltages were measured by applying the Ag/AgCl electrodes through agar–agar salt bridges (Fig. S18c, ESI†).
Conclusions
In summary, we have demonstrated that the ionic and molecular transport properties of reconstructed lamellar membranes can be finely tuned by applying appropriate spacers in right composition. Application of humic acid not only improved the nanofluidic transport of the GO membrane but also enhanced its solution stability and mechanical robustness. Among the GO–HA membranes with different compositions, the 15% membrane showed remarkable enhancement in ionic mobility and molecular permeability and selectivity. The data presented in this manuscript indicate that slight variations in the channels’ dimensions within the Debye-length-overlapping-regime do not deteriorate their selectivity, but significantly enhance permeability and mobility by providing additional pathways for ionic/molecular transportation and reducing the viscosity of the permeates. With such improvement, reconstructed lamellar membranes should be ideal for applications like water desalination and energy harvesting from direct methanol fuel cells and reverse electrodialysis.Methods
Extraction of humic acid
Humic acid was extracted following the standard conjugative alkaline–acid treatment method.48–50 In typical experiments, 100 g of a soil sample was mixed with 300 ml of 0.1 M NaOH solution and stirred for 2 hours at room temperature. The brown coloured supernatant obtained after allowing the reaction mixture to stand overnight was collected by centrifugation. The pH of the brownish dispersion was adjusted to 1, to precipitate out the acid-insoluble humic acid. And the precipitate of humic acid was thoroughly washed with deionized (DI) water and oven dried at 60 °C.Preparation of GO membranes
GO was synthesized following modified Hummers’ method.51 6 g of KMnO4 was gradually added to ice cold sulphuric acid (17 M, 50 ml) mixed with 1 g of graphite powder under constant stirring. The mixture was then stirred at 35 °C for two hours, followed by slow addition of 100 ml of DI water. The reaction was terminated by adding 8 ml of H2O2 (30%) solution. The as-obtained yellow suspension was subjected to two-step washing with HCl (1 M) and acetone. Freestanding membranes were prepared by vacuum filtering aqueous dispersions of GO through a polytetrafluoroethylene (PTFE) membrane.Fabrication of composite membranes
Aqueous dispersions of GO and humic acid (1 mg ml−1 each) were mixed in appropriate amounts (10, 15, and 20% humic acid by weight) and sonicated for 15 minutes. The mixed dispersions were then passed through a cellulose nitrate membrane to prepare GO–HA composite membranes.Surface charge governed ionic transport
The ionic conductivities of the devices were measured by dipping two Ag/AgCl electrodes in the reservoirs filled with electrolyte. A source meter (Keithley 2450 model) instrument was used for recording current and voltage values.Characterisation
The functional groups present in humic acid were characterized by Fourier transform infrared (FTIR) spectroscopy. The morphologies of humic acid and graphene oxide were examined by atomic force microscopy (AFM) (Agilent, Model 5500 series), field emission scanning electron microscopy (FESEM) (Zeiss, Model: Gemini), and field emission transmission electron microscopy (FETEM) (JEOL, Model: 2100F). X-ray diffraction was studied using Bruker D-205505 Cu-Kα radiation (λ = 1.5406 Å). Dye separation experiments were conducted using a UV-Vis spectrophotometer (Systronics, Model: 117).Conflicts of interest
The authors declare no competing financial interest.Acknowledgements
K. R. acknowledges financial support of a Ramanujan Research Grant (SB/S2/RJN-141/2014) of the Science and Engineering Research Board (SERB), India. All the authors thank CIF-IIT Guwahati and DST-FIST-Chemistry at IIT Guwahati and the XRD facility in the Department of Chemistry, Gauhati University, for help with sample characterization. TK, RG, KS and JD are grateful to IITG for PhD fellowships. KR acknowledges Dr Debajyoti Mahanta (GU), Sibani Mazumder (GU) and Kaushik Sharma (NLC) for their help with scientific discussions and sample characterization. Anki Reddy Katha and Abhijit Gogoi acknowledge the Param Ishan high performance computing facility of IIT Guwahati for providing an adequate computational facility to carry out the equilibrium molecular dynamics simulations.References
- P. Abgrall and N. T. Nguyen, Nanofluidics, Artech House, Boston, 4th edn, 2009 Search PubMed.
- A. Van den Berg, H. G. Craighead and P. D. Yang, Chem. Soc. Rev., 2010, 39, 899 RSC.
- W. Sparreboom, A. Van den Berg and J. C. T. Eijkel, Nat. Nanotechnol., 2009, 4, 713 CrossRef PubMed.
- C. H. Duan and A. Majumdar, Nat. Nanotechnol., 2010, 5, 848 CrossRef PubMed.
- P. Mao and J. Y. Han, Lab Chip, 2005, 5, 837 RSC.
- H. Cao, Z. N. Yu, J. Wang, J. O. Tegenfeldt, R. H. Austin, E. Chen, W. Wu and S. Y. Chou, Appl. Phys. Lett., 2002, 81, 174 CrossRef.
- H. T. Liu, J. He, J. Y. Tang, H. Liu, P. Pang, D. Cao, P. Krstic, S. Joseph, S. Lindsay and C. Nuckolls, Science, 2010, 327, 64 CrossRef PubMed.
- J. Z. Ji, Q. Kang, Y. Zhou, Y. P. Feng, X. Chen, J. Y. Yuan, W. Guo, Y. Wei and L. Jiang, Adv. Funct. Mater., 2017, 27, 1603623 CrossRef.
- L. Lin, L. Zhang, L. D. Wang and J. H. Li, Chem. Sci., 2016, 7, 3645 RSC.
- R. K. Joshi, P. Carbone, F. C. Wang, V. G. Kravets, Y. Su, I. V. Grigorieva, H. A. Wu, A. K. Geim and R. R. Nair, Science, 2014, 343, 752 CrossRef PubMed.
- R. R. Nair, H. A. Wu, P. N. Jayaram, I. V. Grigorieva and A. K. Geim, Science, 2012, 335, 442 CrossRef PubMed.
- K. Raidongia and J. Huang, J. Am. Chem. Soc., 2012, 134, 16528 CrossRef PubMed.
- J. J. Shao, K. Raidongia, A. R. Koltonow and J. Huang, Nat. Commun., 2015, 6, 7602 CrossRef PubMed.
- J. Gao, Y. P. Feng, W. Guo and L. Jiang, Chem. Soc. Rev., 2017, 46, 5400 RSC.
- J. Abraham, K. S. Vasu, C. D. Williams, K. Gopinadhan, Y. Su, C. T. Cherian, J. Dix, E. Prestat, S. J. Haigh, I. V. Grigorieva, P. Carbone, A. K. Geim and R. R. Nair, Nat. Nanotechnol., 2017, 12, 546 CrossRef PubMed.
- H. Li, Z. N. Song, X. J. Zhang, Y. Huang, S. G. Li, Y. T. Mao, H. J. Ploehn, Y. Bao and M. Yu, Science, 2013, 342, 95 CrossRef PubMed.
- M. Hu and B. X. Mi, Environ. Sci. Technol., 2013, 47, 3715 CrossRef PubMed.
- Y. Han, Y. Q. Jiang and C. Gao, ACS Appl. Mater. Interfaces, 2015, 7, 8147 CrossRef PubMed.
- J. W. Burress, S. Gadipelli, J. Ford, J. M. Simmons, W. Zhou and T. Yildirim, Angew. Chem., Int. Ed., 2010, 49, 8902 CrossRef PubMed.
- X. Y. Zhou, B. Wang, T. Lan, H. Q. Chen, H. L. Wang, Y. Tao, Z. H. Li, K. Ibrahim, D. Q. Wang and W. Y. Feng, J. Phys. Chem. C, 2016, 120, 25789 CrossRef.
- E. S. M. Duraia and G. W. Beall, Sens. Actuators, B, 2015, 220, 22 CrossRef.
- B. L. Xing, R. F. Yuan, C. X. Zhang, G. X. Huang, H. Guo, Z. F. Chen, L. J. Chen, G. Y. Yi, Y. D. Zhang and J. L. Yu, Fuel Process. Technol., 2017, 165, 112 CrossRef.
- L. J. Cote, J. Kim, V. C. Tung, J. Luo, F. Kim and J. Huang, Pure Appl. Chem., 2011, 83, 95 Search PubMed.
- J. Kim, L. J. Cote, F. Kim, W. Yuan, K. R. Shull and J. Huang, J. Am. Chem. Soc., 2010, 132, 8180 CrossRef PubMed.
- F. Kim, L. J. Cote and J. Huang, Adv. Mater., 2010, 22, 1954 CrossRef PubMed.
- M. Tschapek, C. Wasowski and R. M. T. Sanchez, Plant Soil, 1981, 63, 261 CrossRef.
- M. Klavins and O. Purmalis, Environ. Chem. Lett., 2010, 8, 349 CrossRef.
- D. W. Lee, T. Kim and M. Lee, Chem. Commun., 2011, 47, 8259 RSC.
- Q. Yang, X. Pan, F. Huang and K. Li, J. Phys. Chem. C, 2010, 114, 3811 CrossRef.
- I. A. Schepetkin, A. I. Khlebnikov, S. Y. Ah, S. B. Woo, C. S. Jeong, O. N. Klubachuk and B. S. Kwon, J. Agric. Food Chem., 2003, 51, 5245 CrossRef PubMed.
- K. Ghosh and M. Schnitzer, Can. J. Soil Sci., 1980, 60, 373 CrossRef.
- V. Georgakilas, J. N. Tiwari, K. C. Kemp, J. A. Perman, A. B. Bourlinos, K. S. Kim and R. Zboril, Chem. Rev., 2016, 116, 5464 CrossRef PubMed.
- S. Li, A. N. Aphale, I. G. Macwan, P. K. Patra, W. G. Gonzalez, J. Miksovska and R. M. Leblanc, ACS Appl. Mater. Interfaces, 2012, 4, 7069 CrossRef PubMed.
- B. Wang, X. Zhou, D. Wang, J. J. Yin, H. Chen, X. Gao, J. Zhang, K. Ibrahim, Z. Chai, W. Feng and Y. Zhao, Nanoscale, 2015, 7, 2651 RSC.
- S. Yang, L. Li, Z. Pei, C. Li, X. Q. Shan, B. Wen, S. Zhang, L. Zheng, J. Zhang, Y. Xie and R. Huang, Carbon, 2014, 75, 227 CrossRef.
- K. L. Vincent Joseph, J. Lim, A. Anthonysamy, H. Kim, W. Choib and J. K. Kim, J. Mater. Chem. A, 2015, 3, 232 RSC.
- M. Gorman, J. Chem. Educ., 1957, 34, 304 CrossRef.
- R. B. Schoch and P. Renaud, Appl. Phys. Lett., 2005, 86, 253111 CrossRef.
- R. Fan, S. Huh, R. Yan, J. Arnold and P. D. Yang, Nat. Mater., 2008, 7, 303 CrossRef PubMed.
- D. D. Ordinario, L. Phan, W. G. Walkup, J. M. Jocson, E. Karshalev, N. Husken and A. A. Gorodetsky, Nat. Chem., 2014, 6, 597 CrossRef PubMed.
- H. Huang, Z. Song, N. Wei, L. Shi, Y. Mao, Y. Ying, L. Sun, Z. Xu and X. Peng, Nat. Commun., 2013, 4, 2979 CrossRef PubMed.
- A. Lerf, H. He, M. Forster and J. Klinowski, J. Phys. Chem. B, 1998, 102, 4477 CrossRef.
- H. Tang, D. Liu, Y. Zhao, X. Yang, J. Lu and F. Cui, J. Phys. Chem. C, 2015, 119, 26712 CrossRef.
- C. J. Shih, S. Lin, R. Sharma, M. S. Strano and D. Blankschtein, Langmuir, 2012, 28, 235 CrossRef PubMed.
- I. Nicotera, C. Simari, L. Coppola, P. Zygouri, D. Gournis, S. Brutti, F. D. Minuto, A. S. Arico, D. Sebastian and V. Baglio, J. Phys. Chem. C, 2014, 118, 24357 CrossRef.
- P. Bunlengsuwan, N. Paradee and A. Sirivat, Polym.-Plast. Technol. Eng., 2017, 56, 1695 CrossRef.
- S. W. Lee, H. J. Kim and D. K. Kim, Energies, 2016, 9, 49 CrossRef.
- R. Sutton and G. Sposito, Environ. Sci. Technol., 2005, 39, 9009 CrossRef PubMed.
- M. O. Deserra and M. Schnitze, Can. J. Soil Sci., 1972, 52, 365 CrossRef.
- S. Paul, T. Sharma, D. Saikia, P. P. Saikia, D. Borah and M. K. Baruah, Int. J. Plant Soil Sci., 2015, 6, 218 CrossRef.
- F. Kim, J. Y. Luo, R. Cruz-Silva, L. J. Cote, K. Sohn and J. Huang, Adv. Funct. Mater., 2010, 20, 2867 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available: Characterization of humic acid and GO; mechanical properties; molecular permeability; selectivity and nanofluidic energy harvesting data. See DOI: 10.1039/c8qm00272j |
| This journal is © the Partner Organisations 2018 |