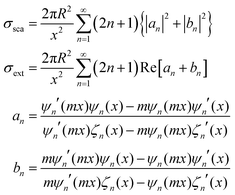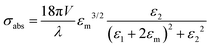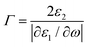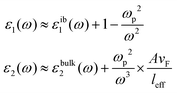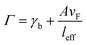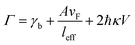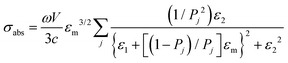Optically active plasmonic resonance in self-assembled nanostructures
Jiaji
Cheng
 a,
Eric H.
Hill
b,
Yuebing
Zheng
a,
Eric H.
Hill
b,
Yuebing
Zheng
 *b,
Tingchao
He
*a and
Yanjun
Liu
*b,
Tingchao
He
*a and
Yanjun
Liu
 *c
*c
aCollege of Physics and Energy, Shenzhen University, Shenzhen 518060, People's Republic of China. E-mail: tche@szu.edu.cn
bDepartment of Mechanical Engineering and Materials Science and Engineering Program, The University of Texas at Austin, Texas, USA. E-mail: zheng@austin.utexas.edu
cDepartment of Electrical and Electronic Engineering, Southern University of Science and Technology, Shenzhen, 518055, China. E-mail: yjliu@sustc.edu.cn
First published on 26th February 2018
Abstract
The rapid development of self-assembled plasmonic chiral nanostructures has proven its promising potential in many applications. The underlying mechanism lies in the localized surface plasmon resonance properties of plasmonic colloids with respect to induced chirality via chiral molecules or chiral geometries. In this review, we summarize recent advances in both experimental phenomena and theoretical modellings, in particular to plasmonic chirality based on geometric motives, to elucidate the underlying origin of chirogenesis so as to provide insights into this fascinating field.
1. Introduction
The invention of metal nanoparticles (NPs) has revolutionized many interdisciplinary fields, triggering the realization of numerous novel materials and their respective applications. The emerging area of plasmonics, for example, is closely related to advanced optical material design and fundamental science in modern optics, where the mechanisms involved are intimately associated with the excitation of plasmons in metallic nanoparticles. When a metal nanoparticle, typically gold or silver, is irradiated by visible light, its electric field separates the negatively charged electrons from the positively charged nuclei. As the opposing charges attract each other the electrons oscillate with a certain frequency, and this oscillation is known as a plasmon. If the frequency of the incident light matches this frequency, the free electrons’ oscillation about the particle and the resulting electric field within the vicinity of the nanoparticle will be greatly enhanced, in turn reinforcing oscillation of the electrons. The coupled excitation between this oscillating electron density (the plasmon) of the nanoparticle and the resonant electromagnetic field near the nanoparticle is known as surface plasmon resonance.1 This fascinating property enables a wide range of applications including single molecule detection using surface-enhanced Raman scattering,2–5 optical energy transfer,6–8 sensing,9–14 and other optical devices.15–17Governed by Maxwell's equations, the characteristics of localized surface plasmon resonance (LSPR) are strongly related to the size, shape, and material of the nanoparticle, as well as its surrounding environment. In general, asymmetric shapes and high aspect ratios result in lower restoring forces and thus lower plasmon resonance frequencies. Closely packed nanoparticles can couple electric fields when their interparticle distance is less than their diameter, leading to lower resonance frequencies and providing opportunities for electromagnetic energy transfer at a length scale below the diffraction limit.18 The coupling effects of nanoparticles can regulate both linear and nonlinear optical properties resulting in novel physical properties for assembled nanostructures.19–23 It is therefore highly appealing to merge the properties of assembled hybrid nanomaterials with the electronic and optical applications in devices.11,24–31
Chirality is often referred to a system that loses mirror and inversion symmetries, like most of chiral organic molecules in which chiral centers are surrounded by four different bonding groups. While in terms of self-assembled systems, this lack of symmetry involves not only the difference in elements, but also often the architecture of overall structures in long range. This allows simple and easy bench top chemical synthesis of chiral structures at both micro- and nano-scale, thus providing alternative approaches to achieving chiral materials with novel properties. In recent years, interests in optically active hybrid nanostructures have been rising rapidly. Optical activity is the ability of a chiral molecule to rotate the plane of plane-polarized light.32 When linearly polarized light, considered as the superposition of left (LCP) and right (RCP) circularly polarized light, propagates through an optically active absorbing system, the absorption of LCP and RCP light will be different due to the difference on speed of light passing the chiral system. This results in turning linearly polarized light to elliptically or circularly polarized light, a phenomenon called circular dichroism (CD). Depending on the absorption properties, electronic circular dichroism (ECD) and vibrational circular dichroism (VCD), and sometimes scattering techniques are employed for measuring the adsorption difference in LCP and RCP light to detect chirality of a measured sample at optical frequencies. However, most chiral materials that have been studied are intrinsically chiral molecules, biomolecules, or inorganic salts at the molecular level. In these cases, the chiroptical effects arise from relatively small dipole moments caused by weak coupling with an external electromagnetic field.33 Recently, chirality has been introduced into plasmonic materials at the nanoscale due to the following merits: (I) optical activity can be greatly enhanced. In some cases, the resonance effects of plasmonic nanostructures creates opportunities to achieve novel materials with interesting optical effects, such as metamaterials with negative refractive indices; (II) generally, colloidal synthesis results in highly symmetrical nanostructures, such as spheres, ellipsoids, and spindles. The next challenge is breaking symmetry by inducing artificial chirality; (III) it is of interest to study the fundamental interactions between chiral molecules and plasmonic nanoparticles or clusters, and particle–particle interactions in chiral configurations.34–37
Generally, chiral responses in self-assembled plasmonic nanostructures arise from two cases: superstructures with chiral configurations in which the particle–particle interactions between plasmonic building blocks are the driving force for chiroptical activity (see Fig. 1B–H), and the plasmon–exciton interactions between a hybrid complex of chiral molecules and achiral plasmonic NPs (Fig. 1A). (Herein we exclude chiral ligand protected metal nanoclusters (<5 nm) because they possess discrete energy bands giving weak or even no obvious localized surface plasmon property. For interested readers, extensive reviews38,39 are published in this field concerning the syntheses, mechanisms, and applications.) Between assembled chiral plasmonic superstructures and complexes of chiral molecules with achiral plasmonic NPs, the latter has been extensively studied during the last ten years with a number of well-summarized reviews34,40–42 published recently. In contrast, cutting-edge research concerning assembled plasmonic nanostructures with defined chiral particle–particle interactions is less frequently reviewed due to the complexity of systematic control over the synthesis and a lack of a priori theoretical analysis. Therefore, understanding the origin of chiroptical effects and manipulating chiral plasmonic interactions in these systems would open the floodgates to a host of new experiments on innovative chiral materials, pushing researchers to re-evaluate the origin of electromagnetic response between light and optically-active matter toward discovering novel avenues in chiral materials’ design.
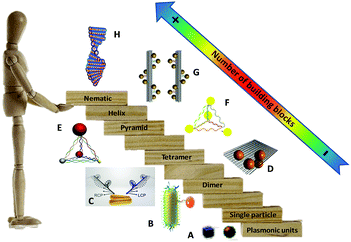 | ||
| Fig. 1 “Stairway” of chiral plasmonic nanostructures in terms of the number of plasmonic building blocks. From downstairs to upstairs, chiral molecules interact with a plasmonic particle (A),40 chiral dimers (B and C),43,44 tetramer (D),45 pyramids (E and F),46,47 short helix (G)48 and helical nematic assemblies (H).49 Adapted with permission from the American Chemical Society, Nature Publishing Group and Wiley. | ||
Herein, we emphasize recent progress on self-assembled chiral nanostructures with two or more plasmonic building blocks in terms of their syntheses, circular dichroism effects at relative optical frequencies, mechanisms of induced optical chirality, and their potential for optical applications. In Section 2, the classical theories for understanding LSPR effects are presented, followed by a more advanced model describing the coupling phenomena of closely packed plasmonic nanoparticles, to explore the optical chirality from a fundamental point of view. Section 3 briefly introduces the origin of induced chirality in plasmonic nanostructures and discusses how CD activities are associated with the species and geometries of the plasmonic building blocks. In Section 4, recent progress exploring mechanisms of induced CD response from metal particle assembles or hybrids of metal and semiconducting nanoparticles will be discussed with respect to the number of building blocks: (i) plasmonic dimers, (ii) tetramers or pyramids, and (iii) higher order plasmonic assemblies, such as short helices and helical nematic structures (Fig. 1). Finally, Section 5 will briefly summarize the applications and potential perspectives of this research area with challenges that remain unsolved to date.
2. Theoretical background on LSPR: Mie scattering and plasmon hybridization theory
Regarding extremely small particles with a size much smaller than the wavelength of incident light, an analytical solution was developed using Maxwell's equations to describe the sub-wavelength particle's light extinction.9,50 To understand the extensive derivation and properties of LSPR, Mie scattering theory arose, which requires combination of dielectric constants of the particle and the environment or surrounding medium's influence.Plasmons are the incompressible electron cloud around the surface of the small particle, and the coherent oscillations from the collective electron cloud. Like a general oscillator, a plasmon also has its own frequency, ωp, which can be used to determine their dielectric constant. If the particle's dielectric constant and environment are known, the absorption spectra of spherical particles can be precisely estimated according to Mie theory, an analytical solution to Maxwell's equations for spheres. Typically, the expression of scattering and extinction for a spherical cross-section are shown in the following equations from Mie theory:
The analytical solution of Mie theory focusing on a spherical nanoparticle is dependent on the number of multipolar modes.51
The extinction can be summed by two cross-sections, absorption and scattering. Plasmons can also re-radiate energy to determine whether absorption or scattering dominates the entire process. In small nanoparticles, electron–electron scattering can quickly convert the energy of LSPR into heat, showing strong absorption. However, in large particles, electron–electron scattering can be significantly confined, and the energy can convert into a strong scattering cross-section as a result of the radiative damping effect.52
For small NPs 10 nm in size, the lowest dipolar l = 1, the absorption cross-section would be described by the expression:
As nanoparticle size increases, the most apparent effect is a red-shift of the plasmon resonance peak to longer wavelengths. This arises due to retardation effects from the incident light no longer polarizing the larger nanoparticle homogeneously, which can result in excitation of higher order modes.
Assuming only dipole contributions in the quasi-static limit l = 1, the linewidth of LSPR can be estimated from the following relation for noble metals:
where A is a constant related to electron scattering, leff is the effective path length of electrons, increasing with large particles, and vF is Fermi velocity. Therefore, with ∣∂ε1/∂ω∣ ≈ 2ωp2/ω3 we can easily calculate the linewidth that is given by:
When we consider radiation damping besides electron–electron scattering for larger size particles,
where κ is a constant describing the efficiency of radiation damping and V is the volume. Apparently, the spectral changes in Fig. 2 can be explained by both effects, i.e., radiation damping at large sizes and electron–electron scattering at small sizes, leading to the linewidth broadening of LSPR.53
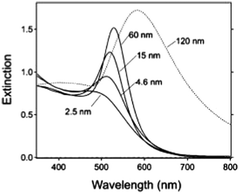 | ||
| Fig. 2 Extinction spectra of different sized gold nanoparticles (AuNPs) in aqueous solution (n = 1.33) reported by G. V. Hartland et al.53 Besides the obvious red-shift resulting from the retardation effect, it clearly demonstrates a broadening of linewidth (apart from 15 nm) for these ensemble nanoparticle observations. Reproduced from ref. 53 by permission of the American Chemical Society. Copyright (2011). | ||
When we consider a more complicated situation, the spherical shape elongated along the z-axis, the optical properties of ellipsoidal NPs has been changed following Gans theory.30,31 This is an analytical solution of Maxwell's equations describing the LSPR of nanoparticles of any aspect ratio including those of metallic nanorods. An approximate solution to the equation is shown:
Aspect ratio (AR) can describe the shape of an ellipsoid. For a sphere the factor weighting εm is 2 in order to meet the SPR condition, but with increasing aspect ratio the weighting factor [(1 − Pj)/Pj] can be much greater than 2 in a nanorod. This outcome leads to an apparent red-shift of plasmon response with increasing AR. For example, the plasmon resonance of gold nanorods can be tuned from the visible region around 640 nm to the near-infrared region >1000 nm when AR increases from 2.4 to 6.6,54 as shown in Fig. 3.
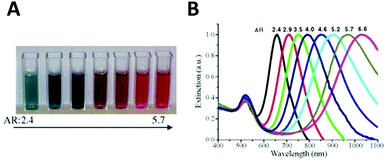 | ||
| Fig. 3 Variation of the nanoparticle shape (in this case, aspect ratio) allows tuning of the plasmon resonance of an Au nanorod from the visible to the near infrared. Different colors of aqueous solutions (A), and corresponding absorption spectra (B) as a function of aspect ratio.54 Reproduced from ref. 54 by permission of Elsevier B.V. Copyright (2010). | ||
In order to predict the plasmonic properties of arbitrary geometries of nanostructures, a number of numerical methods have been well developed, namely the finite-difference time domain (FDTD) method,55 the discrete dipole approximation (DDA),56 Greens-function approach,57 the multiple multipole (MMP) method,58 multiple scattering techniques, transfer-matrix approaches,59 plane wave expansions,60 and the boundary element method (BEM).61 In brief, with the support of proper modeling and theory, the enhancement of the electric field as the intensity of the surface plasmon resonance absorption increases can be exploited for many potential applications.39
On the other hand, although theoretical modeling of the optical response of metallic nanoparticles is well established,62 to better understand the electromagnetic properties of complex plasmonic nanostructures, an analytical theoretical method was suggested by Halas and Nordlander.63 This theory – a plasmon hybridization approach analogous to molecular orbital hybridization theory – suggests that the plasmon modes of a complex nanostructure are expressed in terms of interactions between the plasmon resonances of its elementary components, offering an intuitive description on how the plasmon resonances in assembled hybrid nanomaterials arise from the plasmon modes of their individual components.63,64 As shown in Fig. 4A, an individual plasmonic nanoparticle would couple plasmonic fields with an adjacent nanoparticle under polarized light illumination along the interparticle axis, which is directly analogous to the molecular orbital diagram. With one particle situated next to another, these two electron clouds hybridize according to quantum mechanics and form bonding and anti-bonding orbitals. When coupled, the hybridization between plasmonic pairs leads to a decrease of plasmon energy and corresponding red-shifted absorbance wavelength.
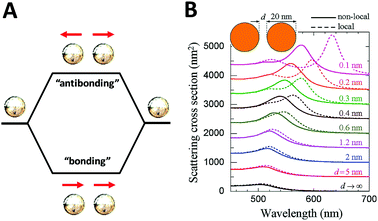 | ||
| Fig. 4 Schematic of plasmon–plasmon coupling of two plasmonic nanoparticles (A) and extinction spectra of dimers formed by spherical gold particles 20 nm in diameter (B) reported by F. J. García de Abajo et al.65 Local (dashed curves) and nonlocal (solid curves) calculations are compared for several separations between the particle surfaces. Reproduced from ref. 65 by permission of the American Chemical Society. Copyright (2008). | ||
The plasmon mode can be split into two collective modes, including a lower energy bonding mode which is aligned along longitudinal dipoles and a higher energy antibonding mode which is perpendicular. The bonding mode can strongly couple with the far field, but the antibonding one cannot and gives no net dipole moment and negligible induced dipole. Fig. 4B shows the scattering spectra of dimers formed by spherical gold particles of 20 nm in diameter.65 Decreased distance between two closely coupled gold particles gives rise to a red-shift of the plasmon peak, which can be explained by the occurrence of strong hybridization between plasmon dimer modes. In addition, it is also of note that when the interparticle distance is small enough (<1 nm), the non-local effect rises as indicated in by the solid lines.
3. Chirality in plasmonic nanostructures
As described before, CD spectroscopy is widely used to study chirality of materials and most studied materials are intrinsically chiral substances such as natural molecules. With the discovery of chiral ligand-protected metal nanoclusters came fundamental studies of induced plasmonic chirality. Principally, it is asserted that the CD response of such a system is induced by an intrinsically chiral metal core, chiral environment or footprint formed by the interactions between chiral ligands and metal core; or even a mixture of both issues. More recent studies claim that assembled plasmonic nanostructures, such as a complex of chiral molecules with achiral plasmonic nanoparticles, and “plasmonic molecules”63,64,66,67 with chiral configurations may have different origins of chirality than ligand-protected nanoclusters. Compared to plasmonic nanoclusters, nanoparticles have basically different LSPR than nanoclusters due to their energy band structures. Thus, it is not necessary to have similar mechanisms for induced plasmonic chirality in these cases. For a complex of chiral molecules with achiral plasmonic nanoparticles, the plasmon–exciton interactions can describe the coupling effect (Fig. 5).68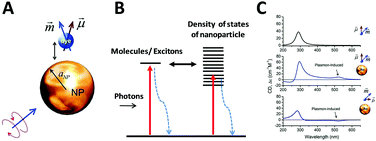 | ||
| Fig. 5 (A) Scheme of a complex composed of a metal nanoparticle and dye molecule. (B) Illustration of exciton–plasmon interaction in a chiral molecule–plasmonic NP complex. (C) Calculated CD signals for a molecule and two complexes from top to bottom, respectively. Insets show the geometry of the complexes.68 Reprinted from ref. 68 by permission of the American Chemical Society. Copyright (2010). | ||
If the absorption of the chiral molecule is located in the UV region, the electromagnetic interaction with a metal nanoparticle is off-resonance, resulting in an active CD response in both the plasmon band and molecular band (Fig. 5C). For this general case, from the definition of CD, one can refer to CD effects of a randomly oriented system as:68
| CD = 〈Q+ − Q−〉Ω, |
where a and R refers to the radius of the metal nanoparticles and the distance between metal core and molecular center, respectively. Notably, when the plasmon resonance of the metal nanoparticle and the molecular absorption band overlap (in-resonance), the CD signal shows a Fano-like shape indicating a strong interference between the molecule and plasmonic nanoparticle, thus the observed CD signal is the sum of the coupling effects of both. In addition, in some core–shell70,71 structures the scattering properties can be just as significant as the issues affecting the overall optical activities of the assemblies. Such contribution from scattering, CDsca, is referred to as the electrodynamic effect, which depends on dielectric properties and geometric parameters such as the size of the structures and shell thickness of individual components.
Yet when a chiral structure is built up by achiral plasmonic nanoparticles with well-defined particle number or superstructures like short helices, the CD response close to the plasmon wavelength is often due to dipole–dipole or plasmon–plasmon interactions. For these interactions, as illustrated previously, it is evident the CD signal is strongly related to the size of nanoparticles and the interparticle distance:41,69
4. Current progress on self-assembled plasmonic nanostructures with chiral configurations
Compared to single plasmonic nanoparticles, assemblies of plasmonic nanoparticles exhibit more sophisticated geometric aspects, which often give rise to collective physical properties absent in single nanoparticles. In terms of chiral self-assembly of metal nanoparticles, one can utilize achiral nanoparticles to obtain chiral plasmonic nanostructures exhibiting chiroptical properties by rationally designing and assembling the achiral building blocks. Owing to the well-established, collective localized properties, and tunable geometries of metal nanoparticles, induced chirality of assembled plasmonic nanostructures is often studied on the basis of assemblies with well-defined particle number, toward elucidating the mechanism for observed optical activities. Therefore, dimers or clusters with a countable number of nanoparticles, such as trimers and tetramers, are considered promising candidates as chiral plasmonic basic units for assembly. Then, more complicated structures such as helices, are treated as higher-ordered superstructures with more representative and collective effects derived from single particle–particle interactions. Herein we will focus on the experimental phenomena and underlying mechanisms of the optical activities derived from various plasmonic chiral systems, as well as their prospective applications.4.1 Assemblies of metal nanoparticles with chiral configurations
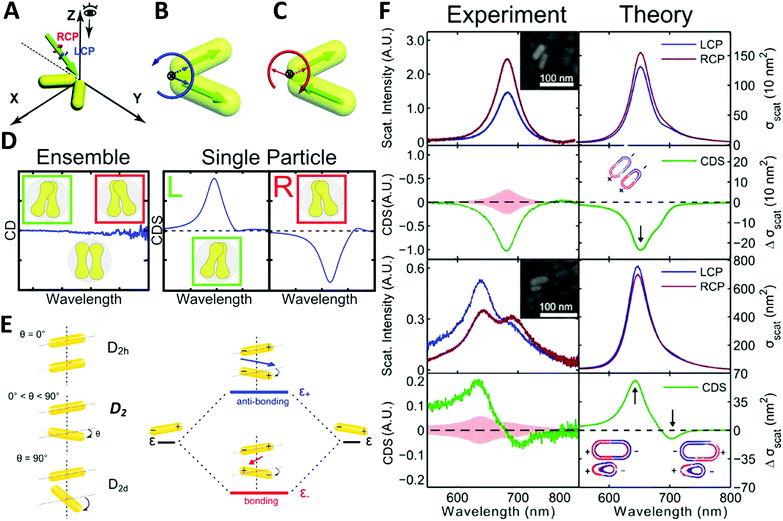 | ||
| Fig. 6 (A) illustration of extrinsically chiral arrangement of a gold nanorod dimer. The green arrow indicates the incident CPL with θ = 60° in the yz-plane, while the gold nanorod dimer lies in the xy-plane. Observation direction for far field scattering is along the z-axis. Interaction between the incident CPL and the dimer in the view of the propagating path is shown as (B). Dipole orientations of the symmetric mode match well with the spatial evolution of electric field vectors of LCP, while they are unfavorable for RCP. For the anti-symmetric mode, a favorable match is found with RCP (C).73 Reproduced from ref. 73 with permission from the Royal Society of Chemistry, Copyright (2014). (D) Chiral optical study of dumbbell-like gold nanorod dimer. Left: CD measurement of ensembled dimers with no chiroptical activity; right: CDS measurement of single particles showing strong chiral signals depending on the chiral geometry.74 Reproduced from ref. 74 with permission from the American Chemical Society, Copyright (2016). (E) Energy diagram describing the plasmonic hybridization of the two modes. The plus and minus signs denote the charge of the plasmon oscillation and the arrows represent the directions of the overall dipole moment. (F) Experimental and calculated scattering and CDS spectra of two AuNR dimers: homodimer and heterodimer.44 Reproduced from ref. 44 with permission from the American Chemical Society, Copyright (2015). | ||
Very recently, Liz-Marzán and Link74 demonstrated that dumbbell-like gold nanorod dimer in a racemic mixture can express strong optical activities in single-particle CDS measurements. Due to the electromagnetic coupling between AuNRs, the twisted AuNR dimer exhibits a characteristic bisignate CDS signal in the vicinity of the plasmon frequency of the AuNRs. Additionally, an interesting finding was that gold nanodumbbell dimers were optically inactive for ensemble measurement in a conventional CD spectrometer while expressing enantioselective CDS activities as a pure single dimer enantiomer, indicating the twist angle between the two constituent AuNRs played a significant role on CDS response (Fig. 6D). Furthermore, Link et al.44 reported chiroptical activity of a twisted side-by-side Au nanorod dimer. The effects of structural symmetry-breaking parameters, such as size difference between the two Au nanorods and twist angles, were studied respectively via CDS spectroscopy and modeling based on simulations. The mechanism of observed chiroptical response was illustrated by the plasmon hybridization theory in which opposite handedness of low-energy “bonding” and high-energy “antibonding” plasmonic modes, defined by the dihedral angle between the nanorods, were considered as the origin of chirality (Fig. 6E and F). It is, however, worth noting that the antibonding mode has the same handedness as the AuNR dimer structure rendering anti-aligned dipoles on each individual AuNR, while the bonding mode has the opposite handedness of aligned longitudinal dipoles in AuNRs, resulting in the two modes possessing CD responses of opposite sign. Additionally, this hybridization theory for induced plasmonic chirogenesis is suitable for some dimers made by NP–NP combinations with strong chiral activity, despite that ellipsoidally shaped NPs can only have a small dihedral angle.75,76
Other than plasmonic dimer systems, more sophisticated nanostructures are also suggested as chiral plasmonic units. The first instructive example is chiral plasmonic pyramids reported by Alivisatos et al.47 where the pyramidal nanostructures were built up by AuNPs conjugated with DNA. The DNA molecules on the AuNP surface served as the scaffold for the pyramid shape with four AuNPs of different sizes located on the vertices presenting a tetrahedral framework, like a chiral carbon atom, which expressed chirality as defined from a geometrical point of view (Fig. 7A). However, no clear CD signals were shown in these nanostructures, probably due to the weak plasmonic coupling between NPs and structural instability caused by single-stranded DNA scaffold. Such chiral assemblies were further studied by Kotov and co-workers,77 in which they obtained AuNPs and DNA pyramids by using the polymerase chain reaction (PCR) technique. The surface density of DNA molecules on the AuNPs and the number of PCR cycles determined the morphologies of the assemblies, revealing the process for the formation of different assemblies. The assemblies showed active CD spectra far from the absorption of DNA molecules but close to the plasmon frequencies of the AuNPs, which are highly sensitive to the morphology of the assemblies. It is therefore suggested that chirality originates from the plasmon–plasmon coupling of the AuNPs (Fig. 7B). However, one should always keep in mind that molecular chirality can cause morphological chirality. AuNPs conjugated with chiral ligands such as DNA or peptides as building blocks sometimes possess chiroptical properties themselves, due to the exciton–plasmon coupling between the chiral molecules and plasmonic nanoparticles. Admittedly, it may be difficult to ascribe the observed CD activities to one of these two mechanisms.
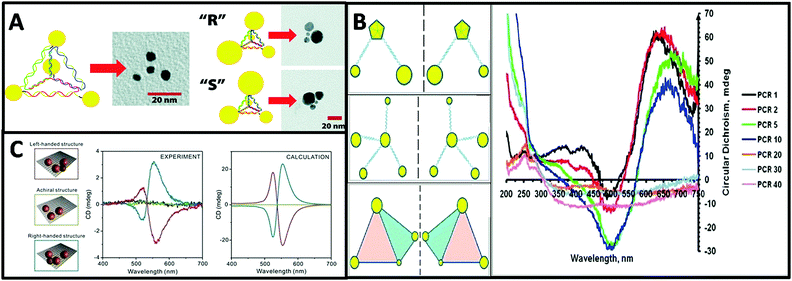 | ||
| Fig. 7 (A) Schematic and TEM images of a DNA–nanocrystal chiral pyramid and its two enantiomers.47 Reproduced from ref. 47 with permission from the American Chemical Society, Copyright (2009). (B) Schematics of chiral NP superstructures synthesized by PCR, and circular dichroism measurements of products of PCR with increasing number of cycles.77 Reprinted from ref. 77 with permission from the American Chemical Society, Copyright (2009). (C) Schematics of DNA-modified AuNPs tetrameters with left- (red), right-handed (blue), and achiral (green) geometry and their corresponding measured and calculated CD spectra.45 Reproduced from ref. 45 with permission from the American Chemical Society, Copyright (2013). | ||
Tetramers. Inspired by the multi-functionality of DNA molecules, plasmonic chiral tetramers made by addressable DNA templates are akin to chiral pyramid structures. Tetramers composed of four identical AuNPs with DNA origami can give a chiral response, confirming the minimum number of identical spherical AuNPs required for three-dimensional chirality.45 Since optical chirality in plasmonic meta-molecules is related to both structural symmetry and plasmonic coupling, the CD response is very sensitive to imperfections in the tetramers. Parameters such as size of the AuNPs, interparticle distance, and solvent effects can dramatically affect the CD lineshape, magnitude, and peak position (Fig. 7C). Later, simulation-based interacting point-dipole approach (PDA) and DDA method from Fan's work78,79 showed that the geometry of the chiral assembly determines the strength of the plasmonic CD effect. Comparing helical and pyramidal structures, an equilateral tetrahedral complex with four NPs has the smallest anisotropy factor, and thus the weakest CD response in the dipole model. The strength of the CD signal scales with interparticle distance R as 1/R9.7 for helices and as 1/R18.1 for equilateral tetrahedral complexes. Nevertheless, closely-packed equilateral tetrahedral assemblies can still show noticeable CD signal due to multipole interactions. An asymmetric chiral frame is the key factor for CD activity in the dipole regime, while in the multipole regime the mismatch in NP size also plays an important role for CD activity. In summary, Fan's calculations on chirality of plasmonic pyramids and tetrapods clusters suggest: (i) a chiral frame is crucial for generating a strong CD response; (ii) complexes with symmetric frames and NPs size of different size may be chiral, albeit with weaker CD signal than (i); (iii) equilateral tetrahedral complexes have very weak CD in the dipolar mode but express CD due to multipolar effects.
Template-assisted assembly of helical superstructures. Unlike traditional wet chemistry, where stringent control of the assembly of noble metal nanoparticles with well-defined morphology still remains challenging, template-assisted methods offer an alternative strategy for fabricating chiral plasmonic superstructures with strong interparticle coupling and collective effects in a controlled manner. In this “bottom up” approach, a patterned and passivated substrate is used to specifically induce or prevent the deposition of nanoparticles in selected areas. Versatile functionalization of the substrate and nanoparticles is required for achieving physical chemical interactions such as electrostatic attraction or repulsion and covalent bonding. An illustrative example of template-assisted chiral assembly of AuNRs is shown in Fig. 8A.80 Here, AuNRs capped by CTAB are co-assembled with an amphiphilic phospholipid template to form liquid crystal (LC) like mesophase hybrid structures with a helical arrangement of encapsulated AuNRs. The obtained plasmonic CD effect was ascribed to the coulombic dipole–dipole interactions between AuNRs. Therefore, parameters such as temperature, additives, and the aggregation state of AuNRs within the hybrid superstructure can be used to regulate the helical configuration of the LC-like AuNR mesophase, resulting in a significant difference in magnitude and sign of plasmonic CD signal. Thereafter, a detailed study was reported by Liz-Marzán and colleagues81 (Fig. 8B) where they used gold nanorods (45 nm long and 17 nm wide) and an anthraquinone-based oxalamide fiber template to synthesize a chiral nanocomposite. A systematic comparisons between this and other relevant plasmonic chiral systems such as chiral metal nanospheres and plasmonic metal particles conjugated with chiral molecules indicated that the anisotropy factor (g-factor) of such hybrid materials(0.022) was four-fold higher than the other systems (0.005), suggesting that anisotropic building blocks such as AuNRs are ideal candidates for obtaining strong plasmonic optical activity.
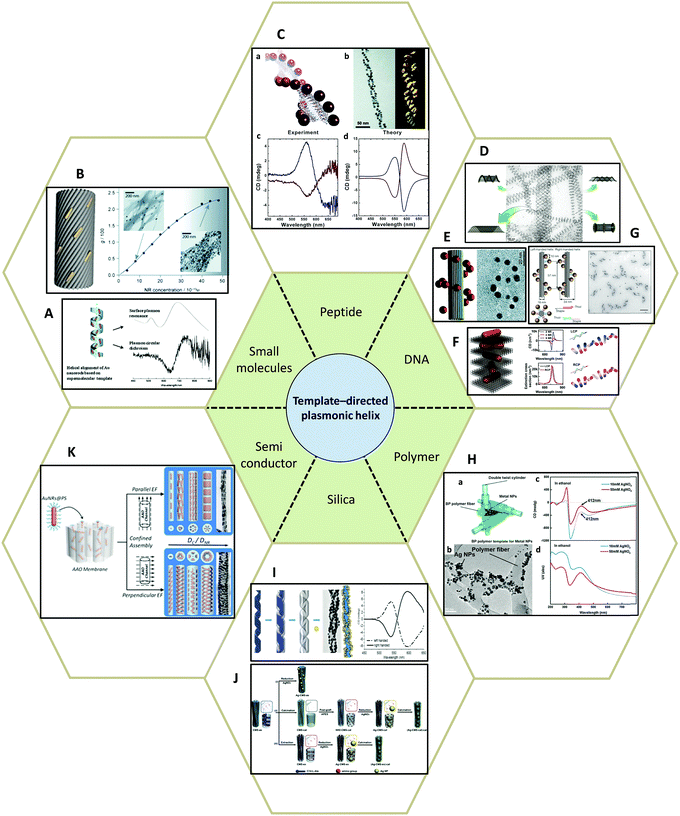 | ||
| Fig. 8 Template-directed synthesis of plasmonic helices. (A and B) Small molecules: (A) phospholipids,80 (B) anthraquinone-based oxalamide fibers.81 (C) Peptides.82–84 (D–G) DNA.48,85–87 (H) Synthetic polymer.89 (I and J) Silica template91,92 and (K) AAO.93 Adapted from the data of the cited papers by permission from the Royal Society of Chemistry, American Chemical Society, American Association for the Advancement of Science, Nature Publishing Group and Wiley. | ||
Peptides, as complex organic molecules with well-defined configurational chirality, are also suitable candidates for chiral deposition of nanoparticles. Rosi and colleagues,82–84 for example, reported the synthesis of highly ordered AuNPs grown on double helices by templating attachment via the peptide sequence (Fig. 8C). The AuNP–peptide conjugates are able to assemble into twisted nanofibers with a regular pitch of approximately 84 nm. However, their CD measurements did not show typical optical activity at the wavelength of AuNPs plasmon absorption. Currently, the chiroptical response of such nanostructures has been obtained by carefully tuning the geometrical parameters, namely pitch length, particle size, interparticle distance, and interhelical distance, which agrees well with simulations based on the DDA method. Moreover, Rosi et al. found that the CD intensity, peak position, and nature of the chiroptical activity can be carefully adjusted via silver overgrowth on as-synthesized gold double helices. When the thickness of the silver layer is grown above 1 nm, the CD signal starts to change sign due to the large blueshift in the plasmon resonances along with an increase in intensity.
Similarly, DNA molecules are effective platforms for chiral plasmonic assemblies with helical shape. In fact, DNA has already been shown to be an effective constituent for chiral co-assemblies, as stated earlier. DNA has also exhibited its convenience and practicality as a chiral template for self-assembly of plasmonic nanoparticles. In 2009, assemblies consisting of single-stranded DNA and AuNPs (Fig. 8D) were demonstrated as a powerful means to fabricate nanotubes of various 3D architectures ranging in shape from stacked rings, single spirals, double spirals, and nested spirals.85 Nanotube conformations can be tuned through the size-dependent steric repulsion effect by varying the AuNP size. The morphological evolution was monitored and revealed left-handed chirality in spiral tubes. Though it is admittedly hard to achieve intrinsically high morphology yield in one specific type of chiral spiral, these complex self-assembled 3D plasmonic nanostructures emphasized the possibility of fabricating chiral plasmonic helical structures at nanometer-scale precision. Shortly after, it was reported that by rolling and stapling a 2D DNA template, AuNPs that were assembled along two linear chains on a rectangular DNA origami sheet could be organized into a 3D helical configuration (Fig. 8E).86 Due to well-defined geometry and easily customized rectangular DNA origami, the deposition of AuNPs can be rationally controlled. The particle size-dependent peak-dip CD signal close to the vicinity of the plasmon resonances of AuNPs were shown to be CD signals arising from plasmon–plasmon interactions of closely packed AuNPs. Not limited to rolling up and stapling, 2D DNA origami templates also provide alternative approaches for the synthesis of chiral plasmonic helices. Wang87 reported that by designing an ‘X’ pattern of complementary DNA strands on both sides of a DNA origami template, AuNRs could be assembled into hierarchical architectures showing left-handed and right-handed helical morphologies (Fig. 8F). Such mirrored structures are finely tuned by adjusting the composition of the DNA molecules. With fixed thickness (14 nm) and inter-rod angle (45°), the helical framework is precisely controlled. The average number of AuNRs in the helix can be manipulated by modulating the ratio of AuNRs to DNA origami in a range from 2 to 4 and 9, which drastically affects the chiroptical activities of the assemblies. The observed intense CD signals show a maximum g-factor close to ∼0.02 when 9 AuNRs (AuNRs![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) DNA origami = 1
DNA origami = 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) are included in one helix. As compared with other similar systems,81 they found less AuNRs are needed to generate the same g-factor, indicating well-controlled asymmetric helical configurations dominate the chiroptical activity, rather than contribution of weak plasmonic coupling among poorly-aligned AuNRs. Their simulations also demonstrated that the chiroptical response of helical AuNR superstructures is derived from the collective oscillation modes of neighboring AuNRs. Therefore, the oscillation modes, parallel or antiparallel, decide characteristic dip-peak bisignate CD line shape.88
1) are included in one helix. As compared with other similar systems,81 they found less AuNRs are needed to generate the same g-factor, indicating well-controlled asymmetric helical configurations dominate the chiroptical activity, rather than contribution of weak plasmonic coupling among poorly-aligned AuNRs. Their simulations also demonstrated that the chiroptical response of helical AuNR superstructures is derived from the collective oscillation modes of neighboring AuNRs. Therefore, the oscillation modes, parallel or antiparallel, decide characteristic dip-peak bisignate CD line shape.88
Meanwhile, work by Kuzyk et al.,48 showed experimentally and theoretically the potential of DNA templates for programmable design of helical plasmonic nanostructures at nanoscale precision (Fig. 8G). Collective plasmon–plasmon interactions of the AuNPs were suggested to be the origin of chirality, from which they envisaged the splitting of the incident light between the longitudinal and transverse modes caused by the plasmonic dipole interactions of AuNPs within the helix, resulting in a peak-dip line shape in the CD spectrum. Plating the gold helix with silver was an effective means to modulate CD peak position and intensity, which provided a feasible way to produce negative refractive index materials without requiring either permittivity or permeability being negative.
Despite silver being less chemically and physically stable than gold, one can hardly deny its potential as a competitive candidate for the synthesis of chiral plasmonic superstructures. Silver possesses the lowest plasmon dissipation property and thus the strongest plasmon resonance of all known metals. A recent study showed that by reducing silver nitrate in presence of blue-phase (BP) polymer template, chiral plasmonic hybrid nanostructures can be obtained (Fig. 8H).89 Like chiral gold nanostructures, such hybrid architectures with silver nanoparticles exhibit optical activity close to the plasmon resonance of silver nanoparticles. Additionally, the hybrid nanostructure shows strong sensitivity to the dielectric environment, such as solvents, indicating that chirality originates from the plasmonic resonance of silver nanoparticles within the helicoidal periodicity of the BP polymer network.
Apart from organic templates, inorganic materials such as silica and metal oxides are also promising template materials. As is widely known, sol–gel chemistry has fashioned the synthesis of nanosized SiO2 or other metal oxide particles with fine controlled morphologies. Among them, chiral mesoporous silica nanostructures for instance, have been synthesized by cooperative self-assembly of chiral or achiral amphiphiles and silica precursors, and many related synthetic works have been well reviewed by Che.78,90 With the capability for robust templating, facile surface functionality and low absorption of visible light, chiral mesoporous silica templates are strong candidates for the synthesis of chiral plasmonic nanostructures. Recent work reported by Cheng et al.,91 exhibited that gold helix hybrid nanostructures could be synthesized via templating of AuNPs on silica nanohelices. The induced chirality of the nanostructures is finely tuned by the chiral geometry of the silica templates, size and concentration of the AuNPs, and the pH of the system. Simulations based on coupled dipole method (CDM) showed that the degree of disorder for the AuNPs deposited on the surface of silica helices plays a critical role for the intensity of the CD signals (Fig. 8I). Similarly, studies from Che's group92 showed that highly ordered achiral Ag nanoparticles assembled on a chiral mesoporous silica template can exhibit strong chiroptical properties. Three possible types of chirality were suggested: (i) the helical hexagonal surface, (ii) the helical pore orientation, and (iii) the helical arrangement of aminopropyl groups on the surface of the mesopores. The synthetic strategy to study the three types of chiral architectures individually is illustrated in Fig. 8J. Although all three types of chirality dramatically impacted the plasmonic CD signals, their further investigation showed the helical pore orientation was the dominant factor for optical response due to asymmetric plasmon interactions of silver nanoparticles within the chiral pores. Also, compared to helical pitch, the total length of the helical channel was dominant in determining the intensity of plasmonic CD effects.
In light of the silica template, metal oxides, such as anodic aluminium oxide (AAO) and titania, provides another means to connect chiral plasmonic materials to the field of light sensitive semiconducting nanomaterials. A recent study by Wang et al.93 illustrated the fabrication of confined assemblies of polystyrene-tethered AuNRs in AAO channels with the assistance of an electric field. By adjusting the electric field direction, pore size in AAO membranes, and molecular weight of polystyrene on the surface of the AuNRs, the morphology of the assemblies could be fine-tuned into highly ordered hierarchical structures such as chiral single-, double-, triple-, or quadruple-helices, achiral linear, and hexagonally packed structures. Among them, electric field orientation was demonstrated to be crucial for affecting the confinement strength, defined as the ratio of the pore size to NRs size, which eventually determined the packing mode of the assembly. Although no study of chiroptical activity was reported in this work, the facile manipulation of plasmonic coupling between the NPs by adjusting interparticle distance via polystyrene chain length unveiled its promising potential for chiral photoelectric device fabrication (Fig. 8K).
Chiral nematic assemblies of metal nanoparticles. Another facile yet effective approach for the synthesis of higher order chiral metal assemblies involves the formation of chiral nematic assemblies. Derived from the concept of nematic liquid crystals, chiral nematic assemblies consist of a chiral nematic liquid crystal matrix and achiral guests such as organic dyes and inorganic nanoparticles (NPs). In particular, when NPs are involved the chiroptical activity of the matrix can potentially interact with the plasmonic properties of metal NPs or excitonic properties of quantum dots, generating novel optical activity to the overall nanostructures. To date, a wide range of representative examples of such assemblies based on mesoporous silica or cholesteric liquid crystal matrices formed by cellulose nanocrystals (CNCs) have been studied. MacLachlan and co-workers,49 for instance, reported in 2011 that AgNPs can be engineered inside mesoporous silica films to form nematic nanostructures which exhibit optical activity close to the SPR frequency of the AgNPs by CD measurement. Their study on the effect of helical pitch on CD signal, and comparison of CD signals of their AgNPs and silica systems formed by mesoporous silica films with and without nematic ordering, revealed that observed chirality comes from the long-range organization of the AgNPs rather than AgNP assemblies within single pores, nor intrinsic chiral shape of the AgNPs (Fig. 9A). Afterwards, cholesteric liquid crystal matrices, especially formed by CNCs, were widely exploited as the chiral matrix for the synthesis. Recently, chiral nematic films made by CNC hosts and AuNRs,94 AuNPs,95 or AgNWs96 guests were synthesized and studied. All these systems showed strong sensitivity of the concentrations of the metal nanoparticles to the CD signals, but in the case of AuNRs,94 while the mechanism is not clear, Kumacheva et al. pointed out that the salt concentration (NaCl) also deeply affected the CD intensity (Fig. 9B). Their recent work97 also demonstrated that concentration of the metal nanoparticles, when compared to size and shape, showed the strongest influence on the properties of the composite films. In particular, when CNC films are loaded with plasmonic NPs with dimensions on the order of 40 nm and a concentration smaller than 2.84 × 10−2 nmol, a second CD peak in the CD spectrum arises due to the local reduction of CNC templates rather than plasmonic chiroptical activity. This can be characterized by Mueller matrix transmission ellipsometry via eliminating the influence of multiple overlapping effects.
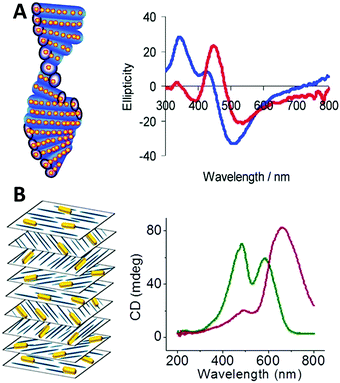 | ||
| Fig. 9 (A) Scheme of chiral nematic assemblies of AgNPs in mesoporous silica film and typical CD spectra of AgNP loaded silica film before (blue) and after (red) soaking with water.49 Reproduced from ref. 49 with permission from the American Chemical Society, Copyright (2011). (B) Illustration of nematic assemblies of AuNRs and cellulose nanocrystals and typical CD spectra of such chiral nematic structures. Red: the single peak was the result of combined CD signal of the CNC matrix and the longitudinal LSPR mode of the NRs; green: the double peaks refer to the chiral activity of CNC host and plasmonic chiroptical activity of the AuNRs at relatively high NaCl concentration.94 Reproduced from ref. 94 with permission from the American Chemical Society, Copyright (2014). | ||
4.2 Optically active Janus nanoparticles consisting of metals and semiconductors
Optically active binary systems made by both metals and semiconductors are also technically feasible. Like always, we start with simple geometries, then progress towards more complicated ones. It is then less surprising that when a plasmonic dimer98 or pyramid system is fabricated with semiconductors and metals, that their mismatched natural physical properties would induce alternative possibilities for symmetry breaking, expressing unexpected collective chiroptical activities. To date, Kotov's group99 demonstrated that when AuNRs assembled with chiral CdTe nanoparticles (CdTe nanoparticles conjugated with chiral organic molecules), different origins of chirality would be observed in CD measurement, depending on the molar excess of chiral CdTe nanoparticles. When such molar excess is small, the system is based on AuNR dimers with “scissor-like” conformation, yielding an “X” shape of the NRs in a dimer. This conformation leads to concomitant polarization rotation, which is sensitive to enantiomeric excess. Dissimilarly, when the molar excess is large, the overall system becomes largely single NRs due to electrostatic repulsion. In this case, the observed optical activity is ascribed to “cross-talk” between the longitudinal and transverse plasmonic modes of the NRs and the excitonic state of CdTe nanoparticles, or plasmon–exciton interactions (Fig. 10A). Their work on pyramid nano-assemblies46 also demonstrated that hetero-particle chiral pyramids can be fabricated via using both metal and semiconductor nanoparticles. Like the metal pyramid structures mentioned before, the synthesis of such hetero-pyramids is also based on DNA strands, which act as the scaffolds for immobilization of nanoparticles. Nonetheless, by adjusting the size or position of the identical metal nanoparticles, various species of nanoparticles such as AuNPs, AgNPs and CdSe/ZnS core/shell QDs were employed as the building blocks, providing a more simple and unique way to manipulate chiroptical activity across a wide range of UV and visible wavelengths. Again, as stated previously, the geometrical disposition of the nanoparticles is the key factor for the chiroptical activity. However, the presence of hetero-particles brings about other possible CD effects i.e. CD signals of QDs due to bandgap transitions, and more enhanced chirality in terms of anisotropy g-factors (∼10−3) due to high asymmetric geometry and enhanced SPR effects (Fig. 10B). In addition, achieving symmetry breaking in the nanoscale is often conducted via bottom-up techniques, but it does not rule out the possibility for top-down methods to be used for such synthesis. Fig. 10C shows chiral plasmonic nanopillars (CPN) made of achiral ZnO nanopillars coated with asymmetric gold nanoshells. Such asymmetric coating of gold is performed via vacuum evaporation at different inclination and rotation angles, resulting in L- or D-nanopillar isomers with symmetry breaking. Intense CD response was found to be related to the aspect ratio of Au nanoshells on the ZnO nanopillars. Moreover, these chiral Au nanoshells endow chiroptical properties to the achiral ZnO nanopillars which exhibit weak CD peaks at around 375 nm. This indicates that the oscillation mode of charge carriers in ZnO nanopillars can couple with the asymmetric plasmon resonance mode of chiral Au nanoshells, explaining the chiral absorption of the achiral ZnO nanopillars.100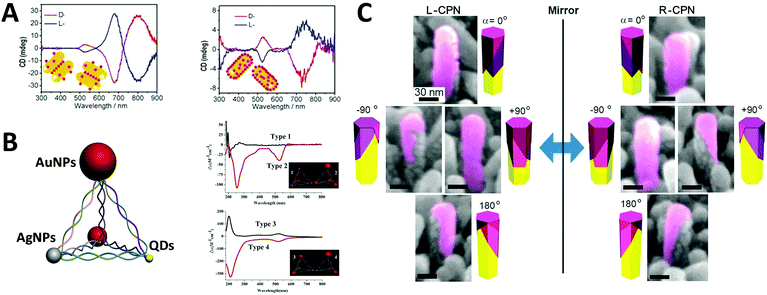 | ||
| Fig. 10 (A) CD spectra of the chiral supra-particles assemblies with (left) low and (right) large molar excess of CdTe quantum dots. Red and blue lines represent D- and L-geometry; the inset is a schematic representation of the proposed structure of the corresponding chiral supra-particles assemblies.99 Reproduced from ref. 99 with permission from the American Chemical Society, Copyright (2014) (B) scheme of chiral NP pyramid made by plasmonic nanoparticles (gold and silver, red and grey) and semiconducting quantum dots (yellow), and CD spectra of self-assembled pyramids made from four 10 nm AuNPs (type 1) and three 15 nm AuNPs + one 25 nm AuNPs (type 2); (B) two 15 nm AuNPs + two CdSe@ZnSQDs (type 3), and one 15 nm AuNPs + one 25 nm AuNPs + two CdSe@ZnS QDs (type 4). Inset: Corresponding illustrations of the 4 types of chiral pyramids.46 Reproduced from ref. 46 with permission from the American Chemical Society, Copyright (2012) (C) tilted SEM images of (left) L-CPN and (right) R-CPN viewed from different angles. The relative direction of the views is given in the corner of each image.100 Reproduced from ref. 100 with permission from the American Chemical Society, Copyright (2013). | ||
5. Conclusion and perspectives
Study of self-assembled nanostructures with chiral plasmonic behavior is a newly flourishing field that has been greatly developed over the past decade and will likely grow in the coming years. With an increasing need for the design and fabrication of innovative materials, chiral plasmonic assemblies may hold the key for developing solutions to many problems, rendering great potential for molecular sensing, environmental remediation, and energy conversion, as well as other optical applications.A conventional direction involves chiral plasmonic sensing. With tailorable SPR and CD activity, a variety of sensors have been fabricated based on chiral plasmonic assembles. In this area, lots of advanced work is reported by Xu and his partners who have successfully utilized chiral plasmonic units for the detection of inorganic ions such as Ag+ and Hg2+, and organic molecules such as prostate-specific antigen (PSA),76,101 peptides/proteins,75 RNA102,103 and DNA.104 Generally, by using chiral plasmonic units, namely AuNP–AgNP dimers, AuNP/AgNP-QD dimers, AuNR–AuNRs/AuNP dimers, AgNPs based pyramids, or even chiral AuNRs assemblies ranging from dimers to pentamers, CD-based sensing methods can be developed to detect the concentration of bridge molecules that are involved in the synthesis of the plasmonic chiral structures. Since chiroplasmonic CD activity is highly sensitive to the geometry of the nanostructures, which can be largely affected by the concentration of the bridge molecules, this sensing method can greatly extend the limit of detection (LOD). This would provide a feasible approach for the detection of biological analytes larger than 2–5 nm, which are often difficult for conventional plasmonic sensing methods (Fig. 11A–C).104 Moreover, with rapid development of chiral sensing, chiroplasmonic therapy105,106 and manipulation of biological activities of cells through chiral plasmonic materials becomes possible.107 Xu's recent work, for example, reports DNA-based self-assembly of plasmonic shell-satellite nanostructures which can be used as chiral photosensitizers. Under circularly polarized light illumination, they can have high reactive oxygen species generating efficiency. This property makes them a useful photodynamic therapy (PDT) agent with remarkable efficiency in tumors targeting and therapy.105
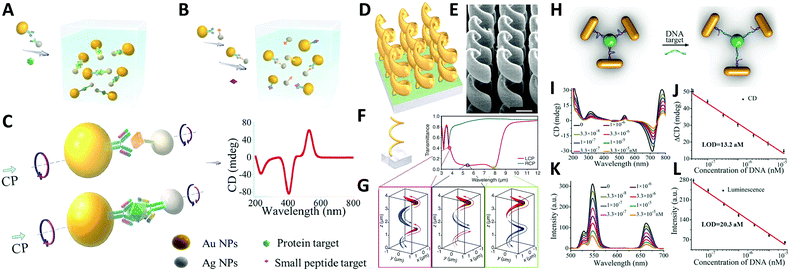 | ||
| Fig. 11 Applications of chiral plasmonic nanostructures. (A–C) Plasmonic sensing via chiral NP dimers. (A and B) The NP dimer was assembled from AuNPs and AgNPs which were functionalized with complementary biomacromolecules (A). The detection of small peptides, exemplified by microcystin-LR. (B) Detection of the fairly large proteins, exemplified by prostate-specific antigen; (C) scheme of the NP dimers bridged by immunocomplexes used in competitive and sandwich immunoassays.104 Reproduced from ref. 104 with permission from Nature Publishing Group, Copyright (2013). (D–G) Chiral gold helical metamaterials made by CVD; (D and E) schematics and SEM images of the gold helices film; (F) two helix pitches (left-handed) and snapshots (G) of the electric current distribution along the metal wire for the three wavelengths [open dots in (F)]. The absolute value of the current is encoded by the curve thickness, the sign by red and blue (see arrows).108 Reproduced from ref. 108 with permission from American Association for the Advancement of Science, Copyright (2009). (H–L) DNA detection by up-conversion luminescent and chiroplasmonic techniques with the NR-UCNP tetramer assembly. (H) Scheme of the DNA biosensing. (I) The CD and (J) up-conversion luminescence curves with increasing concentrations of DNA solution. (K) The CD and (L) up-conversion luminescent calibration curves for DNA detection. The longitudinal absorption peak of NR using for assembly was 750 nm.109 Reproduced from ref. 109 with permission from Wiley, Copyright (2016). | ||
Manipulation of polarized optical effects such as asymmetric transmission110 and polarization conversion111,112 can also be achieved via chiroplasmonic nanostructures. N. I. Zheludev's group proves that in visible to near-IR frequencies, normal incidence transmission of circularly polarized light is asymmetric in the opposite directions when anisotropic planar chiral nanostructures are used, suggesting a novel type of enantiomerically sensitive plasmon excitation.110 P. Biagioni et al.,113 for example, showed that a cross resonant optical antenna, consisting of two perpendicular nanosized gold dipoles, can be used to finely tune the propagating fields of any polarization state into correspondingly polarized, localized, and enhanced fields.
Furthermore, the emerging area of assembled plasmonics114,115 is closely related to refractive index manipulation, where the mechanism and designs of negative effective refractive index media are related to the excitation of plasmons in the nano-metallic particles. However, at a minimum, it is required that either the permittivity or permeability of the materials should be negative to achieve metamaterials at a certain frequency range. The rising interest in chirality offers another alternative without such limits.116,117 Similar to metamaterials designed for linear polarized waves, chiral metamaterials are composed of periodic arrangements of artificial building blocks with chirality.118,119 With the existence of chirality, electromagnetic coupling between the magnetic and electric fields occurs at the plasmon resonance frequency. In order to describe such coupling, chirality parameter κ is introduced to the constitutive relations as:
| D = ε0εE + iκ/c0H |
| B = μ0μH − iκ/c0E |
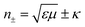 . This means when κ is large enough either n+ or n− becomes negative, rendering negative refraction easier to achieve and offer simpler designs of metamaterials. In fact, negative refraction has been well achieved in microwave range via many planar helicoidal plasmonic structures. Owing to the strong electromagnetic interactions within the chiral building blocks and the local electromagnetic field, giant optical chirality is observed, enabling a negative refractive index by dramatically magnifying the chirality parameter. A typical example is the 3D gold helix with uniaxial orientations made by Gansel et al.,108 in which gold helices were synthesized via CVD method in the square lattice after laser writing on the photoresist. The obtained chiral photonic metamaterial showed selective propagation of light. It basically blocks the circular polarization with the same handedness as the helices, whereas it transmits the other within a certain frequency range. Nevertheless, these chiral metamaterials are all based on top-down methods, such as lithography and chemical or physical deposition, indicating that to achieve chiral metamaterials in the visible frequency is tremendously challenging. The periodicity requires the size of building blocks in metamaterials to be at least ten times smaller than the wavelength of incident light to ensure the macroscopic effective parameters, such as permeability and permittivity, can be used to describe the material. Alternatively, chiral plasmonic assemblies at the nanoscale can provide a different means to approach metamaterials design. Though it is still in its infancy, such nanostructures have revolutionized both the scope of metamaterials into the visible range and synthetic methods to the realm of bottom up approaches with more systematic control (Fig. 11D–G).
. This means when κ is large enough either n+ or n− becomes negative, rendering negative refraction easier to achieve and offer simpler designs of metamaterials. In fact, negative refraction has been well achieved in microwave range via many planar helicoidal plasmonic structures. Owing to the strong electromagnetic interactions within the chiral building blocks and the local electromagnetic field, giant optical chirality is observed, enabling a negative refractive index by dramatically magnifying the chirality parameter. A typical example is the 3D gold helix with uniaxial orientations made by Gansel et al.,108 in which gold helices were synthesized via CVD method in the square lattice after laser writing on the photoresist. The obtained chiral photonic metamaterial showed selective propagation of light. It basically blocks the circular polarization with the same handedness as the helices, whereas it transmits the other within a certain frequency range. Nevertheless, these chiral metamaterials are all based on top-down methods, such as lithography and chemical or physical deposition, indicating that to achieve chiral metamaterials in the visible frequency is tremendously challenging. The periodicity requires the size of building blocks in metamaterials to be at least ten times smaller than the wavelength of incident light to ensure the macroscopic effective parameters, such as permeability and permittivity, can be used to describe the material. Alternatively, chiral plasmonic assemblies at the nanoscale can provide a different means to approach metamaterials design. Though it is still in its infancy, such nanostructures have revolutionized both the scope of metamaterials into the visible range and synthetic methods to the realm of bottom up approaches with more systematic control (Fig. 11D–G).
Another practical direction relates to studies of energy conversion-based applications. Photon upconversion120 is an anti-Stokes process in which the sequential absorption of two or more low energy photons leads to high energy emission of light. The conventional upconversion nanomaterials often suffer from low energy conversion efficiency, for example lanthanide-doped luminescence upconversion nanomaterials generally have luminescence efficiencies less than 1%. An efficient remedy to improve the situation is to use the SPR effect of plasmonic nanoparticles. Recently, Xu's group109 reported that propeller-like chiral assemblies of AuNRs and lanthanide-doped luminescence upconversion nanoparticles (UCNPs) can lead to an enhancement of upconversion luminescence as great as 21.3 fold via plasmonic resonance coupling. As illustrated in Fig. 11H, such chiral plasmonic tetramers are fabricated via co-assembly of DNA-modified AuNRs with DNA-modified UCNPs. By tuning parameters such as the length of DNA molecules, diameter of the UCNP, and the aspect ratios of AuNRs to the UCNPs, intense chiroptical activity can be achieved in the visible plasmonic region due to the unique propeller-like geometry of the assemblies. In addition, up-conversion luminescence (UCL) of Yb/Er doped UCNP was enhanced for emission peaks at 529, 546, and 662 nm. This phenomenon matches well with the DNA hybridization process for tetramer formation, which is largely affected by plasmon resonance interactions i.e. interparticle distances between AuNRs and UCNPs and the size of AuNRs and UCNPs. Furthermore, such materials with both chiroptical activity and UCL have been successfully used for biosensing of oligonucleotides, confirming the versatility of the method (Fig. 11H–L).
In addition, if we extended the plasmonic response of inorganic nanocrystals into metal oxides or doped semiconductors, the LSPR properties of doped semiconductor nanocrystals can also provide a versatile toolbox for obtaining chiral plasmonic nanostructures with induced chirality. Different from metallic nanomaterials whose extinction peak is generally associated to their size, shape and chemical compositions, the extinction peak of doped semiconductor nanocrystals can be easily modulated via changing carrier concentration through chemical doping. To date, a variety of substoichiometry semiconductor nanocrystals such as Cu2−xS,121,122 indium oxide,123 germanium telluride,124 tungsten oxide,125 zinc oxide,126,127 and molybdenum oxide128 have been extensively studied for their LSPR behaviors. Tunable control of their LSPR response was often achieved via defect engineering129 and liquid exfoliation approaches.130 In light of the merits of doped semiconductors nanocrystals, Kotov and colleagues131 synthesized chiral WO3−x nanoparticles via a bio-to-nano chirality transfer approach. The difference in CD response of WO3−x induced by proline (Pro) and aspartic acid (Asp) respectively are related to the degree of distortion of the inorganic crystal lattice, which is confirmed by atomistic molecular dynamics simulations. Although enantioselective preparation of chiral plasmonic nanostructures with doped semiconductors is difficult, the development of this area is still open for more systematic studies on chiral synthesis of higher-order structures and mechanisms for understanding the plasmonic chirality in these materials.
In summary, the skyrocketing development on the design and fabrication of plasmonic chiral nanomaterials presents great potential for this field, giving researchers adequate foundations for obtaining novel advances and practical merits. However, it is worth noting that the study on plasmonic optical chirality is still in its infancy. Progressive investigations on the CD generation and incisive explanations on the origin of chirality as well as theoretical simulations are still expected to improve the field. Detailed studies on the plasmonic NP–chiral molecule and NP–NP interactions supported by interdisciplinary areas such as plasmonic biosensors, chiral metamaterials, and time-resolved nonlinear optics will inevitably trigger further development of this area, providing us new horizons together with brand-new challenges.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
We thank the National Natural Science Foundation of China (NSFC Grant No. 11404219), the Shenzhen Basic Research Project of Science and Technology (Grant No. JCYJ2015032414171163 and JCYJ20170302142433007), and the Army Research Office (W911NF-17-1-0561).Notes and references
- M. Pelton and G. W. Bryant, Introduction to metal-nanoparticle plasmonics, John Wiley & Sons, 2013 Search PubMed.
- E. J. Blackie, E. C. L. Ru and P. G. Etchegoin, J. Am. Chem. Soc., 2009, 131, 14466–14472 CrossRef CAS PubMed.
- R. Tamoto, S. Lecomte, S. Si, S. Moldovan, O. Ersen, M.-H. Delville and R. Oda, J. Phys. Chem. C, 2012, 116, 23143–23152 CAS.
- S. L. Kleinman, E. Ringe, N. Valley, K. L. Wustholz, E. Phillips, K. A. Scheidt, G. C. Schatz and R. P. Van Duyne, J. Am. Chem. Soc., 2011, 133, 4115–4122 CrossRef CAS PubMed.
- J. A. Dieringer, R. B. Lettan, K. A. Scheidt and R. P. Van Duyne, J. Am. Chem. Soc., 2007, 129, 16249–16256 CrossRef CAS PubMed.
- J. Pendry, Science, 1999, 285, 1687–1688 CrossRef CAS.
- S. A. Maier, P. G. Kik, H. A. Atwater, S. Meltzer, E. Harel, B. E. Koel and A. A. Requicha, Nat. Mater., 2003, 2, 229–232 CrossRef CAS PubMed.
- A. O. Govorov, J. Lee and N. A. Kotov, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 76, 125308 CrossRef.
- P. K. Jain, X. Huang, I. H. El-Sayed and M. A. El-Sayed, Plasmonics, 2007, 2, 107–118 CrossRef CAS.
- A. J. Haes, W. P. Hall, L. Chang, W. L. Klein and R. P. Van Duyne, Nano Lett., 2004, 4, 1029–1034 CrossRef CAS.
- K.-S. Lee and M. A. El-Sayed, J. Phys. Chem. B, 2006, 110, 19220–19225 CrossRef CAS PubMed.
- A. D. McFarland and R. P. Van Duyne, Nano Lett., 2003, 3, 1057–1062 CrossRef CAS.
- S. Eustis and M. A. El-Sayed, Chem. Soc. Rev., 2006, 35, 209–217 RSC.
- Y. Kim, R. C. Johnson and J. T. Hupp, Nano Lett., 2001, 1, 165–167 CrossRef CAS.
- S. A. Maier, M. L. Brongersma, P. G. Kik, S. Meltzer, A. A. Requicha and H. A. Atwater, Adv. Mater., 2001, 13, 1501–1505 CrossRef CAS.
- H. A. Atwater and A. Polman, Nat. Mater., 2010, 9, 205–213 CrossRef CAS PubMed.
- S. Lal, S. Link and N. J. Halas, Nat. Photonics, 2007, 1, 641–648 CrossRef CAS.
- S. K. Ghosh and T. Pal, Chem. Rev., 2007, 107, 4797–4862 CrossRef CAS PubMed.
- M. Rycenga, C. M. Cobley, J. Zeng, W. Li, C. H. Moran, Q. Zhang, D. Qin and Y. Xia, Chem. Rev., 2011, 111, 3669–3712 CrossRef CAS PubMed.
- M. B. Cortie and A. M. McDonagh, Chem. Rev., 2011, 111, 3713–3735 CrossRef CAS PubMed.
- M. Rycenga, C. M. Cobley, J. Zeng, W. Li, C. H. Moran, Q. Zhang, D. Qin and Y. Xia, Chem. Rev., 2011, 111, 3669–3712 CrossRef CAS PubMed.
- V. Giannini, A. I. Fernandez-Dominguez, S. C. Heck and S. A. Maier, Chem. Rev., 2011, 111, 3888–3912 CrossRef CAS PubMed.
- M. R. Jones, K. D. Osberg, R. J. Macfarlane, M. R. Langille and C. A. Mirkin, Chem. Rev., 2011, 111, 3736–3827 CrossRef CAS PubMed.
- J. Homola, S. S. Yee and G. Gauglitz, Sens. Actuators, B, 1999, 54, 3–15 CrossRef CAS.
- K. Catchpole and A. Polman, Opt. Express, 2008, 16, 21793–21800 CrossRef CAS PubMed.
- M. G. Kang, T. Xu, H. J. Park, X. Luo and L. J. Guo, Adv. Mater., 2010, 22, 4378–4383 CrossRef CAS PubMed.
- J.-L. Wu, F.-C. Chen, Y.-S. Hsiao, F.-C. Chien, P. Chen, C.-H. Kuo, M. H. Huang and C.-S. Hsu, ACS Nano, 2011, 5, 959–967 CrossRef CAS PubMed.
- M. D. Brown, T. Suteewong, R. S. S. Kumar, V. D’Innocenzo, A. Petrozza, M. M. Lee, U. Wiesner and H. J. Snaith, Nano Lett., 2010, 11, 438–445 CrossRef PubMed.
- J. Pendry, Science, 2004, 306, 1353–1355 CrossRef CAS PubMed.
- C. Sönnichsen, B. M. Reinhard, J. Liphardt and A. P. Alivisatos, Nat. Biotechnol., 2005, 23, 741–745 CrossRef PubMed.
- S. Zhang, D. A. Genov, Y. Wang, M. Liu and X. Zhang, Phys. Rev. Lett., 2008, 101, 047401 CrossRef PubMed.
- L. D. Barron, J. Mol. Struct., 1983, 101(3), 343–344 Search PubMed.
- A. Passaseo, M. Esposito, M. Cuscunà and V. Tasco, Adv. Opt. Mater., 2017, 5, 1601079 CrossRef.
- A. Ben-Moshe, B. M. Maoz, A. O. Govorov and G. Markovich, Chem. Soc. Rev., 2013, 42, 7028–7041 RSC.
- J. T. Collins, C. Kuppe, D. C. Hooper, C. Sibilia, M. Centini and V. K. Valev, Adv. Opt. Mater., 2017, 5, 1700182 CrossRef.
- Y. Luo, C. Chi, M. Jiang, R. Li, S. Zu, Y. Li and Z. Fang, Adv. Opt. Mater., 2017, 1700040 CrossRef.
- W. Ma, L. Xu, A. F. de Moura, X. Wu, H. Kuang, C. Xu and N. A. Kotov, Chem. Rev., 2017, 117, 8041–8093 CrossRef CAS PubMed.
- C. Noguez and I. L. Garzón, Chem. Soc. Rev., 2009, 38, 757–771 RSC.
- A. Guerrero-Martínez, J. L. Alonso-Gómez, B. Auguié, M. M. Cid and L. M. Liz-Marzán, Nano Today, 2011, 6, 381–400 CrossRef.
- X. Lan and Q. Wang, Adv. Mater., 2016, 28(47), 10499–10507 CrossRef CAS PubMed.
- A. O. Govorov, Y. K. Gun'ko, J. M. Slocik, V. A. Gérard, Z. Fan and R. R. Naik, J. Mater. Chem., 2011, 21, 16806–16818 RSC.
- Y. Wang, J. Xu, Y. Wang and H. Chen, Chem. Soc. Rev., 2013, 42, 2930–2962 RSC.
- C. Hao, L. Xu, W. Ma, L. Wang, H. Kuang and C. Xu, Small, 2014, 10, 1805 CrossRef CAS PubMed.
- L.-Y. Wang, K. W. Smith, S. Dominguez-Medina, N. Moody, J. M. Olson, H. Zhang, W.-S. Chang, N. Kotov and S. Link, ACS Photonics, 2015, 2, 1602–1610 CrossRef CAS.
- X. Shen, A. Asenjo-Garcia, Q. Liu, Q. Jiang, F. J. García De Abajo, N. Liu and B. Ding, Nano Lett., 2013, 13, 2128 CrossRef CAS PubMed.
- W. Yan, L. Xu, C. Xu, W. Ma, H. Kuang, L. Wang and N. A. Kotov, J. Am. Chem. Soc., 2012, 134, 15114–15121 CrossRef CAS PubMed.
- A. J. Mastroianni, S. A. Claridge and A. P. Alivisatos, J. Am. Chem. Soc., 2009, 131, 8455–8459 CrossRef CAS PubMed.
- A. Kuzyk, R. Schreiber, Z. Fan, G. Pardatscher, E.-M. Roller, A. Hogele, F. C. Simmel, A. O. Govorov and T. Liedl, Nature, 2012, 483, 311–314 CrossRef CAS PubMed.
- H. Qi, K. E. Shopsowitz, W. Y. Hamad and M. J. MacLachlan, J. Am. Chem. Soc., 2011, 133, 3728–3731 CrossRef CAS PubMed.
- S. M. Morton, D. W. Silverstein and L. Jensen, Chem. Rev., 2011, 111, 3962–3994 CrossRef CAS PubMed.
- K. M. Mayer and J. H. Hafner, Chem. Rev., 2011, 111, 3828–3857 CrossRef CAS PubMed.
- M. Li, S. K. Cushing and N. Wu, Analyst, 2015, 140, 386–406 RSC.
- G. V. Hartland, Chem. Rev., 2011, 111, 3858–3887 CrossRef CAS PubMed.
- X. Huang and M. A. El-Sayed, J. Adv. Res., 2010, 1, 13–28 CrossRef.
- E. K. Miller, J. Electromagnet. Wave, 2012, 8, 1125–1172 CrossRef.
- B. T. Draine and P. J. Flatau, J. Opt. Soc. Am. A, 1994, 11, 1491–1499 CrossRef.
- C. Girard, A. Dereux and O. J. F. Martin, Phys. Rev. Lett., 1996, 76, 2405 CrossRef PubMed.
- C. Hafner and R. Ballisti, COMPEL, 1983, 2, 1–7 CrossRef.
- J. B. Pendry and A. Mackinnon, Phys. Rev. Lett., 1992, 69, 2772 CrossRef CAS PubMed.
- K. M. Leung and Y. F. Liu, Phys. Rev. B: Condens. Matter Mater. Phys., 1990, 41, 10188–10190 CrossRef.
- F. J. García De Abajo and A. Howie, Phys. Rev. Lett., 1998, 80, 5180–5183 CrossRef.
- V. Myroshnychenko, J. Rodríguez-Fernández, I. Pastoriza-Santos, A. M. Funston, C. Novo, P. Mulvaney, L. M. Liz-Marzán and F. J. G. de Abajo, Chem. Soc. Rev., 2008, 37, 1792–1805 RSC.
- N. J. Halas, S. Lal, W.-S. Chang, S. Link and P. Nordlander, Chem. Rev., 2011, 111, 3913–3961 CrossRef CAS PubMed.
- E. Prodan, C. Radloff, N. J. Halas and P. Nordlander, Science, 2003, 302, 419–422 CrossRef CAS PubMed.
- F. J. García de Abajo, J. Phys. Chem. C, 2008, 112, 17983–17987 Search PubMed.
- M. Hentschel, M. Schäferling, T. Weiss, N. Liu and H. Giessen, Nano Lett., 2012, 12, 2542–2547 CrossRef CAS PubMed.
- S. J. Barrow, A. M. Funston, D. E. Gómez, T. J. Davis and P. Mulvaney, Nano Lett., 2011, 11, 4180–4187 CrossRef CAS PubMed.
- A. O. Govorov, Z. Fan, P. Hernandez, J. M. Slocik and R. R. Naik, Nano Lett., 2010, 10, 1374 CrossRef CAS PubMed.
- Z. Fan, H. Zhang, R. Schreiber, T. Liedl, G. Markovich, V. Gérard, Y. Gun'Ko and A. Govorov, Chiral Nanostructures with Plasmon and Exciton Resonances, 2014 Search PubMed.
- X. Wu, L. Xu, W. Ma, L. Liu, H. Kuang, W. Yan, L. Wang and C. Xu, Adv. Funct. Mater., 2015, 25, 987 CrossRef.
- C. Hao, L. Xu, W. Ma, X. Wu, L. Wang, H. Kuang and C. Xu, Adv. Funct. Mater., 2015, 25, 5816–5822 CrossRef CAS.
- L. Xu, M. Sun, W. Ma, H. Kuang and C. Xu, Mater. Today, 2016, 19, 595–606 CrossRef CAS.
- X. Lu, J. Wu, Q. Zhu, J. Zhao, Q. Wang, L. Zhan and W. Ni, Nanoscale, 2014, 6, 14244–14253 RSC.
- K. W. Smith, H. Zhao, H. Zhang, A. Sánchez-Iglesias, M. Grzelczak, Y. M. Wang, W.-S. Chang, P. Nordlander, L. M. Liz-Marzan and S. Link, ACS Nano, 2016, 10(6), 6180–6188 CrossRef CAS PubMed.
- H. Zhao, S. Bian, Y. Yang and X. Wu, Microchim. Acta, 2017, 184(6), 1855–1862 CrossRef CAS.
- X. Wu, L. Xu, L. Liu, W. Ma, H. Yin, H. Kuang, L. Wang, C. Xu and N. A. Kotov, J. Am. Chem. Soc., 2013, 135, 18629–18636 CrossRef CAS PubMed.
- W. Chen, A. Bian, A. Agarwal, L. Liu, H. Shen, L. Wang, C. Xu and N. A. Kotov, Nano Lett., 2009, 9, 2153–2159 CrossRef CAS PubMed.
- Z. Fan, H. Zhang and A. O. Govorov, J. Phys. Chem. C, 2013, 117, 14770–14777 CAS.
- Z. Fan and A. O. Govorov, Nano Lett., 2010, 10(7), 2580 CrossRef CAS PubMed.
- R.-Y. Wang, H. Wang, X. Wu, Y. Ji, P. Wang, Y. Qu and T.-S. Chung, Soft Matter, 2011, 7, 8370–8375 RSC.
- A. Guerrero-Martínez, B. Auguié, J. L. Alonso-Gómez, Z. Džolić, S. Gómez-Graña, M. Žinić, M. M. Cid and L. M. Liz-Marzán, Angew. Chem., Int. Ed., 2011, 50, 5499–5503 CrossRef PubMed.
- C.-L. Chen, P. Zhang and N. L. Rosi, J. Am. Chem. Soc., 2008, 130, 13555–13557 CrossRef CAS PubMed.
- C. L. Chen and N. L. Rosi, J. Am. Chem. Soc., 2010, 132, 6902 CrossRef CAS PubMed.
- C. Song, M. G. Blaber, G. Zhao, P. Zhang, H. C. Fry, G. C. Schatz and N. L. Rosi, Nano Lett., 2013, 13(7), 3256–3261 CrossRef CAS PubMed.
- J. Sharma, R. Chhabra, A. Cheng, J. Brownell, Y. Liu and H. Yan, Science, 2009, 323, 112–116 CrossRef CAS PubMed.
- X. Shen, C. Song, J. Wang, D. Shi, Z. Wang, N. Liu and B. Ding, J. Am. Chem. Soc., 2011, 134, 146–149 CrossRef PubMed.
- X. Lan, X. Lu, C. Shen, Y. Ke, W. Ni and Q. Wang, J. Am. Chem. Soc., 2014, 137, 457–462 CrossRef PubMed.
- A. Christofi, N. Stefanou, G. Gantzounis and N. Papanikolaou, J. Phys. Chem. C, 2012, 116, 16674–16679 CAS.
- Y. Shi, J. Mo, J. Wei and J. Guo, New J. Chem., 2015, 39, 1899–1904 RSC.
- H. Qiu and S. Che, Chem. Soc. Rev., 2011, 40, 1259–1268 RSC.
- J. Cheng, G. Le Saux, J. Gao, T. Buffeteau, Y. Battie, P. Barois, V. Ponsinet, M.-H. Delville, O. Ersen, E. Pouget and R. Oda, ACS Nano, 2017, 11(4), 3806–3818 CrossRef CAS PubMed.
- J. Xie, Y. Duan and S. Che, Adv. Funct. Mater., 2012, 22, 3784–3792 CrossRef CAS.
- K. Wang, S.-M. Jin, J. Xu, R. Liang, K. Shezad, Z. Xue, X. Xie, E. Lee and J. Zhu, ACS Nano, 2016, 10, 4954–4960 CrossRef CAS PubMed.
- A. Querejeta-Fernández, G. G. Chauve, M. Methot, J. Bouchard and E. Kumacheva, J. Am. Chem. Soc., 2014, 136, 4788–4793 CrossRef PubMed.
- A. Lukach, H. l. Thérien-Aubin, A. Querejeta-Fernández, N. Pitch, G. G. Chauve, M. Méthot, J. Bouchard and E. Kumacheva, Langmuir, 2015, 31, 5033–5041 CrossRef CAS PubMed.
- G. Chu, X. Wang, T. Chen, J. Gao, F. Gai, Y. Wang and Y. Xu, ACS Appl. Mater. Interfaces, 2015, 7, 11863–11870 CAS.
- A. Querejeta-Fernández, B. Kopera, K. S. Prado, A. Klinkova, M. Methot, G. Chauve, J. Bouchard, A. S. Helmy and E. Kumacheva, ACS Nano, 2015, 9, 10377–10385 CrossRef PubMed.
- M. Sun, W. Ma, L. Xu, L. Wang, H. Kuang and C. Xu, J. Mater. Chem. C, 2014, 2, 2702–2706 RSC.
- T. Hu, B. P. Isaacoff, J. H. Bahng, C. Hao, Y. Zhou, J. Zhu, X. Li, Z. Wang, S. Liu, C. Xu, J. Biteen and N. A. Kotov, Nano Lett., 2014, 14, 6799–6810 CrossRef CAS PubMed.
- B. Yeom, H. Zhang, H. Zhang, J. I. Park, K. Kim, A. O. Govorov and N. A. Kotov, Nano Lett., 2013, 13, 5277–5283 CrossRef CAS PubMed.
- L. Tang, S. Li, L. Xu, W. Ma, H. Kuang, L. Wang and C. Xu, ACS Appl. Mater. Interfaces, 2015, 7, 12708 CAS.
- W. Ma, M. Sun, P. Fu, S. Li, L. Xu, H. Kuang and C. Xu, Adv. Mater., 2017, 29, 1703410 CrossRef PubMed.
- S. Li, L. Xu, W. Ma, X. Wu, M. Sun, H. Kuang, L. Wang, N. A. Kotov and C. Xu, J. Am. Chem. Soc., 2016, 138, 306 CrossRef CAS PubMed.
- M. Wei, K. Hua, L. Xu, D. Li, C. Xu, L. Wang and N. A. Kotov, Nat. Commun., 2013, 4, 2689 Search PubMed.
- F. Gao, M. Sun, W. Ma, X. Wu, L. Liu, H. Kuang and C. Xu, Adv. Mater., 2017, 29, 1606864 CrossRef PubMed.
- M. Sun, L. Xu, J. H. Banhg, H. Kuang, S. Alben, N. A. Kotov and C. Xu, Nat. Commun., 2017, 8, 1847 CrossRef PubMed.
- X. Zhao, L. Xu, M. Sun, W. Ma, X. Wu, C. Xu and H. Kuang, Nat. Commun., 2017, 8, 2007 CrossRef PubMed.
- J. K. Gansel, M. Thiel, M. S. Rill, M. Decker, K. Bade, V. Saile, F. G. Von, S. Linden and M. Wegener, Science, 2009, 325, 1513 CrossRef CAS PubMed.
- X. Wu, L. Xu, W. Ma, L. Liu, H. Kuang, N. A. Kotov and C. Xu, Adv. Mater., 2016, 28, 5907 CrossRef CAS PubMed.
- V. A. Fedotov, A. S. Schwanecke, N. I. Zheludev, V. V. Khardikov and S. L. Prosvirnin, Nano Lett., 2007, 7, 1996–1999 CrossRef CAS.
- S. L. Prosvirnin and N. I. Zheludev, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2005, 71, 037603 CrossRef CAS PubMed.
- L. P. Sergey and I. Z. Nikolay, J. Opt. A: Pure Appl. Opt., 2009, 11, 074002 CrossRef.
- P. Biagioni, J. S. Huang, L. Duò, M. Finazzi and B. Hecht, Phys. Rev. Lett., 2009, 102, 256801 CrossRef CAS PubMed.
- O. Sakai and K. Tachibana, Plasma Sources Sci. Technol., 2012, 21, 013001 CrossRef.
- A. Alù, A. Salandrino and N. Engheta, Opt. Express, 2006, 14, 1557–1567 Search PubMed.
- J. B. Pendry, Science, 2004, 306, 1353 CrossRef CAS PubMed.
- Y. Liu, G. Si, E. H. Khoo, E. S. P. Leong, W. K. Phua and H. Dai, Sci. Adv. Today, 2015, 1, 25212 Search PubMed.
- E. H. Khoo, E. S. P. Leong, S. J. Wu, W. K. Phua, Y. L. Hor and Y. J. Liu, Sci. Rep., 2016, 6, 19658 CrossRef CAS PubMed.
- E. S. P. Leong, J. Deng, E. H. Khoo, S. Wu, W. K. Phua and Y. J. Liu, RSC Adv., 2015, 5, 96366–96371 RSC.
- B. Zhou, B. Shi, D. Jin and X. Liu, Nat. Nanotechnol., 2015, 10, 924 CrossRef CAS PubMed.
- J. M. Luther, P. K. Jain, T. Ewers and A. P. Alivisatos, Nat. Mater., 2011, 10, 361 CrossRef CAS PubMed.
- F. Wang, Q. Li, L. Lin, H. Peng, Z. Liu and D. Xu, J. Am. Chem. Soc., 2015, 137, 12006 CrossRef CAS PubMed.
- G. Garcia, R. Buonsanti, E. L. Runnerstrom, R. J. Mendelsberg, A. Llordes, A. Anders, T. J. Richardson and D. J. Milliron, Nano Lett., 2011, 11, 4415 CrossRef CAS PubMed.
- M. J. Polking, P. K. Jain, Y. Bekenstein, U. Banin, O. Millo, R. Ramesh and A. P. Alivisatos, Phys. Rev. Lett., 2013, 111, 037401 CrossRef PubMed.
- K. Manthiram and A. P. Alivisatos, J. Am. Chem. Soc., 2012, 134, 3995–3998 CrossRef CAS PubMed.
- R. Buonsanti, A. Llordes, S. Aloni, B. A. Helms and D. J. Milliron, Nano Lett., 2011, 11, 4706 CrossRef CAS PubMed.
- J. A. Faucheaux and P. K. Jain, J. Phys. Chem. Lett., 2013, 4, 3024–3030 CrossRef CAS.
- Y. Li, J. Cheng, Y. Liu, P. Liu, W. Cao, T. He, R. Chen and Z. Tang, J. Phys. Chem. C, 2017, 121, 5208–5214 CAS.
- J. Kim, A. Agrawal, F. Krieg, A. Bergerud and D. J. Milliron, Nano Lett., 2016, 16, 3879–3884 CrossRef CAS PubMed.
- M. M. Alsaif, M. R. Field, T. Daeneke, A. F. Chrimes, W. Zhang, B. Carey, K. J. Berean, S. Walia, J. V. Embden and B. Zhang, ACS Appl. Mater. Interfaces, 2016, 8, 3482 CAS.
- S. Jiang, M. Chekini, Z.-B. Qu, Y. Wang, A. Yeltik, Y. Liu, A. Kotlyar, T. Zhang, B. Li, H. V. Demir and N. A. Kotov, J. Am. Chem. Soc., 2017, 139, 13701–13712 CrossRef CAS PubMed.
| This journal is © the Partner Organisations 2018 |