Nanoscale-driven structural changes and associated superparamagnetism in magnetically diluted Ni–Zn ferrites†
Satu G.
Gawas
a,
Sher Singh
Meena
 b,
Pramod
Bhatt
b and
Vidhyadatta M. S.
Verenkar
b,
Pramod
Bhatt
b and
Vidhyadatta M. S.
Verenkar
 *a
*a
aDepartment of Chemistry, Goa University, Goa – 403 206, India. E-mail: vmsv@rediffmail.com; Fax: +91-832-2452886; Tel: +91-832-6519321
bSolid State Physics Division, Bhabha Atomic Research Centre, Mumbai – 400 085, India
First published on 27th November 2017
Abstract
The investigation under study deals with the combustion synthesis of nanocrystalline Mg substituted nickel zinc ferrites i.e., MgxNi0.6−xZn0.4Fe2O4 (x = 0.0 to 0.6) using malic acid dihydrazide as a novel fuel and the effect of magnesium substitution on the structural and magnetic properties. The nanocrystalline monophasic nature of “as prepared” MgxNi0.6−xZn0.4Fe2O4 (x = 0.0 to 0.6) has been confirmed from XRD and Raman spectroscopic studies and the crystallite sizes were found to be in the range of 19–25 nm which nearly matches with TEM. The RT and low temperature magnetization studies indicate a continuous decrease in magnetization with increase in Mg substitution. In contrast, the hysteretic behaviour diminished and the emergence of superparamagnetism is observed in all the samples as the Mg content increases. The decrease in MS with increase in Mg concentration is attributed to the replacement of magnetic Ni2+ ions with non-magnetic Mg2+ ions and also to the enhancement of the Y–K angle by cation redistribution. The variation of AC susceptibility with temperature exhibits broad maxima, indicating a distribution of particle sizes in the sample with the existence of single domain and superparamagnetic type domain structures. The susceptibility decreases continuously beyond x = 0.4 until 0.6, and the samples exhibit only superparamagnetism. The AC susceptibility studies also show a decrease in Curie temperature (TC) with an increase in x for MgxNi0.6−xZn0.4Fe2O4 (x = 0.0 to 0.6) resulting from weakening of A–B interaction. The ZFC–FC studies along with the Mössbauer studies were also corroborated by the proposed existence of dominant superparamagnetism with an increase in Mg concentration.
Introduction
Nowadays, the fundamental understanding of the physical processes in ferrites and their consequent proposed importance in many technological devices have attracted considerable interest. A noticeable advancement has been taking place in the direction of exploring the improvised effect of nano-sized particles on various electric and magnetic properties. Compared to bulk ferrites, a smaller size of the particles in the magnetic single domain state can bring in innovative variations in the properties of the ferrites. Mainly, when the particles exist in the singe domain state, the domain wall resonance is avoided favouring optimum working conditions for applications in high frequency. Thus, a wide variety of applications ranging from high density storage to energy devices like inductors, power transformers, and telecommunications working in the high frequency region use nanodomain ferrite systems.1 Also, the magnetic characteristics of the materials are strongly affected when the particle sizes are further reduced and the superparamagnetic relaxation effects originate due to the influence of the thermal energy over the magnetic moment orientation at the nanoscale. Moreover, the magnetocrystalline anisotropy is the vital parameter which influences the magnetic moment ordering in ferrites controlling the superparamagnetism in nanodomains. Many newer applications have emerged involving ferrites in the superparamagnetic region mainly in the biomedical field such as site-specific targeted drug delivery, hyperthermia tumor cell treatment, MRI contrast agents, bio-imaging etc.2–5In the ferrite systems, most of the theoretical studies claim that the substitution of a reasonable amount of magnetic ions enhances the magnetization, in which the correlation between magnetism and strength of magnetic interaction between magnetic ions depends on the nature of the cation substituted. Furthermore, emphasis is highlighted on the variation in particle size as a function of sintering/annealing temperature and the effect of finite size and surface spin on the resultant magnetic properties.1 Thus, various types of particle size and surface effect result in spin canting and core shell spin alignment, and the net magnetic interaction leads to the origin of Neel type and Y–K type magnetization, thus affecting the magnetic properties.6,7 Meanwhile, the substitution of magnetic ions by non-magnetic ions in controlled concentration is also known to enhance the magnetic properties of the spinel ferrite system. The magnetic behaviour of ferrites with a high concentration of diamagnetic ions shows a large number of characteristics which are not well explained and correlated. The presence of diamagnetic ions above a certain limit on a sub-lattice has been found to result in non-collinearity of spins on the adjacent sub-lattice. Besides this, magnetic anisotropy also varies with the inclusion of diamagnetic ions and affects the superparamagntic blocking temperature in nano domain states. Thus, it is important to correlate the various properties that exist in the nanodomain states along with the diamagnetic ions in order to explain the magnetism.
Although Ni–Zn ferrites are of extensive research interest owing to their remarkable properties such as high electrical resistivity, high saturation magnetization, low eddy current losses, chemical stability, mechanical hardness, etc., their superparamagnetic behaviour originates mainly from finite size effects and points the way towards biomedical applications.8,9 The reports on the studies of Ni–Zn ferrites with variable Ni and Zn substitution as well as substitution of magnetic ions by non-magnetic Zn or Cd ions or by other transition metal ions like Cr, Mn, Co and Cu are many.2,10–14 In contrast, studies on a fixed concentration of Zn2+ in Ni–Zn ferrites which corresponds to the highest magnetization and then varying the concentration of Ni2+ with some other metal ions have not been exploited fully, especially for the composition Ni0.6Zn0.4Fe2O4.9,15–17
In the previous work of our group, the substitution of magnetic Ni2+ ions by magnetic Co2+ ions was tried but did not show any significant variation in the superparamagnetic properties and blocking temperature.10 Despite the correlation towards the change in magnetic anisotropy by virtue of Co2+ ions and the change in single domain, superparamagnetic properties were observed and explained in detail with the shift in magnetic properties in a single domain ferrimagnetic region. When compared with ferromagnetic elements like Mn and Co, it is expected that non-magnetic substances like Mg may soften the Ni–Zn ferrite by diluting the magneto crystalline anisotropy constant and this in turn will affect the magnetic properties and eddy current losses. Also, it is reported that Mg ions can be a low toxicity alternative for Ni ions in Ni–Zn ferrites forming Mg–Zn ferrites and retaining the various important properties.18 A further peep into the literature on Mg substituted Ni–Zn ferrites reveals studies on the effect of sintering temperature, particle size and cation distribution on the resultant properties, whereas the effect of diamagnetic Mg ion substitution on superparamagnetism is scantly investigated.19–21 Hence, for a better understanding of magnetism and to apply the material as a novel material in the biomedicinal field, we thought it important to study the domain structure which exists as a function of diamagnetic Mg ion substitution and its correlation with change in anisotropy energy.
In the literature, the variations in different properties were explored by considering different methods of synthesis for controlling the size and its distribution.22–34 More particularly, recent trends in synthetic methods use low temperature wet chemical methods like auto-combustion, which is considered one of the prominent methods of synthesis compared to high temperature annealing.33,34 This auto-combustion method is extensively used not only by changing the fuels, which controls the exothermicity of the reaction, but also by varying the metal nitrate to fuel ratio.34 Thus, we are exploring the same principle for the combustion synthesis of MgxNi0.6−xZn0.4Fe2O4 (x = 0.0 to 0.6), wherein a novel fuel has been used after optimization with respect to metal nitrates.
Experimental
Synthesis and optimization of malic acid dihydrazide (fuel)
Hitherto unexplored malic acid dihydrazide (MADH) has been used as a fuel for the first time in the combustion method. The MADH was prepared from diethyl malate and hydrazine hydrate, following the reaction conditions used for the synthesis of malonic acid dihydrazide (MDH) (ESI,† Scheme S1).35 The diethyl malate was synthesized from malic acid by refluxing it for 14 h with ethyl alcohol, under the acidic condition of a catalytic amount of conc. H2SO4. The prepared diethyl malate was reacted with hydrazine hydrate in the molar ratio 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2, to precipitate out malic acid dihydrazide (MADH) as a white solid.
2, to precipitate out malic acid dihydrazide (MADH) as a white solid.
The newly prepared fuel was characterized using FTIR and NMR spectroscopy, and optimized for the favourable combustion reaction with metal nitrates (ESI†). After optimizing it for the best oxidizer to fuel ratio, based on the broadening of the XRD peaks and monophasic nature of the ferrites, the oxidizer to fuel ratio of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.7 was found to be ideal for nanoparticle synthesis. Thus, Mg substituted MgxNi0.6−xZn0.4Fe2O4 samples with x ranging from 0.0 to 0.6 were prepared by following the procedure as discussed below.
0.7 was found to be ideal for nanoparticle synthesis. Thus, Mg substituted MgxNi0.6−xZn0.4Fe2O4 samples with x ranging from 0.0 to 0.6 were prepared by following the procedure as discussed below.
Combustion synthesis of MgxNi0.6−xZn0.4Fe2O4 (x = 0.0 to 0.6)
All the metal nitrates used were of analytical grade without further purification. Stoichiometric amounts of Mg2+, Ni2+, Zn2+ and Fe3+ nitrates were melted in a beaker on a heating plate followed by the addition of MADH to the melt. The fuel was added in such an amount that the oxidizer to fuel ratio was maintained as 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.7. The whole mixture was slowly heated with stirring in-between, until it formed a homogeneous sticky slurry. Further heating attains the ignition temperature of the reaction mixture, where it catches fire and undergoes slow combustion to form a desired nanocrystalline single phase ferrite powder. Finally, the powder was calcined at 500 °C for 5 h in air to remove the unburnt carbonaceous matter.
0.7. The whole mixture was slowly heated with stirring in-between, until it formed a homogeneous sticky slurry. Further heating attains the ignition temperature of the reaction mixture, where it catches fire and undergoes slow combustion to form a desired nanocrystalline single phase ferrite powder. Finally, the powder was calcined at 500 °C for 5 h in air to remove the unburnt carbonaceous matter.
Characterization
The crystal structure and phase purity of all the composition were determined using a RIGAKU ULTIMA IV X-ray powder diffractometer using CuKα radiation (λ = 1.5418 Å) filtered through Ni and operated at the voltage of 40 kV and current of 20 mA. The Raman spectra at RT were recorded to study the associated structural changes in the range of 225–875 cm−1 on a HORIBA JOBIN YVON HR-800 Raman spectrometer equipped with a CCD camera using an Ar+ laser at an excitation wavelength of 488 nm and a power of 10 mW. An Olympus optical microscope with a 50× objective lens was used to focus the laser beam on the sample and collect the scattered radiation. The surface morphology of the samples was recorded on a Carl-Zeiss EV018 scanning electron microscope (SEM) and the elemental analysis was done by Energy Dispersive X-ray Spectroscopy (EDX) using a scanning electron microscope (SEM) coupled with EDX facility on a JEOL JSM-6360. The particle size distribution and selected area electron diffraction (SAED) pattern were recorded by transmission electron microscopy (TEM) using a Philips CM20 electron microscope. The AC susceptibility curves along with the Curie temperature were recorded at 5 kOe using a temperature programmed Data-logger for Science Experiments (DOSE) AC susceptibility Setup standardized with Nickel and supplied by ADEC Embedded Technology and Solutions Pvt. Ltd Corlim-Goa. The magnetic properties were studied as a function of applied field (M–H) and temperature (M–T) on a Quantum Design-Versa Lab Vibrating sample magnetometer (VSM). For M–T studies, zero field cooled–field cooled (ZFC–FC) measurements were carried out at 700 Oe, wherein for ZFC measurements, the sample was first cooled to 50 K without any applied field and magnetization was recorded from 50 K to 400 K by applying a field. For the FC measurement, the samples were cooled in the presence of a field and then the measurements were carried out. The room temperature Mössbauer (RT) spectra were recorded using a Mössbauer spectrometer operated in constant acceleration mode (triangular wave) in transmission geometry. The source employed was Co-57 in a Rh matrix of strength 50 mCi. The calibration of the velocity scale was done by using an enriched α-57Fe metal foil and the line width (inner) of the calibration spectrum was 0.26 mm s−1.Result and discussion
The combustion synthesis of MgxNi0.6−xZn0.4Fe2O4 (x = 0.0 to 0.6) using malic acid dihydrazide as a novel fuel has been successfully tried for the first time, yielding single phase ferrites. The ratio of metal nitrate to malic acid dihydrazide as a combustion mixture was fixed at 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.7 after optimization (Fig. S1, ESI†), keeping in mind the requirement of single phase nanosize ferrites which in turn directly depend upon the heat generated during combustion. Therefore, perfect equilibrium has to be reached in order to avoid either incomplete combustion due to a lower fuel ratio or decomposition of single phase into multiphase due to a higher fuel ratio. The impurity-free phase thus obtained was monitored by X-ray diffraction and Raman spectroscopic studies. The impact of Mg substitution for Ni in Ni0.6Zn0.4Fe2O4 on the magnetic properties has been dealt with in detail and the results were explained utilizing Mössbauer spectroscopic along with A.C. susceptibility data in this section.
0.7 after optimization (Fig. S1, ESI†), keeping in mind the requirement of single phase nanosize ferrites which in turn directly depend upon the heat generated during combustion. Therefore, perfect equilibrium has to be reached in order to avoid either incomplete combustion due to a lower fuel ratio or decomposition of single phase into multiphase due to a higher fuel ratio. The impurity-free phase thus obtained was monitored by X-ray diffraction and Raman spectroscopic studies. The impact of Mg substitution for Ni in Ni0.6Zn0.4Fe2O4 on the magnetic properties has been dealt with in detail and the results were explained utilizing Mössbauer spectroscopic along with A.C. susceptibility data in this section.
Structural properties
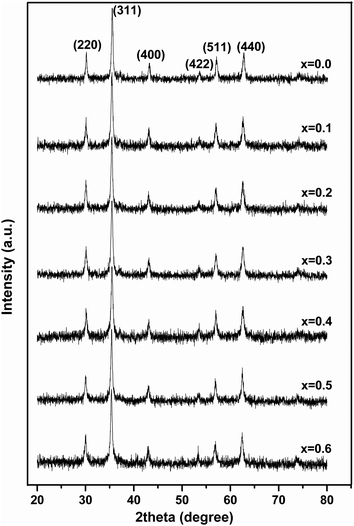
Fig. 1 shows the XRD patterns of MgxNi0.6−xZn0.4Fe2O4 (x = 0.0 to 0.6) samples prepared by the combustion method and calcined at 500 °C (hereafter, referred to as ‘as prepared’ in the text). Analysis of all the XRD patterns confirmed the formation of crystalline structure and all the characteristics peaks were indexed to cubic spinel diffraction planes. The XRD patterns demonstrate that the cubic crystal structure is maintained throughout the substitution without any extra peaks of secondary phase corresponding to MgO, α-Fe2O3, etc. However, the intensity of the (222) peak decreases with the increase in Mg2+ substitution and the spectrum is almost devoid of a (222) peak at x ≥ 0.5. A similar observation has been made in the XRD plots for higher substitution of Mg2+.19,36,37 It has been reported that the intensity of the (222) peak is sensitive to the cations at the octahedral site whereas the intensity of the (220) peak depends on the cations at the tetrahedral site.38 Hence for initial lower substitution of Ni2+ ions by Mg2+ ions, the (222) peak results from the Ni2+ ion at the octahedral site, which successively decreases in intensity with decrease in Ni concentration. The inclusion of Mg2+ ions in the lattice leads to migration of Fe3+ ions from the tetrahedral to octahedral site in place of the substituted Ni2+ ion while Mg2+ occupies the tetrahedral site along with Zn2+/Fe3+ ions. With further increase in Mg ≥ 0.5, the Mg2+ ions may also occupy the octahedral site resulting in the occupation of both the tetrahedral and octahedral sites and simultaneously decreasing the intensity of the octahedral site sensitive (222) peak. Thus, it can be concluded that the Mg2+ ions occupy both the sites at higher concentration, whereas they remain preferably at the tetrahedral site at lower concentration.Moreover, it was also observed that [Fig. 1] the peaks became rather broad and nearly merged with the low intensity (222) peak with increased Mg substitution (Mg ≥ 0.5). The broadening indicates the fine particle nature of the ferrites, suggesting the particle dimensions to be in the nanometric scale. Thus, the average crystallite sizes have been calculated from the full width half maxima (FWHM) values of the most prominent, highly intense diffraction peak i.e., 311 using Scherrer's equation. It was found that the crystallite size decreases from 25 nm to 19 nm with increase in Mg content, almost matching the similar behaviour reported for increase in Mg content.19
Furthermore, the lattice parameter was calculated to monitor the associated changes in the structure using the relation,39
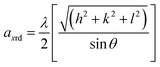 | (1) |
While using the Nelson–Riley extrapolation method as per the relation,40
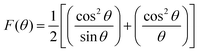 | (2) |
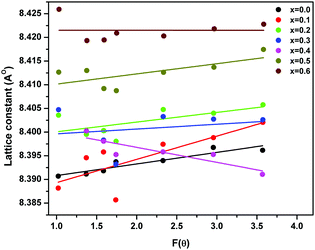 | ||
| Fig. 2 Variation of lattice parameter with F(θ) in ‘as prepared’ MgxNi0.6−xZn0.4Fe2O4 (x = 0.0 to 0.6) nanoparticles. | ||
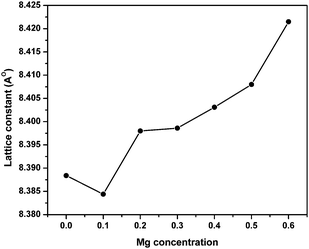 | ||
| Fig. 3 Variation of lattice parameter with Mg substitution in ‘as prepared’ MgxNi0.6−xZn0.4Fe2O4 (x = 0.0 to 0.6) nanoparticles. | ||
Morphology, chemical and particle size analysis
The SEM micrographs of the MgxNi0.6−xZn0.4Fe2O4 (x = 0.0 to 0.6) along with the EDS spectra of the selected composition are shown in Fig. 4. The micrographs revealed that the ferrite samples are composed of nanoparticles which exist as agglomerated lumps with wide size distribution. The extent of agglomerated lump formation decreases with substitution of Mg ions, and the particles appear more dispersed in the micrographs. The EDS analysis spectra give the qualitative and quantitative substitution of the Mg ions in the composition and the ratio of Mg, Ni, Fe and Zn ions is maintained with substitution. It is also clearly visible from the EDS images that the inclusion of Mg for the Ni ion leads to the disappearance of Ni peaks and the appearance of the Mg ion peak. | ||
| Fig. 4 SEM micrographs of ‘as prepared’ MgxNi0.6−xZn0.4Fe2O4 (x = 0.0 to 0.6) and EDS analysis spectra of ‘as prepared’ MgxNi0.6−xZn0.4Fe2O4 (x = 0.0, 0.2 0.4 and 0.6) nanoparticles. | ||
The TEM images of the selected ferrite samples (x = 0.0, 0.2, 0.4 and 0.6) along with the electron diffraction pattern are presented in Fig. 5. From the TEM images, we observe that the particles are almost spherical shapes fused together or exist as agglomerates, also observed in SEM micrographs resulting from mutual magnetic interaction of individual magnetic nanoparticles. The average particle size estimated from the TEM analysis is found to be in the range of 20 to 30 nm and necessarily of the size of single domains with some agglomerates measuring up to 40 nm. The comparison of grain sizes with the average crystallite size obtained from XRD studies indicates that the grains are formed by aggregation of small crystallites. The SAED patterns were indexed with respect to the position of the individual planes in the ferrite system. Clear pattern rings were observed proving the well-crystallized nature of all the compositions and the appearance of bright spots supports agglomeration of the particles in all the compositions.41
 | ||
| Fig. 5 TEM images and SAED pattern of ‘as prepared’ MgxNi0.6−xZn0.4Fe2O4 (x = 0.0, 0.2 0.4 and 0.6) nanoparticles. | ||
Raman spectroscopic studies
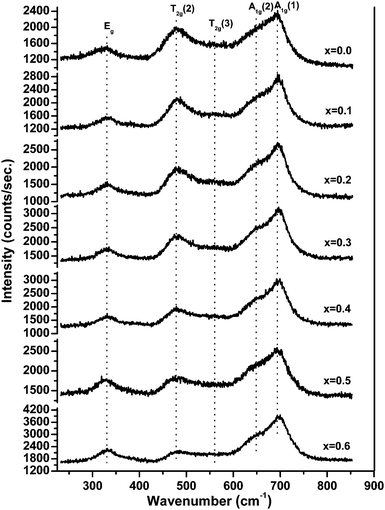
Fig. 6 shows the Raman spectra of ‘as prepared’ MgxNi0.6−xZn0.4Fe2O4 (x = 0.0 to 0.6), and the characteristics of spinel space group, Fd3m, have been assigned to the Raman modes on the basis of factor group analysis.42 Accordingly, the modes above 600 cm−1 were assigned to the tetrahedral site, A1g whereas the lower frequency modes represent the characteristics of the octahedral vibrations, Eg and T2g respectively. In the present compositions, three major broad bands were observed at 330, 470 and 690 cm−1, respectively, in association with two shoulder bands at 560 and 650 cm−1. These shoulder peaks were also called a doublet feature in many literature reports and were assigned to the local cation distribution at available tetrahedral and octahedral sites.43–45 No extra peaks were observed for the formation of γ-Fe2O3, α-Fe2O3, MgO, etc. other than spinel ferrite, thus confirming the monophasic composition throughout. Usually, peaks appear at ∼240 cm−1 and 300 cm−1 assigned to Fe2O3 in the defined range.46 But no such peak was observed at ∼240 cm−1, whereas the low intensity peak at ∼330 cm−1 can be assigned to the Eg mode,47 and provides strong evidence for the absence of such impurity phases in accordance with the XRD analysis.The present studies demonstrating the effect of Mg substitution on structural properties can be easily monitored from the shift in the peak position and from the variation in the relative peak intensity. As inferred from Fig. 6, the relative intensity of the peak at ∼474 cm−1 diminishes with increase in Mg ions, whilst the peak of A1g at ∼690 cm−1 becomes more prominent along with the shoulder peak at ∼650 cm−1. According to Nakagomi et al.48 and da Silva et al.,49 the Mg2+ ions at tetrahedral sites result in splitting of the A1g peak, wherein the higher wave number peak was assigned to the Mg2+ ion and the lower peak was attributed to the Fe3+ ion, respectively. They had also stated that48,49 the relative intensity of the peaks increases along with the red shift in the peak positions as a function of Mg2+ ion at the tetrahedral site. A similar trend has been seen in the present studies with respect to the splitting of the A1g peak, which is less for x = 0.0 i.e., Ni0.6Zn0.4Fe2O4, but successively increases with increase in Mg2+ ions at tetrahedral sites. However, instead of a red shift, a blue shift in the peak position has been observed in the present studies and assigned to the lower atomic mass of Mg2+ ions than Zn2+/Ni2+/Fe3+ ions, which is in accordance with the report by Varshney, and Verma.45 Moreover, the peak assigned to the octahedral site T2g(2) vibration mode was found to decrease in intensity as compared with the A1g modes, whereas the T2g(3) modes become almost invisible for higher substitution of Mg2+ ions. It is a well-accepted fact that Zn2+ ions have strong preference for the tetrahedral site and Ni2+ ions occupy the octahedral site. With the substitution of Mg2+ for Ni2+ ions in the lattice structure, the lattice cation disordering takes place, wherein the Ni2+ ion decreases at the octahedral site with the inclusion of Mg2+ and Zn2+ ions at tetrahedral sites and at the expense of migration of Fe3+ as well as reordering of Mg2+ ions to the octahedral sites for higher substitution of the Mg2+ ion. Thus, lowering of the T2g(3) peak can be assigned to the decrease in octahedral Ni2+ ions, and the enhancement of tetrahedral A1g(1) is mostly due to the Mg2+ ions at the tetrahedral site. The above reasoning agrees with the prediction made on cation distribution observed in XRD studies and the assignments of various Raman peaks are due to cationic disorder.
Magnetization studies
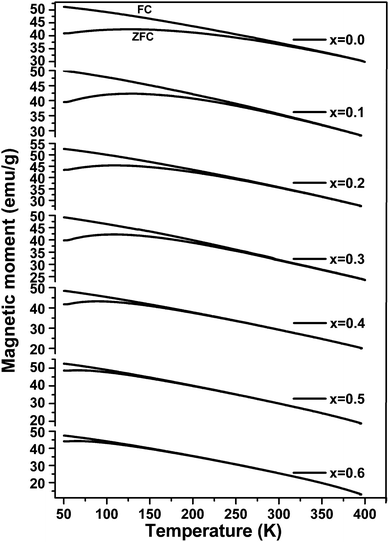
The temperature-dependent zero field cooled–field cooled (ZFC–FC) magnetization plots for ‘as prepared’ nanocrystalline MgxNi0.6−xZn0.4Fe2O4 (x = 0.0 to 0.6) ferrites that were obtained at an applied field of 700 Oe are presented in Fig. 7. As can be observed from the plots, the magnetization increases initially with temperature, reaches a maximum and decreases with further increase in temperature in the case of ZFC studies. While, in the case of FC measurement, magnetization decreases continuously with increase in temperature. Usually, the maxima in ZFC magnetization studies are thought to be the result of two effects, the first causing an increase in magnetization by individual magnetic domains having enough thermal energy to adopt the new alignment at lower energy with the applied field and the second effect resulting from the thermal energy overcoming the alignment of magnetic domains with the field, thus randomizing the magnetic anisotropy and hence lowering the magnetization value.50 Thus, the maximum peak with the highest magnetic moment is obtained in ZFC plots and observed for individual non-interacting single domain particles at a characteristic temperature called the blocking temperature (TB). Below this temperature, the superparamagnetic properties diminish with the sample behaving more like a ferrimagnetic, whereas above TB in the unblocked region magnetization decreases monotonically with increase in temperature. Thus, the characteristic properties of superparamagnetic materials are observed in the case of all the samples below room temperature until the blocking temperature. Apart from this, the peak in all the ZFC curves is broader, which should be due to the presence of a broad distribution of relaxation times for the metastable states resulting from the less and less uniformity in the particle sizes and dipole–dipole interaction at the nano domain states.51–54It is also noticed that the increase in Mg ions tends to shift the blocking temperature to lower temperature. The blocking temperature shift is the resultant effect of anisotropy and particle size distribution given by the relation.
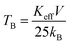 | (3) |
At temperatures slightly above the blocking temperature (TB), the FC curves merge with the ZFC curves, known as the irreversible temperature (Tirr). This irreversible nature of ZFC–FC below Tirr indicates different orientation energy of individual particles and Tirr corresponds to the blocking temperature of the individual largest single domain particle.51,58,59 It is also evident from eqn (3) that each particle size (V) meets a certain blocking temperature (TB), which means that when the composition has maximum homogeneity with all the particles having the same sizes in the nano range, there will be maximum closeness between the TB and Tirr. This is observed for x ≥ 0.5 indicating maximum homogeneity in the compositions. Above Tirr, the merged ZFC–FC curves displaying continuous decrease in magnetization with rise in temperature indicate the net orientation of all particles domain with respect to field direction due to thermal fluctuation within the interacting domains, irrespective of individual anisotropy energy.
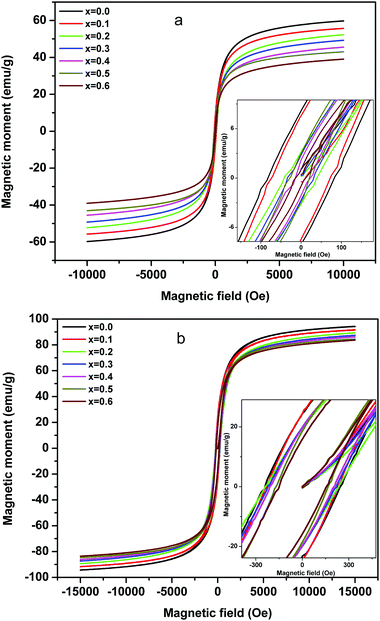
The magnetization studies as a function of applied field (1.5 Tesla) were carried out at room temperature (Fig. 8a) and 50 K (Fig. 8b), wherein the effect of magnetic dilution by the incorporation of non-magnetic Mg ions for magnetic Ni ions in the Ni–Zn ferrite is discussed in detail. As can be observed from Fig. 8a, the room temperature magnetic moment decreases from 59.91 to 39.10 emu g−1 [Table 1] with the substitution of Ni2+ by Mg2+ ions. The field reversal magnetization shows an almost absence of hysteresis with very low remenance and coercivity values and thus the superparamagnetic nature of nanocrystalline MgxNi0.6−xZn0.4Fe2O4 (x = 0.0 to 0.6) ferrites at RT. The non-attainment of saturation for a higher applied field of 1.5 Tesla also supports the presence of superparamagnetic and single domain particles in all the composition.60,61 On the other hand, the low temperature magnetization studies at 50 K (Fig. 8b) which is below blocking temperature (TB) show comparatively higher magnetization values, which decrease from 94.26 to 83.75 emu g−1 [Table 1] with the increase in Mg content. Also, the hysteresis loop begins to open up with detectable remenance and coercivity value and can be accounted for by the more ordered magnetic structure of nanoparticles at lower temperature. This is because the thermal effect results in disorder of the magnetic moment above the blocking temperature (TB) in comparison to the ordered structure at 50 K which leads to variation in magnetic properties.
| Mg | RT | 50 K | ||||
|---|---|---|---|---|---|---|
| M S (emu g−1) | M R (emu g−1) | H C (Oe) | M S (emu g−1) | M R (emu g−1) | H C (Oe) | |
| 0.0 | 59.91 | 8.12 | 82.9 | 94.26 | 24.5 | 240 |
| 0.1 | 55.80 | 7.58 | 74.6 | 91.42 | 24.5 | 235 |
| 0.2 | 52.2 | 3.18 | 42.9 | 89.33 | 19.3 | 230 |
| 0.3 | 49.2 | 2.75 | 34.6 | 87.36 | 20.0 | 220 |
| 0.4 | 45.6 | 2.12 | 25.2 | 86.13 | 19.6 | 210 |
| 0.5 | 43.0 | 3.05 | 20.2 | 84.50 | 18.5 | 176 |
| 0.6 | 39.1 | 1.01 | 12.2 | 83.75 | 15.8 | 150 |
The decrease in magnetic moment with the increase in Mg ions is considered to be the impact of the lower magnetic moment of Mg ions (0 μB) than Ni ions (2 μB) as a major source. According to Neel's two-sublattice model of ferrimagnetism, the variation in magnetization values can be explained by the distribution of cations among the tetrahedral (A) and octahedral (B) sites. According to this model, three types of magnetic interactions take place between the A and B sites, namely A–A, B–B and A–B interaction giving rise to resultant magnetic moment. The A–B type of interaction is the most prominent and strongest one among the three and hence the net magnetization of a unit cell (within the) is calculated as a difference between the magnetic moment of the A and B sites. In Ni–Zn ferrites, Zn2+ has strong preference for the tetrahedral sites, whereas Ni2+ ions mainly occupy the octahedral sites and Fe3+ ions have a preference for both the available A and B sites. On the other hand, Mg2+ ions exist in both the sites but have strong preference for the tetrahedral site.19,21 Thus, the substitution of magnetic Ni2+ ions by non-magnetic Mg2+ ions gives rise to cation reordering which results in a decrease in magnetic moment as well as magnetic interaction and hence the lowering of the magnetization values. Moreover, other factors like particle size effect and cation distribution leading to enhancement in Y–K type magnetism promote the decrease in magnetic moment.6
Below the blocking temperature, i.e., at 50 K, the nanoparticles of Mg substituted Ni–Zn ferrites exhibit hysteresis behaviour and the hysteresis area decreases with increase in Mg substitution. At T < TB, the thermal energy of the nanoparticles is not high enough to compensate for the orientation of the magnetic domain with the applied field direction and to attain equilibrium during the measurement time. Moreover, higher magnetocrystalline anisotropy of less substituted Ni–Zn ferrites leads to shift of blocking temperature to higher values as discussed earlier and also to the enhancement in hysteretic behaviour with lowering of the measurement temperature.
AC susceptibility studies
The alternating current susceptibility studies of the ‘as prepared’ nanoparticle ferrites were measured at 5 kOe in the temperature range of 25 °C until the Curie point is attained. The normalized susceptibility curves for MgxNi0.6−xZn0.4Fe2O4 (x = 0.0 to 0.6) are shown in Fig. 9. The behaviour of the curves in response to the temperature shows the domain nature of the nanoparticles and represents the variation in Curie transition temperature, TC as a function of Mg substitution. The TC is the characteristic magnetic transition temperature which gives an idea about the amount of energy required to disturb the magnetic ordering in the magnetic material. It can be observed from Fig. 9 that all the compositions display very broad transition with the tailing effect near the Curie temperature, which could be due to inhomogeneity in the particle sizes. The broad transition seems to be very significant for lower substitution of Mg with x ≤ 0.3 and indicates the presence of single domain as well as superparamagnetic nanoparticles. In contrast above x ≥ 0.4, steady decrease in susceptibility with continuous tailing indicates dominant superparamagnetic particles. Thus, the AC susceptibility plots depict typical single domain ferrimagnetic type of domain structure behaviour at x ≤ 0.3, which changes to superparamagnetic at x ≥ 0.4 and finally undergoes paramagnetic transition at the Curie temperature (TC).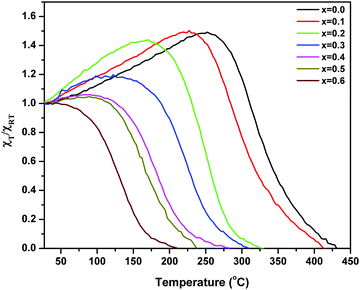 | ||
| Fig. 9 Plots of variation of normalized AC susceptibility with temperature for ‘as prepared’ MgxNi0.6−xZn0.4Fe2O4 (x = 0.0 to 0.6). | ||
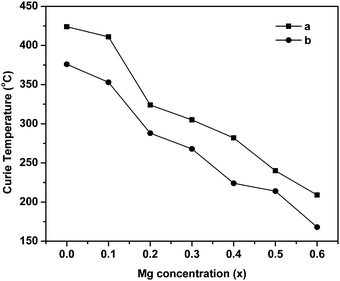
The Curie temperature from the AC susceptibility study is determined by extrapolating the steady decrease in susceptibility to intercept with the x-axis, and also from the subsequent fall in susceptibility to zero values.62 The Curie temperature is plotted as a function of Mg substitution and shown in Fig. 10. It can be seen from the figure that the TC decreases with increase in Mg content. According to Neel's theory of ferrimagnetisms as discussed in magnetization studies, the Curie temperature also depends on the magnitude of A–B interaction of the type A–O–B, which in turn results from the type and number of different ions at the A and B sites. So, as the non-magnetic Mg2+ ions increase in the lattice structure, the strength of magnetic interaction weakens at the A and B sites whereas the B–B interaction enhances leading to Y–K type magnetism and eventually the Curie temperature decreases with increase in Mg content. Besides, the increase in lattice parameter with Mg substitution decreases the interaction among the A and B sites, and also the mutual orientation of magnetic ions. Thus, considering both these parameters, the thermal energy required to off-set the magnetic orientation decreases which in turn decreases the Curie temperature (TC).
Mössbauer spectroscopic analysis
Mössbauer spectroscopy is a powerful and efficient technique to investigate the superparamagnetic relaxation effects in the magnetic nanoparticles which arise out of the impact of intrinsic factors like particle size and magnetic anisotropy, and extrinsic factors like temperature and measurement time window.63 For single domain particles, the superparamagnetism can be accounted on the basis of Néel's relaxation theory, wherein the ferrimagnetically/ferromagnetically aligned magnetic moments fluctuate between the two energetically favoured degenerate states on a time scale given by the Néel–Arrhenius equation.7,56τ = τ0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(KV/kBT) exp(KV/kBT) | (4) |
The Mössbauer spectra for nanocrystalline MgxNi0.6−xZn0.4Fe2O4 (x = 0.0 to 0.6) at room temperature were recorded in the velocity range of −11.5 to 11.5 mm s−1 and presented in Fig. 11. All spectra are fitted with the least square method by assuming the Lorentzian peak shape using the Win-Normos site fit program. The fitting exhibits three Zeeman spit sextets superimposed with a weak disordered magnetic relaxation state doublet. Normally, two Zeeman split sextets were observed, one corresponding to Fe3+ ions at the tetrahedral sites and the other due to Fe3+ ions at the octahedral B-site. However, the observed three sextets can be attributed to random distribution of cations at the tetrahedral and octahedral sites, thus resulting in the splitting of the octahedral site into two sextets as B and B1, respectively. The spectral parameters isomer shift, IS (δ), quadrupole splitting, QS (Δ) and hyperfine splitting (Hhf) calculated from the fitted Mössbauer spectra are summarized in Table 2. The assignment of three sextets to various sites has been made on the basis of isomer shift values calculated, whereas other parameters were obtained based on the distribution of cations around Fe3+/Fe2+ ions. It is well accepted that the isomer shift for the tetrahedral site is always less than that of the octahedral site, resulting from larger overlap of Fe3+–O2− ions at A-sites and leading to greater dispersion of charges at the tetrahedral site than the octahedral site. Thus, the fitted sextet with a lower isomer shift value is assigned to tetrahedral sites and the other sextets with higher values were assigned to the octahedral B and B1 sites. The calculated isomer shift values for both the sites are less than 0.5 mm s−1 and indicate that iron exists in the Fe3+ valence state with high spin configuration.8,65 Moreover, the isomer shift values are comparatively smaller than the expected values of ∼0.8 mm s−1 for Fe2+ ions in a high spin state.66–68 This confirms the presence of Fe3+ ions in the system with no signature of Fe2+ ions.
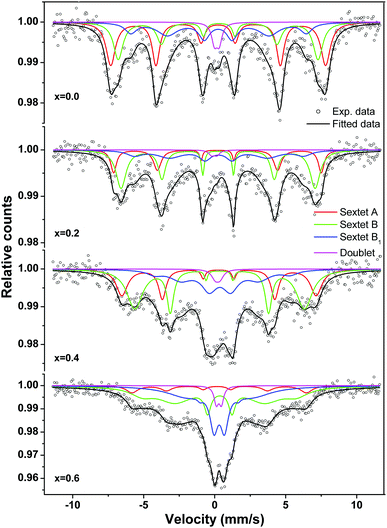 | ||
| Fig. 11 Room temperature Mössbauer spectra of the ‘as prepared’ MgxNi0.6−xZn0.4Fe2O4 (x = 0.0, 0.2, 0.4 and 0.6) nanoparticles. | ||
| Sample comp. (x) | Fe-site | IS (δ) (mm s−1) | QS (Δ) (mm s−1) | H hf (Tesla) | Γ (mm s−1) | R A area (%) |
|---|---|---|---|---|---|---|
| 0.0 | Sextet A | 0.252 | 0.0029 | 46.93 | 0.581 | 38.81 |
| Sextet B | 0.288 | −0.0755 | 43.63 | 0.424 | 20.33 | |
| Sextet B1 | 0.267 | 0.0326 | 38.33 | 0.909 | 38.88 | |
| Doublet | 0.159 | 0.342 | — | 0.465 | 1.98 | |
| 0.2 | Sextet A | 0.181 | −0.0019 | 45.34 | 0.232 | 11.98 |
| Sextet B | 0.228 | −0.0025 | 42.38 | 0.252 | 27.55 | |
| Sextet B1 | 0.269 | 0.0247 | 36.91 | 0.979 | 59.43 | |
| Doublet | −0.0429 | 0.377 | — | 0.465 | 1.04 | |
| 0.4 | Sextet A | 0.275 | 0.0309 | 42.43 | 0.349 | 16.16 |
| Sextet B | 0.327 | 0.0123 | 37.05 | 0.268 | 20.63 | |
| Sextet B1 | 0.445 | 0.1822 | 29.51 | 1.299 | 61.64 | |
| Doublet | 0.188 | 0.3360 | — | 0.614 | 1.57 | |
| 0.6 | Sextet A | 0.236 | 0.1573 | 38.09 | 0.599 | 9.25 |
| Sextet B | 0.346 | −0.0276 | 33.66 | 0.551 | 45.98 | |
| Sextet B1 | 0.318 | −0.0001 | 14.44 | 0.655 | 43.37 | |
| Doublet | 0.293 | 0.358 | — | 0.376 | 1.40 | |
The chemical disorder in the spinel structure results in an electric field gradient of varying magnitude and corresponds to non-zero quadrupole splitting. The quadrupole splitting obtained for the tetrahedral and octahedral sites is nearly zero throughout the substitution and points towards the maintenance of symmetry without any distortion in the cubic structure. However, the Δ obtained for fitted relaxation doublet of octahedral sites indicates the substantial electric field gradient around the Fe nuclei originating from large surface to volume ratio in superparamagnetic nanoparticles and also from the trigonal field present at the B-site.69 The trigonal field distorts the octahedron formed by the six O2− around the Fe3+ ions changing the perfect cubic symmetry and hence non-zero Δ values.
The variation in hyperfine field (Hhf) at tetrahedral (A-site) and octahedral sites (B and B1) as a function of magnesium substitution is depicted in Fig. 12. Here, the Hhf at both the sites decreases with increase in Mg concentration and the Hhf for the tetrahedral site is higher than for the octahedral sites. It is considered and well accepted that the origin of the hyperfine field is due to the resultant effect of factors namely, the polarization of core s-electrons by the magnetic moment of d-electrons (Hcore), the dipolar field of the surrounding magnetic ions (HD) and lastly the super transferred hyperfine fields arising from the magnetic moments of the nearest neighbouring cation (HSTHF) and given by the relation,63,68,70–72
| Hhf = Hcore + HSTHF + HD | (5) |
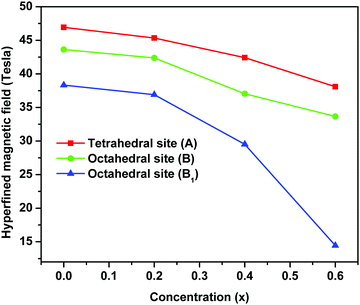 | ||
| Fig. 12 Variation of hyperfine fields at 57Fe nuclei of tetrahedral and octahedral sites of ‘as prepared’ MgxNi0.6−xZn0.4Fe2O4 (x = 0.0, 0.2, 0.4 and 0.6) nanoarticles. | ||
According to the Néel theory, AB exchange interactions are stronger than AA or BB exchange interactions. As both the A and B sites are occupied by Fe3+ ions, the interaction of Fe3+ ions is possible with the Ni2+, Mg2+ and Zn2+ ions and the net magnetic field is mainly due to FeA3+–O–FeB3+ interaction. Thus, the substitution of magnetic Ni2+ ions by non-magnetic Mg2+ ions decreases the magnetic linkages in FeA3+–O–FeB3+, FeA3+–O–ZnA2+ and FeA3+–O–NiB2+ and consequently the Fe3+ ions experience a decrease in magnetic field at the A and B sites.45 Also as mentioned in the magnetization studies, the enhancement of Y–K angle with substitution of Mg2+ ions leads to reordering of the Fe3+ ions. This lowers the magnetic moment at the octahedral sites by FeB3+–O–FeB3+ interaction leading to canting of spins at octahedral sites and concurrently supporting the lowering of Hhf at the octahedral site (B and B1) compared to the tetrahedral site. Moreover, the relative area of the tetrahedral and octahedral sites from Mössbauer sub-spectra determines the fraction of Fe3+ ions at respective sites [Table 2]. This indicates that a larger fraction of Fe3+ ions occupied the octahedral sites, favouring the canting of spin and leading to Y–K type magnetism.6
The relaxation effect pertaining to the presence of superparamagnetic phase can be easily monitored in all the composition as a function of Mg substitution for Ni ions. The primary features for the relaxation of the magnetically ordered system are the significant broadening of the Zeeman sextet and a growth of the inner line at the expense of the outer lines. As can be observed from the spectrum as well as from the data, the intensity of the doublet increases with successive increase in Mg2+ ions, while the sextet peaks broaden. On the other hand for x = 0.0, i.e., Ni0.6Zn0.4 Fe2O4, although the intensity of the doublet peak is higher, all the sextet peaks are well defined with much less broadening. Hence, the initial doublet observed can be either due to superparamagnetic or due to paramagnetic behaviour of the nanoparticles,62,64 however in the present study it is due to superparamagnetic behaviour of the nanoparticles.
Thus, Mössbauer spectroscopy indicates that the nanoparticles are in an ordered ferrimagnetic state and the presence of a doublet could be interpreted as a small fraction of superparamagnetic phase, originating from Mg2+ ions and perhaps due to wide size distribution of ferrite particles as well as due to lowering of L–S coupling by Mg2+ ion substitution.
Conclusions
The newly designed malic acid dihydrazide fuel proves to be very effective for the synthesis of ferrites, necessarily in the nano dimension at relatively lower temperature. The variation of lattice parameter ‘a’ with Mg content is due to structural changes, atomic weight and the replacement of smaller radius Ni2+ ions by larger radius Mg2+ ions. The associated structural changes are inferred from the Raman spectroscopic peak splitting, indicating preferred occupation of tetrahedral sites by Mg2+ ions. The particle size analysis from the TEM and SEM studies proves the distribution of particles from 20 to 30 nm with spherical morphology and that the particles exist as fused agglomerates. The decrease in magnetization with increase in Mg substitution is attributed to the Y–K type magnetism originating from dominant B–B interaction and also to the lower magnetic moment of Mg2+ ions. The decrease in Curie temperature is due to the decrease in A–B interaction, whereas the effective decrease in hysteresis behaviour can be assigned to lower magneto crystalline anisotropy of Mg2+ ions than Ni2+ ions. The Mössbauer spectroscopy and AC susceptibility results confirm the existence of a mixture of single domain ferrimagnetic and superparamagentic domain states in all the samples with successive dominance of superparamagnetic behaviour with increase in Mg substitution.Thus, with the impact of Mg substitution in Ni–Zn ferrites, the ferrimagnetic property diminishes with the enhancement of superparamagnetic behaviour of the nanoparticles at RT, thereby maximizing the applicability of such materials in superparamagnetic applications.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors would like to acknowledge Dr V. Sathe, UGC-DAE Consortium for Scientific Research, Indore, India, for providing the Raman facility and DST-FIST, New Delhi for financial support through the Nanomission project, No. SR/MN/NS-86/2009. One of the authors, S. G. G., gratefully acknowledges the UGC, New Delhi for a SRF under UGC-BSR fellowship, No. F.4-1/2006(BSR)/7-69/2007(BSR).References
- Z. Beji, L. S. Smiri, N. Yaacoub, J. M. Greneche, N. Menguy and S. Ammar, Chem. Mater., 2010, 22, 1350 CrossRef CAS.
- M. Siva Ram Prasad, B. Prasad, B. Rajesh, K. H. Rao and K. V. Ramesh, J. Magn. Magn. Mater., 2011, 323, 2115 CrossRef CAS.
- N. A. Fray, S. Peng, K. Cheng and S. Sun, Chem. Soc. Rev., 2009, 38, 2532 RSC.
- R. Ghosh, L. Pradhan, Y. P. Devi, S. S. Meena, R. Tewari and A. Kumar, J. Mater. Chem., 2011, 21, 13388 RSC.
- Q. A. Pankhurst, J. Connolly, S. K. Jones and J. Dobson, J. Phys. D: Appl. Phys., 2003, 36, 167 CrossRef.
- Y. Yafet and C. Kittel, Phys. Rev., 1952, 87, 290 CrossRef CAS.
- L. Néel, Ann. Phys., 1948, 3, 137 Search PubMed.
- C. Srinivas, B. V. Tirupanyam, S. S. Meena, S. M. Yusuf, C. Seshu Babu and K. S. Ramakrishna, J. Magn. Magn. Mater., 2016, 407, 135 CrossRef CAS.
- D. V. Kurmude, C. M. Kale, P. S. Aghav, D. R. Shengule and K. M. Jadhav, J. Supercond. Novel Magn., 2014, 27, 1889 CrossRef CAS.
- U. B. Gawas, V. M. S. Verenkar, S. R. Barman, S. S. Meena and P. Bhatt, J. Alloys Compd., 2013, 555, 225 CrossRef CAS.
- S. G. Gawas, S. S. Meena, S. M. Yusuf and V. M. S. Verenkar, New J. Chem., 2016, 40, 9275 RSC.
- E. Rezlescu, L. Sachelarie, P. D. Popa and N. Rezlescu, IEEE Trans. Magn., 2000, 36, 3962 CrossRef CAS.
- A. A. Sattar, H. M. El-Sayed, K. M. El-Shokrofy and M. M. El-Tabey, J. Mater. Eng. Perform., 2005, 14, 99 CrossRef CAS.
- A. K. Akther Hossain and M. L. Rahman, J. Magn. Magn. Mater., 2011, 323, 1954 CrossRef CAS.
- J. M. Daniels and A. Rosencwaig, Can. J. Phys., 1970, 48, 381 CrossRef CAS.
- M. Ajmal and A. Maqsood, Mater. Lett., 2008, 62, 2077 CrossRef.
- G. K. Joshi, A. Y. Khot and S. R. Sawant, Solid State Commun., 1988, 65, 1593 CrossRef CAS.
- A. Daigle, J. Modest, A. L. Geiler, S. Gillette, Y. Chen, M. Geiler, B. Hu, S. Kim, K. Stopher, C. Vittoria and V. G. Harris, Nanotechnology, 2011, 22, 305708 CrossRef CAS PubMed.
- D. H. Bobade, S. M. Rathod and M. L. Mane, Physica B, 2012, 407, 3700 CrossRef CAS.
- N. Kavitha and P. Manohar, J. Supercond. Novel Magn., 2016, 29, 2151 CrossRef CAS.
- N. Singh, A. Agarwal, S. Sanghi and P. Singh, Physica B, 2011, 406, 687 CrossRef CAS.
- Y. Liu, J. Li, F. Min, J. Zhu and M. Zhang, J. Magn. Magn. Mater., 2014, 354, 295 CrossRef CAS.
- K. Shafi, Y. Koltypin, A. Gedanken, R. Prozorov, J. Balogh, J. Lendvai and I. Felner, J. Phys. Chem. B, 1997, 101, 6409 CrossRef CAS.
- S. Prasad and N. Gajbhiye, J. Alloys Compd., 1998, 265, 87 CrossRef CAS.
- Y. Shi, J. Ding, X. Liu and J. Wang, J. Magn. Magn. Mater., 1999, 205, 249 CrossRef CAS.
- T. F. Marinca, I. Chicinas, O. Isnard, V. Pop and F. Popa, J. Alloys Compd., 2011, 509, 7931 CrossRef CAS.
- D. V. Kurmude, A. B. Shinde, A. A. Pandit, C. M. Kale, D. R. Shengule and K. M. Jadhav, J. Supercond. Novel Magn., 2015, 28, 1759 CrossRef CAS.
- G. S. Sahane, A. Kumar, M. Arora, R. P. Pant and K. Lal, J. Magn. Magn. Mater., 2010, 322, 1015 CrossRef.
- A. Sutka and G. Mezinskis, Front. Mater. Sci., 2012, 6, 128 CrossRef.
- D. Chen and R. He, Mater. Res. Bull., 2001, 36, 1369 CrossRef CAS.
- A. S. Džunuzovi, N. I. Ilić, M. M. Vijatović Petrović, J. D. Bobić, B. Stojadinović, Z. Dohčević-Mitrović and B. D. Stojanović, J. Magn. Magn. Mater., 2015, 374, 245 CrossRef.
- K. Bhattacharjee, C. K. Ghosh, M. K. Mitra, G. C. Das, S. Mukherjee and K. K. Chattopadhyay, J. Nanopart. Res., 2011, 13, 739 CrossRef CAS.
- R. Parthasarathi, L. Berchmans, R. Preetha, G. Senguttuvan and G. Umapathu, Int. J. Self-Propag. High-Temp. Synth., 2011, 20, 236 CrossRef CAS.
- S. Castro, M. Gayoso and C. Rodriguez, J. Solid State Chem., 1997, 134, 227 CrossRef CAS.
- K. C. Patil, M. S. Hegde, T. Ratan and S. T. Aruna, Chemistry of Nanocrystalline Oxide Materials – Combustion synthesis, Properties and Applications, World Scientific Publishing Co. Pte. Ltd, Singapore, 2008 Search PubMed.
- M. A. Gabal, Y. M. Al Angari and H. M. Zaki, J. Magn. Magn. Mater., 2014, 363, 6 CrossRef CAS.
- M. A. Gabal and W. A. Bayoumy, Polyhedron, 2010, 29, 2569 CrossRef CAS.
- V. Sepelak, D. Baabe, D. Mienert, D. Schultze, F. Krumeich, F. J. Litterst and K. D. Becker, J. Magn. Magn. Mater., 2003, 257, 377 CrossRef CAS.
- B. D. Cullity, Elements of X-ray diffraction, Addison-Wesley Publ. Comp. Inc., Massachusetts, USA, 1956, p. 99 Search PubMed.
- J. B. Nelson and D. P. Riley, Proc. Phys. Soc., London, 1945, 160 CrossRef CAS.
- J. Wang, F. Ren, R. Yi, A. Yan, G. Qiu and L. Xiaohe, J. Alloys Compd., 2009, 479, 791 CrossRef CAS.
- J. Kreisel, G. Lucazeau and H. Vincent, J. Solid State Chem., 1998, 137, 127 CrossRef CAS.
- A. Ahlawat and V. G. Sathe, J. Raman Spectrosc., 2011, 42, 1087 CrossRef CAS.
- J. Jacob and M. Abdul Khadar, J. Appl. Phys., 2010, 107, 114310 CrossRef.
- D. Varshney and K. Verma, Mater. Chem. Phys., 2013, 140, 412 CrossRef CAS.
- D. L. de Faria, S. Venancio and M. T. de Oliveira, J. Raman Spectrosc., 1997, 28, 873 CrossRef CAS.
- A. V. Humbe, A. C. Nawle, A. B. Shinde and K. M. Jadhav, J. Alloys Compd., 2017, 691, 343 CrossRef CAS.
- F. Nakagomi, S. W. da Silva, V. K. Garg, A. C. Oliveira, P. C. Morais and A. Franco Jr., J. Solid State Chem., 2009, 182, 2423 CrossRef CAS.
- S. W. da Silva, F. Nakagomi, A. Franco Jr., V. K. Garg, A. C. Oliveira and P. C. Morais, J. Nanopart. Res., 2012, 14, 798 CrossRef.
- S. Trudel, H. J. Colin and R. H. Hill, J. Mater. Chem., 2007, 17, 2206 RSC.
- S. Dey, S. K. Dey, B. Ghosh, V. R. Reddy and S. Kumar, Mater. Chem. Phys., 2013, 138, 833 CrossRef CAS.
- Y. Hou, J. Yu and S. Gao, J. Mater. Chem., 2003, 13, 1983 RSC.
- K. Maaz, W. Khalid, A. Mumtaz, S. K. Hasanain, J. Liu and J. L. Duan, Physica E, 2009, 41, 593 CrossRef CAS.
- E. de Barco, J. Asenjo, X. X. Zhang, R. Pieczynski, A. Julia and J. Tajeda, Chem. Mater., 2001, 13, 1487 CrossRef.
- Q. Chen, A. J. Rondinone, B. C. Chakoumakos and Z. John Zhang, J. Magn. Magn. Mater., 1999, 194, 1 CrossRef CAS.
- B. K. Nath, P. K. Chakrabarti, S. Das, U. Kumar, P. K. Mukhopadhyay and D. Das, Eur. Phys. J. B, 2004, 39, 417 CrossRef CAS.
- K. Bhattacharjee, S. P. Patil, G. C. Das, D. Das and K. K. Chattopadhyay, J. Appl. Phys., 2014, 116, 233907 CrossRef.
- M. F. Hansen and S. Mørup, J. Magn. Magn. Mater., 1999, 203, 214 CrossRef CAS.
- R. Topkaya, A. Baykal and A. Demir, J. Nanopart. Res., 2013, 15, 1359 CrossRef.
- R. Iyer, R. Desai and R. V. Upadhyay, Bull. Mater. Sci., 2009, 32, 141 CrossRef CAS.
- X. M. Liu and S. Y. Fu, J. Magn. Magn. Mater., 2007, 308, 61 CrossRef CAS.
- P. Yaseneva, M. Bowker and G. Hutchings, Phys. Chem. Chem. Phys., 2011, 13, 18609 RSC.
- S. M. Patange, S. S. Desai, S. S. Meena, S. M. Yusuf and S. E. Shirsath, RSC Adv., 2015, 5, 91482 RSC.
- C. Liu, B. Zou, A. J. Randinone and Z. J. Zhang, J. Am. Chem. Soc., 2000, 122, 6263 CrossRef CAS.
- M. Hashim, S. S. Meena, R. K. Kotnala, S. E. Shirsath, A. S. Roy and P. Ameena, J. Alloys Compd., 2014, 602, 150 CrossRef CAS.
- S. R. Naik, A. V. Salker, S. M. Yusuf and S. S. Meena, J. Alloys Compd., 2013, 566, 54 CrossRef CAS.
- T. R. Tatarchuk, M. Bououdina, N. D. Paliychuk, I. P. Yaremiy and V. V. Moklyak, J. Alloys Compd., 2017, 694, 777 CrossRef CAS.
- S. P. Yadav, S. S. Shinde, P. Bhatt, S. S. Meena and Y. K. Rajpure, J. Alloys Compd., 2015, 646, 550 CrossRef CAS.
- A. K. Nikumbh, A. V. Nagawade, G. S. Gugale and M. G. Chaskar, J. Mater. Sci., 2002, 37, 637 CrossRef CAS.
- W. Marshall, Phys. Rev., 1958, 110, 1280 CrossRef CAS.
- Z. P. Niu, Y. Wang and F. S. Li, Phys. Status Solidi B, 2010, 247, 198 CrossRef CAS.
- M. K. Fayek, F. M. Sayed Ahmed, S. S. Ata-Allah, M. K. Elnimer and M. F. Mostafa, J. Mater. Sci., 1992, 27, 4813 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c7qm00437k |
| This journal is © the Partner Organisations 2018 |